C. Number Systems
Objectives
In this appendix you’ll:
![]() Understand basic number systems concepts such as base, positional value and symbol value.
Understand basic number systems concepts such as base, positional value and symbol value.
![]() Understand how to work with numbers represented in the binary, octal and hexadecimal number systems
Understand how to work with numbers represented in the binary, octal and hexadecimal number systems
![]() Abbreviate binary numbers as octal numbers or hexadecimal numbers.
Abbreviate binary numbers as octal numbers or hexadecimal numbers.
![]() Convert octal numbers and hexadecimal numbers to binary numbers.
Convert octal numbers and hexadecimal numbers to binary numbers.
![]() Convert back and forth between decimal numbers and their binary, octal and hexadecimal equivalents.
Convert back and forth between decimal numbers and their binary, octal and hexadecimal equivalents.
![]() Understand binary arithmetic and how negative binary numbers are represented using two’s complement notation.
Understand binary arithmetic and how negative binary numbers are represented using two’s complement notation.
![]() Understand basic number systems concepts such as base, positional value and symbol value.
Understand basic number systems concepts such as base, positional value and symbol value.
Outline
C.2 Abbreviating Binary Numbers as Octal and Hexadecimal Numbers
C.3 Converting Octal and Hexadecimal Numbers to Binary Numbers
C.4 Converting from Binary, Octal or Hexadecimal to Decimal
C.5 Converting from Decimal to Binary, Octal or Hexadecimal
C.6 Negative Binary Numbers: Two’s Complement Notation
C.1. Introduction
In this appendix, we introduce the key number systems that programmers use, especially when they are working on software projects that require close interaction with machine-level hardware. Projects like this include operating systems, computer networking software, compilers, database systems and applications requiring high performance.
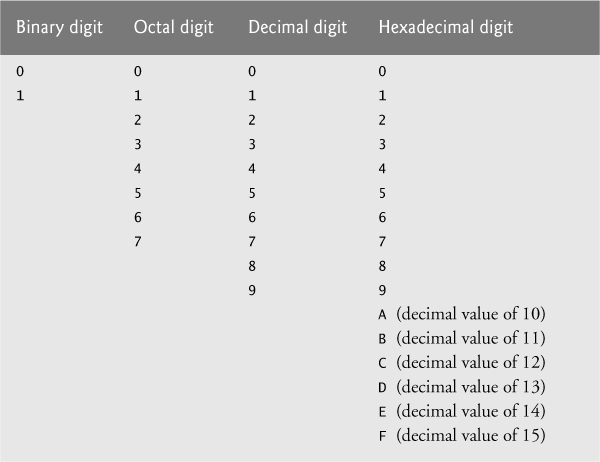
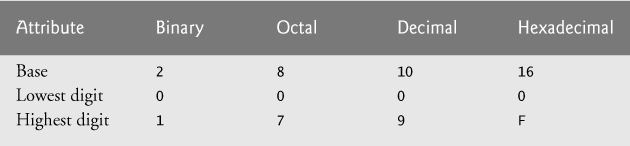
When we write an integer such as 227 or –63 in a program, the number is assumed to be in the decimal (base 10) number system. The digits in the decimal number system are 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9. The lowest digit is 0 and the highest digit is 9—one less than the base of 10. Internally, computers use the binary (base 2) number system. The binary number system has only two digits, namely 0 and 1. Its lowest digit is 0 and its highest digit is 1—one less than the base of 2.
As we’ll see, binary numbers tend to be much longer than their decimal equivalents. Programmers who work in assembly languages and in high-level languages like C that enable programmers to reach down to the machine level find it cumbersome to work with binary numbers. So two other number systems—the octal number system (base 8) and the hexadecimal number system (base 16)—are popular primarily because they make it convenient to abbreviate binary numbers.
In the octal number system, the digits range from 0 to 7. Because both the binary number system and the octal number system have fewer digits than the decimal number system, their digits are the same as the corresponding digits in decimal.
The hexadecimal number system poses a problem because it requires 16 digits—a lowest digit of 0 and a highest digit with a value equivalent to decimal 15 (one less than the base of 16). By convention, we use the letters A through F to represent the hexadecimal digits corresponding to decimal values 10 through 15. Thus in hexadecimal we can have numbers like 876 consisting solely of decimal-like digits, numbers like 8A55F consisting of digits and letters and numbers like FFE consisting solely of letters. Occasionally, a hexadecimal number spells a common word such as FACE or FEED—this can appear strange to programmers accustomed to working with numbers. The digits of the binary, octal, decimal and hexadecimal number systems are summarized in Figs. C.1–C.2.
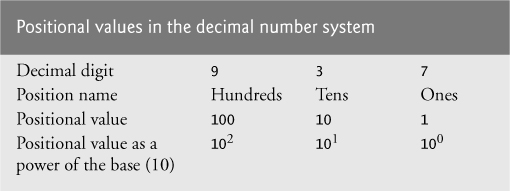
Each of these number systems uses positional notation—each position in which a digit is written has a different positional value. For example, in the decimal number 937 (the 9, the 3 and the 7 are referred to as symbol values), we say that the 7 is written in the ones position, the 3 is written in the tens position and the 9 is written in the hundreds position. Each of these positions is a power of the base (base 10) and these powers begin at 0 and increase by 1 as we move left in the number (Fig. C.3).
For longer decimal numbers, the next positions to the left would be the thousands position (10 to the 3rd power), the ten-thousands position (10 to the 4th power), the hundred-thousands position (10 to the 5th power), the millions position (10 to the 6th power), the ten-millions position (10 to the 7th power) and so on.
In the binary number 101, the rightmost 1 is written in the ones position, the 0 is written in the twos position and the leftmost 1 is written in the fours position. Each position is a power of the base (base 2) and these powers begin at 0 and increase by 1 as we move left in the number (Fig. C.4). So, 101 = 1 * 22 + 0 * 21 + 1 * 20 = 4 + 0 + 1 = 5.
For longer binary numbers, the next positions to the left would be the eights position (2 to the 3rd power), the sixteens position (2 to the 4th power), the thirty-twos position (2 to the 5th power), the sixty-fours position (2 to the 6th power) and so on.
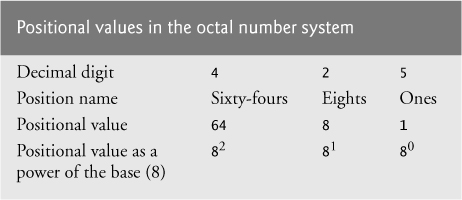
In the octal number 425, we say that the 5 is written in the ones position, the 2 is written in the eights position and the 4 is written in the sixty-fours position. Each of these positions is a power of the base (base 8) and that these powers begin at 0 and increase by 1 as we move left in the number (Fig. C.5).
For longer octal numbers, the next positions to the left would be the five-hundred-and-twelves position (8 to the 3rd power), the four-thousand-and-ninety-sixes position (8 to the 4th power), the thirty-two-thousand-seven-hundred-and-sixty-eights position (8 to the 5th power) and so on.
In the hexadecimal number 3DA, we say that the A is written in the ones position, the D is written in the sixteens position and the 3 is written in the two-hundred-and-fifty-sixes position. Each of these positions is a power of the base (base 16) and these powers begin at 0 and increase by 1 as we move left in the number (Fig. C.6).
For longer hexadecimal numbers, the next positions to the left would be the four-thousand-and-ninety-sixes position (16 to the 3rd power), the sixty-five-thousand-five-hundred-and-thirty-sixes position (16 to the 4th power) and so on.
C.2. Abbreviating Binary Numbers as Octal and Hexadecimal Numbers
The main use for octal and hexadecimal numbers in computing is for abbreviating lengthy binary representations. Figure C.7 highlights the fact that lengthy binary numbers can be expressed concisely in number systems with higher bases than the binary number system.
A particularly important relationship that both the octal number system and the hexadecimal number system have to the binary system is that the bases of octal and hexadecimal (8 and 16 respectively) are powers of the base of the binary number system (base 2). Consider the following 12-digit binary number and its octal and hexadecimal equivalents. See if you can determine how this relationship makes it convenient to abbreviate binary numbers in octal or hexadecimal. The answer follows the numbers.
Binary number Octal equivalent Hexadecimal equivalent
100011010001 4321 8D1
To see how the binary number converts easily to octal, simply break the 12-digit binary number into groups of three consecutive bits each and write those groups over the corresponding digits of the octal number as follows:
100 011 010 001
4 3 2 1
The octal digit you have written under each group of three bits corresponds precisely to the octal equivalent of that 3-digit binary number, as shown in Fig. C.7.
The same kind of relationship can be observed in converting from binary to hexadecimal. Break the 12-digit binary number into groups of four consecutive bits each and write those groups over the corresponding digits of the hexadecimal number as follows:
1000 1101 0001
8 D 1
The hexadecimal digit you wrote under each group of four bits corresponds precisely to the hexadecimal equivalent of that 4-digit binary number as shown in Fig. C.7.
C.3. Converting Octal and Hexadecimal Numbers to Binary Numbers
In the previous section, we saw how to convert binary numbers to their octal and hexadecimal equivalents by forming groups of binary digits and simply rewriting them as their equivalent octal digit values or hexadecimal digit values. This process may be used in reverse to produce the binary equivalent of a given octal or hexadecimal number.
For example, the octal number 653 is converted to binary simply by writing the 6 as its 3-digit binary equivalent 110, the 5 as its 3-digit binary equivalent 101 and the 3 as its 3-digit binary equivalent 011 to form the 9-digit binary number 110101011.
The hexadecimal number FAD5 is converted to binary simply by writing the F as its 4-digit binary equivalent 1111, the A as its 4-digit binary equivalent 1010, the D as its 4-digit binary equivalent 1101 and the 5 as its 4-digit binary equivalent 0101 to form the 16-digit 1111101011010101.
C.4. Converting from Binary, Octal or Hexadecimal to Decimal
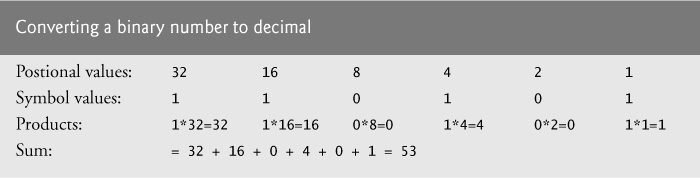
We’re accustomed to working in decimal, and therefore it’s often convenient to convert a binary, octal, or hexadecimal number to decimal to get a sense of what the number is “really” worth. Our tables in Section C.1 express the positional values in decimal. To convert a number to decimal from another base, multiply the decimal equivalent of each digit by its positional value and sum these products. For example, the binary number 110101 is converted to decimal 53, as shown in Fig. C.8.
To convert octal 7614 to decimal 3980, we use the same technique, this time using appropriate octal positional values, as shown in Fig. C.9.
To convert hexadecimal AD3B to decimal 44347, we use the same technique, this time using appropriate hexadecimal positional values, as shown in Fig. C.10.
C.5. Converting from Decimal to Binary, Octal or Hexadecimal
The conversions in Section C.4 follow naturally from the positional notation conventions. Converting from decimal to binary, octal, or hexadecimal also follows these conventions.
Suppose we wish to convert decimal 57 to binary. We begin by writing the positional values of the columns right to left until we reach a column whose positional value is greater than the decimal number. We do not need that column, so we discard it. Thus, we first write:
Positional values: 64 32 16 8 4 2 1
Then we discard the column with positional value 64, leaving:
Positional values: 32 16 8 4 2 1
Next we work from the leftmost column to the right. We divide 32 into 57 and observe that there is one 32 in 57 with a remainder of 25, so we write 1 in the 32 column. We divide 16 into 25 and observe that there is one 16 in 25 with a remainder of 9 and write 1 in the 16 column. We divide 8 into 9 and observe that there is one 8 in 9 with a remainder of 1. The next two columns each produce quotients of 0 when their positional values are divided into 1, so we write 0s in the 4 and 2 columns. Finally, 1 into 1 is 1, so we write 1 in the 1 column. This yields:
Positional values: 32 16 8 4 2 1
Symbol values: 1 1 1 0 0 1
and thus decimal 57 is equivalent to binary 111001.
To convert decimal 103 to octal, we begin by writing the positional values of the columns until we reach a column whose positional value is greater than the decimal number. We do not need that column, so we discard it. Thus, we first write:
Positional values: 512 64 8 1
Then we discard the column with positional value 512, yielding:
Positional values: 64 8 1
Next we work from the leftmost column to the right. We divide 64 into 103 and observe that there is one 64 in 103 with a remainder of 39, so we write 1 in the 64 column. We divide 8 into 39 and observe that there are four 8s in 39 with a remainder of 7 and write 4 in the 8 column. Finally, we divide 1 into 7 and observe that there are seven 1s in 7 with no remainder, so we write 7 in the 1 column. This yields:
Positional values: 64 8 1
Symbol values: 1 4 7
and thus decimal 103 is equivalent to octal 147.
To convert decimal 375 to hexadecimal, we begin by writing the positional values of the columns until we reach a column whose positional value is greater than the decimal number. We do not need that column, so we discard it. Thus, we first write:
Positional values: 4096 256 16 1
Then we discard the column with positional value 4096, yielding:
Positional values: 256 16 1
Next we work from the leftmost column to the right. We divide 256 into 375 and observe that there is one 256 in 375 with a remainder of 119, so we write 1 in the 256 column. We divide 16 into 119 and observe that there are seven 16s in 119 with a remainder of 7 and write 7 in the 16 column. Finally, we divide 1 into 7 and observe that there are seven 1s in 7 with no remainder, so we write 7 in the 1 column. This yields:
Positional values: 256 16 1
Symbol values: 1 7 7
and thus decimal 375 is equivalent to hexadecimal 177.
C.6. Negative Binary Numbers: Two’s Complement Notation
The discussion so far in this appendix has focused on positive numbers. In this section, we explain how computers represent negative numbers using two’s complement notation. First we explain how the two’s complement of a binary number is formed, then we show why it represents the negative value of the given binary number.
Consider a machine with 32-bit integers. Suppose
int value = 13;
The 32-bit representation of value is
00000000 00000000 00000000 00001101
To form the negative of value we first form its one’s complement by applying C’s bitwise complement operator (~):
onesComplementOfValue = ~value;
Internally, ~value is now value with each of its bits reversed—ones become zeros and zeros become ones, as follows:
value:
00000000 00000000 00000000 00001101
~value (i.e., value's ones complement):
11111111 11111111 11111111 11110010
To form the two’s complement of value, we simply add 1 to value’s one’s complement. Thus
Two's complement of value:
11111111 11111111 11111111 11110011
Now if this is in fact equal to –13, we should be able to add it to binary 13 and obtain a result of 0. Let’s try this:
00000000 00000000 00000000 00001101
+11111111 11111111 11111111 11110011
------------------------------------
00000000 00000000 00000000 00000000
The carry bit coming out of the leftmost column is discarded and we indeed get 0 as a result. If we add the one’s complement of a number to the number, the result would be all 1s. The key to getting a result of all zeros is that the twos complement is one more than the one’s complement. The addition of 1 causes each column to add to 0 with a carry of 1. The carry keeps moving leftward until it’s discarded from the leftmost bit, and thus the resulting number is all zeros.
Computers actually perform a subtraction, such as
x = a - value;
by adding the two’s complement of value to a, as follows:
x = a + (~value + 1);
Suppose a is 27 and value is 13 as before. If the two’s complement of value is actually the negative of value, then adding the two’s complement of value to a should produce the result 14. Let’s try this:
a (i.e., 27) 00000000 00000000 00000000 00011011
+(~value + 1) +11111111 11111111 11111111 11110011
------------------------------------
00000000 00000000 00000000 00001110
which is indeed equal to 14.