To Infinity and Beyond
In This Chapter
- Exploring improper integrals
- Working with infinite limits of integration
- Examining discontinuities in the integrand
- Using the Comparison Test for improper integrals
We looked at the Fundamental Theorem of Calculus, and we have concentrated on studying techniques of integration. In this chapter, we will go back to definite integrals and look at problems that either have an infinite bound of integration or an infinite discontinuity in a finite region.
Improper Integrals
In all cases involving improper integrals, we will treat the problem as a limit. If the limit exists, we say that the integral converges and if the limit does not exist, we say that the integral diverges.
Definition
An improper integral is a definite integral that has either or both bounds of integration going to an infinity, or integrands that approach infinity at one or more points in the range of integration.
Infinite Limits of Integration
Consider the area under the graph of 
and above the x-axis on the interval [1, n]. The integral 
computes the amount of area.
Figure 9.1
The area under the curve 
from x = 1 to infinity.
What happens to this area as n gets very large? The larger the value of n, the closer 
gets to 0 and the closer 
gets to 1. That is, 
.
In this case, we can state that 
.
Do we get the same result for 
.
As n gets extremely large, ln(n) also get extremely large so 
fails to exist, and the integral is said to be divergent.
Critical Point
If the integral of f(x) on [a, n] exists for all values of n > a, then 
provided the limit exists and is finite.
We say the integrals are convergent if the limits exist. We say that the integrals are divergent if the limits fail to exist.
Example 1: For what values of p is the integral 
convergent?
Solution:
1. 
.
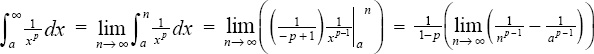2. If p > 1, 
while if p ≤ 1 and not equal to 0, 
diverges.
3. Therefore, 
is convergent for p > 1.
Critical Point
The integral 
will converge whenever p > 1 and will diverge when p ≤ 1. This is called the p-Test for improper integrals.
Example 2: Evaluate 
, if it exists.
Solution: 
.
Example 3: Evaluate 
, if it exists.
Solution:
1. Let’s treat this as two problems: 
and 
.
In a similar manner:
2. Therefore: 
.
Example 4: Evaluate 
dx if it exists.
Solution:
1. We’ll need use integration by parts to evaluate 
. Once we’ve done that, we can work to the bounds of integration.
Let u = x – 4 and dv = e–x dx. The du = dx and v = –e–x.
.
2. Applying the bounds of integration, you get 
3. Use L’Hopital’s Rule to evaluate 
.
4. Therefore, 
.
YOU’VE GOT PROBLEMS
Problem 1: Evaluate 
if it exists.
Example 5: Consider the graph of the function h given by h(x) = e–x2 for 0 ≤ x < ∞. Let R be the unbounded region in the first quadrant below the graph of h. Find the volume of the solid generated when R is revolved about the y-axis.
Solution:
1. Use the cylindrical shell method to find the volume (since the region is being rotated about a vertical line).
2. The volume of the solid is 
, which becomes 
.
Let u = –x2 so that du = –2x dx or 
.
3. Therefore, 
.
Discontinuities in the Integrand
We’ve examined what happens when one or both bounds of integration go to infinity. We now consider how to handle discontinuities within the integrand. There are two cases that we should consider:
- The discontinuity is finite.
- The discontinuity is infinite.
Critical Point
If f(x) is continuous on [a, b) and discontinuous at x = b, 
if the limit exists and is finite. Similarly, If f(x) is continuous on (a, b] and discontinuous at x = a, 
if the limit exists and is finite.
Example 6: Let 
. Evaluate 
if it exists.
Figure 9.2
The graph of 
.
Solution: 
.
1. f(x) = x2 on the interval [0, 3) and f(x) = 2x + 5 on the interval [3, 5]. Therefore, 
.
2. Apply the Fundamental Theorem of Calculus in each case: 
.
3. Therefore, 
.
Critical Point
If f(x) has a discontinuity at x = b with a < b < c, then 
is convergent if both 
and 
are convergent and is divergent if either 
or 
are divergent.
Example 7: Evaluate 
if it exists.
Solution:
1. Because the integrand does not exist at x = 3, we treat 
as 
.
2. 
.
3. As n approaches 3 from the left, 
gets infinitely large, meaning the limit, and therefore the integral, is divergent.
Example 8: Evaluate 
if it exists.
Solution: Since the integrand does not exist at x = 4, we treat 
as 
.
Example 9: Evaluate 
if it exists.
Solution:
1. As we have done before, substitute sec2(x) – 1 for tan2(x).
2. Both the tangent function and the secant function are discontinuous at 
.
3. Therefore, 
should be written as 
.
4. We know that 
and does not present a problem.
5. The question of concern is if 
is convergent.
6. 
. Therefore, 
is divergent.
Be Aware
If we had not checked for the point of discontinuity on the interval [0, π], then 
, and this is incorrect.
YOU’VE GOT PROBLEMS
Problem 2: Evaluate 
if it exists.
Comparison Test for Improper Integrals
There will be times—particularly when we study infinite series—that all we want to know is if an expression in convergent or divergent. The Comparison Test for Improper Integrals helps us with this problem.
Definition
Given f(x) and g(x) are continuous functions for x > a with f(x) ≥ g(x) ≥ 0. If 
converges, then so does 
. If 
diverges, then so does 
. This is called the Comparison Test for Improper Integrals.
Example 10: Is 
convergent?
Solution: Because 
and 
is convergent. (This is one of the integrals of the type 
with p > 1.)
Critical Point
As a practical matter, the p-Test is always a good tool to use when using the Comparison Test for Improper Integrals and part of the integrand to be tested contains a polynomial.
Example 11: Is 
convergent?
Solution: Because 
and 
is divergent, therefore, 
is divergent.
YOU’VE GOT PROBLEMS
Problem 3: Determine if 
converges.
The Least You Need to Know
- When evaluating integrals with infinite bounds of integration, use a limit to determine the value of the integral, if it exists.
- Look for points of discontinuity on a finite interval, either at an endpoint of the interval or in the interior of the interval. If a discontinuity exists, use a limit to evaluate the integral.
- The p-Test is a good tool for comparing an unknown improper integral to a known improper integral.