Infinite Series
In This Chapter
![]()
- Investigating infinite geometric series
- Studying tests of convergence: ratio, comparison, and integral
- Examining alternating series and absolute and conditional convergence
- Estimating sums of alternating series with a maximum error estimate
Whereas a sequence is a listing of numbers that come from a defined pattern, a series is the sum of the terms of the sequence. In the next two chapters, we will examine infinite series. We’ll lay down the basics for infinite series in this chapter and work further with some important series in Chapter 16.
A geometric sequence is defined by the rule an = a1rn – 1. For example, the sequence an = 2(3)n – 1 is 2, 6, 18, … . Do you see why 2 must be the first term? a1 = 2(3)1 – 1 = 2(3)0 = 2. The sum of the first six terms of this series is S6 = 2 + 6 + 18 + 54 + 162 + 486. There are only a few terms in this series so we could add them up by hand. Imagine if we had to find the sum of the first 60 terms, you would want to use a formula. The process is called “eliminating the middle.”
1. We’ll multiply the equation for S6 by the common ratio, 3, to get 3S6 = 6 + 18 + 54 + 162 + 486 + 1458.
2. We subtract this from the equation for S6. S6 – 3S6 = (2 + 6 + 18 + 54 + 162 + 486) – (6 + 18 + 54 + 162 + 486 + 1458) so that –2S6 = 2 – 1458. (Do you see how all the middle terms are eliminated?)
3. Just so that we can get to a more general formula, we’ll rewrite 1458 as 2(3)6. (Grab your calculator to verify that is correct.)
4. So –2S6 = 2 – 2(3)6 so that ![]() .
.
In general, if the first term of the geometric sequence is a1 and the common ratio is r, the sum of the first n terms of the series is ![]() . (We’ll not compute the sum of the first 60 terms as it is in the neighborhood of 4 × 1027.)
. (We’ll not compute the sum of the first 60 terms as it is in the neighborhood of 4 × 1027.)
Example 1: Find the sum of the first 40 terms of the series 2400 + 1800 + 1350 + 1012.5 + ….
Solution: The first is 2400 and the common ratio is ![]() . Therefore,
. Therefore, 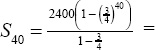 9599.903.
9599.903.
You can see that as n gets larger, the value of an gets smaller. The question is “What happens to Sn?” The ![]() . As n gets larger, rn → 0 because r < 1.
. As n gets larger, rn → 0 because r < 1.

CRITICAL POINT
The sum of an infinite geometric series will converge to ![]() , provided |r| < 1.
, provided |r| < 1.
Example 2: Compute 16 + 8 + 4 + 2 + 1 + ….
Solution: The first term is 16 and the common ratio is ![]() , so the sum is
, so the sum is ![]() .
.
Example 3: Compute 16 – 8 + 4 – 2 + 1 ….
Solution: The first term is 16 and the common ratio is ![]() , so the sum is
, so the sum is ![]() .
.

YOU’VE GOT PROBLEMS
Problem 1: Compute ![]() .
.
Tests of Convergence
If all the terms in a series Σan are positive, the series is called a positive series. (As opposed to an alternating series that we will discuss later in this chapter.) There are a number of tests available to us to determine if a positive series is convergent.
We begin with a very simple, but important statement, called the Divergence Test.

CRITICAL POINT
If ![]() does not equal 0, the series
does not equal 0, the series ![]() diverges.
diverges.
Simply said, if the numbers being added to the series do not get infinitely small, the sum of the terms will continue to grow.
Example 4: Show that the series  diverges.
diverges.
Solution:
1. We’ll go back to the familiar limit theorem, ![]() .
.
2. If we replace x with ![]() becomes
becomes ![]() so that n → ∞ making
so that n → ∞ making ![]() .
.
3. Therefore, series  diverges.
diverges.
When the rule defining the series is a continuous function that can be integrated, you can apply improper integrals to test for the convergence or divergence of a series. This is called the Integral Test.
Definition
If f(x) is a continuous, positive, decreasing function on [1,∞] with f(n) = an for all positive integers n, then the series Σan converges if and only if ![]() converges. This is called the Integral Test.
converges. This is called the Integral Test.
Example 5: Show that ![]() diverges.
diverges.
Solution: ![]() . Because the integral diverges, the series also diverges.
. Because the integral diverges, the series also diverges.

CRITICAL POINT
The series ![]() is called the harmonic series and is related to musical harmonies. To give you a sense of the size of “large” in mathematics, it takes 12,368 terms before the sum of the terms in the harmonic series reaches 10 and it takes more than 1.509 × 1043 terms to reach 100. That is pretty incredible!
is called the harmonic series and is related to musical harmonies. To give you a sense of the size of “large” in mathematics, it takes 12,368 terms before the sum of the terms in the harmonic series reaches 10 and it takes more than 1.509 × 1043 terms to reach 100. That is pretty incredible!
Example 6: Show that ![]() converges.
converges.
Solution: ![]() . Because the integral converges, the series also converges.
. Because the integral converges, the series also converges.

CRITICAL POINT
An important consequence of the Integral Test is referred to as the p-series. (We’ve seen this before when we discussed improper integrals.) Series of the form ![]() will converge when p > 1 and will diverge when p ≤ 1.
will converge when p > 1 and will diverge when p ≤ 1.

YOU’VE GOT PROBLEMS
Problem 2: Show that the series ![]() converges.
converges.
The next test for us to look at is the Comparison Test. This is a good test to use when the unknown series looks like a known convergent or divergent series.
Definition
If two positive series, ![]() and
and ![]() , with the property that ak > bk for k ≥ m then we can conclude two things: If the series
, with the property that ak > bk for k ≥ m then we can conclude two things: If the series ![]() converges, then so does the series
converges, then so does the series ![]() . And if the series
. And if the series ![]() diverges, then so does the series
diverges, then so does the series ![]() . This is called the Comparison Test. In English, there comes a point where the terms in series
. This is called the Comparison Test. In English, there comes a point where the terms in series ![]() are always greater than the terms in series
are always greater than the terms in series ![]() .
.
Example 7: Show that the series  converges.
converges.
Solution:
1. This series looks strikingly similar to the series ![]() , which is a known convergent series.
, which is a known convergent series.
2. We now have to show that there comes a point in which ![]() .
.
3. Both denominators are positive, so we can multiply the inequality by the common denominator without affecting the orientation of the inequality: n2 + 5 > n2.
4. This becomes 5 > 0, which is always true.
5. Because the unknown series is less than the known series for all values of n, the unknown series,  converges.
converges.
Example 8: Show that the series  diverges.
diverges.
Solution:
1. It seems reasonable to compare this series to the divergent harmonic series. When is ![]() ? The answer is never.
? The answer is never.
2. For positive values of n, n is never greater than n + 1.
3. So what do we do? We come up with a different divergent series. Rather than use ![]() , use the series
, use the series ![]() . When is
. When is ![]() ? Always!
? Always!
4. Multiply by the common denominator to get 2n > n + 1 or that n > 1.
5. The unknown series is greater than the known divergent series so the series  diverges.
diverges.
(Did you notice that applying the Integral Test shows that the series  diverges?)
diverges?)
Example 9: Determine whether the series  converges or diverges.
converges or diverges.
Solution:
1. Once again, the series ![]() will make for a good comparison.
will make for a good comparison.
2. When is ![]() ?
?
3. Solve: n2 + 5n – 1250 > n2 becomes 5n – 1250 > 0 or n > 250.
4. The inequality takes 250 terms before it holds true, but eventually it is true that ![]() .
.
5. The series  converges.
converges.

YOU’VE GOT PROBLEMS
Problem 3: Use the Comparison Test to determine if the series ![]() converges or diverges.
converges or diverges.
The Limit Comparison Test also takes advantage of known convergent and divergent series in determining the nature of the convergence of an unknown series.
Definition
Given two positive series ![]() and
and ![]() let
let ![]() . If L is positive and finite, then both
. If L is positive and finite, then both  and
and ![]() converge or diverge. This is the Limit Comparison Test.
converge or diverge. This is the Limit Comparison Test.
This test has the advantage that is saves us from doing some ugly algebra.
Example 10: Show that  diverges.
diverges.
Solution: Use the Limit Comparison Test with the divergent series ![]() .
. ![]() . Therefore, both series diverge.
. Therefore, both series diverge.
Example 11: Show that the series ![]() converges. (Sorry, I got tired of using n as the variable.)
converges. (Sorry, I got tired of using n as the variable.)
Solution: Compare this series to  . Therefore, both series converge.
. Therefore, both series converge.

YOU’VE GOT PROBLEMS
Problem 4: Determine whether the series 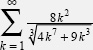 is convergent or divergent.
is convergent or divergent.
Now that we’ve developed ground rules for how to deal with series containing only positive terms, we take on the issue of series with alternating signs. This will be the basis for the work we do with power series in the next chapter.

CRITICAL POINT
Let ![]() with bn > 0 for all n. If (1) bn is decreasing for all n, and (2)
with bn > 0 for all n. If (1) bn is decreasing for all n, and (2) ![]() , then
, then ![]() is convergent.
is convergent.
This statement is called the Alternating Series Test.
Example 12: Show that the alternating harmonic series ![]() converges.
converges.
Solution: The series meets the condition that ![]() decreases (use the derivative if you want; it’s always negative) and
decreases (use the derivative if you want; it’s always negative) and ![]() . Therefore,
. Therefore, ![]() converges.
converges.
Example 13: Determine if the series  is convergent or divergent.
is convergent or divergent.
Solution:
1. We know ![]() , so the conditions of the Alternating Series Test are not met.
, so the conditions of the Alternating Series Test are not met.
2. This does not tell us that the series is divergent, but it does tell us we need to try something else. At this point, the only something else we have is the Divergence Test. If ![]() does not equal 0, then the series diverges.
does not equal 0, then the series diverges.
3. As you can see, ![]() will oscillate between –1 and 1 for very large values of n.
will oscillate between –1 and 1 for very large values of n.
4. The limit fails to exist, so the limit does not equal 0.
5. We can use the Divergence Test to conclude that  is divergent.
is divergent.

YOU’VE GOT PROBLEMS
Problem 5: Determine if the series ![]() is convergent?
is convergent?
So we now know that the harmonic series is divergent but the alternating harmonic series is convergent. This leads us to consider the other series that are related by their absolute values.

CRITICAL POINT
Given the series ![]() , the series is said to be absolutely convergent if the series
, the series is said to be absolutely convergent if the series  converges. The series is said to be conditionally convergent if
converges. The series is said to be conditionally convergent if ![]() converges but
converges but  diverges. If a series is absolutely convergent, it is convergent.
diverges. If a series is absolutely convergent, it is convergent.
Therefore, the alternating harmonic series is conditionally convergent.
Example 14: Is the series ![]() absolutely convergent, conditionally convergent, or neither?
absolutely convergent, conditionally convergent, or neither?
Solution: The series 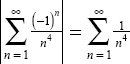 is convergent based on the p-series. Therefore,
is convergent based on the p-series. Therefore, ![]() is absolutely convergent.
is absolutely convergent.
Example 15: Is the series  absolutely convergent, conditionally convergent, or neither?
absolutely convergent, conditionally convergent, or neither?
Solution:
1. The series itself does not represent an alternating series.
2. However, if we consider that –1 ≤ cos(n) ≤ 1, then ![]() .
.
3. Use the Comparison Test to note that ![]() converges conditionally then so does
converges conditionally then so does  .
.

CRITICAL POINT
Given a series ![]() , let
, let ![]() . If r < 1, then
. If r < 1, then ![]() converges. If r > 1, then
converges. If r > 1, then ![]() diverges. If r = 1, then no conclusion about
diverges. If r = 1, then no conclusion about ![]() can be drawn from this test. This is called the Ratio Test.
can be drawn from this test. This is called the Ratio Test.
The Ratio Test is a major player in the study of alternating series. It is especially useful for series involving nth powers and factorials.
Example 16: Determine if the series  is absolutely convergent, conditionally convergent, or neither.
is absolutely convergent, conditionally convergent, or neither.
Solution: Using the Ratio Test,  . By the terms of the Ratio Test,
. By the terms of the Ratio Test,  is absolutely convergent.
is absolutely convergent.
Example 17: Determine if the series ![]() is absolutely convergent, conditionally convergent, or neither.
is absolutely convergent, conditionally convergent, or neither.
Solution: 
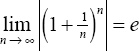 . With e > 0, the series diverges.
. With e > 0, the series diverges.

YOU’VE GOT PROBLEMS
Problem 6: Determine if the series  is absolutely convergent, conditionally convergent, or neither.
is absolutely convergent, conditionally convergent, or neither.
The Root Test is the last of the tests for convergence/divergence that we need to consider.

CRITICAL POINT
Given a series ![]() , let
, let ![]() . If r < 1, then
. If r < 1, then ![]() is absolutely convergent. If r > 1, then
is absolutely convergent. If r > 1, then ![]() divergent. If r = 1, then no conclusion about
divergent. If r = 1, then no conclusion about ![]() can be drawn from this test. This is called the Root Test.
can be drawn from this test. This is called the Root Test.
A useful fact to have when using the Root Test is ![]() .
.
Example 18: Determine if the series  is absolutely convergent, conditionally convergent, or neither.
is absolutely convergent, conditionally convergent, or neither.
Solution: Applying the Root Test,  . The series is absolutely convergent.
. The series is absolutely convergent.
Estimating the Sum of Alternating Series
Let’s reinforce two items about alternating series that will help with the work we are going to do on estimating sums.
- If we define the alternating series as
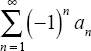 , the terms an are positive and they are decreasing.
, the terms an are positive and they are decreasing. - It is the factor (–1)n that causes the signs to alternate.
The sum of the first n terms of the series, called the partial sum Sn, estimates the true sum. However, there is a difference between partial sum and the true sum. The maximum value of this difference is the next term in the series, an + 1.

CRITICAL POINT
The difference between the sum of an alternating series, S, and a partial sum, Sn, is at most an + 1. That is, ![]() .
.
Example 19: Estimate the maximum error when ![]() is estimated by S15.
is estimated by S15.
Solution: ![]() so the maximum error is
so the maximum error is ![]() .
.
Example 20: How many terms are needed to estimate the sum  so that the maximum error is less than 0.0001?
so that the maximum error is less than 0.0001?
Solution:
1. The maximum error is ![]() .
.
2. ![]() becomes 10000 < (k + 1)!.
becomes 10000 < (k + 1)!.
3. Use your calculator to determine that k + 1 = 8 so k = 7.
4. Use seven terms to insure that the maximum error is less than 0.0001.
5. The sum  , which is approximately –0.632121.
, which is approximately –0.632121.  is –0.632143.
is –0.632143.
6. The first four decimal places are exactly the same.

YOU’VE GOT PROBLEMS
Problem 7: Determine the number of terms needed to estimate the sum ![]() so that the maximum error is less than 0.00001.
so that the maximum error is less than 0.00001.
The Least You Need to Know
- Look to see if
 is equal to 0. If it’s not, the series diverges by the Divergence Test.
is equal to 0. If it’s not, the series diverges by the Divergence Test. - A geometric series converges if |r| < 1; the series diverges if |r| > 1.
- Use the Integral Test when the series has the form of a function that can be integrated.
- Use the Comparison Test when the series looks like a p-series.
- When the series involves the ratio of polynomials, use the Comparison Test or Limit Comparison Test after checking that all the terms of the series are positive.
- Use the Ratio Test when the series involve factorials or constants raised to powers.
- Use the Alternating Series Test when the series have the form (-1)nan.
