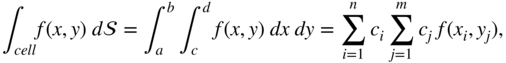Appendix E
Auxiliary Techniques for Partial Element Computations
E.1 Multi-function Partial Element Integration
An important part of the overall solution is a mixture of techniques for the efficient partial element evaluation. We call the overall approach multifunction method (MFM) [1, 2] since it involves different algorithms or functions with the main goal of keeping the compute time for the partial elements low.
The partial 
and 
coefficients formulations given in Appendices C and D represent an important collection of integrals for analytic solutions. The analytic solutions usually lead to the efficient evaluation of the coefficients. However, it is obvious from Appendices C and D that the efficient analytic evaluation of nonorthogonal coefficients is much more challenging.
The overall approach also needs to include numerical integration methods especially for cases where the analytic integration may not exist or is too complicated. Fortunately, more work has been conducted that contributes to the multifunction approach [2] and to the solution of total or partially numerically evaluated coefficients, for example, Ref. [3].
The efficient numerical computation of nonorthogonal partial inductances is very challenging especially if the length-to-width ratio between the sides as large as 1000:1. Numerical integration is more efficient for the smallest dimensions of conductor of the cell. For most nonorthogonal cells, a mixed numerical and analytical solution works best. Therefore, we need to consider techniques suitable for the shorter lengths of the cells.
An important aspect – which is often overlooked – is physically dense parts of the PEEC models. For example, skin-effect models in Chapter 9 require much higher accuracy for the partial inductance evaluation. In general, numerical compute cost can be larger for the evaluation of skin-effect models due to the higher accuracy required.
Another issue of importance is the evaluation of the singular partial self-coefficient 
and 
. The singularity can be eliminated with two analytic integrations over the same surface. Interesting techniques have been worked out for the solution of the singularity problem. For example in Ref. [2], a combination of rectangular and hexahedral shapes is used and nonsingular rectangular subcells are embedded to take care of the singular parts.
The singularity is weaker – if not eliminated – by some of the integrations which are performed analytically. One of the most used approaches is the use of analytical filaments or sheet results given in Appendices C and D for complex orthogonal cases [4]. Quite complex cases can be evaluated for rectangular uniform shapes since the partial self-inductances 
are available for zero thickness sheets and rectangular cross sections. Recently, approximate formulas for partial self-inductances with nonrectangular cross-sectional shapes have been considered [5].
For nonorthogonal shapes, the filament approach has been successfully applied in Refs [6] and [3] where for the partial self-inductances 
an adaptive Simpson numerical integration method is used. In Ref. [2], an adaptive Gauss–Legendre numerical approach is used.
The accuracy issue for close conductors is considered in Section 5.5.2. The observation is that we need four to five digits of accuracy for closely located partial inductances. Compute time is a key issue for these very closely located cells. It has been shown, for example, Ref. [7], that many of the approximate partial inductance formulas [8] are not accurate enough for the near coefficients in physically dense meshing regions.
The partial coefficients of potential in the circuit matrix solution are of the form 
. The number of digits of accuracy in the 
coefficients can be reduced due to the declining ratio for distant elements. We need to make sure that the coefficient ratio is sufficiently small. Hence, we reduce the accuracy or the number of significant digits in the accuracy of off-diagonal elements to speed up the evaluation.
In the multifunction approach, a mixture is used to calculate the integrals for the different geometrical shapes. The challenge is to choose number of subdivisions such that the best compromise is made between accuracy and compute time. For far-coefficients we can reduce the relative error from five digits to four or even three digits. Since the majority of the coupling coefficient is of the physical distant type, this results in a large reduction in the overall compute time.
E.1.1 Appropriate Numerical Integration Methods
Rather than presenting a general overview over integration techniques, we restrict ourselves to suitable approach for the numerical integration for partial element integrals. Unfortunately, compute time for the numerical evaluation of the 3D integrals increases rapidly with the number of subdivisions. Hence, using as few integration points as possible is an important goal. Also, wherever possible, we want to use an analytical evaluation for the overlapping self-integrals that lead to the singularities.
Numerical integration methods are required for some of the integrals of functions without explicit antiderivatives or whose antiderivatives are too complex. Hence, numerical techniques play an important role for integrals that are difficult to solve.
We use an appropriate class of numerical quadrature techniques for the solution. Specifically, each single, general integral numerical quadrature can be represented as
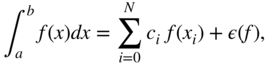
where 
are the integration points, 
is the weight, and 
is the residual error of the numerical integration. All integration points 
are defined within the integration region 
. For some integration methods such as the Simpson and the trapezoidal rule, the end points are included in 
. However, in another class of methods such as the midpoint rule and Gaussian integration, the end points are not part of the discretization points. This is important for nearest neighboring cells, but not necessarily for partial self-element, which will be considered in Section E.1.2.
A category of numerical quadrature methods is called the Newton–Cotes formulas. They are derived by approximating the integrand with interpolating polynomials. The error term in the interpolating polynomial of degree 
involves the 
th derivatives of the function to be approximated. This type of quadrature method is exact if the approximating polynomial is of a lesser degree than or equal to 
.
Newton–Cotes formulas [9] use values of the function at equally spaced points. For a polynomial of order 
, there are 
coefficients. Polynomials with 
coefficients result in, for 
equally spaced, fixed quadrature points with an accuracy up to 
.
Alternatively, if both the quadrature points 
and the weights 
are adjustable, higher accuracy can be achieved due to the 
-freedoms for such a method. A polynomial of order 
has 
coefficients, and it is possible to achieve an accurate integration of a polynomial with an order of 
by using computed quadrature points as well as weights. For this reason, we employ Gaussian integration methods that are of this type.
The Gaussian quadrature methods [9, 10] are based on optimally spaced quadrature points, rather than equally spaced ones. The nodes are 
, 
, …, 
and the weights are 
, 
, …, 
in
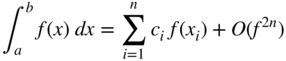
are precomputed and where the error term indicates that Gaussian quadrature can integrate polynomials accurately up to the order of 
.
The following theorem provides the theoretical support of the Gaussian quadrature method.
The Gaussian quadrature points are the roots of the order 
Legendre polynomial 
. Also, the weight 
is the corresponding integration results of Lagrange polynomials. Fortunately, the coefficients are precalculated. We provide a table of Gaussian quadrature coefficient in Table E.1. More elaborate Tables are available, such as [11].
A fundamental issue is the mapping of the integration interval from 
to the interval between 
. The following transformations are used for the mapping
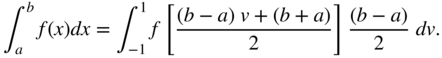
If the Gaussian quadrature points between 
are mapped back to the region 
, the weights can be scaled so that a customized set of Gaussian quadrature points and weights can be used directly as follows:
We should note that the mappings for the solution of nonorthogonal geometries in Chapter 8 also result in the interval 
(Table E.1).
Table E.1 Table for Gaussian quadrature coefficients.
 |
 |
 |
| 2 |  0.577350 |
1.00000 |
| 3 | 0 | 0.888889 |
 0.7745967 |
0.5555556 | |
| 4 |  0.3399810 |
0.6521452 |
 0.8611363 |
0.3478548 | |
| 5 | 0 | 0.5688889 |
 0.5384693 |
0.47862867 | |
 0.9061798 |
0.23692689 | |
| 6 |  0.2386192 |
0.4679139 |
 0.6612094 |
0.3607616 | |
 0.9324695 |
0.1713244 | |
| 10 |  0.14887434 |
0.29552422 |
 0.433395390 |
0.26926672 | |
 0.679409570 |
0.21908636 | |
 0.865063370 |
0.14945134 | |
 0.97390653 |
0.06667134 |
In PEEC, the potential coefficients and partial inductances need the evaluation of multiple integrals. The integrands are frequently related to antiderivative. Hence, Gaussian quadratures can conveniently be applied to get accurate numerical approximate solutions. One example for the multiple integral is a double integral defined over a rectangular region, which is a surface integral defined for a rectangular cell surface
where the weights are given in Table E.1 correspond to (E.7).
E.1.2 Numerical Solution for Singular Self-Coefficients 
or 
The singular situation clearly occurs when the Green's function in the self-coefficients becomes infinite since both integrations are over the same cell. In some cases, the singular behavior can be avoided by using a change of variables given in Ref. [12] or Appendix D in Ref. [13]. Another approach is the numerical integration over the singularity such as an averaging technique [14].
Most of the Green's functions in this text are singular of the form 
if 
. However, if one of the integrations is accomplished analytically, and the singularity is reduced to the basic form 
. If we compare the behavior between the two singularities by using the L'Hôpital rule [15] for this case is
where we assume that 
and 
are constant. Due to the additional analytical integrations, a milder logarithmic singularity results. This is a more suitable singular behavior for numerical integration.
The numerical solution of the still singular integrals is a separate issue. It is clear that such a logarithmic singularity is more suitable for a numarical integration solution. This can be accomplished by so-called adaptive methods. In these methods, the iterative improvement helps the solution of mildly singular problems.
The iterative improvement is difficult for the conventional Gauss integration method presented above due to choice of the steps. For this reason, the adaptive refinement is applied to other methods such as the adaptive Simpson and the adaptive Lobatto methods [10, p. 565]. For example, the Simpson method uses the end point 
and 
of the range where the first approximation of the integral 
for 
is given by
where 
.
In the next iteration, two additional points are added, 
and the right point 
. With this, the next improved solution can be added:
The two Simpson results 
and 
can be combined to find an improved 
result using the Romberg scheme [10, p537]
More steps are taken by further reducing the subdivision 
. In each step, we apply the same scheme for part of the range only. Hence, the same steps are applied to two half regions 
and 
, and so on.
More details and examples are given in Ref. [10] for the solution of moderately singular integrals. The numerical integration of the milder singularity is acceptable if it yields a solution with about five digit accuracy.
E.1.3 Analytical and Numerical Integral Solutions with Variable Subdivisions for Nonself-Partial Elements
If a partial coefficient matrix is of size 
, then the efficient evaluation of the 
partial off-diagonal coupling elements can be very compute time intensive. Of course, the symmetry of the partial elements can be used to reduce the compute time by about a factor of two. In this section, we consider the reduction of the steps 
needed for the numerical integrations.
This part of the MFM algorithm is based on the above-outlined concepts [1]. Again, the majority of applications are for nonorthogonal cells. We assume that the appropriate meshing or space discretization into cells has been applied. For the mid- and high-frequency (FW)PEEC cases, the size of the largest inductive and capacitive cell is less than 
, where 
is the minimum wavelength corresponding to the maximum frequency in the excitation spectrum.
For the prediction algorithm, geometrical quantities are required such as the distance between the cells of interest and the cell size. The first quantity of interest is the distance between the cells in comparison to the size of the larger cell. This is used to determine the number of subdivision for the numerical integration. This part is given as follows:
- Find the maximum size, maxSize, of the two cells.
- Find the center-to-center distance,
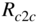, between the two cells. - Find the ratio called farRatio=
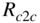/maxSize. 
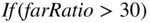, center-to-center point approximation can be used for the distance-oriented part of the integral. Of course retardation must still be considered for full wave solutions.
For smaller distances, a more elaborate algorithm is required, which are considered next.
We should note that this part of the algorithm can be improved to include the retarded element. Fortunately, for sufficiently large problems, the majority of the coefficients fall into the above large distance class. Also, we do not need to store the computed coupling coefficients for very small compute times. The purpose of this is to save storage space.
Algorithms for close spaced cells where the farRatio 
are more challenging. We give an outline of a more elaborate example for such a case. Unless the distance between the cells is very small, the Gauss–Legendre quadrature approach is used, where the subdivisions are determined by the algorithm.
In all cases, the gap between the edges of two close cells, we call 
, is evaluated in each direction 
. Then, a parameter is evaluated for each direction 
as 
for 
. The following decision steps can be applied to determine the integration order used for the evaluation of the near distance coefficients:
then 
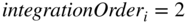
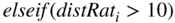then 
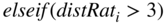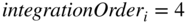
then 
then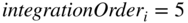 
- else
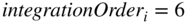
for 
, for eachcell where required. The 
determines the number 
of the subdivisions used in the numerical integration.
The information obtained is utilized in the MFM algorithm to speed up partial element calculations. For very far units, other criteria can be used based on information such as the distance between entire blocks of conductor cells if the distance to obtain further speedup in the partial element evaluations since less checks have to be performed.
More can be accomplished with additional ways to evaluate partial elements as is discussed throughout the book. For example, cells can be divided into several groups for faster evaluation, such as orthogonal or nonorthogonal cells. Evaluation done for groups rather than a cell-by-cell level can lead to further reductions in compute time. We should note that in this section we assumed that numerical integration techniques are used. However, an analytical solutions in cooperation with numerical solutions where necessary yield the best results. An example is a long cell where the length is integrated analytically using formulas like the one in section C.1.1. Then, the arbitrary cross-section may be added using the variable analytic numerical integration outlined in this section where the number of integration steps may depend on the distance to its neighbors.
References
- 1. G. Antonini and A. E. Ruehli. Fast multipole and multi-function PEEC methods. IEEE Transactions on Mobile Computing, 2(4):288–298, October 2003.
- 2. Y. Hackl, P. Scholz, W. Ackermann, and T. Weiland. Multifunction approach and specialized numerical integration algorithms for fast inductance evaluations in nonorthogonal PEEC systems. IEEE Transactions on Electromagnetic Compatibility, 57(5):1155–1163, October 2015.
- 3. A. Muesing, J. Ekman, and J. W. Kolar. Efficient calculation of non-orthogonal partial elements for the PEEC method. IEEE Transactions on Magnetics, 45(3):1140–1142, March 2009.
- 4. A. E. Ruehli. Inductance calculations in a complex integrated circuit environment. IBM Journal of Research and Development, 16(5):470–481, September 1972.
- 5. R. De Smedt. Difference between the partial self-inductance at DC and HF. IEEE Transactions on Electromagnetic Compatibility, 57(4):702–708, April 2015.
- 6. A. Muesing and J. W. Kolar. Efficient partial element calculation and the extension to cylindrical elements for the PEEC method. In 2008 11th Workshop on Control and Modeling for Power Electronics, COMPEL, August 2008.
- 7. A. E. Ruehli and G. Antonini. On modeling accuracy of EMI problems using PEEC. In Proceedings of the IEEE International Symposium on Electromagnetic Compatibility, Boston, MA, August 2003.
- 8. F. W. Grover. Inductance Calculations: Working Formulas and Tables. Dover Publications, New York, 1962.
- 9. R. W. Hamming. Numerical Methods for Scientists and Engineers. Dover Publications, New York, 1986.
- 10. W. Gander, M. Gander, and F. Kwok. Scientific Computing, An introduction using Maple and MATLAB. Springer-Verlag, Berlin and New York, 2014.
- 11. M. Abramowitz and I. A. Stegun. Handbook of Mathematical Functions. U.S. Government Printing Office, Washington, DC, 1964.
- 12. M. G. Duffy. Quadrature over a pyramid or cube of integrands with a singularity at a vertex. SIAM Journal on Numerical Analysis, 19(6):1260–1262, December 1982.
- 13. J. M. Jin. The Finite Element Method in Electromagnetics. John Wiley and Sons, Inc., New York, 2nd edition, 2002.
- 14. M. A. Cracraft. Mobile array design with ANSERLIN antennas and efficient, wide-band PEEC models for interconnect and power distribution network analysis. Ph.D. Dissertation [Online]. Available: http://hdl.handle.net/10355/29582, Missouri University Science and Technology, USA, 2007.
- 15. D. V. Widder. Advanced Calculus. Prentice Hall, Englewood Cliffs, NJ, 1961.