A large number of problems that computational tools are used to solve can be broadly categorized as constraint-satisfaction problems (CSPs). CSPs are composed of variables with possible values that fall into ranges known as domains. Constraints between the variables must be satisfied in order for constraint-satisfaction problems to be solved. Those three core concepts--variables, domains, and constraints--are simple to understand, and their generality underlies the wide applicability of constraint-satisfaction problem solving.
Let’s consider an example problem. Suppose you are trying to schedule a Friday meeting for Joe, Mary, and Sue. Sue has to be at the meeting with at least one other person. For this scheduling problem, the three people--Joe, Mary, and Sue--may be the variables. The domain for each variable may be their respective hours of availability. For instance, the variable Mary has the domain 2 p.m., 3 p.m., and 4 p.m. This problem also has two constraints. One is that Sue has to be at the meeting. The other is that at least two people must attend the meeting. A constraint-satisfaction problem solver will be provided with the three variables, three domains, and two constraints, and it will then solve the problem without having the user explain exactly how. Figure 3.1 illustrates this example.
Programming languages like Prolog and Picat have facilities for solving constraint-satisfaction problems built in. The usual technique in other languages is to build a framework that incorporates a backtracking search and several heuristics to improve the performance of that search. In this chapter, we will first build a framework for CSPs that solves them using a simple recursive backtracking search. Then we will use the framework to solve several different example problems.

Figure 3.1 Scheduling problems are a classic application of constraint-satisfaction frameworks.
3.1 Building a constraint-satisfaction problem framework
Constraints will be defined as subclasses of a Constraint class. Each Constraint consists of the variables it constrains and a method that checks whether it is satisfied(). The determination of whether a constraint is satisfied is the main logic that goes into defining a specific constraint-satisfaction problem.
The default implementation should be overridden. In fact, it must be, because we are defining our Constraint class as an abstract base class. Abstract base classes are not meant to be instantiated. Instead, only their subclasses that override and implement their abstract methods are for actual use.
package chapter3; import java.util.List; import java.util.Map; // V is the variable type, and D is the domain type public abstract class Constraint<V, D> { // the variables that the constraint is between protected List<V> variables; public Constraint(List<V> variables) { this.variables = variables; } public abstract boolean satisfied(Map<V, D> assignment); }
TIP It can be difficult to choose between an abstract class and an interface in Java. Only abstract classes can have instance variables. Since we have the variables instance variable, we opted for an abstract class here.
The centerpiece of our constraint-satisfaction framework will be a class called CSP. CSP is the gathering point for variables, domains, and constraints. It uses generics to make itself flexible enough to work with any kind of variables and domain values (V keys and D domain values). Within CSP, the variables, domains, and constraints collections are of types that you would expect. The variables collection is a List of variables, domains is a Map mapping variables to lists of possible values (the domains of those variables), and constraints is a Map that maps each variable to a List of the constraints imposed on it.
package chapter3;
import java.util.ArrayList;
import java.util.HashMap;
import java.util.List;
import java.util.Map;
public class CSP<V, D> {
private List<V> variables;
private Map<V, List<D>> domains;
private Map<V, List<Constraint<V, D>>> constraints = new HashMap<>();
public CSP(List<V> variables, Map<V, List<D>> domains) {
this.variables = variables;
this.domains = domains;
for (V variable : variables) {
constraints.put(variable, new ArrayList<>());
if (!domains.containsKey(variable)) {
throw new IllegalArgumentException("Every variable should have a domain assigned to it.");
}
}
}
public void addConstraint(Constraint<V, D> constraint) {
for (V variable : constraint.variables) {
if (!variables.contains(variable)) {
throw new IllegalArgumentException("Variable in constraint not in CSP");
}
constraints.get(variable).add(constraint);
}
}
The constructor creates the constraints Map. The addConstraint() method goes through all of the variables touched by a given constraint and adds itself to the constraints mapping for each of them. Both methods have basic error-checking in place and will raise an exception when a variable is missing a domain or a constraint is on a nonexistent variable.
How do we know if a given configuration of variables and selected domain values satisfies the constraints? We will call such a given configuration an assignment. In other words, an assignment is a specific domain value selected for each variable. We need a function that checks every constraint for a given variable against an assignment to see if the variable’s value in the assignment is consistent with the constraints. Here, we implement a consistent() function as a method on CSP.
Listing 3.3 CSP.java continued
// Check if the value assignment is consistent by checking all
// constraints for the given variable against it
public boolean consistent(V variable, Map<V, D> assignment) {
for (Constraint<V, D> constraint : constraints.get(variable)) {
if (!constraint.satisfied(assignment)) {
return false;
}
}
return true;
}
consistent() goes through every constraint for a given variable (it will always be the variable that was just added to the assignment) and checks if the constraint is satisfied, given the new assignment. If the assignment satisfies every constraint, true is returned. If any constraint imposed on the variable is not satisfied, false is returned.
This constraint-satisfaction framework will use a simple backtracking search to find solutions to problems. Backtracking is the idea that once you hit a wall in your search, you go back to the last known point where you made a decision before the wall, and you choose a different path. If you think that sounds like depth-first search from chapter 2, you are perceptive. The backtracking search implemented in the following backtrackingSearch() method is a kind of recursive depth-first search, combining ideas you saw in chapters 1 and 2. We also implement a helper method that just calls backtrackingSearch() with an empty initial Map. The helper method will be useful for starting a search.
Listing 3.4 CSP.java continued
public Map<V, D> backtrackingSearch(Map<V, D> assignment) { // assignment is complete if every variable is assigned (base case) if (assignment.size() == variables.size()) { return assignment; } // get the first variable in the CSP but not in the assignment V unassigned = variables.stream().filter(v -> !assignment.containsKey(v)).findFirst().get(); // look through every domain value of the first unassigned variable for (D value : domains.get(unassigned)) { // shallow copy of assignment that we can change Map<V, D> localAssignment = new HashMap<>(assignment); localAssignment.put(unassigned, value); // if we're still consistent, we recurse (continue) if (consistent(unassigned, localAssignment)) { Map<V, D> result = backtrackingSearch(localAssignment); // if we didn't find the result, we end up backtracking if (result != null) { return result; } } } return null; } // helper for backtrackingSearch when nothing known yet public Map<V, D> backtrackingSearch() { return backtrackingSearch(new HashMap<>()); } }
Let’s walk through backtrackingSearch(), line by line:
if (assignment.size() == variables.size()) { return assignment; }
The base case for the recursive search is having found a valid assignment for every variable. Once we have, we return the first instance of a solution that was valid. (We do not keep searching.)
V unassigned = variables.stream().filter(v -> !assignment.containsKey(v)).findFirst().get();
To select a new variable whose domain we will explore, we simply go through all of the variables and find the first that does not have an assignment. To do this, we create a Stream of variables filtered by whether they are yet in assignment, and we pull the first one that is not assigned using findFirst(). filter() takes a Predicate. A Predicate is a functional interface that describes a function that takes one argument and returns a boolean. Our predicate is a lambda expression (v -> !assignment.containsKey(v)) that returns true if assignment does not contain the argument, which in this case will be a variable for our CSP.
for (D value : domains.get(unassigned)) { Map<V, D> localAssignment = new HashMap<>(assignment); localAssignment.put(unassigned, value);
We try assigning all possible domain values for that variable, one at a time. The new assignment for each is stored in a local map called localAssignment.
if (consistent(unassigned, localAssignment)) { Map<V, D> result = backtrackingSearch(localAssignment); if (result != null) { return result; } }
If the new assignment in localAssignment is consistent with all of the constraints (this is what consistent() checks for), we continue recursively searching with the new assignment in place. If the new assignment turns out to be complete (the base case), we return the new assignment up the recursion chain.
return null;
Finally, if we have gone through every possible domain value for a particular variable, and there is no solution utilizing the existing set of assignments, we return null, indicating no solution. This will lead to backtracking up the recursion chain to the point where a different prior assignment could have been made.
3.2 The Australian map-coloring problem
Imagine you have a map of Australia that you want to color by state/territory (which we will collectively call regions). No two adjacent regions should share a color. Can you color the regions with just three different colors?
The answer is yes. Try it out on your own. (The easiest way is to print out a map of Australia with a white background.) As human beings, we can quickly figure out the solution by inspection and a little trial and error. It is a trivial problem, really, and a great first problem for our backtracking constraint-satisfaction solver. A solution to the problem is illustrated in figure 3.2.
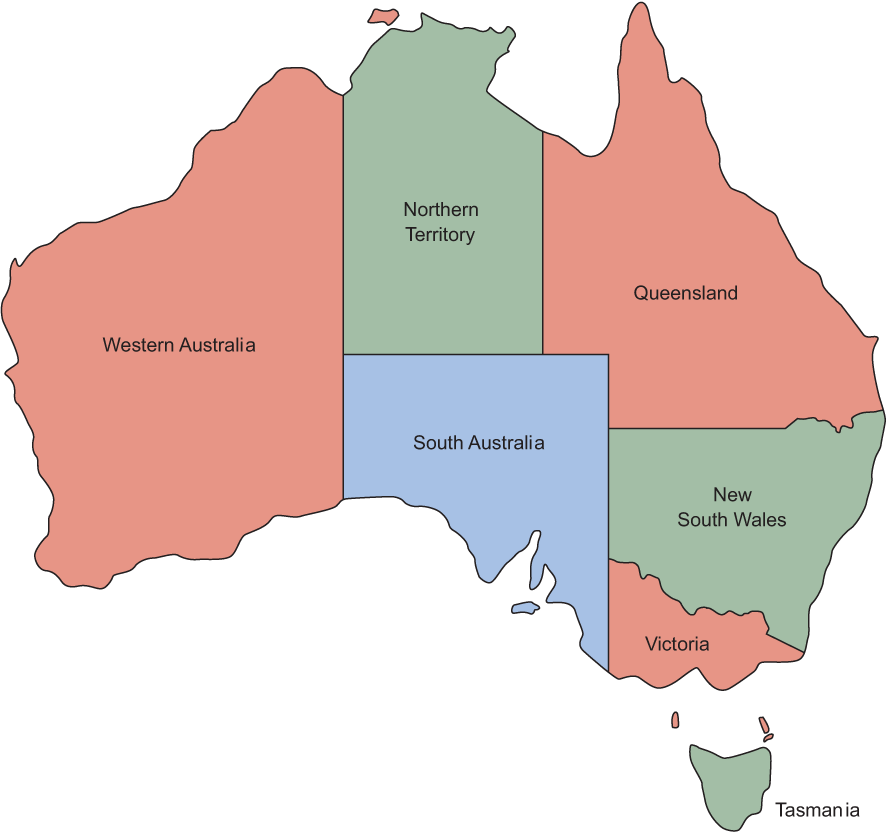
Figure 3.2 In a solution to the Australian map-coloring problem, no two adjacent parts of Australia can be colored with the same color.
To model the problem as a CSP, we need to define the variables, domains, and constraints. The variables are the seven regions of Australia (at least the seven that we will restrict ourselves to): Western Australia, Northern Territory, South Australia, Queensland, New South Wales, Victoria, and Tasmania. In our CSP, they can be modeled with strings. The domain of each variable is the three different colors that can possibly be assigned. (We will use red, green, and blue.) The constraints are the tricky part. No two adjacent regions can be colored with the same color, so our constraints will be dependent on which regions border one another. We can use what are called binary constraints (constraints between two variables). Every two regions that share a border will also share a binary constraint indicating that they cannot be assigned the same color.
To implement these binary constraints in code, we need to subclass the Constraint class. The MapColoringConstraint subclass will take two variables in its constructor: the two regions that share a border. Its overridden satisfied() method will check first whether the two regions have domain values (colors) assigned to them; if either does not, the constraint is trivially satisfied until they do. (There cannot be a conflict when one does not yet have a color.) Then it will check whether the two regions are assigned the same color. Obviously, there is a conflict, meaning that the constraint is not satisfied, when they are the same.
The class is presented here in its entirety except for its main() driver. MapColoringConstraint itself is not generic, but it subclasses a parameterized version of the generic class Constraint that indicates both variables and domains are of type String.
Listing 3.5 MapColoringConstraint.java
package chapter3;
import java.util.HashMap;
import java.util.List;
import java.util.Map;
public final class MapColoringConstraint extends Constraint<String, String> {
private String place1, place2;
public MapColoringConstraint(String place1, String place2) {
super(List.of(place1, place2));
this.place1 = place1;
this.place2 = place2;
}
@Override
public boolean satisfied(Map<String, String> assignment) {
// if either place is not in the assignment, then it is not
// yet possible for their colors to be conflicting
if (!assignment.containsKey(place1) ||
!assignment.containsKey(place2)) {
return true;
}
// check the color assigned to place1 is not the same as the
// color assigned to place2
return !assignment.get(place1).equals(assignment.get(place2));
}
Now that we have a way of implementing the constraints between regions, fleshing out the Australian map-coloring problem with our CSP solver is simply a matter of filling in domains and variables, and then adding constraints.
Listing 3.6 MapColoringConstraint.java continued
public static void main(String[] args) { List<String> variables = List.of("Western Australia", "Northern Territory", "South Australia", "Queensland", "New South Wales", "Victoria", "Tasmania"); Map<String, List<String>> domains = new HashMap<>(); for (String variable : variables) { domains.put(variable, List.of("red", "green", "blue")); } CSP<String, String> csp = new CSP<>(variables, domains); csp.addConstraint(new MapColoringConstraint("Western Australia", "Northern Territory")); csp.addConstraint(new MapColoringConstraint("Western Australia", "South Australia")); csp.addConstraint(new MapColoringConstraint("South Australia", "Northern Territory")); csp.addConstraint(new MapColoringConstraint("Queensland", "Northern Territory")); csp.addConstraint(new MapColoringConstraint("Queensland", "South Australia")); csp.addConstraint(new MapColoringConstraint("Queensland", "New South Wales")); csp.addConstraint(new MapColoringConstraint("New South Wales", "South Australia")); csp.addConstraint(new MapColoringConstraint("Victoria", "South Australia")); csp.addConstraint(new MapColoringConstraint("Victoria", "New South Wales")); csp.addConstraint(new MapColoringConstraint("Victoria", "Tasmania"));
Finally, backtrackingSearch() is called to find a solution.
Listing 3.7 MapColoringConstraint.java continued
Map<String, String> solution = csp.backtrackingSearch(); if (solution == null) { System.out.println("No solution found!"); } else { System.out.println(solution); } } }
A correct solution will include an assigned color for every region:
{Western Australia=red, New South Wales=green, Victoria=red, Tasmania=green, Northern Territory=green, South Australia=blue, Queensland=red}
3.3 The eight queens problem
A chessboard is an eight-by-eight grid of squares. A queen is a chess piece that can move on the chessboard any number of squares along any row, column, or diagonal. A queen is attacking another piece if, in a single move, it can move to the square the piece is on without jumping over any other piece. (In other words, if the other piece is in the line of sight of the queen, then it is attacked by it.) The eight queens problem poses the question of how eight queens can be placed on a chessboard without any queen attacking another queen. One of many potential solutions to the problem is illustrated in figure 3.3.
To represent squares on the chessboard, we will assign each an integer row and an integer column. We can ensure each of the eight queens is not in the same column by simply assigning them sequentially the columns 1 through 8. The variables in our constraint-satisfaction problem can just be the column of the queen in question. The domains can be the possible rows (again, 1 through 8). Listing 3.8 shows the end of our file, where we define these variables and domains.

Figure 3.3 In a solution to the eight queens problem (there are many solutions), no two queens can be threatening each other.
Listing 3.8 QueensConstraint.java
public static void main(String[] args) { List<Integer> columns = List.of(1, 2, 3, 4, 5, 6, 7, 8); Map<Integer, List<Integer>> rows = new HashMap<>(); for (int column : columns) { rows.put(column, List.of(1, 2, 3, 4, 5, 6, 7, 8)); } CSP<Integer, Integer> csp = new CSP<>(columns, rows);
To solve the problem, we will need a constraint that checks whether any two queens are on the same row or diagonal. (They were all assigned different sequential columns to begin with.) Checking for the same row is trivial, but checking for the same diagonal requires a little bit of math. If any two queens are on the same diagonal, the difference between their rows will be the same as the difference between their columns. Can you see where these checks take place in QueensConstraint? Note that the following code is at the top of our source file.
Listing 3.9 QueensConstraint.java continued
package chapter3;
import java.util.HashMap;
import java.util.List;
import java.util.Map;
import java.util.Map.Entry;
public class QueensConstraint extends Constraint<Integer, Integer> {
private List<Integer> columns;
public QueensConstraint(List<Integer> columns) {
super(columns);
this.columns = columns;
}
@Override
public boolean satisfied(Map<Integer, Integer> assignment) {
for (Entry<Integer, Integer> item : assignment.entrySet()) {
// q1c = queen 1 column, q1r = queen 1 row
int q1c = item.getKey();
int q1r = item.getValue();
// q2c = queen 2 column
for (int q2c = q1c + 1; q2c <= columns.size(); q2c++) {
if (assignment.containsKey(q2c)) {
// q2r = queen 2 row
int q2r = assignment.get(q2c);
// same row?
if (q1r == q2r) {
return false;
}
// same diagonal?
if (Math.abs(q1r - q2r) == Math.abs(q1c - q2c)) {
return false;
}
}
}
}
return true; // no conflict
}
All that is left is to add the constraint and run the search. We’re now back at the bottom of the file within the end of main().
Listing 3.10 QueensConstraint.java continued
csp.addConstraint(new QueensConstraint(columns)); Map<Integer, Integer> solution = csp.backtrackingSearch(); if (solution == null) { System.out.println("No solution found!"); } else { System.out.println(solution); } } }
Notice that we were able to reuse the constraint-satisfaction problem-solving framework that we built for map coloring fairly easily for a completely different type of problem. This is the power of writing code generically! Algorithms should be implemented in as broadly applicable a manner as possible unless a performance optimization for a particular application requires specialization.
A correct solution will assign a column and row to every queen:
{1=1, 2=5, 3=8, 4=6, 5=3, 6=7, 7=2, 8=4}
3.4 Word search
A word search is a grid of letters with hidden words placed along rows, columns, and diagonals. A player of a word-search puzzle attempts to find the hidden words by carefully scanning through the grid. Finding places to put the words so that they all fit on the grid is a kind of constraint-satisfaction problem. The variables are the words, and the domains are the possible locations of those words. The problem is illustrated in figure 3.4. Our goal in this section is to generate a word-search puzzle, not to solve one.
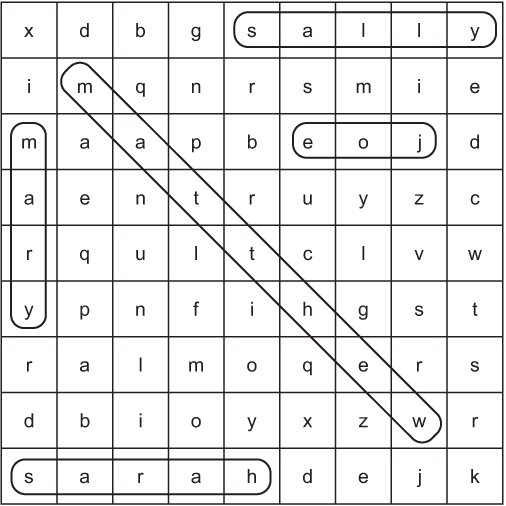
Figure 3.4 A classic word search, such as you might find in a children’s puzzle book
For the purposes of expediency, our word search will not include words that overlap. You can improve it to allow for overlapping words as an exercise.
The grid of this word-search problem is not entirely dissimilar from the mazes of chapter 2. Some of the following data types should look familiar. WordGrid is analogous to Maze, and GridLocation is analogous to MazeLocation.
package chapter3;
import java.util.ArrayList;
import java.util.List;
import java.util.Random;
public class WordGrid {
public static class GridLocation {
public final int row, column;
public GridLocation(int row, int column) {
this.row = row;
this.column = column;
}
// auto-generated by Eclipse
@Override
public int hashCode() {
final int prime = 31;
int result = 1;
result = prime * result + column;
result = prime * result + row;
return result;
}
// auto-generated by Eclipse
@Override
public boolean equals(Object obj) {
if (this == obj) {
return true;
}
if (obj == null) {
return false;
}
if (getClass() != obj.getClass()) {
return false;
}
GridLocation other = (GridLocation) obj;
if (column != other.column) {
return false;
}
if (row != other.row) {
return false;
}
return true;
}
}
Initially, we will fill the grid with random letters of the English alphabet (A-Z). We do this by generating random char codes (integers, effectively) equivalent to where the letters land in ASCII. We will also need a method to mark a word on the grid given a list of locations, and a method for displaying the grid.
Listing 3.12 WordGrid.java continued
private final char ALPHABET_LENGTH = 26; private final char FIRST_LETTER = 'A'; private final int rows, columns; private char[][] grid; public WordGrid(int rows, int columns) { this.rows = rows; this.columns = columns; grid = new char[rows][columns]; // initialize grid with random letters Random random = new Random(); for (int row = 0; row < rows; row++) { for (int column = 0; column < columns; column++) { char randomLetter = (char) (random.nextInt(ALPHABET_LENGTH) + FIRST_LETTER); grid[row][column] = randomLetter; } } } public void mark(String word, List<GridLocation> locations) { for (int i = 0; i < word.length(); i++) { GridLocation location = locations.get(i); grid[location.row][location.column] = word.charAt(i); } } // get a pretty printed version of the grid @Override public String toString() { StringBuilder sb = new StringBuilder(); for (char[] rowArray : grid) { sb.append(rowArray); sb.append(System.lineSeparator()); } return sb.toString(); }
To figure out where words can fit in the grid, we will generate their domains. The domain of a word is a list of lists of the possible locations of all of its letters (List<List<GridLocation>>). Words cannot go just anywhere, though. They must stay within a row, column, or diagonal that is within the bounds of the grid. In other words, they should not go off the end of the grid. The purpose of generateDomain() and its helper “fill” methods is to build these lists for every word.
Listing 3.13 WordGrid.java continued
public List<List<GridLocation>> generateDomain(String word) { List<List<GridLocation>> domain = new ArrayList<>(); int length = word.length(); for (int row = 0; row < rows; row++) { for (int column = 0; column < columns; column++) { if (column + length <= columns) { // left to right fillRight(domain, row, column, length); // diagonal towards bottom right if (row + length <= rows) { fillDiagonalRight(domain, row, column, length); } } if (row + length <= rows) { // top to bottom fillDown(domain, row, column, length); // diagonal towards bottom left if (column - length >= 0) { fillDiagonalLeft(domain, row, column, length); } } } } return domain; } private void fillRight(List<List<GridLocation>> domain, int row, int column, int length) { List<GridLocation> locations = new ArrayList<>(); for (int c = column; c < (column + length); c++) { locations.add(new GridLocation(row, c)); } domain.add(locations); } private void fillDiagonalRight(List<List<GridLocation>> domain, int row, int column, int length) { List<GridLocation> locations = new ArrayList<>(); int r = row; for (int c = column; c < (column + length); c++) { locations.add(new GridLocation(r, c)); r++; } domain.add(locations); } private void fillDown(List<List<GridLocation>> domain, int row, int column, int length) { List<GridLocation> locations = new ArrayList<>(); for (int r = row; r < (row + length); r++) { locations.add(new GridLocation(r, column)); } domain.add(locations); } private void fillDiagonalLeft(List<List<GridLocation>> domain, int row, int column, int length) { List<GridLocation> locations = new ArrayList<>(); int c = column; for (int r = row; r < (row + length); r++) { locations.add(new GridLocation(r, c)); c--; } domain.add(locations); } }
For the range of potential locations of a word (along a row, column, or diagonal), for loops translate the range into a list of GridLocations. Because generateDomain() loops through every grid location from the top left through to the bottom right for every word, it involves a lot of computation. Can you think of a way to do it more efficiently? What if we looked through all of the words of the same length at once, inside the loop?
To check if a potential solution is valid, we must implement a custom constraint for the word search. The satisfied() method of WordSearchConstraint simply checks whether any of the locations proposed for one word are the same as a location proposed for another word. It does this using a Set. Converting a List into a Set will remove all duplicates. If there are fewer items in a Set converted from a List than there were in the original List, that means the original List contained some duplicates. To prepare the data for this check, we will use a flatMap() to combine multiple sublists of locations for each word in the assignment into a single larger list of locations.
Listing 3.14 WordSearchConstraint.java
package chapter3;
import java.util.Collection;
import java.util.Collections;
import java.util.HashMap;
import java.util.HashSet;
import java.util.List;
import java.util.Map;
import java.util.Map.Entry;
import java.util.Random;
import java.util.Set;
import java.util.stream.Collectors;
import chapter3.WordGrid.GridLocation;
public class WordSearchConstraint extends Constraint<String, List<GridLocation>> {
public WordSearchConstraint(List<String> words) {
super(words);
}
@Override
public boolean satisfied(Map<String, List<GridLocation>> assignment) {
// combine all GridLocations into one giant List
List<GridLocation> allLocations = assignment.values().stream()
.flatMap(Collection::stream).collect(Collectors.toList());
// a set will eliminate duplicates using equals()
Set<GridLocation> allLocationsSet = new HashSet<>(allLocations);
// if there are any duplicate grid locations then there is an overlap
return allLocations.size() == allLocationsSet.size();
}
Finally, we are ready to run it. For this example, we have five words (names, in this example) in a nine-by-nine grid. The solution we get back should contain mappings between each word and the locations where its letters can fit in the grid.
Listing 3.15 WordSearchConstraint.java continued
public static void main(String[] args) { WordGrid grid = new WordGrid(9, 9); List<String> words = List.of("MATTHEW", "JOE", "MARY", "SARAH", "SALLY"); // generate domains for all words Map<String, List<List<GridLocation>>> domains = new HashMap<>(); for (String word : words) { domains.put(word, grid.generateDomain(word)); } CSP<String, List<GridLocation>> csp = new CSP<>(words, domains); csp.addConstraint(new WordSearchConstraint(words)); Map<String, List<GridLocation>> solution = csp.backtrackingSearch(); if (solution == null) { System.out.println("No solution found!"); } else { Random random = new Random(); for (Entry<String, List<GridLocation>> item : solution.entrySet()) { String word = item.getKey(); List<GridLocation> locations = item.getValue(); // random reverse half the time if (random.nextBoolean()) { Collections.reverse(locations); } grid.mark(word, locations); } System.out.println(grid); } } }
There is a finishing touch in the code that fills the grid with words. Some words are randomly chosen to be reversed. This is valid, because this example does not allow overlapping words. Your ultimate output should look something like the following. Can you find Matthew, Joe, Mary, Sarah, and Sally?
LWEHTTAMJ MARYLISGO DKOJYHAYE IAJYHALAG GYZJWRLGM LLOTCAYIX PEUTUSLKO AJZYGIKDU HSLZOFNNR
3.5 SEND+MORE=MONEY
SEND+MORE=MONEY is a cryptarithmetic puzzle, meaning that it is about finding digits that replace letters to make a mathematical statement true. Each letter in the problem represents one digit (0-9). No two letters can represent the same digit. When a letter repeats, it means a digit repeats in the solution.
To solve this puzzle by hand, it helps to line up the words.
SEND +MORE =MONEY
It is absolutely solvable by hand, with a bit of algebra and intuition. But a fairly simple computer program can solve it faster by brute-forcing many possible solutions. Let’s represent SEND+MORE=MONEY as a constraint-satisfaction problem.
Listing 3.16 SendMoreMoneyConstraint.java
package chapter3;
import java.util.HashMap;
import java.util.HashSet;
import java.util.List;
import java.util.Map;
public class SendMoreMoneyConstraint extends Constraint<Character, Integer> {
private List<Character> letters;
public SendMoreMoneyConstraint(List<Character> letters) {
super(letters);
this.letters = letters;
}
@Override
public boolean satisfied(Map<Character, Integer> assignment) {
// if there are duplicate values then it's not a solution
if ((new HashSet<>(assignment.values())).size() < assignment.size()) {
return false;
}
// if all variables have been assigned, check if it adds correctly
if (assignment.size() == letters.size()) {
int s = assignment.get('S');
int e = assignment.get('E');
int n = assignment.get('N');
int d = assignment.get('D');
int m = assignment.get('M');
int o = assignment.get('O');
int r = assignment.get('R');
int y = assignment.get('Y');
int send = s * 1000 + e * 100 + n * 10 + d;
int more = m * 1000 + o * 100 + r * 10 + e;
int money = m * 10000 + o * 1000 + n * 100 + e * 10 + y;
return send + more == money;
}
return true; // no conflicts
}
SendMoreMoneyConstraint’s satisfied() method does a few things. First, it checks if multiple letters represent the same digits. If they do, that’s an invalid solution, and it returns false. Next, it checks if all letters have been assigned. If they have, it checks to see if the formula (SEND+MORE=MONEY) is correct with the given assignment. If it is, a solution has been found, and it returns true. Otherwise, it returns false. Finally, if all letters have not yet been assigned, it returns true. This is to ensure that a partial solution continues to be worked on.
Listing 3.17 SendMoreMoneyConstraint.java continued
public static void main(String[] args) { List<Character> letters = List.of('S', 'E', 'N', 'D', 'M', 'O', 'R', 'Y'); Map<Character, List<Integer>> possibleDigits = new HashMap<>(); for (Character letter : letters) { possibleDigits.put(letter, List.of(0, 1, 2, 3, 4, 5, 6, 7, 8, 9)); } // so we don't get answers starting with a 0 possibleDigits.replace('M', List.of(1)); CSP<Character, Integer> csp = new CSP<>(letters, possibleDigits); csp.addConstraint(new SendMoreMoneyConstraint(letters)); Map<Character, Integer> solution = csp.backtrackingSearch(); if (solution == null) { System.out.println("No solution found!"); } else { System.out.println(solution); } } }
You will notice that we preassigned the answer for the letter M. This was to ensure that the answer doesn’t include a 0 for M, because if you think about it, our constraint has no notion of the concept that a number can’t start with zero. Feel free to try it out without that preassigned answer.
The solution should look something like this:
{R=8, S=9, D=7, E=5, Y=2, M=1, N=6, O=0}
3.6 Circuit board layout
A manufacturer needs to fit certain rectangular chips onto a rectangular circuit board. Essentially, this problem asks, “How can several different-sized rectangles all fit snugly inside of another rectangle?” A constraint-satisfaction problem solver can find the solution. The problem is illustrated in figure 3.5.
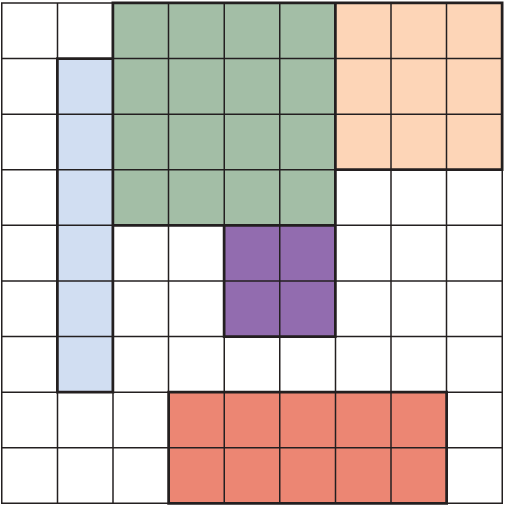
Figure 3.5 The circuit board layout problem is very similar to the word-search problem, but the rectangles are of variable width.
The circuit board layout problem is similar to the word-search problem. Instead of 1 × N rectangles (words), the problem presents M × N rectangles. Like in the word-search problem, the rectangles cannot overlap. The rectangles cannot be put on diagonals, so in that sense the problem is actually simpler than the word search.
On your own, try rewriting the word-search solution to accommodate circuit board layout. You can reuse much of the code, including the code for the grid.
3.7 Real-world applications
As was mentioned in the introduction to this chapter, constraint-satisfaction problem solvers are commonly used in scheduling. Several people need to be at a meeting, and they are the variables. The domains consist of the open times on their calendars. The constraints may involve what combinations of people are required at the meeting.
Constraint-satisfaction problem solvers are also used in motion planning. Imagine a robot arm that needs to fit inside of a tube. It has constraints (the walls of the tube), variables (the joints), and domains (possible movements of the joints).
There are also applications in computational biology. You can imagine constraints between molecules required for a chemical reaction. And, of course, as is common with AI, there are applications in games. Writing a Sudoku solver is one of the following exercises, but many logic puzzles can be solved using constraint-satisfaction problem solving.
In this chapter, we built a simple backtracking, depth-first search, problem-solving framework. But it can be greatly improved by adding heuristics (remember A*?)--intuitions that can aid the search process. A newer technique than backtracking, known as constraint propagation, is also an efficient avenue for real-world applications. For more information, check out chapter 6 of Stuart Russell and Peter Norvig’s Artificial Intelligence: A Modern Approach, third edition (Pearson, 2010).
The simple example frameworks we build in this book are not appropriate for production environments. If you need to solve a more sophisticated constraint problem in Java, you may consider the Choco framework, available at https://choco-solver.org.
3.8 Exercises
-
Revise WordSearchConstraint so that overlapping letters are allowed.
-
Build the circuit board layout problem solver described in section 3.6, if you have not already.
-
Build a program that can solve Sudoku problems using this chapter’s constraint-satisfaction problem-solving framework.
