Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

5Linear model and multilinear model

This chapter covers the following items:

–Algorithm for linear modeling

–Algorithm for multilinear modeling

–Examples and applications

Sir Francis Galton (1822–1911), an English scientist and also one of the cousins of Charles Darwin, contributed significantly to the fields of not only genetics but also psychology. He came up with the concept of regression [1, 2]. He is also regarded as a pioneer in applying statistics to biology. One of the datasets he handled included the heights of fathers and their first sons. Galton focused on the prediction of heights of sons being reliant on the heights of fathers. Having analyzed the scatter-plots regarding these heights, Galton discovered that the trend was linear and in increasing direction. After having fit a line to these data, he realized that the regression line estimated that taller fathers were inclined to have shorter sons, whereas shorter fathers showed the tendency to have taller sons [2, 3]. This held true for fathers whose heights were taller than the average, which showed a regression toward the mean.

In this chapter, we attempt to examine the relationship between one or more variables. Based on this, we have created a model to be utilized for predictive purposes. For instance, consider the following question: “Is there any statistical evidence to draw a conclusion that the Expanded Disability Status Scale (EDSS) score with the relapsing remitting multiple sclerosis (MS) has the greatest incidence of MS?” To answer this is of vital importance if we intent to make appropriate medical decisions, choices as well as decisions regarding lifestyles. Regression analysis will be used while we are analyzing the relationship between variables. What we aim at is creating a model and studying inferential procedures in cases when several independent variables and one dependent are existent. Y denotes the random variable to be predicted, which is also termed as the dependent variable (or response variable) and xi denotes independent (or predictor) variables used to predict or to model Y. For instance, (x, y) represent the weight and height of a man. Let us assume that we are interested in finding the relationship between weight and height from sample measurements of n individuals. The process related to the finding of a mathematical equation that optimally fits the noisy data is termed the regression analysis. Sir Francis Galton introduced the word regression in his seminal book Natural Inheritance in 1894 to describe certain genetic relationships [3]. Regression is one of the most popular statistical techniques if one wishes to study the dependence of one variable in relation to another variable. There exist different forms of regression, which are simple linear, nonlinear, multiple and others. The principal use of a regression model is prediction. When one uses a model for predicting Y for a particular set of values of (x1, x2, ᐧᐧᐧ , xk), he/she may want to make out how large prediction error might be. After collecting the sample data, regression analysis broadly comprises the following steps [4]. The function f (x1, x2, ᐧᐧᐧ , xk; w0,w1,w2, ᐧᐧᐧ , wk) (k ≥ 1) constitutes the independent or predictor variables x1, x2, ᐧᐧᐧ , xk (supposed to be nonrandom) and unknown parameters or weights w0,w1,w2, ᐧᐧᐧ , wk and e denoting the random or error variable. Subsequently, it will be possible to get on with the introduction of the simplest form of a regression model which is termed as simple linear regression [4].

Consider a random sample with n observations of the form (x1, y1) , (x2, y2), ᐧᐧᐧ , (xk, yk). Here x is the independent variable and y is the dependent variable, both of which are scalars. The scatter diagram is a basic descriptive technique to determine the form of relationship between x and y, which can be drawn by plotting the sample observations in Cartesian coordinates. The pattern of points provides a clue of a linear or a nonlinear relationship between the relevant variables. Figure 5.1(a) presents the relationship between x and y, which is quite linear. On the other hand, in Figure 5.1(b), the relationship resembles a parabola, and in Figure 5.1(c) there exists no evident relationship between the variables [5, 6]. When the scatter diagram shows a linear relationship, the problem may be to find the linear model that fits the given data in the best way. For this purpose, we will provide a general definition of a linear statistical model, which is named as the multilinear regression model.

Figure 5.1: Scatter diagram: (a) linear relationship; (b) quadratic relationship; and (c) no relationship. From Ramachandran and Chris [2].

A multilinear regression model in relation to random response Y to a set of predictor variables x1, x2, ᐧᐧᐧ , xk provides an equation of the form Y =w0 + w1x1 +w2x2 + ᐧᐧᐧ +wkxk, where w0,w1,w2, ᐧᐧᐧ ,wk are unknown parameters, x1, x2, ᐧᐧᐧ , xk are independent nonrandom variables and e is a random variable that signifies an error term. We suppose that E (e) = 0, or in an equivalent manner, E(Y) =w0 +w1x1 +w2x2 + ᐧᐧᐧ +wkxk [2, 5–7]. We can handle a single dependent variable Y and a single independent nonrandom variable x to have an understanding of the basic concepts pertaining to regression analysis. If we assume that there exist no measurement errors in xi, we can say that the possible measurement errors in y and the uncertainties in the model assumed are depicted through the random error e. There is an inability inherent to afford an exact model for a natural singularity as is expressed via the random term e. This will have a specified probability distribution (like normal) with mean zero. Hence, you can consider Y as one with a deterministic component, E(Y) and a random component, e. If you take k = 1 in the multilinear regression model, a simple linear regression model is obtained as follows [7–9]:

$E (Y) = w_{0} + w_{1} x + e (5.1)$ $E (Y) = w_{0} + w_{1} x + e (5.1)$

If Y is termed a simple linear regression model, w0 is the Y-intercept of the line and w shows the line slope. Here, e is the error component. Such a basic linear model accepts the presence of a linear relationship between the variables x and y disturbed by a random error e [2, 7–9]. The data points known are the pairs (x1, y1), (x2, y2), ᐧᐧᐧ , (xk, yk) and the problem of simple linear regression is to fit a straight line optimal in an extent to the dataset as provided and is also shown in Figure 5.2.

Figure 5.2: Equation regarding a straight line. From Ramachandran and Chris [2].

At this point, the problem is to find estimators for w0 and w1. When you obtain the “good” estimators ŵ0 and ŵ1 you are able to fit a line for the given data by the prediction equation ŷ = ŵ0 + ŵ1x. The question arises whether this predicted line yields the “best” description of data. The most widely used technique currently is called the method of least squares, which is described so that we can obtain the weights of the parameters or the estimators [10–12].

Many methods have been proposed for the estimation of parameters in a model. We call the method under discussion in this section ordinary least squares (ols), where parameter estimates are selected to minimize the quantity which is termed as the residual sum of squares.

It is known that parameters are unknown quantities characterizing a model. Estimates of parameters are functions of data that can be computed; therefore, they are statistics. The fitted value for case i is given by E (xi). For this, ŷi is used, which can be represented by the shorthand notation [10–12].

${\hat{y}}_{i} = w_{0} + w_{1} x_{i} (5.2)$ ${\hat{y}}_{i} = w_{0} + w_{1} x_{i} (5.2)$

This should be contrasted with the equation for the statistical errors:

$e_{i} = {\hat{y}}_{i} - (w_{0} + w_{1} x_{i}), i = 1, 2, \dots, n (5.3)$ $e_{i} = {\hat{y}}_{i} - (w_{0} + w_{1} x_{i}), i = 1, 2, \dots, n (5.3)$

All of the least squares calculations for simple regression depend solely on averages, sums of cross-products and sums of squares [13–16]. The criterion helps to obtain estimators reliant on residuals. These are geometrically vertical distances between the fitted line and the actual values, and the illustration is shown in Figure 5.3. It is known that the residuals echo the inherent asymmetry in roles of response and predictor for the problems regarding regression.

Figure 5.3: A schematic plot for ols fitting. From Ramachandran and Chris [2].

Figure 5.3 presents a schematic plot for ols fitting. A small circle indicates each data point, and the solid line is the candidate ols line yielded by a specific choice of slope as well as intercept. The residuals are the solid vertical lines between solid line and points. Points that are below the line have negative residuals, whereas points that are above the line have positive residuals. The ols estimators are values w0 and w1 minimizing the function as follows [13–15]:

$RSS (w_{0}, w_{1}) = \sum_{i = 1}^{n} {[y_{i} - (w_{0} + w_{1} x_{i})]}^{2} (5.4)$ $RSS (w_{0}, w_{1}) = \sum_{i = 1}^{n} {[y_{i} - (w_{0} + w_{1} x_{i})]}^{2} (5.4)$

When we make the evaluation at (ŵ0, ŵ1), the quantity is called RSS(ŵ0, ŵ1) (the residual sum of squares or the abbreviation RSS), which can also be used as [13–15]

$\begin{array}{l} {\hat{w}}_{1} = \frac{SAB}{SAA} = r_{x y} \frac{{SD}_{y}}{{SD}_{x}} = r_{x y} {(\frac{SBB}{SAA})}^{2} \\ {\hat{w}}_{0} = \hat{y} - {\hat{w}}_{1} \bar{x} (5.5) \end{array}$ $\begin{array}{l} {\hat{w}}_{1} = \frac{SAB}{SAA} = r_{x y} \frac{{SD}_{y}}{{SD}_{x}} = r_{x y} {(\frac{SBB}{SAA})}^{2} \\ {\hat{w}}_{0} = \hat{y} - {\hat{w}}_{1} \bar{x} (5.5) \end{array}$

Several forms of ŵ1 are all equivalent. The variance σ2 is basically the average squared size of the $e_{i}^{2} .$ $e_{i}^{2} .$ For this reason, it can be expected that its estimator ^σ22 is attained by averaging the squared residuals. Assuming that the errors are uncorrelated random variables that have no zero means and common variance σ2, an unbiased estimate of σ2 is gained through dividing $RSS = \sum {\hat{e}}_{i}^{2}$ $RSS = \sum {\hat{e}}_{i}^{2}$ by its degrees of freedom (df). Here, residual df, in the mean function, represents the number of cases minus the number of parameters. Residual df = n – 2 is valid for simple regression. For this reason, the estimate of σ2 is provided by the following equation [13–15]:

${\hat{σ}}^{2} = \frac{RSS}{n - 2} (5.6)$ ${\hat{σ}}^{2} = \frac{RSS}{n - 2} (5.6)$

Another point to mention is the F-test for regression. In this case, if the sum of squares for regression SSreg is large, the simple regression mean function E (x) = w0 + w1x is supposed to be a significant improvement over the mean function E (x) = w0. This is similar to stating that the additional parameter in the simple regression mean function w1 differs from zero; or E (x) is not constant as it changes. More formally, we can say that in order to be capable of judging how large is “large,” we do a comparison of the regression mean square, SSreg divided by its df, with the residual mean square ^σ2. This ratio is called F, and the formulation is [17, 18]

$F = \frac{\frac{(SBB - RSS)}{1}}{σ^{2}} (5.7)$ $F = \frac{\frac{(SBB - RSS)}{1}}{σ^{2}} (5.7)$

The intercept is employed as in Figure 5.4 so as to show the general form of confidence intervals pertaining to the normally distributed estimates. When you perform a hypothesis test in statistics, a p-value helps to determine the significance of your results. Hypothesis tests are used to test the validity of a claim put forth regarding a population. This claim that’s on trial is named as the null hypothesis. p-Value is the conditional probability of observing a value of the computed statistic with appropriate assumptions. The p-value is a number between 0 and 1 which is interpreted as follows [15–17]:

Figure 5.4: A linear regression surface k = 2 predictors. From Ramachandran and Chris [2].

–A small p-value (typically ≤ 0.05) indicates strong evidence against the null hypothesis, hence one rejects the null hypothesis.

–A large p-value (> 0.05) indicates weak evidence against the null hypothesis, hence one fails to reject the null hypothesis.

–p-Values very close to the cutoff (0.05) are considered to be marginal (that means it may go either way). It is important to report the p-value so that your readers will be able to make inferences of their own.

The value of F is large or larger, extreme or more extreme, than the observed value. We can use the estimated mean function for obtaining the values of response for given values concerning the predictor. This problem has two vital variants regarding estimation and prediction of fitted values. We aim at prediction, which is a more important component, so let us move on with prediction [17, 18]:

With response y and terms x1, ᐧᐧᐧ , xk regarding the general multilinear regression model, the following form is at stake [17–20]:

E (Y) shows that all the terms are being conditioned on the right-hand side of the equation. Likewise, when one is conditioning on specific values for the predictors x1, ᐧᐧᐧ , xk, he/ she will jointly call x as follows [17–20]:

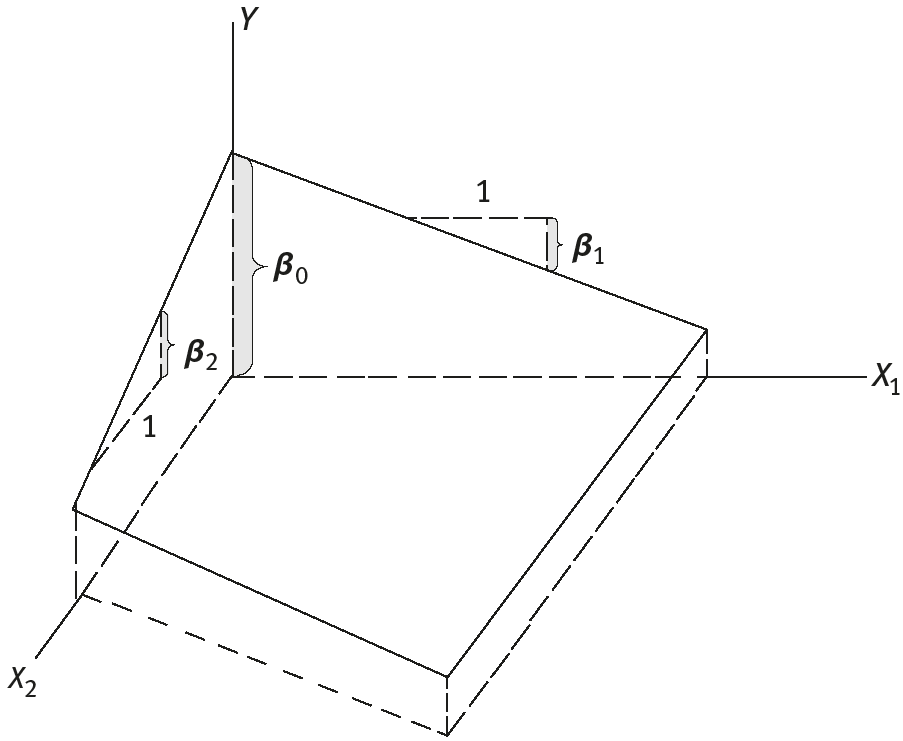
$E (Y) = w_{0} + w_{1} x_{1} + \dots + w_{1} x_{k} (5.8)$ $E (Y) = w_{0} + w_{1} x_{1} + \dots + w_{1} x_{k} (5.8)$

where w represents unknown parameters that require to be estimated. Equation (5.4) is a linear function of the parameters; hence, it is called linear regression. If k = 1, then Y has only one element; if k = 2, then the mean function of eq. (5.4) corresponds to a plane in three dimensions, which are presented in Figure 5.4. If k > t, the fitted mean function is a hyperplane. In generalization of a k-dimensional plane in a (k + 1)-dimensional space, it is not possible that we can draw a general k-dimensional plane in a three-dimensional world [17–20].

We have observed data for n cases or units, which means that at present there is a value of Y and all the terms for each of the n cases. We also have symbols for the response and terms that use matrices and vectors [17–21]:

Equation (5.11) is defined, hence Y is an n × 1 vector and X is an n × (k + 1) matrix. w is also defined to be a (k + 1) × 1 vector of regression coefficients and e as the n × 1 vector of statistical errors [17–20]:

$w = (\begin{matrix} w_{1} \\ w_{2} \\ ⋮ \\ w_{n} \end{matrix}) and e = (\begin{matrix} e_{1} \\ e_{2} \\ ⋮ \\ e_{n} \end{matrix}) (5.11)$ $w = (\begin{matrix} w_{1} \\ w_{2} \\ ⋮ \\ w_{n} \end{matrix}) and e = (\begin{matrix} e_{1} \\ e_{2} \\ ⋮ \\ e_{n} \end{matrix}) (5.11)$

The matrix X yields all the observed values of the terms. The ith row of X is elaborated by the symbol ${x^{'}}_{i}$ ${x^{'}}_{i}$ that is a (k + 1) × 1 vector for mean functions including an intercept. Although xi is row of X, the principle that all vectors are column vectors is used. For this reason, it is required to write ${x^{'}}_{i}$ ${x^{'}}_{i}$ to signify a row. The equation for the mean function evaluated at xi is given as follows [13–21]:

$E (x_{i}) = {x^{'}}_{i} w = w_{0} + w_{1} x_{i 1} + \dots + w_{k} x_{i k} X_{k} (5.12)$ $E (x_{i}) = {x^{'}}_{i} w = w_{0} + w_{1} x_{i 1} + \dots + w_{k} x_{i k} X_{k} (5.12)$

The multilinear regression model is written as

$Y = X w + e (5.13)$ $Y = X w + e (5.13)$

for the matrix notation.

The steps of linear model based on the linear model flowchart (Figure 5.5) are given below:

For the algorithm, let us have a closer look at the steps (Figure 5.6).

The steps for the linear model algorithm (see Figure 5.6) in the relevant order are given below:

Steps (1–3) Simple regression model is handled with x independent variable that has direct correlation with y dependent variable.

Step (4) x independent variable is accepted as a variable that is controllable and measurable through a tolerable error.

Steps (5–7) In the linear model, y dependent variable is dependent on the x independent variable (see eq. (5.1)). If x=0, y =w0. If x ≠ 0, we move on to Steps (8–10) stage for the estimation of w0 and w1 parameters (see eq. (5.1)).

Steps (8–10) Least squares method is used for the estimation of w0 and w1 parameters. Error value (ei) is calculated based on eq. (5.3). Afterwards, E (Y) equation is obtained using eqs. (5.4) and (5.5).

If the solution of our problem is dependent on more than one independent variable, how can we do the linear model analysis?

The answer to the question can be found by applying the multilinear model flowchart in Figure 5.6 and the multilinear model algorithm in Figure 5.7.

The flowchart of multilinear model is shown in Figure 5.7.

Figure 5.7: Multilinear model flowchart.

Based on Figure 5.7, the steps regarding multilinear model are given below.

The steps of multilinear model algorithm (see Figure 5.9) are as follows:

Steps (1–3) Multiregression model that has direct correlation with y dependent variable and that with more than one independent variable X = x1 + x2 + ᐧᐧᐧ + xk is handled.

Step (4) x independent variable with k number can be denoted as multilinear model based on eq. (5.8). w0,w1, ᐧᐧᐧ , wk parameters are accepted as the multiregression coefficients and the model to be formed will denote a hyperplane in k-dimensional space. wk parameter shows the expected change in y dependent variable that corresponds to a unit change in xk independent variable.

Steps (5–10) For each of the unknown multiregression coefficients (w0,w1, ᐧᐧᐧ , wk) the solution of the equation will yield the estimation of the least squares method. Error value (ei) is calculated based on eq. (5.3). Afterwards, E (Y) equation is obtained. (Note: As it is more appropriate to denote multiple regression models in matrix format, eq. (5.10) can be used.)

The flowchart of the linear model and the structure of its algorithm have been provided in Figures 5.7 and 5.8, respectively. Now, let us reinforce our knowledge on linear model through the applications we shall develop.

Figure 5.8: General multilinear modeling.

5.1Linear model analysis for various data

The interrelationship between the attributes in our linear model dataset can be modeled in a linear manner. Linear model analysis has been applied in economy (USA, New Zealand, Sweden [U.N.I.S.]) dataset, Multiple Sclerosis (MS) dataset and Wechsler Adult Intelligence Scale Revised (WAIS-R) dataset in Sections 5.1.1, 5.1.2 and 5.1.3, respectively.

5.1.1Application of economy dataset based on linear model

The attributes of data are years, time to import, time to export and so on. Values for the period 1960–2015 are known. Let’s assume that we would like to develop a linear model with the data available for these four different countries. Before developing the linear model algorithmically for the economy dataset, it could be of use if we can go over Example 5.1 for the reinforcing of linear model.

Example 5.1 Let us consider the following case study: A relationship between the loan demand (in dollars) from the customer of New Zealand Bank in the second quarter of 2003 and the duration (hour) required for the preparation of loans as demanded by customers has been modeled to fit a straight line.

When eq. (5.1) is used:

y = 9.5 + 2.1 x + e

$y = 9.5 + 2.1 x + e$

The loan demand from the customer in the second quarter of 2003 is 20 < x < 80. An anticipated time period (proposed by the New Zealand economy) for the preparation of loan for the customer whose demand for loan is 45 is estimated to be 108 h. Let’s attempt to set if the loan can be offered to the customer within the anticipated time interval or not by means of linear model.

Solution 5.1

Based on eq. (5.1),

\begin{array}{l} y = w_{0} + w_{1} x \\ = 9.5 + 2.1 x \\ = 9.5 + 2.1 (45) \\ = 104 \end{array}

$\begin{array}{l} y = w_{0} + w_{1} x \\ = 9.5 + 2.1 x \\ = 9.5 + 2.1 (45) \\ = 104 \end{array}$

Based on the linear model formed to fit a straight line, the residual error value of y is ŷ = 108 while the actual value was found to be y = 104. As you can see, a difference of 108 – 104 = 4 h has been obtained between the expected value and the actual value. It can be said that the New Zealand Bank can offer the loan to the customer 4 h earlier than the time anticipated.

In order to set a linear model for the economy (U.N.I.S.) dataset, you can have a look at the steps presented in Figure 5.9.

Example 5.2 The application steps of linear modeling are as follows:

Steps (1–3) Simple regression model is handled with x = 9.5 independent variable that has direct correlation with y dependent variable.

Step (4) x independent variable is accepted as the variable that is controllable and measurable through a tolerable error. Based on Example 5.4, y = 9.5 + 2.1x model is set up.

Figure 5.9: Linear modeling for the analysis of the economy (U.N.I.S.) dataset.

Steps (5–7) In the linear model, y dependent variable is dependent on the x independent variable (see eq. 5.1). If x =0, y =w0. If x ≠ 0, we move on to Steps (8–10) stage for the estimation of w0 and w1 parameters (see eq. (5.1)).

Steps (8–10) Least squares method is used for the estimation of w0 and w1 parameters (using eqs. (5.4) and (5.5)). Error value (e) is calculated based on eq. (5.3). Afterward, E (Y) equation is obtained.

Figure 5.10 shows the results of the annual gross domestic product (GDP) per capita (x-coordinate) for the years between 1960 and 2015 (y-coordinate) for the Italy economy dataset, and the linear model is established so that the data are modeled to fit a straight line model.

The relationship between GDP per capita and years (1960–2015) in Figure 5.10(b) is based on the data in the linear diagonal (see Figure 5.10(a)). The statistical results for the standard error (SE) calculated and estimated values are provided below along with their interpretations.

The SE of the coefficients is 93.026.
w1 is regression coefficient obtained as 1,667.3. The linear relation is E (Y) = 1, 667.3x.
t-Statistic for each coefficient for the testing of null hypothesis that the corresponding coefficient is zero against the alternative that it is different from zero, given the other predictors in the model: t-stat = estimate/SE. The t-statistic for the intercept is 1,667.3/93.026 = 17.923. The column that is indicated as the t-stat value is the ratio of the estimate to its SE. The column labeled “t-stat” is the ratio of the estimate to its large-sample SE, which is possible to be used for a test of the null hypothesis that a particular parameter is equal to zero against either a general or one-sided alternative. The column indicated as the “p-value(>|t-stat|)” is the level of significance regarding this test, using a normal reference distribution instead of a t-stat.
The p-value for GDP per capita (2.5368e-25 < 0.05) is smaller than the common level of 0.05. This shows that it is statistically significant.

Figure 5.10: Italy’s GDP per capita and years based on data of linear model. (a) Data of linear model between GDP per capita (x) and years (y) for Italy. (b) Estimated coefficients between GDP per capita and years (1960–2015) for Italy based on linear regression results.

5.1.2Linear model for the analysis of MS

At this point, let us carry out an application over an example based on linear model that analyzes the interrelationship between the attributes in our MS dataset.

As presented in Table 2.12, MS dataset has data from the following groups: 76 samples belonging to relapsing remitting MS (RRMS), 76 samples to secondary progressive MS (SPMS), 76 samples to primary progressive MS (PPMS) and 76 samples to healthy subjects of control group. The attributes of the control group are data regarding brain stem (MRI [magnetic resonance imaging] 1), corpus callosum periventricular (MRI 2), upper cervical (MRI 3) lesion diameter size (mm) in the MRI and EDSS score. Data are made up of a total of 112 attributes. By using these attributes of 304 individuals, we can know that whether the data belong to the MS subgroup or healthy group. How can we make the classification as to which MS patient belongs to which subgroup of MS including healthy individuals and those diagnosed with MS (based on the lesion diameters (MRI 1, MRI 2, MRI 3) and the number of lesion size for (MRI 1, MRI 2, MRI 3) as obtained from MRI and EDSS scores)? D matrix has a dimension of (304 × 112), which means it includes the MS dataset of 304 individuals along with their 112 attributes (see Table 2.12 for the MS dataset). For the classification of D matrix through linear model algorithm, the first step training procedure is to be employed. For the training procedure, 66.66% of the D matrix can be split for the training dataset (203 × 112) and 33.33% as the test dataset (101 × 112). For MS dataset, we would like to develop a linear model for MS patients and healthy individuals whose data are available.

Before developing the linear model algorithmically for the MS dataset, it will be for the benefit of the reader to study Example 5.2 for the reinforcing of linear model.

Example 5.3 Based on the research carried out in neurology clinic for an SPMS patient, the linear model set for the lesion diameter (x) in the MRI and EDSS score (y) is given below:

When eq. (5.1) is applied

y = 1 + 1.5 x

$y = 1 + 1.5 x$

Based on this model, for w0 a 0.5 mmincrease in the lesion diameter will lead to 1 unit increase in the EDSS score. This could be assumed based on the given parameters. Thus, it can also be assumed that the EDSS score value for an individual who is for the first time diagnosed with SPMS will be 1. At this point, let’s address a hypothetical question to the reader. Can we predict, based on this model, what the EDSS score will be for an individual whose lesion diameter is 6 in line with the linear regression model?

Solution 5.3

\begin{array}{l} x = 6 \\ y = 0.5 + 1 (6) = 6.5 \end{array}

$\begin{array}{l} x = 6 \\ y = 0.5 + 1 (6) = 6.5 \end{array}$

Based on the linear model set, it can be estimated that an SPMS patient with lesion diameter as 6 will have an EDSS of 6.5 (see Table 2.10 for details).

In order to set a linear model for the MS dataset, you can have a look at the steps presented in Figure 5.10.

Example 5.4 The application of the linear model algorithm (Figure 5.11) is given below:

Steps (1–3) Simple regression model is handled with x = 6 independent variable that has direct correlation with y dependent variable.

Step (4) x independent variable is accepted as one that is controllable and measurable through a tolerable error.

Steps (5–7) In the linear model, y dependent variable is dependent on the x independent variable (see eq. (5.1)). If x=0, y =w0. If x ≠ 0, then we move on to Steps (8–10) stage for the estimation of w0 and w1 parameters (see eq. (5.1)).

Steps (8–10) Least squares method is used for the estimation of w0 and w1 parameters (using eqs. (5.4) and (5.5)) and error value (e) is calculated based on eq. (5.3). Afterwards, E (Y) equation is obtained.

Figure 5.11: Linear modeling for the analysis of MS dataset.

Figure 5.12(a) presents the results obtained in line with linear model set for EDSS (x-coordinate) and SPMS, PPMS, RRMS, healthy classes (y-coordinate). From the EDSS and classes (MS subgroups data: SPMS [labeled in y-axis by 1], PPMS [labeled in y-axis by 2], RRMS [labeled in y-axis by 3] and healthy [labeled in y axis by 4]), find the linear regression relation E(Y)=w1x between the EDSS and classes of a least squares regression.

Figure 5.12(a) shows the linear model between EDSS attribute (x) and classes (MS subgroups and healthy) (y).

The relationship between EDSS and classes (MS subgroups, healthy) in Figure 5.12(b) is based on the data in the linear diagonal (see Figure 5.12(a)). The statistical results for the SE calculated and estimated values are provided with their interpretations.

SE of the coefficients is 0.33102.
w1 is the regression coefficient obtained as 5.8127. The linear relation is E(Y) = 5.8127x.
t-Statistic for each coefficient to test the null hypothesis that the corresponding coefficient is zero against the alternative that it is different from zero, given the other predictors in the model. Note that t-stat = estimate/ SE. The t-statistic for the intercept is 5.8127/0.33102 = 17.56. The column indicating the t-stat value is the ratio of the estimate to its SE. The column labeled “t-stat” is the ratio of the estimate to its large-sample SE and can be used for the null hypothesis test that a particular parameter is equal to zero against either a general or one-sided alternative. The column indicating the “p-value(>|t-stat|)” is the level of significance with regard to this test, using a normal reference distribution instead of a t-stat.
The coefficient value obtained from t-statistic is used with predictors different from zero (zero against) in order to test the null hypothesis. Note: t-stat = estimate/SE is calculated. For the intercept, t-stat value has been calculated as 5.8127/0.33102 = 17.56. t-Stat row represents the SE and is used for the test of the null hypothesis (general or one dimensional). “p-Value” uses a normal reference distribution vis-à-vis sStat, defining the significance level of the null hypothesis.
The p-value for EDSS (4.6492e-48 < 0.05) is smaller than the common level of 0.05. This shows that it is statistically significant.

Figure 5.12: Linear model for the EDSS–MS subgroups and healthy group: (a) Linear model for the EDSS attribute (x) and classes (MS subgroups and healthy) (y) and (b) estimated coefficients of EDSS attribute and classes (MS subgroups and healthy group) based on linear regression results.

5.1.3Linear model for the analysis of mental functions

Let us see an application over an example based on linear model that analyzes the interrelationship between the attributes in our WAIS-R dataset.

WAIS-R dataset in Table 2.19 includes data of 200 samples belonging to healthy group and 200 samples in control group. The attributes of data that belong to control group are school education, gender, ..., DM information. Using these attributes of 400 individuals, it is known which individuals are healthy or patient. For WAIS-R dataset we would like to develop a linear model for control group subjects and healthy individuals whose data are available.

Before developing the linear model algorithmically for the WAIS-R dataset, it will be for the benefit of the reader to study Example 5.5 for the reinforcing of linear model.

Example 5.5 Based on the research carried out in psychology clinic on male patients, the linear regression model set stemming from the correlation between the variables of age (x) and assembly ability (y) is described later:

When eq. (5.1) is used

y = 3.42 + 0.326 x

$y = 3.42 + 0.326 x$

Based on this model, a 1 unit increase in the age variable will lead to a 0.326 unit increase in the assembly ability value. Thus, it can be said that a newborn baby boy will have (x = 0) and assembly ability (x = 0) as 3.42. At this point, let’s pose a related question: can we predict, based on this model, what the assembly ability value will be for an individual who is 50 years in line with the linear model?

Solution 5.5

For x = 50,

y = 3.42 + 0.326 \times (50) = 19.52

$y = 3.42 + 0.326 \times (50) = 19.52$

Based on the linear model set, it can be estimated that a man aged 50 will have the assembly ability value as 19.52.

In order to set a linear model for the WAIS-R dataset, please have a look at the steps presented in Figure 5.13.

Figure 5.13: Linear modeling for the analysis of WAIS-R dataset.

Example 5.6 The application steps of linear modeling are as follows:

Steps (1–3) Simple regression model includes x = 50 independent variables that have direct correlation with the dependent variable.

Step (4) x independent variable is accepted as the variable that is controllable and measurable through tolerable error. Based on Example 5.5, y = 3.42 + 0.326x model is set up.

Figure 5.14: Linear model set for QIV–classes (patient and healthy). (a) Linear model between QIV (x) and classes (patient or healthy) (y) fitting. (b) Estimated coefficients between QIV and classes (patient and healthy) group based on linear regression results.

Steps (5–7) In the linear model, y dependent variable is dependent on the x independent variable (see eq. (4.1)). If x=0, y =w0. If x ≠ 0, we move on to Steps (8–10) stage for the estimation of w0 and w1 parameters (see eq. (5.1)).

Steps (8–10) Least squares method is used for the estimation of w0 and w1 parameters (using eqs. (5.4) and (5.5)). Error value e is calculated based on eq. (5.3).

Afterwards, E (Y) equation is obtained.

In Figure 5.15, according to the linear model set for the WAIS-R dataset (x-coordinate: verbal IQ [QIV]; y-coordinate: patient or healthy class), the results obtained are presented in Figure 5.14.

Figure 5.14(a) shows the linear model between QIV and classes (patient–healthy). The relationship between QIV and classes (patient–healthy) in Figure 5.14(b) is based on the data in the linear diagonal (see Figure 5.14(a)). The statistical results for the SE calculated and estimated values are provided below along with their interpretations.

The SE of the coefficients is 0.094401.
w1 is the regression coefficient obtained as 1.2657. The linear relation is E(Y) = 1.2657x.
t-Statistic for each coefficient to test the null hypothesis that the corresponding coefficient is zero against the alternative that it is different from zero, given the other predictors in the model. Note that t-stat = estimate/SE. The t-statistic for the intercept is 1.2657/0.094401 = 1.3407. The *pillar marked t-stat value is the ratio of the estimate to its SE. The column labeled “t-stat” is the ratio of the estimate to its large-sample SE and can be used for a test of the null hypothesis that a particular parameter is equal to zero against either a general or one-sided alternative. The column marked “p-value(>|t-stat|)” is the significance level for this test, using a normal reference distribution rather than a t-stat.
The p-value for EDSS (1.2261e-31 < 0.05) is smaller than the common level of 0.05. This shows that it is statistically significant.

5.2Multilinear model algorithms for the analysis of various data

Multilinear model is capable of modeling the relationship between the attributes in our dataset with multivariate data. Multilinear model is applied in Sections 5.2.1, 5.2.2 and 5.2.3 – economy (U.N.I.S.) dataset, MS dataset and WAIS-R dataset, respectively.

5.2.1Multilinear model for the analysis of economy (U.N.I.S.) dataset

Let us see an application over an example based on linear model that analyzes the interrelationship between the attributes in our economy dataset (including economies of U.N.I.S.). Data for these countries’ economies from 1960 to 2015 are defined based on the attributes presented in Table 2.8. Data belonging to U.N.I.S. economies from 1960 to 2015 are defined based on the attributes given in Table 2.8 economy dataset (http:// data.worldEconomy.org), which is used in the following sections. The attributes of data are years, time to import (days), time to export (days) and others. Values for the period 1960–2015, the values over the years, are known. Let’s assume that we would like to develop a linear model with the data available for four different countries.

Before developing the multivariate linear model algorithmically for the economy dataset, it will be useful if we can go over the steps provided in Figure 5.15.

For this, let us have a look at the steps provided in Figure 5.15 in order to establish the data to fit a straight line for a multivariate linear model:

Based on Figure 5.15, the steps of the multilinear model algorithm applied to economy (U.N.I.S.) dataset are as follows:

Steps (1–3) Multilinear regression model will be formed with direct correlation to the dependent variable (GDP per capita) in the dataset with Italy economy (between 1960 and 2013) including independent variables such as years and time to import (days).

Step (4) We denote the x1, x2, x3 independent variables as multilinear regression model. The interrelation of the regression coefficients w0,w1,w2,w3 on three-dimensional plane will be calculated in Steps (5–10).

Steps (5–10) For each of the unknown regression coefficients (w0,w1,w2,w3), least squares model is applied and the following results have been obtained, respectively, 2.4265, 0.0005, 0.0022, 0. In Italy for the three variables in the economy dataset (GDP per capita, years [1960–2015] and time to import [days]) multilinear model plot (see Figure 5.16), the multilinear regression coefficients are presented as w0 = 2.4265, w1 = 0.0005,w2 = 0.0022, w3 = 0. The error value (ei) of the y equation calculated is computed based on eq. (5.3).

Figure 5.15: Multilinear modeling for the analysis of economy (U.N.I.S.) dataset.

For the Italy economy dataset, the multiple regression analysis established for the data to be modeled to fit a straight line between GDP per capita, years and time to import (days) figure is provided in Figure 5.16.

Based on Figure 5.17, a relation has been established for the data to be modeled to fit a straight line between GDP per capita, years and time to import (days) as stated in the equations in the multilinear regression model.

When eq. (5.8) is used:

\begin{array}{l} y = 2.4265 - 0.0005 x_{1} + 0.0022 x_{2} - (0) x_{3} \\ y = 2.4265 - 0.0005 x_{1} + 0.0022 x_{2} \end{array}

$\begin{array}{l} y = 2.4265 - 0.0005 x_{1} + 0.0022 x_{2} - (0) x_{3} \\ y = 2.4265 - 0.0005 x_{1} + 0.0022 x_{2} \end{array}$

All these show that each year evens on the average 0.0005 and for Italy economy it is 0.0022 to the time to import (days). w0 coefficient (>0), GDP per capita coefficient (= −0.0005) and years coefficient affects (=0.0022) are significant attributes.

5.2.2Multilinear model for the analysis of MS

Let us do an application over an example based on linear model that analyzes the interrelationship between the attributes in our MS dataset.

As presented in Table 2.12, MS dataset has data from the following groups: 76 samples belonging to RRMS, 76 samples to SPMS, 76 samples to PPMS and 76 samples to healthy subjects of control group. The attributes of the control group are data regarding brain stem (MRI 1), corpus callosum periventricular (MRI 2), upper cervical (MRI 3) lesion diameter size (mm) in the MRI and EDSS score. Data are made up of a total of 112 attributes. By using these attributes of 304 individuals, we can know that whether the data belong to the MS subgroup or healthy group. How can we make the classification as to which MS patient belongs to which subgroup of MS including healthy individuals and those diagnosed with MS (based on the lesion diameters (MRI 1, MRI 2, MRI 3) and the number of lesion size for (MRI 1, MRI 2, MRI 3) as obtained from MRI and EDSS scores)? D matrix has a dimension of (304 × 112), which means D matrix includes the MS dataset of 304 individuals along with their 112 attributes (see Table 2.12 for the MS dataset). For the classification of D matrix through naive Bayesian algorithm, the first step training procedure is to be employed. For the training procedure, 66.66% of the D matrix can be split for the training dataset (203 × 112) and 33.33% as the test dataset (101 × 112). For this, let us have a look at the steps provided in Figure 5.17 to establish the data to fit a straight line regarding a multivariate linear model:

Figure 5.16: (a) Multilinear model mesh plot for GDP per capita, years and time to import attributes for Italy. (b) Multilinear model plot for GDP per capita, years and time to import attributes for Italy.

Figure 5.17: Multilinear modeling for the analysis of MS dataset.

For the MS dataset, the multiple regression analysis established for the data to be modeled to fit a straight line between the MRI data MRI 1, MRI 2 and the individuals’ EDSS three-dimensional space figure is provided in Figure 5.18.

Based on Figure 5.18, the linear model steps applied to MS dataset (see Table 2.12) linear model are given below.

Steps (1–3) Multilinear regression model will be formed with MRI that has direct correlation with dependent variable (EDSS score) with data belonging to 304 individuals, including these independent variables: lesion count (in the first and second regions of the brain).

Step (4) We denote the x1, x2, x3 independent variables as the multilinear regression model. The interrelation of the regression coefficients w0,w1,w2,w3 on three-dimensional plane will be calculated in Steps (5–10).

Steps (5–10) For each of the unknown regression coefficients (w0,w1,w2,w3), least squares model is applied and the following results have been obtained, respectively: 0.0483, 0.1539, 0.1646, 0.0495. For the three variables in the MS dataset (EDSS, MRI 1, MRI 2 attributes) multilinear model plot (see Figure 5.18), the interrelations of the multilinear regression coefficients are presented as w0 = 0.0483,w1 = 0.1539,w2 = 0.1646,w3 = 0.0495. The error value ei of the y equation calculated is computed based on eq. (5.3).

In the multilinear regression model established for the data modeled to fit a straight line as in Figure 5.18, the following equations show the relation between the EDSS score of the individuals, the lesion count of the first region and the lesion count of the second region.

If we use eq. (5.8),

Figure 5.18: (a) Multilinear model mesh plot for EDSS, MRI 1, MRI 2 attributes. (b) Multilinear model plot for EDSS, MRI 1, MRI 2 attributes.

y = 0.0483 + 0.1539 x_{1} + 0.1646 x_{2} + 0.0495 x_{3}

$y = 0.0483 + 0.1539 x_{1} + 0.1646 x_{2} + 0.0495 x_{3}$

All these show that each EDSS score adds on the average 0.1539 and each lesion count of the second region corresponds to 0.1646 as the lesion count of the first region. Based on w0 coefficient (>0), MRI 1 coefficient (=0.1646) and MRI 2 coefficient (=0.0495), the coefficients obtained for the EDSS score affects (=0.1539) reveal that they are significant attributes.

5.2.3Multilinear model for the analysis of mental functions

Let us do an application over an example based on linear model that analyzes the interrelationship between the attributes in our WAIS-R dataset.

WAIS-R dataset as provided in Table 2.19 includes data of 200 samples belonging to healthy group and 200 samples in control group. The attributes of data that belong to control group are school education, gender, . . ., DMinformation. Using these attributes of 400 individuals, it is known which individuals are healthy or patient. For WAIS-R dataset we would like to develop a linear model for control group subjects and healthy individuals whose data are available.

Before developing the multivariate linear model algorithmically for the WAIS-R dataset, it will be for the benefit of the reader to study Figure 5.19 for the reinforcing of linear model.

Figure 5.19: Multilinear modeling for the analysis of WAIS-R dataset.

According to Figure 5.19, the steps of the multilinear model applied to WAIS-R dataset can be explained as follows:

Steps (1–3) Multilinear regression model will be formed with direct correlation to the dependent variable (gender) in the WAIS-R dataset (with a total of 400 individuals) including independent variables such as QIV and information.

Step (4) We denote x1, x2, x3 independent variables as multilinear regression model. The interrelation of the regression coefficients w0,w1,w2,w3 on three-dimensional plane will be calculated in Steps (5–10).

Steps (5–10) For each of the unknown regression coefficients (w0,w1,w2,w3), least squares model is applied and the following results have been obtained, respectively, 38.7848, 1.5510, 5.8622, 1.6936. For the three variables in the WAIS-R dataset (QIV, gender and information) multilinear model plot (see Figure 5.20), the interrelation of the multilinear regression coefficients is presented as w0 = 38.7848, w1 = 1.5510, w2 = 5.8622, w3 = 1.6936. The error value (ei) of the y equation calculated is computed based on eq. (5.3).

For the WAIS-R dataset, the multiple regression analysis established to fit a straight line between gender, information and QIV score three-dimensional space figure is provided in Figure 5.20.

Figure 5.20: (a) Multilinear model mesh plot for QIV, gender and information attributes. (b) Multilinear model plot for QIV, gender and information attributes.

A relation has been established between gender, information and QIV as stated in the following equations based on Figure 5.20.

When eq. (5.8) is used,

y = 38.7848 - 1.5510 x_{1} - 5.8622 x_{2} - 1.6936 x_{3}

$y = 38.7848 - 1.5510 x_{1} - 5.8622 x_{2} - 1.6936 x_{3}$

All these reveal that each QIV score evens on the average 1.5510 and gender 5.8622 to the information. According to w0 coefficient (>0), QIV coefficient (= −1.5510), information coefficient (= −1.6936), the coefficient obtained for gender affects (= −5.8622) so this shows that they are significant attributes.

References

[1]Dobson AJ, Barnett AG. An introduction to generalized linear models. USA: CRC Press, 2008.

[2]Ramachandran KM, Chris PT. Mathematical statistics with applications in R.USA: Academic Press, Elsevier, 2014.

[3]C, Zidek J, Lindsey J. An introduction to generalized linear models. New York, USA: CRC Press, 2010.

[4]Rencher AC, Schaalje GB. Linear models in statistics. USA: John Wiley & Sons, 2008.

[5]Neter J, Kutner MH, Nachtsheim CJ, Wasserman W. Applied linear statistical models. New York, NY, USA: The McGraw-Hill Compan Inc., 2005.

[6]John F. Regression diagnostics: An introduction . USA: Sage Publications, Vol. 79, 1991.

[7]John F. Applied regression analysis and generalized linear models. USA: Sage Publications, 2015.

[8]Allison PD, Event History and Survival Analysis: Regression for Longitudinal Event Data. USA: Sage Publications, Inc., 2014.

[9]Weisberg S. Applied linear regression. USA: John Wiley & Sons, Inc., 2005.

[10]Berry WD, Feldman S. Multiple regression in practice. USA: Sage Publications, Inc.,1985.

[11]Everitt BS, Dunn G. Applied multivariate data analysis. USA: John Wiley & Sons, Ltd., 2001.

[12]Agresti A. Foundations of linear and generalized linear models. Hoboken, NJ: John Wiley & Sons, 2015.

[13]Raudenbush SW, Bryk A S. Hierarchical linear models: Applications and data analysis methods (Vol. 1). USA: Sage Publications, Inc., 2002.

[14]Darlington RB, Hayes AF. Regression analysis and linear models: Concepts, applications, and implementation, New York: The Guilford Press, 2016.

[15]Stroup WW. Generalized linear mixed models: modern concepts, methods and applications. USA: CRC press, 2012.

[16]Searle SR., Gruber MH. Linear models. Hoboken, New Jersey, John Wiley & Sons, Inc., 2016.

[17]Faraway JJ. Extending the linear model with R: generalized linear, mixed effects and nonparametric regression models (Vol. 124). USA: CRC press, 2016.

[18]Hansen LP, Sargent TJ. Recursive models of dynamic linear economies. USA: Princeton University Press, 2013.

[19]Bingham NH, Fry JM. Regression: Linear models in statistics. London: Springer Science & Business Media, 2010.

[20]Karaca Y, Onur O, Karabudak R. Linear modeling of multiple sclerosis and its subgroubs. Turkish Journal of Neurology, 2015, 21(1), 7–12.

[21]Reddy TA, Claridge DE. Using synthetic data to evaluate multiple regression and principal component analyses for statistical modeling of daily building energy consumption. Energy and buildings, 1994, 21(1), 35-44.

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 5 Linear model and multilinear model

Create new playlist

Sign In

Sign Up