4.1.1What is the flowchart of an algorithm?

A flowchart is a pictorial or graphical representation of an algorithm by means of different shapes, arrows or symbols so that one can show a program or a process. We can understand a program with ease owing to algorithms. The main purpose of a flowchart is to analyze different processes [6]. Shapes in the flowchart change depending on the algorithm used and they may have different meanings accordingly. The shapes and meanings to be used in the algorithms to be handled in the following sections are provided in Table 4.1.

Table 4.1: Shapes and meanings used in the flowchart of algorithms.

Shape	Description
	Start, End: Start and end procedures are standard in an algorithm. Forthis reason, each flow chart starts with the shape of “start” and endswith the shape “end”. The procedures in algorithm are conductedbetween start and end.
	Data input: The shape which represents the data input encoded bythe user.
	Procedure: This is used for the denotation of the procedures tobe conducted during the execution of the procedures during theprogram. The procedures like formula and assigning the resultsof the procedures are written as they are. When the proceduralflow reaches this step, the procedures written in this box areexecuted.
	Decision: It is the shape that represents the decision and comparisonprocedures. It is also called condition or branching shape. Itcorresponds to the following in the programming language:if (condition) is true …else …
	Repetition Statement: Different procedures are repeatedin differentplaces. This repetitive procedure is called loop or iteration. The initialvalue, end value and increase value are assigned in the repetitionstatement shape. It corresponds to the following in the programminglanguage:
	for (; ;)
	for each ( )
	do-while (condition)
	while (condition)

4.1.2Fundamental concepts of programming

It is important to know what token, variable and expression concepts mean in order to better understand the algorithms to be covered in the following sections. Let us analyze these fundamental concepts [4–8]:

Token concept: The smallest unit that bears a meaning in a programming language is called token. Tokens are the plainest elements that cannot be further split into more meaningful units in the algorithm.

We can categorize atoms as follows:

{

;

,

}

Expression: The combination of variable, operator and constant is called expression.

The following examples explain who we can show the variables and procedure operator within algorithm:

Example 4.1 Let us define a, b, c variables and + procedure operator within the algorithm.

The expression is made up of a+b//a, b, c variable and + procedure operator.

Example 4.2 Let us define d variable, 2 constant and – procedure operator within algorithm.

The expression is made up of d – 2//d variable, 2 constant and – procedure operator.

Left side value: The expressions that depict object (variable) are called left side values. Since the assignment operator is on the left (=: equation), these expressions are called left side values.

Example 4.3 How can k variable value with 5 within the algorithm be defined as the left side value?

In order to define the value of k variable, a variable like c (integer, float, etc.) should be defined within the algorithm.

Right side value: Expressions that do not show object are called right side value. Since they are positioned on the right of the assigning operator (=: equation), they are named as right side values.

Example 4.4 Let us take k and l as variables (integer, double, etc.). Can we define k + l expression within the algorithm as right side value?

In other words, by adding values of k and l variables, how can we make the interpretation by writing them as the right side value (which means on the right of the equation)?

The result of the summing of k + l values within the algorithm given above is assigned to a variable like m, which means it shows that k + l expression is a right side value.

4.1.2.1Notification and identification concepts

Giving information about the attributes of the objects prior to their use is called variable definition.

In the following sections, the giving of information on attributes before using objects in algorithms has been defined outside the blocks[7].

What do we mean by the block concept? The sites in between the set brackets are called blocks.

There are two blocks in Figure 4.1; the second block is within the first block.

Example 4.5 How do we define the priority about procedures in blocks in which variables are defined in the algorithm?

There are two blocks in the following algorithm. Different procedures will be done in two different blocks. The priority for the procedure is given to the block that is defined in the innermost part of the algorithm. The procedure of the block that is in the innermost section is completed and it goes on with the outermost block from inside to the external side.

a = a * 2 procedure within the algorithm calculates before the a * b operation in the first block.

Constant concept: Data are loaded as constant directly or within the objects. Constants are the data that are not in the form of object (integer, float, etc.).

Example 4.6 How can we transfer the summation operation of values in the algorithm pertaining to a and b variables to a variable like c?

In the algorithm, the value obtained from the summation operation within a and b variables is transferred to c variable.

4.1.3Expressions and repetition statements

Expressions are a group of token that is made up of expression and terminator (as split from one another with semicolon)[7].

Example 4.7 i = a * b – d is an expression because (a * b − d) expression is not split with semicolon (;) or, in other words, with the terminator.

Example 4.8 i = a * b − d is an expression because (a * b − d) expression is split with semicolon (;) or, in other words, with the terminator.

In the following sections, expressions within the algorithms have been used for three purposes:

1. Simple expressions are formed by bringing a terminator (;) to the end of an expression within the algorithm.

For example, let us do the application of calculation for a = b + 3 operation in the algorithm.

2. Compound expressions constitute the summation of more than one expression within a block.

For example, let us do the application of calculation for a = b + k – c and b++ operation as compound expressions:

Here, operations a and b++ are done at the same time within the operational block, so a compound expression is at stake.

3. Control expressions are the ones used for controlling the program flow.

The compiler calculates the numerical value of an expression within the if parenthesis. It interprets this numerical value computed logically as follows: True (if it is a value other than zero) or False (if it is 0). If the result of the expression is True, the part up to else keyword is handled as operation. If the result of the expression is False, the part following the else keyword is taken under operation (or executed) (see Figure 4.2).

Let us now see how if expressions are applied to the algorithm through Example 4.9.

Example 4.9 Let us show if the value 5 assigned to variable x by an algorithm is an even or an odd number.

Steps (1–3) The numerical value of the expression within if parenthesis is calculated.

Is the mode of the x variable 1 according to 2 or not?

if x = 5 has a mode that is 1 according to 2, in the algorithm it is operated with

Statement 1.

Result: Correct, which means x = 5 has a mode 1 according to 2 and it is operated with Statement 1 in the algorithm.

Steps (3–4) Since the statement is True, the part up to the else keyword (Statement 1) is executed.

Steps (5–8) By skipping the else part, Statements 2 and 3 are executed.

Repetition statements enable the execution of a part of the algorithm in an iterative manner. It is an indispensable component of algorithms. Let us illustrate at this point for, while, do-while and foreach repetition statements:

1. for repetition statement: It is used to ensure a certain number of iteration in the for repetition statement.

Example 4.10 Let us apply the algorithm that makes the numbers from 1 to 100 count with for repetition statement:

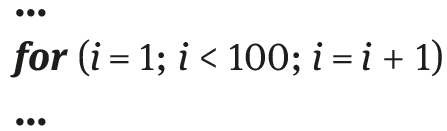
The variable i of for loop makes us count one by one starting from 1 up until 100 (1, 2, 3, 4,…, 100).

2. while repetition statement: In such repetition statements, the condition is generally given based on the variable.

Example 4.11 Let’s apply an algorithm that makes numbers from 1 to 100 count through while repetition statement.

In Example 4.11, the i variable started with 1 (i = 1).

i++ operation is increased by 1 until the i variable reaches the value 100. As a result, by an incremental increase of 1, the while loop initiated with 1 reaches 100 and along this process it enables a counting from 1 to 100 (1, 2, 3, 4, …, 100).

3. foreach repetition statement: foreach is a repetition statement that proceeds over the array elements.

The general use of this repetition statement is as follows:

Example 4.12 Let us obtain all the numbers in a number set through foreach repetition statement:

A = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};

foreach repetition statement in Example 4.12 enables the obtaining of each element separately within the number set of A array 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 from the i variable value.

4.2.1Pixel coordinates

A digital image constitutes rows and columns of pixels. A pixel in such an image can be identified by stating which column and which row include it. A pixel can be identified by a pair of integers in terms of coordinates, yielding the column number and the row number. For instance, the pixel with coordinates (4,8) lies in column number 4 and row number 8. Columns are usually numbered from left to right, and they start with zero. Including the ones to be handled in this book, most graphic systems have the number rows from top to bottom, and they start from zero [10–14].

In Figure 4.3, you can see the 5 × 9 pixel grid, as depicted with row and column numbers. Rows are numbered from top to bottom.

Consider that the pixel identified by a pair of coordinates (x, y) is dependent on the choice of a coordinate system.

Row and column numbers specify a pixel, not a point. A pixel includes many points. It mathematically contains an infinite number of points. Computer graphics is not essentially oriented to color pixels and the goal is in fact to create and manipulate images. In ideal cases, an image should be defined by identifying a color for each point, and not just for each pixel. If it is assumed that there exists a true and ideal image to be displayed, then any image we display by coloring pixels will be an approximation.

4.2.2Color models

Here what we discuss is the most basic and essential foundations regarding computer graphics: one of which is the coordinate systems and the other one is the color which is actually a complex and surprising subject matter. All of the modern monitors take digital input for the “value” of a pixel and makes conversion of this into an intensity level. When they are off, real monitors have nonzero intensity since the screen reflects some light. For the current purposes, we can regard this as “black” and monitor fully on as “white.” We assume a numeric description of pixel color varying from zero to one. Black is zero, white is 1 and gray halfway between black and white (BW) is 0.5 [11–13].

The colors on a computer screen are generated as combinations of red, green and blue light. Different colors are made by varying the intensity of each type of light. It is possible to specify a color by three numbers, with the intensity of red, green and blue in the color. Intensity can be stated as a number in the range zero, for minimum intensity, to one, for maximum intensity. We call this method of specifying the color the RGB color model where RGB means red/green/blue. For instance, the number triple (1, 0, 0) signifies the color obtained by setting red to full intensity, whereas green and blue to half the intensity in the RGB color model [13–17]. The red, green and blue values for a color are termed as color components.

Figure 4.4(a) shows the RGB quantized form and Figure 4.4(b) shows XR, XG, XB, which are the weights applied to RGB colors to be able to figure out X. Figure 4.4(c) shows XB, XW which are the weights applied to BW colors to be able to figure out X.

Actual RGB levels are often given in quantized form. Each component is indicated with an integer. One byte each is the most common size for these integers. Therefore, each of the three RGB components is an integer between 0 and 255. The three integers together take three bytes, corresponding to 24 bits. Hence, a system with “24 bit color” has 256 possible levels for each of the primary color.

4.3.1Statistical application with algorithms: BW image on coordinate systems

BW image is an image in which each pixel can either be black or white and nothing else. Grayscale image has gray values that vary from 0 to 255 where 0 = black and 255 = white, while the BW image has only 0 and 1 values where 0 = black and 1 = white.

Figure 4.6(a) and (b) shows a BW image from MRI of an RRMS patient.

Images used in Examples 4.13–4.17 belong to the RRMS patient of MS. The MRI images pertain to BW. For BW MRI images that have different colors and dimensions, mean, median, range, variance and standard deviation have been calculated.

How the original MRI of an RRMS patient can be calculated through algorithms with statistical methods in coordinates of BW is provided in the following steps:

Step 1 First of all, the pixel values that correspond to x- and y-coordinate axes in the image used are obtained.

Step 2 Statistical methods are used along with the algorithm through the pixel values obtained (Figure 4.5).

Now, let us apply the algorithm for an image data for the calculation of BW image of an RRMS patient (see Figure 4.6(b)) using statistical methods such as mean XE, median, range, variance and standard deviation in Examples 4.13–4.17.

Example 4.13 The application of BW image in Figure 4.7 for the Mean function algorithm has been elaborated step by step. The mean function algorithm has steps as elicited in Figure 4.7. In Figure 4.8, you can see how BW is applied to the MRI image of a patient suffering from RRMS.

The histogram graphs are provided, owing to the application of Steps (1–8) for the Mean() function algorithm (see Figure 4.7) for the BW image in Figure 4.8.

Figure 4.8(a) shows in BW MRI image, x-axis x = (x1, x2, ..., x200) row and y-axis y = (y1, y2, ..., y212) column as the corresponding pixel values.

In the BW MRI image of histogram (Figure 4.8(b)), x-axis represents the results as obtained by calculating the mean value in Figure 4.8(a) (for each pixel values in x- and y-axes) and y-axis represents the iteration numbers in Figure 4.8(a) (iteration i = 1, 2, …, 200) (mean values for pixel values in x- and y-axes).

In order to calculate the mean value in BW image (200 × 212 dimension), the following iteration steps are applied ((i): 1–200) along with the steps of Mean() function algorithm (Figure 4.7) (which means while passing from Figure 4.8(a) BW MRI image for pixel value to Figure 4.8(b) BW MRI image of histogram for Mean()).

For BW MRI image,

Iteration (i) = 1

Step (1) When (i = 1), with the loop to be formed for (xi, yj) = y1, ..., the (x1, y212), pixel values that correspond to x- and y-coordinate axes are obtained.

Step (2) When (i = 1), for j = 1, ..., 212, with the pixel values obtained in the first iteration, the mean values are calculated.

...

...

...

Iteration (i) = 200

Step (1) When (i = 200), for ( xi, yj )= (x200, y1, ..., y212), the pixel values that correspond to x- and y-coordinate axes are obtained.

Step (2) When (i = 200), for j = 1, ..., 212, with the pixel values obtained in the first iteration, mean value is calculated.

The mean (M) values above $\left(M_{\text{BW}{}_i}=M_{{\text{BW}}_1},M_{{\text{BW}}_2},\dots ,M_{{\text{BW}}_{200}}\right):$ for the iteration of (i = 1, 2, …, 200) and for the pixel values in all columns in the y-axis ( j=1, 2, …, 212) corresponding to x-coordinate axis (i = 1), the calculation of mean values is done until (i = 200).

In Table 4.2, the mean values in Figure 4.8 are calculated along with the application of Mean() function algorithm for (i = 1, …, 200).

Example 4.14: Application of BW image in Figure 4.9 for the Median function algorithm has been provided step by step. The steps of median function algorithm are shown in Figure 4.9. In Figure 4.10, BW is applied to the MRI image of a patient who is afflicted with RRMS.

The histogram graphs are provided owing to the application of Steps (1–8) for the Median() function algorithm (see Figure 4.9) for the BW image in Figure 4.10.

Figure 4.10(a) shows in BW MRI image, x-axisx = (x1, x2, ..., x200) row and y-axis y = (y1, y2, ..., y212) column as the corresponding pixel values.

In BW MRI image of histogram (Figure 4.10(b)), x-axis represents the results as obtained by calculating the median value in Figure 4.10(a) (for each pixel values in x- and y-axes) and y-axis represents the iteration numbers in Figure 4.10(a) (iteration i = 1, 2, …, 200) (median values for pixel values in x- and y-axes).

In order to calculate the median value in BW image (200 × 212 dimension), the following iteration steps are applied ((i): 1–200) along with the steps of Median() function algorithm (Figure 4.9) (where medians pass from Figure 4.10(a) BW MRI image for pixel value to Figure 4.10(b) BW MRI image of histogram for Median()).

For BW MRI image,

Iteration (i) = 1

Step (1) When (i = 1), with the loop to be formed for (xi, yj )= (x1, y2, ..., y212), the pixel values that correspond to x- and y-coordinate axes are obtained.

Table 4.2: The detailed illustration of black and white MRI image Mean() calculation.

Step (2) When (i = 1), for j = 1, ..., 212, with the pixel values obtained in the first iteration, the median values are calculated.

...

...

...

Iteration (i) = 200

Step (1) When (i = 200), for ( xi, yj )= (x200, y1, ..., y212), the pixel values that correspond to x- and y-coordinate axes are obtained.

Step (2): When (i = 200), for j = 1, ..., 212, with the pixel values obtained in the first iteration, median value is calculated.

The median (Mdn) values above (MdnBWi = MdnBW1 , MdnBW2 , ..., MdnBW200 ): for the iteration of (i = 1, 2, …, 200) and for the pixel values in all columns in the y-axis (j = 1, 2,…, 212) corresponding to x-coordinate axis (i = 1), the calculation of medianvalues is done until (i = 200).

In Table 4.3, the median values in Figure 4.10 are calculated along with the application of Median() function algorithm for (i = 1,…, 200).

Example 4.15: The application of BW image in Figure 4.11 for the Range function algorithm has been provided step by step. The steps of range function algorithm have been elicited in Figure 4.11. In Figure 4.12, you can see how BW is applied to the MRI image of a patient who is afflicted with RRMS.

The histogram graphs are provided owing to the application of Steps (1–8) for the Range() function algorithm (see Figure 4.11) for the BW image in Figure 4.12.

Figure 4.12(a) shows in BW MRI image, x-axis x = (x1, x2, ..., x200) row and y-axis y = (y1, y2, ..., y212) column as the corresponding pixel values.

In BW MRI image of histogram (Figure 4.12(b)), x-axis represents the results as obtained by calculating the range value in Figure 4.12(a) (for each pixel values in x- and y-axes) and y-axis represents the iteration numbers in Figure 4.12(a) (iteration i = 1, 2, …, 200) (range values for pixel values in x- and y-axes).

In order to calculate the range value in BW image (200 × 212 dimension), the following iteration steps are applied ((i): 1–200) along with the steps of Range() function algorithm (Figure 4.11) (where ranges pass from Figure 4.12(a) BW MRI image for pixel value to Figure 4.12(b) BW MRI image of histogram for Range()).

For BW MRI image,

Iteration (i) = 1

Step (1) When (i = 1), with the loop to be formed for ( xi, yj )= (x1, y1, ..., y212), the pixel values that correspond to x- and y-coordinate axes are obtained.

Table 4.3: The detailed illustration of black and white MRI image Median() calculation.

Step (2) When (i = 1), for j = 1, ..., 212, with the pixel values obtained in the first iteration, the range values are calculated.

...

...

...

Iteration (i) = 200

Step (1) When (i = 200), for ( xi, yj )= (x200, y1, ..., y212), the pixel values that correspond to x- and y-coordinate axes are obtained.

Step (2) When (i = 200), for j = 1, ..., 212, with the pixel values obtained in the first iteration, range value is calculated.

The range (R) values above $\left(R_{{\text{BW}}_i}=R_{{\text{BW}}_1},R_{{\text{BW}}_2},\dots ,R_{{\text{BW}}_{200}}\right):$ for the iteration of (i = 1, 2, …, 200), for the pixel values in all the columns in the y-axis (j = 1,2, …, 212) corresponding to x-coordinate axis (i = 1), the calculation of range values is done until (i = 200).

In Table 4.4, the range values in Figure 4.12 are calculated along with the application of Range() function algorithm for (i = 1,…, 200).

Example 4.16 The application for BW image in Figure 4.13 for the Variance function algorithm has been provided step by step. The steps of Variance function algorithm elicited in Figures 4.13 and 4.14 show how BW is applied to the MRI image of a patient who is afflicted with RRMS.

The histogram graphs are provided owing to the application of Steps (1–8) for the Variance() function algorithm (see Figure 4.13) for the BW image in Figure 4.14.

Figure 4.14(a) shows in BW MRI image, x-axis x = (x1, x2, ..., x200) row and y-axis y = (y1, y2, ..., y212) column as the corresponding pixel values.

In BW MRI image of histogram (Figure 4.14(b)), x-axis represents the results as obtained by calculating the variance value in Figure 4.14(a) (for each pixel values in x- and y-axes) and y-axis represents the iteration numbers in Figure 4.14(a) (iteration i = 1, 2, …, 200) (variance values for pixel values in x- and y-axes).

Table 4.4: The detailed illustration of black and white MRI image Range () calculation.

In order to calculate the variance value in BW image (200 × 212 dimension), the following iteration steps are applied ((i): 1–200) along with the steps of Variance() function algorithm (Figure 4.14) (where variances pass from Figure 4.14(a) BW MRI image for pixel value to Figure 4.14(b) BW MRI image of histogram for Variance()).

For BW MRI image,

Iteration (i) = 1

Step (1) When (i = 1), with the loop to be formed for ( xi, yj )= y1, ..., the pixel (x1, y212), values that correspond to x- and y-coordinate axes are obtained.

Step (2) When (i = 1), for j = 1, ..., 212, with the pixel values obtained in the first iteration, the variance values are calculated.

...

...

...

Iteration (i) = 200

Step (1) When (i = 200), for ( xi, yj ) = (x200, y1, ..., y212), the pixel values that correspond to x- and y-coordinate axes are obtained.

Step (2) When (i = 200), for j = 1, ..., 212, with the pixel values obtained in the first iteration, variance value is calculated.

The variance (σ2 ) values above $\left({\sigma }_{\text{BW}}^2={\sigma }_{{\text{BW}}_1}^2,{\sigma }_{{\text{BW}}_2}^2,\dots ,{\sigma }_{{\text{BW}}_{200}}^2\right):$ for the iteration of (i = 1, 2, …, 200) and for pixel values in all columns in the y-axis (j = 1, 2, …, 212) corresponding to x-coordinate axis (i = 1), the calculation of variance values is done until (i = 200).

In Table 4.5, the variance values in Figure 4.13 are calculated along with the application of Variance() function algorithm for (i = 1,…, 200).

Example 4.17 The application of BW image in Figure 4.15 for the standard deviation function algorithm has been provided step by step. The steps of standard deviation function algorithm as elicited in Figures 4.15 and 4.16 show how BW is applied to the MRI image of a patient who is afflicted with RRMS.

The histogram graphs are provided owing to the application of Steps (1–9) for the StandardDeviation() function algorithm (see Figure 4.15) for the BW image in Figure 4.16.

Figure 4.16(a) shows in BW MRI image, x-axis x = (x1, x2, ..., x200) row and y-axis y = (y1, y2, ..., y212) column as the corresponding pixel values.

In BW MRI image of histogram (Figure 4.16(b)), x-axis represents the results as obtained by calculating the standard deviation value in Figure 4.16(a) (for each pixel values in x- and y-axes) and y-axis represents the iteration numbers in Figure 4.16(a) (iteration i = 1, 2,,…, 200) (standard deviation values for pixel values in x- and y-axes).

In order to calculate the standard deviation value in BW image (200 × 212 dimension), the following iteration steps are applied ((i): 1–200) along with the algorithm steps of StandardDeviation() function algorithm (Figure 4.16) (where standard deviations pass from Figure 4.16(a) BW MRI image for pixel value to Figure 4.16(b) BW MRI image of histogram for StandardDeviation().

For BW MRI image,

Iteration(i) = 1

Step (1) When (i = 1), with the loop to be formed for ( xi, yj )= (x1, y1, ..., y212), the pixel values that correspond to x- and y-coordinate axes are obtained.

Step (2) When (i = 1), for j = 1, ..., 212, with the pixel values obtained in the first iteration, the standard deviation values are calculated.

...

...

...

Table 4.5: The detailed illustration of black and white MRI image Variance() calculation.

Iteration (i) = 200

Step (1) When (i = 200), for ( xi, yj )= (x200, y1, ..., y212), the pixel values that correspond to x- and y-coordinate axes are obtained.

Step (2) When (i = 200), for j = 1, ..., 212, with the pixel values obtained in the first iteration, standard deviation value is calculated.

The standard deviation (SD =σ) values above ${\text{SD}}_i={\text{SD}}_{{\text{BW}}_1},{\text{SD}}_{{\text{BW}}_2},\dots ,{\text{SD}}_{{\text{BW}}_{200}}):$ for the iteration of (i = 1, 2, …, 200) and for the pixel values in all columns in the y-axis (j = 1, 2,…, 212) corresponding to x-coordinate axis (i = 1), the calculation of standard deviation values is done until (i = 200).

In Table 4.6, the standard deviation values in Figure 4.16 are calculated along with the application of StandardDeviation() function algorithm for (i = 1,…, 200).

Table 4.6: The detailed illustration of black and white MRI image StandardDeviation() calculation.

4.3.2Statistical application with algorithms: RGB image on coordinate systems

In each pixel, the color is the function $\left(x_i,y_j\right).$ In )particular, for an RGB image in each pixel xi , yj , three values R xi , yj ,G xi , yj andB xi , yj are defined, each one ranging from 0 to 255; the resulting color in xi , yj is given by the combination as follows [15]:

$\frac{R\left(x_i,y_j\right)+G\left(x_i,y_j\right)+B\left(x_i,y_j\right)}{3}\left(4.1\right)$

How the original MRI of an RRMS patient can be calculated through algorithms with statistical methods in coordinates of RGB is provided below:

Step (1) First of all, pixel values that correspond to x- and y-coordinate axes in the image used are obtained.

Step (2) Statistical methods are used along with the algorithm through the pixel values obtained (Figure 4.5).

Now, let us apply the algorithm for an image data for calculating RGB image of an RRMS patient (see Figure 4.17(b)) using statistical methods such as mean, median, range, variance and standard deviation in Examples 4.18–4.22.

Example 4.18: The application for RGB image in Figure 4.17 for the Mean function algorithm has been provided step by step. The steps of the mean function algorithm as elicited in Figures 4.18 and 4.19 show how RGB is applied to the MRI image of a patient who is afflicted with RRMS.

The histogramgraphs are provided owing to the application of Steps 1–8 for the Mean() function algorithm (see Figure 4.18) for the RGB image in Figure 4.19.

Figure 4.19(a) shows in RGB MRI image, x-axis x = (x1, x2, ..., x196) row and y-axis y = (y1, y2, ..., y216) column as the corresponding pixel values.

In RGB MRI image of histogram (Figure 4.19(b)), x-axis represents the results as obtained by calculating the mean value in Figure 4.19(a) (for each pixel values in x- and y-axes) and y-axis represents the iteration numbers in Figure 4.19 (a) (iteration i = 1, 2, …, 196) (mean values for pixel values in x- and y-axes).

In order to calculate the mean value in RGB image (196 × 216 dimension), the following iteration steps are applied ((i): 1–196) along with the steps of Mean() function algorithm (Figure 4.18) (which means while passing from Figure 4.19(a) RGB MRI image for pixel value to Figure 4.19(b) RGB MRI image of histogram for Mean()).

For RGB MRI image,

Iteration (i) = 1

Step (1) When (i = 1), with the loop to be formed for ( xi, yj )= (x1, y1, ..., y216), the pixel values that correspond to x- and y-coordinate axes are obtained.

Step (2) When (i = 1), for j = 1, ..., 216, with the pixel values obtained in the first iteration, the mean values are calculated.

...

...

...

Iteration (i) = 196

Step (1) When (i = 196), for ( xi, yj )= (x196, y1, ..., y216), the pixel values that correspond to x- and y-coordinate axes are obtained.

Step (2) When (i = 196), for the pixel values obtained in the first iteration, mean value is calculated.

The mean (M) values above $\left(M_{{\text{RGB}}_i}=M_{{\text{RGB}}_1},M_{{\text{RGB}}_2},\dots ,M_{{\text{RGB}}_{196}}\right):\left(i=1,2,\dots ,196\right)$ for the pixel values in all columns in the y-axis (j = 1, 2,…, 216) corresponding to x-coordinate axis (i = 1), the calculation of mean values is done until (i = 196).

In Table 4.7, the mean values in Figure 4.19 are calculated along with the application of Mean() function algorithm for (i = 1,…, 196).

Example 4.19: The application of RGB image in Figure 4.20 for the Median function algorithm has been provided step by step. The steps of median function algorithm elicited in Figures 4.20 and 4.21 show how RGB is applied to the MRI image of a patient who is afflicted with RRMS.

The histogram graphs are provided owing to the application of Steps (1–8) for the Median() function algorithm (see Figure 4.20) for the RGB image in Figure 4.21.

Figure 4.21 (b) in RGB MRI image of histogram., x-axis represents the results as obtained by calculating the median value in Figure 4.21(a) (for each pixel values in x- and y-axes). y-Axis represents the iteration numbers in Figure 4.21(a) (iteration = 1,2, …, 196) (median values for pixel value in x- and y-axes).

In order to calculate the median value in RGB image (196 × 216 dimension), the following iteration steps are applied ((i): 1–196) along with the steps of Median() function algorithm (Figure 4.21) (where medians pass from Figure 4.21(a) RGB MRI image for pixel value to Figure 4.18(b) RGB MRI image of histogram for Median()).

For RGB MRI image,

Iteration (i) = 1

Step (1) When (i = 1), with the loop to be formed for ( xi, yj )= (x1, y1, ..., y216), the pixel values that correspond to x- and y-coordinate axes are obtained.

Step (2) When (i = 1), for j = 1, ..., 216, with the pixel values obtained in the first iteration, the median values are calculated.

...

...

...

Table 4.7: The detailed illustration of red/green/blue MRI image Mean() calculation.

Iteration (i) = 196

Step (1) When (i = 196), for ( xi, yj )= (x196, y1, ..., y216), the pixel values that correspond to x- and y-coordinate axes are obtained.

Step (2) When (i = 196), for with the pixel values obtained in the first iteration, median value is calculated.

The median (Mdn) values above $\left({\text{Mdn}}_{{\text{RGB}}_i}={\text{Mdn}}_{{\text{RGB}}_1},{\text{Mdn}}_{{\text{RGB}}_2},\dots ,{\text{Mdn}}_{{\text{RGB}}_{196}}\right):$ for the pixel values in all columns in the y-axis (j = 1, 2,…, 216) corresponding to x-coordinate axis (i = 1), the calculation of mean values is done until (i = 196).

In Table 4.8, the mean values in Figure 4.20 are calculated along with the application of Median() function algorithm for (i = 1,…, 196).

Example 4.20 The application of RGB image in Figure 4.22 for the range function algorithm has been provided step by step. The range function algorithm is shown in Figure 4.22. Figure 4.23 shows how RGB is applied to the MRI image of a patient who is afflicted with RRMS.

Table 4.8: The detailed illustration of red/green/blue MRI image Median() calculation.

The histogram graphs are provided owing to the application of Steps (1–8) for the Range() function algorithm (see Figure 4.22) for the RGB image in Figure 4.23.

Figure 4.23(a) shows in RGB MRI image, x-axis x = (x1, x2, ..., x196) row and y-axis y = (y1, y2, ..., y216) column as the corresponding pixel values.

In RGB MRI image of histogram (Figure 4.23(b)), x-axis represents the results as obtained by calculating the range value in Figure 4.24(a) (for each pixel values in x- and y-axes) and y-axis represents the iteration numbers in Figure 4.23(a) (i = 1,2,…, 196) (range values for pixel values in x- and y-axes).

In order to calculate the range value in RGB image (196 × 216 dimension), the following iteration steps are applied ((i): 1–196) along with the steps of Range() function algorithm (Figure 4.22) (where ranges pass from Figure 4.22(a) RGB MRI image for pixel value to Figure 4.23(b) RGB MRI image of histogram for Range()).

For RGB MRI image,

Iteration (i) = 1

Step (1) When (i = 1), with the loop to be formed for ( xi, yj )= (x1, y1, ..., y216) the pixel values that correspond to x- and y-coordinate axes are obtained.

Step (2) When (i = 1), for j = 1, ..., 216, with the pixel values obtained in the first iteration, the range values are calculated.

...

...

...

Iteration (i) = 196

Step (1) When (i = 196), for ( xi, yj )= (x196, y1, ..., y216) the pixel values that correspond to x- and y-coordinate axes are obtained.

Step (2) When (i = 196), for the pixel values obtained in the first iteration, range value is calculated.

The range values above $\left({\text{R}}_{{\text{RGB}}_i}=R_{{\text{RGB}}_1},R_{{\text{RGB}}_2},\dots ,R_{{\text{RGB}}_{196}}\right):$ for the pixel values in all columns in the y-axis (j = 1, 2, …, 216) corresponding to x-coordinate axis (i = 1), the calculation of range values is done until (i = 196).

In Table 4.9, the range values in Figure 4.23 are calculated along with the application of Range() function algorithm for (i = 1,…, 196).

Example 4.21 The application for RGB image in Figure 4.24 for the Variance function algorithm has been provided step by step. The steps of Variance function algorithm elicited in Figure 4.25 show how RGB is applied to the MRI image of a patient who is afflicted with RRMS.

The histogram graphs are provided owing to the application of Steps (1–8) for the Variance() function algorithm (see Figure 4.24) of the RGB image in Figure 4.25.

Figure 4.25(a) shows in RGB MRI image, x-axis x = (x1, x2, ..., x196) row and y-axis y = (y1, y2, ..., y216) column as the corresponding pixel values.

In RGB MRI image of histogram (Figure 4.25(b)), x-axis represents the results as obtained by calculating the variance value in Figure 4.26(a) (for each pixel values in x- and y-axes) and y-axis represents the iteration numbers in Figure 4.26(a) (iteration i = 1,2,…, 196) (variance values for pixel value in x- and y-axes).

Table 4.9: The detailed illustration of red/green/blue MRI image Range() calculation.

In order to calculate the variance value in RGB image (196 × 216 dimension), the following iteration steps are applied ((i): 1–196) along with the steps of Variance() function algorithm (Figure 4.25) (where variances pass from Figure 4.25 (a) RGB MRI image for pixel value to Figure 4.25(b) RGB MRI image of histogram for Variance()).

For RGB MRI image,

Iteration (i) = 1

Step (1) When (i = 1), with the loop to be formed for ( xi, yj )= (x1, y1, ..., y216), the pixel values that correspond to x- and y-coordinate axes are obtained.

Step (2) When (i = 1), for j = 1, ..., 216, with the pixel values obtained in the first iteration, the variance values are calculated.

...

...

...

Iteration (i) = 196

Step (1) When (i = 196), for ( xi, yj )= (x196, y1, ..., y216), the pixel values that correspond to x- and y-coordinate axes are obtained.

Step (2) When (i = 196), for the pixel values obtained in the first iteration, variance value is calculated.

The variance values above $\left({\sigma }_{{\text{RGB}}_i}^2={\sigma }_{{\text{RGB}}_1}^2,{\sigma }_{{\text{RGB}}_2}^2,\dots ,{\sigma }_{{\text{RGB}}_{196}}^2\right):$ for the pixel values in all the columns in the y-axis j = 1, 2, …, 216) corresponding to x-coordinate axis (i = 1), the calculation of variance values is done until (i = 196).

In Table 4.10, the variance values in Figure 4.25 are calculated along with the application of Variance() function algorithm for (i = 1,…, 196).

Example 4.22 The application of RGB image in Figure 4.27 for the standard deviation function algorithm has been provided step by step. The steps of standard deviation function algorithm elicited in Figure 4.28 show how BW is applied to the MRI image of a patient who is afflicted with RRMS.

The histogram graphs are provided owing to the application of Steps (1–9) for the StandardDeviation() function algorithm (see Figure 4.26) for the RGB image in Figure 4.27.

In RGB MRI image of histogram (Figure 4.27(b)), x-axis represents the results as obtained by calculating the standard deviation value in Figure 4.27(a) (for each pixel values in x- and y-axes). y-Axis represents the iteration numbers in Figure 4.27(a) (iteration i = 1, 2, …, 196) (standard deviation values for pixel values in x- and y-axes).

In order to calculate the standard deviation value in RGB image (196 × 216 dimension), the following iteration steps are applied ((i): 1–196) along with the algorithm steps of StandardDeviation() function algorithm (Figure 4.26) (where standard deviations pass from Figure 4.27(a) RGB MRI image for pixel value to Figure 4.27 (b) RGB MRI image of histogram for StandardDeviation()).

For RGB MRI image,

Iteration (i) = 1

Step (1) When (i = 1), with the loop to be formed for ( xi, yj )= (x1, y1, ..., y216) the pixel values that correspond to x- and y-coordinate axes are obtained.

Step (2) When (i = 1), for j = 1, ..., 216, with the pixel values obtained in the first iteration, the standard deviation values are calculated.

...

...

...

Iteration (i) = 196

Step (1) When (i = 196), for ( xi, yj )= (x196, y1, ..., y216) the pixel values that correspond to x- and y-coordinate axes are obtained.

Table 4.10: The detailed illustration of red/green/blue MRI image Variance() calculation.

Table 4.11: The detailed illustration of red/green/blue MRI StandardDeviation()calculation.

Step (2) When (i = 196), for the pixel values obtained in the first iteration, standard deviation value is calculated.

The standard deviation (SD) values above $\left({\text{SD}}_{{\text{RGB}}_i}={\text{SD}}_{{\text{RGB}}_1},{\text{SD}}_{{\text{RGB}}_2},\dots ,{\text{SD}}_{{\text{RGB}}_{196}}\right):$ for the pixel values in all columns in the y-axis (j = 1, 2, …, 216) corresponding to x-coordinate axis (i = 1), the calculation of standard deviation values is done until (i = 196).

In Table 4.11, the standard deviation values in Figure 4.27 are calculated along with the application of StandardDeviation() function algorithm for i = 1,…, 196.