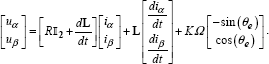Chapter 9

Control of the Stepping Motor ¹

9.1. Introduction

This chapter deals with control of the stepping motor, or rather controls of stepping motors. There are, in fact, different stepping motor technologies possessing particular properties that need adapted supply converters. These different types of motors are represented by specific models. The technology used in these motors and their converters as well as the development of their models are not covered in the framework of this chapter which is devoted to control. This is why, after having briefly indicated the particularities of the different types of stepping motors, the principles of control will be presented and illustrated on the basis of the most common models: those of the permanent magnet motor and the hybrid motor.

9.2. Modeling

9.2.1. Main technologies

We usually distinguish three families of stepping motors:

– The motor with variable reluctance exploits the principle of natural evolution towards the minimum magnetic potential energy or maximum flux rule. The torque being a function of the square of the supply current intensity, a unipolar converter that is simple and economical is sufficient. On the other hand, to increase the number of stable positions, we need to increase the number of teeth, which requires precise and costly machining. For this reason, it is not often used.

– The permanent magnet motor implements the interaction force between the magnetic field generated by the stator windings and the magnetic field of a magnet inserted at the rotor. According to the stator technology, simple or double windings, may or may not require a bipolar supply converter. The technology of the rotor influences the inertia moment and thus the dynamic performance. The claw-pole motor, with its cylindrical magnet with radial polarization, is economical but less precise and slower than the motor with a radially magnetized disk, which costs more to produce.

– Finally, the hybrid motor carries an axial magnet on its rotor axis. The magnet polarizes two toothed disks, the north and south disks being shifted by electrical radians. This configuration allows us to reach higher torques than previously and the angular combinations between the stator teeth and those of the disks increase precision, thanks to the higher number of steps per revolution. These advantages, which are particular to the hybrid structure, mean that this is the type of motor that is most often used [ABI 91].

9.2.2. The modeling hypotheses

Stepping motors are linked to synchronous machines whose main structures and models are known [SAR 04]. In this chapter we consider a generic two-phase stepping motor, whose phases in quadrature are indexed and . Moreover, the following hypotheses allow us to simplify the model without reducing the understanding of the control principles.

The two main phenomena concerning conductors are:

– the resistance to the electrical current; and

– the skin effect.

At motor functioning frequencies (of a few dozens of Hertz), the skin effect can be disregarded, because the skin is about 1 cm thick. When the motor has a voltage supply, we have to take into account the resistance of the conductors. It is this, in fact, which limits the current in the windings when the motor is in static position on a step.

There are three main defects of the ferromagnetic material in the magnetic circuit. These are:

– its non-zero conductivity, which allows the circulation of eddy currents;

– the existence of a saturation phenomenon and a hysteresis cycle in the magnetic characteristic; and

– a relative magnetic permeability that is not infinite.

The first two defects lead to losses in variable field regime. The third requires a non-zero magnetization current to generate the flux. The effects of the eddy currents and of the hysteresis can be disregarded if the model is not being used for a precise energy study, but rather aims to define the controls.

These hypotheses about the magnetic circuit confer linear properties that allow us to model the use of notions of self-inductance and mutual inductance. To retain their meaning, i.e. to not tend towards infinity, it is however necessary to retain the third defect mentioned, about permeability.

When the magnet exists, it is usual to assume that its functioning point, which is situated near the point with maximum specific energy, evolves under the joint action of current and reluctance variations and that it moves on a backward line. If the slope is sufficiently small, we can assume that the flux is constant. This decreases the harmonic content of the motor torque momentum.

Finally, the mechanical construction allows us to justify other simplifying hypotheses. The hypothesis of sinusoidal spatial distribution of the permeability, in particular, allows the restriction of the harmonic development of inductances. The construction symmetry, as far as it is concerned, is assumed to be sufficient for the mutual inductance fluxes in the two-phase motor to have at saliency of polar pieces of sole origin. Furthermore, as the leakage fluxes are not being involved in electromechanical conversion, the leakage inductances can be disregarded in the model.

To account for the mechanical dynamics, it is necessary to take into account the inertia moment and viscous friction of the motor. The marginal effect of dry friction can often be disregarded. It is true that dry friction shows a nonlinearity of sign type at the change in rotational direction. It is not, however, about an essential nonlinearity, i.e. one of those that naturally confer the stepping function on the motor. Moreover, at usual supply frequencies, inversion in direction does not occur and the effect of this nonlinearity, therefore, has no influence on behavior in this case1 . It can hence possibly be disregarded in the control model.

9.2.3. The model

The dynamics of the motor are described in a four-dimensional state space by the evolution of the state vector and are the currents in the two stator phases. and refer to the angular position and angular speed respectively. We can write the electrical angle, e, as: e = p, where p is the number of steps per rotation of the motor2 . The resistance of a coil is written R.

The inductance matrix is in the form L = [L0] + [L2] with:

[9.1] 

given the hypotheses: M0 = 0.

By making the maximum total flux of the magnet in a coil and the electromechanical constant, the flux vector of the magnet in the phases is:

[9.2] 

We then obtain the first two differential equations of the model inferred from Ohm’s and Faraday’s laws:

[9.3] 

By writing the current vector as as well as the magnetic coenergy with all the currents switched off as wc () [MAT 04], given the linearity hypothesis of the magnetic circuit, the momentum of the torque developed by the motor is expressed by superposition in the following way:

[9.4] 

Under the hypotheses given in the previous section, by assuming the flux in the magnet is constant and by restricting the development of inductances and coenergy to the first harmonic, , we get:

[9.5] 

with m being the number of contacts of the stator and Kd the coefficient of the cogging torque.

The torque in the motor has three origins:

– The electrodynamic torque is generated by the interaction between the stator field generated by the currents and the rotor field of the magnet.

– The detent torque comes from the external permeability variation of the magnet according to the position that introduces a flux variation in the absence of current.

– Finally, the reluctance torque originates from the variations of self and mutual inductances during the rotation.

Equation [9.5] develops the most complete expression of the torque in a permanent magnet motor. However, in this type of motor, it is the electrodynamic torque that is dominant, the reluctance torque being insignificant. The reluctance torque is the main torque of the motor with variable reluctance. Finally, the cogging torque is taken advantage of along with the electrodynamic torque, in the hybrid motor. The model of the hybrid motor is therefore very similar to that of a permanent magnet motor.

The reluctance motors, on principle insensitive to the polarity of magnetizing currents, implement more complex electromechanical structures so that it remains possible to control their rotational direction. In multiple stator-stack motors, for instance, we have at least three magnetically independent stators within which a single rotor is inserted. Another solution, that is more economical but does not produce such a high performance in terms of dynamics, is the single stator-stack toothed motor. This has a single rotor but three or four phases. The models of these motors require specific developments that are not directly derived from expression [9.5].

Table 9.1 summarizes the expressions of torque of a few motors and their essential features.

To ensure the coherence and clarity of the presentation the principles of control in open loop (section 9.3) and closed loop (section 9.4) will be presented in relation to permanent magnetic motors, namely by putting L2 = 0 and Kd = 0 into expression [9.5].

By applying the fundamental principle of dynamics and, by taking into account dry friction, we can determine the third equation of the model:

[9.6] 

where J is the inertia moment, f the fluid friction coefficient, D the dry friction and Tc the load torque.

The fourth equation simply links speed and position:

[9.7] 

Finally, we obtain the dynamic model of the permanent magnet stepping motor in the form of a nonlinear non-autonomous four-dimensional differential system:

[9.8] 

It is quite common that the dry friction torque associated with the sign function is disregarded in the model. This approximation is all the more justified when the motor is speed controlled without pausing at the equilibrium positions. The dry friction can then possibly be accumulated with the resistant torque. In the neighborhood of the stop at the equilibrium positions or in a vibratory functioning mode at an average speed of 0, the approximation must be discussed according to the relative orders of magnitude of the different torques present.

9.3. Control in open loop

9.3.1. The types of supply

As for every electromechanical converter, the safest way to control the dynamics consists of imposing flux via current sources. The cost of producing such a motor, which is linked to the sophistication of the supply converter, depends on their dynamic and energy performances. In this case, with currents being imposed, the dynamic model [9.8] becomes two-dimensional by being restricted to the last two equations.

However, working either at fixed or free chopping frequency, the current supplies always present a limitation in terms of step frequency. This limitation is due to the settling time of the current, which inevitably degrades their functioning in a voltage source functioning for frequencies that are too high. In fact, if the derivatives of currents and rotational speed are too high, the first two equations in [9.8] imply that we have sources with non-realistic voltage at our disposal.

The simplest way to control the stepping motors is to use the voltage sources. According to the type and technology of the motor, they can be unipolar or bipolar. The structure of the supply converter also influences the dynamic performance, by ensuring a relatively efficient demagnetization of phases and a relatively quick rise in current. We can infer from [9.8] that the final values of the currents depend only on supply voltages and the coil resistance. If the electrical dynamics is much faster than the mechanical dynamics, the decoupling of the two gives us the option of ignoring the first and considering that the currents are established almost instantaneously, which is then equivalent to controlling the current. In the opposite case, i.e. at high speed, the whole model rules the evolution of the variables, both electrical and mechanical.

The current control is the most effective control. It is well adapted to slow movements but we need to be cautious about the reality as soon as the speed of the motor increases. The voltage control, which is a less effective control, is more economical to produce. This is not a secondary aspect of the problem because stepping motors are specially appreciated for their ability to control position at the lowest cost.

9.3.2. The supply modes

Solving singular points of the differential system [9.8], in which we have disregarded dry friction, allows us to express the angular position of the rotor as a function of currents established in the stator coils. The speed being 0, it is hence about equilibrium positions that also depend on the load torque.

[9.9] 

By retaining only the stable equilibrium points, the last equation becomes:

[9.10] 

The first term marks the position defined by the control; whereas the second translates the shifting introduced by the resistant torque with respect to this reference. The intensities of supply currents usually take their values in , with In and being fixed by a dual voltage supply in the absence of a current supply.

The supply modes are defined by the sequence of values given to and . Table 9.2 summarizes the equilibrium positions inferred from equation [9.10] by disregarding the load torque. The maximum load torque − also called the holding torque − and the corresponding position are inferred from equation [9.6] at equilibrium.

The logic sequencer drives the motor supplies by describing the lines of this table according to an order that defines the four main supply modes:

– Mode 1: only one of two phases is supplied at a time by alternating the polarity. The sequencer describes the odd lines of the table, which leads to the incremental displacement by electrical quarter turn.

– Mode 2: the two phases are always supplied simultaneously, the sequencer only describing the even lines. The incremental displacement remains the same as previously, but the equilibrium positions are intermediate to the previous ones. The obvious advantage of this mode lies in the increase in torque by a factor of . For this reason, it is the most frequent supply mode.

– Mode 3: in this mode, the half-step advance is done by sequentially describing all the lines of the table. The positioning is more precise but this mode has the drawback of having different static (and dynamic) behaviors from one half-step to the next, the holding torque alternating between two values.

– Mode 4: this mode attempts to remedy the drawback of mode 3, by increasing the intensity of supply current on the odd lines by a factor of . We thus ally the advantage of mode 2 in terms of torque and that of mode 3 in terms of precision. However, this is only possible at the expense of a bivoltage supply or a current supply with variable reference.

Generalizing the approach introduced by mode 4, it is possible to define a fifth supply mode, referred to as a microstep. In fact, equation [9.10] allows us to establish that for no load the equilibrium position is entirely defined by the intensity ratio of the two supply currents. It is enough to have a supply able to do:

[9.11] 

on a set of discrete values of e, thus theoretically defining as many microsteps as desired with the same performance as in mode 2. However, this approach has several limits that quickly put a strain on economic interest in the stepping motor:

– the precision and stability of the intensities of constant currents, which can lead to the need to resort to linear supplies;

– the high quality of mechanical construction necessary to approach a really sinusoidal spatial evolution of the motor torque;

– the precise knowledge of the load torque, which must not fluctuate ortherwise incremental resolution desired loses all sense.

9.3.3. Case of slow movement

The previous section has dealt with control by only considering the equilibrium states, their successions and their static properties. In this section, the control of displacements is analyzed within the framework of the hypothesis of quasistationarity. As detailed in section 9.3.1, it consists of disregarding the influence of the mechanical dynamics on currents. We consider that the currents have quickly reached their final values, in the case of a voltage supply, or their reference values in the case of a current supply, with the reservations mentioned. The last two equations of model [9.8] then suffice to describe the mechanical dynamics by assuming that the currents are piecewise constant intervals and that the dry friction can be disregarded.

9.3.3.1. Start

Relationship [9.6] allows us to establish the maximum load torque that the motor can support at equilibrium. This is the holding torque, which is denoted Tm. Its value depends on the supply mode, as can be seen in Table 1.1. Here, we establish the maximum load torque that will allow the motor to advance by one step when the supplies switch. This is the start torque, which is denoted Td.

From relationship [9.10], we can infer the equilibrium position before the advance impulse. For instance, on line 1 of Table 1.1:

[9.12] 

Immediately after switching, the motor still being stopped, the start torque is inferred from relationship [9.6]:

[9.13] 

The condition to fulfill being Td > 0, the advance control on one step is only possible if:

[9.14] 

Similarly, we infer that the advance control on a half-step supports a higher load torque:

[9.15] 

9.3.3.2. Oscillating response

To generalize the sentiments, the dynamic equation can be reformulated by using the following dimensionless variables:

– electrical angle: e = p · ;

– the load torque scaled with respect to the holding torque:

– the time scaled with respect to the natural period:

Moreover, by defining the following parameters:

– the natural pulsation

– the damping coefficient

we obtain:

[9.16] 

Variables and here represent the control states and take their values in { − 1, 0, 1}, in accordance with Table 1.1. Without loss of generality, we consider the advance in the particular position defined by the first line of this table:

[9.17] 

The damped oscillating response, which can be inferred is a major handicap for quick and precise positioning, and is greater when the motor is not heavily loaded. The expression of the damping coefficient shows the negative influence of inertia on response, which could require the addition of a reducer in order to be attenuated. We can also consider increasing the viscous friction on purpose to increase the damping or we can obtain a certain electrical damping by adding free wheel diodes at the terminals of the coils. However, these solutions considerably reduce the performances of the motor at high speed. The best approach consists of dealing with the damping of oscillations using the control.

9.3.3.3. Microstep control

The first approach consists of decreasing the oscillation amplitude by decreasing the steps of the motor torque generated by the current. If we have a current supply at our disposal, we can opt for control in mode 5. Let us assume that this control imposes currents of amplitude In with a microstep index n defining n – 1 intermediate positions, denoted i, between the natural equilibria of the no load rotor. From equations [9.11] and [9.16], we can infer:

[9.18] 

If index n is sufficient, it is possible to linearize the sinus. Furthermore, by translation we can define the angular gap with respect to the equilibrium around the resistant torque: . This leads us to a linear equation with constant coefficient:

[9.19] 

from which we know that the step response shows an overshoot proportional to the gap between the initial and final positions. This gap being inversely proportional to n, we can conclude that microstep control allows us more effectively to dampen the oscillation with a larger number of microsteps.

This approach holds, however, provided that the equilibrium is reached between each microstep, which leads to a relatively slow control.

9.3.3.4. Bang-Bang control on one step

This section is about optimizing control to enable the advance of one step, without overshooting and in a minimum period of time. The principle consists of breaking down the advance of one step into two intervals. In the first interval, taking a duration of τ1, we develop the accelerating torque by applying the control corresponding to the next step. In the second interval, of a duration of τ2, we perform electrical braking by reapplying the previous control. If the two intervals are properly distributed, the speed cancels out at exactly the time the next equilibrium position is reached. It is then sufficient to reapply the control that corresponds to the position to keep it in equilibrium.

The dotted line in Figure 9.1 illustrates the no load response on a step by applying mode 1 control on the step going from 0 to . The damping coefficient, , is 0.25. With the unbroken line, we notice the application of a negative torque impulse during the braking phase. The speed very quickly decreases and the phase portrait shows that the motor quickly returns to its equilibrium position. The response time is considerably decreased, as can be seen with the position curves.

The optimal time to reach equilibrium without overshoot does not depend much on the load torque. It is generally in the neighborhood of 3.0. At no load, the ratio of the first and second interval, is about 2.0. It increases with the load torque.

In practice, the duration of the two intervals can be evaluated in the following way.

By applying an impulse of step advance of variable duration, τ1, we look for the tangency point of the position with its final value. The graphs in the top line of Figure 9.2 illustrate the results obtained for different durations of advance impulse. When optimal duration τ1 is determined, we can calibrate the duration of braking impulse to obtain that the motor stops exactly at the equilibrium position, exactly at the end of braking pulse. The graphs on the bottom line in Figure 9.2 illustrates the consequences of breaking that takes too long or is too fast, and the result when duration τ2 is optimal.

Using the same approach, similar controls have been designed to instigate control in a minimum time in two or three steps [GOE 84].

9.3.4. Case of quick movement

9.3.4.1. Start−stop zone

A displacement at high speed begins with an acceleration phase and ends with a deceleration phase. Yet, the most elementary control of a stepping motor involves applying step impulses at a fixed frequency to the sequencer and stopping it by switching off the impulses. In this case, the control frequency is temporally discontinuous whereas, for energy reasons, the speed of the motor is continuous.

The first steps being the slowest, the control goes ahead of the motor. The loss of synchronism can only be avoided when the torques developed in the following steps are sufficient to allow the rotor to catch up with its delay. This phenomenon therefore imposes a maximum start frequency, which depends on total inertia and load torque. It is usually specified in the form of a boundary curve in the torque−frequency plane, given for the inertia of the motor alone.

The motor being totally reversible, the start zone is also a stopping zone as shown in Figure 9.3. For a load torque neighbor of the starting torque, the start frequency is close to zero; whereas the highest start frequency is possible when the motor has no load.

9.3.4.2. Driving zone

Once the motor is in rotation, it is possible to use the inertia torque to pass more quickly from one step to the other, provided we do not stop at any equilibrium positions. The functioning analysis can then be led by using the notion of mean torque, as we do for any other rotating machine in an established regime.

The instantaneous electrodynamic torque is defined by relationship [9.5] and takes different expressions according to the combinations of currents and . The maximum mean torque is obtained by switching the currents in order to select the torque function of highest value at each time, exactly as we do with voltages in a diode rectifier. Any shift in switching angles with respect to these particular values leads to a decrease in mean torque, and then to the canceling out or even inversion of the torque. Figure 9.4 illustrates the sentiment in mode 1.

We now spot the switching angle that is used to supply a phase with respect to the specific angle that would cancel out the mean torque. We write this as . It is similar to the internal angle of a synchronous machine. Mean motor torque is inferred by the following relationship:

[9.20] 

The maximum mean torque is inferred from this. It is contained between the starting torque and the holding torque:

[9.21] 

On one hand, this analysis of mean torque is valid provided that it really benefits the dynamic smoothing effect brought by inertia, i.e. quite a long way from the start, in the neighborhood of the maximum of the curve presented in Figure 9.3. On the other hand, for higher frequencies, the currents tend to be degraded because the decoupling hypothesis between the mechanical and electrical dynamics is no longer justified. The rise and fall times of currents no longer being insignificant compared to the duration of the step, the mean torque is thus degraded.

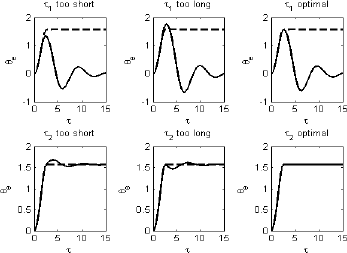
In the driving zone, different transients of speed can be put in place to lead the motor from the initial frequency fi to the desired speed, i.e. to control frequency, fc. The corresponding frequency transients can be programmed by taking into account the available accelerating (or decelerating) torque. We usually take a safety margin below the boundary curve of the driving zone, as shown in Figure 9.5.

Inertia being the most important phenomenon in driving, the dynamics in this zone can be summarized with:

[9.22] 

The switching angles can be calculated and programmed so that at each time, during the variations of speed and hence frequency, the motor torque remains below the safety margin. If the programmed movement requires an accelerating torque greater than that available at a given frequency, the motor loses steps.

9.3.4.3. Linear acceleration

To obtain a uniformly varied movement, the motor must be controlled so that the accelerating torque is constant. Let TaL be the accelerating torque, i and i the initial position and speed, and p the angular step. By integration of equation [9.22], we obtain:

[9.23] 

On the one hand, the uniformly varied movement is such that: . On the other hand, the synchronism warrants: = fp. The elimination of time in equation [9.23] gives:

[9.24] 

The accelerating torque that we want to use is the torque available at frequency fc. We infer the number of steps to program in acceleration phase as well as its duration by using:

[9.25] 

The control of the acceleration can be easily implemented but has the drawback of not exploiting all the accelerating torque available at intermediate frequencies between fi and fc.

9.3.4.4. Exponential acceleration

For a faster increase in speed, the control must remain close to the maximum torque. The torque line:

[9.26] 

generally remains close to the maximum torque, as shown in Figure 9.5.

By integration of equation [9.22], we obtain:

[9.27] 

[9.28] 

The time constant of the exponential is negative.

The duration of the acceleration phase as well as the number of steps to be programmed are inferred in the following way:

[9.29] 

[9.30] 

9.3.4.5. Programming of a speed profile

The previous developments about accelerations can be applied to deal with the linear and exponential decelerations in the same way. In the case of linear deceleration, the motor torque and resistant torque combine their effects and generate braking faster than acceleration. Let us also note that, in the case of exponential deceleration, the time constant of the exponential is positive, which causes very efficient braking.

To carry out a quick displacement between two positions, we separately program a phase of Na acceleration steps, followed by Nv steps at constant speed to finish with a deceleration phase of Nd steps.

It appears obvious in Figure 9.6 that the exponential controls provide better performance than the linear controls, both in acceleration and braking. The implantation of the exponential control being noticeably more complicated than that of the linear control, however, it is frequently approximated for a control giving linear response by intervals by using a series of constant accelerating torques distributed at an interval of fc − fi.

Calculation of the series of switching times, or more precisely step duration, can be programmed recurrently.

[9.27] 

Let ti be the step duration:

Applied to two consecutive steps, formula [9.24] gives:

[9.31] 

[9.32] 

If the displacement is predetermined, the switching times calculated are tabulated in memory to be used by a low-cost processor of the dsPIC type. If the control must be calculated in real time, the previous expression can be simplified by a development limited to the first order to limit the calculation time:

[9.33] 

TaL, J and p being constants.

We proceed similarly to control the Nd deceleration steps with a braking torque that is negative. During the constant speed phase, however, the control is reduced to: ti+1 = ti.

9.4. Controls in closed loop

Control in open loop is the favorite way to control the step motor because it has a very economical implantation that is consistent with the low cost of many stepping motors. As we have seen, however, it is necessary to implement a torque margin to secure functioning by avoiding loss of step. This leads to overdimensioning of the motor. To avoid overdimensioning but also to improve reliability, we resort to control in closed loop [KUO 79].

Controls in closed loop all require the use of an incremental coder, except in the case of voltage supplied motors. In this case, the observation of back electromotive force (emf) is sufficient to design the self-control, provided that the rotational speed is fast enough. Generally, the performances of these controls are largely dependent on those of the coder. Given its price and that of the calculation unit, the total cost of the installation can be doubled. Such coders must therefore be kept for demanding applications and associated with motors that are themselves high performance.

Certain motors integrate an economic coder. In this case, it is not used to design the control, but simply to control the amplitude of movement a posteriori.

9.4.1. Linear models

The application of a continuous analog control to a process that is essentially discrete remains a topic of discussion.

Is the stepping motor not, by nature, an incremental electromechanical converter? The answer is yes, when we take the time to stop at each equilibrium position. This is less obvious when the motor continuously evolves (i.e. without stopping) from its initial position to its final position. The position and the rotor speed are, in any case, continuous variables.

What about control? It can be synthesized analogically via continuous correctors. It is finally control impulses, however, that are generated in discrete form and transmitted to the sequencer. In fact, these impulses are specified by an angle or by their frequency, so it is clear that their features only mean something in the interval defined by the polar step.

Under this subheading, we present analog controls whose validity is restricted to an intermediate speed range. At very low speed, incremental dynamics are dominant and the notion of continuous control is questionable. At high speeds, electrical dynamics are not insignificant compared to the mechanical dynamics and the simplifications introduced in the control models are no longer valid.

9.4.1.1. Modeling of the torque

The two controls that follow are designed from linear dynamic models with the usual restrictions about validity around the functioning points where the parameters are evaluated. The hypothesis common to these models assumes that the currents are very quickly established in the phases, which allows us to abandon the two electrical equations of the initial model [9.8].

The model being established around a mean speed, the instantaneous electrodynamic torque formulated in equation [9.5] can be abandoned for the benefit of mean torque, , which is expressed in equation [9.20]. However, it appears that angle being orientated from a rotor position not yet reached, it cannot be exploited from the control point of view.

We therefore define a new switching angle:

where angle γ, orientated from the switching angle to the detent position of the supplied phase, is referred to as control angle. Figure 9.7 completes Figure 9.4 by including these two new angles.

The third equation of model [9.8] then becomes:

[9.34] 

In an established regime, this relationship allows us to express the relationship between the speed and switching angle, according to the load torque:

[9.35] 

This relationship establishes that with angle control imposing the mean torque, it is the load torque that sets the rotational speed. Reciprocally, when a frequency control sets the speed, the switching angle is able to evolve in order to balance the torque.

To obtain the dynamic model, we consider the speed and angle variations around the functioning point by noting:

By noticing that for all 0 ≠ 0, sgn = sgn 0, we get3 :

[9.36] 

9.4.1.2. Modelfor angle control

Within the framework of restriction at low speeds (hypothesis of piecework constant currents), since the mean torque is dependent on the switching angle alone, its expression can be linearized by differentiation:. The linearization of [9.36] and the Laplace transform lead to the dynamic model:

[9.37] 

Consistent with the hypothesis, the dynamics of the speed in response to variations in the switching angle are of a first-order system reduced to the sole mechanical time constant.

At high speed, the settling time of currents being of the same order of magnitude as the mechanical time constant, the expression of mean torque is noticeably more complex. It requires us to calculate the instantaneous fluxes and infer the instantaneous torque before expressing its mean. The method is rigorous and takes into account the electrical transients [GOE 84]. Another possibility consists of restricting the dynamics of currents to the first harmonic. This allows us to analytically integrate the differential system [9.8] with greater ease [HAM 92]. In any case, the mean torque is then dependent on the rotational speed, also since it influences the current transients.

In this case the linearization of equation [9.36] becomes:

Model [9.37] is modified in the following way:

[9.38] 

The responses to the perturbations of control angle or load torque remain of the first order; the mechanical time constant depending on the mean rotational speed being:

[9.39] 

Since the mean torque decreases with speed, coefficient B is negative. As a consequence, the mechanical time constant tends to decrease at high speed.

Let us remind ourselves that the performance of this model is compromised by:

– the approach of the torque in mean value;

– linearization; and

– processing of the control angle in the same way as a continuous variable, although it only makes sense discretely on a step of the motor.

9.4.1.3. Model for frequency control

Even if control of the angle appears to be the most natural, the stepping motor is the most often controlled in frequency in order to set its rotational speed using the frequency of its impulses. A step of the control angle corresponds to a Dirac impulse on frequency.

The control angle is normally defined discretely in an electrical step. To harmonize the nature of this angle with a continuous approach to control, however, it is preferable to redefine the angle by the difference between the electrical angle (continuous variable linked to the mechanical position of the rotor4 ) and the switching angle .

[9.40] 

The mechanical speed is derived from the electrical angle and the switching angle follows the variations in impulse frequency:

[9.41] 

[9.42] 

From relationships [9.40] to [9.42], we can infer the dynamics of the control angle:

[9.43] 

Figure 9.9 shows how we can naturally complete the structure of frequency control from the control angle by using equation [9.43]. After reorganization, Figure 9.10 presents the block diagram of the frequency control.

By noticing that A< 0, we get:

[9.44] 

Figure 9.11a shows the damped oscillating response of speed in response to successive steps of the frequency which controls the motor. Figure 9.11b shows that a perturbation of load torque causes a temporary oscillation in instantaneous speed. The control angle evolves naturally and cancels out the speed error.

9.4.1.4. Choice criteria of control

One of the advantages of the stepping motor being its low cost, the economic aspect is an important criterion in the choice of control. By taking into account the demands of the application, the easiest control is obviously preferred.

For that reason, the choice frequency control appears to be more natural because it is the easiest. This is done economically, in open loop. The second-order model allows us to predetermine the response of the motor to the frequency variations and torque perturbations, around a functioning point. It is therefore well suited to the load displacements whose parameters (mass, inertia, friction, etc.) are known and are constant.

The angle control is more difficult and costly to implement. It requires the addition of an incremental coder whose quality and resolution influence directly the performance of control. Moreover, this control, operated in closed loop, requires precise adjustment of the coder with respect to the detent positions of the motor. We must also foresee a procedure for starting in open loop, since the control impulses are generated from those of the coder. We then understand that angle control is kept for the most demanding applications, which require us to take full advantage of the capabilities of the motor.

Functioning safety is another factor to take into account in the choice of control. As we have seen, frequency control does not show any static error in the speed. When some load parameters vary, however, particularly but not only the torque, the motor can suddenly stall and stop. This can happen due to an overload or due to a simple torque cough whose amplitude prevents the motor from regaining normal functioning. In the case of an angle control that controls the torque, the speed is free to decrease during the cough in order to adapt itself to the characteristic of the motor, then to return to its initial value after the disappearance of the perturbation. This automatic adaptation of speed works until the speed is 0 and to guarantee that the motor does not lose a step. The angle control is hence the favored control from the point of view of running safety.

9.4.2. Servo-control of speed

Here we consider the stepping motor whose step frequency is controlled by servo-control of its speed. A servo-control of the rotational frequency is shown in Figure 9.12. It requires a speed sensor or, at least, something to determine the instantaneous rotational frequency that is required prior to the motor being started. Input V0 sets the reference speed (frequency) of the motor.

Let the frequency transfer function of the motor be:

[9.45] 

The synthesis of the corrector can be carried out by algebraic or other methods for analog or digital implementation. The choices are made taking into account specifications, the cost of control and use of the technology available.

9.4.2.1. Development in Taylor series

A simple approach proposed in [HAM 92] determines the parameters of transfer function C(s)of the corrector, knowing model M (s) of the motor, so that the transfer function of the system in closed loop, TS (s), is close to a theoretical second-order system, TT (s). We assume that the voltage controled oscillator (VCO) is modeled by a gain KF (Hz/V), similarly to the speed sensor (frequency), KΩ (V/Hz).

The choices of damping coefficient 0 and natural pulsation 0 completely define the second order of reference:

[9.46] 

A development limited to third order allows us to synthesize a three-parameter corrector such as a PID (propotional integral derivate). It is obtained by polynomial division:

[9.47] 

The transfer function of the system in closed loop is given by:

[9.48] 

Its limited development is obtained similarly. Namely:

[9.49] 

The identification from [9.49] to [9.46] gives the parameters of the corrector.

The application of this method to setting classical regulators such as PID is not of any interest to us. It provides good results for developments in series at higher orders and then concerns more sophisticated correctors with more parameters that need to be set.

9.4.2.2. Naslin polynomial

Another approach consists of using the Naslin polynomial [HAU 97, NAS 58]. The transfer function of the system in open loop is:

[9.50] 

Let the Naslin polynomial be:

[9.51] 

Naslin defines the following characteristic ratios:

[9.52] 

The Naslin polynomial is referred to as normal when all the ratios are equal. Each of the ratios depends on the parameters of the corrector. The Naslin criterion sets the equality of as many ratios as the number of parameters of the corrector allow. It is about solving an algebraic system of n equations with n unknowns, if the corrector possesses n setting parameters.

By setting the first equal ratios to 2, we obtain a behavior close to that of a second-order system with a damping coefficient close to 0.7. It remains to check that the ratios of higher ranks, which are not adjustable, are greater than 2. If this is not the case, we can increase the first ratios a bit without going beyond 2.2.

A drawback of this method is the great sensitivity of the response to the value of the first characteristic ratios. For instance, going beyond 2.3 leads to a closed loop system that is over-damped; and below a ratio of 1.7, the damping of oscillations are insufficient.

9.4.2.3. Correction by phase advance

A corrector with phase advance is sometimes enough to efficiently damp the oscillations of the speed of the motor.

The transfer function of this corrector is:

[9.53] 

Setting the phase margin in open loop between 50° and 60° is generally satisfactory. Coefficient is calculated to obtain phase advance necessary for this result. Time constant TAV is then calculated to center the action of the corrector on the cutoff pulsation c of the transfer function in open loop before correction. We set the gain KAV so that the value of the cutoff frequency of the closed loop transfer function after correction is the same as the value of the cutoff frequency of the closed loop transfer function before correction. This leads to the following relationships:

[9.54] 

9.4.2.4. PID correction

A PID industrial corrector can also be used. The integral term added by this corrector allows us to cancel out the static error that the corrector with phase advance has the tendency to induce. The transfer function of this corrector is:

[9.55] 

This corrector can be set empirically. The time constant of the derived term Td can be set in the same way as previously described. The integral time constant is set so that it does not excessively degrade the response time and maintains it in the same order of magnitude as previously. The proportional gain is then adjusted to act on the overshoot. From this initial setting, it is possible to more finely adjust these three parameters to refine the result.

9.5. Advanced control: the control of chaos

9.5.1. Chaotic behavior

As has been indicated above, the most natural control of the stepping motor is control in open loop. It has been shown in [ROB 00] and [PER 00], however, that performances at high speed are considerably degraded. It has been established in [REI 03] that functioning modes that are not only quasi-periodic but also chaotic appear when the supply frequency enters the instability zone.

The control of chaos consists of stabilizing one of the unstable periodic orbits that are embedded in infinite number in the chaotic attractor. The trajectory describing the dynamics in state space must be kept in this orbit when a system parameter is varied. In the case of the stepping motor, controling the chaos means forcing of the electrical angle to produce periodic behavior, i.e. to impose a rotational speed that remains synchronous with the supply frequency.

The control of chaos has aroused a lot of interest since the seminal works presented in [OTT 90]. Different control strategies have been proposed since [BAS 97, BLE 96, PYR 92, PYR 95]. The synthesis of the controller can be implemented by a linear [BAS 98] or a nonlinear approach [FEK 03, YAN 02].

In the next section, we present a method allowing us to control the chaotic behaviors of the stepping motor in the instability zone at high speed. By using the theory of absolute stability [KHA 92], it is possible to synthesize a linear controller capable of stabilizing one of the periodic orbits initially embedded in the chaotic attractor over a large supply frequency range. The motor is supplied by voltage, in mode two, and the control variables are the supply voltages. We therefore have control in closed loop requiring the control of the output voltage of the supply choppers. This control remains relatively economical because it does not require any position/speed sensor but only current sensors to measure the instantaneous intensities of the supply currents.

9.5.2. The model

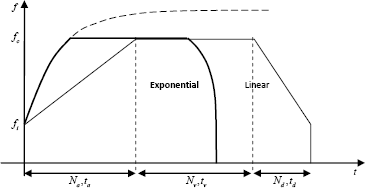
The great instability of simulations in chaotic mode, owing to the sensitivity to initial conditions of the dynamic system, requires us, among other things, to conform with model [9.8] in order to solve certain numerical problems [ALI 02]. Basically, it is about using dimensionless variables as well as a dimensionless temporal variable with respect to the control period. Moreover, to improve the generality with respect to model [9.8], here we use a model taking into account the cogging torque, Kd ≠ 0.

Let the generic model of the hybrid model be:

[9.56] 

The rectangular supply voltages are defined as follows:

The dimensionless state variables are:

The parameters are expressed in the following way:

By writing the state vector as , the input vector as and the output as Y, system [9.55] can be put in the form:

[9.57] 

in which B1 is the injection matrix and C1 is the output matrix:

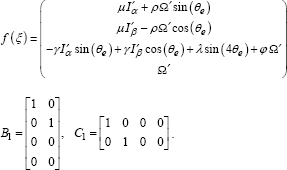
9.5.3. Orbit stabilization

The goal here is not to stabilize the motor at an equilibrium point but to stabilize it along an orbit of period T = 1, in scaled time. We can extend the notion of equilibrium to the periodic dynamics in the following way. Let us first notice that, if the natural dynamics of the motor at control frequency are really chaotic, there is always at least one unstable orbit, p (t), of period-one embedded in the attractor. The stability of this orbit can be analyzed in the Lyapunov sense.

We define a new state vector x (t) =(t)−p (t), so that the origin x = 0 is an equilibrium point of the following system:

[9.58] 

The behavior of the solutions to equation [9.57] close to p (t) is equivalent to that of solutions to equation [9.58] close to x = 0. As a consequence, the stability of p(t) can be similarly characterized from the stability of equilibrium, x = 0. In particular, the periodic solution p(t) of equation [9.57] is uniformly asymptotically stable if x = 0 is an equilibrium point of equation [9.58] that is uniformly asymptotically stable.

The stability issue can be dealt with by linearizing equation [9.57] around x = 0 and adding an excitation input to stabilize the periodical orbit.

[9.59] 

The partial derivative with respect to the state can be broken down into two parts: a linear invariant part (linear time invariant (LTI)) called A, expressed in equation [9.60] and a linear variable part (linear time variable (LTV)), called Av.

[9.60] 

The reformulation is done by defining a matrix Δp (t) which is a diagonal of rank 7 whose elements are the non-zero elements of Av:

[9.61] 

System [9.59] is now written in the following form:

[9.62] 

Figure 9.14 represents the linearized system whose transfer function, G (s), is expressed in the following way:

[9.63] 

The goal is to synthesize a linear controller admitting -y as input and u as output, as shown in Figure 9.14.

The transfer function between z and v in closed loop is given by:

[9.64] 

We need to notice that (t, z) is a class of nonlinearities dependent on time and without memory effect. It depends on the periodical orbit, and hence on the supply frequency. The analysis of the stability of a system interconnecting a linear part with a nonlinear function of this type can be led by means of the theory of absolute stability.

9.5.4. Absolute stability

Here we remind ourselves briefly of the principal elements of the theory of absolute stability.

DEFINITION 9.1.– (sector condition)

A memoryless nonlinearity is said to satisfy a sector condition if:

[9.65] 

For some real matrices, Kmin and Kmax, so that Ksec = Kmax − Kmin is a symmetric positive definite matrix and the interior of Γ is connected and contains the origin. If Γ = p, then (·,·) globally fulfills the sector condition, in which case it is said that (·,·) belongs to a sector [Kmin, Kmax].

DEFINITION 9.2.– (absolute stability)

Consider the nonlinear system where (·,·) satisfies the sector condition. The system is absolutely stable if the origin is globally, uniformly, asymptotically stable for every nonlinearity belonging to the given sector.

THEOREM 9.1.– consider the nonlinear system described above, where triplet {A, B, C} is controllable and observable and (·,·) globally fulfills the sector condition. The system is absolutely stable if:

[9.66] 

is Hurwitz and:

[9.67] 

is strictly positive-real.

REMARK 9.1.– if the system is absolutely stable, then it suffices to analyze the linear system Hzv (s) to comprehend the behavior of the nonlinear system. This is interesting because the unknown periodic orbits are not needed for the controller design.

9.5.5. Synthesis of the controller

By applying sector condition [9.65] to nonlinearities of the motor, we get:

[9.68] 

We can choose:

Among other chaos properties, we need to remind ourselves that a strange attractor is bounded. As a consequence, whether the motor dynamics are periodical or chaotic, the excursion of variable is limited in the state space. We infer that Kmin and Kmax exist and are bounded. The sector condition is hence globally fulfilled in the state space of the motor.

Without loss of generality [FEK 05], we put Kmin = 0. From equations [9.66] and [9.67], we obtain:

[9.69] 

We notice, from equation [9.64], that the synthesis of K(s) from a general constraint on Hzv (s) will be very difficult. To simplify things, we can use a parameterized form of K (s). From equation [9.64], by putting:

[9.70] 

we obtain:

[9.71] 

All calculations done, we get:

[9.72] 

Transfer function, Q (s), is a matrix of the following form:

[9.73] 

The Pyraguas control principle consists of not creating new orbits or modifying the pre-existing orbits, but in stabilizing one of them. As a consequence, transfer matrix K (s) must be:

[9.74] 

With this goal in mind, elements Qii (s) are in the form where:

[9.75] 

and τ is a positive constant usually chosen to be equal to1/c and is determined to satisfy conditions [9.65] and [9.66] imposed by the theorem. In the case of the stepping motor to control, the development of Q0 (s) can be limited to N0 = 1 without compromising the performances of the controller. Parameters q0, q1 and q2 are dependent on the control frequency.

[9.76] 

9.5.6. Examples

The first example presents the stabilization of a periodical orbit in a zone where the functioning mode is quasiperiodic in the absence of control. It is not about chaos control but, with clarity in mind, it is preferable to begin by illustrating the action of the controller on dynamics that are easier to represent than chaotic dynamics.

The trajectory of the state vector should be represented in a four-dimensional space, which is obviously not possible. To ease the interpretation of the observed curve, we represent the projection of this trajectory in the plane of supply currents . Figure 9.15 shows, in fine line, the projection of the trajectory in the absence of control. The shape of the (open) curve wrapping at the surface of a hypertorus is characteristic of the quasiperiodic dynamics [ROB 00]. By synthesizing the controller as indicated in section 9.5.5, without knowing it a priori, we stabilize the naturally unstable periodical trajectory represented in a bold line.

The second example presents the case of chaotic behavior. The trajectory of a chaotic dynamics converges towards a geometrical object of fractal nature, referred to as a strange attractor. The extreme (geometrical) complexity of these attractors does not allow us to directly represent the trajectory or even what the project is. In this case we resort to a Poincaré section and, more particularly, in the case of an excited drived system with fixed period (supply frequency), to a stroboscopic Poincaré section. With this mode of representation, it is obvious that a periodical functioning at the driven frequency will be reduced to a point in the plane (and a finite number of points in the case of sub-harmonic regimes).

The graph in Figure 9.16 is achieved by sampling the currents once per supply period. The cloud of 20,000 points sketches the strange attractor, giving us a glimpse of the self-similarity and the folding that give it the laminated aspect characteristic of this type of attractor. Figure 9.16b is a close-up of the portion of Figure 9.16a that is surrounded by a bex. These visual considerations must be confirmed by the estimation of a certain number of geometrical and dynamic invariants that allow us to more formally characterize the chaotic dynamics [CAS 10a, CAS 10b]. The target placed on the figure spots the location of the unique point corresponding to the section of the stabilized periodical trajectory.

Another way to visualize the action of the control consists of representing the waveform of one of the two currents before and after the application of control. This is shown in Figure 9.17a.

For each value of the supply frequency, the three parameters of the corrector (q0, q1, q2) are to be determined. Parameter q1is constant throughout the whole domain studied. Figure 9.17b represents the evolutions of the two other parameters.

To finish, Figure 9.18 shows the superposition of the Feigenbaum (improper bifurcation) diagrams before the application of controls and after. For each value of supply frequency (as abscissa), the sampled values of one of the currents are reported to the vertical of the abscissa. All aperiodical modes functioning takes on the appearance of a line segment densely populated with points. Only the Poincaré sections and the analysis of invariants allow us to distinguish chaotic regimes from quasiperiodic regimes. The bold line shows us the superimposition of the Feigenbaum diagram with control application. For each abscissa (except for one) a single point is depicted on the vertical. This means that to within an exception, the controller allows us to stabilize a periodical orbit across the whole functioning domain. The shift between the two diagrams, in the naturally periodical zones, is due to the development of Q0 (s), which has been limited to N0 = 1.

9.6. Bibliography

[ABI 91] ABIGNOLI M., GOELDEL C., “Moteurs pas à pas”, Techniques de l'Ingénieur, Génie Electrique, D3 III, D3690-1 – D3690-21, Techniques de l'Ingénieur, Paris, 1991.

[ALI 02] ALIN F., ROBERT B., GOELDEL C., “On the limits of chaotic simulations by classic software – Application to the step motor”, Proceedings of IEEE International Conference on Industrial Technology, CD-ROM, Bangkok, Thailand, December 11-14, 2002.

[BAR 94] BARBOT J.P., BIC J-C., GOLLREITER R., GRIGAT M., KADEL G., LEVY A.J., LORENZ R., MOHR W., STRASSER G., WALBERER A., “Channel modelling for advanced TDMA mobile access”, Proceedings RACE MPLA Workshop, Amsterdam, pp. 683-687, May 1994.

[BAS 97] BASSO M., GENESIO R., TESI A., “Stabilizing priodic orbits of forced systems via generalized pyragas controllers”, IEEE Trans. Circuits Systems I, vol. 44, no. 10, pp. 1023–1027, 1997.

[BAS 98] BASSO M., GENESIO R., GIOVANARDI, L. TESI, A. TORRINI G., “On optimal stabilization of periodic orbits via time delayed feedback control”, Int. J. Bifurcation Chaos, vol. 8, no. 8, pp. 1699–1706, 1998.

[BER 95] BERG J.-E., “A recursive method for street microcell path loss calculations”, PIMRC’95, Toronto, Canada, pp. 140-143, September 1995.

[BLE 96] BLEICH M.E., SOCOLAR J.E.S, “Stability of periodic orbits controlled by time-delay feedback”, Physics Letters A, vol. 210, pp. 87–94, 1996.

[CAS 10a] DE CASTRO M.R., ROBERT B.G.M., GOELDEL C., “Experimental chaos and fractals in a linear switched reluctance motor”, EPE-PEM Conference, Ohrid, Republic of Macedonia, September 6-8, 2010.

[CAS 10b] DE CASTRO M.R., ROBERT B.G.M., GOELDEL C., “Analysis of aperiodic and chaotic motions in a switched reluctance linear motor”, Proceeding of IEEE International Symposium on Circuits and Systems, ISCAS Conference, Paris, France, May 30–June 2, 2010.

[FEK 03] FEKI M., “An adaptive feedback control of linearizable chaotic systems”, Chaos, Solitons& Fractals, vol. 15, pp. 883–890, 2003.

[FEK 05] FEKI M., ROBERT B., ALIN F., GOELDEL C., “Chaotic ehavior of the stepper motor”, Proceedings of the Electrimacs Conference, Hammamet, Tunisia, April 17-20, 2005.

[GOE 84] GOELDEL C., Contribution à la modélisation, à l'alimentation et la commande de moteurs pas à pas, PhD thesis, Nancy, p. 173-179, 1984.

[HAU 97] J.-P. HAUTIER, J.-P. CARON, Systèmes Automatiques, Tome 2: Commande des Processus, Ellipses, 1997.

[HAM 92] HAMZAOUI A., Modèles dynamiques et commandes en boucle fermée d'un moteur pas à pas, PhD thesis, Reims, 1992.

[KHA 92] KHALIL H.-K., Nonlinear Systems, Macmillan, New York, 1992. [KUO 79] KUO B.C., Step Motors and Control System, SRL Publishing, 1979.

[LOU 04a] LOUIS J-P. (ed.), Modélisation des Machines Électriques en vue de Leur Commande, Hermes-Lavoisier, 2004.

[LOU 04b] LOUIS J-P., Modèles pour la Commande des Actionneurs Électriques, Hermes-Lavoisier, 2004.

[MAT 04] MATAGNE E., DA SILVA GARRIDO M., “Conversion électromécanique d’énergie : du phénomène physique à la modélisation dynamique”,in: LOUIS J-.P. (ed.), Modélisation des Machines Électriques en vue de Leur Commande, Hermes-Lavoisier, 2004.

[NAS 58] NASLIN P., Technologie et Calcul Pratique des Systèmes Asservis, Dunod, 1958.

[OTT 90] OTT E., GREBOGI C., YORKE J.A., “Controlling chaos”, Physical Review Letters, vol. 64, pp. 1196–1199, 1990.

[PER 00] PERA M-C., ROBERT B., GOELDEL C., “Nonlinear dynamics in electromechanical systems-application to a hybrid stepping motor”, Electromotion, vol. 7, pp. 31–42, 2000.

[PYR 92] PYRAGAS K., “Continuous control of chaos by self-controlling feedback”, Physics Letters A, vol. 170, pp. 421–428, 1992.

[PYR 95] PYRAGAS K., “Control of chaos via extended delay feedback”, Physics Letters A, vol. 206, pp. 323–330, 1995.

[REI 03] REISS J., ROBERT B., ALIN F., SANDLER M., “Flip phenomena and co-existing attractors in an incremental actuator”, Proceedings of IEEE International Conference on Industrial Technology, CD-ROM Maribor, Slovenia, December 9-12, 2003.

[ROB 00] ROBERT B., PERA M.-C., GOELDEL C., “Dynamiques apériodiques et chaotiques du moteur pas à pas”, Revue Internationale de Génie Electrique, vol. 3, pp. 375–410, 2000.

[SAR 04] SARGOS F-M., MEIBODY-TABAR F., “Modèles dynamiques des machines synchrones”, in: LOUIS J-P. (ed.), Modélisation des Machines Électriques en vue de Leur Commande, Hermes-Lavoisier, 2004.

[YAN 02] YANG S-K., CHEN C-L., YAU H-T., “Control of chaos in Lorenz system”, Chaos, Solitons & Fractals, vol. 13, pp. 767–780, 2002.

---

1 Chapter written by Bruno ROBERT and Moez FEKI.

1 We need to signal that at the highest frequencies the functioning becomes vibratory and the nonlinearity of dry friction type can become perceptible.

2 According to the structure of the motor, the expression of the electrical angle, which depends on the number of rotor teeth, the number of stator teeth and the number of magnet pole pairs can vary.

3 This remark excludes the analysis of functioning in the neighborhood of stable equilibrium, which is out of context for the model in mean torque, but also for vibratory type functioning, i.e. at a mean speed of 0.

4 See footnote 2 on page 332.