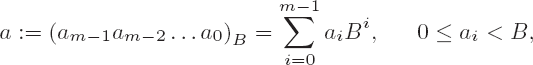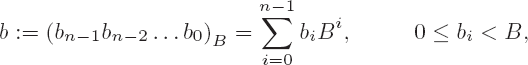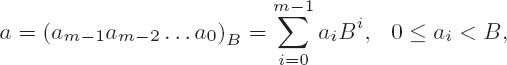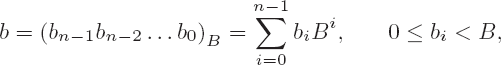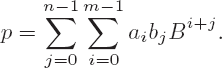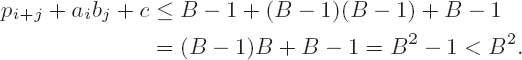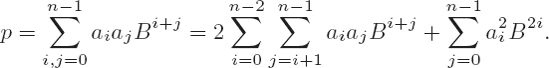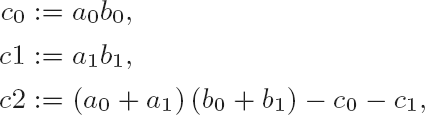Thus calculation can be seen as the basis and foundation of all the arts.
And you, poor creature, you are completely useless. Look at me. Everyone needs me.
There is one small prerequisite for mastering the mathemagic tricks in this chapter—you need to know the multiplication tables through 10 ... backward and forward.
The fundamental building blocks of any software package for computer arithmetic are the functions that carry out the basic operations of addition, subtraction, multiplication, and division. The efficiency of the entire package hangs on the last two of these, and for that reason great care must be taken in the selection and implementation of the associated algorithms. Fortunately, volume 2 of Donald Knuth's classic The Art of Computer Programming contains most of what we need for this portion of the FLINT/C functions.
In anticipation of their representation to come, the functions developed in the following sections use the operations cpy_l(), which copies one CLINT object to another in the sense of an allocation, and cmp_l(), which makes a comparison of the sizes of two CLINT values. For a more precise description see Sections 7.4 and 8.
Let us mention at this point that for the sake of clarity, in this chapter the functions for the fundamental arithmetic operations are developed all of a piece, while in Chapter 5 it will prove practical to split some of the functions into their respective "core" operations and from there develop additional steps such as the elimination of leading zeros and the handling of overflow and underflow, where, however, the syntax and semantics of the functions are kept intact. For an understanding of the relations described in this chapter this is irrelevant, so that for now we can forget about these more difficult issues.
This notion of "further counting" means, "to the integer n1 add the integer n2," and the integer s at which one arrives by this further counting is called "the result of addition" or the "sum of n1 and n2" and is represented by n1 + n2.
Since addition and subtraction are in principle the same operation with differing signs, the underlying algorithms are equivalent, and we can deal with them together in this section. We consider operands a and b with representations
where we assume a ≥ b. For addition this condition represents no restriction, since it can always be achieved by interchanging the two summands. For subtraction it means that the difference is positive or zero and therefore can be represented as a CLINT object without reduction modulo (Nmax + 1).
Addition consists essentially of the following steps.
Algorithm for the addition a + b
Set i ← 0 and c ← 0.
Set t ← ai + bi + c, si ← t mod B, and c ←

Set i ← i + 1; if i ≤ n − 1, go to step 2.
Set t ← ai + c, si ← t mod B, and c ←

Set i ← i +1; if i ≤ m − 1, go to step 4.
Set sm ← c.
Output s = (smsm−1 ...s0)B.
The digits of the summands, together with the carry, are added in step 2, with the less-significant part stored as a digit of the sum, while the more-significant part is carried to the next digit. If the most-significant digit of one of the summands is reached, then in step 4 any remaining digits of the other summand are added to any remaining carries one after the other. Until the last summand digit is processed, the less-significant part is stored as a digit of the sum, and the more-significant part is used as a carry to the next digit. Finally, if there is a leftover carry at the end, it is stored as the most-significant digit of the sum. The output of this digit is suppressed if it has the value zero.
Steps 2 and 4 of the algorithm appear in a similar form in the case of subtraction, multiplication, and division. The associated code, which is illustrated by the following lines, is typical for arithmetic functions:[7]
s = (USHORT)(carry = (ULONG)a + (ULONG)b + (ULONG)(USHORT)(carry >> BITPERDGT));
The intermediate value t that appears in the algorithm is represented by the variable carry, of type ULONG, which holds the sum of the digits ai and bi as well as the carry of the previous operation. The new summation digit si is stored in the less-significant part of carry, from where it is taken by means of a cast as a USHORT. The resulting carry from this operation is held in the more-significant part of carry for the next operation.
The implementation of this algorithm by our function add_l() deals with a possible overflow of the sum, where in this case a reduction of the sum modulo (Nmax + 1) is carried out.
Function: | addition |
Syntax: |
|
Input: |
|
Output: |
|
Return: |
|
int
add_l (CLINT a_l, CLINT b_l, CLINT s_l)
{
clint ss_l[CLINTMAXSHORT + 1];
clint *msdptra_l, *msdptrb_l;
clint *aptr_l, *bptr_l, *sptr_l = LSDPTR_L (ss_l);
ULONG carry = 0L;
int OFL = E_CLINT_OK;Note
The pointers for the addition loop are set. Here it is checked which of the two summands has the greater number of digits. The pointers aptr_l and msdaptr_l are initialized such that they point respectively to the least-significant and most-significant digits of the summand that has the most digits, or to those digits of a_l if both summands are of the same length. This holds analogously for the pointers bptr_l and msdbptr_l, which point to the least-significant and most-significant digits of the shorter summand, or to those digits of b_l. The initialization is carried out with the help of the macro LSDPTR_L() for the least-significant digits and MSDPTR_L() for the most-significant digits of a CLINT object. The macro DIGITS_L (a_l) specifies the number of digits of the CLINT object a_l, and with SETDIGITS_L(a_l, n) the number of digits of a_l is set to the value n.
if (DIGITS_L (a_l) < DIGITS_L (b_l))
{
aptr_l = LSDPTR_L (b_l);
bptr_l = LSDPTR_L (a_l);
msdptra_l = MSDPTR_L (b_l);
msdptrb_l = MSDPTR_L (a_l);
SETDIGITS_L (ss_l, DIGITS_L (b_l));
}
else
{
aptr_l = LSDPTR_L (a_l);
bptr_l = LSDPTR_L (b_l);
msdptra_l = MSDPTR_L (a_l);
msdptrb_l = MSDPTR_L (b_l);
SETDIGITS_L (ss_l, DIGITS_L (a_l));
}Note
In the first loop of add_l the digits of a_l and b_l are added and stored in the result variable ss_l. Any leading zeros cause no problem, and they are simply used in the calculation and filtered out when the result is copied to s_l. The loop runs from the least-significant digit of b_l to the most-significant digit. This corresponds exactly to the process of pencil-and-paper addition as learned at school. As promised, here is the implementation of the carry.
while (bptr_l <= msdptrb_l)
{
*sptr_l++ = (USHORT)(carry = (ULONG)*aptr_l++
+ (ULONG)*bptr_l++ + (ULONG)(USHORT)(carry >> BITPERDGT));
}Note
The two USHORT values *aptr and *bptr are copied via a cast to ULONG representation and added. To this the carry from the last interation is added. The result is a ULONG value that contains the carry from the addition step in its higher-valued word. This value is allocated to the variable carry and there reserved for the next iteration. The value of the resulting digit is taken from the lower-valued word of the addition result via a cast to the type USHORT. The carry saved in the higher-valued word of carry is included in the next iteration by a shift to the right by the number BITPERDGT of bits used for the representation of USHORT and a cast to USHORT.
In the second loop only the remaining digits of a_l are added to a possible existing carry and stored in s_l.
while (aptr_l <= msdptra_l)
{
*sptr_l++ = (USHORT)(carry = (ULONG)*aptr_l++
+ (ULONG)(USHORT)(carry >> BITPERDGT));
}Note
If after the second loop there is a carry, the result is one digit longer than a_l. If it is determined that the result exceeds the maximal value Nmax representable by the CLINT type, then the result is reduced modulo (Nmax + 1) (see Chapter 5), analogously to the treatment of standard unsigned types. In this case the status announcement of the error code E_CLINT_OFL is returned.
if (carry & BASE)
{
*sptr_l = 1;
SETDIGITS_L (ss_l, DIGITS_L (ss_l) + 1);
}
if (DIGITS_L (ss_l) > (USHORT)CLINTMAXDIGIT) /* overflow? */
{
ANDMAX_L (ss_l); /* reduce modulo (Nmax + 1) */
OFL = E_CLINT_OFL;
}
cpy_l (s_l, ss_l);
return OFL;
}The run time t of all the procedures given here for addition and subtraction is t = O(n), and thus proportional to the number of digits of the larger of the two operands.
Now that we have seen addition, we shall present the algorithm for subtraction of two numbers a and b with representations
to base B.
Algorithm for the subtraction a − b
Set i ← 0 and c ← 1.
If c = 1, sett ← B + ai − bi; otherwise, sett ← B − 1 + ai − bi.
Set di ← t mod B and c ←

Set i ← i + 1; if i ≤ n − 1, go to step 2.
If c = 1, set t ← B + ai; otherwise, sett ← B − 1 + ai.
Set di ← t mod B and c ←

Set i ← i + 1; if i ≤ m − 1, go to step 5.
Output d = (dm − 1 dm − 2 ...d0)B.
The implementation of subtraction is identical to that of addition, with the following exceptions:
The
ULONGvariablecarryis used to "borrow" from the next-higher digit of the minuend if a digit of the minuend is smaller than the corresponding digit of the subtrahend.Instead of an overflow one must be on the lookout for a possible underflow, in which case the result of the subtraction would actually be negative; however, since
CLINTis anunsignedtype, there will be a reduction modulo (Nmax + 1) (see Chapter 5). The function returns the error codeE_CLINT_UFLto indicate this situation.Finally, any existing leading zeros are eliminated.
Thus we obtain the following function, which subtracts a CLINT number b_l from a number a_l.
Function: | subtraction |
Syntax: | |
Input: |
|
Output: |
|
Return: |
|
int
sub_l (CLINT aa_l, CLINT bb_l, CLINT d_l)
{
CLINT b_l;
clint a_l[CLINTMAXSHORT + 1]; /* allow 1 additional digit in a_l */
clint *msdptra_l, *msdptrb_l;
clint *aptr_l = LSDPTR_L (a_l);
clint *bptr_l = LSDPTR_L (b_l);
clint *dptr_l = LSDPTR_L (d_l);
ULONG carry = 0L;
int UFL = E_CLINT_OK;
cpy_l (a_l, aa_l);
cpy_l (b_l, bb_l);
msdptra_l = MSDPTR_L (a_l);
msdptrb_l = MSDPTR_L (b_l);Note
In the following the case a_l < b_l is considered, in which b_l is subtracted not from a_l, but from the largest possible value, Nmax. Later, the value (minuend+1) is added to this difference, so that altogether the calculation is carried out modulo (Nmax + 1). To generate the value Nmax the auxiliary function setmax_l() is used.
if (LT_L (a_l, b_l))
{
setmax_l (a_l);
msdptra_l = a_l + CLINTMAXDIGIT;
SETDIGITS_L (d_l, CLINTMAXDIGIT);
UFL = E_CLINT_UFL;
} else
{
SETDIGITS_L (d_l, DIGITS_L (a_l));
}
while (bptr_l <= msdptrb_l)
{
*dptr_l++ = (USHORT)(carry = (ULONG)*aptr_l++
- (ULONG)*bptr_l++ - ((carry & BASE) >> BITPERDGT));
}
while (aptr_l <= msdptra_l)
{
*dptr_l++ = (USHORT)(carry = (ULONG)*aptr_l++
- ((carry & BASE) >> BITPERDGT));
}
RMLDZRS_L (d_l);Note
The required addition of (minuend + 1) to the difference Nmax − b_l stored in d_l is carried out before the output of d_l.
if (UFL)
{
add_l (d_l, aa_l, d_l);
inc_l (d_l);
}
return UFL;
}In addition to the functions add_l() and sub_l() two special functions for addition and subtraction are available, which operate on a USHORT as the second argument instead of a CLINT. These are called mixed functions and identified by a function name with a prefixed "u," as in the functions uadd_l() and usub_l() to follow. The use of the function u2clint_l() for converting a USHORT value into a CLINT object follows in anticipation of its discussion in Chapter 8.
Function: | mixed addition of a |
Syntax: | |
Input: |
|
Output: |
|
Return: |
|
int
uadd_l (CLINT a_l, USHORT b, CLINT s_l)
{
int err;
CLINT tmp_l;
u2clint_l (tmp_l, b);
err = add_l (a_l, tmp_l, s_l);
return err;
}Function: | subtraction of a |
Syntax: | |
Input: |
|
Output: |
|
Return: |
|
int
usub_l (CLINT a_l, USHORT b, CLINT d_l)
{
int err;
CLINT tmp_l; u2clint_l (tmp_l, b);
err = sub_l (a_l, tmp_l, d_l);
return err;
}Two further useful special cases of addition and subtraction are realized in the functions inc_l() and dec_l(), which increase or decrease a CLINT value by 1. These functions are designedas accumulator routines: The operandisoverwritten with the return value, which has proved practical in the implementation of many algorithms.
It is not surprising that the implementations of inc_l() and dec_l() are similar to those of the functions add_l() and sub_l(). They test for overflow and underflow, respectively, and return the corresponding error codes E_CLINT_OFL and E_CLINT_UFL.
Function: | |
Syntax: |
|
Input: |
|
Output: |
|
Return: |
|
int
inc_l (CLINT a_l)
{
clint *msdptra_l, *aptr_l = LSDPTR_L (a_l);
ULONG carry = BASE;
int OFL = E_CLINT_OK;
msdptra_l = MSDPTR_L (a_l);
while ((aptr_l <= msdptra_l) && (carry & BASE))
{
*aptr_l = (USHORT)(carry = 1UL + (ULONG)*aptr_l);
aptr_l++;
}
if ((aptr_l > msdptra_l) && (carry & BASE))
{
*aptr_l = 1;
SETDIGITS_L (a_l, DIGITS_L (a_l) + 1);
if (DIGITS_L (a_l) > (USHORT) CLINTMAXDIGIT) /* overflow ? */
{
SETZERO_L (a_l); /* reduce modulo (Nmax + 1) */
OFL = E_CLINT_OFL;
}
}
return OFL;
}Function: | |
Syntax: | |
Input: |
|
Output: |
|
Return: |
|
int
dec_l (CLINT a_l)
{
clint *msdptra_l, *aptr_l = LSDPTR_L (a_l);
ULONG carry = DBASEMINONE;
if (EQZ_L (a_l)) /* underflow ? */
{
setmax_l (a_l); /* reduce modulo max_l */
return E_CLINT_UFL;
}
msdptra_l = MSDPTR_L (a_l);
while ((aptr_l <= msdptra_l) && (carry & (BASEMINONEL << BITPERDGT)))
{
*aptr_l = (USHORT)(carry = (ULONG)*aptr_l - 1L);
aptr_l++;
}
RMLDZRS_L (a_l);
return E_CLINT_OK;
}If the individual summands n1, n2, n3, ..., nr are all equal to one and the same integer n, then one calls the addition "multiplication of the integer n by the multiplier r" and sets n1 + n2 + n3 + ••• + nr = rn.
Multiplication is one of the most critical functions of the entire FLINT/C package due to the computation time required for its execution, since together with division it determines the execution time of many algorithms. In contrast to our experience heretofore with addition and subtraction, the classical algorithms for multiplication and division have execution times that are quadratic in the number of digits of the arguments, and it is not for nothing that Donald Knuth asks in one of his chapter headings, "How fast can we multiply?"
In the literature there have been published various procedures for rapid multiplication of large and very large integers, among which are some rather difficult methods. An example of this is the procedure developed by A. Schönhage and V. Strassen for multiplying large numbers by application of fast Fourier transforms over finite fields. The running time in terms of the number of digits n in the arguments is bounded above by O(n log n log log n) (see [Knut], Section 4.3.3). These techniques encompass the fastest known multiplication algorithms, but their advantage in speed over the classical O (n2) methods comes into play only when the number of binary digits is in the range 8,000–10,000. Based on the demands of cryptographic systems, such numbers, at least for the present, are far beyond the range envisioned in the application domain of our functions.
For our realization of multiplication for the FLINT/C package we would like first to use as a basis the grade school method based on "Algorithm M" given by Knuth (see [Knut], Section 4.3.1), and we shall make an effort to achieve as efficient an implementation of this procedure as possible. Then we shall occupy ourselves in a close examination of the calculation of squares, which offers great potential for savings, and for both cases we shall finally look at the multiplication procedure of Karatsuba, which is asymptotically better than O (n2).[8] The Karatsuba multiplication arouses our curiosity, since it seems simple, and one could pleasantly occupy a (preferably rainy) Sunday afternoon trying it out. We shall see whether this procedure has anything to contribute to the FLINT/C library.
We are considering multiplication of two numbers a and b with representations
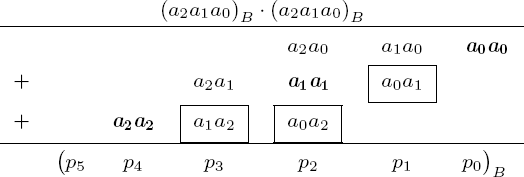
to the base B. According to the procedure that we learned in school, the product ab can be computed for m = n = 3 as shown in Figure 4-1.
First, the partial products (a2a1a0)B • bj for j = 0, 1, 2, are calculated: The values aibj are the least-significant digits of the terms (aibj + carry) with the inner products aibj, and the c2j are the more-significant digits of the p2j. The partial products are summed at the end to form the product p = (p5p4p3p2p1 p0) B.
In the general case the product p = ab has the value
The result of a multiplication of two operands with m and n digits has at least m + n − 1 and at most m + n digits. The number of elementary multiplication steps (that is, multiplications by factors smaller than the base B) is mn.
A multiplication function that followed exactly the schema outlined above would first calculate all partial products, store these values, and then sum them up, each provided with the appropriate scaling factor. This school method is quite suitable for calculating with pencil and paper, but for the possibilities of a computer program it is somewhat cumbersome. A more efficient alternative consists in adding the inner products aibj at once to the accumulated values in the result digit pi+j, to which are added the carries c from previous steps. The resulting value for each pair (i, j) is assigned to a variable t:
where t can be represented as
and we then have
The current value of the result digit is taken by the assignment pi+j ← l from this representation of t. As the new carry we set c ← k.
The multiplication algorithm thus consists entirely of an outer loop for calculating the partial products ai (bn−1bn−2... b0) B and an inner loop for calculating the inner products aibj, j = 0, ..., n − 1, and the values t and pi + j. The algorithm then appears as follows.
Algorithm for multiplication
Setpi ← 0 for i = 0, ..., n − 1.
Set i ← 0.
Set j ← 0 and c ← 0.
Set t ← pi+j + aibj + c, pi+j ← t mod B, and c ←

Set j ← j + 1; if j ≤ n − 1, go to step 4.
Setpi+n ← c.
Set i ← i + 1; if i ≤ m − 1, go to step 3.
Output p = (pm+n − 1 pm+n − 2 ... p0)B.
The following implementation of multiplication contains at its core this main loop. Corresponding to the above estimate, in step 4 the lossless representation of a value less than B2 in the variable t is required. Analogously to how we proceeded in the case of addition, the inner products t are thus represented as ULONG types. The variable t is nonetheless not used explicitly, and the setting of the result digits pi+j and the carry c occurs rather within a single expression, analogous to the process already mentioned in connection with the addition function (see page 25). For initialization a more efficient procedure will be chosen than the one shown in step 1 of the algorithm.
Function: | multiplication |
Syntax: | |
Input: |
|
Output: |
|
Return: |
|
int
mul_l (CLINT f1_l, CLINT f2_l, CLINT pp_l)
{
register clint *pptr_l, *bptr_l;
CLINT aa_l, bb_l;
CLINTD p_l;
clint *a_l, *b_l, *aptr_l, *csptr_l, *msdptra_l, *msdptrb_l;
USHORT av;
ULONG carry;
int OFL = E_CLINT_OK;Note
First the variables are declared; p_l will hold the result and thus is of double length. The ULONG variable carry will hold the carry. In the first step the case is dealt with in which one of the factors, and therefore the product, is zero. Then the factors are copied into the workspaces aa_l and bb_l, and leading zeros are purged.
if (EQZ_L (f1_l) || EQZ_L (f2_l))
{
SETZERO_L (pp_l);
return E_CLINT_OK;
}
cpy_l (aa_l, f1_l);
cpy_l (bb_l, f2_l);Note
According to the declarations the pointers a_l and b_l are given the addresses of aa_l and bb_l, where a logical transposition occurs if the number of digits of aa_l is smaller than that of bb_l. The pointer a_l always points to the operand with the larger number of digits.
if (DIGITS_L (aa_l) < DIGITS_L (bb_l))
{
a_l = bb_l;
b_l = aa_l;
}
else
{
a_l = aa_l;
b_l = bb_l;
}
msdptra_l = a_l + *a_l;
msdptrb_l = b_l + *b_l;Note
To save time in the computation, instead of the initialization required above, the partial product (bn − 1bn − 2 ... b0)B • a0 is calculated in a loop and stored in pn,pn − 1,...,p0.
carry = 0;
av = *LSDPTR_L (a_l)
for (bptr_l = LSDPTR_L (b_l), pptr_l = LSDPTR_L (p_l);
bptr_l <= msdptrb_l; bptr_l++, pptr_l++)
{
*pptr_l = (USHORT)(carry = (ULONG)av * (ULONG)*bptr_l +
(ULONG)(USHORT)(carry >> BITPERDGT));
}
*pptr_l = (USHORT)(carry >> BITPERDGT);Note
Next follows the nested multiplication loop, beginning with the digit a_l[2] of a_l.
for (csptr_l = LSDPTR_L (p_l) + 1, aptr_l = LSDPTR_L (a_l) + 1;
aptr_l <= msdptra_l; csptr_l++, aptr_l++)
{
carry = 0;
av = *aptr_l;
for (bptr_l = LSDPTR_L (b_l), pptr_l = csptr_l;
bptr_l <= msdptrb_l; bptr_l++, pptr_l++) {
*pptr_l = (USHORT)(carry = (ULONG)av * (ULONG)*bptr_l +
(ULONG)*pptr_l + (ULONG)(USHORT)(carry >> BITPERDGT));
}
*pptr_l = (USHORT)(carry >> BITPERDGT);
}Note
The largest possible length of the result is the sum of the numbers of digits of a_l and b_l. If the result has one digit fewer, this is determined by the macro RMLDZRS_L.
SETDIGITS_L (p_l, DIGITS_L (a_l) + DIGITS_L (b_l)); RMLDZRS_L (p_l);
Note
If the result is larger than can be accommodated in a CLINT object, it is reduced, and the error flag OFL is set to the value E_CLINT_OFL. Then the reduced result is assigned to the object pp_l.
if (DIGITS_L (p_l) > (USHORT)CLINTMAXDIGIT) /* overflow ? */
{
ANDMAX_L (p_l); /* reduce modulo (Nmax + 1) */
OFL = E_CLINT_OFL;
}
cpy_l (pp_l, p_l);
return OFL;
}With t = O(mn) the run time t for the multiplication is proportional to the product of the numbers of digits m and n of the operands. For multiplication, too, the analogous mixed function is implemented, which processes a CLINT type and as second argument a USHORT type. This short version of CLINT multiplication requires O(n) CPU multiplications, which is the result not of any particular refinement of the algorithm, but of the shortness of the USHORT argument. Later, we shall set this function implicitly within a special exponentiation routine for USHORT bases (see Chapter 6, the function wmexp_l()).
For the implementation of the umul_l() function we return primarily to a code segment of the mul_l() function and reuse it with a few modifications.
Function: | multiplication of a |
Syntax: |
|
Input: |
|
Output: |
|
Return: |
|
int
umul_l (CLINT aa_l, USHORT b, CLINT pp_l)
{
register clint *aptr_l, *pptr_l;
CLINT a_l;
clint p_l[CLINTMAXSHORT + 1];
clint *msdptra_l;
ULONG carry;
int OFL = E_CLINT_OK;cpy_l (a_l, aa_l);
if (EQZ_L (a_l) || 0 == b)
{
SETZERO_L (pp_l);
return E_CLINT_OK;
}Note
After these preliminaries, the CLINT factor is multiplied in a pass through a loop by the USHORT factor, and at the end the carry is stored in the most-significant USHORT digit of the CLINT value.
msdptra_l = MSDPTR_L (a_l);
carry = 0;
for (aptr_l = LSDPTR_L (a_l), pptr_l = LSDPTR_l (p_l);
aptr_l <= msdptra_l; aptr_l++, pptr_l++)
{
*pptr_l = (USHORT)(carry = (ULONG)b * (ULONG)*aptr_l +
(ULONG)(USHORT)(carry >> BITPERDGT));
}
*pptr_l = (USHORT)(carry >> BITPERDGT);
SETDIGITS_L (p_l, DIGITS_L (a_l) + 1);
RMLDZRS_L (p_l);
if (DIGITS_L (p_l) > (USHORT)CLINTMAXDIGIT) /* overflow ? */
{
ANDMAX_L (p_l); /* reduce modulo (Nmax + 1) */
OFL = E_CLINT_OFL;
}
cpy_l (pp_l, p_l);
return OFL;
}The calculation of a large square is accomplished with significantly fewer multiplications than in the case of the multiplication of large numbers. This is a result of the symmetry in the multiplication of identical operands. This observation is very important, since when it comes to exponentiation, which involves not one, but hundreds, of squarings, we shall be able to achieve considerable savings in speed. We again look at the well-known multiplication schema, this time with two identical factors (a2a1a0)B (see Figure 4-2).
We recognize that the inner products aiaj for i = j appear once (in boldface in Figure 4-2) and twice for i ≠ j (in boxes in the figure). Thus we can save three out of nine multiplications by multiplying the sum aiaj Bi+j for i<j by 2. The sum of the inner products of a square can then be written as
The number of required elementary multiplications is thus reduced with respect to the school method from n2 to n(n + 1)/2.
A natural algorithmic representation of squaring calculates the above expression with the two summands in two nested loops.
Algorithm 1 for squaring
Set pi ← 0 for i = 0 ,...,n − 1.
Set i ← 0.
Set t ← p2i + ai2, p2i ← t mod B, and c ←

Set j ← i + 1. If j = n, go to step 7.
Sett ← pi+j + 2aiaj + c, pi+j ← t (modB), andc ←

Set j ← j + 1; if j ≤ n − 1, go to step 5.
Setpi+n ← c.
Set j ← i + 1; if i = n − 1, go to step 7.
Outputp = (p2n − 1 p2n − 2 ...p 0)B.
In selecting the necessary data types for the representation of the variables we must note that t can assume the value
(B − 1) + 2(B − 1)2 + (B − 1) = 2B2 − 2B
(in step 5 of the algorithm). But this means that for representing t to base B more than two digits to base B will be needed, since we also have B2 − 1 < 2B2 −2B <
2B2 − 1, and so a ULONG will not suffice for representing t (the inequality above is derived from the fact that one additional binary digit is needed). While this poses no problem for an assembler implementation, in which one has access to the carry bit of the CPU, it is difficult in C to handle the additional binary digit. To get around this dilemma, we alter the algorithm in such a way that in step 5 the required multiplication by 2 is carried out in a separate loop. It is then required that step 3 be carried out in its own loop, whereby for a slight extra expenditure of effort in loop management we are spared the additional binary digit. The altered algorithm is as follows.
Initialization: Set pi ← 0 for i = 0,...,n − 1.
Calculate the product of digits of unequal index: Set i ← 0.
Set j ← i + 1 and c ← 0.
Set t ← pi + j + aiaj + c, pi + j ← t mod B, and c ←

Set j ← j + 1; if j ≤ n − 1, go to step 4.
Set pi+n ← c.
Set i ← i + 1; if i ≤ n − 2, go to step 3.
Multiplication of inner products by 2: Set i ← 1 and c ← 0.
Set t ← 2pi + c, pi ← t mod B, and c ←

Set i ← i + 1; if i ≤ 2n − 2, go to step 9.
Set p2n−1 ← c.
Addition of the inner squares: Set i ← 0 and c ← 0.
Set t ← p2i + a2 i + c, p2i ← t mod B, and c ←

Set t ← p2i+1 + c, p2i+1 ← t mod B, and c ←

Set i ← i +1; if i ≤ n − 1, go to step 13.
Setp2n−1 ← p2n−1 + c; outputp = (p2n − 1 p2n−2 ...p 0)B•
In the C function for squaring the initialization in step 1 is likewise, in analogy to multiplication, replaced by the calculation and storing of the first partial product a0 (an − 1 an − 2 ...a1)B•
Function: | squaring |
Syntax: | |
Input: |
|
Output: |
|
Return: |
|
int
sqr_l (CLINT f_l, CLINT pp_l)
{
register clint *pptr_l, *bptr_l;
CLINT a_l;
CLINTD p_l;
clint *aptr_l, *csptr_l, *msdptra_l, *msdptrb_l, *msdptrc_l;
USHORT av;
ULONG carry;
int OFL = E_CLINT_OK;
cpy_l (a_l, f_l);
if (EQZ_L (a_l))
{
SETZERO_L (pp_l);
return E_CLINT_OK;
}
msdptrb_l = MSDPTR_L (a_l);
msdptra_l = msdptrb_l - 1;Note
The initialization of the result vector addressed by pptr_l is carried out by means of the partial product a0 (an − 1 an − 2 ... a1)B, in analogy with multiplication. The digit p0 is here not assigned; it must be set to zero.
*LSDPTR_L (p_l) = 0;
carry = 0;
av = *LSDPTR_L (a_l);
for (bptr_l = LSDPTR_L (a_l) + 1, pptr_l = LSDPTR_L (p_l) + 1;
bptr_l <= msdptrb_l; bptr_l++, pptr_l++){
*pptr_l = (USHORT)(carry = (ULONG)av * (ULONG)*bptr_l +
(ULONG)(USHORT)(carry >> BITPERDGT));
}
*pptr_l = (USHORT)(carry >> BITPERDGT);Note
The loop for summing the inner products aiaj.
for (aptr_l = LSDPTR_L (a_l) + 1, csptr_l = LSDPTR_L (p_l) + 3;
aptr_l <= msdptra_l; aptr_l++, csptr_l += 2)
{
carry = 0;
av = *aptr_l;
for (bptr_l = aptr_l + 1, pptr_l = csptr_l; bptr_l <= msdptrb_l;
bptr_l++, pptr_l++)
{
*pptr_l = (USHORT)(carry = (ULONG)av * (ULONG)*bptr_l + (ULONG)*pptr_l +
(ULONG)(USHORT)(carry >> BITPERDGT));
}
*pptr_l = (USHORT)(carry >> BITPERDGT);
}
msdptrc_l = pptr_l;Note
Then comes multiplication of the intermediate result in pptr_l by 2 via shift operations (see also Section 7.1).
carry = 0;
for (pptr_l = LSDPTR_L (p_l); pptr_l <= msdptrc_l; pptr_l++)
{
*pptr_l = (USHORT)(carry = (((ULONG)*pptr_l) << 1) +
(ULONG)(USHORT)(carry >> BITPERDGT));
}
*pptr_l = (USHORT)(carry >> BITPERDGT);Note
Now we compute the "main diagonal."
carry = 0;
for (bptr_l = LSDPTR_L (a_l), pptr_l = LSDPTR_L (p_l);
bptr_l <= msdptrb_l; bptr_l++, pptr_l++){
*pptr_l = (USHORT)(carry = (ULONG)*bptr_l * (ULONG)*bptr_l +
(ULONG)*pptr_l + (ULONG)(USHORT)(carry >> BITPERDGT));
pptr_l++;
*pptr_l = (USHORT)(carry = (ULONG)*pptr_l + (carry >> BITPERDGT));
}SETDIGITS_L (p_l, DIGITS_L (a_l) << 1);
RMLDZRS_L (p_l);
if (DIGITS_L (p_l) > (USHORT)CLINTMAXDIGIT) /* overflow ? */
{
ANDMAX_L (p_l); /* reduce modulo (Nmax + 1) */
OFL = E_CLINT_OFL;
}
cpy_l (pp_l, p_l);
return OFL;
}The run time for squaring is, with O (n2), likewise quadratic in the number of digits of the operators, but with n(n + 1)/2 elementary multiplications it is about twice as fast as multiplication.
The antispirit of multiplication and division deconstructed everything and then focused only on a specific part of the whole.
As announced, we shall now consider a method of multiplication named for the Russian mathematician A. Karatsuba, who has published several variants of it (See [Knut], Section 4.3.3). We assume that a and b are natural numbers with n = 2k digits to base B, so thatwe can write a = (a1a0)Bk and b = (b1b0) Bk with digits a0 and a1, respectively b0 and b1, to base Bk. Were we to multiply a and b in the traditional manner, then we would obtain the expression
ab = B2k a1 b1 + Bk (a0b1 + a1b0) + a0b0,
with four multiplications to base Bk and thus n2 = 4k2 elementary multiplications to base B. However, if we set
then we have
For calculating ab it now appears that only three more multiplications by numbers to base Bk, or 3k2 multiplications to base B, are necessary in addition to some additions and shifting operations (multiplication by Bk can be accomplished by left shifting by k digits to base B; see Section 7.1). Let us assume that the number of digits n of our factors a and b is a power of 2, with the result that by recursive application of the procedure on the remaining partial products we can end with having to carry out only elementary multiplications to base B, and this yields a total of 3log2n = nlog23 ≈ n1.585 elementary multiplications, as opposed to n2 in the classical procedure, in addition to the time for additions and shift operations.
For squaring, this process can be simplified somewhat: With
| c0 := a02, |
| c1 := a12, |
| c2 := (a0 + a1) − c0 − c1, |
we have
Furthermore, to our advantage, the factors in the squaring always have the same number of digits, which is not generally the case in multiplication. With all these advantages, we should, however, mention that recursion within a program function always costs something, so that we may hope to experience a savings in time over the classical method, which manages without the added burden of recursion, only when the numbers get large.
To obtain information on the actual time performance of the Karatsuba procedure the functions kmul() and ksqr() are provided. The division of the factors into two halves takes place in situ, and so a copying of the halves is unnecessary. But it is necessary that the functions be passed pointers to the least-significant digits of the factors and that the numbers of digits be passed separately.
The functions presented below in experimental form use the recursive procedure for factors having more than a certain number of digits determined by a macro, while for smaller factors we turn to conventional multiplication or squaring. For the case of nonrecursive multiplication the functions kmul() and ksqr() use the auxiliary functions mult() and sqr(), in which multiplication and squaring are implemented as kernel functions without the support of identical argument addresses (accumulator mode) or reduction in the case of overflow.
void
kmul (clint *aptr_l, clint *bptr_l, int len_a, int len_b, CLINT p_l)
{
CLINT c01_l, c10_l;
clint c0_l[CLINTMAXSHORT + 2];
clint c1_l[CLINTMAXSHORT + 2];
clint c2_l[CLINTMAXSHORT + 2];
CLINTD tmp_l;
clint *a1ptr_l, *b1ptr_l;
int l2;
if ((len_a == len_b) && (len_a >= MUL_THRESHOLD)
&& (0 == (len_a & 1)) )
{Note
If both factors possess the same even number of digits above the value MUL_THRESHOLD, then recursion is entered with the splitting of the factors into two halves. The pointers aptr_l, a1ptr_l, bptr_l, b1ptr_l are passed to the corresponding least-significant digits of one of the halves. By not copying the halves, we save valuable time. The values c0 and c1 are calculated by recursively calling kmul() and then stored in the CLINT variables c0_l and c1_l.
l2 = len_a/2; a1ptr_l = aptr_l + l2; b1ptr_l = bptr_l + l2; kmul (aptr_l, bptr_l, l2, l2, c0_l); kmul (a1ptr_l, b1ptr_l, l2, l2, c1_l);
Note
The value c2 := (a0 + a1)(b0) + (b1) − c0 − c1 is computed with two additions, a call to kmul(), and two subtractions. The auxiliary function addkar() takes pointers to the least-significant digits of two equally long summands together with their number of digits, and outputs the sum of the two as a CLINT value.
addkar (a1ptr_l, aptr_l, l2, c01_l);
addkar (b1ptr_l, bptr_l, l2, c10_l);
kmul (LSDPTR_L (c01_l), LSDPTR_L (c10_l),
DIGITS_L (c01_l), DIGITS_L (c10_l), c2_l);
sub (c2_l, c1_l, tmp_l);
sub (tmp_l, c0_l, c2_l);Note
The function branch ends with the calculation of Bk (Bk c1 + c2) + c0, which used the auxiliary function shiftadd(), which during the addition left shifts the first of the two CLINT summands by a given number of places to base B.
shiftadd (c1_l, c2_l, l2, tmp_l); shiftadd (tmp_l, c0_l, l2, p_l); }
Note
If one of the input conditions is not fulfilled, the recursion is interrupted and the nonrecursive multiplication mult() is called. As a requirement for calling mult() the two factor halves in aptr_l and bptr_l are brought into CLINT format.
else
{
memcpy (LSDPTR_L (c1_l), aptr_l, len_a * sizeof (clint));
memcpy (LSDPTR_L (c2_l), bptr_l, len_b * sizeof (clint));
SETDIGITS_L (c1_l, len_a);
SETDIGITS_L (c2_l, len_b);
mult (c1_l, c2_l, p_l);
RMLDZRS_L (p_l);
}
}The Karatsuba squaring process proceeds analogously to this and will not be described in detail. For calling kmul() and ksqr() we make use of the functions kmul_l() and ksqr_l(), which are equipped with the standard interface.
Function: | |
Syntax: | int kmul_l (CLINT a_l, CLINT b_l, CLINT p_l); int ksqr_l (CLINT a_l, CLINT p_l); |
Input: |
|
Output: |
|
Return: |
|
The implementation of the Karatsuba functions are contained in the source file kmul.c in the downloadable source code (www.apress.com).
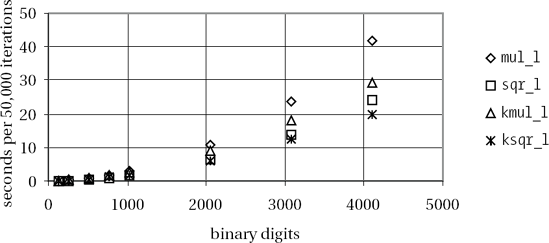
Extensive tests with these functions (on a Pentium III processor at 500 MHz under Linux) have given best results when the nonrecursive multiplication routine is called for a digit count under 40 (corresponding to 640 binary digits). The computation time of our implementation appears in Figure 4-3).
We conclude from this overview what we expected, that between standard multiplication and squaring there is a difference in performance of about 40 percent, and that for numbers of over 2000 binary digits a pronounced spread of the measured times becomes noticeable, with the Karatsuba routine in the lead. It is interesting to note that "normal" squaring sqr_l() is noticeably faster than Karatsuba multiplication, and Karatsuba squaring ksqr_l() takes the lead only above 3000 binary digits.
The large drop in performance of the Karatsuba functions for smaller numbers that was remarked on in the first edition of this book has in the meantime been eliminated. Yet there is still potential for improvement. The observable discontinuity in the calculation times of kmul_l() indicates that the recursion breaks off earlier than specified by the threshold value if the factors of a recursion step do not have an even number of digits. In the worst case this occurs right at the beginning of the multiplication, and even for very large numbers we are no better off than we were in the standard case. It would seem worthwhile, then, to extend the Karatsuba functions to be able to process arguments with differing numbers of digits and odd numbers of digits.
At the Max Planck Institute in Saarbrücken, J. Ziegler [Zieg] developed a portable implementation of Karatsuba multiplication and squaring for a 64-bit CPU (Sun Ultra-1) that overtakes the conventional method at 640 binary digits. With squaring an improvement in performance of 10% occurred at 1024 binary digits and 23% at 2048 binary digits.
C. Burnikel and J. Ziegler [BuZi] have developed an interesting recursive division procedure based on Karatsuba multiplication that from about 250 decimal digits on is increasingly faster than the school method.
Once again, however, the Karatsuba functions have no particular advantage for our cryptographic applications without considerable optimization, for which reason we shall prefer to fall back on the functions mul_l() and sqr_l(), which realize the conventional procedures (and their variants in assembly language optimized by hand; see Chapter 19). For applications for which the Karatsuba functions seem suited one could simply substitute those functions for mul_l() and sqr_l().
And marriage and death and division Make barren our lives.
We still need to place the last stone in our edifice of the fundamental arithmetic processes on large numbers, namely, division, which is the most complex of them all. Since we are calculating with natural numbers, we have only natural numbers at our disposal to express the results of a division. The principle of division that we are about to expound will be called division with remainder. It is based on the following relation. Given a,b € •, b > 0, there are unique integers q and r that satisfy a = qb + r with 0 ≤ r < b. We call q the quotient and r the remainder of the division of a by b.
Frequently, we are interested only in the remainder and couldn't care less about the quotient. In Chapter 5 we shall see the importance of the operation of calculating remainders, since it is used in many algorithms, always in conjunction with addition, subtraction, multiplication, and exponentiation. Thus it will be worth our while to have at our disposal as efficient a division algorithm as possible.
For natural numbers a and b the simplest way of executing a division with remainder consists in subtracting the divisor b from the dividend a continually until the remaining quantity r is smaller than the divisor. By counting how often we have carried out the subtraction we will have calculated the quotient. The quotient q and the remainder r have the values q =
This process of division by means of repeated subtraction is, of course, terribly boring. Even the grade school method of long division uses a significantly more efficient algorithm, in which the digits of the quotient are determined one by one and are in turn used as factors by which the divisor is multiplied. The partial products are subtracted in turn from the dividend. As an example consider the division exercise depicted in Figure 4-4.
Already at the determination of the first digit, 8, of the quotient we are required to make an estimate or else discover it by trial and error. If one makes an error, then one discovers either that the product (quotient digit times divisor) is too large (in the example, larger than 3549), or that the remainder after subtraction of the partial product from the digits of the dividend is larger than the divisor. In the first case the chosen quotient digit is too large, while in the second it is too small, and in either case it must be corrected.
This heuristic modus operandi must be replaced in an implementation of a division algorithm by a more precise process. In [Knut], Section 4.3.1, Donald Knuth has described how such rough calculations can be made precise. Let us look more closely at our example.
Let a = (am+n−1 am+n−2 ...a0)B and b = (bn−1 bn−2...b0)B be two natural numbers, represented to the base B, and for bn−1, the most-significant digit of b, we have bn−1 > 0. We are looking for the quotient q and remainder r such that a = qb + r, 0 ≤ r < b.
Following the long division above, for the calculation of q and r a quotient digit qj :=
For programming this procedure we must repeatedly determine, for two large numbers R = (rnrn − 1...r0) B and b = (bn − 1 bn − 2 ... b0)B with
Let
If bn −1 ≥
By scaling the operands a and b this can always be achieved. We choose d > 0 such that
The choice of
Algorithm for division with remainder of
Determine the scaling factor d as given above.
Set
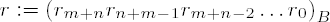
Set i ← m+n, j ← m.
Set
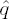
If
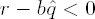
Set
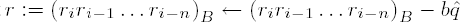
Set i ← i ← 1 and j ← j − 1; if i ≥ n, go to step 4.
Output
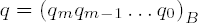
If the divisor has only a single digit b0, then the process can be shortened by initializing r with r ← 0 and dividing the two digits (rai)B by b0 with remainder. Here r is overwritten by the remainder, r ← (rai)B ← qib0, and ai runs through all the digits of the dividend. At the end, r contains the remainder and
Now that we have at hand all the requisite processes for implementing division, we present the C function for the above algorithm.
Function: | division with remainder |
Syntax: | int div_l (CLINT d1_l, CLINT d2_l, CLINT quot_l,
CLINT rem_l); |
Input: |
|
Output: |
|
Return: |
|
int
div_l (CLINT d1_l, CLINT d2_l, CLINT quot_l, CLINT rem_l)
{
register clint *rptr_l, *bptr_l;
CLINT b_l;
/* Allow double-length dividend plus 1 digit */
clint r_l[2 + (CLINTMAXDIGIT << 1)];
clint *qptr_l, *msdptrb_l, *lsdptrr_l, *msdptrr_l;
USHORT bv, rv, qhat, ri, ri_1, ri_2, bn_1, bn_2;
ULONG right, left, rhat, borrow, carry, sbitsminusd;
unsigned int d = 0;
int i;Note
The dividend
We allow the dividend to possess up to double the number of digits determined in MAXB. This makes possible the later use of division in the functions of modular arithmetic. The storage allotment for a doubly long quotient must always be available to the calling function.
cpy_l (r_l, d1_l); cpy_l (b_l, d2_l); if (EQZ_L (b_l)) return E_CLINT_DBZ;
Note
A test is made as to whether one of the simple cases is at hand: dividend = 0, dividend < divisor, or dividend = divisor. In these cases we are done.
if (EQZ_L (r_l))
{
SETZERO_L (quot_l);
SETZERO_L (rem_l);
return E_CLINT_OK ;
}
i = cmp_l (r_l, b_l);if (i == −1)
{
cpy_l (rem_l, r_l);
SETZERO_L (quot_l);
return E_CLINT_OK ;
}
else if (i == 0)
{
SETONE_L (quot_l);
SETZERO_L (rem_l);
return E_CLINT_OK ;
}Note
In the next step we check whether the divisor has only one digit. In this case a branch is made to a faster variant of division, which we shall discuss further below.
if (DIGITS_L (b_l) == 1) goto shortdiv;
Note
Now begins the actual division. First the scaling factor d is determined as the exponent of a power of two. As long as bn−1 ≥ BASEDIV2 :=
msdptrb_l = MSDPTR_L (b_l);
bn_1 = *msdptrb_l;
while (bn_1 < BASEDIV2)
{
d++;
bn_1 <<= 1;
}
sbitsminusd = (int)(BITPERDGT - d);Note
If d > 0, then the two most-significant digits
if (d > 0)
{
bn_1 += *(msdptrb_l −1) >> sbitsminusd;
if (DIGITS_L (b_l) > 2)
{
bn_2 = (USHORT)(*(msdptrb_l - 1) << d) + (*(msdptrb_l - 2) >> sbitsminusd);
}
else
{
bn_2 = (USHORT)(*(msdptrb_l - 1) << d);
}
}
else
{
bn_2 = (USHORT)(*(msdptrb_l −1));
}Note
Now the pointers msdptrr_l and lsdptrr_l are set to the most-significant, respectively least-significant, digit of
msdptrb_l = MSDPTR_L (b_l); msdptrr_l = MSDPTR_L (r_l) + 1; lsdptrr_l = MSDPTR_L (r_l) - DIGITS_L (b_l) + 1; *msdptrr_l = 0; qptr_l = quot_l + DIGITS_L (r_l) - DIGITS_L (b_l) + 1;
Note
We now enter the main loop. The pointer lsdptrr_l runs over the digits
while (lsdptrr_l <= LSDPTR_L (r_l))
{Note
As preparation for determining
ri = (USHORT)((*msdptrr_l << d) + (*(msdptrr_l - 1) >> sbitsminusd));
ri_1 = (USHORT)((*(msdptrr_l - 1) << d) + (*(msdptrr_l - 2) >> sbitsminusd));
if (msdptrr_l - 3 > r_l) /* there are four dividend digits */
{
ri_2 = (USHORT)((*(msdptrr_l - 2) << d) +
(*(msdptrr_l −3) >> sbitsminusd));
}
else /* there are only three dividend digits */
{
ri_2 = (USHORT)(*(msdptrr_l - 2) << d);
}Note
Now comes the determination of
if (ri != bn_1) /* almost always */
{
qhat = (USHORT)((rhat = ((ULONG)ri << BITPERDGT) + (ULONG)ri_1) / bn_1);
right = ((rhat = (rhat - (ULONG)bn_1 * qhat)) << BITPERDGT) + ri_2;Note
If bn_2 * qhat > right, then qhat is too large by at least 1 and by at most 2.
if ((left = (ULONG)bn_2 * qhat) > right)
{
qhat--;Note
The test is now repeated only if we have rhat = rhat + bn_1 < BASE due to the decrementing of qhat (otherwise, we already have bn_2 * qhat < BASE2 ≤ rhat * BASE).
if ((rhat + bn_1) < BASE)
{
if ((left - bn_2) > (right + ((ULONG)bn_1 << BITPERDGT)))
{
qhat--;
}
}
}
}
elseNote
In the second, rare, case, ri = bn_1, first
{
qhat = BASEMINONE;
right = ((ULONG)(rhat = (ULONG)bn_1 + (ULONG)ri_1) << BITPERDGT) + ri_2;
if (rhat < BASE)
{
if ((left = (ULONG)bn_2 * qhat) > right)
{
qhat--;
if ((rhat + bn_1) < BASE)
{
if ((left - bn_2) > (right + ((ULONG)bn_1 << BITPERDGT)))
{
qhat--;
}
}
}
}
}Note
Then comes the subtraction of qhat • b from the part
The products
qhat• bj can have two digits. Both digits are saved for the time being in theULONGvariablecarry. The more-significant word ofcarryis dealt with as a carry in the subtraction of the next-higher digit.For the case that
qhatis still too large by 1 and the difference u −qhat• b is negative, as a precaution the value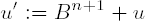
borrow = BASE;
carry = 0;
for (bptr_l = LSDPTR_L (b_l), rptr_l = lsdptrr_l;
bptr_l <= msdptrb_l; bptr_l++, rptr_l++)
{
if (borrow >= BASE)
{
*rptr_l = (USHORT)(borrow = ((ULONG)*rptr_l + BASE
(ULONG)(USHORT)(carry = (ULONG)*bptr_l *
qhat + (ULONG)(USHORT)(carry >> BITPERDGT))));
}
else
{
*rptr_l = (USHORT)(borrow = ((ULONG)*rptr_l + BASEMINONEL -
(ULONG)(USHORT)(carry = (ULONG)*bptr_l * qhat +
(ULONG)(USHORT)(carry >> BITPERDGT))));
}
}
if (borrow >= BASE) {
*rptr_l = (USHORT)(borrow = ((ULONG)*rptr_l + BASE -
(ULONG)(USHORT)(carry >> BITPERDGT)));
}
else
{
*rptr_l = (USHORT)(borrow = ((ULONG)*rptr_l + BASEMINONEL -
(ULONG)(USHORT)(carry >> BITPERDGT)));
}Note
The quotient digit is stored, subject to a possible necessary correction.
*qptr_l = qhat;
Note
As promised, now a test is made as to whether the quotient digit is too large by 1. This is extremely seldom the case (further below, special test data will be presented) and is indicated by the high-valued word of the ULONG variable borrow being equal to zero; that is, that borrow < BASE. If this is the case, then
if (borrow < BASE)
{
carry = 0;
for (bptr_l = LSDPTR_L (b_l), rptr_l = lsdptrr_l;
bptr_l <= msdptrb_l; bptr_l++, rptr_l++)
{
*rptr_l = (USHORT)(carry = ((ULONG)*rptr_l + (ULONG)(*bptr_l) +
(ULONG)(USHORT)(carry >> BITPERDGT)));
}
*rptr_l += (USHORT)(carry >> BITPERDGT);
(*qptr_l)--;
}Note
Now the pointers are set to the remainder and the quotient, and we return to the beginning of the main loop.
msdptrr_l--; lsdptrr_l--; qptr_l--; }
The length of the remainder and that of the quotient are determined. The number of digits is at most 1 more than the number of digits of the dividend minus the number of digits of the divisor. The remainder possesses at most the number of digits of the divisor. In both cases the exact length is set by the removal of leading zeros.
SETDIGITS_L (quot_l, DIGITS_L (r_l) -DIGITS_L (b_l) + 1); RMLDZRS_L (quot_l); SETDIGITS_L (r_l, DIGITS_L (b_l)); cpy_l (rem_l, r_l); return E_CLINT_OK;
Note
In the case of "short division" the divisor possesses only the digit b0, by which the two digits (rai)B are to be divided, where ai runs through all digits of the dividend; r is initialized with r ← 0 and assumes the difference r ← (rai)B ← qb0. The value r is represented by the USHORT variable rv. The value of (rai)B is stored in the ULONG variable rhat.
shortdiv:
rv=0;
bv = *LSDPTR_L (b_l);
for (rptr_l = MSDPTR_L (r_l), qptr_l = quot_l + DIGITS_L (r_l);
rptr_l >= LSDPTR_L (r_l); rptr_l--, qptr_l--)
{
*qptr_l = (USHORT)((rhat = ((((ULONG)rv) << BITPERDGT) + (ULONG)*rptr_l)) / bv);
rv = (USHORT)(rhat - (ULONG)bv * (ULONG)*qptr_l);
}
SETDIGITS_L (quot_l, DIGITS_L (r_l));
RMLDZRS_L (quot_l);
u2clint_l (rem_l, rv);
return E_CLINT_OK;
}With t = O(mn),the runtime t of the division is analogous to that for multiplication, where m and n are the numbers of digits of the dividend and divisor, respectively, to the base B.
In the sequel we shall describe a number of variants of division with remainder, all of which are based on the general division function. First we have the mixed version of the division of a CLINT type by a USHORT type. For this we return once again to the routine for small divisors of the function div_l(),where it is placed almost without alteration into its own function. We thus present only the interface of the function.
division of a | |
Syntax: | int udiv_l (CLINT dv_l, USHORT uds, CLINT q_l,
CLINT r_l); |
Input: |
|
Output: |
|
Return: |
|
We have already indicated that for a given calculation the quotient of a division is not required, and only the remainder is of interest. This will not result in a great savings of time, but in such cases, at least the passing of a pointer to the storage location of the quotient is burdensome. It is therefore worthwhile to create an independent function for computing remainders, or "residues." The mathematical background of the use of this function is discussed more fully in Chapter 5.
Function: | Remainders (reduction modulo n) |
Syntax: | |
Input: |
|
Output: |
|
Return: |
|
Simpler than the general case is the construction of the remainder modulo apower of 2, namely 2k, which is worth implementing in its own function. The remainder of the dividend in a division by 2k results from truncating its binary digits after the kth bit, where counting begins with 0. This truncation corresponds to a bitwise joining of the dividend to 2k − 1 = (111111 ...1)2, the value of k binary ones, by a logical AND (cf. Section 7.2). The operation is concentrated on the digit of the dividend in its representation to base B that contains the kth bit; all higher-valued dividend digits are irrelevant. For specifying the divisor the following function mod_l() is passed only the exponent k.
Function: | remainder modulo a power of 2 (reduction modulo 2k) |
Syntax: | |
Input: |
|
Return: |
|
int
mod2_l (CLINT d_l, ULONG k, CLINT r_l)
{
int i;Note
Since 2k > 0, there is no test for division by 0. First d_l is copied to r_l and a test is made as to whether k exceeds the maximal binary length of a CLINT number, in which case the function is terminated.
cpy_l (r_l, d_l); if (k > CLINTMAXBIT) return E_CLINT_OK;
Note
The digit in r_l in which something changes is determined and is stored as an index in i. If i is greater than the number of digits of r_l, thenweare done.
i=1+(k >> LDBITPERDGT); if (i > DIGITS_L (r_l)) return E_CLINT_OK;
Note
Now the determined digit of r_l (counting from 1) is joined by a logical AND to the value 2k mod BITPERDGT − 1 (= 2kmod 16 − 1 in this implementation). The new length i of r_l is stored in r_l[0]. After the removal of leading zeros the function is terminated.
r_l[i] &= (1U << (k & (BITPERDGT - 1))) −1U; SETDIGITS_L (r_l, i); RMLDZRS_L (r_l); return E_CLINT_OK; }
The mixed variant of calculating residues employs a USHORT type as divisor and represents the remainder again as a USHORT type, where here again only the interface is given, and we refer the reader to the FLINT/C source code for the short functions.
Function: | remainders, division of a |
Syntax: | |
Input: |
|
Return: | nonnegative remainder if all is ok |
For testing the division there are—as for all other functions as well—some considerations to be taken into account (see Chapter 13). In particular, it is important that step 5 be tested explicitly, though in randomly selected test cases it will appear with a probability of only about 2/B (= 2−15 in our implementation) (see [Knut], Section 4.3.1, Exercise 21).
In the following the given dividend a and divisor b with associated quotient q and remainder r have the effect that the program sequence associated to step 5 of the division algorithm is run through twice, and can therefore be used as test data for this particular case. Additional values with this property are contained in the test program testdiv.c.
The display of test numbers below shows the digits in hexadecimal, running from right to left in ascending order, without specifying the length:
Test values for step 5 of the division
a = e3 7d 3a bc 90 4b ab a7 a2 ac 4b 6d 8f 78 2b 2b f8 49 19
d2 91 73 47 69 0d 9e 93 dc dd 2b 91 ce e9 98 3c 56 4c f1
31 22 06 c9 1e 74 d8 0b a4 79 06 4c 8f 42 bd 70 aa aa 68
9f 80 d4 35 af c9 97 ce 85 3b 46 57 03 c8 ed ca
b = 08 0b 09 87 b7 2c 16 67 c3 0c 91 56 a6 67 4c 2e 73 e6 1a
1f d5 27 d4 e7 8b 3f 15 05 60 3c 56 66 58 45 9b 83 cc fd
58 7b a9 b5 fc bd c0 ad 09 15 2e 0a c2 65
q = 1c 48 a1 c7 98 54 1a e0 b9 eb 2c 63 27 b1 ff ff f4 fe 5c
0e 27 23
r = ca 23 12 fb b3 f4 c2 3a dd 76 55 e9 4c 34 10 b1 5c 60 64
bd 48 a4 e5 fc c3 3d df 55 3e 7c b8 29 bf 66 fb fd 61 b4
66 7f 5e d6 b3 87 ec 47 c5 27 2c f6 fb[7] The C expression in this compact form is due to my colleague Robert Hammelrath.
[8] When we say that the calculation time is asymptotically better, we mean that the larger the numbers in question, the greater the effect. One should not fall victim to premature euphoria, and for our purposes such an improvement may have no significance whatsoever.
[9] Note that for a < 0 with q = − ⌈|a|/b⌉ and r = b − (|a| + qb) if a ∤ b, respectively r = 0 if a | b, division with remainder is reduced to the case a, b €