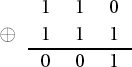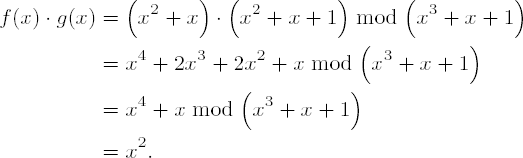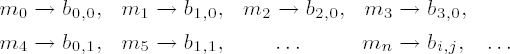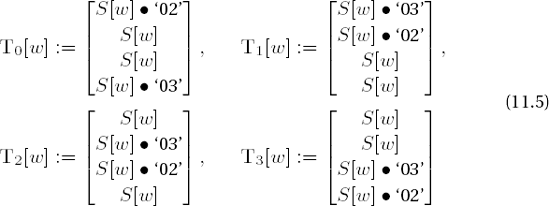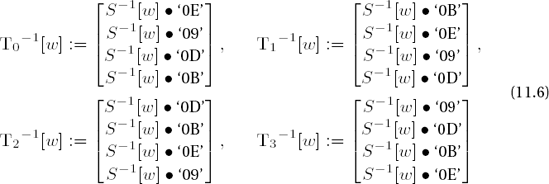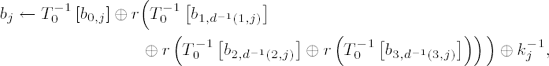I don't know if we have any real chance. He can multiply and all we can do is add. He represents progress and I just drag my feet.
The american national institute of Standards and Technology (NIST) launched a competition in 1997 under the aegis of an Advanced Encryption Standard (AES) with the goal of creating a new national standard (federal information processing standard, or FIPS) for encryption with a symmetric algorithm. Although we have concentrated our attention in this book on asymmetric cryptography, this development is important enough that we should give it some attention, if only cursorily. Through the new standard FIPS 197 [F197], an encryption algorithm will be established that satisfies all of today's security requirements and that in all of its design and implementation aspects will be freely available without cost throughout the world. Finally, it replaces the dated data encryption standard (DES), which, however, as triple DES remains available for use in government agencies. However, the AES represents the cryptographic basis of the American administration for the protection of sensitive data.
The AES competition received a great deal of attention abroad as well as in the USA, not only because whatever happens in the United States in the area of cryptography produces great effects worldwide, but because international participation was specifically encouraged in the development of the new block encryption procedure.
From an original field of fifteen candidates who entered the contest in 1998, by 1999 ten had been eliminated, a process with involvement of an international group of experts. There then remained in competition the algorithms MARS, of IBM; RC6, of RSA Laboratories; Rijndael, of Joan Daemen and Vincent Rijmen; Serpent, of Ross Anderson, Eli Biham, and Lars Knudson; and Twofish, of Bruce Schneier et al. Finally, in October 2000 the winner of the selection process was announced. The algorithm with the name "Rijndael," by Joan Daemen and Vincent Rijmen, of Belgium, was named as the future advanced encryption standard (cf. [NIST]).[32] Rijndael is a successor of the block cipher "Square," published earlier by the same authors (cf. [Squa]), which, however, had proved to be not as powerful. Rijndael was especially strengthened to attack the weaknesses of Square. The AES report of NIST gives the following basis for its decision.
Security
All candidates fulfill the requirements of the AES with respect to security against all known attacks. In comparison to the other candidates, the implementations of Serpent and Rijndael can at the least cost be protected against attacks that are based on measurements of the time behavior of the hardware (so-called timing attacks) or changes in electrical current use (so-called power or differential power analysis attacks).[33] The degradation in performance associated with such protective measures is least for Rijndael, Serpent, and Twofish, with a greater advantage to Rijndael.
Speed
Rijndael is among the candidates that permit the most rapid implementation, and it is distinguished by equally good performance across all platforms considered, such as 32-bit processors, 8-bit microcontrollers, smart cards, and implementations in hardware (see below). Of all the candidates Rijndael allows the most rapid calculation of round keys.
Memory requirement
Rijndael makes use of very limited resources of RAM and ROM memory and is thus an excellent candidate for use in restricted-resource environments. In particular, the algorithm offers the possibility to calculate round keys separately "on the fly" for each round. These properties have great significance for applications on microcontrollers such as used in smart cards. Due to the structure of the algorithm, the requirements on ROM storage are least when only one direction, that is, either encryption or decryption, is realized, and they increase when both functions are needed. Nonetheless, with respect to resource requirements Rijndael is not beaten by any of the other four contestants.
Implementation in hardware
Rijndael and Serpent are the candidates with the best performance in hardware implementations, with a slight advantage going to Rijndael due to its better performance in output and cipher feedback modes.
The report offers further criteria that contributed to the decision in favor of Rijndael, which are collected into a closing summary (see [NIST], Section 7):
There are many unknowns regarding future computing platforms and the wide range of environments in which the AES will be implemented. However, when considered together, Rijndael's combination of security, performance, efficiency, implementability, and flexibility make it an appropriate selection for the AES for use in the technology of today and in the future.
Given the openness of the selection process and the politically interesting fact that with Rijndael an algorithm of European vintage was selected, one might expect future speculation about secret properties, hidden trap doors, and deliberately built-in weaknesses to be silenced, which never quite succeeded with DES.
Before we get involved with the functionality of Rijndael, we would like as preparation to go on a brief excursion into the arithmetic of polynomials over finite fields, which leans heavily on the presentation in [DaRi], Section 2.
We start by looking at arithmetic in the field • 2n, the finite field with 2n elements, where an element of • 2n is represented as a polynomial f(x) = an− 1xn−1 + an−2xn−2 + ... + a1x+ a0 with coefficients ai in • 2 (which is isomorphic to •2). Equivalently, an element of •2n can be represented simply as an n-tuple of polynomial coefficients, each representation offering its own advantages. The polynomial representation is well suited for manual calculation, while the representation as a tuple of coefficients corresponds well to a computer's binary representation of numbers. To demonstrate this, we notate •23 as a sequence of eight polynomials and again as eight 3-tuples with their associated numerical values (see Table 11-1).
Addition of polynomials proceeds by adding the coefficients in •2: If f(x) := x2 + x and g(x) := x2 + x + 1, then f(x) + g(x) = 2x2 + 2x + 1 = 1, since 1+1 = 0 in •2. We can carry out addition of 3-tuples in •23 column by column. We see, then, for example, that the sum of (1 1 0) and (1 1 1) is (0 0 1):
The addition of digits takes place in •2 and is not to be confused with binary addition, which can involve a carry. This process is reminiscent of our XOR function in Section 7.2, which executes the same operation in •n for large n.
Multiplication in •23 is accomplished by multiplying each term of the first polynomial by each term of the second and then summing the partial products. The sum is then reduced by an irreducible polynomial of degree 3 (in our example modulo m(x) := x3 + x + 1):[34]
This corresponds to the product of 3-tuples (1 1 0) • (1 1 1) = (1 0 0), or, expressed numerically, '06' • '07' = '04'.
The abelian group laws hold in •23 with respect to addition and in •23 {0} with respect to multiplication (cf. Chapter 5). The distributive law holds as well.
The structure and arithmetic of •23 can be carried over directly to the field •28, which is the field that is actually of interest in studying Rijndael. Addition and multiplication are carried out as in our above example, the only differences being that •28 has 256 elements and that an irreducible polynomial of degree 8 will be used for reduction. For Rijndael this polynomial is m(x) := x8 + x4 + x3 + x + 1, which in tuple representation is (1 0 0 0 1 1 0 1 1), corresponding to the hexadecimal number '011B'.
Multiplication of a polynomial
by x (corresponding to a multiplication • '02') is particularly simple:
where the reduction modulo m(x) is required only in the case a7 ≠ 0, and then it can be carried out by subtracting m(x), that is, by a simple XOR of the coefficients.
For programming one therefore regards the coefficients of a polynomial as binary digits of integers and executes a multiplication by x by a left shift of one bit, followed by, if a7 = 1, a reduction by an XOR operation with the eight least-significant digits '1B' of the number '011B' corresponding to m(x) (whereby a7 is simply "forgotten"). The operation a • '02' for a polynomial f, or its numerical value a, is denoted by Daemen and Rijmen by b = xtime(a). Multiplication by powers of x can be executed by successive applications of xtime().
For example, multiplication of f(x) by x + 1 (or '03') is carried out by shifting the binary digits of the numerical value a of f one place to the left and XOR-ing the result with a. Reduction modulo m(x) proceeds exactly as with xtime. Two lines of C code demonstrate the procedure:
f ^= f << 1; /* multiplication of f by (x + 1) */ if (f & 0x100) f ^= 0x11B; /* reduction modulo m(x) */
Multiplication of two polynomials f and h in •28 {0} can be speeded up by using logarithms: Let g(x) be a generating polynomial[35] of •28 {0}. Then there exist m and n such that f ≡ gm and h ≡ gn. Thus f • h ≡ gm+n mod m(x).
From a programming point of view this can be transposed with the help of two tables, into one of which we place the 255 powers of the generator polynomial g(x) := x + 1 and into the other the logarithms to the base g(x) (see Tables 11-2 and 11-3). The product f • h is now determined by three accesses to these tables: From the logarithm table are taken values m and n for which gm = f and gn = h. From the table of powers the value g((n+m)mod255) is taken (note that gord(g) = 1) Table 11-2 contains the powers of g twice in succession, and so one can avoid having to reduce the exponent of g in f • h = gn+m.
With the help of this mechanism we can also carry out polynomial division in •28. Thus for f, g € •28 {0},
This procedure for polynomial multiplication in •28 is illustrated in the function polymul():
Table 11-2. Powers of g(x) = x + 1, ascending left to right
03 | 05 | 0F | 11 | 33 | 55 | FF | 1A | 2E | 72 | 96 | A1 | F8 | 13 | 35 | |
5F | E1 | 38 | 48 | D8 | 73 | 95 | A4 | F7 | 02 | 06 | 0A | 1E | 22 | 66 | AA |
E5 | 34 | 5C | E4 | 37 | 59 | EB | 26 | 6A | BE | D9 | 70 | 90 | AB | E6 | 31 |
53 | F5 | 04 | 0C | 14 | 3C | 44 | CC | 4F | D1 | 68 | B8 | D3 | 6E | B2 | CD |
4C | D4 | 67 | A9 | E0 | 3B | 4D | D7 | 62 | A6 | F1 | 08 | 18 | 28 | 78 | 88 |
83 | 9E | B9 | D0 | 6B | BD | DC | 7F | 81 | 98 | B3 | CE | 49 | DB | 76 | 9A |
B5 | C4 | 57 | F9 | 10 | 30 | 50 | F0 | 0B | 1D | 27 | 69 | BB | D6 | 61 | A3 |
FE | 19 | 2B | 7D | 87 | 92 | AD | EC | 2F | 71 | 93 | AE | E9 | 20 | 60 | A0 |
FB | 16 | 3A | 4E | D2 | 6D | B7 | C2 | 5D | E7 | 32 | 56 | FA | 15 | 3F | 41 |
C3 | 5E | E2 | 3D | 47 | C9 | 40 | C0 | 5B | ED | 2C | 74 | 9C | BF | DA | 75 |
9F | BA | D5 | 64 | AC | EF | 2A | 7E | 82 | 9D | BC | DF | 7A | 8E | 89 | 80 |
9B | B6 | C1 | 58 | E8 | 23 | 65 | AF | EA | 25 | 6F | B1 | C8 | 43 | C5 | 54 |
FC | 1F | 21 | 63 | A5 | F4 | 07 | 09 | 1B | 2D | 77 | 99 | B0 | CB | 46 | CA |
45 | CF | 4A | DE | 79 | 8B | 86 | 91 | A8 | E3 | 3E | 42 | C6 | 51 | F3 | 0E |
12 | 36 | 5A | EE | 29 | 7B | 8D | 8C | 8F | 8A | 85 | 94 | A7 | F2 | 0D | 17 |
39 | 4B | DD | 7C | 84 | 97 | A2 | FD | 1C | 24 | 6C | B4 | C7 | 52 | F6 | 01 |
03 | 05 | 0F | 11 | 33 | 55 | FF | 1A | 2E | 72 | ... | ... | ... | F6 |
Function: | multiplication of polynomials in •28 |
Syntax: |
|
Input: |
|
Return: | the product |
UCHAR
polymul (unsigned int f, unsigned int h)
{
if ((f != 0) && (h != 0))
{return (AntiLogTable[LogTable[f] + LogTable[h]]);
}
else
{
return 0;
}
}Table 11-3. Logarithms to base g(x) = x + 1 (e.g., logg(x) 2 = 25 = 19 in hexadecimal, logg(x) 255 = 7).
00 | 19 | 01 | 32 | 02 | 1A | C6 | 4B | C7 | 1B | 68 | 33 | EE | DF | 03 | |
64 | 04 | E0 | 0E | 34 | 8D | 81 | EF | 4C | 71 | 08 | C8 | F8 | 69 | 1C | C1 |
7D | C2 | 1D | B5 | F9 | B9 | 27 | 6A | 4D | E4 | A6 | 72 | 9A | C9 | 09 | 78 |
65 | 2F | 8A | 05 | 21 | 0F | E1 | 24 | 12 | F0 | 82 | 45 | 35 | 93 | DA | 8E |
96 | 8F | DB | BD | 36 | D0 | CE | 94 | 13 | 5C | D2 | F1 | 40 | 46 | 83 | 38 |
66 | DD | FD | 30 | BF | 06 | 8B | 62 | B3 | 25 | E2 | 98 | 22 | 88 | 91 | 10 |
7E | 6E | 48 | C3 | A3 | B6 | 1E | 42 | 3A | 6B | 28 | 54 | FA | 85 | 3D | BA |
2B | 79 | 0A | 15 | 9B | 9F | 5E | CA | 4E | D4 | AC | E5 | F3 | 73 | A7 | 57 |
AF | 58 | A8 | 50 | F4 | EA | D6 | 74 | 4F | AE | E9 | D5 | E7 | E6 | AD | E8 |
2C | D7 | 75 | 7A | EB | 16 | 0B | F5 | 59 | CB | 5F | B0 | 9C | A9 | 51 | A0 |
7F | 0C | F6 | 6F | 17 | C4 | 49 | EC | D8 | 43 | 1F | 2D | A4 | 76 | 7B | B7 |
CC | BB | 3E | 5A | FB | 60 | B1 | 86 | 3B | 52 | A1 | 6C | AA | 55 | 29 | 9D |
97 | B2 | 87 | 90 | 61 | BE | DC | FC | BC | 95 | CF | CD | 37 | 3F | 5B | D1 |
53 | 39 | 84 | 3C | 41 | A2 | 6D | 47 | 14 | 2A | 9E | 5D | 56 | F2 | D3 | AB |
44 | 11 | 92 | D9 | 23 | 20 | 2E | 89 | B4 | 7C | B8 | 26 | 77 | 99 | E3 | A5 |
67 | 4A | ED | DE | C5 | 31 | FE | 18 | 0D | 63 | 8C | 80 | C0 | F7 | 70 | 07 |
We now ratchet the complexity level up one notch and consider arithmetic with polynomials of the form f(x) = f3x3 + f2x2 + f1x + f0 with coefficients fi in •28, that is, coefficients that are themselves polynomials. The coefficients of such polynomials can be represented as fields of four bytes each. Now things begin to get interesting: While addition of such polynomials f(x) and g(x) again takes place by means of a bitwise XOR of the coefficients, the product h(x) = f(x)g(x) is calculated to be
with coefficients
After reduction of h(x) by a polynomial of degree 4, one again obtains a polynomial of degree 3 over •28.
For this Rijndael uses the polynomial m(x) := x4 + 1. Usefully, xj mod M(x) = xjmod4, so that h(x) mod m(x) can be easily computed as
with
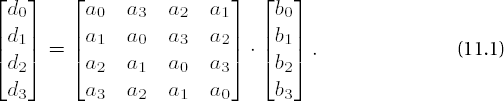
From this one concludes that the coefficients di can be computed by matrix multiplication over •28:
It is precisely this operation with the constant, invertible modulo M(x), polynomial a(x) := a3x3 + a2x2 + a1x + a0 over •28, with coefficients a0(x) = x, a1(x) = 1, a2(x) = 1, and a3(x) = x + 1, that is executed in the so-called MixColumns transformation, which constitutes a principal component of the round transformations of Rijndael.
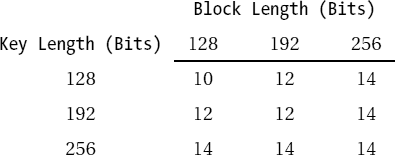
Rijndael is a symmetric block encryption algorithm with variable block and key lengths. It can process blocks of 128, 192, and 256 bits and keys of the same lengths, where all combinations of block and key lengths are possible. The accepted key lengths correspond to the guidelines for AES, though the "official" block length is only 128 bits. Each block of plain text is encrypted several times with a repeating sequence of various functions, in so-called rounds. The number of rounds is dependent on the block and key lengths (see Table 11-4).
Rijndael is not a Feistel algorithm, whose essential characteristic is that blocks are divided into left and right halves, the round transformations applied to one half, and the result XOR-ed with the other half, after which the two halves are exchanged. DES is the best-known block algorithm built along these lines. Rijndael, on the other hand, is built up of separate layers, which successively apply various effects to an entire block. For the encryption of a block the following transformations are sequentially applied:
The first round key is XOR-ed with the block.
Lr - 1 regular rounds are executed.
A terminal round is executed, in which the
MixColumnstransformation of the regular rounds is omitted.
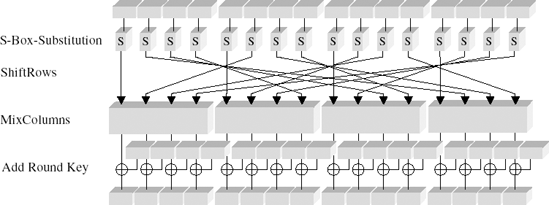
Each regular round of step 2 consists of four individual steps, which we shall now examine:
Substitution:Each byte of a block is replaced by application of an S-box.
Permutation:The bytes of the block are permuted in a ShiftRows transformation.
Diffusion:The MixColumns transformation is executed.
Round key addition:The current round key is XOR-ed with the block.
The layering of transformations within a round is shown schematically in Figure 11-1.
Each layer exercises a particular effect within a round and thus on each block of plain text:
Influence of the key
XOR-ing with the round key before the first round and as the last step within each round has an effect on every bit of the round result. In the course of encryption of a block there is no step whose result is not dependent in every bit on the key.
Nonlinear layer
The substitution effected via the S-box is a nonlinear operation. The construction of the S-box provides almost ideal protection against differential and linear cryptanalysis (see [BiSh] and [NIST]).
Linear layer
The
ShiftRowsandMixColumnstransformations ensure an optimal mixing up of the bits of a block.
In the following description of the internal Rijndael functions Lb will denote the block length in 4-byte words, Lk the length of the user key in 4-byte words (that is, Lb, Lk € {4, 6, 8})), and Lr the number of rounds as indicated in Table 11-4.
Plain text and encrypted text are input, respectively output, as fields of bytes. A block of plain text, passed as a field m0,...,m4Lb − 1, will be regarded in the following as a two-dimensional structure
Table 11-5. Representation of message blocks
b0,0 | b0,1 | b0,2 | b0,3 | b0,4 | ... | b0,Lb−1 |
b1,0 | b1,1 | b1,2 | b1,3 | b1,4 | ... | b1,Lb−1 |
b2,0 | b2,1 | b2,2 | b2,3 | b2,4 | ... | b2,Lb−1 |
b3,0 | b3,1 | b3,2 | b3,3 | b3,4 | ... | b3,Lb−1 |
where the bytes of plain text are sorted according to the following ordering:
with i = n mod 4 and j =
Access to
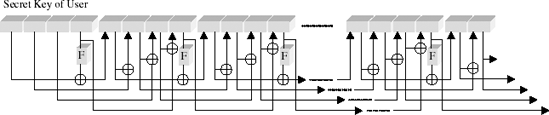
Encryption and decryption each require the generation of Lr round keys, called collectively the key schedule. This occurs through expansion of the secret user key by attaching recursively derived 4-byte words ki = (k0,i, k1,i, k2,i, k3,i)) to the user key.
The first Lk words k0, ..., kLk−1 of the key schedule are formed from the secret user key itself. For Lk € {4,6} the next 4-byte word ki is determined by XOR-ing the preceding word ki−1 with ki-Lk. If i ≡ 0 mod Lk, then a function FLk (k,i) is applied before the XOR operation, which is composed of a cyclic left shift (left rotation) r(k) of k bytes, a substitution S(r(k)) from the Rijndael S-box (we shall return to this later), and an XOR with a constant c (
The constants c(j) are defined by c(j) := (rc(j)0, 0, 0), where rc(j) are recursively determined elements from •28: rc(1) := 1, rc(j) := rc(j − 1) • x = xj−1 . Expressed in numerical values, this is equivalent to rc(1) := '01', rc(j) := rc(j − 1) • '02'. From the standpoint of programming, rc(j) is computed by a (j − 1)-fold execution of the function xtime described above, beginning with the argument 1, or more rapidly by access to a table (Tables 11-6 and 11-7).
Table 11-6. rc(j) constants (hexadecimal)
'01' | '02' | '04' | '08' | '10' | '20' | '40' | '80' | '1B' | '36' |
'6C | 'D8' | 'AB' | '4D' | '9A | '2F' | '5E' | 'BC | '63' | 'C6' |
'97' | '35' | '6A' | 'D4' | 'B3' | '7D' | 'FA | 'EF' | 'C5' | '91' |
For keys of length 256 bits (that is, Lk = 8) an additional S-box operation is inserted: If i ≡ 4 mod Lk, then before the XOR operation ki−1 is replaced by S (ki−1).
Table 11-7. rc(j) constants (binary)
00000001 | 00000010 | 00000100 | 00001000 | 00010000 |
00100000 | 01000000 | 10000000 | 00011011 | 00110110 |
01101100 | 11011000 | 10101011 | 01001101 | 10011010 |
00101111 | 01011110 | 10111100 | 01100011 | 11000110 |
10010111 | 00110101 | 01101010 | 11010100 | 10110011 |
01111101 | 11111010 | 11101111 | 11000101 | 10010001 |
Thus a key schedule is built up of Lb • (Lr + 1) 4-byte words, including the secret user key. At each round i = 0, ..., Lr - 1 the next Lb 4-byte words kLb•i through kLb•(i+1) are taken as round keys from the key schedule. The round keys are conceptualized, in analogy to the structuring of the message blocks, as a two-dimensional structure of the form depicted in Table 11-8.
Table 11-8. Representation of the round keys
k0,0 | k0,1 | k0,2 | k0,3 | k0,4 | ... | k0,Lb−1 |
k1,0 | k1,1 | k1,2 | k1,3 | k1,4 | ... | k1,Lb−1 |
k2,0 | k2,1 | k2,2 | k2,3 | k2,4 | ... | k2,Lb−1 |
k3,0 | k3,1 | k3,2 | k3,3 | k3,4 | ... | k3,Lb−1 |
For key lengths of 128 bits key generation can be understood from an examination of Figure 11-2.
There are no weak keys known, those whose use would weaken the procedure.
The substitution box, or S-box, of the Rijndael algorithm specifies how in each round each byte of a block is to be replaced by another value.
The S-box has the task of minimizing the susceptibility of the algorithm to methods of linear and differential cryptanalysis and to algebraic attacks. To accomplish this, the S-box operation should possess a high algebraic complexity in •28 and thus create a good extension to the ShiftRows and MixColumns operations. Not having such a function would support attacks within •28 and thereby decisively weaken the procedure.
In addition to the requirement of complexity the S-box function must of course be invertible; it must have no fixed points S(a) = a or complementary fixed points S(a) = ā; and it must also execute rapidly and be easy to implement.
All these desiderata were achieved through a combination of multiplicative inversion in •28 and the previously mentioned affine mapping from •28 to itself. The S-box consists of a list of 256 bytes, which are constructed by first thinking of each nonzero byte as a representative of •28 and replacing it with its multiplicative inverse (zero remains unchanged). Then an affine transformation over •2 is calculated as a matrix multiplication and addition of (1 1 0 0 0 1 1 0):
In this representation x0 and y0 denote the least-significant, and x7 and y7 the most-significant, bits of a byte, where the 8-tuple (1 1 0 0 0 1 1 0) corresponds to the hexadecimal value '63'.
Through this construction, all of the requisite design criteria were satisfied. The substitution is thereby an ideal strengthening of the algorithm. Successive application of the construction plan to the values 0 to 255 leads to Table 11-9 (in hexadecimal form; read horizontally from left to right).
For decryption the S-box must be used backwards: The affine inverse transformation is used, followed by multiplicative inversion in •28. The inverted S-box appears in Table 11-10.
The next step in the cycle of a round consists in the permutation of a block at the byte level. To this end the bytes are exchanged within the individual lines (bi,0, bi,1, bi,2, . . ., bi, Lb − 1) of a block according to the schemata depicted in Tables 11-11 through 11-13.
Table 11-9. The values of the S-box
63 | 7C | 77 | 7B | F2 | 6B | 6F | C5 | 30 | 01 | 67 | 2B | FE | D7 | AB | 76 |
CA | 82 | C9 | 7D | FA | 59 | 47 | F0 | AD | D4 | A2 | AF | 9C | A4 | 72 | C0 |
B7 | FD | 93 | 26 | 36 | 3F | F7 | CC | 34 | A5 | E5 | F1 | 71 | D8 | 31 | 15 |
04 | C7 | 23 | C3 | 18 | 96 | 05 | 9A | 07 | 12 | 80 | E2 | EB | 27 | B2 | 75 |
09 | 83 | 2C | 1A | 1B | 6E | 5A | A0 | 52 | 3B | D6 | B3 | 29 | E3 | 2F | 84 |
53 | D1 | 00 | ED | 20 | FC | B1 | 5B | 6A | CB | BE | 39 | 4A | 4C | 58 | CF |
D0 | EF | AA | FB | 43 | 4D | 33 | 85 | 45 | F9 | 02 | 7F | 50 | 3C | 9F | A8 |
51 | A3 | 40 | 8F | 92 | 9D | 38 | F5 | BC | B6 | DA | 21 | 10 | FF | F3 | D2 |
CD | 0C | 13 | EC | 5F | 97 | 44 | 17 | C4 | A7 | 7E | 3D | 64 | 5D | 19 | 73 |
60 | 81 | 4F | DC | 22 | 2A | 90 | 88 | 46 | EE | B8 | 14 | DE | 5E | 0B | DB |
E0 | 32 | 3A | 0A | 49 | 06 | 24 | 5C | C2 | D3 | AC | 62 | 91 | 95 | E4 | 79 |
E7 | C8 | 37 | 6D | 8D | D5 | 4E | A9 | 6C | 56 | F4 | EA | 65 | 7A | AE | 08 |
BA | 78 | 25 | 2E | 1C | A6 | B4 | C6 | E8 | DD | 74 | 1F | 4B | BD | 8B | 8A |
70 | 3E | B5 | 66 | 48 | 03 | F6 | 0E | 61 | 35 | 57 | B9 | 86 | C1 | 1D | 9E |
E1 | F8 | 98 | 11 | 69 | D9 | 8E | 94 | 9B | 1E | 87 | E9 | CE | 55 | 28 | DF |
8C | A1 | 89 | 0D | BF | E6 | 42 | 68 | 41 | 99 | 2D | 0F | B0 | 54 | BB | 16 |
In each first row (row index i = 0) no exchange takes place. In lines i = 1, 2, 3 the bytes are rotated left by cLb,i positions, from position j to position j - cLb,i mod Lb, where cLb,i is taken from Table 11-14.
For inverting this step, positions j in rows i = 1, 2, 3 are shifted to positions j + cLb,i mod Lb.
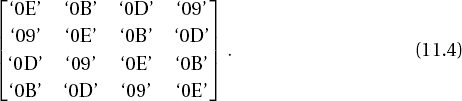
After the rowwise permutation in the last step, in this step each column (bi,j), i = 0 ,..., 3, j = 0 ,..., Lb of a block is taken to be a polynomial over •28 and multiplied by the constant polynomial a(x) := a3x3 + a2x2 + a1x + a0, with coefficients a0(x) = x, a1(x) = 1, a2(x) = 1, a3(x) = x + 1, and reduced modulo M(x) := x4 + 1. Each byte of a column thus interacts with every other byte of the column. The rowwise operating ShiftRows transformation has the effect that in each round, other bytes are mixed with one another, resulting in strong diffusion.
Table 11-10. The values of the inverted S-box
52 | 09 | 6A | D5 | 30 | 36 | A5 | 38 | BF | 40 | A3 | 9E | 81 | F3 | D7 | FB |
7C | E3 | 39 | 82 | 9B | 2F | FF | 87 | 34 | 8E | 43 | 44 | C4 | DE | E9 | CB |
54 | 7B | 94 | 32 | A6 | C2 | 23 | 3D | EE | 4C | 95 | 0B | 42 | FA | C3 | 4E |
08 | 2E | A1 | 66 | 28 | D9 | 24 | B2 | 76 | 5B | A2 | 49 | 6D | 8B | D1 | 25 |
72 | F8 | F6 | 64 | 86 | 68 | 98 | 16 | D4 | A4 | 5C | CC | 5D | 65 | B6 | 92 |
6C | 70 | 48 | 50 | FD | ED | B9 | DA | 5E | 15 | 46 | 57 | A7 | 8D | 9D | 84 |
90 | D8 | AB | 00 | 8C | BC | D3 | 0A | F7 | E4 | 58 | 05 | B8 | B3 | 45 | 06 |
D0 | 2C | 1E | 8F | CA | 3F | 0F | 02 | C1 | AF | BD | 03 | 01 | 13 | 8A | 6B |
3A | 91 | 11 | 41 | 4F | 67 | DC | EA | 97 | F2 | CF | CE | F0 | B4 | E6 | 73 |
96 | AC | 74 | 22 | E7 | AD | 35 | 85 | E2 | F9 | 37 | E8 | 1C | 75 | DF | 6E |
47 | F1 | 1A | 71 | 1D | 29 | C5 | 89 | 6F | B7 | 62 | 0E | AA | 18 | BE | 1B |
FC | 56 | 3E | 4B | C6 | D2 | 79 | 20 | 9A | DB | C0 | FE | 78 | CD | 5A | F4 |
1F | DD | A8 | 33 | 88 | 07 | C7 | 31 | B1 | 12 | 10 | 59 | 27 | 80 | EC | 5F |
60 | 51 | 7F | A9 | 19 | B5 | 4A | 0D | 2D | E5 | 7A | 9F | 93 | C9 | 9C | EF |
A0 | E0 | 3B | 4D | AE | 2A | F5 | B0 | C8 | EB | BB | 3C | 83 | 53 | 99 | 61 |
17 | 2B | 04 | 7E | BA | 77 | D6 | 26 | E1 | 69 | 14 | 63 | 55 | 21 | 0C | 7D |
Table 11-11. ShiftRows for blocks oflength 128 bits (Lb = 4)
|
| ||||||||
|---|---|---|---|---|---|---|---|---|---|
0 | 4 | 8 | 12 | 0 | 4 | 8 | 12 | ||
1 | 5 | 9 | 13 | 5 | 9 | 13 | 1 | ||
2 | 6 | 10 | 14 | 10 | 14 | 2 | 6 | ||
3 | 7 | 11 | 15 | 15 | 3 | 7 | 11 |
We have already seen (see page 244) how this step can be reduced to a matrix multiplication
with multiplication and addition carried out over •28. For multiplication by '02' (respectively x) the function xtime() has already been defined; multiplication by '03' (respectively x +1) has already been handled similarly (cf. page 247).
For inverting the MixColumns transformation every column (bi,j) of a block is multiplied by the polynomial r (x) := r3x3 + r2x2 + r1x + r0 with coefficients
r0(x) = x3+x2+x, r1(x) = x3+1, r2(x) = x3+x2+1, and r3(x) = x3+x+1 and reduced modulo M(x) := x4+1. The corresponding matrix is
The last step of a round carries out an XOR of the round key with the block:
for j = 0,..., Lb − 1. In this way, every bit of the result of a round is made dependent on every key bit.
Encryption with Rijndael is encapsulated in the following pseudocode according to [DaRi], Section 4.2–4.4. The arguments are passed as pointers to fields of bytes or 4-byte words. The interpretation of the fields, variables, and functions employed is provided in Tables 11-15 through 11-17.
Table 11-15. Interpretation of variables
|
|
|---|---|
| length Lk of the secret user key in 4-byte words |
| block length Lb in 4-byte words |
| round number Lr according to the table above |
Table 11-16. Interpretation of fields
|
|
|
|---|---|---|
|
| secret user key |
|
| field of 4-byte words to hold the round key |
|
| field of 4-byte words as constant c(j) := (rc(j),0,0,0)[a] |
|
| field for input and output of plain text and encrypted blocks |
|
| round key, segment of |
[a] It suffices to store the constants rc(j) in a field of size | ||
Table 11-17. Interpretation of functions
|
|
|---|---|
| generation of round key |
| left rotation of a 4-byte word by 1 byte: |
| S-box substitution |
| regular round |
| last round without |
|
|
|
|
| addition of a round key |
Key generation:
KeyExpansion (byte CipherKey, word ExpandedKey)
{
for (i = 0; i < Nk; i++)
ExpandedKey[i] = (CipherKey[4*i], CipherKey[4*i + 1],
CipherKey[4*i + 2], CipherKey[4*i + 3]);
for (i = Nk; i < Nb * (Nr + 1); i++)
{
temp = ExpandedKey[i - 1];
if (i % Nk == 0)
temp = SubBytes (RotBytes (temp)) ^ Rcon[i/Nk];
else if ((Nk == 8) && (i % Nk == 4))
temp = SubBytes (temp);
ExpandedKey[i] = ExpandedKey[i - Nk] ^ temp;
}
}Round functions:
Round (word State, word RoundKey)
{
SubBytes (State);
ShiftRows (State);
MixColumns (State);
AddRoundKey (State, RoundKey)
}
FinalRound (word State, word RoundKey)
{
SubBytes (State);
ShiftRows (State);
AddRoundKey (State, RoundKey)
}Entire operation for encrypting a block:
Rijndael (byte State, byte CipherKey)
{
KeyExpansion (CipherKey, ExpandedKey);
AddRoundKey (State, ExpandedKey);
for (i = 1; i < Nr; i++)
Round (State, ExpandedKey + Nb*i);
FinalRound (State, ExpandedKey + Nb*Nr);
}There exists the possibility of preparing the round key outside of the function Rijndael and to pass the key schedule ExpandedKey instead of the user key CipherKey. This is advantageous when it is necessary in the encryption of texts that are longer than a block to make several calls to Rijndael with the same user key.
Rijndael (byte State, byte ExpandedKey)
{
AddRoundKey (State, ExpandedKey);
for (i = 1; i < Nr; i++)
Round (State, ExpandedKey + Nb*i);
FinalRound (State, ExpandedKey + Nb*Nr);
}Especially for 32-bit processors it is advantageous to precompute the round transformation and to store the results in tables. By replacing the permutation and matrix operations by accesses to tables, a great deal of CPU time is saved, yielding improved results for encryption, and, as we shall see, for decryption as well. With the help of four tables each of 256 4-byte words of the form
(for w = 0, ..., 255, S(w) denotes, as above, the S-box replacement), the transformation of a block b = (b0,j,b1,j,b2,j,b3,j), j = 0,...,Lb − 1, can be determined quickly for each round by the substitution
with d(i,j) := j + cLb, i mod Lb (cf. ShiftRows, Table 11-14) and kj = (k0,j, k1,j, k2,j, k3,j) as the jth column of the round key.
For the derivation of this result, see [DaRi], Section 5.2.1. In the last round the MixColumns transformation is omitted, and thus the result is determined by
Clearly, it is also possible to use a table of 256 4-byte words, in which
with a right rotation r(a, b, c, d) = (d, a, b, c) by one byte. For environments with limited memory this can be a useful compromise, the price being only a slightly increased calculation time for the three rotations.
For Rijndael decryption one runs the encryption process in reverse order with the inverse transformations. We have already considered the inverses of the transformations SubBytes, ShiftRows, and MixColumns, which in the following are represented in pseudocode by the functions InvSubBytes, InvShiftRows, and InvMixColumns. The inverted S-box, the distances for inversion, the ShiftRows transformation, and the inverted matrix for the inversion of the MixColumns transformation are given on pages 251-252. The inverse round functions are the following:
InvFinalRound (word State, word RoundKey)
{
AddRoundKey (State, RoundKey);
InvShiftRows (State);
InvSubBytes (State);
}
InvRound (word State, word RoundKey)
{
AddRoundKey (State, RoundKey);
InvMixColumns (State);
InvShiftRows (State);
InvSubBytes (State);
}The entire operation for decryption of a block is as follows:
InvRijndael (byte State, byte CipherKey)
{
KeyExpansion (CipherKey, ExpandedKey);
InvFinalRound (State, ExpandedKey + Nb*Nr);
for (i = Nr - 1; i > 0; i--)
InvRound (State, ExpandedKey + Nb*i);
AddRoundKey (State, ExpandedKey);
}The algebraic structure of Rijndael makes it possible to arrange the transformations for encryption in such a way that here, too, tables can be employed. Here one must note that the substitution S and the InvShiftRows transformation commute, so that within a round their order can be switched. Because of the homomorphism property f(x + y) = f(x) + f(y) of linear transformations the InvMixColumns transformation and addition of the round key can be exchanged when InvMixColumns was used previously on the round key. Within a round the following course is taken:
InvFinalRound (word State, word RoundKey)
{
AddRoundKey (State, RoundKey);
InvSubBytes (State);
InvShiftRows (State);
}
InvRound (word State, word RoundKey)
{
InvMixColumns (State);
AddRoundKey (State, InvMixColumns (RoundKey));
InvSubBytes (State);
InvShiftRows (State);
}Without changing the sequence of transformations over both functions ordered one after the other, they can be redefined as follows:
AddRoundKey (State, RoundKey);
InvRound (word State, word RoundKey)
{
InvSubBytes (State);
InvShiftRows (State);
InvMixColumns (State);
AddRoundKey (State, InvMixColumns (RoundKey));
}
InvFinalRound (word State, word RoundKey)
{
InvSubBytes (State);
InvShiftRows (State);
AddRoundKey (State, RoundKey);
}With this is created the analogous structure to that for encryption. For reasons of efficiency the application of InvMixColumns to the round key in InvRound() is postponed until the key expansion, where the first and last round keys of InvMixColumns are left untouched. The "inverse" round keys are generated with
InvKeyExpansion (byte CipherKey, word InvEpandedKey)
{
KeyExpansion (CipherKey, InvExpandedKey);
for (i = 1; i < Nr; i++)
InvMixColumns (InvExpandedKey + Nb*i);
}The entire decryption operation of a block is now as follows:
InvRijndael (byte State, byte CipherKey)
{
InvKeyExpansion (CipherKey, InvExpandedKey);
AddRoundKey (State, InvExpandedKey + Nb*Nr);
for (i = Nr - 1; i > 0; i--)
InvRound (State, InvExpandedKey + Nb*i);
InvFinalRound (State, InvExpandedKey);
}In analogy to encryption, tables can be precomputed for this form of decryption. With
(for w = 0, ...,255, S−1(w) denotes the inverse S-box replacement) the result of an inverse round operation on a block b = (b0,j,b1,j,b2,j,b3,j), j = 0, ..., Lb − 1, can be determined by
for j = 0, ..., Lb − 1 with d−1 (i, j) := j − cLb,i mod Lb (cf. page 250) and the jth column
Again in the last round the MixColumns transformation is omitted, and thus the result of the last round is given by
To save memory one can also make do in decryption with a table of only 256 4-byte words, in which
with a right rotation r(a, b, c, d) = (d, a, b, c) of one byte.
Implementations for various platforms have verified the superior performance of Rijndael. The bandwidth suffices for realizations for small 8-bit controllers with small amounts of memory and key generation on the fly up through current 32-bit processors. For purposes of comparison, Table 11-18 provides encryption rates for the candidates RC6, Rijndael, and Twofish, as well as for the older 8051 controller and the Advanced Risc Machine (ARM) as a modern 32-bit chip card controller.
Table 11-18. Comparative Rijndael performance in bytes per second, after [Koeu]
|
| |
|---|---|---|
RC6 | 165 | 151260 |
Rijndael | 3005 | 311492 |
Twofish | 525 | 56 289 |
Because of the more complex InvMixColumns operation, the times for decryption and encryption can diverge, depending on the implementation, though this effect can be completely compensated by using the tables described previously. Of course, the times depend on, in addition to the key length, the block length and the number of rounds (see Table 11-4). For comparison, on a Pentium III/200 MHz, throughput of about 8 MByte per second for a key of length 128 bits, about 7 Mbyte per second for 192-bit keys, and about 6 MByte per second for 256-bit keys for blocks of length 128 bits is achievable in both directions. On the same platform, the DES in C can encrypt and decrypt about 3.8 MByte per second (see [Gldm], http://fp.gladman.plus.com).
The classical operating modes Electronic Code Book (ECB), Cipher Block Chaining (CBC), Cipher Feedback (CFB), and Output Feedback (OFB) for block ciphers were updated by NIST for use with AES and provided with appropriate test vectors (see [FI81, N38A]). Consideration of additional operating modes, which had begun already in the framework of standardization of AES and which relates to the use of modes of operation in Internet communication, has resulted in the following operating modes:
Counter Mode (CTR): A block keystream is generated and joined to the plain text blocks using XOR.
CCM Mode: To ensure the reliability and integrity of a message, the counter mode is combined with a message authentication code (MAC) based on cipher block chaining (see [N38C]).
RMAC: Using a randomized message authentication code, which is still in development, the validity of a message can be checked with respect to both its content and its source (see [N38B]).
For further details, investigations into security and cryptanalysis, computational times, and current information on AES and Rijndael the reader is referred to the literature cited above as well as the Internet sites of NIST and Vincent Rijmen, which in turn contain many links to further sources of information:
http://csrc.nist.gov/CryptoToolkit/tkencryption.html |
http://csrc.nist.gov/CryptoToolkit/modes |
http://www.esat.kuleuven.ac.be/~rijmen/rijndael |
In the downloadable source code to this book there is an implementation of AES in the file aes.c, which can be used to deepen an understanding of the procedure and to do some experimentation.
[32] The name "Rijndael" is a portmanteau word derived from the names of the authors. Sources tell me that the correct pronunciation is somewhere between "rain doll" and "Rhine dahl." Per haps NIST should include in the standard a pronunciation key in the international phonetic alphabet.
[33] Power analysis attacks (simple PA/differential PA) are based on correlations between individual bits or groups of bits of a secret cryptographic key and the average consumption of electricity for the execution of individual instructions or code sequences depending on the key (see, for example, [KoJJ], [CJRR], [GoPa]).
[34] A polynomial is said to be irreducible if it divisible (without remainder) only by itself and 1.
[35] g generates •28 {0} if g has order 255. That is, the powers of g run through all the elements of •28 {0}.