Chapter 4

Dealing with Nonnormality via Response Transformations

No experiments are useless.

Thomas Edison

At the end of Chapter 3, we showed you how to check for normality—a fundamental assumption of the statistical analysis for design of experiments (DOE). In this chapter, we discuss how to deal with nonnormality (and nonconstant variance) via transformation of the response data. The most common transformation, the logarithm, is illustrated with a case study. This is the most complex DOE shown thus far: a two-level design on four factors, requiring 16 runs for all the combinations. After detailing this DOE, we will use fractional designs to squeeze more factors into the same number of runs.

Skating on Thin Ice

The data in this chapter comes from an exercise called tabletop hockey. It works well as an in-class experiment for workshops on DOE. The objective of the hockey experiment is to learn how to shoot a puck for distance with a flexible, 15-centimeter (cm) ruler. The puck is made of two or more quarters (25-cent coins) stuck together with a gum adhesive. A simple wooden block acts as a fixture for the ruler. The response is the distance the puck slides over a smooth tabletop.

After some brainstorming, a team of workshop students decided to study four factors at the levels shown in Table 4.1.

Figure 4.1 is a template for the tabletop hockey exercise. The circles show the various locations for the factor named stick length. The marks below the line of the ruler relate to the factor called windup. The last factor, named puck place, is not shown on the figure. The low level for puck place is 0%, which means it is kept at the original position in front of the ruler and slapped. The high level for puck place is 100%, which puts it against the ruler so it can be flung forward, much like a wrist shot in the real game of hockey.

Table 4.2 lists the runs in standard order with factors in coded form. The actual experiment was performed in random order. The response (Y) covers a broad range, from 3 to 190 centimeters; more than a 60-fold change. When data spans an order of magnitude (10-fold) or more, model fitting is often simplified by applying a logarithm to the response. Therefore, we added a column for the log base 10 of the response. This is called a transformation.

Ultimately, we will show that the logarithmic scale works best, but for comparison sake, let’s first analyze the data without a transformation. (In Table 4.2 and those that follow, ignore the column(s) labeled “Log10” for now.) From the 16 unique combinations that result from the 24 factorial (2 * 2 * 2 * 2 = 16), 15 effects can be estimated, as shown in Table 4.3. A computer does the calculations much faster and more accurately than most people, with the possible exception of statisticians. The tricky part for nonstatisticians is understanding the terminology and interpreting the outputs, but the reader who has gone over all the nuts and bolts of two-level factorials in Chapter 3 has nothing to fear.

Once again you see data transformed by the logarithm. We will be getting back to the “logged” data very soon, but for now let’s proceed with the analysis of the data as it was originally collected, before being transformed mathematically. The next step is to view the untransformed effects (Figure 4.2).

The students working on the experiment could not see any obvious division of effects on this plot, so they simply focused on the largest effect, C. The analysis of variance (ANOVA) (not shown) did produce a significant probability for the resulting model (intercept plus main effect C), but the residual plots looked odd (Figure 4.3a,b,b).

The residuals did not line up on the normal plot and they clearly increased with the predicted level, forming the unwanted megaphone pattern. The students knew enough from prior training to recognize that these patterns indicate problems in the statistics. The analysis required a different approach.

Log Transformation Saves the Data

The tabletop hockey data demonstrates a very common characteristic—as the response increases, the variance does too. This is a case of constant percent error. For example, a system may exhibit 10% error, so at a level of 10 the standard deviation is 1; however, at a level of 100, the standard deviation becomes 10, and so on. Transforming such a response with the logarithm will stabilize the variance.

Luckily, we anticipated the need for a log after seeing the wide range of response. Using the transformed effects from Table 4.3, the workshop participants generated the half-normal plot shown in Figure 4.4.

The transformation was amazing, revealing a subset of relatively large effects, including interaction BD. Moreover, as one would expect from seeing such a dramatic half-normal plot, the subsequent analysis of variance indicated that all four chosen effects (B, C, D, and BD) were highly significant (Table 4.4).

The residuals from the transformed model now looked much better (Figure 4.5a,b).

In the final analysis, the students found that the distance of the shot is most affected by factor C: the windup of the ruler (Figure 4.6).

As hockey aficionados might expect, larger windups produced longer shots. The weight of the puck (Factor A) had no effect, at least over the range tested. On the other hand, the significant interaction between B and D (Figure 4.7) yielded results that may be surprising.

The effect of stick length (B) depends on puck placement (D). The D+ (100% setting) line is flat, with overlapping least significant difference (LSD) bars at either end. This indicates that stick length from 7.5 to 15 cm makes no difference when you fling the puck at the D+ level. However, when the puck is left at the original ruler line (0% setting) and slapped at this D− level, the longest shot comes with the shorter stick (B−). This is counterintuitive for most students who participate in this exercise, and thus it provides a good lesson on why one ought to conduct experiments rather than relying only on instinct.

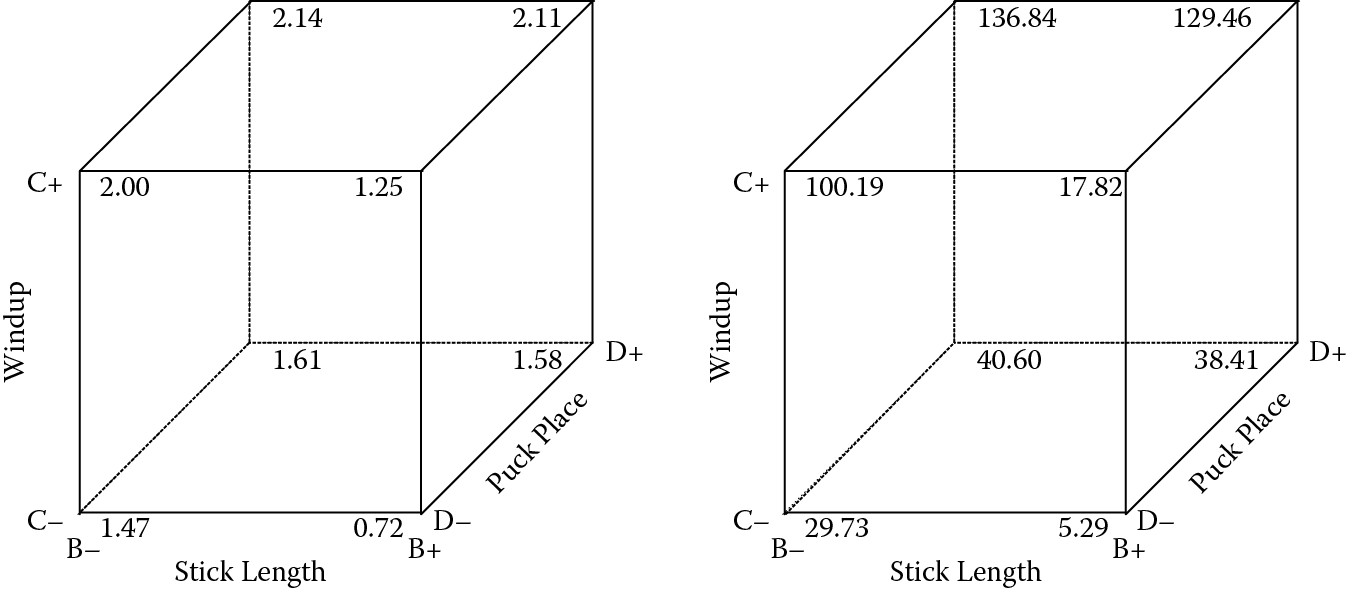
To see the combined effect of the three significant factors, view the cube plots in Figure 4.8a,b. The left cube is in transformed units to be consistent with the previous effect graphs done in the as-analyzed (log) metric. But, what you really want to know is the distance in original units. This can be generated by taking the antilog of the predicted responses. The right cube in Figure 4.8a,b presents the results after taking this reverse transformation.

The best results, well over 100 centimeters, can be seen at the upper, back side with long windup (C+) and the puck placed against the stick (D+). At these settings of C and D, the stick length makes little difference, but by choosing the shorter level (B−) you lessen the impact of potential variations in the placement of the puck.

Now that we are back in original scale, let’s revisit the interaction plot, illustrated in Figure 4.9. It was produced with factor C set at its optimal level: high (+).

After untransforming the responses to put them back in the original scale of distance in centimeters, two things become noticeable:

• The curvilinear shape that is most pronounced at the low level of “puck place” (D−).
• How small the LSD bar gets at the short distance resulting from longest stick length (15 cm) at D−.

It makes sense that variation will be much reduced at this extremely low median response level of 5.29 centimeters versus what you would expect at (median) 136.84 centimeters, the predicted extremes in original scale (you can read these values off the right-hand cube in Figure 4.8a,b). Now you really see the reason for applying the log transformation to stabilize variances at all levels of response so they can be properly pooled for statistical purposes.

Choosing the Right Transformation

The abnormal residual plots shown on Figure 4.3a,b exhibit a relatively common “power law” relationship between the standard deviation and the mean response. Statistically, this situation is symbolized as follows:

${\sigma }_y\propto {\mu }^{\alpha }$

where the Greek letter sigma is the true standard deviation (of response y), which is proportional to the true mean (mu) to some power (alpha). Table 4.5 shows just a few of the possibilities for this power law, along with the appropriate transformations.

Ideally, there is no power law relationship (α = 0), so no transformation is needed. In some cases, such as counts of imperfections, the standard deviation increases with the mean to the 0.5 power. The direct power relation (α = 1) implies that the error is a constant percent of the response. This is a very common problem, which is remedied by a log transformation. In some cases, particularly when the response is a rate (e.g., liters per second), the standard deviation increases with the square of the mean (power of 2). Then the inverse transformation is indicated (e.g., seconds per liter).

Transformations, such as those shown in Table 4.5, may stabilize the residual variance, satisfying the assumptions for ANOVA. They may be supported by scientific knowledge of the underlying relationship between factor(s) and response. For example, material scientists studying spider silk discovered a remarkable exponential relationship between extension (x) and the external force (f): f = ex/k where k is a constant (see H. Zhou, Polymers and Filaments: The Elasticity of Silk, Max Planck Institute Biannual Report 2003–2004, p. 122). In this and similar cases, a log transformation is the obvious remedy for linear modeling.

If you are uncertain whether or not a transformation will help, try one. However, if you don’t see a definite improvement in the ANOVA (F-test) and residuals, you may find that the transformation actually complicates matters. If you do use a transformation, remember to reverse the process by applying the inverse function, such as the antilog for a logged response. Otherwise you might get some grief about your goofy predictions!

Practice Problem

Problem 4.1

This problem demonstrates that design of experiments can be applied to any system, even one that does not involve manufacturing. It addresses a question debated by producers of goods and services aimed at a technical audience: Would this data-driven personality type react favorably to fancy four-color printing on a direct mail piece? Conventional wisdom says the answer will be yes, but, on second thought, this “yes” may not be absolute. While it may apply to nontechnical consumers, a cheaper, two-color printing might work as well (or better) for technical types.

In addition to considering the color factor, market researchers looked at two postcard sizes (small versus big) and two types of paper stock (thin versus thick). The eight resulting postcard designs (23) were sent to eight equal segments of the company’s client list, chosen at random. To garner more response, the researcher offered a free technical report to anyone who faxed back the reply side of the postcard. The postcards incorporated the standard two-level code to facilitate measurement. For example, the first and last combinations in standard order were coded:

• − − − (= two-color, small card on thin stock)
• + + + (= four-color, big card on thick stock)

Table 4.6 shows the number of requests generated by each postcard configuration.

The cost of printing the cards is also shown for reference. This is a “deterministic” response because it depends only on the factor levels. The four-color, large, thick postcard was the most expensive combination.

Analyze this data. Given that this section of the book focuses on the use of transformations, consider trying one. (Hint: The response is a count.) Determine the combination that maximizes response. You might be surprised by the results.

(Suggestion: Use the software provided with the book. Set up a factorial design, similar to the one you did for the tutorial that comes with the program, for three factors in 8 runs with two responses. Sort the design by standard order to match Table 4.6, enter the data, and do the analysis as outlined in the tutorial. Then go back and reanalyze after first choosing the square root as a response transformation. Compare the model and resulting residual plots before and after doing the transformation.)