Sampling picks out values f(nT) from a signal f(t), at regular intervals. This is equivalent to the multiplication of f(t) with the signal s(t), given by the expression:
![]()
where (t) is a delta function.
The Fourier transform Fs(ω) of fs(t) is given by the expression:
![]()
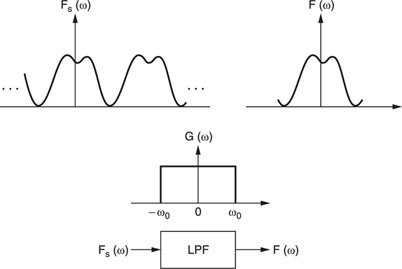
where ωs= 2π/T. When two functions are multiplied in time their transforms in the frequency domain are convoluted. For this reason, the spectrum F(ω) is repeated at multiples of the sampling frequency. Function f(t) may be recovered from Fs(ω) by first multiplying by a gating function G(ω), illustrated in Figure A2.1. This results in the expression:
![]()
Now, the inverse transform of G(ω) is given by the expression:
![]()
Figure A2.1 Recovery of a sampled signal.
and if:
![]()
then:
![]()
so that:
![]()
where the symbol * denotes convolution. This gives:
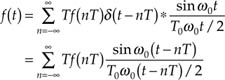
And, when T0= 2T:
![]()
This result, the sampling theorem, relates the samples f(nT) taken at regular intervals to the function f(t).
The sampling theorem is important when considering the bandwidth of a sampled signal. For example, a function f(t) can only be properly reconstructed when samples have been taken at the Nyquist rate, 1/T = 2/T0. In practical terms, this means that the sampling frequency should be twice that of the highest signal component frequency, i.e.:
and so, to make sure that signal component frequencies greater than half the sampling frequency are not sampled, an anti-aliasing filter is used.