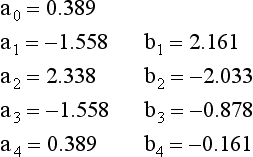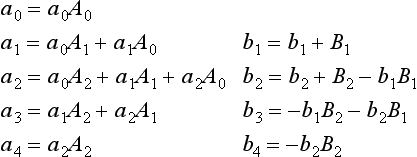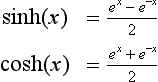The z-Transform
Just as analog filters are designed using the Laplace transform, recursive digital filters are developed with a parallel technique called the z-transform. The overall strategy of these two transforms is the same: probe the impulse response with sinusoids and exponentials to find the system’s poles and zeros. The Laplace transform deals with differential equations, the s-domain, and the s-plane. Correspondingly, the z-transform deals with difference equations, the z-domain, and the z-plane. However, the two techniques are not a mirror image of each other; the s-plane is arranged in a rectangular coordinate system, while the z-plane uses a polar format. Recursive digital filters are often designed by starting with one of the classic analog filters, such as the Butterworth, Chebyshev, or elliptic. A series of mathematical conversions are then used to obtain the desired digital filter. The z-transform provides the framework for this mathematics. The Chebyshev filter design program presented in Chapter 20 uses this approach, and is discussed in detail in this chapter.
The Nature of the z-Domain
To reinforce that the Laplace and z-transforms are parallel techniques, we will start with the Laplace transform and show how it can be changed into the z-transform. From the last chapter, the Laplace transform is defined by the relationship between the time domain and s-domain signals:
where x(t) and X(s) are the time domain and s-domain representation of the signal, respectively. As discussed in the last chapter, this equation analyzes the time domain signal in terms of sine and cosine waves that have an exponentially changing amplitude. This can be understood by replacing the complex variable, s, with its equivalent expression, σ + jω. Using this alternate notation, the Laplace transform becomes:
If we are only concerned with real time domain signals (the usual case), the top and bottom halves of the s-plane are mirror images of each other, and the term, e−jωt, reduces to simple cosine and sine waves. This equation identifies each location in the s-plane by the two parameters, σ and ω. The value at each location is a complex number, consisting of a real part and an imaginary part. To find the real part, the time domain signal is multiplied by a cosine wave with a frequency of ω, and an amplitude that changes exponentially according to the decay parameter, σ. The value of the real part of X(σ,ω) is then equal to the integral of the resulting waveform. The value of the imaginary part of X(σ,ω) is found in a similar way, except using a sine wave. If this doesn’t sound very familiar, you need to review the previous chapter before continuing.
The Laplace transform can be changed into the z-transform in three steps. The first step is the most obvious: change from continuous to discrete signals. This is done by replacing the time variable, t, with the sample number, n, and changing the integral into a summation:
Notice that X(σ, ω) uses parentheses, indicating it is continuous, not discrete. Even though we are now dealing with a discrete time domain signal, x[n], the parameters σ and ω can still take on a continuous range of values. The second step is to rewrite the exponential term. An exponential signal can be mathematically represented in either of two ways:
As illustrated in Fig. 33-1, both these equations generate an exponential curve. The first expression controls the decay of the signal through the parameter, σ. If σ is positive, the waveform will decrease in value as the sample number, n, becomes larger. Likewise, the curve will progressively increase if σ is negative. If σ is exactly zero, the signal will have a constant value of one.
FIGURE 33-1 Exponential signals. Exponentials can be represented in two different mathematical forms. The Laplace transform uses one way, while the z-transform uses the other.
The second expression uses the parameter, r, to control the decay of the waveform. The waveform will decrease if r> 1, and increase if r<1. The signal will have a constant value when r = 1. These two equations are just different ways of expressing the same thing. One method can be swapped for the other by using the relation:
The second step of converting the Laplace transform into the z-transform is completed by using the other exponential form:
While this is a perfectly correct expression of the z-transform, it is not in the most compact form for complex notation. This problem was overcome in the Laplace transform by introducing a new complex variable, s, defined to be: s = σ + jω. In this same way, we will define a new variable for the z-transform:
This is defining the complex variable, z, as the polar notation combination of the two real variables, r and ω. The third step in deriving the z-transform is to replace: r and ω, with z. This produces the standard form of the z-transform:
The z-transform. The z-transform defines the relationship between the time domain signal, x[n], and the z-domain signal, X(z).
Why does the z-transform use rn instead of e−σn, and z instead of s? As described in Chapter 19, recursive filters are implemented by a set of recursion coefficients. To analyze these systems in the z-domain, we must be able to convert these recursion coefficients into the z-domain transfer function, and back again. As we will show shortly, defining the z-transform in this manner (rn and z) provides the simplest means of moving between these two important representations. In fact, defining the z-domain in this way makes it trivial to move from one representation to the other.
Figure 33-2 illustrates the difference between the Laplace transform’s s-plane, and the z-transform’s z-plane. Locations in the s-plane are identified by two parameters: σ, the exponential decay variable along the horizontal axis, and ω, the frequency variable along the vertical axis. In other words, these two real parameters are arranged in a rectangular coordinate system. This geometry results from defining s, the complex variable representing position in the s-plane, by the relation: s = σ + jω.
FIGURE 33-2 Relationship between the s-plane and the z-plane. The s-plane is a rectangular coordinate system with σ expressing the distance along the real (horizontal) axis, and ω the distance along the imaginary (vertical) axis. In comparison, the z-plane is in polar form, with r being the distance to the origin, and ω the angle measured to the positive horizontal axis. Vertical lines in the s-plane, such as illustrated by the example poles and zeros in this figure, correspond to circles in the z-plane.
In comparison, the z-domain uses the variables: r and ω, arranged in polar coordinates. The distance from the origin, r, is the value of the exponential decay. The angular distance measured from the positive horizontal axis, ω, is the frequency. This geometry results from defining z by: z = re−jω. In other words, the complex variable representing position in the z-plane is formed by combining the two real parameters in a polar form.
These differences result in vertical lines in the s-plane matching circles in the z-plane. For example, the s-plane in Fig. 33-2 shows a pole-zero pattern where all of the poles and zeros lie on vertical lines. The equivalent poles and zeros in the z-plane lie on circles concentric with the origin. This can be understood by examining the relation presented earlier: σ = −1n(r). For instance, the s-plane’s vertical axis (i.e., σ = 0) corresponds to the z-plane’s unit circle (that is, r = 1). Vertical lines in the left half of the s-plane correspond to circles inside the z-plane’s unit circle. Likewise, vertical lines in the right half of the s-plane match with circles on the outside of the z-plane’s unit circle. In other words, the left and right sides of the s-plane correspond to the interior and the exterior of the unit circle, respectively. For instance, a continuous system is unstable when poles occupy the right half of the s-plane. In this same way, a discrete system is unstable when poles are outside the unit circle in the z-plane. When the time domain signal is completely real (the most common case), the upper and lower halves of the z-plane are mirror images of each other, just as with the s-domain.
Pay particular attention to how the frequency variable, ω, is used in the two transforms. A continuous sinusoid can have any frequency between DC and infinity. This means that the s-plane must allow ω to run from negative to positive infinity. In comparison, a discrete sinusoid can only have a frequency between DC and one-half the sampling rate. That is, the frequency must be between 0 and 0.5 when expressed as a fraction of the sampling rate, or between 0 and π when expressed as a natural frequency (i.e., ω = 2πf). This matches the geometry of the z-plane when we interpret ω to be an angle expressed in radians. That is, the positive frequencies correspond to angles of 0 to π radians, while the negative frequencies correspond to 0 to −π radians. Since the z-plane express frequency in a different way than the s-plane, some authors use different symbols to distinguish the two. A common notation is to use Ω (an upper-case omega) to represent frequency in the z-domain, and ω (a lower-case omega) for frequency in the s-domain. In this book we will use ω to represent both types of frequency, but look for this in other DSP material.
In the s-plane, the values that lie along the vertical axis are equal to the frequency response of the system. That is, the Laplace transform, evaluated at σ = 0, is equal to the Fourier transform. In an analogous manner, the frequency response in the z-domain is found along the unit circle. This can be seen by evaluating the z-transform (Eq. 33-1) at r = 1, resulting in the equation reducing to the discrete time Fourier transform (DTFT). This places zero frequency (DC) at a value of one on the horizontal axis in the s-plane. The spectrum’s positive frequencies are positioned in a counter-clockwise pattern from this DC position, occupying the upper semicircle. Likewise the negative frequencies are arranged from the DC position along the clockwise path, forming the lower semicircle. The positive and negative frequencies in the spectrum meet at the common point of ω = π and ω = −π. This circular geometry also corresponds to the frequency spectrum of a discrete signal being periodic. That is, when the frequency angle is increased beyond π, the same values are encountered as between 0 and π. When you run around in a circle, you see the same scenery over and over.
Analysis of Recursive Systems
As outlined in Chapter 19, a recursive filter is described by a difference equation:
where x[ ] and y[ ] are the input and output signals, respectively, and the “a” and “b” terms are the recursion coefficients. An obvious use of this equation is to describe how a programmer would implement the filter. An equally important aspect is that it represents a mathematical relationship between the input and output that must be continually satisfied. Just as continuous systems are controlled by differential equations, recursive discrete systems operate in accordance with this difference equation. From this relationship we can derive the key characteristics of the system: the impulse response, step response, frequency response, pole-zero plot, etc.
We start the analysis by taking the z-transform (Eq. 33-1) of both sides of Eq. 33-2. In other words, we want to see what this controlling relationship looks like in the z-domain. With a fair amount of algebra, we can separate the relation into: Y[z]/X[z], that is, the z-domain representation of the output signal divided by the z-domain representation of the input signal. Just as with the Laplace transform, this is called the system’s transfer function, and designate it by H[z]. Here is what we find:
Transfer function in polynomial form. The recursion coefficients are directly identifiable in this relation.
This is one of two ways that the transfer function can be written. This form is important because it directly contains the recursion coefficients. For example, suppose we know the recursion coefficients of a digital filter, such as might be provided from a design table:
Without having to worry about nasty complex algebra, we can directly write down the system’s transfer function:
Notice that the “b” coefficients enter the transfer function with a negative sign in front of them. Alternatively, some authors write this equation using additions, but change the sign of all the “b” coefficients. Here’s the problem. If you are given a set of recursion coefficients (such as from a table or filter design program), there is a 50–50 chance that the “b” coefficients will have the opposite sign from what you expect. If you don’t catch this discrepancy, the filter will be grossly unstable.
Equation 33-3 expresses the transfer function using negative powers of z, such as: z−1, z−2, z−3, etc. After an actual set of recursion coefficients has been plugged in, we can convert the transfer function into a more conventional form that uses positive powers: i.e., z, z2, z3, 
. By multiplying both the numerator and denominator of our example by z4, we obtain:
Positive powers are often easier to use, and they are required by some z-domain techniques. Why not just rewrite Eq. 33-3 using positive powers and forget about negative powers entirely? We can’t! The trick of multiplying the numerator and denominator by the highest power of z (such as z4 in our example) can only be used if the number of recursion coefficients is already known. Equation 33-3 is written for an arbitrary number of coefficients. The point is, both positive and negative powers are routinely used in DSP and you need to know how to convert between the two forms.
The transfer function of a recursive system is useful because it can be manipulated in ways that the recursion coefficients cannot. This includes such tasks as: combining cascade and parallel stages into a single system, designing filters by specifying the pole and zero locations, converting analog filters into digital, etc. These operations are carried out by algebra performed in the z-domain, such as: multiplication, addition, and factoring. After these operations are completed, the transfer function is placed in the form of Eq. 33-3, allowing the new recursion coefficients to be identified.
Just as with the s-domain, an important feature of the z-domain is that the transfer function can be expressed as poles and zeros. This provides the second general form of the z-domain:
Each of the poles (p1, p2, p3, ) and zeros (z1, z2, z3 ) is a complex number. To move from Eq. 33-4 to 33-3, multiply out the expressions and collect like terms. While this can involve a tremendous amount of algebra, it is straightforward in principle and can easily be written into a computer routine. Moving from Eq. 33-3 to 33-4 is more difficult because it requires factoring of the polynomials. As discussed in Chapter 32, the quadratic equation can be used for the factoring if the transfer function is second order or less (i.e., there are no powers of z higher than z2). Algebraic methods cannot generally be used to factor systems greater than second order and numerical methods must be employed. Fortunately, this is seldom needed; digital filter design starts with the pole-zero locations (Eq. 33-4) and ends with the recursion coefficients (Eq. 33-3), not the other way around.
As with all complex numbers, the pole and zero locations can be represented in either polar or rectangular form. Polar notation has the advantage of being more consistent with the natural organization of the z-plane. In comparison, rectangular form is generally preferred for mathematical work; that is, it is usually easier to manipulate σ + jω, as compared with rejω.
As an example of using these equations, we will design a notch filter by the following steps: (1) specify the pole-zero placement in the z-plane, (2) write down the transfer function in the form of Eq. 33-4, (3) rearrange the transfer function into the form of Eq. 33-3, and (4) identify the recursion coefficients needed to implement the filter. Fig. 33-3 shows the example we will use: a notch filter formed from two poles and two zeros located at
FIGURE 33-3 Notch filter designed in the z-domain. The design starts by locating two poles and two zeros in the z-plane, as shown in (a). The resulting impulse and frequency response are shown in (b) and (c), respectively. The sharpness of the notch is controlled by the distance of the poles from the zeros.
To understand why this is a notch filter, compare this pole-zero plot with Fig. 32-6, a notch filter in the s-plane. The only difference is that we are moving along the unit circle to find the frequency response from the z-plane, as opposed to moving along the vertical axis to find the frequency response from the s-plane. From the polar form of the poles and zeros, it can be seen that the notch will occur at a natural frequency of π/4, corresponding to 0.125 of the sampling rate. Since the pole and zero locations are known, the transfer function can be written in the form of Eq. 33-4 by simply plugging in the values:
To find the recursion coefficients that implement this filter, the transfer function must be rearranged into the form of Eq. 33-3. To start, expand the expression by multiplying out the terms:
Next, we collect like terms and reduce. As long as the upper half of the z-plane is a mirror image of the lower half (which is always the case if we are dealing with a real impulse response), all of the terms containing a “j” will cancel out of the expression:
While this is in the form of one polynomial divided by another, it does not use negative exponents of z, as required by Eq. 33-3. This can be changed by dividing both the numerator and denominator by the highest power of z in the expression, in this case, z2:
Since the transfer function is now in the form of Eq. 33-3, the recursive coefficients can be directly extracted by inspection:
This example provides the general strategy for obtaining the recursion coefficients from a pole-zero plot. In specific cases, it is possible to derive simpler equations directly relating the pole-zero positions to the recursion coefficients. For example, a system containing two poles and two zeros, called as biquad, has the following relations:
Biquad design equations. These equations give the recursion coefficients, a0, a1, a2, b1,b2, from the position of the poles: rp & ωp, and the zeros: r0 & ω0.
After the transfer function has been specified, how do we find the frequency response? There are three methods: one is mathematical and two are computational (programming). The mathematical method is based on finding the values in the z-plane that lie on the unit circle. This is done by evaluating the transfer function, H(z), at r = 1. Specifically, we start by writing down the transfer function in the form of either Eq. 33-3 or 33-4. We then replace each z with e−jω (that is, re−jω with r = 1). This provides a mathematical equation of the frequency response, H(ω). The problem is, the resulting expression is in a very inconvenient form. A significant amount of algebra is usually required to obtain something recognizable, such as the magnitude and phase. While this method provides an exact equation for the frequency response, it is difficult to automate in computer programs, such as needed in filter design packages.
The second method for finding the frequency response also uses the approach of evaluating the z-plane on the unit circle. The difference is that we only calculate samples of the frequency response, not a mathematical solution for the entire curve. A computer program loops through, perhaps, 1000 equally spaced frequencies between ω = 0 and ω = π. Think of an ant moving between 1000 discrete points on the upper half of the z-plane’s unit circle. The magnitude and phase of the frequency response are found at each of these location by evaluating the transfer function.
This method works well and is often used in filter design packages. Its major limitation is that it does not account for round-off noise affecting the system’s characteristics. Even if the frequency response found by this method looks perfect, the implemented system can be completely unstable!
This brings up the third method: find the frequency response from the recursion coefficients that are actually used to implement the filter. To start, we find the impulse response of the filter by passing an impulse through the system. In the second step, we take the DFT of the impulse response (using the FFT, of course) to find the system’s frequency response. The only critical item to remember with this procedure is that enough samples must be taken of the impulse response so that the discarded samples are insignificant. While books could be written on the theoretical criteria for this, the practical rules are much simpler. Use as many samples as you think are necessary. After finding the frequency response, go back and repeat the procedure using twice as many samples. If the two frequency responses are adequately similar, you can be assured that the truncation of the impulse response hasn’t fooled you in some way.
Cascade and Parallel Stages
Sophisticated recursive filters are usually designed in stages to simplify the tedious algebra of the z-domain. Figure 33-4 illustrates the two common ways that individual stages can be arranged: cascaded stages and parallel stages with added outputs. For example, a low-pass and high-pass stage can be cascaded to form a band-pass filter. Likewise, a parallel combination of low-pass and high-pass stages can form a band-reject filter. We will call the two stages being combined system 1 and system 2, with their recursion coefficients being called: a0,a1,a2,b1,b2 and A0,A1,A2,B1,B2, respectively. Our goal is to combine these stages (in cascade or parallel) into a single recursive filter, which we will call system 3, with recursion coefficients given by: a0, a1, a2, a3, a4, b1, b2, b3, b4.
FIGURE 33-4 Combining cascade and parallel stages. The z-domain allows recursive stages in a cascade, (a), or in parallel, (b), to be combined into a single system, (c).
As you recall from previous chapters, the frequency responses of systems in a cascade are combined by multiplication. Also, the frequency responses of systems in parallel are combined by addition. These same rules are followed by the z-domain transfer functions. This allows recursive systems to be combined by moving the problem into the z-domain, performing the required multiplication or addition, and then returning to the recursion coefficients of the final system.
As an example of this method, we will work out the algebra for combining two biquad stages in a cascade. The transfer function of each stage is found by writing Eq. 33-3 using the appropriate recursion coefficients. The transfer function of the entire system, H[z], is then found by multiplying the transfer functions of the two stage:
Multiplying out the polynomials and collecting like terms:
Since this is in the form of Eq. 33-3, we can directly extract the recursion coefficients that implement the cascaded system:
The obvious problem with this technique is the large amount of algebra needed to multiply and rearrange the polynomial terms. Fortunately, the entire algorithm can be expressed in a short computer program, shown in Table 33-1. Although the cascade and parallel combinations require different mathematics, they use nearly the same program. In particular, only one line of code is different between the two algorithms, allowing both to be combined into a single program.
TABLE 33-1
Combining cascade and parallel stages. This program combines the recursion coefficients of stages in cascade or parallel. The recursive coefficients for the two stages being combined enter the program in the arrays: A1[ ], B1[ ],& A2[ ], B2[ ]. The recursion coefficients that implement the entire system leave the program in the arrays: A3[ ], B3[ ].
This program operates by changing the recursive coefficients from each of the individual stages into transfer functions in the form of Eq. 33-3 (lines 220–270). After combining these transfer functions in the appropriate manner (lines 290–380), the information is moved back to being recursive coefficients (lines 400 to 430).
The heart of this program is how the transfer function polynomials are represented and combined. For example, the numerator of the first stage being combined is: a0+a1z−1+a2z−2+a3z−3. This polynomial is represented in the program by storing the coefficients: a0, a1, a2, a3 , in the array: A1[0], A1[1], A1[2], A1[3] . Likewise, the numerator for the second stage is represented by the values stored in: A2[0], A2[1], A2[2], A2[3] , and the numerator for the combined system in: A3[0], A3[1], A3[2], A3[3] . The idea is to represent and manipulate polynomials by only referring to their coefficients. The question is, how do we calculate A3[ ], given that A1 [ ], A2[ ], and A3[ ] all represent polynomials? The answer is that when two polynomials are multiplied, their coefficients are convolved. In equation form: A1[ ] * A2[ ] = A3[ ]. This allows a standard convolution algorithm to find the transfer function of cascaded stages by convolving the two numerator arrays and the two denominator arrays.
The procedure for combining parallel stages is slightly more complicated. In algebra, fractions are added according to:
Since each of the transfer functions is a fraction (one polynomial divided by another polynomial), we combine stages in parallel by multiplying the denominators, and adding the cross products in the numerators. This means that the denominator is calculated in the same way as for cascaded stages, but the numerator calculation is more elaborate. In line 340, the numerators of cascaded stages are convolved to find the numerator of the combined transfer function. In line 350, the numerator of the parallel stage combination is calculated as the sum of the two numerators convolved with the two denominators. Line 360 handles the denominator calculation for both cases.
Spectral Inversion
Chapter 14 describes an FIR filter technique called spectral inversion. This is a way of changing the filter kernel such that the frequency response is flipped top-for-bottom. All the passbands are changed into stopbands, and vice versa. For example, a low-pass filter is changed into high-pass, a band-pass filter into band-reject, etc. A similar procedure can be done with recursive filters, although it is far less successful.
As illustrated in Fig. 33-5, spectral inversion is accomplished by subtracting the output of the system from the original signal. This procedure can be viewed as combining two stages in parallel, where one of the stages happens to be the identity system (the output is identical to the input). Using this approach, it can be shown that the “b” coefficients are left unchanged, and the modified “a” coefficients are given by:
FIGURE 33-5 Spectral inversion. This procedure is the same as subtracting the output of the system from the original signal.
Spectral inversion. The frequency response of a recursive filter can be flipped top-for-bottom by modifying the “a” coefficients according to these equations. The original coefficients are shown in italics, and the modified coefficients in roman. The “b” coefficients are not changed. This method usually provides poor results.
Figure 33-6 shows spectral inversion for two common frequency responses: a low-pass filter, (a), and a notch filter, (c). This results in a high-pass filter, (b), and a band-pass filter, (d), respectively. How do the resulting frequency responses look? The high-pass filter is absolutely terrible! While the band-pass is better, the peak is not as sharp as the notch filter from which it was derived. These mediocre results are especially disappointing in comparison to the excellent performance seen in Chapter 14. Why the difference? The answer lies in something that is often forgotten in filter design: the phase response.
FIGURE 33-6 Examples of spectral inversion. Figure (a) shows the frequency response of a 6 pole low-pass Butterworth filter. Figure (b) shows the corresponding high-pass filter obtained by spectral inversion; its a mess! A more successful case is shown in (c) and (d) where a notch filter is transformed in to a band-pass frequency response.
To illustrate how phase is the culprit, consider a system called the Hilbert transformer. The Hilbert transformer is not a specific device, but any system that has the frequency response: Magnitude = 1 and phase = 90 degrees, for all frequencies. This means that any sinusoid passing through a Hilbert transformer will be unaffected in amplitude, but changed in phase by one-quarter of a cycle. Hilbert transformers can be analog or discrete (that is, hardware or software), and are commonly used in communications for various modulation and demodulation techniques.
Now, suppose we spectrally invert the Hilbert transformer by subtracting its output from the original signal. Looking only at the magnitude of the frequency responses, we would conclude that the entire system would have an output of zero. That is, the magnitude of the Hilbert transformer’s output is identical to the magnitude of the original signal, and the two will cancel. This, of course, is completely incorrect. Two sinusoids will exactly cancel only if they have the same magnitude and phase. In reality, the frequency response of this composite system has a magnitude of 
, and a phase shift of −45 degrees. Rather than being zero (our naive guess), the output is larger in amplitude than the input!
Spectral inversion works well in Chapter 14 because of the specific kind of filter used: zero phase. That is, the filter kernels have a left-right symmetry. When there is no phase shift introduced by a system, the subtraction of the output from the input is dictated solely by the magnitudes. Since recursive filters are plagued with phase shift, spectral inversion generally produces unsatisfactory filters.
Gain Changes
Suppose we have a recursive filter and need to modify the recursion coefficients such that the output signal is changed in amplitude. This might be needed, for example, to insure that a filter has unity gain in the passband. The method to achieve this is very simple: multiply the “a” coefficients by whatever factor we want the gain to change by, and leave the “b” coefficients alone.
Before adjusting the gain, we would probably like to know its current value. Since the gain must be specified at a frequency in the passband, the procedure depends on the type of filter being used. Low-pass filters have their gain measured at a frequency of zero, while high-pass filters use a frequency of 0.5, the maximum frequency allowable. It is quite simple to derive expressions for the gain at both these special frequencies. Here’s how it is done.
First, we will derive an equation for the gain at zero frequency. The idea is to force each of the input samples to have a value of one, resulting in each of the output samples having a value of G, the gain of the system we are trying to find. We will start by writing the recursion equation, the mathematical relationship between the input and output signals:
Next, we plug in one for each input sample, and G for each output sample. In other words, we force the system to operate at zero frequency. The equation becomes:
Solving for G provides the gain of the system at zero frequency, based on its recursion coefficients:
To make a filter have a gain of one at DC, calculate the existing gain by using this relation, and then divide all the “a” coefficients by G.
The gain at a frequency of 0.5 is found in a similar way: we force the input and output signals to operate at this frequency, and see how the system responds. At a frequency of 0.5, the samples in the input signal alternate between −1 and 1. That is, successive samples are: 1, −1, 1, −1, 1, −1, 1, etc. The corresponding output signal also alternates in sign, with an amplitude equal to the gain of the system: G, −G, G, −G, G, −G, etc. Plugging these signals into the recursion equation:
Solving for G provides the gain of the system at a frequency of 0.5, using its recursion coefficients:
Gain at maximum frequency. This relation gives the recursive filter’s gain at a frequency of 0.5, based on the system’s recursion coefficients.
Just as before, a filter can be normalized for unity gain by dividing all of the “a” coefficients by this calculated value of G. Calculation of Eq. 33-8 in a computer program requires a method for generating negative signs for the odd coefficients, and positive signs for the even coefficients. The most common method is to multiply each coefficient by (−1)k, where k is the index of the coefficient being worked on. That is, as k runs through the values: 0, 1, 2, 3, 4, 5, 6 etc., the expression, (−1)k, takes on the values: 1, −1, 1, −1, 1, −1, 1 etc.
Chebyshev-Butterworth Filter Design
A common method of designing recursive digital filters is shown by the Chebyshev-Butterworth program presented in Chapter 20. It starts with a pole-zero diagram of an analog filter in the s-plane, and converts it into the desired digital filter through several mathematical transforms. To reduce the complexity of the algebra, the filter is designed as a cascade of several stages, with each stage implementing one pair of poles. The recursive coefficients for each stage are then combined into the recursive coefficients for the entire filter. This is a very sophisticated and complicated algorithm; a fitting way to end this book. Here’s how it works.
Loop Control
Figure 33-7 shows the program and flowchart for the method, duplicated from Chapter 20. After initialization and parameter entry, the main portion of the program is a loop that runs through each pole-pair in the filter. This loop is controlled by block 11 in the flowchart, and the FOR-NEXT loop in lines 320 & 460 of the program. For example, the loop will be executed three times for a 6 pole filter, with the loop index, P%, taking on the values 1,2,3. That is, a 6 pole filter is implemented in three stages, with two poles per stage.
FIGURE 33-7 Chebyshev-Butterworth filter design. This program was previously presented as Table 20-4 and Table 20-5 in Chapter 20. Figure 33-8 shows the program and flowchart for subroutine 1000, called from line 340 of this main program.
Combining Coefficients
During each loop, subroutine 1000 (listed in Fig. 33-8) calculates the recursive coefficients for that stage. These are returned from the subroutine in the five variables: A0, A1, A2, B1, B2. In step 10 of the flowchart (lines 360-440), these coefficients are combined with the coefficients of all the previous stages, held in the arrays: A[ ] and B[ ]. At the end of the first loop, A[ ] and B[ ] hold the coefficients for stage one. At the end of the second loop, A[ ] and B[ ] hold the coefficients of the cascade of stage one and stage two. When all the loops have been completed, A[ ] and B[ ] hold the coefficients needed to implement the entire filter.
FIGURE 33-8 Subroutine called from Figure 33-7.
The coefficients are combined as previously outlined in Table 33-1, with a few modifications to make the code more compact. First, the index of the arrays, A[ ] and B[ ], is shifted by two during the loop. For example, a0 is held in A[2], a1 & b1 are held in A[3] & B[3], etc. This is done to prevent the program from trying to access values outside the defined arrays. This shift is removed in block 12 (lines 480–520), such that the final recursion coefficients reside in A[ ] and B[ ] without an index offset.
Second, A[ ] and B[ ] must be initialized with coefficients corresponding to the identity system, not all zeros. This is done in lines 180 to 240. During the first loop, the coefficients for the first stage are combined with the information initially present in these arrays. If all zeros were initially present, the arrays would always remain zero. Third, two temporary arrays are used, TA[ ] and TB[ ]. These hold the old values of A[ ] and B[ ] during the convolution, freeing A[ ] and B[ ] to hold the new values.
To finish the program, block 13 (lines 540-670) adjusts the filter to have a unity gain in the passband. This operates as previously described: calculate the existing gain with Eq. 33-7 or 33-8, and divide all the “a” coefficients to normalize. The intermediate variables, SA and SB, are the sums of the “a” and “b” coefficients, respectively.
Calculate Pole Locations in the s-Plane
Regardless of the type of filter being designed, this program begins with a Butterworth low-pass filter in the s-plane, with a cutoff frequency of ω = 1. As described in the last chapter, Butterworth filters have poles that are equally spaced around a circle in the s-plane. Since the filter is low-pass, no zeros are used. The radius of the circle is one, corresponding to the cutoff frequency of ω = 1. Block 3 of the flowchart (lines 1080 & 1090) calculate the location of each pole-pair in rectangular coordinates. The program variables, RP and IP, are the real and imaginary parts of the pole location, respectively. These program variables correspond to σ and ω, where the pole-pair is located at σ ±jω. This pole location is calculated from the number of poles in the filter and the stage being worked on, the program variables: NP and P%, respectively.
Warp from Circle to Ellipse
To implement a Chebyshev filter, this circular pattern of poles must be transformed into an elliptical pattern. The relative flatness of the ellipse determines how much ripple will be present in the passband of the filter. If the pole location on the circle is given by: σ and ω, the corresponding location on the ellipse, σ’ and ω’, is given by:
Circular to elliptical transform. These equations change the pole location on a circle to a corresponding location on an ellipse. The variables, NP and PR, are the number of poles in the filter, and the percent ripple in the passband, respectively. The location on the circle is given by σ and ω, and the location on the ellipse by σ’ and ω’. The variables e, V, and k, are used only to make the equations shorter.
where
These equations use hyperbolic sine and cosine functions to define the ellipse, just as ordinary sine and cosine functions operate on a circle. The flatness of the ellipse is controlled by the variable PR, which is numerically equal to the percentage of ripple in the filter’s passband. The variables: e, v and k are used to reduce the complexity of the equations, and are represented in the program by: ES, VX and KX, respectively. In addition to converting from a circle to an ellipse, these equations correct the pole locations to keep a unity cutoff frequency. Since many programming languages do not support hyperbolic functions, the following identities are used:
These equations produce illegal operations for PR ≥ 30 and PR = 0. To use this program to calculate Butterworth filters (i.e., zero ripple, PR = 0), the program lines that implement these equations must be bypassed (line 1120).
Continuous to Discrete Conversion
The most common method of converting a pole-zero pattern from the s-domain into the z-domain is the bilinear transform. This is a mathematical technique of conformal mapping, where one complex plane is algebraically distorted or warped into another complex plane. The bilinear transform changes H(s), into H(z), by the substitution:
The Bilinear transform. This substitution maps every point in the s-plane into a corresponding piont in the z-plane.
That is, we write an equation for H(s), and then replace each s with the above expression. In most cases, T = 2 tan(1/2) = 1.093 is used. This results in the s-domain’s frequency range of 0 to π radians/second being mapped to the z-domain’s frequency range of 0 to infinity radians. Without going into more detail, the bilinear transform has the desired properties to convert from the s-plane to the z-plane, such as vertical lines being mapped into circles. Here is an example of how it works. For a continuous system with a single pole-pair located at p1 = σ +jω and p2 = σ −jω, the s-domain transfer function is given by:
The bilinear transform converts this into a discrete system by replacing each s with the expression given in Eq. 33-10. This creates a z-domain transfer function also containing two poles. The problem is, the substitution leaves the transfer function in a very unfriendly form:
Working through the long and tedious algebra, this expression can be placed in the standard form of Eq. 33-3, and the recursion coefficients identified as:
Bilinear transform for two poles. The pole-pair is located at σ ± ω in the s-plane, and a0, a1, a2, b1, b2 are the recursion coefficients for the discrete system.
where
The variables M, T, and D have no physical meaning; they are simply used to make the equations shorter.
Lines 1200–1290 use these equations to convert the location of the s-domain pole-pair, held in the variables, RP and IP, directly into the recursive coefficients, held in the variables, X0, X1, X2, Y1, Y2. In other words, we have calculated an intermediate result: the recursion coefficients for one stage of a low-pass filter with a cutoff frequency of one.
Low-pass to Low-pass Frequency Change
Changing the frequency of the recursive filter is also accomplished with a conformal mapping technique. Suppose we know the transfer function of a recursive low-pass filter with a unity cutoff frequency. The transfer function of a similar low-pass filter with a new cutoff frequency, W, is obtained by using a low-pass to low-pass transform. This is also carried out by substituting variables, just as with the bilinear transform. We start by writing the transfer function of the unity cutoff filter, and then replace each z−1 with the following:
Low-pass to low-pass transform. This is a method of changing the cutoff frequency of low-pass filters. The original filter has a cutoff frequency of unity, while the new filter has a cutoff frequency of W, in the range of 0 to π.
where
This provides the transfer function of the filter with the new cutoff frequency. The following design equations result from applying this substitution to the biquad, i.e., no more than two poles and two zeros:
Low-pass to High-pass Frequency Change
The above transform can be modified to change the response of the system from low-pass to high-pass while simultaneously changing the cutoff frequency. This is accomplished by using a low-pass to high-pass transform, via the substitution:
Low-pass to high-pass transform. This substitution changes a low-pass filter into a high-pass filter. The cutoff frequency of the low-pass filter is one, while the cutoff frequency of the high-pass filter is W.
As before, this can be reduced to design equations for changing the coefficients of a biquad stage. As it turns out, the equations are identical to those of Eq. 33-13, with only two minor changes. The value of k is different (as given in Eq. 33-14), and two coefficients, a1 and b1, are negated in value. These equations are carried out in lines 1330 to 1410 in the program, providing the desired cutoff frequency, and the choice of a high-pass or low-pass response.
The Best and Worst of DSP
This book is based on a simple premise: most DSP techniques can be used and understood with a minimum of mathematics. The idea is to provide scientists and engineers tools for solving the DSP problems that arise in their non-DSP research or design activities.
These last four chapters are the other side of the coin: DSP techniques that can only be understood through extensive math. For example, consider the Chebyshev-Butterworth filter just described. This is the best of DSP, a series of elegant mathematical steps leading to an optimal solution. However, it is also the worst of DSP, a design method so complicated that most scientists and engineers will look for another alternative.
Where do you fit into this scheme? This depends on who you are and what you plan on using DSP for. The material in the last four chapters provides the theoretical basis for signal processing. If you plan on pursuing a career in DSP, you need to have a detailed understanding of this mathematics. On the other hand, specialists in other areas of science and engineering only need to know how DSP is used, not how it is derived. To this group, the theoretical material is more of a background, rather than a central topic.