As the use of minicomputers and microprocessors rapidly expanded in the 1960s, people grew tired of manipulating long strings of ones and zeros on paper and began to use more convenient ways to represent binary numbers. One way to express a binary number is an octal format, with its base of eight. Converting from binary to octal is as simple as separating the binary number into three-bit groups starting from the right. For example, the binary number 10101001₂ can be converted to octal format as

Each of the three groups of bits above are easily converted from their binary formats to a single octal digit because, for three-bit words, the octal and decimal formats are the same. That is, starting with the left group of bits, 10₂ = 2₁₀ = 2₈, 101₂ = 5₁₀ = 5₈, and 001₂ = 1₁₀ = 1₈. The octal format also uses the place value system meaning that 251₈ = (2 · 8² + 5 · 8¹ + 1 · 8⁰). Octal format enables us to represent the eight-digit 10101001₂ with the three-digit 251₈. Of course, the only valid digits in the octal format are 0 to 7—the digits 8 and 9 have no meaning in octal representation.

Another popular binary format is the hexadecimal number format using 16 as its base. Converting from binary to hexadecimal is done, this time, by separating the binary number into four-bit groups starting from the right. The binary number 10101001₂ is converted to hexadecimal format as

If you haven't seen the hexadecimal format used before, don't let the A9 digits confuse you. In this format, the characters A, B, C, D, E, and F represent the digits whose decimal values are 10, 11, 12, 13, 14, and 15 respectively. We convert the two groups of bits above to two hexadecimal digits by starting with the left group of bits, 1010₂ = 10₁₀ = A₁₆, and 1001₂ = 9₁₀ = 9₁₆. Hexadecimal format numbers also use the place value system, meaning that A9₁₆ = (A · 16¹ + 9 · 16⁰). For convenience, then, we can represent the eight-digit 10101001₂ with the two-digit number A9₁₆. Table 12-1 lists the permissible digit representations in the number systems discussed thus far.

Fractions (numbers whose magnitudes are greater than zero and less than one) can also be represented by binary numbers if we use a binary point identical in function to our familiar decimal point. In the binary numbers we've discussed so far, the binary point is assumed to be fixed just to the right of the rightmost digit. Using the symbol ◊ to denote the binary point, the six-bit binary fraction 11_◊ 0101 is equal to decimal 3.3125 as shown by

Equation 12-4. 

For the example in Eq. (12-4), the binary point is set between the second and third most significant bits. Having a stationary position for the binary point is why binary numbers are often called fixed-point binary.

For some binary number formats (like the floating-point formats that we'll cover shortly), the binary point is fixed just to the left of the most significant bit. This forces the number values to be restricted to the range between zero and one. In this format, the largest and smallest values possible for a b-bit fractional word are 1–2^–b and 2^–b, respectively. Taking a six-bit binary fraction, for example, the largest value is _◊111111₂, or

Equation 12-5. 

which is in decimal. The smallest nonzero value is _◊000001₂, equaling a decimal .

For binary numbers to be at all useful in practice, they must be able to represent negative values. Binary numbers do this by dedicating one of the bits in a binary word to indicate the sign of a number. Let's consider a popular binary format known as sign-magnitude. Here, we assume that a binary word's leftmost bit is a sign bit and the remaining bits represent the magnitude of a number which is always positive. For example, we can say that the four-bit number 0011₂ is +3₁₀ and the binary number 1011₂ is equal to –3₁₀, or

Of course, using one of the bits as a sign bit reduces the magnitude of the numbers we can represent. If an unsigned binary number's word length is b bits, the number of different values that can be represented is 2^b. An eight-bit word, for example, can represent 2⁸ = 256 different integral values. With zero being one of the values we have to express, a b-bit unsigned binary word can represent integers from 0 to 2^b–1. The largest value represented by an unsigned eight-bit word is 2⁸–1 = 255₁₀ = 11111111₂. In the sign-magnitude binary format a b-bit word can represent only a magnitude of ±2^b–1–1, so the largest positive or negative value we can represent by an eight-bit sign-magnitude word is ±2^8–1–1 = ±127.

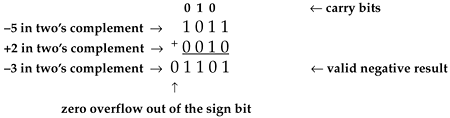
Another common binary number scheme, known as the two's complement format, also uses the leftmost bit as a sign bit. The two's complement format is the most convenient numbering scheme from a hardware design standpoint, and has been used for decades. It enables computers to perform both addition and subtraction using the same hardware adder logic. To get the negative version of a positive two's complement number, we merely complement (change a one to a zero and change a zero to a one) each bit and add a one to the complemented word. For example, with 0011₂ representing a decimal 3 in two's complement format, we obtain a negative decimal 3 through the following steps:

In the two's complement format, a b-bit word can represent positive amplitudes as great as 2^b–1–1, and negative amplitudes as large as –2^b–1. Table 12-2 shows four-bit word examples of sign-magnitude and two's complement binary formats.

While using two's complement numbers, we have to be careful when adding two numbers of different word lengths. Consider the case where a four-bit number is added to a eight-bit number:

No problem so far. The trouble occurs when our four-bit number is negative. Instead of adding a +3 to the +15, let's try to add a –3 to the +15:

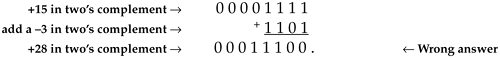
The above arithmetic error can be avoided by performing what's called a sign-extend operation on the four-bit number. This process, typically performed automatically in hardware, extends the sign bit of the four-bit negative number to the left, making it an eight-bit negative number. If we sign-extend the –3 and, then perform the addition, we'll get the correct answer:

Another useful binary number scheme is known as the offset binary format. While this format is not as common as two's complement, it still shows up in some hardware devices. Table 12-2 shows offset binary format examples for four-bit words. Offset binary represents negative numbers by subtracting 2^b–1 from an unsigned binary value. For example, in the second row of Table 12-2, the offset binary number is 1110₂. When this number is treated as an unsigned binary number, it's equivalent to 14₁₀. For four-bit words b = 4 and 2^b–1 = 8, so 14₁₀ – 8₁₀ = 6₁₀, which is the decimal equivalent of 1110₂ in offset binary. The difference between the unsigned binary equivalent and the actual decimal equivalent of the offset binary numbers in Table 12-2 is always –8. This kind of offset is sometimes referred to as a bias when the offset binary format is used. (It may interest the reader that we can convert back and forth between the two's complement and offset binary formats merely by complementing a word's most significant bit.)

The history, arithmetic, and utility of the many available number formats is a very broad field of study. A thorough and very readable discussion of the subject is given by Knuth in Reference [2].

Practical A/D converters are constrained to have binary output words of finite length. Commercial A/D converters are categorized by their output word lengths, which are normally in the range from 8 to 16 bits. A typical A/D converter input analog voltage range is from –1 to +1 volt. If we used such an A/D converter having eight-bit output words, the least significant bit would represent

Equation 12-7. 

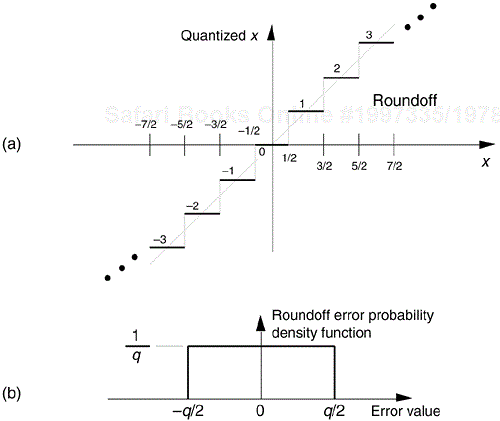
What this means is that we can represent continuous (analog) voltages perfectly as long as they're integral multiples of 7.81 millivolts—any intermediate input voltage will cause the A/D converter to output a best estimate digital data value. The inaccuracies in this process are called quantization errors because an A/D output least significant bit is an indivisible quantity. We illustrate this situation in Figure 12-1(a), where the continuous waveform is being digitized by an eight-bit A/D converter whose output is in the sign-magnitude format. When we start sampling at time t = 0, the continuous waveform happens to have a value of 31.25 millivolts (mv), and our A/D output data word will be exactly correct for sample x(0). At time T when we get the second A/D output word for sample x(1), the continuous voltage is between 0 and –7.81 mv. In this case, the A/D converter outputs a sample value of 10000001 representing –7.81 mv, even though the continuous input was not quite as negative as –7.81mv. The 10000001 A/D output word contains some quantization error. Each successive sample contains quantization error because the A/D's digitized output values must lie on a horizontal dashed line in Figure 12-1(a). The difference between the actual continuous input voltage and the A/D converter's representation of the input is shown as the quantization error in Figure 12-1(b). For an ideal A/D converter, the quantization error, a kind of roundoff noise, can never be greater than ±1/2 an lsb, or ±3.905 mv.

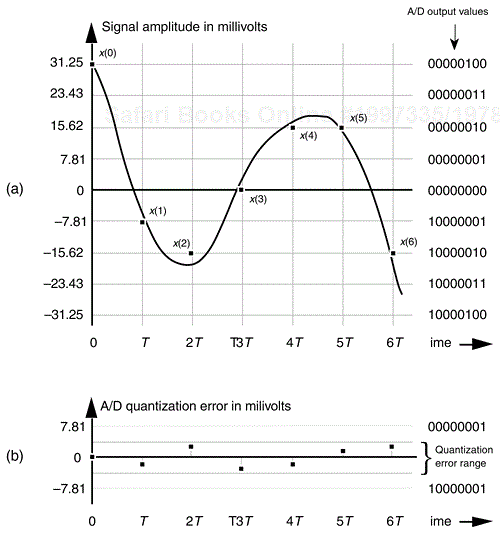
Figure 12-1. Quantization errors: (a) digitized x(n) values of a continuous signal; (b) quantization error between the actual analog signal values and the digitized signal values.

While Figure 12-1(b) shows A/D quantization noise in the time domain, we can also illustrate this noise in the frequency domain. Figure 12-2(a) depicts a continuous sinewave of one cycle over the sample interval shown as the dotted line and a quantized version of the time-domain samples of that wave as the dots. Notice how the quantized version of the wave is constrained to have only integral values, giving it a stair step effect oscillating above and below the true unquantized sinewave. The quantization here is 4 bits, meaning that we have a sign bit and three bits to represent the magnitude of the wave. With three bits, the maximum peak values for the wave are ±7. Figure 12-2(b) shows the discrete Fourier transform (DFT) of a discrete version of the sinewave whose time-domain sample values are not forced to be integers, but have high precision. Notice in this case that the DFT has a nonzero value only at m = 1. On the other hand, Figure 12-2(c) shows the spectrum of the 4-bit quantized samples in Figure 12-2(a), where quantization effects have induced noise components across the entire spectral band. If the quantization noise depictions in Figures 12-1(b) and 12-2(c) look random, that's because they are. As it turns out, even though A/D quantization noise is random, we can still quantify its effects in a useful way.

In the field of communications, people often use the notion of output signal-to-noise ratio, or SNR = (signal power)/(noise power), to judge the usefulness of a process or device. We can do likewise and obtain an important expression for the output SNR of an ideal A/D converter, SNR_A/D, accounting for finite word-length quantization effects. Because quantization noise is random, we can't explicitly represent its power level, but we can use its statistical equivalent of variance to define SNR_A/D measured in decibels as

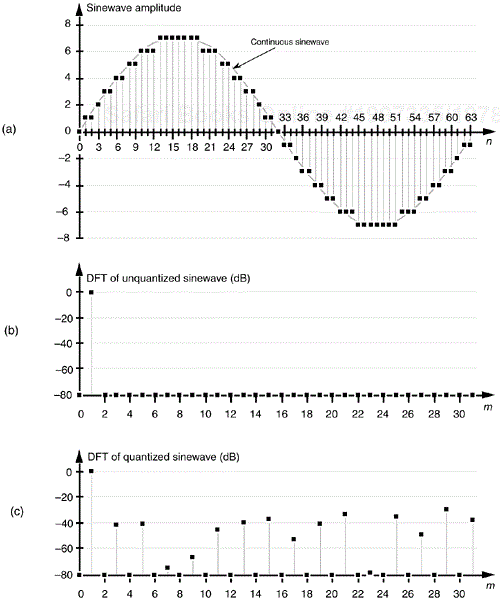
Figure 12-2. Quantization noise effects: (a) input sinewave applied to a 64-point DFT; (b) theoretical DFT magnitude of high-precision sinewave samples; (c) DFT magnitude of a sinewave quantized to 4 bits.

Equation 12-8. 

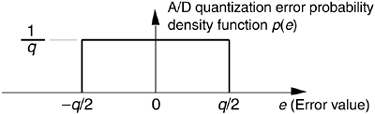
Next, we'll determine an A/D converter's quantization noise variance relative to the converter's maximum input peak voltage V_p. If the full scale (–V_p to +V_p volts) continuous input range of a b-bit A/D converter is 2Vp, a single quantization level q is that voltage range divided by the number of possible A/D output binary values, or q = 2V_p/2^b. (In Figure 12-1, for example, the quantization level q is the lsb value of 7.81 mv.) A depiction of the likelihood of encountering any given quantization error value, called the probability density function p(e) of the quantization error, is shown in Figure 12-3.

Figure 12-3. Probability density function of A/D conversion roundoff error (noise).

This simple rectangular function has much to tell us. It indicates that there's an equal chance that any error value between –q/2 and +q/2 can occur. By definition, because probability density functions have an area of unity (i.e., the probability is 100 percent that the error will be somewhere under the curve), the amplitude of the p(e) density function must be the area divided by the width, or p(e) = 1/q. From Figure D-4 and Eq. (D-12) in Appendix D, the variance of our uniform p(e) is

Equation 12-9. 

We can now express the A/D noise error variance in terms of A/D parameters by replacing q in Eq. (12-9) with q = 2V_p/2^b to get

Equation 12-10. 

OK, we're halfway to our goal—with Eq. (12-10) giving us the denominator of Eq. (12-8), we need the numerator. To arrive at a general result, let's express the input signal in terms of its root mean square (rms), the A/D converter's peak voltage, and a loading factor LF defined as

Equation 12-11. 

With the loading factor defined as the input rms voltage over the A/D converter's peak input voltage, we square and rearrange Eq. (12-11) to show the signal variance as

Equation 12-12. 

Substituting Eqs. (12-10) and (12-12) in Eq. (12-8),

Equation 12-13. 

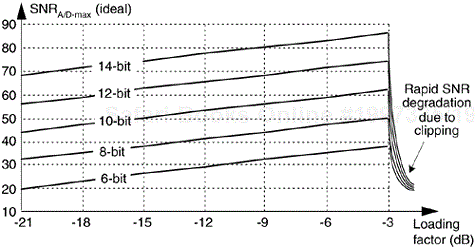
Eq. (12-13) gives us the SNR_A/D of an ideal b-bit A/D converter in terms of the loading factor and the number of bits b. Figure 12-4 plots Eq. (12-13) for various A/D word lengths as a function of the loading factor. Notice that the loading factor in Figure 12-4 is never greater than –3dB, because the maximum continuous A/D input peak value must not be greater than V_p volts. Thus, for a sinusoid input, its rms value must not be greater than volts (3 dB below V_p).

Figure 12-4. SNR_A/D of ideal A/D converters as a function of loading factor in dB.

† Recall from Appendix D, Section D.2 that, although the variance σ² is associated with the power of a signal, the standard deviation is associated with the rms value of a signal.

When the input sinewave's peak amplitude is equal to the A/D converter's full-scale voltage V_p, the full-scale LF is

Equation 12-14. 

Under this condition, the maximum A/D output SNR from Eq. (12-13) is

Equation 12-15. 

This discussion of SNR relative to A/D converters means three important things to us:

A word of caution is appropriate here concerning our analysis of A/D converter quantization errors. The derivations of Eqs. (12-13) and (12-15) are based upon three assumptions:

To conclude our discussion of A/D converters, let's consider one last topic. In the literature the reader is likely to encounter the expression

Equation 12-16. 

Equation (12-16) is used by test equipment manufacturers to specify the sensitivity of test instruments using a b_eff parameter known as the number of effective bits, or effective number of bits (ENOB) [3–8]. Equation (12-16) is merely Eq. (12-15) solved for b. Test equipment manufacturers measure the actual SNR of their product indicating its ability to capture continuous input signals relative to the instrument's inherent noise characteristics. Given this true SNR, they use Eq. (12-16) to determine the b_eff value for advertisement in their product literature. The larger b_eff, the greater the continuous voltage that can be accurately digitized relative to the equipment's intrinsic quantization noise.

The next finite, word-length effect we'll consider is called overflow. Overflow is what happens when the result of an arithmetic operation has too many bits, or digits, to be represented in the hardware registers designed to contain that result. We can demonstrate this situation to ourselves rather easily using a simple four-function, eight-digit pocket calculator. The sum of a decimal 9.9999999 plus 1.0 is 10.9999999, but on an eight-digit calculator the sum is 10.999999 as

The hardware registers, which contain the arithmetic result and drive the calculator's display, can hold only eight decimal digits; so the least significant digit is discarded (of course). Although the above error is less than one part in ten million, overflow effects can be striking when we work with large numbers. If we use our calculator to add 99,999,999 plus 1, instead of getting the correct result of 100 million, we'll get a result of 1. Now that's an authentic overflow error!

Let's illustrate overflow effects with examples more closely related to our discussion of binary number formats. First, adding two unsigned binary numbers is as straightforward as adding two decimal numbers. The sum of 42 plus 39 is 81, or

In this case, two 6-bit binary numbers required 7 bits to represent the results. The general rule is the sum of m individual b-bit binary numbers can require as many as [b + log₂(m)] bits to represent the results. So, for example, a 24-bit result register (accumulator) is needed to accumulate the sum of sixteen 20-bit binary numbers, or 20 + log₂(16) = 24. The sum of 256 eight-bit words requires an accumulator whose word length is [8 + log₂(256)], or 16 bits, to ensure that no overflow errors occur.

In the preceding example, if our accumulator word length was 6 bits, an overflow error occurs as

Here, the most significant bit of the result overflowed the 6-bit accumulator, and an error occurred.

With regard to overflow errors, the two's complement binary format has two interesting characteristics. First, under certain conditions, overflow during the summation of two numbers causes no error. Second, with multiple summations, intermediate overflow errors cause no problems if the final magnitude of the sum of the b-bit two's complement numbers is less than 2^b–1. Let's illustrate these properties by considering the four-bit two's complement format in Figure 12-5, whose binary values are taken from Table 12-2.

Figure 12-5. Four-bit two's complement binary numbers.

The first property of two's complement overflow, which sometimes causes no errors, can be shown by the following examples:

Then again, the following examples show how two's complement overflow sometimes does cause errors:

The rule with two's complement addition is if the carry bit into the sign bit is the same as the overflow bit out of the sign bit, the overflow bit can be ignored, causing no errors; if the carry bit into the sign bit is different from the overflow bit out of the sign bit, the result is invalid. An even more interesting property of two's complement numbers is that a series of b-bit word summations can be performed where intermediate sums are invalid, but the final sum will be correct if its magnitude is less than 2^b–1. We show this by the following example. If we add a +6 to a +7, and then add a –7, we'll encounter an intermediate overflow error but our final sum will be correct as

The magnitude of the sum of the three four-bit numbers was less than 2^4–1 (<8), so our result was valid. If we add a +6 to a +7, and next add a –5, we'll encounter an intermediate overflow error, and our final sum will also be in error because its magnitude is not less than 8.

Another situation where overflow problems are conspicuous is during the calculation of the fast Fourier transform (FFT). It's difficult at first to imagine that multiplying complex numbers by sines and cosines can lead to excessive data word growth—particularly because sines and cosines are never greater than unity. Well, we can show how FFT data word growth occurs by considering a decimation-in-time FFT butterfly from Figure 4-14(c) repeated here as Figure 12-6, and grinding through a little algebra. The expression for the x' output of this FFT butterfly, from Eq. (4-26), is

Equation 12-17. 

Figure 12-6. Single decimation-in-time FFT butterfly.

Breaking up the butterfly's x and y inputs into their real and imaginary parts and remembering that , we can express Eq. (12-17) as

Equation 12-18. 

If we let α be the twiddle factor angle of 2πk/N, and recall that e^–jα = cos(α) – jsin(α), we can simplify Eq. (12-18) as

Equation 12-19. 

If we look, for example, at just the real part of the x' output, x'_real, it comprises the three terms

Equation 12-20. 

If x_real, y_real, and y_imag are of unity value when they enter the butterfly and the twiddle factor angle α = 2πk/N happens to be π/4 = 45^o, then, x'_real can be greater than 2 as

Equation 12-21. 

So we see that the real part of a complex number can more than double in magnitude in a single stage of an FFT. The imaginary part of a complex number is equally likely to more than double in magnitude in a single FFT stage. Without mitigating this word growth problem, overflow errors could render an FFT algorithm useless.

OK, overflow problems are handled in one of two ways—by truncation or rounding—each inducing its own individual kind of quantization errors, as we shall see.

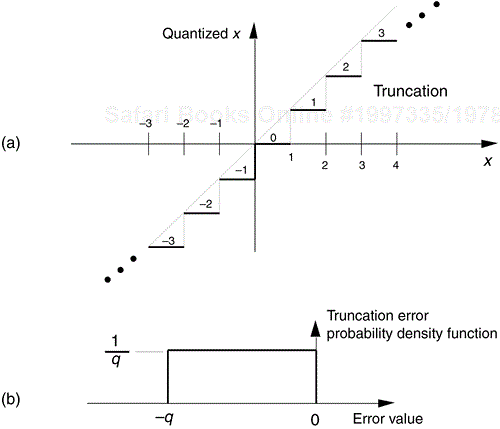
Truncation is the process where a data value is represented by the largest quantization level that is less than or equal to that data value. If we're quantizing to integral values, for example, the real value 1.2 would be quantized to 1. An example of truncation to integral values is shown in Figure 12-7(a), where all values of x in the range of 0 ≤ x < 1 are set equal to 0, values of x in the range of 1 ≤ x < 2 are set equal to 1, x values in the range of 2 ≤ x < 3 are set equal to 2, and so on.

Figure 12-7. Truncation: (a) quantization nonlinearities; (b) error probability density function.

As we did with A/D converter quantization errors, we can call upon the concept of probability density functions to characterize the errors induced by truncation. The probability density function of truncation errors, in terms of the quantization level, is shown in Figure 12-7(b). In Figure 12-7(a) the quantization level q is 1, so, in this case, we can have truncation errors as great as –1. Drawing upon our results from Eqs. (D-11) and (D-12) in Appendix D, the mean and variance of our uniform truncation probability density function are expressed as

Equation 12-22. 

and

Equation 12-23. 

In a sense, truncation error is the price we pay for the privilege of using integer binary arithmetic. One aspect of this is the error introduced when we use truncation to implement division by some integral power of 2. We often speak of a quick way of dividing a binary value by 2^T is to shift that binary word T bits to the right; that is, we're truncating the data value (not the data word) by lopping off the rightmost T bits after the shift. For example, let's say we have the value 31 represented by the five-bit binary number 11111₂, and we want to divide it by 16 through shifting the bits T = 4 places to the right and ignoring (truncating) those shifted bits. After the right shift and truncation, we'd have a binary quotient of 31/16 = 00001₂. Well, we see the significance of the problem because our quick division gave us an answer of one instead of the correct 31/16 = 1.9375. Our division-by-truncation error here is almost 50 percent of the correct answer. Had our original dividend been a 63 represented by the six-bit binary number 111111₂, dividing it by 16 through a four-bit shift would give us an answer of binary 000011₂, or decimal three. The correct answer, of course, is 63/16 = 3.9375. In this case the percentage error is 0.9375/3.9375, or about 23.8 percent. So, the larger the dividend, the lower the truncation error.

If we study these kinds of errors, we'll find that the resulting truncation error depends on three things: the number of value bits shifted and truncated, the values of the truncated bits (were those dropped bits ones or zeros), and the magnitude of the binary number left over after truncation. Although a complete analysis of these truncation errors is beyond the scope of this book, we can quantify the maximum error that can occur with our division-by-truncation scheme when using binary integer arithmetic. The worst case scenario is when all of the T bits to be truncated are ones. For binary integral numbers the value of T bits, all ones, to the right of the binary point is 1 – 2^–T. If the resulting quotient N is small, the significance of those truncated ones aggravates the error. We can normalize the maximum division error by comparing it to the correct quotient using a percentage. So the maximum percentage error of the binary quotient N after truncation for a T-bit right shift, when the truncated bits are all ones, is

Equation 12-24. 

Let's plug a few numbers into Eq. (12-24) to understand its significance. In the first example above, 31/16, where T = 4 and the resulting binary quotient was N = 1, the percentage error is

Plotting Eq. (12-24) for three different shift values as functions of the quotient, N, after truncation results in Figure 12-8.

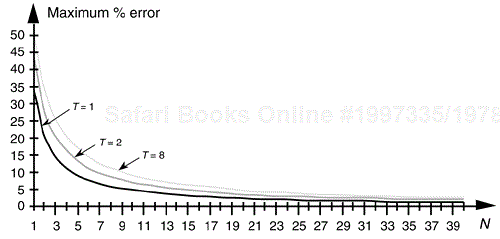
Figure 12-8. Maximum error when data shifting and truncation are used to implement division by 2^T. T = 1 is division by 2; T = 2 is division by 4; and T = 8 is division by 256.

So, to minimize this type of division error, we need to keep the resulting binary quotient N, after the division, as large as possible. Remember, Eq. (12-24) was a worst case condition where all of the truncated bits were ones. On the other hand, if all of the truncated bits happened to be zeros, the error will be zero. In practice, the errors will be somewhere between these two extremes. A practical example of how division-by-truncation can cause serious numerical errors is given in Reference [9].

Rounding is an alternate process of dealing with overflow errors where a data value is represented by, or rounded off to, its nearest quantization level. If we're quantizing to integral values, the number 1.2 would be quantized to 1, and the number 1.6 would be quantized to 2. This is shown in Figure 12-9(a), where all values of x in the range of –0.5 ≤ x < 0.5 are set equal to 0, values of x in the range of 0.5 ≤ x < 1.5 are set equal to 1, x values in the range of 1.5 ≤ x < 2.5 are set equal to 2, etc. The probability density function of the error induced by rounding, in terms of the quantization level, is shown in Figure 12-9(b). In Figure 12-9(a), the quantization level q is 1, so, in this case, we can have truncation error magnitudes no greater than q/2, or 1/2. Again, using our Eqs. (D-11) and (D-12) results from Appendix D, the mean and variance of our uniform roundoff probability density function are expressed as

Figure 12-9. Roundoff: (a) quantization nonlinearities; (b) error probability density function.

Equation 12-25. 

and

Equation 12-26. 

Because the mean (average) and maximum error possibly induced by roundoff is less than that of truncation, rounding is generally preferred, in practice, to minimize overflow errors.

In digital signal processing, statistical analysis of quantization error effects is exceedingly complicated. Analytical results depend on the types of quantization errors, the magnitude of the data being represented, the numerical format used, and which of the many FFT or digital filter structures we happen to use. Be that as it may, digital signal processing experts have developed simplified error models whose analysis has proved useful. Although discussion of these analysis techniques and their results is beyond the scope of this introductory text, many references are available for the energetic reader[10–18]. (Reference [11] has an extensive reference list of its own on the topic of quantization error analysis.)

Again, the overflow problems using fixed-point binary formats—that we try to alleviate with truncation or roundoff—arise because so many digital signal processing algorithms comprise large numbers of additions or multiplications. This obstacle, particularly in hardware implementations of digital filters and the FFT, is avoided by hardware designers through the use of floating-point binary formats.

Attempting to determine the dynamic range of an arbitrary floating-point number format is a challenging exercise. We start by repeating the expression for a number system's dynamic range from Eq. (12-6) as

Equation 12-35. 

When we attempt to determine the largest and smallest possible values for a floating-point number format, we quickly see that they depend on such factors as

Trying to develop a dynamic range expression that accounts for all the possible combinations of the above factors is impractical. What we can do is derive a rule of thumb expression for dynamic range that's often used in practice[8,22,24].

Let's assume the following for our derivation: the exponent is a b_e-bit offset binary number, the fraction is a normalized sign-magnitude number having a sign bit and b_m magnitude bits, and a hidden bit is used just left of the binary point. Our hypothetical floating-point word takes the following form:

First we'll determine what the largest value can be for our floating-point word. The largest fraction is a one in the hidden bit, and the remaining b_m fraction bits are all ones. This would make fraction The first 1 in this expression is the hidden bit to the left of the binary point, and the value in parentheses is all b_m bits equal to ones to the right of the binary point. The greatest positive value we can have for the b_e-bit offset binary exponent is . So the largest value that can be represented with the floating-point number is the largest fraction raised to the largest positive exponent, or

Equation 12-36. 

The smallest value we can represent with our floating-point word is a one in the hidden bit times two raised to the exponent's most negative value, , or

Equation 12-37. 

Plugging Eqs. (12-36) and (12-37) into Eq. (12-35),

Equation 12-38. 

Now here's where the thumb comes in—when b_m is large, say over seven, the value approaches zero; that is, as b_m increases, the all ones fraction value in the numerator approaches 1. Assuming this, Eq. (12-38) becomes

Equation 12-39. 

Using Eq. (12-39) we can estimate, for example, the dynamic range of the single-precision IEEE P754 standard floating-point format with its eight-bit exponent:

Equation 12-40. 

Although we've introduced the major features of the most common floating-point formats, there are still more details to learn about floating-point numbers. For the interested reader, the references given in this section provide a good place to start.