The Hilbert transform (HT) is a mathematical process performed on a real signal x_r(t) yielding a new real signal x_ht(t), as shown in Figure 9-1.

Figure 9-1. The notation used to define the continuous Hilbert transform.

Our goal here is to ensure that x_ht(t) is a 90^o phase-shifted version of x_r(t). So, before we carry on, let's make sure we understand the notation used in Figure 9-1. The variables are defined as:

We'll clarify that x_ht(t) = h(t)_*x_r(t), where the _* symbol means convolution. In addition, we can define the spectrum of x_ht(t) as X_ht(ω) = H(ω)·X_r(ω). (These relationships sure make the HT look like a filter, don't they? We'll cogitate on this notion again later in this chapter.)

Describing how the new x_ht(t) signal, the HT of x_r(t), differs from the original x_r(t) is most succinctly done by relating their Fourier transforms, X_r(ω) and X_ht(ω). In words, we can say that all of x_ht(t)'s positive frequency components are equal to x_r(t)'s positive frequency components shifted in phase by –90^o. Also, all of x_ht(t)'s negative frequency components are equal to x_r(t)'s negative frequency components shifted in phase by +90^o. Mathematically, we recall:

Equation 9-1. 

where H(ω) = –j over the positive frequency range, and H(ω) = +j over the negative frequency range. We show the non-zero imaginary part of H(ω) in Figure 9-2(a).

Figure 9-2. The complex frequency response of H(ω).

To fully depict the complex H(ω), we show it as floating in a three-dimensional space in Figure 9-2(b). The bold curve is our complex H(ω). On the right side is an upright plane on which we can project the imaginary part of H(ω). At the bottom of Figure 9-2(b) is a flat plane on which we can project the real part of H(ω). In rectangular notation, we say that H(ω) = 0 +j1 for negative frequencies and H(ω) = 0 –j1 for positive frequencies. (We introduce the three-dimensional axes of Figure 9-2(b) now because we'll be using it to look at other complex frequency-domain functions later in this discussion.)

To show a simple example of a HT, and to reinforce our graphical viewpoint, Figure 9-3(a) shows the three-dimensional time and frequency representations of a real cosine wave cos(ωt). Figure 9-3(b) shows the HT of cos(ωt) to be the sinewave sin(ωt).

Figure 9-3. The Hilbert transform: (a) cos(ωt); (b) its transform is sin(ωt).

The complex spectrum on the right side of Figure 9-3(b) shows how the HT rotates the cosine wave's positive frequency spectral component by –j, and the cosine wave's negative frequency spectral component by +j. You can see on the right side of Figure 9-3 that our definition of the +j multiplication operation is a +90^o rotation of a spectral component counterclockwise about the frequency axis. (The length of those spectral components is half the peak amplitude of the original cosine wave.) We're assuming those sinusoids on the left in Figure 9-3 exist for all time, and this allows us to show their spectra as infinitely narrow impulses in the frequency domain.

Now that we have this frequency response of the HT defined, it's reasonable for the beginner to ask: “Why would anyone want a process whose frequency domain response is that weird H(ω) in Figure 9-2(b)?”

The answer is: we need to understand the HT because it's useful in so many complex-signal (quadrature) processing applications. A brief search on the Internet reveals HT-related signal processing techniques being used in the following applications:

All of these applications employ the HT either to generate or measure complex time-domain signals, and that's where the HT's power lies. The HT delivers to us, literally, another dimension of signal processing capabilities as we move from two-dimensional real signals to three-dimensional complex signals. Here's how.

Let's consider a few mathematical definitions. If we start with a real time-domain signal x_r(t), we can associate with it a complex signal x_c(t), defined as:

Equation 9-2. 

The complex x_c(t) signal is known as an analytic signal (because it has no negative-frequency spectral components), and its real part is equal to the original real input signal x_r(t). The key here is that x_c(t)'s imaginary part, x_i(t), is the HT of the original x_r(t) as shown in Figure 9-4.

Figure 9-4. Functional relationship between the x_c(t) and x_r(t) signals.

As we'll see shortly, in many real-world signal processing situations x_c(t) is easier, or more meaningful, to work with than the original x_r(t). Before we see why that is true, we'll explore x_c(t) further to attempt to give it some physical meaning. Consider a real x_r(t) = cos(ω_ot) signal that's simply four cycles of a cosine wave and its HT x_i(t) sinewave as shown in Figure 9-5. The x_c(t) analytic signal is the bold corkscrew function.

Figure 9-5. The Hilbert transform and the analytic signal of cos(ω_ot).

We can describe x_c(t) as a complex exponential using one of Euler's equations. That is:

Equation 9-3. 

The spectra of those signals in Eq. (9-3) are shown in Figure 9-6. Notice three things in Figure 9-6. First, following the relationships in Eq. (9-3), if we rotate X_i(ω) by +90^o counterclockwise (+j) and add it to X_r(ω), we get X_c(ω) = X_r(ω)+jX_i(ω). Second, note how the magnitude of the component in X_c(ω) is double the magnitudes in X_r(ω). Third, notice how X_c(ω) is zero over the negative frequency range. This property of zero spectral content for negative frequencies is why X_c(ω) is called an analytic signal. Some people call X_c(ω) a one-sided spectrum.

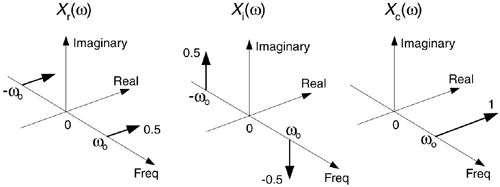
Figure 9-6. HT spectra: (a) spectrum of cos(ω_ot); (b) spectrum of the Hilbert transform of cos(ω_ot), sin(ω_ot); (c) spectrum of the analytic signal of cos(ω_ot), .

To appreciate the physical meaning of our discussion here, let's remember that the x_c(t) signal is not just a mathematical abstraction. We can generate x_c(t) in our laboratory and route it via cables to the laboratory down the hall. (This idea is described in Section 8.3.)

To illustrate the utility of this analytic signal x_c(t) notion, let's see how analytic signals are very useful in measuring instantaneous characteristics of a time domain signal: measuring the magnitude, phase, or frequency of a signal at some given instant in time. This idea of instantaneous measurements doesn't seem so profound when we think of characterizing, say, a pure sinewave. But if we think of a more complicated signal, like a modulated sinewave, instantaneous measurements can be very meaningful. If a real sinewave x_r(t) is amplitude modulated so its envelope contains information, from an analytic version of the signal we can measure the instantaneous envelope E(t) value using:

Equation 9-4. 

That is, the envelope of the signal is equal to the magnitude of x_c(t). We show a simple example of this AM demodulation idea in Figure 9-7(a), where a sinusoidal signal is amplitude modulated by a low-frequency sinusoid (dashed curve). To recover the modulating waveform, traditional AM demodulation would rectify the amplitude modulated sinewave, x_r(t), and pass the result through a lowpass filter. The filter's output is represented by the solid curve in Figure 9-7(b) representing the modulating waveform. If, instead, we compute the HT of x_r(t) yielding x_i(t) and use that to generate the x_c(t) = x_r(t) + jx_i(t) analytic version of x_r(t). Finally, we compute the magnitude of x_c(t) using Eq. (9-4) to extract the modulating waveform shown as the bold solid curve in Figure 9-7(c). The |x_c(t)| function is a much more accurate representation of the modulating waveform than the solid curve in Figure 9-7(b).

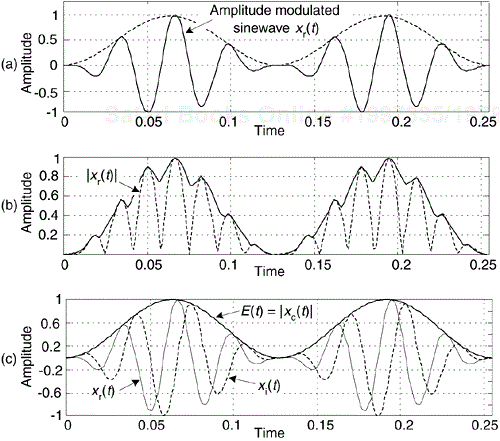
Figure 9-7. Envelope detection: (a) input x_r(t) signal; (b) traditional lowpass filtering of |x_r(t)|; (c) complex envelope detection result |x_c(t)|.

Suppose, on the other hand, some real x_r(t) sinewave is phase modulated. We can estimate x_c(t)'s instantaneous phase ø(t), using:

Equation 9-5. 

Computing ø(t) is equivalent to phase demodulation of x_r(t). Likewise (and more oftentimes implemented), should a real sinewave carrier be frequency modulated we can measure its instantaneous frequency F(t) by calculating the instantaneous time rate of change of x_c(t)'s instantaneous phase using:

Equation 9-6. 

Calculating F(t) is equivalent to frequency demodulation of x_r(t). By the way, if ø(t) is measured in radians, then F(t) in Eq. (9-6) is measured in radians/second. Dividing F(t) by 2π will give it dimensions of Hz. (Another frequency demodulation method is discussed in Section 13.22.)

For another HT application, consider a real x_r(t) signal whose |X_r(ω)| spectral magnitude is centered at 25 kHz as shown in Figure 9-8(a). Suppose we wanted to translate that spectrum to be centered at 20 kHz. We could multiply x_r(t) by the real sinusoid cos(2π5000t) to obtain a real signal whose spectrum is shown in Figure 9-8(b). The problem with this approach is we'd need an impractically high-performance filter (the dashed curve) to eliminate those unwanted high-frequency spectral images.

Figure 9-8. Spectra associated with frequency translation of a real signal x_r(t).

One the other hand, if we compute the HT of x_r(t) to obtain x_i(t), combine the two signals to form the analytic signal x_c(t) = x_r(t)+jx_i(t), we'll have the complex x_c(t) whose one-sided spectrum is given in Figure 9-8(c). Next we multiply the complex x_c(t) by the complex e^–j2π5000t, yielding a frequency-translated x_out(t) complex signal whose spectrum is shown in Figure 9-8(d). Our final step is to take the real part of x_out(t) to obtain a real signal with the desired spectrum centered about 20 kHz, as shown in Figure 9-8(e).

Now that we're convinced of the utility of the HT, let's determine the HT's time-domain impulse response and use it to build Hilbert transformers.

Instead of following tradition and just writing down the impulse response equation for a device that performs the HT, we'll show how to arrive at that expression. To determine the HT's impulse response expression, we take the inverse Fourier transform of the HT's frequency response H(ω). The garden-variety continuous inverse Fourier transform of an arbitrary frequency function X(f) is defined as:

Equation 9-7. 

where f is frequency measured in cycles/second (hertz). We'll make three changes to Eq. (9-7). First, in terms of our original frequency variable ω = 2πf radians/second, and because df = dω/2π, we substitute dω/2π in for the df term. Second, because we know our discrete frequency response will be periodic with a repetition interval of the sampling frequency ω_s, we'll evaluate Eq. (9-7) over the frequency limits of –ω_s/2 to +ω_s/2. Third, we partition the original integral into two separate integrals. This algebraic massaging gives us the following:

Equation 9-8. 

Whew! OK, we're going to plot this impulse response shortly, but first we have one hurdle to overcome. Heartache occurs when we plug t = 0 into Eq. (9-8) because we end up with the indeterminate ratio 0/0. Hardcore mathematics to the rescue here. We merely pull out the Marquis de L'Hopital's Rule, take the time derivatives of the numerator and denominator in Eq. (9-8), and then set t = 0 to determine h(0). Following through on this:

Equation 9-9. 

So now we know that h(0) = 0. Let's find the discrete version of Eq. (9-8) because that's the form we can model in software and actually use in our DSP work. We can go digital by substituting the discrete time variable nt_s in for the continuous time variable t in Eq. (9-8). Using the following definitions

we can rewrite Eq. (9-8) in discrete form as:

Equation 9-10. 

Substituting 2πf_s for ω_s, and 1/f_s for t_s, we have:

Equation 9-11. 

Finally, we plot HT's h(n) impulse response in Figure 9-9. The f_s term in Eq. (9-11) is simply a scale factor; its value does not affect the shape of h(n). An informed reader might, at this time, say, “Wait a minute. Eq. (9-11) doesn't look at all like the equation for the HT's impulse response that's in my other DSP textbook. What gives?” The reader would be correct, because one popular expression in the literature for h(n) is:

Equation 9-12. 

Figure 9-9. The Hilbert transform's discrete impulse response when f_s = 1.

Here's the answer; first, the derivation of Eq. (9-12) is based on the assumption that the f_s sampling rate is normalized to unity. Next, if you blow the dust off your old mathematical reference book, inside you'll find a trigonometric power relations identity stating: sin²(α) = [1 – cos(2α)]/2. If in Eq. (9-11) we substitute 1 for f_s, and substitute 2sin²(πn/2) for [1 – cos(πn)], we see Eqs. (9-11) and (9-12) to be equivalent.

Looking again at Figure 9-9, we can reinforce the validity of our h(n) derivation. Notice that for n > 0 the values of h(n) are non-zero only when n is odd. In addition, the amplitudes of those non-zero values decrease by factors of 1/1, 1/3, 1/5, 1/7, etc. Of what does that remind you? That's right, the Fourier series of a periodic squarewave! This makes sense because our h(n) is the inverse Fourier transform of the squarewave-like H(ω) in Figure 9-2. Furthermore, our h(n) is anti-symmetric, and this is consistent with a purely imaginary H(ω). (If we were to make h(n) symmetrical by inverting its values for all n < 0, the new sequence would be proportional to the Fourier series of a periodic real squarewave.)

Now that we have the expression for the HT's impulse response h(n), let's use it to build a discrete Hilbert transformer.

Discrete Hilbert transformations can be implemented in either the time or frequency domains. Let's look at time-domain Hilbert transformers first.

Time-Domain Hilbert Transformation: FIR Filter Implementation

Looking back at Figure 9-4, and having h(n) available, we want to know how to generate the discrete x_i(n). Recalling the frequency-domain product in Eq. (9-1), we can say x_i(n) is the convolution of x_r(n) and h(k). Mathematically, this is:

Equation 9-13. 

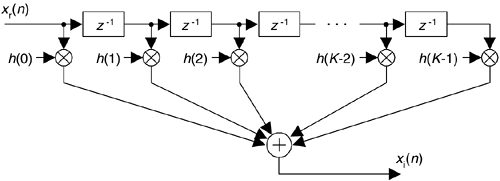
So this means we can implement a Hilbert transformer as a discrete nonrecursive finite impulse response (FIR) filter structure as shown in Figure 9-10.

Figure 9-10. FIR implementation of a K-tap Hilbert transformer.

Designing a traditional time-domain FIR Hilbert transformer amounts to determining those h(k) values so the functional block diagram in Figure 9-4 can be implemented. Our first thought is merely to take the h(n) coefficient values from Eq. (9-11), or Figure 9-9, and use them for the h(k)'s in Figure 9-10. That's almost the right answer. Unfortunately, the Figure 9-9 h(n) sequence is infinite in length, so we have to truncate the sequence. Figuring out what the truncated h(n) should be is where the true design activity takes place.

To start with, we have to decide if our truncated h(n) sequence will have an odd or even length. We make this decision by recalling that FIR implementations having anti-symmetric coefficients and an odd, or even, number of taps are called a Type III, or a Type IV, system respectively[1-3]. These two anti-symmetric filter types have the following unavoidable restrictions with respect to their frequency magnitude responses |H(ω)|:

h(n) length: →	Odd (Type III)	Even (Type IV)
	|H(0)| = 0	|H(0)| = 0
	|H(ωs/2)| = 0	|H(ωs/2)| no restriction

What this little table tells us is odd-tap Hilbert transformers always have a zero magnitude response at both zero Hz and at half the sample rate. Even-tap Hilbert transformers always have a zero magnitude response at zero Hz. Let's look at some examples.

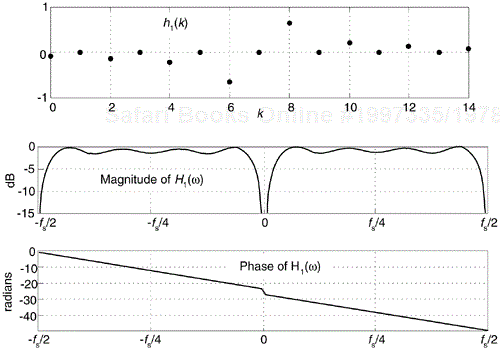
Figure 9-11 shows the frequency response of a 15-tap (Type III, odd-tap) FIR Hilbert transformer whose coefficients are designated as h₁(k). These plots have much to teach us.

Figure 9-11. H₁(ω) frequency response of h₁(k), a 15-tap Hilbert transformer.

1. For example, an odd-tap FIR implementation does indeed have a zero magnitude response at 0 Hz and ±f_s/2 Hz. This means odd-tap (Type III) FIR implementations turn out to be bandpass in performance.

2. There's ripple in the H₁(ω) passband. We should have expected this because we were unable to use an infinite number of h₁(k) coefficients. Here, just as it does when we're designing standard lowpass FIR filters, truncating the length of the time-domain coefficients causes ripples in the frequency domain. (When we abruptly truncate a function in one domain, Mother Nature pays us back by invoking the Gibbs phenomenon, resulting in ripples in the other domain.) You guessed it. We can reduce the ripple in |H₁(ω)| by windowing the truncated h₁(k) sequence. However, windowing the coefficients will narrow the bandwidth of H₁(ω) somewhat, so using more coefficients may be necessary after windowing is applied. You'll find windowing the truncated h₁(k) sequence to be to your advantage.

3. It's exceedingly difficult to compute the HT of low-frequency signals. We can widen (somewhat) and reduce the transition region width of H₁(ω)'s magnitude response, but that requires many filter taps.

4. The phase response of H₁(ω) is linear, as it should be when the coefficients' absolute values are symmetrical. The slope of the phase curve (that is constant in our case) is proportional to the time delay a signal sequence experiences traversing the FIR filter. More on this in a moment. That discontinuity in the phase response at 0 Hz corresponds to π radians, as Figure 9-2 tells us it should. Whew, good thing. That's what we were after in the first place!

In our relentless pursuit of correct results, we're forced to compensate for the linear phase shift of H₁(ω)—that constant time value equal to the group delay of the filter—when we generate our analytic x_c(n). We do this by delaying, in time, the original x_r(n) by an amount equal to the group delay of the h₁(k) FIR Hilbert transformer. Recall that the group delay G of a K-tap FIR filter, measured in samples, is G = (K–1)/2 samples. So our block diagram for generating a complex x_c(n) signal, using an FIR structure, is given in Figure 9-12(a). There we delay x_r(n) by G = (7–1)/2 = 3 samples, generating the delayed sequence x'_r(n). This delayed sequence now aligns properly in time with x_i(n).

Figure 9-12. Generating an x_c(n) sequence when h(k) is a 7-tap FIR Hilbert filter: (a) processing steps; (b) filter structure.

If you're building your odd-tap FIR Hilbert transform in hardware, an easy way to obtain x'_r(n) is to tap off the original x_r(n) sequence at the center tap of the FIR Hilbert transformer structure as in Figure 9-12(b). If you're modeling Figure 9-12(a) in software, the x'_r(n) sequence can be had by inserting G = 3 zeros at the beginning of the original x_r(n) sequence.

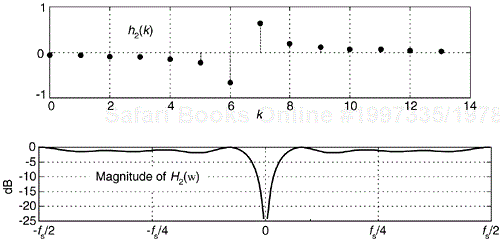
We can, for example, implement an FIR Hilbert transformer using a Type IV FIR structure, with its even number of taps. Figure 9-13 shows this notion where the coefficients are, say, h₂(k). See how the frequency magnitude response is non-zero at ±f_s/2 Hz. Thus this even-tap filter approximates an ideal Hilbert transformer somewhat better than an odd-tap implementation.

Figure 9-13. H₂(ω) frequency response of h₂(k), a 14-tap Hilbert transformer.

One of the problems with this traditional Hilbert transformer is that the passband gain in |H₂(ω)| is not unity for all frequencies, as is the x'_r(n) path in Figure 9-12. So to minimize errors, we must use many h₂(k) coefficients (or window the coefficients) to make |H₂(ω)|'s passband as flat as possible.

Although not shown here, the negative slope of the phase response of H₂(ω) corresponds to a filter group delay of G = (14–1)/2 = 6.5 samples. This requires us to delay the original x_r(n) sequence by a non-integer (fractional) number of samples in order to achieve time alignment with x_i(n). Fractional time delay filters is beyond the scope of this material, but Reference [4] is a source of further information on the topic.

Let's recall that alternate coefficients of a Type III (odd-tap) FIR are zeros. Thus the odd-tap Hilbert transformer is more attractive than an even-tap version from a computational workload standpoint. Almost half of the multiplications in Figure 9-10 can be eliminated for a Type III FIR Hilbert transformer. Designers might even be able to further reduce the number of multiplications by a factor of two by using the folded FIR structure (discussed in Section 13.7) that's possible with symmetric coefficients (keeping in mind that half the coefficients are negative).

A brief warning: here's a mistake sometimes even the professionals make. When we design standard linear-phase FIR filters, we calculate the coefficients and then use them in our hardware or software designs. Sometimes we forget to flip the coefficients before we use them in an FIR filter. This forgetfulness usually doesn't hurt us because typical FIR coefficients are symmetrical. Not so with FIR Hilbert filters, so please don't forget to reverse the order of your coefficients before you use them for convolutional filtering. Failing to flip the coefficients will distort the desired HT phase response.

As an aside, Hilbert transformers can be built with IIR filter structures, and in some cases they're more computationally efficient than FIR Hilbert transformers at the expense of a slight degradation in the 90^o phase difference between x_r(n) and x_i(n)[5,6].

Frequency-Domain Hilbert Transformation

Here's a frequency-domain Hilbert processing scheme deserving mention because the HT of x_r(n) and the analytic x_c(n) sequence can be generated simultaneously. We merely take an N-point DFT of a real even-length-N x_r(n) signal sequence, obtaining the discrete X_r(m) spectrum given in Figure 9-14(a). Next, create a new spectrum X_c(m) = 2X_r(m). Set the negative-frequency X_c(m) samples, that's (N/2)+1 ≤ m ≤ N–1, to zero leaving us with a new one-sided X_c(m) spectrum as in Figure 9-14(b). Next divide the X_c(0) (the DC term) and the X_c(N/2) spectral samples by two. Finally, we perform an N-point inverse DFT of the new X_c(m), the result being the desired analytic x_c(n) time-domain sequence. The real part of x_c(n) is the original x_r(n), and the imaginary part of x_c(n) is the HT of x_r(n). Done!

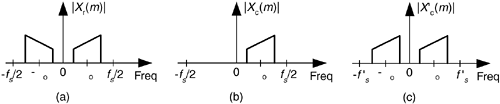
Figure 9-14. Spectrum of original x_r(n) sequence, and the one-sided spectrum of analytic x_c(n) sequence.

There are several issues to keep in mind concerning this straightforward frequency-domain analytic signal generation scheme:

1. If possible, restrict the x_r(n) input sequence length to an integer power of two so the radix-2 FFT algorithm can be used to efficiently compute the DFT.

2. Make sure the X_c(m) sequence has the same length as the original X_r(m) sequence. Remember, you zero out the negative-frequency X_c(m) samples; you don't discard them.

3. The factor of 2 in the above X_c(m) = 2X_r(m) assignment compensates for the amplitude loss by a factor of 2 in losing the negative-frequency spectral energy.

4. If your HT application is block-oriented in the sense that you only have to generate the analytic sequence from a fixed-length real time sequence, this technique is sure worth thinking about because there's no time delay heartache associated with time-domain FIR implementations to worry about. With the advent of fast hardware DSP chips and pipelined FFT techniques, the above analytic signal generation scheme may be viable for a number of applications. One scenario to consider is using the efficient 2N-point real FFT technique, described in Section 13.5.2, to compute the forward DFT of the real-valued x_r(n). Of course, the thoughtful engineer would conduct a literature search to see what algorithms are available for efficiently performing inverse FFTs when many of the frequency-domain samples are zeros.

Should you desire a decimated-by-two analytic x'_c(n) sequence based on x_r(n), it's easy to do, thanks to Reference [7]. First, compute the N-point X_r(m). Next, create a new spectral sequence X'_c(k) = 2X_r(k) for 1 ≤ k ≤ (N/2)-1. Set X'_c(0) equal to X_r(0) + X_r(N/2). Finally, compute the (N/2)-point inverse DFT of X'_c(m) yielding the decimated-by-two analytic x'_c(n). The x'_c(n) sequence has a sample rate of f'_s = f_s/2, and the spectrum shown in Figure 9-14(c).

In Section 13.28.2 we discuss a scheme to generate interpolated analytic signals from x_r(n).

In digital communications applications, the FIR implementation of the HT (such as that in Figure 9-12(b)) is used to generate a complex analytic signal x_c(n). Some practitioners now use a time-domain complex filtering technique to achieve analytic signal generation when dealing with real bandpass signals[8]. This scheme, which does not specifically perform the HT of an input sequence x_r(n), uses a complex filter implemented with two real FIR filters with essentially equal magnitude responses, but whose phase responses differ by exactly 90^o, as shown in Figure 9-15.

Figure 9-15. Generating an x_c(n) sequence with a complex filter (two real FIR filters).

Here's how it's done. A standard K-tap FIR lowpass filter is designed, using your favorite FIR design software, to have a two-sided bandwidth slightly wider than the original real bandpass signal of interest. The real coefficients of the lowpass filter, h_LP(k), are then multiplied by the complex exponential , using the following definitions:

The results of the multiplication are complex coefficients whose rectangular-form representation is

Equation 9-14. 

creating a complex bandpass filter centered at f_o Hz.

Next we use the real and imaginary parts of the filter's h_BP(k) coefficients in two separate real-valued coefficient FIR filters as shown in Figure 9-15. In DSP parlance, the filter producing the x_I(n) sequence is called the I-channel for in-phase, and the filter generating x_Q(n) is called the Q-channel for quadrature phase. There are several interesting aspects of this mixing analytic signal generation scheme in Figure 9-15:

Keep in mind now, the x_Q(n) sequence in Figure 9-15 is not the Hilbert transform of the x_r(n) input. That wasn't our goal here. Our intent was to generate an analytic x_c(n) sequence whose x_Q(n) quadrature component is the Hilbert transform of the x_I(n) in-phase sequence.

Time-domain FIR Hilbert transformer design is essentially an exercise in lowpass filter design. As such, an ideal discrete FIR Hilbert transformer, like an ideal lowpass FIR filter, cannot be achieved in practice. Fortunately, we can usually ensure that the bandpass of our Hilbert transformer covers the bandwidth of the original signal we're phase shifting by ± 90^o. Using more filter taps improves the transformer's performance (minimizing passband ripple), and the choice of an odd or even number of taps depends on whether the gain at the folding frequency should be zero or not, and whether an integer-sample delay is mandatory. Those comments also apply to the complex-filter method (Figure 9-15) for generating a complex signal from a real signal. A possible drawback of that method is that the real part of the generated complex signal is not equal to the original real input signal. (That is, x_I(n) does not equal x_r(n).)

Using a floating point number format, the complex filtering scheme yields roughly a 0.15 dB peak-peak passband ripple difference between the two real filters with 100 taps each, while the FIR Hilbert filter scheme requires something like 30 taps to maintain that same passband ripple level. These numbers are for the scenario where no filter coefficient windowing is performed. Thus the FIR Hilbert filter method is computationally more efficient than the complex filtering scheme. For very high-performance analytic signal generation (where the equivalent Hilbert transformer bandwidth must be very close to the full f_s/2 bandwidth, and passband ripple must be very small), the DFT method should be considered.

The complex filtering scheme exhibits an amplitude loss of one half, where the DFT and FIR Hilbert filtering methods have no such loss. The DFT method provides the most accurate method for generating a complex analytic signal from a real signal, and with the DFT the real part of x_c(n) is equal to the real input x_r(n). Choosing which method to use in any given application requires modeling with your target computing hardware, using your expected number format (integer versus floating point), against the typical input signals you intend to process.