7.4* The Rational Canonical Form
Until now we have used eigenvalues, eigenvectors, and generalized eigenvectors in our analysis of linear operators with characteristic polynomials that split. In general, characteristic polynomials need not split, and indeed, operators need not have eigenvalues! However, the unique factorization theorem for polynomials (see page 562) guarantees that the characteristic polynomial f(t) of any linear operator T on an n-dimensional vector space factors uniquely as
where the ϕi(t)’s (1≤i≤k) are distinct irreducible monic polynomials and the ni’s are positive integers. In the case that f(t) splits, each irreducible monic polynomial factor is of the form ϕi(t)=t−λi, where λi is an eigenvalue of T, and there is a one-to-one correspondence between eigenvalues of T and the irreducible monic factors of the characteristic polynomial. In general, eigenvalues need not exist, but the irreducible monic factors always exist. In this section, we establish structure theorems based on the irreducible monic factors of the characteristic polynomial instead of eigenvalues.
In this context, the following definition is the appropriate replacement for eigenspace and generalized eigenspace.
Definition.
Let T be a linear operator on a finite-dimensional vector space V with characteristic polynomial
where the ϕi(t)’s (1≤i≤k) are distinct irreducible monic polynomials and the ni’s are positive integers. For 1≤i≤k, we define the subset Kϕi of V by
We show that each Kϕi is a nonzero T-invariant subspace of V. Note that if ϕi(t)=t−λ is of degree one, then Kϕi is the generalized eigenspace of T corresponding to the eigenvalue λ.
Having obtained suitable generalizations of the related concepts of eigenvalue and eigenspace, our next task is to describe a canonical form of a linear operator suitable to this context. The one that we study is called the rational canonical form. Since a canonical form is a description of a matrix representation of a linear operator, it can be defined by specifying the form of the ordered bases allowed for these representations.
Here the bases of interest naturally arise from the generators of certain cyclic subspaces. For this reason, the reader should recall the definition of a T-cyclic subspace generated by a vector and Theorem 5.21 (p. 314). We briefly review this concept and introduce some new notation and terminology.
Let T be a linear operator on a finite-dimensional vector space V, and let x be a nonzero vector in V. We use the notation Cx for the T-cyclic subspace generated by x. Recall (Theorem 5.21) that if dim(Cx)=k, then the set
is an ordered basis for Cx. To distinguish this basis from all other ordered bases for Cx, we call it the T-cyclic basis generated by x and denote it by βx. Let A be the matrix representation of the restriction of T to Cx in the ordered basis βx. Recall from the proof of Theorem 5.21 that
where
Furthermore, the characteristic polynomial of A is given by
The matrix A is called the companion matrix of the monic polynomial h(t)=a0+a1t+⋯+ak−1tk−1+tk. Every monic polynomial has a companion matrix, and the characteristic polynomial of the companion matrix of a monic polynomial g(t) of degree k is equal to (−1)kg(t). (See Exercise 19 of Section 5.4.) By Theorem 7.15 (p. 512), the monic polynomial h(t) is also the minimal polynomial of A. Since A is the matrix representation of the restriction of T to Cx, h(t) is also the minimal polynomial of this restriction. By Exercise 15 of Section 7.3, h(t) is also the T-annihilator of x.
It is the object of this section to prove that for every linear operator T on a finite-dimensional vector space V, there exists an ordered basis β for V such that the matrix representation [T]β is of the form
where each Ci is the companion matrix of a polynomial (ϕ(t))m such that ϕ(t) is a monic irreducible divisor of the characteristic polynomial of T and m is a positive integer. A matrix representation of this kind is called a rational canonical form of T. We call the accompanying basis a rational canonical basis for T.
The next theorem is a simple consequence of the following lemma, which relies on the concept of T-annihilator, introduced in the Exercises of Section 7.3.
Lemma.
Let T be a linear operator on a finite-dimensional vector space V, let x be a nonzero vector in V, and suppose that the T-annihilator of x is of the form (ϕ(t))p for some irreducible monic polynomial ϕ(t). Then ϕ(t) divides the minimal polynomial of T, and x∈Kϕ.
Proof.
By Exercise 15(b) of Section 7.3, (ϕ(t))p divides the minimal polynomial of T. Therefore ϕ(t) divides the minimal polynomial of T. Furthermore, x∈Kϕ by the definition of Kϕ.
Theorem 7.17.
Let T be a linear operator on a finite-dimensional vector space V, and let β be an ordered basis for V. Then β is a rational canonical basis for T if and only if β is the disjoint union of T-cyclic bases βvi, where each vi lies in Kϕ for some irreducible monic divisor ϕ(t) of the characteristic polynomial of T.
Proof.
Exercise.
Example 1
Suppose that T is a linear operator on R8 and
is a rational canonical basis for T such that
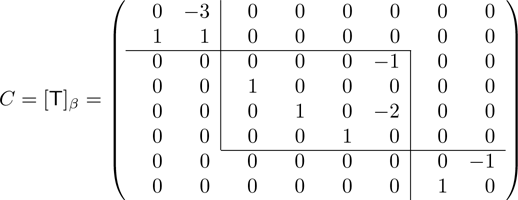
is a rational canonical form of T. In this case, the submatrices C1, C2, and C3 are the companion matrices of the polynomials ϕ1(t), (ϕ2(t))2, and ϕ2(t), respectively, where
In the context of Theorem 7.17, β is the disjoint union of the T-cyclic bases; that is,
By Exercise 39 of Section 5.4, the characteristic polynomial f(t) of T is the product of the characteristic polynomials of the companion matrices:
The rational canonical form C of the operator T in Example 1 is constructed from matrices of the form Ci, each of which is the companion matrix of some power of a monic irreducible divisor of the characteristic polynomial of T. Furthermore, each such divisor is used in this way at least once.
In the course of showing that every linear operator T on a finite dimensional vector space has a rational canonical form C, we show that the companion matrices Ci that constitute C are always constructed from powers of the monic irreducible divisors of the characteristic polynomial of T. A key role in our analysis is played by the subspaces Kϕ, where ϕ(t) is an irreducible monic divisor of the minimal polynomial of T. Since the minimal polynomial of an operator divides the characteristic polynomial of the operator, every irreducible divisor of the former is also an irreducible divisor of the latter. We eventually show that the converse is also true; that is, the minimal polynomial and the characteristic polynomial have the same irreducible divisors.
We begin with a result that lists several properties of irreducible divisors of the minimal polynomial. The reader is advised to review the definition of T-annihilator and the accompanying Exercises 15 of Section 7.3.
Theorem 7.18.
Let T be a linear operator on a finite-dimensional vector space V, and suppose that
is the minimal polynomial of T, where the ϕi(t)‘s (1≤i≤k) are the distinct irreducible monic factors of p(t) and the mi’s are positive integers. Then the following statements are true.
-
(a) Kϕi is a nonzero T-invariant subspace of V for each i.
-
(b) If x is a nonzero vector in some Kϕi, then the T-annihilator of x is of the form (ϕi(t))p for some integer p.
-
(c) Kϕi∩Kϕj={0} for i≠j.
-
(d) Kϕi is invariant under ϕj(T) for i≠j, and the restriction of ϕj(T) to Kϕi is one-to-one and onto.
-
(e) Kϕi=N((ϕi(T))mi) for each i.
Proof.
If k=1, then (a), (b), and (e) are obvious, while (c) and (d) are vacuously true. Now suppose that k>1.
-
(a) The proof that Kϕi is a T-invariant subspace of V is left as an exercise. Let fi(t) be the polynomial obtained from p(t) by omitting the factor (ϕi(t))mi. To prove that Kϕi is nonzero, first observe that fi(t) is a proper divisor of p(t); therefore there exists a vector z∈V such that x=fi(T)(z)≠0. Then x∈Kϕi because
(ϕi(T))mi(x)=(ϕi(T))mifi(T)(z)=p(T)(z)=0. -
(b) Assume the hypothesis. Then (ϕi(T))q(x)=0 for some positive integer q. Hence the T-annihilator of x divides (ϕi(t))q by Exercise 15(b) of Section 7.3, and the result follows.
-
(c) Assume i≠j. Let x∈Kϕi∩Kϕj, and suppose that x≠0. By (b), the T-annihilator of x is a power of both ϕi(t) and ϕj(t). But this is impossible because ϕi(t) and ϕj(t) are relatively prime (see Appendix E). We conclude that x=0.
-
(d) Assume i≠j. Since Kϕi is T-invariant, it is also ϕj(T)-invariant. Suppose that ϕj(T)(x)=0 for some x∈Kϕi. Then x∈Kϕi∩Kϕj={0} by (c). Therefore the restriction of ϕj(T) to Kϕi is one-to-one. Since V is finite-dimensional, this restriction is also onto.
-
(e) Suppose that 1≤i≤k. Clearly, N((ϕi(T))mi)⊆Kϕi. Let fi(t) be the polynomial defined in (a). Since fi(t) is a product of polynomials of the form ϕj(t) for j≠i, we have by (d) that the restriction of fi(T) to Kϕi is onto. Let x∈Kϕi. Then there exists y∈Kϕi such that fi(T)(y)=x. Therefore
((ϕi(T))mi)(x)=((ϕi(T))mi)fi(T)(y)=p(T)(y)=0,
and hence x∈N((ϕi(T))mi). Thus Kϕi=N((ϕi(T))mi).
Since a rational canonical basis for an operator T is obtained from a union of T-cyclic bases, we need to know when such a union is linearly independent. The next major result, Theorem 7.19, reduces this problem to the study of T-cyclic bases within Kϕ, where ϕ(t) is an irreducible monic divisor of the minimal polynomial of T. We begin with the following lemma.
Lemma.
Let T be a linear operator on a finite-dimensional vector space V, and suppose that
is the minimal polynomial of T, where the ϕi’s (1≤i≤k) are the distinct irreducible monic factors of p(t) and the mi’s are positive integers. For 1≤i≤k, let vi∈Kϕi be such that
Then vi=0 for all i.
Proof.
The result is trivial if k=1, so suppose that k>1. Consider any i. Let fi(t) be the polynomial obtained from p(t) by omitting the factor (ϕi(t))mi. As a consequence of Theorem 7.18, fi(T) is one-to-one on Kϕi, and fi(T)(vj)=0 for i≠j. Thus, applying fi(T) to (2), we obtain fi(T)(vi)=0, from which it follows that vi=0.
Theorem 7.19.
Let T be a linear operator on a finite-dimensional vector space V, and suppose that
is the minimal polynomial of T, where the ϕi‘s (1≤i≤k) are the distinct irreducible monic factors of p(t) and the mi’s are positive integers. For 1≤i≤k, let Si be a linearly independent subset of Kϕi. Then
-
Si∩Sj=∅ for i≠j
-
S1∪S2∪⋯∪Sk is linearly independent.
Proof.
If k=1, then (a) is vacuously true and (b) is obvious. Now suppose that k>1. Then (a) follows immediately from Theorem 7.18(c). Furthermore, the proof of (b) is identical to the proof of Theorem 5.5 (p. 261) with the eigenvectors replaced by the generalized eigenvectors.
In view of Theorem 7.19, we can focus on bases of individual spaces of the form Kϕ, where ϕ(t) is an irreducible monic divisor of the minimal polynomial of T. The next several results give us ways to construct bases for these spaces that are unions of T-cyclic bases. These results serve the dual purposes of leading to the existence theorem for the rational canonical form and of providing methods for constructing rational canonical bases.
For Theorems 7.20 and 7.21 and the latter’s corollary, we fix a linear operator T on a finite-dimensional vector space V and an irreducible monic divisor ϕ(t) of the minimal polynomial of T.
Theorem 7.20.
Let v1, v2, …, vk be distinct vectors in Kϕ such that
is linearly independent. For each i, suppose there exists wi∈V such that ϕ(T)(wi)=vi. Then
is also linearly independent.
Proof.
Consider any linear combination of vectors in S2 that sums to zero, say,
For each i, let fi(t) be the polynomial defined by
Then (3) can be rewritten as
Apply ϕ(T) to both sides of (4) to obtain
This last sum can be rewritten as a linear combination of the vectors in S1 so that each fi(T)(vi) is a linear combination of the vectors in βvi. Since S1 is linearly independent, it follows that
Therefore the T-annihilator of vi divides fi(t) for all i. (See Exercise 15 of Section 7.3.) By Theorem 7.18(b), ϕ(t) divides the T-annihilator of vi, and hence ϕ(t) divides fi(t) for all i. Thus, for each i, there exists a polynomial gi(t) such that fi(t)=gi(t)ϕ(t). So (4) becomes
Again, linear independence of S1 requires that
But fi(T)(wi) is the result of grouping the terms of the linear combination in (3) that arise from the linearly independent set βwi. We conclude that for each i, aij=0 for all j. Therefore S2 is linearly independent.
We now show that Kϕ has a basis consisting of a union of T-cycles.
Lemma.
Let W be a T-invariant subspace of Kϕ, and let β be a basis for W. Then the following statements are true.
-
(a) Suppose that x∈N(ϕ(T)), but x∉W. Then β∪βx is linearly independent.
-
(b) For some w1, w2, …, ws in N(ϕ(T)), β can be extended to the linearly independent set
β′=β∪βw1∪βw2∪⋯∪βws,whose span contains N(ϕ(T)).
Proof.
(a) Let β={v1, v2, …, vk}, and suppose that
where d is the degree of ϕ(t). Then z∈Cx∩W, and hence Cz⊆Cx∩W. Suppose that z≠0. Then z has ϕ(t) as its T-annihilator, and therefore
It follows that Cx∩W=Cx, and consequently x∈W, contrary to hypothesis. Therefore z=0, from which it follows that bj=0 for all j. Since β is linearly independent, it follows that ai=0 for all i. Thus β∪βx is linearly independent.
(b) Suppose that W does not contain N(ϕ(T)). Choose a vector w1∈N(ϕ(T)) that is not in W. By (a), β1=β∪βw1 is linearly independent. Let W1=span(β1). If W1 does not contain N(ϕ(T)), choose a vector w2 in N(ϕ(T)), but not in W1, so that β2=β1∪βw2=β∪βw1∪βw2 is linearly independent. Continuing this process, we eventually obtain vectors w1, w2, …, ws in N(ϕ(T)) such that the union
is a linearly independent set whose span contains N(ϕ(T)).
Theorem 7.21.
If the minimal polynomial of T is of the form p(t)=(ϕ(t))m, then there exists a rational canonical basis for T.
Proof.
The proof is by mathematical induction on m. Suppose that m=1. Apply (b) of the lemma to W={0} to obtain a linearly independent subset of V of the form βv1∪βv2∪⋯∪βvk, whose span contains N(ϕ(T)). Since V=N(ϕ(T)), this set is a rational canonical basis for V.
Now suppose that, for some integer m>1, the result is valid whenever the minimal polynomial of T is of the form (ϕ(t))k, where k<m, and assume that the minimal polynomial of T is p(t)=(ϕ(t))m. Let r=rank(ϕ(T)). Then R(ϕ(T)) is a T-invariant subspace of V, and the restriction of T to this subspace has (ϕ(t))m−1 as its minimal polynomial. Therefore we may apply the induction hypothesis to obtain a rational canonical basis for the restriction of T to R(T). Suppose that v1, v2, …, vk are the generating vectors of the T-cyclic bases that constitute this rational canonical basis. For each i, choose wi in V such that vi=ϕ(T)(wi). By Theorem 7.20, the union β of the sets βwi is linearly independent. Let W=span(β). Then W contains R(ϕ(T)). Apply (b) of the lemma and adjoin additional T-cyclic bases βwk+1, βwk+2, …, βws to β, if necessary, where wi is in N(ϕ(T)) for i≥k, to obtain a linearly independent set
whose span W′ contains both W and N(ϕ(T)).
We show that W′=V. Let U denote the restriction of ϕ(T) to W′, which is ϕ(T)-invariant. By the way in which W′ was obtained from R(ϕ(T)), it follows that R(U)=R(ϕ(T)) and N(U)=N(ϕ(T)). Therefore
Thus W′=V, and β′ is a rational canonical basis for T.
Corollary.
Kϕ has a basis consisting of the union of T-cyclic bases.
Proof.
Apply Theorem 7.21 to the restriction of T to Kϕ.
We are now ready to study the general case.
Theorem 7.22.
Every linear operator on a finite-dimensional vector space has a rational canonical basis and, hence, a rational canonical form.
Proof.
Let T be a linear operator on a finite-dimensional vector space V, and let p(t)=(ϕ1(t))m1(ϕ2(t))m2⋯(ϕk(t))mk be the minimal polynomial of T, where the ϕi(t)’s are the distinct irreducible monic factors of p(t) and mi>0 for all i. The proof is by mathematical induction on k. The case k=1 is proved in Theorem 7.21.
Suppose that the result is valid whenever the minimal polynomial contains fewer than k distinct irreducible factors for some k>1, and suppose that p(t) contains k distinct factors. Let U be the restriction of T to the T-invariant subspace W=R((ϕk(T))mk), and let q(t) be the minimal polynomial of U. Then q(t) divides p(t) by Exercise 10 of Section 7.3. Furthermore, ϕk(t) does not divide q(t). For otherwise, there would exist a nonzero vector x∈W such that ϕk(U)(x)=0 and a vector y∈V such that x=(ϕk(T))mk(y). It follows that (ϕk(T))mk+1(y)=0, and hence y∈Kϕk and x=(ϕk(T))mk(y)=0 by Theorem 7.18(e), a contradiction. Thus q(t) contains fewer than k distinct irreducible divisors. So by the induction hypothesis, U has a rational canonical basis β1 consisting of a union of U-cyclic bases (and hence T-cyclic bases) of vectors from some of the subspaces Kϕi, 1≤i≤k−1. By the corollary to Theorem 7.21, Kϕk has a basis β2 consisting of a union of T-cyclic bases. By Theorem 7.19, β1 and β2 are disjoint, and β=β1∪β2 is linearly independent. Let s denote the number of vectors in β.Then
We conclude that β is a basis for V. Therefore β is a rational canonical basis, and T has a rational canonical form.
In our study of the rational canonical form, we relied on the minimal polynomial. We are now able to relate the rational canonical form to the characteristic polynomial.
Theorem 7.23.
Let T be a linear operator on an n-dimensional vector space V with characteristic polynomial
where the ϕi(t)’s (1≤i≤k) are distinct irreducible monic polynomials and the ni’s are positive integers. Then the following statements are true.
-
(a) ϕ1(t), ϕ2(t), …, ϕk(t) are the irreducible monic factors of the minimal polynomial.
-
(b) For each i, dim(Kϕi)=dini, where di is the degree of ϕi(t).
-
(c) If β is a rational canonical basis for T, then βi=β∩Kϕi is a basis for Kϕi for each i.
-
(d) If γi is a basis for Kϕi for each i, then γ=γ1∪γ2∪⋯∪γk is a basis for V. In particular, if each γi is a disjoint union of T-cyclic bases, then γ is a rational canonical basis for T.
Proof.
(a) By Theorem 7.22, T has a rational canonical form C. By Exercise 39 of Section 5.4, the characteristic polynomial of C, and hence of T, is the product of the characteristic polynomials of the companion matrices that compose C. Therefore each irreducible monic divisor ϕi(t) of f(t) divides the characteristic polynomial of at least one of the companion matrices, and hence for some integer p, (ϕi(t))p is the T-annihilator of a nonzero vector of V. We conclude that (ϕi(t))p, and so ϕi(t), divides the minimal polynomial of T. Conversely, if ϕ(t) is an irreducible monic polynomial that divides the minimal polynomial of T, then ϕ(t) divides the characteristic polynomial of T because the minimal polynomial divides the characteristic polynomial.
(b), (c), and (d) Let C=[T]β, which is a rational canonical form of T. Consider any i i(1≤i≤k). Since f(t) is the product of the characteristic polynomials of the companion matrices that compose C, we may multiply those characteristic polynomials that arise from the T-cyclic bases in βi to obtain the factor (ϕi(t))ni of f(t). Since this polynomial has degree nidi, and the union of these bases is a linearly independent subset βi of Kϕi, we have
Furthermore, n=k∑i=1dini, because this sum is equal to the degree of f(t).
Now let s denote the number of vectors in γ. By Theorem 7.19, γ is linearly independent, and therefore
Hence n=s, and dini=dim(Kϕi) for all i. It follows that γ is a basis for V and βi is a basis for Kϕi for each i.
Uniqueness of the Rational Canonical Form
Having shown that a rational canonical form exists, we are now in a position to ask about the extent to which it is unique. Certainly, the rational canonical form of a linear operator T can be modified by permuting the T-cyclic bases that constitute the corresponding rational canonical basis. This has the effect of permuting the companion matrices that make up the rational canonical form. As in the case of the Jordan canonical form, we show that except for these permutations, the rational canonical form is unique, although the rational canonical bases are not.
To simplify this task, we adopt the convention of ordering every rational canonical basis so that all the T-cyclic bases associated with the same irreducible monic divisor of the characteristic polynomial are grouped together. Furthermore, within each such grouping, we arrange the T-cyclic bases in decreasing order of size. Our task is to show that, subject to this order, the rational canonical form of a linear operator is unique up to the arrangement of the irreducible monic divisors.
As in the case of the Jordan canonical form, we introduce arrays of dots from which we can reconstruct the rational canonical form. For the Jordan canonical form, we devised a dot diagram for each eigenvalue of the given operator. In the case of the rational canonical form, we define a dot diagram for each irreducible monic divisor of the characteristic polynomial of the given operator. A proof that the resulting dot diagrams are completely determined by the operator is also a proof that the rational canonical form is unique.
In what follows, T is a linear operator on a finite-dimensional vector space with rational canonical basis β, ϕ(t) is an irreducible monic divisor of the characteristic polynomial of βv1, βv2, …, βvk are the T-cyclic bases of β that are contained in Kϕ; and d is the degree of ϕ(t). For each j, let (ϕ(t))pj be the annihilator of vj. This polynomial has degree dpj; therefore, by Exercise 15 of Section 7.3, βvj contains dpj vectors. Furthermore, p1≥p2≥⋯≥pk since the T-cyclic bases are arranged in decreasing order of size. We define the dot diagram of ϕ(t) to be the array consisting of k columns of dots with pj dots in the jth column, arranged so that the jth column begins at the top and terminates after pj dots. For example, if k=3, p1=4, p2=2, and p3=2, then the dot diagram is

Although each column of a dot diagram corresponds to a T-cyclic basis βvi in Kϕ, there are fewer dots in the column than there are vectors in the basis.
Example 2
Recall the linear operator T of Example 1 with the rational canonical basis β and the rational canonical form C=[T]β. Since there are two irreducible monic divisors of the characteristic polynomial of T, ϕ1(t)=t2−t+3 and ϕ2(t)=t2+1, there are two dot diagrams to consider. Because ϕ1(t) is the T-annihilator of v1 and βv1 is a basis for Kϕ1, the dot diagram for ϕ1(t) consists of a single dot. The other two T-cyclic bases, βv3 and βv7, lie in Kϕ2. Since v3 has T-annihilator (ϕ2(t))2 and v7 has T-annihilator ϕ2(t), in the dot diagram of ϕ2(t) we have p1=2 and p2=1. These diagrams are as follows:
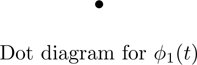
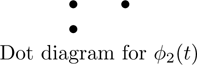
In practice, we obtain the rational canonical form of a linear operator from the information provided by dot diagrams. This is illustrated in the next example.
Example 3
Let T be a linear operator on a finite-dimensional vector space over R, and suppose that the irreducible monic divisors of the characteristic polynomial of T are
Suppose, furthermore, that the dot diagrams associated with these divisors are as follows:
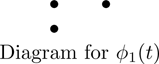
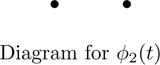
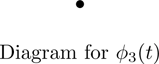
Since the dot diagram for ϕ1(t) has two columns, it contributes two companion matrices to the rational canonical form. The first column has two dots, and therefore corresponds to the 2×2 companion matrix of (ϕ1(t))2=(t−1)2. The second column, with only one dot, corresponds to the 1×1 companion matrix of ϕ1(t)=t−1. These two companion matrices are given by
The dot diagram for ϕ2(t)=t2+2 consists of two columns. each containing a single dot; hence this diagram contributes two copies of the 2×2 companion matrix for ϕ2(t), namely,
The dot diagram for ϕ3(t)=t2+t+1 consists of a single column with a single dot contributing the single 2×2 companion matrix
Therefore the rational canonical form of T is the 9×9 matrix
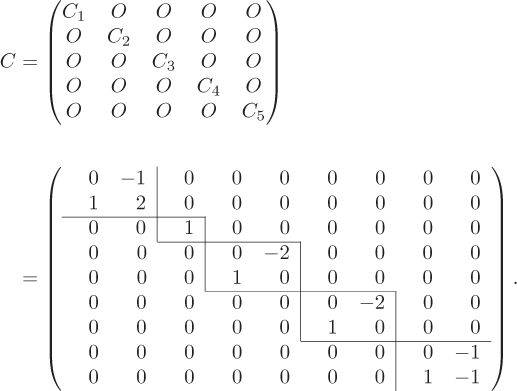
We return to the general problem of finding dot diagrams. As we did before, we fix a linear operator T on a finite-dimensional vector space and an irreducible monic divisor ϕ(t) of the characteristic polynomial of T. Let U denote the restriction of the linear operator ϕ(T) to Kϕ. By Theorem 7.18(d), Uq=T0 for some positive integer q. Consequently, by Exercise 12 of Section 7.2, the characteristic polynomial of U is (−1)mtm, where m=dim(Kϕ). Therefore Kϕ is the generalized eigenspace of U corresponding to λ=0, and U has a Jordan canonical form. The dot diagram associated with the Jordan canonical form of U gives us a key to understanding the dot diagram of T that is associated with ϕ(t). We now relate the two diagrams.
Let β be a rational canonical basis for T, and βv1, βv2, …, βvk be the T-cyclic bases of β that are contained in Kϕ. Consider one of these T-cyclic bases βvj, and suppose again that the T-annihilator of vj is (ϕ(t))pj. Then βvj consists of dpj vectors in β. For 0≤i<d, let γi be the cycle of generalized eigenvectors of U corresponding to λ=0 with end vector Ti(vj), where T0(vj)=bj. Then
By Theorem 7.1 (p. 478), γi is a linearly independent subset of Cvi. Now let
Notice that αj contains dpj vectors.
Lemma 1.
αj is an ordered basis for Cvj.
Proof. The key to this proof is Theorem 7.4 (p. 480). Since αj is the union of cycles of generalized eigenvectors of U corresponding to λ=0, it suffices to show that the set of initial vectors of these cycles
is linearly independent. Consider any linear combination of these vectors
where not all of the coefficients are zero. Let g(t) be the polynomial defined by g(t)=a0+a1t+⋯+ad−1td−1. Then g(t) is a nonzero polynomial of degree less than d, and hence (ϕ(t))pj−1g(t) is a nonzero polynomial with degree less than dpj. Since (ϕ(t))pj is the T-annihilator of vj, it follows that (ϕ(T))pj−1g(T)(vj)≠0. Therefore the set of initial vectors is linearly independent. So by Theorem 7.4, αj is linearly independent, and the γi’s are disjoint. Consequently, αj consists of dpj linearly independent vectors in Cvj, which has dimension dpj. We conclude that αj is a basis for Cvj.
Thus we may replace βvj by αj as a basis for Cvj. We do this for each j to obtain a subset α=α1∪α2∪⋯∪αk of Kϕ.
Lemma 2.
α is a Jordan canonical basis for Kϕ.
Proof. Since βv1∪βv2∪⋯∪βvk is a basis for Kϕ, and since span(αi)=span(βvi)=Cvi, Exercise 9 implies that α is a basis for Kϕ. Because α is a union of cycles of generalized eigenvectors of U, we conclude that α is a Jordan canonical basis.
We are now in a position to relate the dot diagram of T corresponding to ϕ(t) to the dot diagram of U, bearing in mind that in the first case we are considering a rational canonical form and in the second case we are considering a Jordan canonical form. For convenience, we designate the first diagram D1, and the second diagram D2. For each j, the presence of the T-cyclic basis βxj results in a column of pj dots in D1. By Lemma 1, this basis is replaced by the union αj of d cycles of generalized eigenvectors of U, each of length pj, which becomes part of the Jordan canonical basis for U. In effect, αj determines d columns each containing pj dots in D2. So each column in D1 determines d columns in D2 of the same length, and all columns in D2 are obtained in this way. Alternatively, each row in D2 has d times as many dots as the corresponding row in D1. Since Theorem 7.10 (p. 493) gives us the number of dots in any row of D2, we may divide the appropriate expression in this theorem by d to obtain the number of dots in the corresponding row of D1. Thus we have the following result.
Theorem 7.24.
Let T be a linear operator on a finite-dimensional vector space V, let ϕ(t) be an irreducible monic divisor of the characteristic polynomial of T of degree d, and let ri denote the number of dots in the ith row of the dot diagram for ϕ(t) with respect to a rational canonical basis for T. Then
-
(a) r1=1d[dim(V)−rank(ϕ(T))];
-
(b) ri=1d[rank((ϕ(T))i−1)−rank((ϕ(T))i)] for i>1.
Thus the dot diagrams associated with a rational canonical form of an operator are completely determined by the operator. Since the rational canonical form is completely determined by its dot diagrams, we have the following uniqueness condition.
Corollary.
Under the conventions described earlier, the rational canonical form of a linear operator is unique up to the arrangement of the irreducible monic divisors of the characteristic polynomial.
Since the rational canonical form of a linear operator is unique, the polynomials corresponding to the companion matrices that determine this form are also unique. These polynomials, which are powers of the irreducible monic divisors, are called the elementary divisors of the linear operator. Since a companion matrix may occur more than once in a rational canonical form, the same is true for the elementary divisors. We call the number of such occurrences the multiplicity of the elementary divisor.
Conversely, the elementary divisors and their multiplicities determine the companion matrices and, therefore, the rational canonical form of a linear operator.
Example 4
Let
be viewed as a subset of F(R, R), the space of all real-valued functions defined on R, and let V=span(β). Then V is a four-dimensional subspace of F(R, R), and β is an ordered basis for V. Let D be the linear operator on V defined by D(y)=y′, the derivative of y, and let A=[D]β. Then
and the characteristic polynomial of D, and hence of A, is
Thus ϕ(t)=t2−2t+5 is the only irreducible monic divisor of f(t). Since ϕ(t) has degree 2 and V is four-dimensional, the dot diagram for ϕ(t) contains only two dots. Therefore the dot diagram is determined by r1, the number of dots in the first row. Because ranks are preserved under matrix representations, we can use A in place of D in the formula given in Theorem 7.24. Now
and so
It follows that the second dot lies in the second row, and the dot diagram is as follows:

Hence V is a D-cyclic space generated by a single function with D-annihilator (ϕ(t))2. Furthermore, its rational canonical form is given by the companion matrix of (ϕ(t))2=t4−4t3+14t2−20t+25, which is
Thus (ϕ(t))2 is the only elementary divisor of D, and it has multiplicity 1. For the cyclic generator, it suffices to find a function g in V for which ϕ(D)(g)≠0. Since ϕ(A)(e3)≠0, it follows that ϕ(D)(xexcos 2x)≠0; therefore g(x)=xexcos 2x can be chosen as the cyclic generator. Hence
is a rational canonical basis for D. Notice that the function h defined by h(x)=xexsin2x can be chosen in place of g. This shows that the rational canonical basis is not unique.
It is convenient to refer to the rational canonical form and elementary divisors of a matrix, which are defined in the obvious way.
Definitions.
Let A∈Mn×n(F). The rational canonical form of A is defined to be the rational canonical form of LA. Likewise, for A, the elementary divisors and their multiplicities are the same as those of LA.
Let A be an n×n matrix, let C be a rational canonical form of A, and let β be the appropriate rational canonical basis for LA. Then C=[LA]β, and therefore A is similar to C. In fact, if Q is the matrix whose columns are the vectors of β in the same order, then Q−1AQ=C.
Example 5
For the following real matrix A, we find the rational canonical form C of A and a matrix Q such that Q−1AQ=C.
The characteristic polynomial of A is f(t)=−(t2+2)2(t−2); therefore ϕ1(t)=t2+2 and ϕ2(t)=t−2 are the distinct irreducible monic divisors of f(t). By Theorem 7.23, dim(Kϕ1)=4 and dim(Kϕ2)=1. Since the degree of ϕ1(t) is 2, the total number of dots in the dot diagram of ϕ1(t) is 4/2=2, and the number of dots r1 in the first row is given by
Thus the dot diagram of ϕ1(t) is

and each column contributes the companion matrix
for ϕ1(t)=t2+2 to the rational canonical form C. Consequently ϕ1(t) is an elementary divisor with multiplicity 2. Since dim(Kϕ2)=1, the dot diagram of ϕ2(t)=t−2 consists of a single dot, which contributes the 1×1 matrix (2). Hence ϕ2(t) is an elementary divisor with multiplicity 1. Therefore the rational canonical form C is
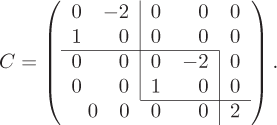
We can infer from the dot diagram of ϕ1(t) that if β is a rational canonical basis for LA, then β∩Kϕ1 is the union of two cyclic bases βv1 and βv2, where v1 and v2 each have annihilator ϕ1(t). It follows that both v1 and v2 lie in N(ϕ1(LA)). It can be shown that
is a basis for N(ϕ1(LA)). Setting v1=e1, we see that
Next choose v2 in Kϕ1=N(ϕ(LA)), but not in the span of βv1={v1, Av1}. For example, v2=e2. Then it can be seen that
and βv1∪βv2 is a basis for Kϕ1.
Since the dot diagram of ϕ2(t)=t−2 consists of a single dot, any nonzero vector in Kϕ2 is an eigenvector of A corresponding to the eigenvalue λ=2. For example, choose
By Theorem 7.23, β={v1, Av1, v2, Av2, v3} is a rational canonical basis for LA. So setting
we have Q−1AQ=C.
Example 6
For the following matrix A, we find the rational canonical form C and a matrix Q such that Q−1AQ=C.
Since the characteristic polynomial of A is f(t)=(t−2)4, the only irreducible monic divisor of f(t) is ϕ(t)=t−2, and so Kϕ=R4. In this case, ϕ(t) has degree 1; hence in applying Theorem 7.24 to compute the dot diagram for ϕ(t), we obtain
and
where ri is the number of dots in the ith row of the dot diagram. Since there are dim(R4)=4 dots in the diagram, we may terminate these computations with r3. Thus the dot diagram for A is

Since (t−2)3 has the companion matrix
and (t−2) has the companion matrix (2), the rational canonical form of A is given by
Next we find a rational canonical basis for LA. The preceding dot diagram indicates that there are two vectors v1 and v2 in R4 with annihilators (ϕ(t))3 and ϕ(t), respectively, and such that
is a rational canonical basis for LA. Furthermore, v1∉N((LA−2I)2), and v2∈N(LA−2I). It can easily be shown that
and
The standard vector e3 meets the criteria for v1; so we set v1=e3. It follows that
Next we choose a vector v2∈N(LA−2I) that is not in the span of βv1. Clearly, v2=e4 satisfies this condition. Thus
is a rational canonical basis for LA.
Finally, let Q be the matrix whose columns are the vectors of β in the same order:
Then C=Q−1AQ.
Direct Sums*
The next theorem is a simple consequence of Theorem 7.23.
Theorem 7.25. (Primary Decomposition Theorem)
Let T be a linear operator on an n-dimensional vector space V with characteristic polynomial
where the ϕi(t)'s(1≤i≤k) are distinct irreducible monic polynomials and the ni’s are positive integers. Then the following statements are true.
-
V=Kϕ1⊕Kϕ2⊕⋯⊕Kϕk.
-
If Ti(1≤i≤k) is the restriction of T to Kϕi and Ci is the rational canonical form of Ti, then C1⊕C2⊕⋯⊕Ck is the rational canonical form of T.
Proof.
Exercise.
The next theorem is a simple consequence of Theorem 7.17.
Theorem 7.26.
Let T be a linear operator on a finite-dimensional vector space V. Then V is a direct sum of T-cyclic subspaces Cvi, where each vi lies in Kϕ for some irreducible monic divisor ϕ(t) of the characteristic polynomial of T.
Proof.
Exercise.
Exercises
-
Label the following statements as true or false.
-
(a) Every rational canonical basis for a linear operator T is the union of T-cyclic bases.
-
(b) If a basis is the union of T-cyclic bases for a linear operator T, then it is a rational canonical basis for T.
-
(c) There exist square matrices having no rational canonical form.
-
(d) A square matrix is similar to its rational canonical form.
-
(e) For any linear operator T on a finite-dimensional vector space, any irreducible factor of the characteristic polynomial of T divides the minimal polynomial of T.
-
(f) Let ϕ(t) be an irreducible monic divisor of the characteristic polynomial of a linear operator T. The dots in the diagram used to compute the rational canonical form of the restriction of T to Kϕ are in one-to-one correspondence with the vectors in a basis for Kϕ.
-
(g) If a matrix has a Jordan canonical form, then its Jordan canonical form and rational canonical form are similar.
-
-
For each of the following matrices A∈Mn×n(F), find the rational canonical form C of A and a matrix Q∈Mn×n(F) such that Q−1AQ=C.
-
(a) A=(310031003)F=R
-
(b) A=(0−11−1)F=R
-
(c) A=(0−11−1)F=C
-
(d) A=(0−714−61−46−30−49−40−411−5)F=R
-
(e) A=(0−412−71−13−30−16−40−18−5)F=R
-
-
For each of the following linear operators T, find the elementary divisors, the rational canonical form C, and a rational canonical basis β.
-
(a) T is the linear operator on P3(R) defined by
T(f(x))=f(0)x−f′(1). -
(b) Let S={sinx, cosx, xsinx, xcosx}, a subset of F(R, R), and let V=span(S). Define T to be the linear operator on V such that
T(f)=f′. -
(c) T is the linear operator on M2×2(R) defined by
T(A)=(01−11)·A. -
(d) Let S={sinxsiny, sinxcosy, cosxsiny, cosxcosy}, a subset of F(R×R, R), and let V=span(S). Define T to be the linear operator on V such that
T(f)(x, y)=∂f(x, y)∂x+∂f(x, y)∂y.
-
-
Let T be a linear operator on a finite-dimensional vector space V with minimal polynomial (ϕ(t))m for some positive integer m.
-
(a) Prove that R(ϕ(T))⊆N((ϕ(T))m−1).
-
(b) Give an example to show that the subspaces in (a) need not be equal.
-
(c) Prove that the minimal polynomial of the restriction of T to R(ϕ(T)) equals (ϕ(t))m−1.
-
-
Let T be a linear operator on a finite-dimensional vector space. Prove that the rational canonical form of T is a diagonal matrix if and only if T is diagonalizable. Visit goo.gl/
tK8pru for a solution. -
Let T be a linear operator on a finite-dimensional vector space V with characteristic polynomial f(t)=(−1)nϕ1(t)ϕ2(t), where ϕ1(t) and ϕ2(t) are distinct irreducible monic polynomials and n=dim(V).
-
(a) Prove that there exist v1, v2∈V such that v1 has T-annihilator ϕ1(t), v2 has T-annihilator ϕ2(t), and βv1∪βv2 is a basis for V.
-
(b) Prove that there is a vector v3∈V with T-annihilator ϕ1(t)ϕ2(t) such that βv3 is a basis for V.
-
(c) Describe the difference between the matrix representation of T with respect to βv1∪βv2 and the matrix representation of T with respect to βv3.
Thus, to assure the uniqueness of the rational canonical form, we require that the generators of the T-cyclic bases that constitute a rational canonical basis have T-annihilators equal to powers of irreducible monic factors of the characteristic polynomial of T.
-
-
Let T be a linear operator on a finite-dimensional vector space with minimal polynomial
f(t)=(ϕ1(t))m1(ϕ2(t))m2⋯(ϕk(t))mk,where the ϕi(t)’s are distinct irreducible monic factors of f(t). Prove that for each i, mi is the number of entries in the first column of the dot diagram for ϕi(t).
-
Let T be a linear operator on a finite-dimensional vector space V. Prove that for any irreducible polynomial ϕ(t), if ϕ(T) is not one-to-one, then ϕ(t) divides the characteristic polynomial of T. Hint: Apply Exercise 15 of Section 7.3.
-
Let V be a vector space and β1, β2, …, βk be disjoint subsets of V whose union is a basis for V. Now suppose that γ1, γ2, …, γk are linearly independent subsets of V such that span(γi)=span(βi) for all i. Prove that γ1∪γ2∪⋯∪γk is also a basis for V.
-
Let T be a linear operator on a finite-dimensional vector space, and suppose that ϕ(t) is an irreducible monic factor of the characteristic polynomial of T. Prove that if ϕ(t) is the T-annihilator of vectors x and y, then x∈Cy if and only if Cx=Cy.
Exercises 11 and 12 are concerned with direct sums.
-
Prove Theorem 7.25.
-
Prove Theorem 7.26.
