Chapter 3

Dimensional Analysis

The treatment of this chapter goes far beyond the field of fluid mechanics. Although the concepts of dimensional analysis apply in all the fields of science, it finds extensive use in fluid mechanics as a tool for studying various phenomena. It, therefore, occupies center stage in this book. This chapter elaborates on several topics:

– It sets out the consequences of a system’s behavior being independent from the system of units used to describe it. This idea is linked to the notion of homogeneity that should be verified by any mathematical expression describing a physical system.

– Dimensional analysis helps to establish the general form of a relation that exists between the various parameters involved in a problem. Let us consider the example of a fluid flow in a pipe with a diameter D and a length L, which we discuss later. This flow is generated by the pressure change between the inlet and outlet, shifting from P₁ to P₂. The streamwise velocity, U, is therefore expressed by a relation in the form F(P₁, P₂, U, D, L, v, ρ, …) = 0 between the different physical parameters that define the system. Dimensional analysis shows that this relation should associate the parameters in a way respecting consistency in regards to units attached to the parameters. It also enables us to identify a reduction in the number of variables in the relation describing the system.

– An offshoot of dimensional analysis is the theory of similarities, which sets out a way to model a physical system at a different scale without altering its nature. This theory is commonly used in mechanics, as well as in chemical engineering, whenever a “pilot experiment” is involved. Similarity theory is based on defining “dimensionless numbers” to describe a physical phenomenon.

The principles of dimensional analysis are difficult to understand for a student who is studying them for the first time. This is natural because one apparently presumes to understand a phenomenon without actually being familiar with the equations which govern its behavior. The examples discussed in this chapter show that it is desirable to identify such equations correctly (even though we do not solve them) to count the parameters involved in a first stage and, to express relevant dimensionless numbers in a second stage. For the above-mentioned flow in a pipe, the parameter count is a consequence of the finding that the phenomenon is described using Navier–Stokes equations alone; solving them would suffice to arrive at the exact answer. The parameters involved in a problem may have different roles. A simple procedure, but one that is necessary to use dimensional analysis efficiently, consists of identifying the physical parameters that cause the phenomenon (the pressure difference between the ends of the pipe — why does the fluid flow inside the pipe?), those that characterize the consequence (the area-averaged streamwise velocity of the flow), and the other parameters (viscosity, geometrical dimensions, etc), which simply have an effect on the phenomenon.

3.1. Principle of dimensional analysis, Vaschy–Buckingham theorem

The Vaschy–Buckingham theorem is stated below:

Consider a phenomenon involving n variables. Let those n variables, in turn, involve p units. The phenomenon can then be described by a relation linking (n–p) dimensionless numbers.

Dimensional analysis, therefore, enables a reduction of the number of variables in the functional relation linking the physical quantities that describe the behavior of a system. To understand the Vaschy–Buckingham theorem, let us return to the example of the pipe flow. Initially, the system’s parameters include the following:

– P₁ is the pressure at the pipe’s inlet,

– P₂ is the pressure at the pipe’s outlet,

– L is the length of the pipe,

– D is the diameter of the pipe,

– ν is the kinematic viscosity of the fluid, and

– U is the area-averaged streamwise velocity of the fluid.

The first five parameters are set by the user who wishes to make a fluid, whose properties he/she specifies, flow inside a chosen pipe. The sixth one, i.e. the velocity, is set based on the values of the previous five. It is this quantity (the unknown of the problem) that we want to determine based on the knowledge of the other parameters. Other, more or less relevant, parameters such as those given below can also be taken into account:

– e, the roughness of the pipe (unit m), and

– the age of the captain (unit s) who actuates the valve.

Let us retain all these parameters.¹ We thus wish to express the velocity as a function of the other parameters, i.e. a functional of the form

Including the quantity we wish to determine, we have n = 7 parameters in the functional, which are listed with their units in Table 3.1:

The parameters involve three units. The Vaschy–Buckingham theorem specifies that there exists, for determining the velocity, a functional relation between four dimensionless numbers. Dimensionless numbers are easily identified, starting by taking the ratio of quantities that have the same dimensions: P₁ / P₂, L / D, and e / D. These first three numbers are independent from one another, as each of them brings in at least one quantity that is not present in the others. The fourth dimensionless number necessarily involves the kinematic viscosity, which had not yet been taken into account, e.g. by writing UD / ν. The Vaschy–Buckingham theorem actually enables us to understand that the functional linking of all the seven parameters can be written in the form:

[3.1]

Other formulations, involving different numbers, could also be used. Further, any other combination of dimensionless numbers can also be expressed using the four numbers we have defined.

Although the Vashy–Buckingham theorem is not based on physics, using dimensional analysis should not rule out considering the physics; for, quite the contrary is true. Regarding the example treated here, it is very clear that expression [3.1] is unsustainable from a physical standpoint, because:

– We know that the flow is generated due to the pressure difference between the inlet and outlet. It would, therefore, be more judicious to obtain a functional of the form:

[3.2]

– Function [3.2] is not pertinent either, in a physical sense, as the solution depends on the pressure level P₂ at the outlet, rather than just the difference in pressure between the inlet and outlet. A review of the dimensions thus indicates that we are short of a parameter that involves mass.

The previous parameter count was intentionally incomplete; this is to convey the fact that reverting repeatedly to a physical analysis of a phenomena enables one to utilize dimensional analysis to express meaningful relations. The additional parameter involving the mass is easily obtained. One simply has to observe again that the phenomenon is governed by Navier–Stokes equations, which involve the density of the fluid (ρ). We therefore incorporate pinto the parameter count, and withdraw P₂ since only the pressure difference between the inlet and the outlet modifies the velocity. This leads us to arrive at a functional between the parameters in Table 3.2.

Once again, four dimensionless numbers need to be determined. They are, for example:

[3.3]

This functional is more appealing because it brings back quantities that have a physical meaning, such as kinetic energy, the pressure difference between the inlet and outlet, and the Reynolds number. Without having solved the equations of the problem, the use of simple results from the general principles of physics has enabled us to bring to the fore some dimensionless numbers, which compare quantities that “interplay together within the principles of physics”.

This can be taken even further, by calling upon a result that we have found before with Poiseuille flows: the flow rate is induced not by the pressure difference, but by the pressure difference per unit length of the pipe. This means that it is physically possible to introduce the quantity (P₁ − P₂ ) / L alone, instead of the three parameters L, P₁, and P₂. Function [3.3] then reduces to a relation between three dimensionless numbers:

[3.4]

As seen in Chapter 4, the pressure drop laws for steady flows in pipes are expressed using a relation similar to this form, using the following dimensionless numbers:

[3.5]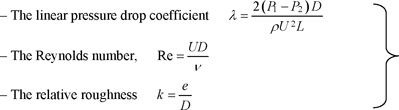

Dimensional analysis, combined with simple physical considerations, makes it possible to set out numerous dimensional forms through which physical results can be expressed. It helps to number the parameters involved in a problem while removing extraneous ones. A fruitful use of the Vaschy–Buckingham theorem can only ensue from a meaningful parameter count. The lesser the parameters, the more informative the result from dimensional analysis will be.

The notion of independent parameters and independent dimensionless numbers needs to be emphasized. As each dimensionless number contained a quantity not present in the rest, we ensured that the defined dimensionless numbers are independent. By using Washy–Buckingham theorem, we usually want to investigate the dependence of one quantity (presently the flow velocity in the pipe) with other parameters. It is also important checking that these other parameters are independent. For the pipe flow problem, this notion is simple: the length and diameter are clearly independent, since we can choose the pipe length on the one hand and its diameter on the other. Nevertheless, adding the dynamics viscosity μ to the parameters in Table 3.2 would not be sensible, as it is simply linked by μ = ρv to other parameters already taken into account. The notion of independence also leads to subtler questions. We have not taken temperature into account in the example we have discussed above, although the principles of physics and experience indicate unequivocally that temperature influences changes in the flow rate for a given pressure drop. This is because temperature’s only effect is to alter the viscosity. Insofar as thermal physics is not taken into account in the phenomenon, the equation that governs its dynamics is limited to the Navier–Stokes equation, while the temperature remains an indirect parameter of the problem. Identifying the nature of the physical phenomena governing a system is indispensable to perform a meaningful dimensional analysis of a problem.

Counting the units that appear in a problem can sometimes be complex. If, e.g. the units of length (m) and time (s) systematically appear in velocity-type parameters (m/s), then only one unit (m/s) should be counted, instead of two.²

3.1.1. Example — the oscillating pendulum

Consider the case of a pendulum, oscillating within the gravity field, whose oscillation frequency we wish to determine. The a priori parameters of the problem are the angular frequency, ω (s⁻¹) — the quantity to be determined — the pendulum’s mass, M (kg), the length of the wire, l (m), the gravitational acceleration, g (m·s⁻²), and the maximum angle of oscillation, θ_o (dimensionless). Based on five parameters and three dimensions, there should therefore be two dimensionless numbers. The first is obviously³ θ_o. The mass M, therefore, does not intervene in the physical problem, as no other parameter depends on the unit of mass. Consequent to this, the only option is to write:

For small angles, we obtain the well-known pendulum relation:

Constant A is undetermined as per dimensional analysis. However, based on dimensional analysis the fact that the oscillation frequency is not dependent on the mass is justified.

3.2.Dimensional study of Navier–Stokes equations

The examples so far given, and the one we discuss fully in section 3.4 (the fall of a ball in a fluid under the effect of gravity), illustrate the fact that a problem can only be treated through dimensional analysis in a meaningful way if one comprehends the nature of its determining phenomena. In the case of the oscillating pendulum, e.g. it is necessary to realize that the pendulum oscillates because it is located within the gravity field. If this property is not identified, the error that results most often is the omission of the gravitational acceleration from the parameter count.

Dimensional analysis of the equations that govern a system enables the identification of the relevant dimensionless numbers for the problem. It also ensures that all parameters have been taken into account, and that they are independent. We illustrate this principle below with the example of Navier–Stokes equations, written in vector form:

[3.6]

A critical interpretation of equation [3.6] helps us to generate a list of parameters involved in Navier–Stokes equations:

– the density, ρ, which we assume here to be homogeneous and constant,

– the gravitational acceleration, g,

– the dynamic viscosity, μ,

– the space dimensions (x, y, z), for which a length scale L is introduced,

– the velocity components (u_x, u_y, and u_z), whose scale is denoted by U,

– the pressure, p, whose scale we denote by P, and

– time t, whose scale is denoted by T.

Of the seven scales defined to represent the dynamics of Navier–Stokes equations, the first three are actual parameters of the problem. Their value is known and fixed, at least in the case where density is homogeneous. On the other hand, the length, velocity, pressure, and time scales are not defined precisely. The length scale can be defined arbitrarily using any existing geometrical dimensions (such as the diameter of the pipe), but this physical dimension is not necessarily a typical scale of the fluid flow. In complex cases (e.g. turbulence or boundary layer), several scales may exist in the flow. We shall assume in the present case that the length scale is the same along all the three directions in space. This is not necessarily correct (there may be the length and width of a pipe). The same considerations apply to the velocity dimensions.

The seven scales involve three units (time, length, and mass). Four dimensionless numbers should, therefore, be defined to represent the flow. These numbers are determined naturally by evaluating the order of magnitude of the various terms in Navier–Stokes equation. By writing:

[3.7]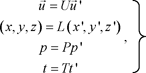

we bring in the velocity, length scales (x′,y′, and z′), pressure p′, and time t′, which are dimensionless variables. Substituting [3.7] into [3.6] leads to:

[3.8]

Dividing this equation by ρU² / L yields:

[3.9]

equation [3.9] naturally brings the four numbers we require, namely:

– the reduced frequency, , which evaluates the significance of unsteadiness,

– the Euler number, , which gives the ratio of pressure to kinetic energy,

– the Froude number, , which evaluates kinetic energy in relation to variations in potential energy,

– the Reynolds number, which evaluates the effect of viscosity in the dynamics of the flow.

These four dimensionless numbers have a physical significance, because they compare the orders of magnitude of the different forces that govern the dynamics of the flow.

Navier–Stokes equations can, therefore, be regarded as a functional relationship between these four dimensionless numbers. The solution of Navier–Stokes equations depends on the values of the different dimensionless numbers. Unsteady effects are negligible if γ<<1. The gravitational force is negligible if Fr >>1. Lastly, dynamic equilibriums are independent from viscosity if Re >>1. This formulation means that the flow’s length, velocity, pressure, and time scales are linked by a relation. For example, in the case where, simultaneously, γ<<1, Fr >>1 and Re >>1, the predominant terms in [3.9] are such that:

[3.10]

The Euler number is of order 1 (if that is not the case, then the scales were improperly chosen). The flow is characterized by the exchanges between pressure energy and kinetic energy. This is the case of a flow governed by Bernoulli’s theorem, for an ideal fluid, and in the absence of gravity.

The approach presented here is the most commonly used when two terms dominate the Navier–Stokes equation. The flow can then be characterized by the value of a single dimensionless number. This is illustrated in section 3.4 with the classical example of the fall of a ball in a viscous fluid (Stokes’ experiment).

The Euler, Froude, and Reynolds numbers are well known. The reduced frequency is less; so, the time scale is often given on the basis of velocity and length scales by writing T = L/U so that γ = 1. This relation is used for a turbulent flow. Time appears as an independent parameter in the case of oscillating flows such as, e.g. the flow generated by the oscillation of a wall at a given frequency.⁴

3.3.Similarity theory

Similarity theory is used to study a physical phenomenon at a reduced scale compared to the real scale (there are also cases where one wishes to enlarge the scale, although this is rather infrequent). The classical example in fluid mechanics is the use of wind tunnel models to study an aircraft prototype before considering its real-size construction. The same process is followed in chemical engineering when building a pilot experiment.

To represent a given phenomenon at a different scale, it should be ensured that the physics of the phenomenon is preserved through the change of scale. Depending on the case, the equations of continuum mechanics, Navier–Stokes equations, the transport equations for thermal energy, etc. will provide the appropriate framework to identify, through dimensional analysis, the dimensionless numbers characterizing the problem. If the dimensionless numbers retain the same value when changing from the real scale to the reduced scale, there is a guarantee that the same physical phenomenon is being represented.

As a continuation of the previous section, let us take the example of a flow governed by Navier–Stokes equations. In the steady-state case, the values of the Euler number, the Reynolds number, and the Froude number should be preserved through the change of scale. Denoting by U, L, P, ρ, and µ as the characteristic quantities of the real flow and U_m, L_m, P_m, ρ_m, and µ_m as the characteristic quantities of the “model” flow, the following relations should be verified:

[3.11]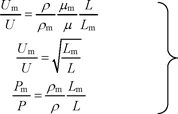

bringing to the fore the consequences of the change in geometrical scale.

The first two relations (equality of Reynolds and Froude numbers) show that it is not possible to change the geometrical scale without changing the fluid (density and viscosity), if the first two conditions are to be fulfilled. If they are, the third condition will also be fulfilled in the flow, insofar as the full-scale and model-scale pressure boundary conditions are adapted to verify the latter condition.

In practice, it is rarely the case that all similarity conditions are verified. It is often necessary to identify the dimensionless numbers that are the most characteristic of the flow dynamics. The constraints associated with a change of fluid are usually rather stringent (cost, availability of products, toxicity, etc.). Quite often, in marine hydrodynamics, in aerospace, or for impact studies of natural flows, the Reynolds similarity is not enforced between the real scale and the scale model. However, care is taken to ensure that the Reynolds number is sufficiently large on the scale model, in order to be in a turbulent regime on the scale model as well as in real size. Since the effect of viscosity is small in both configurations, the difference in Reynolds number between the scale model and the real-size case is of less consequence for the structure of the flow. Studying a flow in air by simulating it on a scale model in water is an engineer’s trick that allows a reduction in the Reynolds number difference between the real scale and the scale model (the kinematic viscosity of air is about 15 times greater than that of water).

3.4.An application example: fall velocity of a spherical particle in a viscous fluid at rest

We observe the fall, under the effect of gravity, of a spherical ball with a diameter D and a density ρ_p in a fluid with density ρ_f and kinematic viscosity v. We assume that ρ_p > ρ_f so that the particle has a falling movement within the fluid. After an acceleration phase, it is observed that the ball falls at a constant velocity, W_c. We wish to establish the dependence of W_c upon the parameters of the problem.

3.4.1. Application of the Vaschy–Buckingham theorem

As the ball is falling because it is located in the gravitational field, the acceleration due to gravity, g, should be added to the catalog of parameters suggested above. It is also clearly understood that the viscosity of the fluid is an important parameter. Friction forces slow down the particle and prevent it from exceeding a certain velocity. The catalog of parameters is listed in Table 3.3. With six parameters and three dimensions, the Vaschy–Buckingham theorem indicates that the fall dynamics of the ball is governed by three dimensionless numbers.

A simplistic, “blind” analysis of the dimensions of different parameters naturally leads us to suggest the following dimensionless numbers:

[3.12]

Such a suggestion is hardly acceptable from the standpoint of physics governing the fall of the ball. We have merely stated that the ball is falling because it is situated in the gravitational field and because ρ_p > ρ_f. To take this further, it is useful to consider, in sequence, two aspects of the phenomenon’s physics:

1. The dynamics of the ball’s fall, regarded as a solid system.

2. The dynamics of the flow past the ball, which slows down its fall.

3.4.2. Forces exerted on the ball

Three forces are exerted on the ball:

1. the weight (downwards);

2. the buoyancy force exerted by the fluid (upwards); and

3. the hydrodynamic force exerted by the fluid on the particle F_R (W_c, D, ρ_f,ν) (upwards). This hydrodynamic force does not depend directly on the density ρ_p of the particle, since it results from the flow of the fluid past the ball. It depends on it indirectly through W_c.

When the ball falls at a constant velocity, the equilibrium between these three forces is verified, in accordance with the fundamental law of dynamics. We can, therefore, write:

[3.13]

Not knowing F_R(W_c,D, ρ_f, v), equation [3.13] does not seem to take us much further. However, it highlights the fact that the density of the particle, ρ_p, and the gravitational acceleration, g, only intervene in the problem through the quantity ( ρ_p − ρ_f)g. Table 3.3 is therefore modified accordingly as presented in Table 3.4.

The problem is thus described by only two dimensionless numbers. We introduce the following two dimensionless numbers:

[3.14]

[3.15]

The use of the Reynolds and Archimedes numbers stands out as the most natural among a number of possibilities. The fall velocity is the unknown of the problem, whose conditions are set by other parameters. Hence, the fall velocity is introduced only in the Reynolds number, while Archimedes number characterizes the properties of the ball and fluid (the conditions of the phenomenon).

Consequently, the fall velocity of the ball is governed by a relation between these two numbers:

[3.16]

The formulation for determining the fall velocity is explicit, knowing the value of Archimedes number.

3.4.3. The hydrodynamic force opposing the particle’s movement relative to the fluid

The analysis of the hydrodynamic force opposing the particle’s movement relative to the fluid enables us to determine the dimensional form of the fall velocity in two asymptotical cases, when the Reynolds number is small or when it is large. The hydrodynamic force results from two contributions:

[3.17]

[3.18]

Both these forces are proportional to the area of the ball, which is homogeneous to D². The viscous friction force involves the viscous stress for a Newtonian fluid (Table 1.1 of Chapter 1). We obtain [3.17] by estimating that the velocity gradient in the vicinity of the ball is of the order W_c/D, since W_c is the velocity scale and D is the only length scale in the problem. The length scale of movements generated in the fluid by the motion of the ball is necessarily similar to the size of the ball. The pressure field changes with the value of the Reynolds number.

3.4.4. Fall velocity for a small Reynolds number

When the Reynolds number is small, the dominant term in [3.9] is the viscous term. The Euler number has the order of the reciprocal of the Reynolds number, ( E ≈1/ Re ). The dynamics of the flow is governed by equilibrium between the pressure field and the viscous stress.⁵ The pressure scale, then, has the same order of magnitude as the viscous stress:

[3.19]

and the resistant hydrodynamic force is:

[3.20]

The equilibrium between the forces exerted on the ball (equation [3.13]) leads to the dimensional form of Stokes law:

[3.21]

An exact calculation of the flow past the ball shows that the value of the constant is A = 1/18.

3.4.5. Fall velocity for a large Reynolds number

When the Reynolds number is large, the viscous term is negligible in [3.9]. The Euler number is of the order of 1, since we are in the situation described by [3.10]. The pressure scale is:

[3.22]

Since the Reynolds number is large, the pressure force (equation [3.18]) outweighs the viscous force (equation [3.17]). The hydrodynamic force is:

[3.23]

The equilibrium between the forces exerted on the ball (equation [3.13]) now leads to Newton’s law:

[3.24]

Only the value of constant B is undetermined.

The results of this application exercise are taken up again in section 14.1 of Chapter 14. As can be seen, dimensional analysis is very critical and crucial in the analysis of physical phenomena, at a first level by determining the association of physical parameters that enable results to be expressed, and at a second level, when the exact case arises, by predicting the dimensional form of physical laws for certain asymptotical situations. We have reached this second level in this example.

3.5.Application exercises

Exercise 3.I: Time of residence and chemical reaction in a stirred reactor

We are interested in performing, in a perfectly stirred reactor with volume V, the following chemical reaction:

which is a first-order reaction with respect to each of the constituents. The kinetics of the reaction are, therefore, written as:

by incorporating the kinetic constant, k. Both constituents are fed at time t = 0 with concentrations [A]_o and [B]_o.

Determine, by dimensional analysis reasoning, the order of magnitude of the residence time in the stirred reactor so that the concentration of product B at the reactor outlet is 1/100 of what it was at the inlet (it is assumed that [A]_o > [B]_o).

HINT.– This application of the Vaschy–Buckingham theorem leads us to question the notion of unit.

Exercise 3. II: Boundary layer on an oscillating plate

Consider a fluid bounded by a flat plate at its bottom. The plate oscillates at a vibration frequency ω in a horizontal plane (as indicated in Figure 2.II.1 by the double arrow). The magnitude of the plate’s vibrational motion is 2a. The fluid is a Newtonian fluid having a kinematic viscosity ν and a density ρ. Due to the effect of viscosity, the vibrational motion induces movements in the fluid, which are restricted to a boundary layer having a thickness δ.

1. Through dimensional analysis reasoning, determine a set of dimensionless numbers with which to express the dependency of δ on the parameters of the problem.

2. When the amplitude of oscillations is sufficiently small, experiments show that the thickness, δ, of the boundary layer does not depend on the amplitude 2a of the oscillations. Can you then provide a simple expression of the boundary layer thickness?

Exercise 3.III: Head capacity curve of a centrifugal pump

The head capacity curve of a pump, plotted in Figure 3.III.1, is described by the following function, which links the flow rate delivered Q with the head change ΔH between the inlet and outlet of the pump:

[3.III.1]

with ΔH_max,1 =10⁵Pa and α₁ =5.76×10⁹Pa·s²/m⁶. This pump has a rotor diameter D₁ = 200 mm and runs at a speed of 180 rpm.

1. What is the maximum flow rate deliverable by the pump, and what is the maximum height to which the pump can lift the fluid?

2. The company that manufactures this pump offers in its catalog another pump having a diameter D₂ = 150 mm, which runs at a speed of 150 rpm.

The two pumps are related by a scale factor, i.e. all geometrical dimensions are in proportion with the ratio of rotor diameters. For example, the diameters of the discharge ports are such that d₁ / d₂ = D₁ / D₂ (index 1 refers to pump 1 and index 2 to pump 2).

The flow conditions are such that the pumps operate in a turbulent regime, with a large Reynolds number. Which parameter can we infer that the head capacity curve is independent from?

As this company has not posted the head capacity curve of that second pump on its website, your boss asks you to determine it.

Demonstrate, by a dimensional analysis argument, that the head capacity curve of the second pump is of the form ΔH = ΔH_max,₂ − α₂Q². Determine the values of ΔH_max,₂, and α₂, having knowing those of ΔH_max,1, and α₁.

What are the maximum flow rate deliverable by pump 2, and the maximum height to which it can lift the fluid?

This exercise does not require any specific knowledge of the operation of centrifugal pumps, apart from understanding that it is the rotational speed of the rotor that produces the pumping action, and that the flow rate and head change between the inlet and outlet of the pump also depend on the geometrical dimensions of the device.

NOTE.– While many manufacturers express the output head as a water-column height, it is crucial in this exercise to express the head as an energy per unit volume (H = P + ρV²/2), as gravity has nothing to do with the pump’s operation.

---

1 Except, obviously, for the age of the captain. This silly proposal aims at pointing out that, for using dimensional analysis, we should tend to count only the parameters that are significant for the phenomenon and not all parameters that may eventually have an effect in some circumstances.

2 This difficulty is encountered when solving Exercise 3.I at the end of this chapter.

3 Is the notion that simple? An angle is expressed by a unit (radians, degrees, etc.). For a dimensional analysis problem, we consider that an angle is a dimensionless quantity, because the length of a circular arc is the product of the angle by the radius. The angle, therefore, has no dimension as such.

4 See Exercise 3.II at the end of this chapter.

5 This category of flows, called “creeping flows”, is abundantly documented, in particular for lubrication problems. Chapter 16 discusses creeping flows around a small particle.