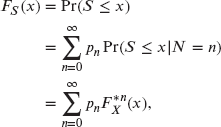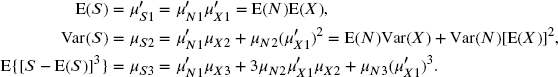9
Aggregate Loss Models
9.1 Introduction
An insurance enterprise exists because of its ability to pool risks. By insuring many people, the individual risks are combined into an aggregate risk that is manageable and can be priced at a level that will attract customers. Consider the following simple example.
![]()
The goal of this chapter is to build a model for the total payments by an insurance system (which may be the entire company, a line of business, those covered by a group insurance contract, or even a single policy). The building blocks are random variables that describe the number of claims and the amounts of those claims, subjects covered in the previous chapters.
There are two ways to build a model for the amount paid on all claims occurring in a fixed time period on a defined set of insurance contracts. The first is to record the payments as they are made and then add them up. In that case, we can represent the aggregate losses as a sum, S, of a random number, N, of individual payment amounts ![]() . Hence,
. Hence,
where ![]() when
when ![]() .
.
The second model, the one used in Example 9.1, assigns a random variable to each contract.
The individual risk model is used to add together the losses or payments from a fixed number of insurance contracts or sets of insurance contracts. It is used in modeling the losses of a group life or health insurance policy that covers a group of n employees. Each employee can have different coverage (life insurance benefit as a multiple of salary) and different levels of loss probabilities (different ages and health statuses).
In the special case where the ![]() are identically distributed, the individual risk model becomes a special case of the collective risk model, with the distribution of N being the degenerate distribution with all of the probability at
are identically distributed, the individual risk model becomes a special case of the collective risk model, with the distribution of N being the degenerate distribution with all of the probability at ![]() , that is,
, that is, ![]() .
.
The distribution of S in (9.1) is obtained from the distribution of N and the common distribution of the ![]() . Using this approach, the frequency and the severity of claims are modeled separately. The information about these distributions is used to obtain information about S. An alternative to this approach is to simply gather information about S (e.g. total losses each month for a period of months) and to use some model from the earlier chapters to model the distribution of S. Modeling the distribution of N and the distribution of the
. Using this approach, the frequency and the severity of claims are modeled separately. The information about these distributions is used to obtain information about S. An alternative to this approach is to simply gather information about S (e.g. total losses each month for a period of months) and to use some model from the earlier chapters to model the distribution of S. Modeling the distribution of N and the distribution of the ![]() separately has seven distinct advantages:
separately has seven distinct advantages:
- The expected number of claims changes as the number of insured policies changes. Growth in the volume of business needs to be accounted for in forecasting the number of claims in future years based on past years' data.
- The effects of general economic inflation and additional claims inflation are reflected in the losses incurred by insured parties and the claims paid by insurance companies. Such effects are often masked when insurance policies have deductibles and policy limits that do not depend on inflation and aggregate results are used.
- The impact of changing individual deductibles and policy limits is easily implemented by changing the specification of the severity distribution.
- The impact on claims frequencies of changing deductibles is better understood.
- Data that are heterogeneous in terms of deductibles and limits can be combined to obtain the hypothetical loss size distribution. This approach is useful when data from several years in which policy provisions were changing are combined.
- Models developed for noncovered losses to insureds, claim costs to insurers, and claim costs to reinsurers can be mutually consistent. This feature is useful for a direct insurer when studying the consequence of shifting losses to a reinsurer.
- The shape of the distribution of S depends on the shapes of both distributions of N and X. The understanding of the relative shapes is useful when modifying policy details. For example, if the severity distribution has a much heavier tail than the frequency distribution, the shape of the tail of the distribution of aggregate claims or losses will be determined by the severity distribution and will be relatively insensitive to the choice of frequency distribution.
In summary, a more accurate and flexible model can be constructed by examining frequency and severity separately.
In constructing the model (9.1) for S, if N represents the actual number of losses to the insured, then the ![]() can represent (i) the losses to the insured, (ii) the claim payments of the insurer, (iii) the claim payments of a reinsurer, or (iv) the deductibles (self-insurance) paid by the insured. In each case, the interpretation of S is different and the severity distribution can be constructed in a consistent manner.
can represent (i) the losses to the insured, (ii) the claim payments of the insurer, (iii) the claim payments of a reinsurer, or (iv) the deductibles (self-insurance) paid by the insured. In each case, the interpretation of S is different and the severity distribution can be constructed in a consistent manner.
Because the random variables N, ![]() , and S provide much of the focus for this chapter, we want to be especially careful when referring to them. To that end, we refer to N as the claim count random variable and refer to its distribution as the claim count distribution. The expression number of claims is also used and, occasionally, just claims. Another term commonly used is frequency distribution. The
, and S provide much of the focus for this chapter, we want to be especially careful when referring to them. To that end, we refer to N as the claim count random variable and refer to its distribution as the claim count distribution. The expression number of claims is also used and, occasionally, just claims. Another term commonly used is frequency distribution. The ![]() are the individual or single-loss random variables. The modifier individual or single is dropped when the reference is clear. In Chapter 8, a distinction is made between losses and payments. Strictly speaking, the
are the individual or single-loss random variables. The modifier individual or single is dropped when the reference is clear. In Chapter 8, a distinction is made between losses and payments. Strictly speaking, the ![]() are payments because they represent a real cash transaction. However, the term loss is more customary, and we continue with it. Another common term for the
are payments because they represent a real cash transaction. However, the term loss is more customary, and we continue with it. Another common term for the ![]() is severity. Finally, S is the aggregate loss random variable or the total loss random variable.
is severity. Finally, S is the aggregate loss random variable or the total loss random variable.
![]()
9.1.1 Exercises
- 9.1 Show how the model in Example 9.1 could be written as a collective risk model.
- 9.2 For each of the following situations, determine which model (individual or collective) is more likely to provide a better description of aggregate losses.
- A group life insurance contract where each employee has a different age, gender, and death benefit.
- A reinsurance contract that pays when the annual total medical malpractice costs at a certain hospital exceeds a given amount.
- A dental policy on an individual pays for at most two checkups per year per family member. A single contract covers any size family at the same price.
9.2 Model Choices
In many cases of fitting frequency or severity distributions to data, several distributions may be good candidates for models. However, some distributions may be preferable for a variety of practical reasons.
In general, it is useful for the severity distribution to be a scale distribution (see Definition 4.2) because the choice of currency (e.g. US dollars or British pounds) should not affect the result. Also, scale families are easy to adjust for inflationary effects over time (this is, in effect, a change in currency; e.g. from 1994 US dollars to 1995 US dollars). When forecasting the costs for a future year, the anticipated rate of inflation can be factored in easily by adjusting the parameters.
A similar consideration applies to frequency distributions. As an insurance company's portfolio of contracts grows, the number of claims can be expected to grow, all other things being equal. Models that have probability generating functions of the form
for some parameter ![]() have the expected number of claims proportional to
have the expected number of claims proportional to ![]() . Increasing the volume of business by 100r% results in expected claims being proportional to
. Increasing the volume of business by 100r% results in expected claims being proportional to ![]() . This approach is discussed in Section 7.4. Because r is any value satisfying
. This approach is discussed in Section 7.4. Because r is any value satisfying ![]() , the distributions satisfying (9.2) should allow
, the distributions satisfying (9.2) should allow ![]() to take on any positive value. Such distributions can be shown to be infinitely divisible (see Definition 7.6).
to take on any positive value. Such distributions can be shown to be infinitely divisible (see Definition 7.6).
A related consideration, the concept of invariance over the time period of the study, also supports using frequency distributions that are infinitely divisible. Ideally, the model selected should not depend on the length of the time period used in the study of claims frequency. In particular, the expected frequency should be proportional to the length of the time period after any adjustment for growth in business. In this case, a study conducted over a period of 10 years can be used to develop claims frequency distributions for periods of one month, one year, or any other period. Furthermore, the form of the distribution for a one-year period is the same as for a one-month period with a change of parameter. The parameter ![]() corresponds to the length of a time period. For example, if
corresponds to the length of a time period. For example, if ![]() in (9.2) for a one-month period, then the identical model with
in (9.2) for a one-month period, then the identical model with ![]() is an appropriate model for a one-year period.
is an appropriate model for a one-year period.
Distributions that have a modification at zero are not of the form (9.2). However, it may still be desirable to use a zero-modified distribution if the physical situation suggests it. For example, if a certain proportion of policies never make a claim, due to duplication of coverage or other reason, it may be appropriate to use this same proportion in future periods for a policy selected at random.
9.2.1 Exercises
- 9.3 For pgfs satisfying (9.2), show that the mean is proportional to
 .
. - 9.4 Which of the distributions in Appendix B satisfy (9.2) for any positive value of
 ?
?
9.3 The Compound Model for Aggregate Claims
Let S denote aggregate losses associated with a set of N observed claims ![]() satisfying the independence assumptions following (9.1). The approach in this chapter involves the following three steps:
satisfying the independence assumptions following (9.1). The approach in this chapter involves the following three steps:
- Develop a model for the distribution of N based on data.
- Develop a model for the common distribution of the
 based on data.
based on data. - Using these two models, carry out necessary calculations to obtain the distribution of S.
Completion of the first two steps follows the ideas developed elsewhere in this text. We now presume that these two models are developed and that we only need to carry out numerical work in obtaining solutions to problems associated with the distribution of S.
9.3.1 Probabilities and Moments
The random sum
(where N has a counting distribution) has distribution function
where ![]() is the common distribution function of the
is the common distribution function of the ![]() and
and ![]() . The distribution of S is called a compound distribution In (9.3),
. The distribution of S is called a compound distribution In (9.3), ![]() is the “n-fold convolution” of the cdf of X. It can be obtained as
is the “n-fold convolution” of the cdf of X. It can be obtained as

and
The tail may then be written, for all ![]() , as
, as
If X is a continuous random variable with probability zero on nonpositive values, (9.4) reduces to
For ![]() , this equation reduces to
, this equation reduces to ![]() . By differentiating, the pdf is
. By differentiating, the pdf is
Therefore, if X is continuous, then S has a pdf, which, for ![]() , is given by
, is given by
and a discrete mass point, ![]() at
at ![]() . Note that
. Note that ![]() .
.
If X has a discrete counting distribution, with probabilities at ![]() , (9.4) reduces to
, (9.4) reduces to

The corresponding pf is
For notational purposes, let ![]() and
and ![]() for
for ![]() . Then, in this case, S has a discrete distribution with pf
. Then, in this case, S has a discrete distribution with pf
Arguing as in Section 7.1, the pgf of S is
due to the independence of ![]() for fixed n. The pgf is typically used when S is discrete. With regard to the moment generating function, we have
for fixed n. The pgf is typically used when S is discrete. With regard to the moment generating function, we have
The pgf of compound distributions is discussed in Section 7.1 where the “secondary” distribution plays the role of the claim size distribution in this chapter. In that section, the claim size distribution is always discrete.
In the case where ![]() (i.e. N is itself a compound distribution),
(i.e. N is itself a compound distribution), ![]() , which in itself produces no additional difficulties.
, which in itself produces no additional difficulties.
From (9.8), the moments of S can be obtained in terms of the moments of N and the ![]() . The first three moments are
. The first three moments are
Here, the first subscript indicates the appropriate random variable, the second subscript indicates the order of the moment, and the superscript is a prime (′) for raw moments (moments about the origin) and is unprimed for central moments (moments about the mean). The moments can be used on their own to provide approximations for probabilities of aggregate claims by matching the first few model and sample moments.
![]()
![]()
![]()
9.3.2 Stop-Loss Insurance
It is common for insurance to be offered in which a deductible is applied to the aggregate losses for the period. When the losses occur to a policyholder, it is called insurance coverage, and when the losses occur to an insurance company, it is called reinsurance coverage. The latter version is a common method for an insurance company to protect itself against an adverse year (as opposed to protecting against a single, very large claim). More formally, we present the following definition.
For any aggregate distribution,
If the distribution is continuous for ![]() , the net stop-loss premium can be computed directly from the definition as
, the net stop-loss premium can be computed directly from the definition as
Similarly, for discrete random variables,
Any time there is an interval with no aggregate probability, the following result may simplify calculations.
![]()
Further simplification is available in the discrete case provided that S places probability at equally spaced values.
![]()
In the discrete case with probability at equally spaced values, a simple recursion holds.
This result is easy to use because, when ![]() ,
, ![]() , which can be obtained directly from the frequency and severity distributions.
, which can be obtained directly from the frequency and severity distributions.
![]()
9.3.3 The Tweedie Distribution
The Tweedie distribution [123] brings together two concepts. First, for certain parameter values it is a compound Poisson distribution with a gamma severity distribution. Hence it may be a useful model for aggregate claims. Second, it is a member of the linear exponential family as discussed in Section 5.4. As such, it can be a useful distributional model when constructing generalized linear models to relate claims to policyholder characteristics.
We begin by looking at this compound Poisson distribution. Let N have a Poisson distribution with mean ![]() and let X have a gamma distribution with parameters
and let X have a gamma distribution with parameters ![]() and
and ![]() (which is used in place of
(which is used in place of ![]() as that letter is used in the definition of the linear exponential family). We then have, for the compound distribution
as that letter is used in the definition of the linear exponential family). We then have, for the compound distribution ![]() , that
, that

The second equation arises from the fact that the n-fold convolution of a gamma distribution is also gamma, with the shape parameter ![]() multiplied by n.
multiplied by n.
The Tweedie distribution is often reparameterized through the relations
where ![]() ,
, ![]() , and
, and ![]() . Substitution of the above three formulas into the moment equations yields
. Substitution of the above three formulas into the moment equations yields
This provides a convenient relationship between the variance and the mean that can help in deciding if this is an appropriate model for a given problem.
As mentioned, the Tweedie distribution is a member of the linear exponential family. Definition 5.9 states that members of this family have the form
where ![]() may include parameters other than
may include parameters other than ![]() . For this discussion, we write the general form of the linear exponential distribution as
. For this discussion, we write the general form of the linear exponential distribution as
The two differences are that ![]() is replaced by
is replaced by ![]() and the parameter
and the parameter ![]() is introduced. The replacement is just a reparameterization. The additional parameter is called the dispersion parameter. As can be seen in (9.11), this parameter allow for additional flexibility with respect to how the variance relates to the mean. For a demonstration that the Tweedie distribution is a member of the linear exponential family, see Clark and Thayer [24].
is introduced. The replacement is just a reparameterization. The additional parameter is called the dispersion parameter. As can be seen in (9.11), this parameter allow for additional flexibility with respect to how the variance relates to the mean. For a demonstration that the Tweedie distribution is a member of the linear exponential family, see Clark and Thayer [24].
The Tweedie distribution exists for other values of p. All nonnegative values other than ![]() are possible. Some familiar distributions that are special cases are normal (
are possible. Some familiar distributions that are special cases are normal (![]() ), Poisson (
), Poisson (![]() ), gamma (
), gamma (![]() ), and inverse Gaussian (
), and inverse Gaussian (![]() ). Note that for
). Note that for ![]() we have, from (9.11), that
we have, from (9.11), that ![]() . Hence, to obtain the Poisson distribution as a special case, we must have
. Hence, to obtain the Poisson distribution as a special case, we must have ![]() . When
. When ![]() takes on values larger than one, the distribution is called the overdispersed Poisson distribution. It will not be discussed further in this text, but is often used when constructing generalized linear models for count data.
takes on values larger than one, the distribution is called the overdispersed Poisson distribution. It will not be discussed further in this text, but is often used when constructing generalized linear models for count data.
9.3.4 Exercises
- 9.5 From (9.8), show that the relationships between the moments in (9.9) hold.
- 9.6 (*) When an individual is admitted to the hospital, the hospital charges have the following characteristics:
Charges Mean Standard deviation Room 1,000 500 Other 500 300 - The covariance between an individual's room charges and other charges is 100,000.
An insurer issues a policy that reimburses 100% for room charges and 80% for other charges. The number of hospital admissions has a Poisson distribution with parameter 4. Determine the mean and standard deviation of the insurer's payout for the policy.
- 9.7 Aggregate claims have been modeled by a compound negative binomial distribution with parameters
 and
and  . The claim amounts are uniformly distributed on the interval (0,10). Using the normal approximation, determine the premium such that the probability that claims will exceed premium is 0.05.
. The claim amounts are uniformly distributed on the interval (0,10). Using the normal approximation, determine the premium such that the probability that claims will exceed premium is 0.05. - 9.8 Automobile drivers can be divided into three homogeneous classes. The number of claims for each driver follows a Poisson distribution with parameter
 . Determine the variance of the number of claims for a randomly selected driver, using the data in Table 9.4.
. Determine the variance of the number of claims for a randomly selected driver, using the data in Table 9.4.
Table 9.4 The data for Exercise 9.8.
Class Proportion of population 
1 0.25 5 2 0.25 3 3 0.50 2 - 9.9 (*) Assume that
 ,
,  , and
, and  are mutually independent loss random variables with probability functions as given in Table 9.5. Determine the pf of
are mutually independent loss random variables with probability functions as given in Table 9.5. Determine the pf of 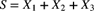 .
.
Table 9.5 The distributions for Exercise 9.9.
x 


0 0.90 0.50 0.25 1 0.10 0.30 0.25 2 0.00 0.20 0.25 3 0.00 0.00 0.25 - 9.10 (*) Assume that
 ,
, 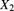 , and
, and  are mutually independent random variables with probability functions as given in Table 9.6. If
are mutually independent random variables with probability functions as given in Table 9.6. If  and
and 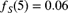 , determine p.
, determine p.
Table 9.6 The distributions for Exercise 9.10.
x 


0 p 0.6 0.25 1 
0.2 0.25 2 0 0.1 0.25 3 0 0.1 0.25 - 9.11 (*) Consider the following information about AIDS patients:
- The conditional distribution of an individual's medical care costs given that the individual does not have AIDS has mean 1,000 and variance 250,000.
- The conditional distribution of an individual's medical care costs given that the individual does have AIDS has mean 70,000 and variance 1,600,000.
- The number of individuals with AIDS in a group of m randomly selected adults has a binomial distribution with parameters m and
 .
.
An insurance company determines premiums for a group as the mean plus 10% of the standard deviation of the group's aggregate claims distribution. The premium for a group of 10 independent lives for which all individuals have been proven not to have AIDS is P. The premium for a group of 10 randomly selected adults is Q. Determine
 .
. - 9.12 (*) You have been asked by a city planner to analyze office cigarette smoking patterns. The planner has provided the information in Table 9.7 about the distribution of the number of cigarettes smoked during a workday.
Table 9.7 The data for Exercise 9.12.
Male Female Mean 6 3 Variance 64 31 The number of male employees in a randomly selected office of N employees has a binomial distribution with parameters N and 0.4. Determine the mean plus the standard deviation of the number of cigarettes smoked during a workday in a randomly selected office of eight employees.
- 9.13 (*) For a certain group, aggregate claims are uniformly distributed over (0,10). Insurer A proposes stop-loss coverage with a deductible of 6 for a premium equal to the expected stop-loss claims. Insurer B proposes group coverage with a premium of 7 and a dividend (a premium refund) equal to the excess, if any, of 7k over claims. Calculate k such that the expected cost to the group is equal under both proposals.
- 9.14 (*) For a group health contract, aggregate claims are assumed to have an exponential distribution, where the mean of the distribution is estimated by the group underwriter. Aggregate stop-loss insurance for total claims in excess of 125% of the expected claims is provided by a gross premium that is twice the expected stop-loss claims. You have discovered an error in the underwriter's method of calculating expected claims. The underwriter's estimate is 90% of the correct estimate. Determine the actual percentage loading in the premium.
- 9.15 (*) A random loss, X, has the probability function given in Table 9.8. You are given that
 and
and  . Determine d.
. Determine d.
Table 9.8 The data for Exercise 9.15.
x 
0 0.05 1 0.06 2 0.25 3 0.22 4 0.10 5 0.05 6 0.05 7 0.05 8 0.05 9 0.12 - 9.16 (*) A reinsurer pays aggregate claim amounts in excess of d, and in return it receives a stop-loss premium
 . You are given
. You are given  ,
,  , and the probability that the aggregate claim amounts are greater than 80 and less than or equal to 120 is zero. Determine the probability that the aggregate claim amounts are less than or equal to 80.
, and the probability that the aggregate claim amounts are greater than 80 and less than or equal to 120 is zero. Determine the probability that the aggregate claim amounts are less than or equal to 80. - 9.17 (*) A loss random variable X has pdf
 ,
,  . Two policies can be purchased to alleviate the financial impact of the loss:
. Two policies can be purchased to alleviate the financial impact of the loss:

and

where A and B are the amounts paid when the loss is x. Both policies have the same net premium, that is,
 . Determine k.
. Determine k. - 9.18 (*) For a nursing home insurance policy, you are given that the average length of stay is 440 days and 30% of the stays are terminated in the first 30 days. These terminations are distributed uniformly during that period. The policy pays 20 per day for the first 30 days and 100 per day thereafter. Determine the expected benefits payable for a single stay.
- 9.19 (*) An insurance portfolio produces N claims, where
n 
0 0.5 1 0.4 3 0.1 Individual claim amounts have the following distribution:
x 
1 0.9 10 0.1 Individual claim amounts and N are mutually independent. Calculate the probability that the ratio of aggregate claims to expected claims will exceed 3.0.
- 9.20 (*) A company sells group travel-accident life insurance, with m payable in the event of a covered individual's death in a travel accident. The gross premium for a group is set equal to the expected value plus the standard deviation of the group's aggregate claims. The standard premium is based on the following two assumptions:
- All individual claims within the group are mutually independent.
 , where q is the probability of death by travel accident for an individual.
, where q is the probability of death by travel accident for an individual.
In a certain group of 100 lives, the independence assumption fails because three specific individuals always travel together. If one dies in an accident, all three are assumed to die. Determine the difference between this group's premium and the standard premium.
- 9.21 (*) A life insurance company covers 16,000 lives for one-year term life insurance, as in Table 9.9.
Table 9.9 The data for Exercise 9.21.
Benefit amount Number covered Probability of claim 1 8,000 0.025 2 3,500 0.025 4 4,500 0.025 All claims are mutually independent. The insurance company's retention limit is two units per life. Reinsurance is purchased for 0.03 per unit. The probability that the insurance company's retained claims, S, plus the cost of reinsurance will exceed 1,000 is
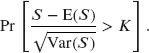
Determine K using a normal approximation.
- 9.22 (*) The probability density function of individual losses Y is
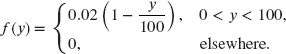
The amount paid, Z, is 80% of that portion of the loss that exceeds a deductible of 10. Determine
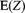 .
. - 9.23 (*) An individual loss distribution is normal with
 and
and  . The distribution for the number of claims, N, is given in Table 9.10. Determine the probability that aggregate claims exceed 100.
. The distribution for the number of claims, N, is given in Table 9.10. Determine the probability that aggregate claims exceed 100.
Table 9.10 The distribution for Exercise 9.23.
n 
0 0.5 1 0.2 2 0.2 3 0.1 - 9.24 (*) An employer self-insures a life insurance program with the following two characteristics:
- Given that a claim has occurred, the claim amount is 2,000 with probability 0.4 and 3,000 with probability 0.6.
- The number of claims has the distribution given in Table 9.11.
Table 9.11 The distribution for Exercise 9.24.
n 
0 1/16 1 1/4 2 3/8 3 1/4 4 1/16 The employer purchases aggregate stop-loss coverage that limits the employer's annual claims cost to 5,000. The aggregate stop-loss coverage costs 1,472. Determine the employer's expected annual cost of the program, including the cost of stop-loss coverage.
- 9.25 (*) The probability that an individual admitted to the hospital will stay k days or less is
 for
for  . A hospital indemnity policy provides a fixed amount per day for the 4th day through the 10th day (i.e. for a maximum of 7 days). Determine the percentage increase in the expected cost per admission if the maximum number of days paid is increased from 7 to 14.
. A hospital indemnity policy provides a fixed amount per day for the 4th day through the 10th day (i.e. for a maximum of 7 days). Determine the percentage increase in the expected cost per admission if the maximum number of days paid is increased from 7 to 14. - 9.26 (*) The probability density function of aggregate claims, S, is given by
 . The relative loading
. The relative loading  and the value
and the value  are selected so that
are selected so that

Calculate
 and
and  .
. - 9.27 (*) An insurance policy reimburses aggregate incurred expenses at the rate of 80% of the first 1,000 in excess of 100, 90% of the next 1,000, and 100% thereafter. Express the expected cost of this coverage in terms of
 for different values of d.
for different values of d. - 9.28 (*) The number of accidents incurred by an insured driver in a single year has a Poisson distribution with parameter
 . If an accident occurs, the probability that the damage amount exceeds the deductible is 0.25. The number of claims and the damage amounts are independent. What is the probability that there will be no damages exceeding the deductible in a single year?
. If an accident occurs, the probability that the damage amount exceeds the deductible is 0.25. The number of claims and the damage amounts are independent. What is the probability that there will be no damages exceeding the deductible in a single year? - 9.29 (*) The aggregate loss distribution is modeled by an insurance company using an exponential distribution. However, the mean is uncertain. The company uses a uniform distribution (2,000,000, 4,000,000) to express its view of what the mean should be. Determine the expected aggregate losses.
- 9.30 (*) A group hospital indemnity policy provides benefits at a continuous rate of 100 per day of hospital confinement for a maximum of 30 days. Benefits for partial days of confinement are prorated. The length of hospital confinement in days, T, has the following continuance (survival) function for
 :
:

For a policy period, each member's probability of a single hospital admission is 0.1 and that of more than one admission is zero. Determine the pure premium per member, ignoring the time value of money.
- 9.31 (*) Medical and dental claims are assumed to be independent with compound Poisson distributions as follows:
Claim type Claim amount distribution 
Medical claims Uniform (0,1,000) 2 Dental claims Uniform (0,200) 3 Let X be the amount of a given claim under a policy that covers both medical and dental claims. Determine
 , the expected cost (in excess of 100) of any given claim.
, the expected cost (in excess of 100) of any given claim. - 9.32 (*) For a certain insured, the distribution of aggregate claims is binomial with parameters
 and
and  . The insurer will pay a dividend, D, equal to the excess of 80% of the premium over claims, if positive. The premium is 5. Determine
. The insurer will pay a dividend, D, equal to the excess of 80% of the premium over claims, if positive. The premium is 5. Determine  .
. - 9.33 (*) The number of claims in one year has a geometric distribution with mean 1.5. Each claim has a loss of 100. An insurance policy pays zero for the first three claims in one year and then pays 100 for each subsequent claim. Determine the expected insurance payment per year.
- 9.34 (*) A compound Poisson distribution has
 and claim amount distribution
and claim amount distribution  ,
,  , and
, and  . Determine the probability that aggregate claims will be exactly 600.
. Determine the probability that aggregate claims will be exactly 600. - 9.35 (*) Aggregate payments have a compound distribution. The frequency distribution is negative binomial with
 and
and  , and the severity distribution is uniform on the interval (0,8). Use the normal approximation to determine the premium such that the probability is 5% that aggregate payments will exceed the premium.
, and the severity distribution is uniform on the interval (0,8). Use the normal approximation to determine the premium such that the probability is 5% that aggregate payments will exceed the premium. - 9.36 (*) The number of losses is Poisson with
 . Loss amounts have a Burr distribution with
. Loss amounts have a Burr distribution with  ,
,  , and
, and  . Determine the variance of aggregate losses.
. Determine the variance of aggregate losses.
9.4 Analytic Results
For most choices of distributions of N and the ![]() , the compound distributional values can only be obtained numerically. Subsequent sections in this chapter are devoted to such numerical procedures.
, the compound distributional values can only be obtained numerically. Subsequent sections in this chapter are devoted to such numerical procedures.
However, for certain combinations of choices, simple analytic results are available, thus reducing the computational problems considerably.
![]()
As is clear from Example 9.7, useful formulas may result with exponential claim sizes. The following example considers this case in more detail.
![]()
For frequency distributions that assign positive probability to all nonnegative integers, (9.15) can be evaluated by taking sufficient terms in the first summation. For distributions for which ![]() , the first summation becomes finite. For example, for the binomial frequency distribution, (9.15) becomes
, the first summation becomes finite. For example, for the binomial frequency distribution, (9.15) becomes

The following theorem provides a shortcut when adding independent compound Poisson random variables. This may arise, for example, in a group insurance contract in which each member has a compound Poisson model for aggregate losses and we are interested in computing the distribution of total aggregate losses. Similarly, we may want to evaluate the combined losses from several independent lines of business. The theorem implies that it is not necessary to compute the distribution for each line or group member and then determine the distribution of the sum. Instead, a weighted average of the loss severity distributions of each component may be used as a severity distribution and the Poisson parameters added to obtain the frequency distribution. Then, a single aggregate loss distribution calculation is sufficient.
![]()
![]()
9.4.1 Exercises
- 9.37 A compound negative binomial distribution has parameters
 ,
, 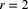 , and severity distribution
, and severity distribution  . How do the parameters of the distribution change if the severity distribution is
. How do the parameters of the distribution change if the severity distribution is  but the aggregate claims distribution remains unchanged?
but the aggregate claims distribution remains unchanged? - 9.38 Consider the compound logarithmic distribution with exponential severity distribution.
- Show that the density of aggregate losses may be expressed as

- Reduce this to

- Show that the density of aggregate losses may be expressed as
- 9.39 For a compound distribution, N has a binomial distribution with parameters
 and
and  and X has an exponential distribution with a mean of 100. Calculate
and X has an exponential distribution with a mean of 100. Calculate  .
. - 9.40 A company sells three policies. For policy A, all claim payments are 10,000 and a single policy has a Poisson number of claims with mean 0.01. For policy B, all claim payments are 20,000 and a single policy has a Poisson number of claims with mean 0.02. For policy C, all claim payments are 40,000 and a single policy has a Poisson number of claims with mean 0.03. All policies are independent. For the coming year, there are 5,000, 3,000, and 1,000 of policies A, B, and C, respectively. Calculate the expected total payment, the standard deviation of total payment, and the probability that total payments will exceed 30,000.
9.5 Computing the Aggregate Claims Distribution
The computation of the compound distribution function
or the corresponding probability (density) function is generally not an easy task, even in the simplest of cases. In this section, we discuss several approaches to numerical evaluation of (9.18) for specific choices of the frequency and severity distributions as well as for arbitrary choices of one or both distributions.
One approach is to use an approximating distribution to avoid direct calculation of (9.18). This approach is used in Example 9.4, where the method of moments is used to estimate the parameters of the approximating distribution. The advantage of this method is that it is simple and easy to apply. However, the disadvantages are significant. First, there is no way of knowing how good the approximation is. Choosing different approximating distributions can result in very different results, particularly in the right-hand tail of the distribution. Of course, the approximation should improve as more moments are used, but after four moments, we quickly run out of distributions!
The approximating distribution may also fail to accommodate special features of the true distribution. For example, when the loss distribution is of the continuous type and there is a maximum possible claim (e.g. when there is a policy limit), the severity distribution may have a point mass (“atom” or “spike”) at the maximum. The true aggregate claims distribution is of the mixed type, with spikes at integral multiples of the maximum corresponding to 1,2,3,… claims at the maximum. These spikes, if large, can have a significant effect on the probabilities near such multiples. These jumps in the aggregate claims distribution function cannot be replicated by a smooth approximating distribution.
The second method to evaluate (9.18) or the corresponding pdf is direct calculation. The most difficult (or computer-intensive) part is the evaluation of the n-fold convolutions of the severity distribution for ![]() . The convolutions need to be evaluated numerically using
. The convolutions need to be evaluated numerically using
When the losses are limited to nonnegative values (as is usually the case), the range of integration becomes finite, reducing (9.19) to
These integrals are written in Lebesgue–Stieltjes form because of possible jumps in the cdf ![]() at zero and at other points.1 Evaluation of (9.20) usually requires numerical integration methods. Because of the first term inside the integral, (9.20) needs to be evaluated for all possible values of x. This approach quickly becomes technically overpowering.
at zero and at other points.1 Evaluation of (9.20) usually requires numerical integration methods. Because of the first term inside the integral, (9.20) needs to be evaluated for all possible values of x. This approach quickly becomes technically overpowering.
As seen in Example 9.5, when the severity distribution is discrete, the calculations reduce to numerous multiplications and additions. For continuous severities, a simple way to avoid these technical problems is to replace the severity distribution by a discrete distribution defined at multiples ![]() of some convenient monetary unit such as 1,000.
of some convenient monetary unit such as 1,000.
In practice, the monetary unit can be made sufficiently small to accommodate spikes at maximum insurance amounts. The spike must be a multiple of the monetary unit to have it located at exactly the right point. As the monetary unit of measurement becomes small, the discrete distribution function needs to approach the true distribution function. The simplest approach is to round all amounts to the nearest multiple of the monetary unit; for example, round all losses or claims to the nearest 1,000. More sophisticated methods are discussed later in this chapter.
When the severity distribution is defined on nonnegative integers ![]() , calculating
, calculating ![]() for integral x requires
for integral x requires ![]() multiplications. Then, carrying out these calculations for all possible values of k and x up to n requires a number of multiplications that are of order
multiplications. Then, carrying out these calculations for all possible values of k and x up to n requires a number of multiplications that are of order ![]() , written as
, written as ![]() , to obtain the distribution of (9.18) for
, to obtain the distribution of (9.18) for ![]() to
to ![]() . When the maximum value, n, for which the aggregate claims distribution is calculated is large, the number of computations quickly becomes prohibitive, even for fast computers. For example, in real applications n can easily be as large as 1,000 and requires about 109 multiplications. Further, if
. When the maximum value, n, for which the aggregate claims distribution is calculated is large, the number of computations quickly becomes prohibitive, even for fast computers. For example, in real applications n can easily be as large as 1,000 and requires about 109 multiplications. Further, if ![]() and the frequency distribution is unbounded, an infinite number of calculations is required to obtain any single probability. This is because
and the frequency distribution is unbounded, an infinite number of calculations is required to obtain any single probability. This is because ![]() for all n and all x, and so the sum in (9.18) contains an infinite number of terms. When
for all n and all x, and so the sum in (9.18) contains an infinite number of terms. When ![]() , we have
, we have ![]() for
for ![]() and so (9.18) will have no more than
and so (9.18) will have no more than ![]() positive terms. Table 9.3 provides an example of this latter case.
positive terms. Table 9.3 provides an example of this latter case.
An alternative method to more quickly evaluate the aggregate claims distribution is discussed in Section 9.6. This method, the recursive method, reduces the number of computations discussed previously to ![]() , which is a considerable savings in computer time, a reduction of about 99.9% when
, which is a considerable savings in computer time, a reduction of about 99.9% when ![]() compared to direct calculation. However, the method is limited to certain frequency distributions. Fortunately, it includes all of the frequency distributions discussed in Chapter 6 and Appendix B.
compared to direct calculation. However, the method is limited to certain frequency distributions. Fortunately, it includes all of the frequency distributions discussed in Chapter 6 and Appendix B.
9.6 The Recursive Method
Suppose that the severity distribution ![]() is defined on
is defined on ![]() representing multiples of some convenient monetary unit. The number m represents the largest possible payment and could be infinite. Further, suppose that the frequency distribution,
representing multiples of some convenient monetary unit. The number m represents the largest possible payment and could be infinite. Further, suppose that the frequency distribution, ![]() , is a member of the
, is a member of the ![]() class and therefore satisfies
class and therefore satisfies
Then, the following result holds.
![]()
Note that when the severity distribution has no probability at zero, the denominator of (9.21) and (9.22) equals 1. Further, in the case of the Poisson distribution, (9.22) reduces to
The starting value of the recursive schemes (9.21) and (9.22) is ![]() following Theorem 7.3 with an appropriate change of notation. In the case of the Poisson distribution, we have
following Theorem 7.3 with an appropriate change of notation. In the case of the Poisson distribution, we have
Starting values for other frequency distributions are found in Appendix D.
![]()
![]()
9.6.1 Applications to Compound Frequency Models
When the frequency distribution can be represented as a compound distribution (e.g. Neyman Type A, Poisson–inverse Gaussian) involving only distributions from the ![]() or
or ![]() classes, the recursive formula (9.21) can be used two or more times to obtain the aggregate claims distribution. If the frequency distribution can be written as
classes, the recursive formula (9.21) can be used two or more times to obtain the aggregate claims distribution. If the frequency distribution can be written as
then the aggregate claims distribution has pgf
which can be rewritten as
where
Now (9.25) has the same form as an aggregate claims distribution. Thus, if ![]() is in the
is in the ![]() or
or ![]() class, the distribution of
class, the distribution of ![]() can be calculated using (9.21). The resulting distribution is the “severity” distribution in (9.25). Thus, a second application of (9.21) to (9.24) results in the distribution of S.
can be calculated using (9.21). The resulting distribution is the “severity” distribution in (9.25). Thus, a second application of (9.21) to (9.24) results in the distribution of S.
The following example illustrates the use of this algorithm.
![]()
When the severity distribution has a maximum possible value at m, the computations are speeded up even more because the sum in (9.21) will be restricted to at most m nonzero terms. In this case, then, the computations can be considered to be of order ![]() .
.
9.6.2 Underflow/Overflow Problems
The recursion (9.21) starts with the calculated value of ![]() . For large insurance portfolios, this probability is very small, sometimes smaller than the smallest number that can be represented on the computer. When this happens, it is stored in the computer as zero and the recursion (9.21) fails. This problem can be overcome in several different ways (see Panjer and Willmot [99]). One of the easiest ways is to start with an arbitrary set of values for
. For large insurance portfolios, this probability is very small, sometimes smaller than the smallest number that can be represented on the computer. When this happens, it is stored in the computer as zero and the recursion (9.21) fails. This problem can be overcome in several different ways (see Panjer and Willmot [99]). One of the easiest ways is to start with an arbitrary set of values for ![]() such as
such as ![]() , where k is sufficiently far to the left in the distribution so that the true value of
, where k is sufficiently far to the left in the distribution so that the true value of ![]() is still negligible. Setting k to a point that lies six standard deviations to the left of the mean is usually sufficient. Recursion (9.21) is used to generate values of the distribution with this set of starting values until the values are consistently less than
is still negligible. Setting k to a point that lies six standard deviations to the left of the mean is usually sufficient. Recursion (9.21) is used to generate values of the distribution with this set of starting values until the values are consistently less than ![]() . The “probabilities” are then summed and divided by the sum so that the “true” probabilities add to 1. Trial and error will dictate how small k should be for a particular problem.
. The “probabilities” are then summed and divided by the sum so that the “true” probabilities add to 1. Trial and error will dictate how small k should be for a particular problem.
Another method to obtain probabilities when the starting value is too small is to carry out the calculations for a subset of the portfolio. For example, for the Poisson distribution with mean ![]() , find a value of
, find a value of ![]() so that the probability at zero is representable on the computer when
so that the probability at zero is representable on the computer when ![]() is used as the Poisson mean. (Equation 9.21) is now used to obtain the aggregate claims distribution when
is used as the Poisson mean. (Equation 9.21) is now used to obtain the aggregate claims distribution when ![]() is used as the Poisson mean. If
is used as the Poisson mean. If ![]() is the pgf of the aggregate claims using Poisson mean
is the pgf of the aggregate claims using Poisson mean ![]() , then
, then ![]() . Hence we can obtain successively the distributions with pgfs
. Hence we can obtain successively the distributions with pgfs ![]() ,
, ![]() ,
, ![]() by convoluting the result at each stage with itself. This approach requires an additional n convolutions in carrying out the calculations but involves no approximations. It can be carried out for any frequency distributions that are closed under convolution. For the negative binomial distribution, the analogous procedure starts with
by convoluting the result at each stage with itself. This approach requires an additional n convolutions in carrying out the calculations but involves no approximations. It can be carried out for any frequency distributions that are closed under convolution. For the negative binomial distribution, the analogous procedure starts with ![]() . For the binomial distribution, the parameter m must be integer valued. A slight modification can be used. Let
. For the binomial distribution, the parameter m must be integer valued. A slight modification can be used. Let ![]() when
when ![]() indicates the integer part of the function. When the n convolutions are carried out, we still need to carry out the calculations using (9.21) for parameter
indicates the integer part of the function. When the n convolutions are carried out, we still need to carry out the calculations using (9.21) for parameter ![]() . This result is then convoluted with the result of the n convolutions. For compound frequency distributions, only the primary distribution needs to be closed under convolution.
. This result is then convoluted with the result of the n convolutions. For compound frequency distributions, only the primary distribution needs to be closed under convolution.
9.6.3 Numerical Stability
Any recursive formula requires accurate computation of values because each such value will be used in computing subsequent values. Recursive schemes suffer the risk of errors propagating through all subsequent values and potentially blowing up. In the recursive formula (9.21), errors are introduced through rounding at each stage because computers represent numbers with a finite number of significant digits. The question about stability is: How fast do the errors in the calculations grow as the computed values are used in successive computations? This work has been done by Panjer and Wang [98]. The analysis is quite complicated and well beyond the scope of this book. However, we can draw some general conclusions.
Errors are introduced in subsequent values through the summation
in recursion (9.21). In the extreme right-hand tail of the distribution of S, this sum is positive (or at least nonnegative), and subsequent values of the sum will be decreasing. The sum will stay positive, even with rounding errors, when each of the three factors in each term in the sum is positive. In this case, the recursive formula is stable, producing relative errors that do not grow fast. For the Poisson and negative binomial-based distributions, the factors in each term are always positive.
However, for the binomial distribution, the sum can have negative terms because a is negative, b is positive, and ![]() is a positive function not exceeding 1. In this case, the negative terms can cause the successive values to blow up with alternating signs. When this occurs, the nonsensical results are immediately obvious. Although it does not happen frequently in practice, you should be aware of this possibility in models based on the binomial distribution.
is a positive function not exceeding 1. In this case, the negative terms can cause the successive values to blow up with alternating signs. When this occurs, the nonsensical results are immediately obvious. Although it does not happen frequently in practice, you should be aware of this possibility in models based on the binomial distribution.
9.6.4 Continuous Severity
The recursive method as presented here requires a discrete severity distribution, while it is customary to use a continuous distribution for severity. In the case of continuous severities, the analog of the recursion (9.21) is an integral equation, the solution of which is the aggregate claims distribution.
The proof of this result is beyond the scope of this book. For a detailed proof, see Theorems 6.14.1 and 6.16.1 of Panjer and Willmot [100], along with the associated corollaries. They consider the more general ![]() class of distributions, which allow for arbitrary modification of m initial values of the distribution. Note that the initial term is
class of distributions, which allow for arbitrary modification of m initial values of the distribution. Note that the initial term is ![]() , not
, not ![]() as in (9.21). Also, (9.26) holds for members of the
as in (9.21). Also, (9.26) holds for members of the ![]() class as well.
class as well.
Integral equations of the form (9.26) are Volterra integral equations of the second kind. Numerical solution of this type of integral equation has been studied in the text by Baker [10]. Instead, we consider an alternative approach for continuous severity distributions. It is to use a discrete approximation of the severity distribution in order to use the recursive method (9.21) and avoid the more complicated methods of Baker [10].
9.6.5 Constructing Arithmetic Distributions
The easiest approach to constructing a discrete severity distribution from a continuous one is to place the discrete probabilities on multiples of a convenient unit of measurement h, the span. Such a distribution is called arithmetic because it is defined on the nonnegative integers. In order to arithmetize a distribution, it is important to preserve the properties of the original distribution both locally through the range of the distribution and globally – that is, for the entire distribution. This should preserve the general shape of the distribution and at the same time preserve global quantities such as moments.
The methods suggested here apply to the discretization (arithmetization) of continuous, mixed, and nonarithmetic discrete distributions.
9.6.5.1 The Method of Rounding (Mass Dispersal)
Let ![]() denote the probability placed at jh,
denote the probability placed at jh, ![]() . Then, set2
. Then, set2

This method concentrates all the probability one-half span on either side of jh and places it at jh. There is an exception for the probability assigned to zero. This, in effect, rounds all amounts to the nearest convenient monetary unit, h, the span of the distribution. When the continuous severity distribution is unbounded, it is reasonable to halt the discretization process at some point once most of the probability has been accounted for. If the index for this last point is m, then ![]() . With this method, the discrete probabilities are never negative and sum to 1, ensuring that the resulting distribution is legitimate.
. With this method, the discrete probabilities are never negative and sum to 1, ensuring that the resulting distribution is legitimate.
9.6.5.2 The Method of Local Moment Matching
In this method, we construct an arithmetic distribution that matches p moments of the arithmetic and the true severity distributions. Consider an arbitrary interval of length ph, denoted by ![]() . We locate point masses
. We locate point masses ![]() at points
at points ![]() ,
, ![]() so that the first p moments are preserved. The system of
so that the first p moments are preserved. The system of ![]() equations reflecting these conditions is
equations reflecting these conditions is
where the notation “−0” at the limits of the integral indicates that discrete probability at ![]() is to be included but discrete probability at
is to be included but discrete probability at ![]() is to be excluded.
is to be excluded.
Arrange the intervals so that ![]() and so that the endpoints coincide. Then, the point masses at the endpoints are added together. With
and so that the endpoints coincide. Then, the point masses at the endpoints are added together. With ![]() , the resulting discrete distribution has successive probabilities:
, the resulting discrete distribution has successive probabilities:
By summing (9.27) for all possible values of k, with ![]() , it is clear that the first p moments are preserved for the entire distribution and that the probabilities add to 1 exactly. It only remains to solve the system of (equations 9.27).
, it is clear that the first p moments are preserved for the entire distribution and that the probabilities add to 1 exactly. It only remains to solve the system of (equations 9.27).
![]()
![]()
This method of local moment matching was introduced by Gerber and Jones [44] and Gerber [43], and further studied by Panjer and Lutek [97] for a variety of empirical and analytic severity distributions. In assessing the impact of errors on aggregate stop-loss net premiums (aggregate excess-of-loss pure premiums), Panjer and Lutek [97] found that two moments were usually sufficient and that adding a third moment requirement adds only marginally to the accuracy. Furthermore, the rounding method and the first-moment method ![]() had similar errors, while the second-moment method
had similar errors, while the second-moment method ![]() provided significant improvement. The specific formulas for the method of rounding and the method of matching the first moment are given in Appendix E. A reason to favor matching zero or one moment is that the resulting probabilities will always be nonnegative. When matching two or more moments, this cannot be guaranteed.
provided significant improvement. The specific formulas for the method of rounding and the method of matching the first moment are given in Appendix E. A reason to favor matching zero or one moment is that the resulting probabilities will always be nonnegative. When matching two or more moments, this cannot be guaranteed.
The methods described here are qualitatively similar to numerical methods used to solve Volterra integral equations such as (9.26) developed in numerical analysis (see, e.g. Baker [10]).
9.6.6 Exercises
- 9.41 Show that the method of local moment matching with
 (matching total probability and the mean) using (9.28) and (9.29) results in
(matching total probability and the mean) using (9.28) and (9.29) results in

and that
 forms a valid distribution with the same mean as the original severity distribution. Using the formula given here, verify the formula given in Example 9.13.
forms a valid distribution with the same mean as the original severity distribution. Using the formula given here, verify the formula given in Example 9.13. - 9.42 You are the agent for a baseball player who desires an incentive contract that will pay the amounts given in Table 9.13. The number of times at bat has a Poisson distribution with
 . The parameter x is determined so that the probability of the player earning at least 4,000,000 is 0.95. Determine the player's expected compensation.
. The parameter x is determined so that the probability of the player earning at least 4,000,000 is 0.95. Determine the player's expected compensation.
Table 9.13 The data for Exercise 9.42.
Type of hit Probability of hit per time at bat Compensation per hit Single 0.14 x Double 0.05 2x Triple 0.02 3x Home run 0.03 4x - 9.43 A weighted average of two Poisson distributions

has been used by some authors (e.g. Tröbliger [121]) to treat drivers as either “good” or “bad.”
- Find the pgf
 of the number of losses in terms of the two pgfs
of the number of losses in terms of the two pgfs  and
and  of the number of losses of the two types of drivers.
of the number of losses of the two types of drivers. - Let
 denote a severity distribution defined on the nonnegative integers. How can (9.23) be used to compute the distribution of aggregate claims for the entire group?
denote a severity distribution defined on the nonnegative integers. How can (9.23) be used to compute the distribution of aggregate claims for the entire group? - Can your approach from (b) be extended to other frequency distributions?
- Find the pgf
- 9.44 (*) A compound Poisson aggregate loss model has five expected claims per year. The severity distribution is defined on positive multiples of 1,000. Given that
 and
and  , determine
, determine  .
. - 9.45 (*) For a compound Poisson distribution,
 and individual losses have pf
and individual losses have pf  . Some of the pf values for the aggregate distribution S are given in Table 9.14. Determine
. Some of the pf values for the aggregate distribution S are given in Table 9.14. Determine  .
.
Table 9.14 The data for Exercise 9.45.
x 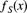
3 0.0132 4 0.0215 5 0.0271 6 
7 0.0410 - 9.46 Consider the
 class of frequency distributions and any severity distribution defined on the positive integers
class of frequency distributions and any severity distribution defined on the positive integers  , where M is the maximum possible single loss.
, where M is the maximum possible single loss.
- Show that, for the compound distribution, the following backward recursion holds:

- For the binomial
 frequency distribution, how can the preceding formula be used to obtain the distribution of aggregate losses?
frequency distribution, how can the preceding formula be used to obtain the distribution of aggregate losses?
- Show that, for the compound distribution, the following backward recursion holds:
- 9.47 (*) Aggregate claims are compound Poisson with
 , and
, and  . For a premium of 6, an insurer covers aggregate claims and agrees to pay a dividend (a refund of premium) equal to the excess, if any, of 75% of the premium over 100% of the claims. Determine the excess of premium over expected claims and dividends.
. For a premium of 6, an insurer covers aggregate claims and agrees to pay a dividend (a refund of premium) equal to the excess, if any, of 75% of the premium over 100% of the claims. Determine the excess of premium over expected claims and dividends. - 9.48 On a given day, a physician provides medical care to
 adults and
adults and  children. Assume that
children. Assume that 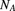 and
and  have Poisson distributions with parameters 3 and 2, respectively. The distributions of length of care per patient are as follows:
have Poisson distributions with parameters 3 and 2, respectively. The distributions of length of care per patient are as follows:
Adult Child 1 hour 0.4 0.9 2 hour 0.6 0.1 Let
 ,
,  , and the lengths of care for all individuals be independent. The physician charges 200 per hour of patient care. Determine the probability that the office income on a given day is less than or equal to 800.
, and the lengths of care for all individuals be independent. The physician charges 200 per hour of patient care. Determine the probability that the office income on a given day is less than or equal to 800. - 9.49 (*) A group policyholder's aggregate claims, S, has a compound Poisson distribution with
 and all claim amounts equal to 2. The insurer pays the group the following dividend:
and all claim amounts equal to 2. The insurer pays the group the following dividend:

Determine
 .
. - 9.50 You are given two independent compound Poisson random variables,
 and
and  , where
, where  , are the two single-claim size distributions. You are given
, are the two single-claim size distributions. You are given  ,
, 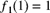 , and
, and  . Let
. Let  be the single-claim size distribution function associated with the compound distribution
be the single-claim size distribution function associated with the compound distribution  . Calculate
. Calculate  .
. - 9.51 (*) The variable S has a compound Poisson claims distribution with the following characteristics:
- Individual claim amounts equal to 1, 2, or 3.
 .
. .
.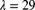 .
.
Determine the expected number of claims of size 2.
- 9.52 (*) For a compound Poisson distribution with positive integer claim amounts, the probability function follows:

The expected value of aggregate claims is 1.68. Determine the expected number of claims.
- 9.53 (*) For a portfolio of policies, you are given the following:
- The number of claims has a Poisson distribution.
- Claim amounts can be 1, 2, or 3.
- A stop-loss reinsurance contract has net premiums for various deductibles as given in Table 9.15.
Table 9.15 The data for Exercise 9.53.
Deductible Net premium 4 0.20 5 0.10 6 0.04 7 0.02 Determine the probability that aggregate claims will be either 5 or 6.
- 9.54 (*) For group disability income insurance, the expected number of disabilities per year is 1 per 100 lives covered. The continuance (survival) function for the length of a disability in days, Y, is

The benefit is 20 per day following a five-day waiting period. Using a compound Poisson distribution, determine the variance of aggregate claims for a group of 1,500 independent lives.
- 9.55 A population has two classes of drivers. The number of accidents per individual driver has a geometric distribution. For a driver selected at random from Class I, the geometric distribution parameter has a uniform distribution over the interval (0,1). Twenty-five percent of the drivers are in Class I. All drivers in Class II have expected number of claims 0.25. For a driver selected at random from this population, determine the probability of exactly two accidents.
- 9.56 (*) A compound Poisson claim distribution has
 and individual claim amount distribution
and individual claim amount distribution  and
and 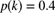 where
where  . The expected cost of an aggregate stop-loss insurance with a deductible of 5 is 28.03. Determine the value of k.
. The expected cost of an aggregate stop-loss insurance with a deductible of 5 is 28.03. Determine the value of k. - 9.57 (*) Aggregate losses have a compound Poisson claim distribution with
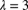 and individual claim amount distribution
and individual claim amount distribution  ,
,  ,
,  , and
, and 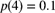 . Determine the probability that aggregate losses do not exceed 3.
. Determine the probability that aggregate losses do not exceed 3. - 9.58 Repeat Exercise 9.57 with a negative binomial frequency distribution with
 and
and  .
.
Note: Exercises 9.59 and 9.60 require the use of a computer.
- 9.59 A policy covers physical damage incurred by the trucks in a company's fleet. The number of losses in a year has a Poisson distribution with
 . The amount of a single loss has a gamma distribution with
. The amount of a single loss has a gamma distribution with  and
and  . The insurance contract pays a maximum annual benefit of 20,000. Determine the probability that the maximum benefit will be paid. Use a span of 100 and the method of rounding.
. The insurance contract pays a maximum annual benefit of 20,000. Determine the probability that the maximum benefit will be paid. Use a span of 100 and the method of rounding. - 9.60 An individual has purchased health insurance, for which he pays 10 for each physician visit and 5 for each prescription. The probability that a payment will be 10 is 0.25, and the probability that it will be 5 is 0.75. The total number of payments per year has the Poisson–Poisson (Neyman Type A) distribution with
 and
and  . Determine the probability that total payments in one year will exceed 400. Compare your answer to a normal approximation.
. Determine the probability that total payments in one year will exceed 400. Compare your answer to a normal approximation. - 9.61 Demonstrate that if the exponential distribution is discretized by the method of rounding, the resulting discrete distribution is a ZM geometric distribution.
9.7 The Impact of Individual Policy Modifications on Aggregate Payments
In Section 8.6 the manner in which individual deductibles (both ordinary and franchise) affect both the individual loss amounts and the claim frequency distribution is discussed. In this section, we consider the impact on aggregate losses. It is worth noting that both individual coinsurance and individual policy limits have an impact on the individual losses but not on the frequency of such losses, so in what follows we focus primarily on the deductible issues. We continue to assume that the presence of policy modifications does not have an underwriting impact on the individual loss distribution through an effect on the risk characteristics of the insured population, an issue discussed in Section 8.6. That is, the ground-up distribution of the individual loss amount X is assumed to be unaffected by the policy modifications, and only the payments themselves are affected.
From the standpoint of the aggregate losses, the relevant facts are now described. Regardless of whether the deductible is of the ordinary or franchise type, we shall assume that an individual loss results in a payment with probability v. The individual ground-up loss random variable X has policy modifications (including deductibles) applied, so that a payment is then made. Individual payments may then be viewed on a per-loss basis, where the amount of such payment, denoted by ![]() , will be zero if the loss results in no payment. Thus, on a per-loss basis, the payment amount is determined on each and every loss. Alternatively, individual payments may also be viewed on a per-payment basis. In this case, the amount of payment is denoted by
, will be zero if the loss results in no payment. Thus, on a per-loss basis, the payment amount is determined on each and every loss. Alternatively, individual payments may also be viewed on a per-payment basis. In this case, the amount of payment is denoted by ![]() , and on this basis payment amounts are only determined on losses that actually result in a nonzero payment being made. Therefore, by definition,
, and on this basis payment amounts are only determined on losses that actually result in a nonzero payment being made. Therefore, by definition, ![]() , and the distribution of
, and the distribution of ![]() is the conditional distribution of
is the conditional distribution of ![]() given that
given that ![]() . Notationally, we write
. Notationally, we write ![]() . Therefore, the cumulative distribution functions are related by
. Therefore, the cumulative distribution functions are related by
because ![]() (recall that
(recall that ![]() has a discrete probability mass point
has a discrete probability mass point ![]() at zero, even if X and hence
at zero, even if X and hence ![]() and
and ![]() have continuous probability density functions for
have continuous probability density functions for ![]() ). The moment generating functions of
). The moment generating functions of ![]() and
and ![]() are thus related by
are thus related by
which may be restated in terms of expectations as
It follows from Section 8.6 that the number of losses ![]() and the number of payments
and the number of payments ![]() are related through their probability generating functions by
are related through their probability generating functions by
where ![]() and
and ![]() .
.
We now turn to the analysis of the aggregate payments. On a per-loss basis, the total payments may be expressed as ![]() , with
, with ![]() if
if ![]() , and where
, and where ![]() is the payment amount on the jth loss. Alternatively, ignoring losses on which no payment is made, we may express the total payments on a per-payment basis as
is the payment amount on the jth loss. Alternatively, ignoring losses on which no payment is made, we may express the total payments on a per-payment basis as ![]() , with
, with ![]() if
if ![]() , and
, and ![]() is the payment amount on the jth loss, which results in a nonzero payment. Clearly, S may be represented in two distinct ways on an aggregate basis. Of course, the moment generating function of S on a per-loss basis is
is the payment amount on the jth loss, which results in a nonzero payment. Clearly, S may be represented in two distinct ways on an aggregate basis. Of course, the moment generating function of S on a per-loss basis is
whereas on a per-payment basis we have
Obviously, (9.32) and (9.33) are equal, as may be seen from (9.30) and (9.31). That is,
Consequently, any analysis of the aggregate payments S may be done on either a per-loss basis (with compound representation (9.32) for the moment generating function) or on a per-payment basis (with (9.33) as the compound moment generating function). The basis selected should be determined by whatever is more suitable for the particular situation at hand. While by no means a hard-and-fast rule, we have found it more convenient to use the per-loss basis to evaluate moments of S. In particular, the formulas given in Section 8.5 for the individual mean and variance are on a per-loss basis, and the mean and variance of the aggregate payments S may be computed using these and (9.9), but with N replaced by ![]() and X by
and X by ![]() .
.
If the (approximated) distribution of S is of more interest than the moments, then a per-payment basis is normally to be preferred. The reason for this choice is that on a per-loss basis, underflow problems may result if ![]() is large, and computer storage problems may occur due to the presence of a large number of zero probabilities in the distribution of
is large, and computer storage problems may occur due to the presence of a large number of zero probabilities in the distribution of ![]() , particularly if a franchise deductible is employed. Also, for convenience, we normally elect to apply policy modifications to the individual loss distribution first and then discretize (if necessary), rather than discretizing and then applying policy modifications to the discretized distributions. This issue is only relevant, however, if the deductible and policy limit are not integer multiples of the discretization span. The following example illustrates these ideas.
, particularly if a franchise deductible is employed. Also, for convenience, we normally elect to apply policy modifications to the individual loss distribution first and then discretize (if necessary), rather than discretizing and then applying policy modifications to the discretized distributions. This issue is only relevant, however, if the deductible and policy limit are not integer multiples of the discretization span. The following example illustrates these ideas.
![]()
9.7.1 Exercises
- 9.62 Suppose that the number of ground-up losses
 has probability generating function
has probability generating function  , where
, where  is a parameter and B is functionally independent of
is a parameter and B is functionally independent of  . The individual ground-up loss distribution is exponential with cumulative distribution function
. The individual ground-up loss distribution is exponential with cumulative distribution function  . Individual losses are subject to an ordinary deductible of d and coinsurance of
. Individual losses are subject to an ordinary deductible of d and coinsurance of  . Demonstrate that the aggregate payments, on a per-payment basis, have a compound moment generating function given by (9.33), where
. Demonstrate that the aggregate payments, on a per-payment basis, have a compound moment generating function given by (9.33), where  has the same distribution as
has the same distribution as  but with
but with  replaced by
replaced by  , and
, and  has the same distribution as X, but with
has the same distribution as X, but with  replaced by
replaced by  .
. - 9.63 A ground-up model of individual losses has a gamma distribution with parameters
 and
and 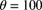 . The number of losses has a negative binomial distribution with
. The number of losses has a negative binomial distribution with  and
and  . An ordinary deductible of 50 and a loss limit of 175 (before imposition of the deductible) are applied to each individual loss.
. An ordinary deductible of 50 and a loss limit of 175 (before imposition of the deductible) are applied to each individual loss.
- Determine the mean and variance of the aggregate payments on a per-loss basis.
- Determine the distribution of the number of payments.
- Determine the cumulative distribution function of the amount
 of a payment, given that a payment is made.
of a payment, given that a payment is made. - Discretize the severity distribution from (c) using the method of rounding and a span of 40.
- Use the recursive formula to calculate the discretized distribution of aggregate payments up to a discretized amount paid of 120.
9.8 The Individual Risk Model
9.8.1 The Model
The individual risk model represents the aggregate loss as a fixed sum of independent (but not necessarily identically distributed) random variables:
This formula is usually thought of as the sum of the losses from n insurance contracts, for example, n persons covered under a group insurance policy.
The individual risk model was originally developed for life insurance, in which the probability of death within a year is ![]() and the fixed benefit paid for the death of the jth person is
and the fixed benefit paid for the death of the jth person is ![]() . In this case, the distribution of the loss to the insurer for the jth policy is
. In this case, the distribution of the loss to the insurer for the jth policy is

The mean and variance of aggregate losses are
and

because the ![]() are assumed to be independent. Then, the pgf of aggregate losses is
are assumed to be independent. Then, the pgf of aggregate losses is
In the special case where all the risks are identical with ![]() and
and ![]() , the pgf reduces to
, the pgf reduces to
and in this case S has a binomial distribution.
The individual risk model can be generalized as follows. Let ![]() , where
, where ![]() are independent. The random variable
are independent. The random variable ![]() is an indicator variable that takes on the value 1 with probability
is an indicator variable that takes on the value 1 with probability ![]() and the value 0 with probability
and the value 0 with probability ![]() . This variable indicates whether the jth policy produced a payment. The random variable
. This variable indicates whether the jth policy produced a payment. The random variable ![]() can have any distribution and represents the amount of the payment in respect of the jth policy given that a payment was made. In the life insurance case,
can have any distribution and represents the amount of the payment in respect of the jth policy given that a payment was made. In the life insurance case, ![]() is degenerate, with all probability on the value
is degenerate, with all probability on the value ![]() .
.
The mgf corresponding to (9.34) is
If we let ![]() and
and ![]() , then
, then
and
You are asked to verify these formulas in Exercise 9.64. The following example is a simple version of this situation.
![]()
With regard to calculating the probabilities, there are at least three options. One is to do an exact calculation, which involves numerous convolutions and almost always requires more excessive computing time. Recursive formulas have been developed, but they are cumbersome and are not presented here. For one such method, see De Pril [27]. One alternative is a parametric approximation as discussed for the collective risk model. Another alternative is to replace the individual risk model with a similar collective risk model and then do the calculations with that model. These two approaches are presented here.
9.8.2 Parametric Approximation
A normal, gamma, lognormal, or any other distribution can be used to approximate the distribution, usually done by matching the first few moments. Because the normal, gamma, and lognormal distributions each have two parameters, the mean and variance are sufficient.
![]()
9.8.3 Compound Poisson Approximation
Because of the computational complexity of calculating the distribution of total claims for a portfolio of n risks using the individual risk model, it has been popular to attempt to approximate the distribution by using the compound Poisson distribution. As seen in Section 9.6, use of the compound Poisson allows calculation of the total claims distribution by using a very simple recursive procedure.
To proceed, note that the indicator random variable ![]() has pgf
has pgf ![]() , and thus (9.35) may be expressed as
, and thus (9.35) may be expressed as
Note that ![]() has a binomial distribution with parameters
has a binomial distribution with parameters ![]() and
and ![]() . To obtain the compound Poisson approximation, assume that
. To obtain the compound Poisson approximation, assume that ![]() has a Poisson distribution with mean
has a Poisson distribution with mean ![]() . If
. If ![]() , then the Poisson mean is the same as the binomial mean, which should provide a good approximation if
, then the Poisson mean is the same as the binomial mean, which should provide a good approximation if ![]() is close to zero. An alternative to equating the mean is to equate the probability of no loss. For the binomial distribution, that probability is
is close to zero. An alternative to equating the mean is to equate the probability of no loss. For the binomial distribution, that probability is ![]() , and for the Poisson distribution, it is
, and for the Poisson distribution, it is ![]() . Equating these two probabilities gives the alternative approximation
. Equating these two probabilities gives the alternative approximation ![]() . This second approximation is appropriate in the context of a group life insurance contract where a life is “replaced” upon death, leaving the Poisson intensity unchanged by the death. Naturally the expected number of losses is greater than
. This second approximation is appropriate in the context of a group life insurance contract where a life is “replaced” upon death, leaving the Poisson intensity unchanged by the death. Naturally the expected number of losses is greater than ![]() . An alternative choice is proposed by Kornya [76]. It uses
. An alternative choice is proposed by Kornya [76]. It uses ![]() and results in an expected number of losses that exceeds that using the method that equates the no-loss probabilities (see Exercise 9.65).
and results in an expected number of losses that exceeds that using the method that equates the no-loss probabilities (see Exercise 9.65).
Regardless of the approximation used, Theorem 9.7 yields, from (9.38) using ![]() ,
,
where

and so X has pf or pdf
which is a weighted average of the n individual severity densities.
If ![]() as in life insurance, then (9.39) becomes
as in life insurance, then (9.39) becomes
The numerator sums all probabilities associated with amount ![]() .
.
![]()
![]()
9.8.4 Exercises
- 9.64 Derive (9.36) and (9.37).
- 9.65 Demonstrate that the compound Poisson model given by
 and (9.40) produces a model with the same mean as the exact distribution but with a larger variance. Then show that the one using
and (9.40) produces a model with the same mean as the exact distribution but with a larger variance. Then show that the one using  must produce a larger mean and an even larger variance, and, finally, show that the one using
must produce a larger mean and an even larger variance, and, finally, show that the one using  must produce the largest mean and variance of all.
must produce the largest mean and variance of all. - 9.66 (*) Individual members of an insured group have independent claims. Aggregate payment amounts for males have mean 2 and variance 4, while females have mean 4 and variance 10. The premium for a group with future claims S is the mean of S plus 2 times the standard deviation of S. If the genders of the members of a group of m members are not known, the number of males is assumed to have a binomial distribution with parameters m and
 . Let A be the premium for a group of 100 for which the genders of the members are not known and let B be the premium for a group of 40 males and 60 females. Determine A/B.
. Let A be the premium for a group of 100 for which the genders of the members are not known and let B be the premium for a group of 40 males and 60 females. Determine A/B. - 9.67 (*) An insurance company assumes that the claim probability for smokers is 0.02, while for nonsmokers it is 0.01. A group of mutually independent lives has coverage of 1,000 per life. The company assumes that 20% of the lives are smokers. Based on this assumption, the premium is set equal to 110% of expected claims. If 30% of the lives are smokers, the probability that claims will exceed the premium is less than 0.20. Using the normal approximation, determine the minimum number of lives that must be in the group.
- 9.68 (*) Based on the individual risk model with independent claims, the cumulative distribution function of aggregate claims for a portfolio of life insurance policies is as shown in Table 9.18. One policy with face amount 100 and probability of claim 0.20 is increased in face amount to 200. Determine the probability that aggregate claims for the revised portfolio will not exceed 500.
Table 9.18 The distribution for Exercise 9.68
x 
0 0.40 100 0.58 200 0.64 300 0.69 400 0.70 500 0.78 600 0.96 700 1.00 - 9.69 (*) A group life insurance contract covering independent lives is rated in the three age groupings as given in Table 9.19. The insurer prices the contract so that the probability that claims will exceed the premium is 0.05. Using the normal approximation, determine the premium that the insurer will charge.
Table 9.19 The data for Exercise 9.69.
Age group Number in age group Probability of claim per life Mean of the exponential distribution of claim amounts 18–35 400 0.03 5 36–50 300 0.07 3 51–65 200 0.10 2 - 9.70 (*) The probability model for the distribution of annual claims per member in a health plan is shown in Table 9.20. Independence of costs and occurrences among services and members is assumed. Using the normal approximation, determine the minimum number of members that a plan must have such that the probability that actual charges will exceed 115% of the expected charges is less than 0.10.
Table 9.20 The data for Exercise 9.70
Distribution of annual charges given that a claim occurs Service Probability of claim Mean Variance Office visits 0.7 160 4,900 Surgery 0.2 600 20,000 Other services 0.5 240 8,100 - 9.71 (*) An insurer has a portfolio of independent risks as given in Table 9.21. The insurer sets
 and k such that aggregate claims have expected value 100,000 and minimum variance. Determine
and k such that aggregate claims have expected value 100,000 and minimum variance. Determine  .
.
Table 9.21 The data for Exercise 9.71.
Class Probability of claim Benefit Number of risks Standard 0.2 k 3,500 Substandard 0.6 
2,000 - 9.72 (*) An insurance company has a portfolio of independent one-year term life policies as given in Table 9.22. The actuary approximates the distribution of claims in the individual model using the compound Poisson model, in which the expected number of claims is the same as in the individual model. Determine the maximum value of x such that the variance of the compound Poisson approximation is less than 4,500.
Table 9.22 The data for Exercise 9.72.
Class Number in class Benefit amount Probability of a claim 1 500 x 0.01 2 500 2x 0.02 - 9.73 (*) An insurance company sold one-year term life insurance on a group of 2,300 independent lives as given in Table 9.23. The insurance company reinsures amounts in excess of 100,000 on each life. The reinsurer wishes to charge a premium that is sufficient to guarantee that it will lose money 5% of the time on such groups. Obtain the appropriate premium by each of the following ways:
- Using a normal approximation to the aggregate claims distribution.
- Using a lognormal approximation.
- Using a gamma approximation.
- Using the compound Poisson approximation that matches the means.
Table 9.23 The data for Exercise 9.73.
Class Benefit amount Probability of death Number of policies 1 100,000 0.10 500 2 200,000 0.02 500 3 300,000 0.02 500 4 200,000 0.10 300 5 200,000 0.10 500 - 9.74 A group insurance contract covers 1,000 employees. An employee can have at most one claim per year. For 500 employees, there is a 0.02 probability of a claim, and when there is a claim, the amount has an exponential distribution with mean 500. For 250 other employees, there is a 0.03 probability of a claim and amounts are exponential with mean 750. For the remaining 250 employees, the probability is 0.04 and the mean is 1,000. Determine the exact mean and variance of total claims payments. Next, construct a compound Poisson model with the same mean and determine the variance of this model.