8
Frequency and Severity with Coverage Modifications
8.1 Introduction
We have seen a variety of examples that involve functions of random variables. In this chapter, we relate those functions to insurance applications. Throughout this chapter, we assume that all random variables have support on all or a subset of the nonnegative real numbers. At times in this chapter and later in the text, we need to distinguish between a random variable that measures the payment per loss (so zero is a possibility, taking place when there is a loss without a payment) and a variable that measures the payment per payment (the random variable is not defined when there is no payment). For notation, a per-loss variable is denoted ![]() and a per-payment variable is denoted
and a per-payment variable is denoted ![]() . When the distinction is not material (e.g. setting a maximum payment does not create a difference), the superscript is omitted.
. When the distinction is not material (e.g. setting a maximum payment does not create a difference), the superscript is omitted.
8.2 Deductibles
Insurance policies are often sold with a per-loss deductible of d. When the loss, x, is at or below d, the insurance pays nothing. When the loss is above d, the insurance pays ![]() . In the language of Chapter 3, such a deductible can be defined as follows.
. In the language of Chapter 3, such a deductible can be defined as follows.
This concept has already been introduced along with formulas for determining its moments. The per-payment variable is

while the per-loss variable is

Note that the per-payment variable ![]() . That is, the per-payment variable is the per-loss variable conditioned on the loss being positive. For the excess loss/per-payment variable, the density function is
. That is, the per-payment variable is the per-loss variable conditioned on the loss being positive. For the excess loss/per-payment variable, the density function is
noting that for a discrete distribution, the density function need only be replaced by the probability function. Other key functions are

Note that as a per-payment variable, the excess loss variable places no probability at zero.
The left censored and shifted variable has discrete probability at zero of ![]() , representing the probability that a payment of zero is made because the loss did not exceed d. Above zero, the density function is
, representing the probability that a payment of zero is made because the loss did not exceed d. Above zero, the density function is
while the other key functions are1 (for ![]() )
)
It is important to recognize that when counting claims on a per-payment basis, changing the deductible will change the frequency with which payments are made (while the frequency of losses will be unchanged). The nature of these changes is discussed in Section 8.6.
![]()
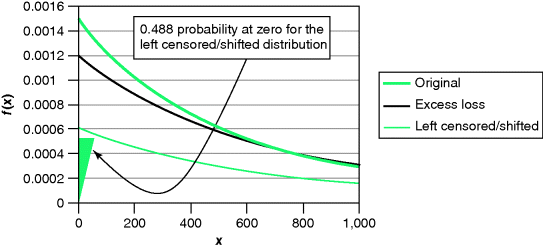
Figure 8.1 The densities for Example 8.1.
An alternative to the ordinary deductible is the franchise deductible. This deductible differs from the ordinary deductible in that, when the loss exceeds the deductible, the loss is paid in full. One example is in disability insurance where, for example, if a disability lasts seven or fewer days, no benefits are paid. However, if the disability lasts more than seven days, daily benefits are paid retroactively to the onset of the disability.
The terms left censored and shifted and excess loss are not used here. Because this modification is unique to insurance applications, we use per-payment and per-loss terminology. The per-loss variable is

while the per-payment variable is

Note that, as usual, the per-payment variable is a conditional random variable. The related functions are now

for the per-loss variable and

for the per-payment variable.
![]()
Expected costs for the two types of deductible may also be calculated.
![]()
![]()
8.2.1 Exercises
- 8.1 Perform the calculations in Example 8.1 for the following distribution, using an ordinary deductible of 5,000:

- 8.2 Repeat Exercise 8.1 for a franchise deductible.
- 8.3 Repeat Example 8.3 for the model in Exercise 8.1 and a 5,000 deductible.
- 8.4 (*) Risk 1 has a Pareto distribution with parameters
 and
and  . Risk 2 has a Pareto distribution with parameters
. Risk 2 has a Pareto distribution with parameters 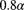 and
and  . Each risk is covered by a separate policy, each with an ordinary deductible of k. Determine the expected cost per loss for risk 1. Determine the limit as k goes to infinity of the ratio of the expected cost per loss for risk 2 to the expected cost per loss for risk 1.
. Each risk is covered by a separate policy, each with an ordinary deductible of k. Determine the expected cost per loss for risk 1. Determine the limit as k goes to infinity of the ratio of the expected cost per loss for risk 2 to the expected cost per loss for risk 1. - 8.5 (*) Losses (prior to any deductibles being applied) have a distribution as reflected in Table 8.1. There is a per-loss ordinary deductible of 10,000. The deductible is then raised so that half the number of losses exceed the new deductible as exceeded the old deductible. Determine the percentage change in the expected cost per payment when the deductible is raised.
Table 8.1 The data for Exercise 8.5.
| x | ||
| 10,000 | 0.60 | 6,000 |
| 15,000 | 0.70 | 7,700 |
| 22,500 | 0.80 | 9,500 |
| 32,500 | 0.90 | 11,000 |
| 1.00 | 20,000 |
8.3 The Loss Elimination Ratio and the Effect of Inflation for Ordinary Deductibles
A ratio that can be meaningful in evaluating the effect of a deductible is the loss elimination ratio (LER).
While many types of coverage modifications can decrease the expected payment, the term loss elimination ratio is reserved for the effect of changing the deductible. Without the deductible, the expected payment is ![]() . With the deductible, the expected payment (from Theorem 8.3) is
. With the deductible, the expected payment (from Theorem 8.3) is ![]() . Therefore, the loss elimination ratio is
. Therefore, the loss elimination ratio is
provided that ![]() exists.
exists.
![]()
Inflation increases costs, but it turns out that when there is a deductible, the effect of inflation is magnified. First, some events that formerly produced losses below the deductible will now lead to payments. Second, the relative effect of inflation is magnified because the deductible is subtracted after inflation. For example, suppose that an event formerly produced a loss of 600. With a 500 deductible, the payment is 100. Inflation at 10% will increase the loss to 660 and the payment to 160, a 60% increase in the cost to the insurer.
![]()
![]()
8.3.1 Exercises
- 8.6 Determine the loss elimination ratio for the distribution given here, with an ordinary deductible of 5,000. This is the same model as used in Exercise 8.1.
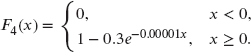
- 8.7 Determine the effect of inflation at 10% on an ordinary deductible of 5,000 applied to the distribution in Exercise 8.6.
- 8.8 (*) Losses have a lognormal distribution with
 and
and  . There is a deductible of 2,000, and 10 losses are expected each year. Determine the loss elimination ratio. If there is uniform inflation of 20% but the deductible remains at 2,000, how many payments will be expected?
. There is a deductible of 2,000, and 10 losses are expected each year. Determine the loss elimination ratio. If there is uniform inflation of 20% but the deductible remains at 2,000, how many payments will be expected? - 8.9 (*) Losses have a Pareto distribution with
 and
and  . There is an ordinary deductible of 2k. Determine the loss elimination ratio before and after 100% inflation.
. There is an ordinary deductible of 2k. Determine the loss elimination ratio before and after 100% inflation. - 8.10 (*) Losses have an exponential distribution with a mean of 1,000. There is a deductible of 500. Determine the amount by which the deductible would have to be raised to double the loss elimination ratio.
- 8.11 (*) The values in Table 8.2 are available for a random variable X. There is a deductible of 15,000 per loss and no policy limit. Determine the expected cost per payment using X and then assuming 50% inflation (with the deductible remaining at 15,000).
- 8.12 (*) Losses have a lognormal distribution with
 and
and  . Determine the ratio of the loss elimination ratio at 10,000 to the loss elimination ratio at 1,000. Then determine the percentage increase in the number of losses that exceed 1,000 if all losses are increased by 10%.
. Determine the ratio of the loss elimination ratio at 10,000 to the loss elimination ratio at 1,000. Then determine the percentage increase in the number of losses that exceed 1,000 if all losses are increased by 10%. - 8.13 (*) Losses have a mean of 2,000. With a deductible of 1,000, the loss elimination ratio is 0.3. The probability of a loss being greater than 1,000 is 0.4. Determine the average size of a loss, given that it is less than or equal to 1,000.
Table 8.2 The data for Exercise 8.11.
| x | ||
| 10,000 | 0.60 | 6,000 |
| 15,000 | 0.70 | 7,700 |
| 22,500 | 0.80 | 9,500 |
| 1.00 | 20,000 |
8.4 Policy Limits
The opposite of a deductible is a policy limit. The typical policy limit arises in a contract where for losses below u the insurance pays the full loss but for losses above u the insurance pays only u. The effect of the limit is to produce a right censored random variable. It will have a mixed distribution with distribution and density function given by (where Y is the random variable after the limit has been imposed)

and

The effect of inflation can be calculated as follows.
![]()
For policy limits, the concepts of per payment and per loss are not relevant. All losses that produced payments prior to imposing the limit will produce payments after the limit is imposed.
![]()

Figure 8.2 The density function for Example 8.6.
A policy limit and an ordinary deductible go together in the sense that, whichever applies to the insurance company's payments, the other applies to the policyholder's payments. For example, when the policy has a deductible of 500, the cost per loss to the policyholder is a random variable that is right censored at 500. When the policy has a limit of 3,000, the policyholder's payments are a variable that is left truncated and shifted (as in an ordinary deductible). The opposite of the franchise deductible is a coverage that right truncates any losses (see Exercise 3.12). This coverage is rarely, if ever, sold. (Would you buy a policy that pays you nothing if your loss exceeds u?)
8.4.1 Exercises
- 8.14 Determine the effect of 10% inflation on a policy limit of 150,000 on the following distribution. This is the same distribution as used in Exercises 8.1 and 8.6.

- 8.15 (*) Let X have a Pareto distribution with
 and
and  . Determine the range of the mean excess loss function
. Determine the range of the mean excess loss function  as d ranges over all positive numbers. Then, let
as d ranges over all positive numbers. Then, let 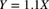 . Determine the range of the ratio
. Determine the range of the ratio  as d ranges over all positive numbers. Finally, let Z be X right censored at 500 (i.e. a limit of 500 is applied to X). Determine the range of
as d ranges over all positive numbers. Finally, let Z be X right censored at 500 (i.e. a limit of 500 is applied to X). Determine the range of  as d ranges over the interval 0 to 500.
as d ranges over the interval 0 to 500.
8.5 Coinsurance, Deductibles, and Limits
The final common coverage modification is coinsurance. In this case, the insurance company pays a proportion, ![]() , of the loss and the policyholder pays the remaining fraction. If coinsurance is the only modification, this changes the loss variable X to the payment variable,
, of the loss and the policyholder pays the remaining fraction. If coinsurance is the only modification, this changes the loss variable X to the payment variable, ![]() . The effect of multiplication has already been covered. When all four items covered in this chapter are present (ordinary deductible, limit, coinsurance, and inflation), we create the following per-loss random variable:
. The effect of multiplication has already been covered. When all four items covered in this chapter are present (ordinary deductible, limit, coinsurance, and inflation), we create the following per-loss random variable:

For this definition, the quantities are applied in a particular order. In particular, the coinsurance is applied last. For the illustrated contract, the policy limit is ![]() , the maximum amount payable. In this definition, u is the loss above which no additional benefits are paid and is called the maximum covered loss. For the per-payment variable,
, the maximum amount payable. In this definition, u is the loss above which no additional benefits are paid and is called the maximum covered loss. For the per-payment variable, ![]() is undefined for
is undefined for ![]() .
.
Previous results can be combined to produce the following theorem, presented without proof.
Higher moments are more difficult. Theorem 8.8 gives the formula for the second moment. The variance can then be obtained by subtracting the square of the mean.
![]()
![]()
8.5.1 Exercises
- 8.16 (*) You are given that
 ,
,  ,
,  , and
, and  is the excess loss variable for
is the excess loss variable for 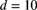 . Determine the variance of
. Determine the variance of  .
. - 8.17 (*) The loss ratio
 is defined as total losses
is defined as total losses  divided by earned premiums
divided by earned premiums  . An agent will receive a bonus
. An agent will receive a bonus  if the loss ratio on his business is less than 0.7. The bonus is given as
if the loss ratio on his business is less than 0.7. The bonus is given as 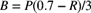 if this quantity is positive; otherwise, it is zero. Let
if this quantity is positive; otherwise, it is zero. Let  and L have a Pareto distribution with parameters
and L have a Pareto distribution with parameters  and
and  . Determine the expected value of the bonus.
. Determine the expected value of the bonus. - 8.18 (*) Losses this year have a distribution such that
 for
for  . Next year, losses will be uniformly higher by 10%. An insurance policy reimburses 100% of losses subject to a deductible of 11 up to a maximum reimbursement of 11. Determine the ratio of next year's reimbursements to this year's reimbursements.
. Next year, losses will be uniformly higher by 10%. An insurance policy reimburses 100% of losses subject to a deductible of 11 up to a maximum reimbursement of 11. Determine the ratio of next year's reimbursements to this year's reimbursements. - 8.19 (*) Losses have an exponential distribution with a mean of 1,000. An insurance company will pay the amount of each claim in excess of a deductible of 100. Determine the variance of the amount paid by the insurance company for one claim, including the possibility that the amount paid is zero.
- 8.20 (*) Total claims for a health plan have a Pareto distribution with
 and
and  . The health plan implements an incentive to physicians that will pay a bonus of 50% of the amount by which total claims are less than 500; otherwise, no bonus is paid. It is anticipated that with the incentive plan the claim distribution will change to become Pareto with
. The health plan implements an incentive to physicians that will pay a bonus of 50% of the amount by which total claims are less than 500; otherwise, no bonus is paid. It is anticipated that with the incentive plan the claim distribution will change to become Pareto with  and
and  . With the new distribution, it turns out that expected claims plus the expected bonus is equal to expected claims prior to the bonus system. Determine the value of K.
. With the new distribution, it turns out that expected claims plus the expected bonus is equal to expected claims prior to the bonus system. Determine the value of K. - 8.21 (*) In year a, total expected losses are 10,000,000. Individual losses in year a have a Pareto distribution with
 and
and 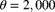 . A reinsurer pays the excess of each individual loss over 3,000. For this, the reinsurer is paid a premium equal to 110% of expected covered losses. In year b, losses will experience 5% inflation over year a, but the frequency of losses will not change. Determine the ratio of the premium in year b to the premium in year a.
. A reinsurer pays the excess of each individual loss over 3,000. For this, the reinsurer is paid a premium equal to 110% of expected covered losses. In year b, losses will experience 5% inflation over year a, but the frequency of losses will not change. Determine the ratio of the premium in year b to the premium in year a. - 8.22 (*) Losses have a uniform distribution from 0 to 50,000. There is a per-loss deductible of 5,000 and a policy limit of 20,000 (meaning that the maximum covered loss is 25,000). Determine the expected payment given that a payment has been made.
- 8.23 (*) Losses have a lognormal distribution with
 and
and  . For losses below 50,000, no payment is made. For losses between 50,000 and 100,000, the full amount of the loss is paid. For losses in excess of 100,000, the limit of 100,000 is paid. Determine the expected cost per loss.
. For losses below 50,000, no payment is made. For losses between 50,000 and 100,000, the full amount of the loss is paid. For losses in excess of 100,000, the limit of 100,000 is paid. Determine the expected cost per loss. - 8.24 (*) The loss severity random variable X has an exponential distribution with mean 10,000. Determine the coefficient of variation of the variables
 and
and  based on
based on  .
. - 8.25 (*) The claim size distribution is uniform over the intervals (0,50), (50,100), (100,200), and (200,400). Of the total probability, 30% is in the first interval, 36% in the second interval, 18% in the third interval, and 16% in the fourth interval. Determine
 .
. - 8.26 (*) Losses follow a two-parameter Pareto distribution with
 and
and  . An insurance policy pays the following for each loss. There is no insurance payment for the first 1,000. For losses between 1,000 and 6,000, the insurance pays 80%. Losses above 6,000 are paid by the insured until the insured has made a total payment of 10,000. For any remaining part of the loss, the insurance pays 90%. Determine the expected insurance payment per loss.
. An insurance policy pays the following for each loss. There is no insurance payment for the first 1,000. For losses between 1,000 and 6,000, the insurance pays 80%. Losses above 6,000 are paid by the insured until the insured has made a total payment of 10,000. For any remaining part of the loss, the insurance pays 90%. Determine the expected insurance payment per loss. - 8.27 (*) The amount of a loss has a Poisson distribution with mean
 . Consider two insurance contracts. One has an ordinary deductible of 2. The second one has no deductible and a coinsurance in which the insurance company pays
. Consider two insurance contracts. One has an ordinary deductible of 2. The second one has no deductible and a coinsurance in which the insurance company pays  of the loss. Determine the value of
of the loss. Determine the value of  so that the expected cost of the two contracts is the same.
so that the expected cost of the two contracts is the same. - 8.28 (*) The amount of a loss has cdf
 ,
,  . An insurance policy pays 80% of the amount of a loss in excess of an ordinary deductible of 20. The maximum payment is 60 per loss. Determine the expected payment, given that a payment has been made.
. An insurance policy pays 80% of the amount of a loss in excess of an ordinary deductible of 20. The maximum payment is 60 per loss. Determine the expected payment, given that a payment has been made.
8.6 The Impact of Deductibles on Claim Frequency
An important component in analyzing the effect of policy modifications pertains to the change in the frequency distribution of payments when the deductible (ordinary or franchise) is imposed or changed. When a deductible is imposed or increased, there will be fewer payments per period, while if a deductible is lowered, there will be more payments.
We can quantify this process if it can be assumed that the imposition of coverage modifications does not affect the process that produces losses or the type of individual who will purchase insurance. For example, those who buy a 250 deductible on an automobile property damage coverage may (correctly) view themselves as less likely to be involved in an accident than those who buy full coverage. Similarly, an employer may find that the rate of permanent disability declines when reduced benefits are provided to employees in the first few years of employment.
To begin, suppose that ![]() , the severity, represents the ground-up loss on the jth such loss and there are no coverage modifications. Let
, the severity, represents the ground-up loss on the jth such loss and there are no coverage modifications. Let ![]() denote the number of losses. Now consider a coverage modification such that v is the probability that a loss will result in a payment. For example, if there is a deductible of d,
denote the number of losses. Now consider a coverage modification such that v is the probability that a loss will result in a payment. For example, if there is a deductible of d, ![]() . Next, define the indicator random variable
. Next, define the indicator random variable ![]() by
by ![]() if the jth loss results in a payment and
if the jth loss results in a payment and ![]() otherwise. Then,
otherwise. Then, ![]() has a Bernoulli distribution with parameter v and the pgf of
has a Bernoulli distribution with parameter v and the pgf of ![]() is
is ![]() . Then,
. Then, ![]() represents the number of payments. If
represents the number of payments. If ![]() are mutually independent and are also independent of
are mutually independent and are also independent of ![]() , then
, then ![]() has a compound distribution with
has a compound distribution with ![]() as the primary distribution and a Bernoulli secondary distribution. Thus
as the primary distribution and a Bernoulli secondary distribution. Thus
In the important special case where the distribution of ![]() depends on a parameter
depends on a parameter ![]() such that
such that
where ![]() is functionally independent of
is functionally independent of ![]() (as in Theorem 7.4), then
(as in Theorem 7.4), then

This result implies that ![]() and
and ![]() are both from the same parametric family and only the parameter
are both from the same parametric family and only the parameter ![]() need be changed.
need be changed.
![]()
This result may be generalized for zero-modified and zero-truncated distributions. Suppose that ![]() depends on parameters
depends on parameters ![]() and
and ![]() such that
such that
Note that ![]() and so is the modified probability at zero. It is also the case that, if
and so is the modified probability at zero. It is also the case that, if ![]() is itself a pgf, then the pgf given in (8.3) is that for the corresponding zero-modified distribution. However, it is not necessary for
is itself a pgf, then the pgf given in (8.3) is that for the corresponding zero-modified distribution. However, it is not necessary for ![]() to be a pgf in order for
to be a pgf in order for ![]() as given in (8.3) to be a pgf. In particular,
as given in (8.3) to be a pgf. In particular, ![]() yields the ZM logarithmic distribution, even though there is no distribution with
yields the ZM logarithmic distribution, even though there is no distribution with ![]() as its pgf. Similarly,
as its pgf. Similarly, ![]() for
for ![]() yields the ETNB distribution. A few algebraic steps reveal (see Exercise 8.35) that for (8.3)
yields the ETNB distribution. A few algebraic steps reveal (see Exercise 8.35) that for (8.3)
where ![]() . It is expected that the imposition of a deductible will increase the value of
. It is expected that the imposition of a deductible will increase the value of ![]() because periods with no payments will become more likely. In particular, if
because periods with no payments will become more likely. In particular, if ![]() is zero truncated,
is zero truncated, ![]() will be zero modified.
will be zero modified.
![]()
In applications, it may be the case that we want to determine the distribution of ![]() from that of
from that of ![]() . For example, data may have been collected on the number of payments in the presence of a deductible and from that data the parameters of
. For example, data may have been collected on the number of payments in the presence of a deductible and from that data the parameters of ![]() can be estimated. We may then want to know the distribution of payments if the deductible is removed. Arguing as before,
can be estimated. We may then want to know the distribution of payments if the deductible is removed. Arguing as before,
This result implies that the formulas derived previously hold with v replaced by ![]() . However, it is possible that the resulting pgf for
. However, it is possible that the resulting pgf for ![]() is not valid. In this case, one of the modeling assumptions is invalid (e.g. the assumption that changing the deductible does not change claim-related behavior). It is instructive to note that the resulting pgf for
is not valid. In this case, one of the modeling assumptions is invalid (e.g. the assumption that changing the deductible does not change claim-related behavior). It is instructive to note that the resulting pgf for ![]() is guaranteed to be a valid pgf [regardless of the value of
is guaranteed to be a valid pgf [regardless of the value of ![]() ] if and only if the pgf for
] if and only if the pgf for ![]() is of mixed Poisson form (for a proof of this fact, see Grandell [47, pp. 25–26]). This provides yet another strong motivation for the use of mixed Poisson models for insurance claim counts. The following two examples illustrate this point.
is of mixed Poisson form (for a proof of this fact, see Grandell [47, pp. 25–26]). This provides yet another strong motivation for the use of mixed Poisson models for insurance claim counts. The following two examples illustrate this point.
![]()
All members of the ![]() and
and ![]() classes meet the conditions of this section. Table 8.3 indicates how the parameters change when moving from
classes meet the conditions of this section. Table 8.3 indicates how the parameters change when moving from ![]() to
to ![]() . If
. If ![]() has a compound distribution, then we can write
has a compound distribution, then we can write ![]() and therefore
and therefore
Thus ![]() will also have a compound distribution with the secondary distribution modified as indicated. If the secondary distribution has an
will also have a compound distribution with the secondary distribution modified as indicated. If the secondary distribution has an ![]() distribution, then it can modified as in Table 8.3. The following example indicates the adjustment to be made if the secondary distribution has an
distribution, then it can modified as in Table 8.3. The following example indicates the adjustment to be made if the secondary distribution has an ![]() distribution.
distribution.
Table 8.3 Frequency adjustments.
| Parameters for |
|
| Poisson | |
| ZM Poisson | |
| Binomial | |
| ZM binomial | |
| ZM binomial | |
| Negative binomial | |
| ZM negative binomial | |
| ZM binomial | |
| ZM logarithmic | |
| ZM binomial |
![]()
The results can be further generalized to an increase or decrease in the deductible. Let ![]() be the frequency when the deductible is d and let
be the frequency when the deductible is d and let ![]() be the frequency when the deductible is
be the frequency when the deductible is ![]() . Let
. Let ![]() , and then Table 8.3 can be used to move from the parameters of
, and then Table 8.3 can be used to move from the parameters of ![]() to the parameters of
to the parameters of ![]() . As long as
. As long as ![]() , we will have
, we will have ![]() and the formulas will lead to a legitimate distribution for
and the formulas will lead to a legitimate distribution for ![]() . This includes the special case of
. This includes the special case of ![]() that was used at the start of this section. If
that was used at the start of this section. If ![]() , then
, then ![]() and there is no assurance that a legitimate distribution will result. This includes the special case
and there is no assurance that a legitimate distribution will result. This includes the special case ![]() (removal of a deductible) covered earlier.
(removal of a deductible) covered earlier.
It should be noted that policy limits have no effect on the frequency distribution. Imposing, removing, or changing a limit will not change the number of payments made.
Finally, it is important to restate that all the results in this section depend on an assumption that may not hold. The assumption is that changing the deductible (or other coverage modifications) does not change the number of loss-producing incidents or the amount of losses.
8.6.1 Exercises
- 8.29 A group life insurance policy has an accidental death rider. For ordinary deaths, the benefit is 10,000; however, for accidental deaths, the benefit is 20,000. The insureds are approximately the same age, so it is reasonable to assume that they all have the same claim probabilities. Let them be 0.97 for no claim, 0.01 for an ordinary death claim, and 0.02 for an accidental death claim. A reinsurer has been asked to bid on providing an excess reinsurance that will pay 10,000 for each accidental death.
- The claim process can be modeled with a frequency component that has the Bernoulli distribution (the event is claim/no claim) and a two-point severity component (the probabilities are associated with the two claim levels, given that a claim occurred). Specify the probability distributions for the frequency and severity random variables.
- Suppose that the reinsurer wants to retain the same frequency distribution. Determine the modified severity distribution that will reflect the reinsurer's payments.
- Determine the reinsurer's frequency and severity distributions when the severity distribution is to be conditional on a reinsurance payment being made.
- 8.30 Individual losses have a Pareto distribution with
 and
and  . With a deductible of 500, the frequency distribution for the number of payments is Poisson–inverse Gaussian with
. With a deductible of 500, the frequency distribution for the number of payments is Poisson–inverse Gaussian with  and
and  . If the deductible is raised to 1,000, determine the distribution for the number of payments. Also, determine the pdf of the severity distribution (per payment) when the new deductible is in place.
. If the deductible is raised to 1,000, determine the distribution for the number of payments. Also, determine the pdf of the severity distribution (per payment) when the new deductible is in place. - 8.31 Losses have a Pareto distribution with
 and
and  . The frequency distribution for a deductible of 500 is zero-truncated logarithmic with
. The frequency distribution for a deductible of 500 is zero-truncated logarithmic with  . Determine a model for the number of payments when the deductible is reduced to 0.
. Determine a model for the number of payments when the deductible is reduced to 0. - 8.32 Suppose that the number of losses
 has the Sibuya distribution (see Exercise 6.7 ) with pgf
has the Sibuya distribution (see Exercise 6.7 ) with pgf  , where
, where  . Demonstrate that the number of payments has a zero-modified Sibuya distribution.
. Demonstrate that the number of payments has a zero-modified Sibuya distribution. - 8.33 (*) The frequency distribution for the number of losses when there is no deductible is negative binomial with
 and
and  . Loss amounts have a Weibull distribution with
. Loss amounts have a Weibull distribution with  and
and  . Determine the expected number of payments when a deductible of 200 is applied.
. Determine the expected number of payments when a deductible of 200 is applied. - 8.34 Consider the situation in Exercise 8.28. Suppose that with the deductible in place, the number of payments has a Poisson distribution with
 . Determine the expected number of payments if the deductible is removed.
. Determine the expected number of payments if the deductible is removed. - 8.35 Suppose that the number of losses has pgf

where
 is a function and
is a function and  . Also, suppose that the probability that a loss leads to a payment is v.
. Also, suppose that the probability that a loss leads to a payment is v.- Show that the number of payments has pgf

where

- Assume that
 and
and 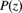 is the pgf of a zero-truncated distribution. Using (a), explain why
is the pgf of a zero-truncated distribution. Using (a), explain why  is the pgf of a zero-modified distribution. Then, further assume that
is the pgf of a zero-modified distribution. Then, further assume that  is the pgf of a zero-truncated member of the
is the pgf of a zero-truncated member of the  class. Explain why
class. Explain why  is the pgf of a member of the
is the pgf of a member of the  class.
class. - Show that if
 and
and  , then
, then  is the logarithmic series pgf.
is the logarithmic series pgf.
- Show that the number of payments has pgf
