19
Simulation
19.1 Basics of Simulation
Simulation has had an on-again, off-again history in actuarial practice. For example, in the 1970s, aggregate loss calculations were commonly done by simulation, because the analytic methods available at the time were not adequate. However, the typical simulation often took a full day on the company's mainframe computer, a serious drag on resources. In the 1980s, analytic methods such as the recursive formula discussed in Chapter 9 and others were developed and found to be significantly faster and more accurate. Today, desktop computers have sufficient power to run complex simulations that allow for the analysis of models not amenable to analytic approaches.
In a similar vein, as investment vehicles become more complex, insurance contracts may include interest-sensitive components and financial guarantees related to stock market performance. These products must be analyzed on a stochastic basis. To accommodate these and other complexities, simulation has become the technique of choice.
In this chapter, we provide some illustrations of how simulation can be used to address some complex modeling problems in insurance, or as an alternative to other methods. It is not our intention to cover the subject in great detail but, rather, to give you an idea of how simulation can help. Study of simulation texts such as Ripley [105] and Ross [108] provides many important additional insights. In addition, simulation can also be an aid in evaluating some of the statistical techniques covered in earlier chapters. This use of simulation will be covered here, with an emphasis on the bootstrap method.
19.1.1 The Simulation Approach
The beauty of simulation is that once a model is created, little additional creative thought is required.1 When the goal is to determine values relating to the distribution of a random variable S, the entire process can be summarized in the following four steps:
- Build a model for S that depends on random variables
 , where their distributions and any dependencies are known.
, where their distributions and any dependencies are known. - For
 generate pseudorandom values
generate pseudorandom values  and then compute
and then compute 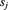 using the model from step 1.
using the model from step 1. - The cdf of S may be approximated by
 , the empirical cdf based on the pseudorandom sample
, the empirical cdf based on the pseudorandom sample  .
. - Compute quantities of interest, such as the mean, variance, percentiles, or probabilities, using the empirical cdf.
Two questions remain. One is postponed until Section 19.3. The other one is: What does it mean to generate a pseudorandom variable? Consider a random variable X with cdf ![]() . This is the real random variable produced by some phenomenon of interest. For example, it may be the result of the experiment “collect one automobile bodily injury medical payment at random and record its value.” We assume that the cdf is known. For example, it may be the Pareto cdf,
. This is the real random variable produced by some phenomenon of interest. For example, it may be the result of the experiment “collect one automobile bodily injury medical payment at random and record its value.” We assume that the cdf is known. For example, it may be the Pareto cdf,

Now consider a second random variable, ![]() , resulting from some other process but with the same Pareto distribution. A random sample from
, resulting from some other process but with the same Pareto distribution. A random sample from ![]() , say
, say ![]() , is impossible to distinguish from one taken from X. That is, given the n numbers, we could not tell if they arose from automobile claims or something else. Thus, instead of learning about X by observing automobile claims, we could learn about it by observing
, is impossible to distinguish from one taken from X. That is, given the n numbers, we could not tell if they arose from automobile claims or something else. Thus, instead of learning about X by observing automobile claims, we could learn about it by observing ![]() . Obtaining a random sample from a Pareto distribution is still probably difficult, so we have not yet accomplished much.
. Obtaining a random sample from a Pareto distribution is still probably difficult, so we have not yet accomplished much.
We can make some progress by making a concession. Let us accept as a replacement for a random sample from ![]() a sequence of numbers
a sequence of numbers ![]() , which is not a random sample at all, but simply a sequence of numbers that may not be independent, or even random, but was generated by some known process that is related to the random variable
, which is not a random sample at all, but simply a sequence of numbers that may not be independent, or even random, but was generated by some known process that is related to the random variable ![]() . Such a sequence is called a pseudorandom sequence because anyone who did not know how the sequence was created could not distinguish it from a random sample from
. Such a sequence is called a pseudorandom sequence because anyone who did not know how the sequence was created could not distinguish it from a random sample from ![]() (and, therefore, from X). Such a sequence is satisfactory for our purposes.
(and, therefore, from X). Such a sequence is satisfactory for our purposes.
The field of developing processes for generating pseudorandom sequences of numbers has been well developed. One fact that makes it easier to provide such sequences is that it is sufficient to be able to generate them for the uniform distribution on the interval (0,1). That is because, if U has the uniform(0,1) distribution, then ![]() when the inverse exists will have
when the inverse exists will have ![]() as its cdf. Therefore, we simply obtain uniform pseudorandom numbers
as its cdf. Therefore, we simply obtain uniform pseudorandom numbers ![]() and then let
and then let ![]() . This is called the inversion method of generating random variates. Specific methods for particular distributions have been developed and some will be discussed here. There is a considerable literature on the best ways to generate pseudorandom uniform numbers and a variety of tests have been proposed to evaluate them. Make sure the method you use is a good one.
. This is called the inversion method of generating random variates. Specific methods for particular distributions have been developed and some will be discussed here. There is a considerable literature on the best ways to generate pseudorandom uniform numbers and a variety of tests have been proposed to evaluate them. Make sure the method you use is a good one.
![]()
Table 19.1 The chi-square test of simulated Pareto observations.
| Interval | Observed | Expected | Chi-square |
| 0–100 | 2,519 | 2,486.85 | 0.42 |
| 100–250 | 2,348 | 2,393.15 | 0.85 |
| 250–500 | 2,196 | 2,157.04 | 0.70 |
| 500–750 | 1,071 | 1,097.07 | 0.62 |
| 750–1,000 | 635 | 615.89 | 0.59 |
| 1,000–1,500 | 589 | 610.00 | 0.72 |
| 1,500–2,500 | 409 | 406.76 | 0.01 |
| 2,500–5,000 | 192 | 186.94 | 0.14 |
| 5,000–10,000 | 36 | 38.78 | 0.20 |
| 10,000– | 5 | 7.51 | 0.84 |
| Total | 10,000 | 10,000 | 5.10 |
When the distribution function of X is continuous and strictly increasing, the equation ![]() will have a unique value of x for any given value of u and a unique value of u for any given x. In that case, the inversion method reduces to solving the equation for x. In other cases, some care must be taken. Suppose that
will have a unique value of x for any given value of u and a unique value of u for any given x. In that case, the inversion method reduces to solving the equation for x. In other cases, some care must be taken. Suppose that ![]() has a jump at
has a jump at ![]() so that
so that ![]() and
and ![]() . If the uniform number is such that
. If the uniform number is such that ![]() , the equation has no solution. In that situation, choose c as the simulated value.
, the equation has no solution. In that situation, choose c as the simulated value.
![]()

Figure 19.1 The inversion of the distribution function for Example 19.2.
It is also possible for the distribution function to be constant over some interval. In that case, the equation ![]() will have multiple solutions for x if u corresponds to the constant value of
will have multiple solutions for x if u corresponds to the constant value of ![]() over that interval. Our convention (to be justified shortly) is to choose the largest possible value in the interval.
over that interval. Our convention (to be justified shortly) is to choose the largest possible value in the interval.
![]()
Discrete distributions have both features. The distribution function has jumps at the possible values of the variable and is constant in between.
![]()
Many random number generators can produce a value of 0 but not a value of 1 (though some produce neither one). This is the motivation for choosing the largest value in an interval where the cdf is constant.
The second question is: What value of n should be used? This will be answered after some special simulation cases are discussed.
19.1.2 Exercises
- 19.1 Use the inversion method to simulate three values from the Poisson(3) distribution. Use 0.1247, 0.9321, and 0.6873 for the uniform random numbers.
- 19.2 Use the uniform random numbers 0.2, 0.5, and 0.7 to simulate values from

19.2 Simulation for Specific Distributions
In this section, we will look at a few special cases where either the inversion method may not be the best (or easiest) choice or the situation warrants some additional thoughts.
19.2.1 Discrete Mixtures
Recall from Section 4.2.3 that the distribution function for a discrete mixture can be written as
It may be difficult to invert this function, but it may be easy to invert the individual cdfs. This suggests a two-step process for simulating from a mixture distribution.
- Simulate a value from the discrete random variable J, where
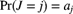 .
. - Use an appropriate method (usually inversion) to simulate an observation from a random variable with distribution function
 .
.
![]()
19.2.2 Time or Age of Death from a Life Table
When following the progress of a portfolio of life insurance or annuity policies, it is necessary to simulate the time or age of death or other decrements. Two approaches will be discussed here.
First, suppose that the portfolio of policies is to be followed from period to period. This may be necessary because other random factors, such as investment earning, may need to be updated as well. If we are looking at a single policy, then there is a probability for each decrement that applies. For example, a policy that is a certain age and duration may have, in the next period, a death probability of 0.01, a lapse probability of 0.09, a disability probability of 0.03, and a probability of continuing as a healthy policyholder of 0.87. Simulating the outcome is simply obtaining a value from a discrete random variable with four possible outcomes. Now suppose that the portfolio contains 250 policyholders with these probabilities and the individual outcomes are independent. This is a multinomial distribution, but it can be broken down into three steps using a result from this distribution.
![]()
The second case is where all that is needed is the age or time at which an event occurs. In a single-decrement setting, this is a discrete distribution and a single lookup will provide the answer. The multiple-decrement setting is a bit more complicated. However, simulation can be accomplished with a single lookup provided that some care is taken.
![]()
19.2.3 Simulating from the (a, b, 0) Class
Consider Example 19.6, where it was necessary to simulate a value from a binomial distribution with ![]() and
and ![]() . The creation of a table requires 251 rows, one for each possible outcome. While some computer applications make the table lookup process easy, writing code for this situation will require a looping process where each value in the table is checked until the desired answer is reached. In some cases, there may be a more efficient approach based on a stochastic process. Such processes generate a series of events and the time of each event. Counting of the number of outcomes in a fixed time period, such as one year, produces the simulated result. The simulation of the event times may be of use in some situations. However, it should be noted that it is the timing that ensures the modeled distribution, not the reverse. That is, for example, it is possible to have a binomially distributed number of events in a given time period with a different process (from the one used here) generating the random times. While the random variable is being interpreted as the number of events in a fixed time period, no such time period is required for the actual situation being simulated. The theory that supports this method is available in Section 6.6.3 of the third edition of this book [73].
. The creation of a table requires 251 rows, one for each possible outcome. While some computer applications make the table lookup process easy, writing code for this situation will require a looping process where each value in the table is checked until the desired answer is reached. In some cases, there may be a more efficient approach based on a stochastic process. Such processes generate a series of events and the time of each event. Counting of the number of outcomes in a fixed time period, such as one year, produces the simulated result. The simulation of the event times may be of use in some situations. However, it should be noted that it is the timing that ensures the modeled distribution, not the reverse. That is, for example, it is possible to have a binomially distributed number of events in a given time period with a different process (from the one used here) generating the random times. While the random variable is being interpreted as the number of events in a fixed time period, no such time period is required for the actual situation being simulated. The theory that supports this method is available in Section 6.6.3 of the third edition of this book [73].
The process that creates the timing of the events starts by having an exponential distribution for the time of the first event. The time for the second event will also have an exponential distribution, with the mean depending on the number of previous events. To simplify matters, the time period in question will always be of length 1. If the period is other than 1, the times that are simulated can be viewed as the proportion of the relevant period. The process is, in general, noting that the first event carries an index of 0, the second event an index of 1, and so on:
- Simulate the time of the first event as an exponential variable with mean
 . Determine this time as
. Determine this time as  , where
, where  is a pseudouniform random number.
is a pseudouniform random number. - Let
 be the time of the most recently simulated event. Simulate the time to the next event using an exponential variable with mean
be the time of the most recently simulated event. Simulate the time to the next event using an exponential variable with mean  . Determine this time as
. Determine this time as  .
. - The time of the next event is then
 .
. - Repeat steps 2 and 3 until
 .
. - The simulated value is k.
All that remains is to determine the formulas for the exponential means.
19.2.3.1 Poisson
This is the simplest case. To simulate values from a Poisson distribution with mean ![]() , set
, set ![]() for all k.
for all k.
![]()
19.2.3.2 Binomial
As usual, let the binomial parameters be m and q. From them, calculate ![]() and
and ![]() . Then,
. Then, ![]() .
.
![]()
It should be noted that because the binomial distribution cannot produce a value greater than m, if ![]() , then the simulation stops and the simulated value is set equal to m. Note that
, then the simulation stops and the simulated value is set equal to m. Note that ![]() for all binomial distributions, so if the algorithm were to continue, the next simulated time would be at infinity, regardless of the value of
for all binomial distributions, so if the algorithm were to continue, the next simulated time would be at infinity, regardless of the value of ![]() .
.
19.2.3.3 Negative Binomial
The process is the same as for the binomial distribution, but with different formulas for c and d. With parameters r and ![]() , the formulas are
, the formulas are ![]() and
and ![]() .
.
![]()
This procedure provides additional insight for the negative binomial distribution. In Section 6.3, the distribution was derived as a gamma mixture of Poisson distributions. A motivation is that the distribution is the result for a portfolio of drivers, each of which has a Poisson-distributed number of claims, but their Poisson means vary by a gamma distribution. However, there is also some evidence that individual drivers have a negative binomial distribution. In the above simulation, the value of d is always positive. Thus, with each claim the parameter ![]() increases in value. This reduces the expected time to the next claim. Thus, if we believe that drivers who have claims are more likely to have further claims, then the negative binomial distribution may be a reasonable model.2.
increases in value. This reduces the expected time to the next claim. Thus, if we believe that drivers who have claims are more likely to have further claims, then the negative binomial distribution may be a reasonable model.2.
19.2.4 Normal and Lognormal Distributions
It is always sufficient to be able to simulate Z, a standard normal random variable. Then, if ![]() , let
, let ![]() . If X is lognormal with parameters
. If X is lognormal with parameters ![]() and
and ![]() , let
, let ![]() . The inversion method is usually available (for example, the NORM.INV function in Excel®). However, this method is not as good in the tails as it is in the central part of the distribution, being likely to underrepresent more extreme values. A simple alternative is the Box–Muller transformation [16]). The method begins with the generation of two independent pseudouniform random numbers
. The inversion method is usually available (for example, the NORM.INV function in Excel®). However, this method is not as good in the tails as it is in the central part of the distribution, being likely to underrepresent more extreme values. A simple alternative is the Box–Muller transformation [16]). The method begins with the generation of two independent pseudouniform random numbers ![]() and
and ![]() . Then, two independent standard normal values are obtained from
. Then, two independent standard normal values are obtained from ![]() and
and ![]() . An improvement is the polar method, which also begins with two pseudouniform values. The steps are as follows:
. An improvement is the polar method, which also begins with two pseudouniform values. The steps are as follows:
- Calculate
 and
and  .
. - Calculate
 .
. - If
 , repeat steps 1 and 2; else proceed to step 4.
, repeat steps 1 and 2; else proceed to step 4. - Calculate
 .
. - Calculate
 and
and  .
.
The polar method requires more programming work due to the rejection possibility at step 3, but is superior to other methods.
![]()
19.2.5 Exercises
- 19.3 Simulate two observations from a distribution that is a mixture of a Pareto distribution with
 and
and  and an inverse Weibull distribution with
and an inverse Weibull distribution with  and
and  . The weight on the Pareto distribution is 0.4. Use the pairs of uniform random numbers (0.372,0.693) and (0.701,0.284), where the first number is used to determine the distribution to use and the second number is used to simulate an outcome from that distribution.
. The weight on the Pareto distribution is 0.4. Use the pairs of uniform random numbers (0.372,0.693) and (0.701,0.284), where the first number is used to determine the distribution to use and the second number is used to simulate an outcome from that distribution. - 19.4 At any time, a member of a pension plan is in one of three states: employed (e), alive but no longer employed (n), or dead (d). Let
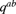 denote the probability that a current or former member of the plan is in state b at the end of a year given that the member was in state a at the beginning of that year. The probabilities are constant over time and independent of age. They are:
denote the probability that a current or former member of the plan is in state b at the end of a year given that the member was in state a at the beginning of that year. The probabilities are constant over time and independent of age. They are:  ,
,  ,
,  ,
,  ,
,  , and
, and  . Any probabilities not listed are zero. At the beginning of a particular year there are 200 members, all of whom are employed. Using the approach from Example 19.6, simulate the number of members in each of the three states two years from now. Use the uniform random numbers 0.123, 0.876, 0.295, 0.623, and 0.426.
. Any probabilities not listed are zero. At the beginning of a particular year there are 200 members, all of whom are employed. Using the approach from Example 19.6, simulate the number of members in each of the three states two years from now. Use the uniform random numbers 0.123, 0.876, 0.295, 0.623, and 0.426. - 19.5 Use the method of this section to simulate one observation from a binomial distribution with
 and
and  . Use the uniform random numbers 0.143, 0.296, 0.003, and 0.192.
. Use the uniform random numbers 0.143, 0.296, 0.003, and 0.192. - 19.6 Simulate two values from a lognormal distribution with
 and
and  . Use the polar method and the uniform random numbers 0.942, 0.108, 0.217, and 0.841.
. Use the polar method and the uniform random numbers 0.942, 0.108, 0.217, and 0.841.
19.3 Determining the Sample Size
A question asked at the beginning of this chapter remains unanswered: How many simulations are needed to achieve a desired level of accuracy? We know that any consistent estimator will be arbitrarily close to the true value with high probability as the sample size is increased. In particular, empirical estimators have this attribute. With a little effort, we should be able to determine the number of simulated values needed to get us as close as we want with a specified probability. Often, the central limit theorem will help, as in the following example.
![]()
The method for working with percentiles is not as satisfying as the other two examples. When the goal is to estimate the mean or a probability, we were able to work directly with a normal approximation and an estimate of the standard deviation of the estimator. A similar approach can be taken with the estimated percentiles. However, the formula for the asymptotic variance is
The problem is that while p is known and ![]() can be replaced by its estimate, the density function of the simulated variable is not known (recall that we are performing simulations because basic quantities such as the pdf and cdf are not available). Thus, it is likely to be difficult to obtain an estimated value of the variance that can, in turn, be used to estimate the required sample size.
can be replaced by its estimate, the density function of the simulated variable is not known (recall that we are performing simulations because basic quantities such as the pdf and cdf are not available). Thus, it is likely to be difficult to obtain an estimated value of the variance that can, in turn, be used to estimate the required sample size.
19.3.1 Exercises
- 19.7 Demonstrate that
 for
for  and
and  as defined in Example 19.12.
as defined in Example 19.12. - 19.8 You are simulating observations from an exponential distribution with
 . How many simulations are needed to be 90% certain of being within 2% of each of the mean and the probability of being below 200? Conduct the required number of simulations and note if the 2% goal has been reached.
. How many simulations are needed to be 90% certain of being within 2% of each of the mean and the probability of being below 200? Conduct the required number of simulations and note if the 2% goal has been reached. - 19.9 Simulate 1,000 observations from a gamma distribution with
 and
and  . Perform the chi-square goodness-of-fit and Kolmogorov–Smirnov tests to see if the simulated values were actually from that distribution.
. Perform the chi-square goodness-of-fit and Kolmogorov–Smirnov tests to see if the simulated values were actually from that distribution. - 19.10 (*) To estimate
 , you have simulated five observations from the random variable X. The values are 1, 2, 3, 4, and 5. Your goal is to have the standard deviation of the estimate of
, you have simulated five observations from the random variable X. The values are 1, 2, 3, 4, and 5. Your goal is to have the standard deviation of the estimate of  be less than 0.05. Estimate the total number of simulations needed.
be less than 0.05. Estimate the total number of simulations needed.
19.4 Examples of Simulation in Actuarial Modeling
19.4.1 Aggregate Loss Calculations
The recursive method for calculating aggregate loss distribution, presented in Chapter 9, has three features. First, the recursive method is exact up to the level of the approximation introduced. The only approximation involves replacing the true severity distribution with an arithmetized approximation. The approximation error can be reduced by increasing the number of points (that is, reducing the span). Second, it assumes that aggregate claims can be written as ![]() with
with ![]() independent and the
independent and the ![]() identically distributed. Third, the recursive method assumes that the frequency distribution is in the
identically distributed. Third, the recursive method assumes that the frequency distribution is in the ![]() or
or ![]() classes.
classes.
There is no need to be concerned about the first feature because the approximation error can be made as small as desired, though at the expense of increased computing time. However, the second restriction may prevent the model from reflecting reality. The third restriction means that if the frequency distribution is not in one of these classes (or can be constructed from them, such as with compound distributions), we will need to find an alternative to the recursive method. Simulation is one such alternative.
In this section, we indicate some common ways in which the independence or identical distribution assumptions may fail to hold and then demonstrate how simulation can be used to obtain numerical values of the distribution of aggregate losses.
When the ![]() are i.i.d., it does not matter how we go about labeling the losses, that is, which loss is called
are i.i.d., it does not matter how we go about labeling the losses, that is, which loss is called ![]() , which one
, which one ![]() , and so on. With the assumption removed, the labels become important. Because S is the aggregate loss for one year, time is a factor. One way of identifying the losses is to let
, and so on. With the assumption removed, the labels become important. Because S is the aggregate loss for one year, time is a factor. One way of identifying the losses is to let ![]() be the first loss,
be the first loss, ![]() be the second loss, and so on. Then let
be the second loss, and so on. Then let ![]() be the random variable that records the time of the jth loss. Without going into much detail about the claims-paying process, we do want to note that
be the random variable that records the time of the jth loss. Without going into much detail about the claims-paying process, we do want to note that ![]() may be the time at which the loss occurred, the time it was reported, or the time payment was made. In the latter two cases, it may be that
may be the time at which the loss occurred, the time it was reported, or the time payment was made. In the latter two cases, it may be that ![]() , which occurs when the report of the loss or the payment of the claim takes place at a time subsequent to the end of the time period of the coverage, usually one year. If the timing of the losses is important, we will need to know the joint distribution of
, which occurs when the report of the loss or the payment of the claim takes place at a time subsequent to the end of the time period of the coverage, usually one year. If the timing of the losses is important, we will need to know the joint distribution of ![]() .
.
19.4.2 Examples of Lack of Independence
There are two common situations in which the assumption of independence does not hold. One is through accounting for time (and, in particular, the time value of money) and the other is through coverage modifications. The latter may have a time factor as well. The following examples provide some illustrations.
![]()
![]()
19.4.3 Simulation Analysis of the Two Examples
We now complete the two examples using the simulation approach. The models have been selected arbitrarily, but we should assume they were determined by a careful estimation process using the techniques presented earlier in this text.
![]()
![]()
19.4.4 The Use of Simulation to Determine Risk Measures
If the distribution of interest is too complex to admit an analytic form, simulation may be used to estimate risk measures such as VaR and TVaR. Because VaR is simply a specific percentile of the distribution, this case has already been discussed. The estimation of TVaR is also fairly straightforward. Suppose that ![]() is an ordered simulated sample from the random variable of interest. If the percentile being used is p, let
is an ordered simulated sample from the random variable of interest. If the percentile being used is p, let ![]() , where [·] indicates the greatest integer function. Then, the two estimators are
, where [·] indicates the greatest integer function. Then, the two estimators are

We know that the variance of a sample mean can be estimated by the sample variance divided by the sample size. While ![]() is a sample mean, this estimator will underestimate the true value. This is because the observations being averaged are dependent and, as a result, there is more variability than is reflected by the sample variance. Let the sample variance be
is a sample mean, this estimator will underestimate the true value. This is because the observations being averaged are dependent and, as a result, there is more variability than is reflected by the sample variance. Let the sample variance be

Manistre and Hancock [85] show that an asymptotically unbiased estimator of the variance of the estimator of TVaR is

![]()
19.4.5 Statistical Analyses
Simulation can help in a variety of ways when analyzing data. Two are discussed here, both of which have to do with evaluating a statistical procedure. The first is the determination of the p-value (or critical value) for a hypothesis test. The second is to evaluate the MSE of an estimator. We begin with the hypothesis testing situation.
![]()
When testing hypotheses, p-values and significance levels are calculated assuming the null hypothesis to be true. In other situations, there is no known population distribution from which to simulate. For such situations, a technique called the bootstrap may help (for thorough coverage of this subject, see Efron and Tibshirani [34]). The key is to use the empirical distribution from the data as the population from which to simulate values. Theoretical arguments show that the bootstrap estimate will converge asymptotically to the true value. This result is reasonable because as the sample size increases, the empirical distribution becomes more and more like the true distribution. The following example shows how the bootstrap works and also indicates that, at least in the case illustrated, it gives a reasonable answer.
![]()
In many situations, determination of the MSE is not so easy, and then the bootstrap becomes an extremely useful tool. While simulation was not needed for the example, note that an original sample size of 3 led to 27 possible bootstrap values. Once the sample size gets beyond 6, it becomes impractical to enumerate all the cases. In that case, simulating observations from the empirical distribution becomes the only feasible choice.
![]()
19.4.6 Exercises
- 19.11 (*) Insurance for a city's snow removal costs covers four winter months. There is a deductible of 10,000 per month. Monthly costs are independent and normally distributed with
 and
and  . Monthly costs are simulated using the inversion method. For one simulation of a year's payments, the four uniform pseudorandom numbers are 0.5398, 0.1151, 0.0013, and 0.7881. Calculate the insurer's cost for this simulated year.
. Monthly costs are simulated using the inversion method. For one simulation of a year's payments, the four uniform pseudorandom numbers are 0.5398, 0.1151, 0.0013, and 0.7881. Calculate the insurer's cost for this simulated year. - 19.12 (*) After one period, the price of a stock is X times its price at the beginning of the period, where X has a lognormal distribution with
 and
and  . The price at time zero is 100. The inversion method is used to simulate price movements. The pseudouniform random numbers are 0.1587 and 0.9332 for periods 1 and 2. Determine the simulated prices at the end of each of the first two periods.
. The price at time zero is 100. The inversion method is used to simulate price movements. The pseudouniform random numbers are 0.1587 and 0.9332 for periods 1 and 2. Determine the simulated prices at the end of each of the first two periods. - 19.13 (*) You have insured 100 people, each age 70. Each person has probability 0.03318 of dying in the next year and the deaths are independent. Therefore, the number of deaths has a binomial distribution with
 and
and  . Use the inversion method to determine the simulated number of deaths in the next year based on
. Use the inversion method to determine the simulated number of deaths in the next year based on  .
. - 19.14 (*) For a surplus process, claims occur according to a Poisson process at the rate of two per year. Thus the time between claims has the exponential distribution with
 . Claims have a Pareto distribution with
. Claims have a Pareto distribution with  and
and  . The initial surplus is 2,000 and premiums are collected at a rate of 2,200. Ruin occurs any time the surplus is negative, at which time no further premiums are collected or claims paid. All simulations are done with the inversion method. For the time between claims, use 0.83, 0.54, 0.48, and 0.14 as the pseudorandom numbers. For claim amounts, use 0.89, 0.36, 0.70, and 0.61. Determine the surplus at time 1.
. The initial surplus is 2,000 and premiums are collected at a rate of 2,200. Ruin occurs any time the surplus is negative, at which time no further premiums are collected or claims paid. All simulations are done with the inversion method. For the time between claims, use 0.83, 0.54, 0.48, and 0.14 as the pseudorandom numbers. For claim amounts, use 0.89, 0.36, 0.70, and 0.61. Determine the surplus at time 1. - 19.15 (*) You are given a random sample of size 2 from some distribution. The values are 1 and 3. You plan to estimate the population variance with the estimator
 . Determine the bootstrap estimate of the MSE of this estimator.
. Determine the bootstrap estimate of the MSE of this estimator. - 19.16 A sample of three items from the uniform(0,10) distribution produced the following values: 2, 4, and 7.
- Calculate the Kolmogorov–Smirnov test statistic for the null hypothesis that the data came from the uniform(0,10) distribution.
- Simulate 10,000 samples of size 3 from the uniform(0,10) distribution and compute the Kolmogorov–Smirnov test statistic for each. The proportion of times the value equals or exceeds your answer to part (a) is an estimate of the p-value.
- 19.17 A sample of three items from the
 distribution produced the following values: 2, 4, and 7. Consider the estimator of
distribution produced the following values: 2, 4, and 7. Consider the estimator of  ,
,

From Example 10.12 the MSE of this unbiased estimator was shown to be
 .
.- Estimate the MSE by replacing
 with its estimate.
with its estimate. - Obtain the bootstrap estimate of the variance of the estimator. (It is not possible to use the bootstrap to estimate the MSE because you cannot obtain the true value of
 from the empirical distribution, but you can obtain the expected value of the estimator.)
from the empirical distribution, but you can obtain the expected value of the estimator.)
- Estimate the MSE by replacing
- 19.18 Losses on an insurance contract have a Pareto distribution with parameters
 and
and  . Expenses to process claims have an exponential distribution with mean 400. The dependence structure is modeled with a Gaussian copula with correlation
. Expenses to process claims have an exponential distribution with mean 400. The dependence structure is modeled with a Gaussian copula with correlation  . Losses have a deductible of 500. When the deductible is not met, there are no processing expenses. Also, when there is a payment in excess of 10,000, a reinsurer pays the excess. In addition, the primary insurer and reinsurer split the processing expenses in proportion to their share of the payments to the insured. Use the uniform random pairs (0.983,0.453) and (0.234,0.529), where the first number simulates the loss and the second the expense, to simulate the results of two loss events. Calculate the total amounts of these losses paid by the insured, the primary insurer, and the reinsurer.
. Losses have a deductible of 500. When the deductible is not met, there are no processing expenses. Also, when there is a payment in excess of 10,000, a reinsurer pays the excess. In addition, the primary insurer and reinsurer split the processing expenses in proportion to their share of the payments to the insured. Use the uniform random pairs (0.983,0.453) and (0.234,0.529), where the first number simulates the loss and the second the expense, to simulate the results of two loss events. Calculate the total amounts of these losses paid by the insured, the primary insurer, and the reinsurer. - 19.19 Repeat Exercise 19.18 using a t copula with
 . Use the same uniform numbers from that exercise to generate the multivariate normal values. Use 0.319 and 0.812 to simulate the scaling factors required for this simulation.
. Use the same uniform numbers from that exercise to generate the multivariate normal values. Use 0.319 and 0.812 to simulate the scaling factors required for this simulation. - 19.20 (*) A dental benefit has a deductible of 100 applied to annual charges. The insured is then reimbursed for 80% of excess charges to a maximum reimbursement of 1,000. Annual charges have an exponential distribution with mean 1,000. Four years' charges are simulated by the inversion method using the uniform random numbers 0.30, 0.92, 0.70, and 0.08. Determine the average annual reimbursement for this simulation.
- 19.21 (*) Paid losses have a lognormal distribution with parameters
 and
and  . The ratio, y, of unpaid losses to paid losses is
. The ratio, y, of unpaid losses to paid losses is  , where
, where 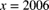 minus the contract purchase year. The inversion method is used, with the uniform random numbers 0.2877, 0.1210, 0.8238, and 0.6179 to simulate paid losses. Estimate the average unpaid losses for purchase year 2005.
minus the contract purchase year. The inversion method is used, with the uniform random numbers 0.2877, 0.1210, 0.8238, and 0.6179 to simulate paid losses. Estimate the average unpaid losses for purchase year 2005. - 19.22 (*) You plan to use simulation to estimate the mean of a nonnegative random variable. The population standard deviation is known to be 20% larger than the population mean. Use the central limit theorem to estimate the smallest number of trials needed so that you will be at least 95% confident that your simulated mean is within 5% of the population mean.
- 19.23 (*) Simulation is used to estimate the value of the cumulative distribution function at 300 of the exponential distribution with mean 100. Determine the minimum number of simulations so that there is at least a 99% probability that the estimate is within 1% of the correct value.
- 19.24 (*) For a policy that covers both fire and wind losses, you are given that a sample of fire losses was 3 and 4 and a sample of wind losses for the same period was 0 and 3. Fire and wind losses are independent and do not have identical distributions. Based on the sample, you estimate that adding a deductible of 2 per wind claim will eliminate 20% of total losses. Determine the bootstrap approximation to the MSE of the estimate.
