4
Information
In the previous chapter, the foundations of probability theory were presented as a way to characterize uncertainty in systems or processes. Despite this fact, we have not provided any direct quantification of uncertainty in relation to the random variables or processes defined by the different probability distributions. This chapter follows Adami's interpretation of Shannon's seminal work [1], summarized in a friendly manner in [2], where the entropy function measures the uncertainty in relation to a given observation protocol and the experiment. Therefrom, the informative value of events – or simply information – can be mathematically defined. After [1], this particular branch of probability theory applied to state the fundamental limits of engineered communications systems emerged as an autonomous research field called Information Theory.
Our objective here is not to review such a theory but rather to provide its very basic concepts that have opened up new research paths from philosophy to biology, from technology to physics [3]. To this end, we will first establish what can be called information in our theoretical construction for cyber‐physical systems, eliminating possible misuses or misinterpretations of the term, and then present a useful typology for information. This chapter is an attempt to move beyond Shannon by explicitly incorporating semantics [3, 4] but still in a generalized way as indicated by [2, 5–7].
4.1 Introduction
Information is a term that may indicate different things in different contexts. As discussed in previous chapters, this might be problematic for scientific theories, where concepts cannot be ambiguous. To clean the path for defining information as our theoretical concept, we will first critically analyze its dictionary definitions, which are presented next.
These different definitions indicate that the term “information” can be used in different domains, from very specific technical ones like 1b, 1c, 1d, or 4 to more general ones like 1a, 2, and 3. Information is then related to some kind of new knowledge or to some specific kind of data in technical fields. In some cases, information can be seen as something that brings novelty in knowledge, whereas in other cases, information is a sort of representation of data or uncertainty. Although some definitions might be more appealing for our purpose, we would like to propose a different one that will allow us to formally establish a concept for information.
With this definition, we are ready to start. Our first task is to differentiate what is data and what is information, as well as their interrelation.
4.2 Data and Information
Data and information are usually considered synonymous, as indicated in Definition 4.1. However, if we follow Definition 4.2, we can deduce that not all data are informative because some data may not be relevant for resolving the uncertainty related to specific processes. For example, the outcome of the lottery is not informative with respect to the weather forecast, but it is informative for the tax office. Information is then composed of data, but not all data are information. To formalize this, we will state the following proposition.
In other words, this proposition indicates that, to potentially be information, data must be interpretable (i.e. follow a syntax and be meaningful). Such meaningful structured data also need to carry a true (correct, trustworthy) reflection of ![]() . If such data decrease the uncertainty about some well‐defined aspect of
. If such data decrease the uncertainty about some well‐defined aspect of ![]() , then the data are information. Information is then a concept that depends on the uncertainty before and after it is acquired.
, then the data are information. Information is then a concept that depends on the uncertainty before and after it is acquired.
The following two examples illustrate these ideas.
As those examples indicate, data and information may appear in different forms, and thus, it is worth using a typology to support their analysis [3]. Data may be either analog or digital. For example, the voice of a person in the room is analog, while the same voice stored as a computer file in an mp3 format is digital. Analog data may be recorded in, for example, vinyl discs. Computer files associated with audio are not recorded in this way; they are actually encoded by state machines via logical bits, i.e. 0s and 1s that can be physically represented by circuits [9]. Bits can then be represented semantically by true or false answers [10], mathematically based on Boolean algebra [11], and physically by circuits. It is then possible to construct machines that can [p. 29][3] (…) recognize bits physically, behave logically on the basis of such recognition and therefore manipulate data in ways which we find meaningful. As we are going to see later, this fact is the basis of the cyber domain of every cyber‐physical system.
Beyond this more fundamental classification, we can list the following types of data (adapted from [4]):
- Primary data: Data that are directly accessible as numbers in spreadsheets, traffic lights, or a binary string; these are the data we usually talk about.
- Secondary data: The absence of data that may be informative (e.g. if a person cannot hear any sound from the office beside his/hers, this silence – lack of data – indicates that no one is there).
- Metadata: Data about other data as, for instance, the location where a photo was taken.
- Operational data: Data related to the operations of a system or process, including its performance (e.g. blinking yellow traffic lights indicate that the signaling system that supports the traffic in that street is not working properly).
- Derivative data: Data that are obtained through other data as indirect sources; for example, the electricity consumption of a household (primary data) also indicates the activity of persons living there (derivative data).
It is easy to see that data can be basically anything, including incorrect or uninterpretable representations and relations. This supports our proposal of differentiating data and information, as stated in Proposition 4.1. In this case, classifying data according to the proposed typology may be helpful in the process of identifying what has the potential to be considered information. Nevertheless, Examples 4.1 and 4.2 indicate how broad these concepts are. The first example can be fully described using probability theory, while the second cannot (although some may argue that it is always possible to build such a model). This is the challenge we should face.
Our approach will be to follow Proposition 4.1, and thus, establish generic relations involving data, information, and uncertainty with respect to well‐defined scenarios. The following proposition states such relations.
These are general statements that are usually presented in a different manner without differentiating data and information. As we will see in the next section, this may be problematic. At this point, we will illustrate this statement with the following example.
As in probability theory, the evaluation of uncertainty about a given aspect of a system or process depends on a few certainties that are considered as givens. The example above demonstrates that an undefined uncertainty about the observation process that is associated with the aspect whose uncertainty we are willing to evaluate makes such an analysis unfeasible. Even in this situation, we could take additional assumptions and evaluate the extreme scenarios. The following proposition states additional properties of the uncertainty function ![]() .
.
It is intuitive that if there is no uncertainty in the characteristic ![]() , there is no uncertainty and
, there is no uncertainty and ![]() . Considering that the set
. Considering that the set ![]() is well defined, then the worst‐case scenario is when all its elements are equally probable to be observed (i.e. they have the same chances to be the outcome of the observation process that will determine the actual value
is well defined, then the worst‐case scenario is when all its elements are equally probable to be observed (i.e. they have the same chances to be the outcome of the observation process that will determine the actual value ![]() that the characteristic
that the characteristic ![]() assumes). With these properties in mind, it is possible to mathematically define
assumes). With these properties in mind, it is possible to mathematically define ![]() as follows.
as follows.
It is interesting to note that (4.4) can be derived from basic axioms as presented in [5] or in [10]. The definition of joint and conditional entropy functions can be readily defined following (4.4) by using the joint and conditional probability mass functions. Figure 4.1 presents a pedagogical illustration of how the conditional and joint entropy are related in the case of two variables ![]() and
and ![]() as presented in Proposition 4.3. Note this is a usual visual representation of mathematical concepts that might be misleading in many ways.
as presented in Proposition 4.3. Note this is a usual visual representation of mathematical concepts that might be misleading in many ways.
It is also possible to extend this definition to continuous random variables as already presented in [1], but the definition would be more complicated since it would involve integrals instead of summations (the principles are nevertheless the same). Another important remark is related to the term “entropy” because it has been used in different scientific fields such as physics, information theory, statistics, and biology. As clearly presented in [5], the formulation of entropy presented in Definition 4.3 is always valid for memoryless and Markov processes, being very similar regardless of the research field; the only differences are the way it is presented and possible constants for normalization (mainly in physics). For complex systems that are related to, for instance, history‐dependent or reinforcement processes, the entropy function needs to be reviewed because the axioms used to derive (4.4) are violated. These alternative formulations are presented in [5].
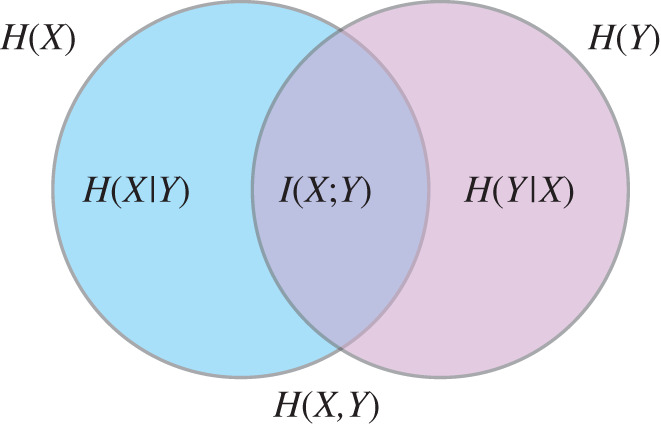
Figure 4.1 Relation between entropy functions and mutual information for two random variables  and
and  .
.
Although important, those advances in both information theory and entropy measures for complex systems are well beyond the scope of this book. To finish this section, we will provide a numerical example to calculate the uncertainty of the lottery previously analyzed.
4.3 Information and Its Different Forms
In the previous section, data and information as concepts were distinguished, the second being a subset of the first whose elements are interpretable and can resolve the uncertainty related to the specific characteristics of a given system or process. We have also introduced a way to mathematically formalize and quantify uncertainty and information by entropy, which is valid for some particular cases. This section will provide another angle on the analysis of information that focuses on the different forms in which that information exists. Following [3], information can be: (a) mathematical, (b) semantic, (c) biological, or (d) physical.
4.3.1 Mathematical Information and Communication
Shannon, in his seminal paper [1], established a mathematical theory of communications, where
(…) the fundamental problem of communication is that of reproducing at one point either exactly or approximately a message selected at another point. Frequently the messages have meaning; that is they refer to or are correlated according to some system with certain physical or conceptual entities. These semantic aspects of communication are irrelevant to the engineering problem. The significant aspect is that the actual message is one selected from a set of possible messages. The system must be designed to operate for each possible selection, not just the one which will actually be chosen since this is unknown at the time of design.
The engineering problem is depicted in Figure 4.3.
Shannon mathematically described the data messages regardless of their semantics and gave them a probabilistic characterization by random variables ![]() and
and ![]() that are associated with the transmitted and received messages, respectively. To do so, Shannon introduced the entropy function to measure the uncertainty of the random variables and then maximize the mutual information between them; these equations were introduced in the previous section. This paper by Shannon is considered the starting point of information theory, a remarkable scientific milestone. The main strength of Shannon's theory is the generality of the results, establishing the fundamental limits of communication channels and also data compression (e.g. [10, 12]). We can say that this generality is also its main weakness because it eliminates the semantics of particular problems to be solved. In simple words, Shannon states the limits of an error‐free transmission of information that no past, existing, or future technology can surpass, which might be of less importance at the semantic level where many problems related to the information transmission can be suppressed (for example, a missing data point related to the temperature sensor can be fairly well estimated from the past) while new ones appear. Semantic problems are usually history‐dependent processes also associated with changes in the sample spaces so that Shannon's key results need to be revisited [5, 7]. More details about semantic information are given next.
that are associated with the transmitted and received messages, respectively. To do so, Shannon introduced the entropy function to measure the uncertainty of the random variables and then maximize the mutual information between them; these equations were introduced in the previous section. This paper by Shannon is considered the starting point of information theory, a remarkable scientific milestone. The main strength of Shannon's theory is the generality of the results, establishing the fundamental limits of communication channels and also data compression (e.g. [10, 12]). We can say that this generality is also its main weakness because it eliminates the semantics of particular problems to be solved. In simple words, Shannon states the limits of an error‐free transmission of information that no past, existing, or future technology can surpass, which might be of less importance at the semantic level where many problems related to the information transmission can be suppressed (for example, a missing data point related to the temperature sensor can be fairly well estimated from the past) while new ones appear. Semantic problems are usually history‐dependent processes also associated with changes in the sample spaces so that Shannon's key results need to be revisited [5, 7]. More details about semantic information are given next.
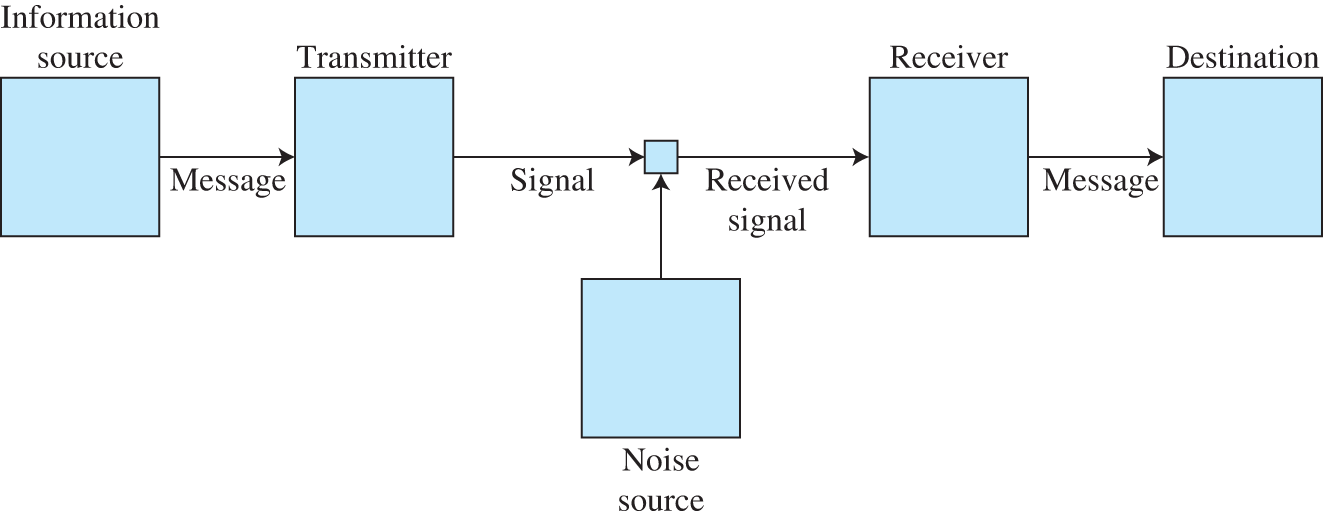
Figure 4.3 Diagram of a general communication system by Shannon.
4.3.2 Semantic Information
Semantics refers to the meaning of data and therefore, of information. Semantic information can be classified as [3]:
- Instructional: Data or information that prescribes actions in a “how to” manner. For example, a recipe that states the procedure to make a chocolate cake.
- Factual: Data that can be declared true or false. Information is then defined as data that are true while misinformation is false data that are unintentional and disinformation false data that are intentional. For example, a scientific paper with new results can be considered factual information. However, it may also be factual misinformation when the measurement devices have not been calibrated and the authors are not aware of it, and thus, the results are unintentionally false. Making fake results to publish a paper is a case of factual disinformation.
- Environmental: Data or information that is independent of an intelligent producer. For example, a tree outside an office indicates the season of the year (green leaves, no leaf, fruits, flowers, etc.). Engineering systems are also designed to be a source of environmental information, such as a thermometer. In general, environmental information is defined as the coupling of two (or more) processes where observable states of one or more processes carry information about the state of other process(es).
In summary, semantic data must be judged with respect to its associated meaning or its purpose, and thus, it is different from – and in many senses more general than – Shannon's mathematical theory. For instance, an error‐free communication in Shannon's sense might be associated with misinformation, like in the case when a perfect communication link transmits the data of a poorly calibrated sensor that misinforms the application that will use such data. As Shannon himself has indicated in his paper, processes like “natural language” could be analyzed by his probabilistic theory but without any ambition to fully characterize it. Natural language can be seen as an evolutionary (history‐dependent) process that is built upon semantics that cannot be reduced to syntactical/logical relations alone.
While semantics is associated with meaning and hence with the social domain, we could also analyze how life is associated with data and information.
4.3.3 Biological Information
The growing scientific understanding of different biological processes including physiology, pathology, genetics, and evolution of species indicate the necessity of “data storage, transmission, and processing” for the production and reproduction of life in its different forms [13]. Biological information broadly refers to how the organization in living beings could (i) emerge from chemical reactions, (ii) be maintained allowing reproduction of life, and (iii) be associated with the emergence of new species [14]. Different from semantic information associated with socially constructed meanings, biological information concerns data that are transmitted by chemical signals that are constitutive of living organisms that evolve over time.
As indicated in [13], Shannon's Information Theory has had a great influence on biology. Even more interesting is the fact that Shannon himself, before moving to Bell Labs, wrote his Ph.D. thesis about theoretical genetics [15]. Biological information can be used as a tool to understand the emergence of new species, cell differentiation, embryonic development, the effects of hormones in physiology, and nervous systems, among many others. It is worth noting that, despite the elegance and usefulness of some mathematical models, the peculiarity of biological objects and concepts must be preserved. In this sense, biological information is still a controversial topic [13]. Nevertheless, we would like to stress the importance of the different existing approaches that use the concept of biological information to develop technologies in, for instance, biochemistry, pharmacology, biomedical engineering, genetic engineering, brain–machine or human–machine interfaces, and molecular communications.
We follow here [3] by arguing that biological information deserves to be considered in its own particularities. Biological information cannot be reduced or derived from Shannon's mathematical information, or semantic information. On the contrary, the scientific knowledge of biological information needs to be constructed with respect to living organisms, even though mathematical and semantic information may be useful in some cases.
4.3.4 Physical Information
As indicated by the Maxwell's demon examples in the previous chapters, there seems to be a fundamental relation between physical and computational processes. Storing, processing, transmitting, and receiving data are physical processes that consume energy, and thus, their fundamental limits are stated by thermodynamics. Landauer theoretically proved in [16] and Berut et al. experimentally demonstrated in [17] that the erasure of a bit is an irreversible process, and thus, dissipates heat. Similarly, Koski et al. proved in [18] that the transfer of information associated with their experimental setting of Maxwell's demon dissipates heat. The dissipated heat and the information entropy are then fundamentally linked: Landauer's principle states the lower bound of irreversible data processing. In Landauer's interpretation [19], this result indicates that “information is physical.”
The fundamental relation between energy and information motivates the study of reversible computation, and also ways to improve the energy efficiency of existing irreversible computing methods by stating their ultimate lower bound. Despite its evident importance, such a fundamental result has had, until now, far less impact on technological development than Shannon's work. However, this may change because of large‐scale data centers with their extremely high energy demand not only to supply the energy to run the data processing tasks but also for cooling pieces of hardware that indeed dissipate heat. What is important to understand here is that any data process must have a material implementation, and thus, requires energy.
In this sense, the limits stated by physical information are valid for all classes of information. Both biochemical processes related to biological information and interpretative processes related to semantic information consume energy, and hence, have their fundamental limits established by Shannon and Landauer. Note that the fundamental limits are valid even for processes whose mathematical characterization defined by the mathematical information is not possible.
The concept of physical information also brings another interesting aspect already indicated in the previous sections: information is a relational concept defined as a trustworthy uncertainty resolution, which is always defined with respect to a specific characteristic of a process or a system. It is then intuitive to think that information should refer, directly or indirectly, to something that materially exists. This is the topic of our next section.
4.4 Physical and Symbolic Realities
The scientific results related to information, whose foundations were just presented, are many times counterintuitive and against the common sense of a given historical period. As discussed in Chapter 1, this may lead to a philosophical interpretation (and distortion) of scientific findings. For example, there is a good deal of heated debates about the nature of information (i.e. metaphysics of information). For example, the already cited works [2–4, 16, 20] have their own positions about it.
In this book, we follow a materialist position, and thus, we are not interested in the nature of information; for us, information exists. In our view, this is the approach taken by Shannon, and only in this way science can evolve. Despite our critical position about Wiener's cybernetics presented in Chapter 1 [21], he precisely stated there how information should be understood:
The mechanical brain does not secrete thought “as the liver does bile,” as the earlier materialists claimed, nor does it put it out in the form of energy, as the muscle puts out its activity. Information is information, not matter or energy. No materialism which does not admit this can survive at the present day.
Information exists, as matter and energy do, but it operates in its own reality, which we call here symbolic reality. The relation between symbolic and physical realities is given by the following proposition.
In other words, this proposition tells that data processes are physical and constitute relations that are not only physical but also symbolic. Information as a product of data processes is then physical and exists in the symbolic reality. It is also possible to define processes that are constituted in the symbolic reality related to symbolic relations. These processes can be classified into levels with respect to the physical reality, as stated in the following definition.
From this very simple example, it is possible to see that the space of analysis could grow larger and larger because symbolic processes are unbounded. Note that higher levels tend to require more data processing, and thus, consume more energy. When the physical reality is mapped into the data forming a symbolic reality, the number of ways that these acquired data can be combined grows to infinity. However, as stated in Proposition 4.1, data that have the potential to become information constitute a very restricted subset of all data about a specific process or system. Given these facts, there are limits in the symbolic relation that cannot be passed, as presented in the following proposition.

Figure 4.4 Car in a highway and level of processes.
In this case, all data processing is limited by energy and, more restrictively, the requirements that the data must fulfill to become information constrain even more what could potentially be an informative symbolic reality, which is the foundation of the cyber domain of cyber‐physical systems. In the cyber domain, the symbolic relation is usually called logical relations in contrast to physical relations. The next step is to understand how physical and symbolic relations can be defined through networks.
4.5 Summary
This chapter introduced the concept of information. We defined it as a subset of all data about a specific process or system that is structured and meaningful, and thus, capable of providing a trustworthy representation. Information is then related to uncertainty resolution, which always involves the processing of data. For some cases, we explained how to measure the uncertainty from a probabilistic characterization of random variables (as presented in Chapter 3) by Shannon's entropy. Therefrom, we presented how to compute the mutual information between two random variables, as well as their conditional and joint entropies. We also presented a discussion about different types of data and information, indicating the fundamental limits of processes involving manipulation of data.
For readers interested in the topic, the book by Floridi [3] provides a brief overview of the subject. The entries of the Stanford Encyclopedia of Philosophy [4, 13, 20] go deeper into different views and controversies related to this theme. Adami provides a speaking‐style introduction of the mathematical basis of information theory [2]. However, the must‐read is the paper by Shannon himself [1] where the fundamental limits of information are pedagogically stated. Landauer's paper [19] is also very instructive to think about the relation between information and thermodynamics.
Exercises
- 4.1 Data and information. The goal of this task is to explore how data and information are related by following Proposition 4.1.
- Define in your own words how data and information are related.
- Propose one example similar to Example 4.1.
- Extend your example by proposing a list of data that are not informative.
- 4.2 Entropy and mutual information. The discussions about climate change always point to the dangers of global warming, which is usually measured by an increase of
 degrees Celsius. This value
degrees Celsius. This value 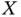 is taken as an average over different places during a specific period of time. Negationists, in their turn, argue that global warming is not true because a given city A reached a temperature
is taken as an average over different places during a specific period of time. Negationists, in their turn, argue that global warming is not true because a given city A reached a temperature 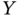 that was the coldest in decades. In this exercise, we consider that
that was the coldest in decades. In this exercise, we consider that 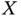 and
and 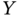 are obtained through data processes
are obtained through data processes  and
and 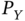 and can be analyzed as random variables.
and can be analyzed as random variables.
- Which data process,
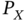 or
or 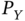 , has a greater level in the sense presented in Definition 4.4? Why?
, has a greater level in the sense presented in Definition 4.4? Why? - Consider a random variable
 associated with the answer of the question: is the global warming true? What is the relation between the entropies
associated with the answer of the question: is the global warming true? What is the relation between the entropies  ,
, 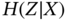 , and
, and  ?
? - Now, consider another random variable
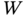 associated with the answer of the question: how was the weather of city A during last winter? What is the relation between the entropies
associated with the answer of the question: how was the weather of city A during last winter? What is the relation between the entropies 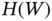 ,
,  , and
, and 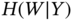 ?
? - What could be said about the mutual information
 ,
, 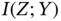 ,
, 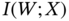 ,
,  , and
, and  ?
? - What is the problem of the argument used by negationists?
- Which data process,
- 4.3 Information and energy in an AND gate. Consider a logical gate AND with
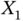 and
and  as inputs, and
as inputs, and  as output. In this case,
as output. In this case,
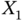


0 0 0 0 1 0 1 0 0 1 1 1 Assume that
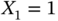 is associated with a probability
is associated with a probability  and
and 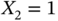 with a probability
with a probability  .
.- Formalize the problem as introduced in Chapter 3 and then find the probability mass functions of
 ,
, 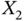 , and
, and 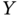 , as well as all conditional and joint probabilities between
, as well as all conditional and joint probabilities between  ,
,  , and
, and  .
. - What are
 ,
, 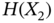 , and
, and  assuming that
assuming that 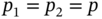 ?
? - What is the mutual information
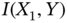 and
and  when
when 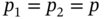 ?
? - Does the AND gate operation generate heat? Why?
- Formalize the problem as introduced in Chapter 3 and then find the probability mass functions of
References
- 1 Shannon CE. A mathematical theory of communication. The Bell System Technical Journal. 1948;27(3):379–423.
- 2 Adami C. What is information? Philosophical Transactions of The Royal Society A. 2016;374(2063):20150230.
- 3 Floridi L. Information: A Very Short Introduction. OUP Oxford; 2010.
- 4 Floridi L, Zalta EN, editor. Semantic Conceptions of Information. Metaphysics Research Lab, Stanford University; 2019. Last accessed 8 January 2021. https://plato.stanford.edu/archives/win2019/entries/information-semantic/.
- 5 Thurner S, Hanel R, Klimek P. Introduction to the Theory of Complex Systems. Oxford University Press; 2018.
- 6 Li M, Vitányi P, et al. An Introduction to Kolmogorov Complexity and its Applications. vol. 3. Springer; 2008.
- 7 Kountouris M, Pappas N. Semantics‐empowered communication for networked intelligent systems. IEEE Communications Magazine, 2021;59(6):96–102, doi: 10.1109/MCOM.001.2000604.
- 8 Merriam‐Webster Dictionary. Information; 2021. Last accessed 11 January 2021. https://www.merriam-webster.com/dictionary/information.
- 9 Shannon CE. A symbolic analysis of relay and switching circuits. Electrical Engineering. 1938;57(12):713–723. Available at: http://hdl.handle.net/1721.1/11173. Last accessed 11 November 2020.
- 10 Ash RB. Information Theory. Dover books on advanced mathematics. Dover Publications; 1990.
- 11 Boole G. The Mathematical Analysis of Logic. Philosophical Library; 1847.
- 12 Popovski P. Wireless Connectivity: An Intuitive and Fundamental Guide. John Wiley & Sons; 2020.
- 13 Godfrey‐Smith P, Sterelny K, Zalta EN, editor. Biological Information. Metaphysics Research Lab, Stanford University; 2016. https://plato.stanford.edu/archives/sum2016/entries/information-biological/.
- 14 Prigogine I, Stengers I. Order Out of Chaos: Man's New Dialogue with Nature. Verso Books; 2018.
- 15 Shannon CE. An algebra for theoretical genetics; 1940. Ph.D. thesis. Massachusetts Institute of Technology.
- 16 Landauer R. Irreversibility and heat generation in the computing process. IBM Journal of Research and Development. 1961;5(3):183–191.
- 17 Bérut A, Arakelyan A, Petrosyan A, Ciliberto S, Dillenschneider R, Lutz E. Experimental verification of Landauer's principle linking information and thermodynamics. Nature. 2012;483(7388):187–189.
- 18 Koski JV, Kutvonen A, Khaymovich IM, Ala‐Nissila T, Pekola JP. On‐chip Maxwell's demon as an information‐powered refrigerator. Physical Review Letters. 2015;115(26):260602.
- 19 Landauer R, et al. Information is physical. Physics Today. 1991;44(5):23–29.
- 20 Adriaans P, Zalta EN, editor. Information. Metaphysics Research Lab, Stanford University; 2020. Last accessed 8 January 2021. https://plato.stanford.edu/archives/fall2020/entries/information/.
- 21 Wiener N. Cybernetics or Control and Communication in the Animal and the Machine. MIT press; 2019.
