CHAPTER 4
The Single Most Important Measurement in Cybersecurity
We hope Chapter 2 cleared up how the term “measurement” is used in decision science as well as the empirical sciences in general. We contend that this is the most relevant understanding of measurement for cybersecurity. Chapter 3 gave you an introduction to the most basic level of quantitative risk analysis. But why did we choose to focus on some methods as the solution and not others? How do we know some methods are better than others? There will be a lot more to cover regarding the details of the methods of measurement, but for now we propose that our first target should be a measurement of risk analysis itself.
The authors have observed experts throughout the field with passionately held positions on the relative merits of different cybersecurity risk‐assessment methods. One easy observation we could make is that both sides of polar‐opposite positions were often argued by highly qualified cybersecurity experts, all with decades of experience. One knowledgeable expert will argue, for example, that a particular framework based on qualitative scores improves decisions, builds consensus, and avoids the problems of more quantitative methods. Another equally qualified expert will argue this is an illusion and that such methods simply “do the math wrong.” Since we know at least one (if not both) must be wrong, then we know qualifications and expertise in cybersecurity alone are not sufficient to determine if a given opinion on this topic is correct.
This leaves us with several hard questions. How do we decide which methods work better? Is it possible that the risk analysis methods cybersecurity experts have used for decades—methods in which many cybersecurity experts have a high degree of confidence—could actually not work? Is it possible that the perceived benefits of widely used tools could be an illusion? What do we even mean when we say a method “works,” and how would that be measured? We propose that the single most important measurement in cybersecurity risk assessment, or any other risk assessment, is to measure how well the risk assessment methods themselves work.
More fundamentally, does it even matter whether risk analysis works? Is it sufficient to merely put on a show for compliance or do we expect a method to measurably improve decisions and reduce risks? We will take what we believe to be an obvious position that shouldn't really be controversial:
- We believe it matters whether risk analysis actually works.
- What we mean by whether it “works” is whether it measurably reduces risks relative to alternative methods with the same resources. That is, we believe that risk analysis in any field, including cybersecurity, is not just a matter of putting on a show for the appearance of compliance.
- Regulators and standards organizations must measure the performance of methods they require. If complying with standards and regulations does not actually improve risk management, then those standards and regulations must change.
- We also think it is entirely reasonable to insist that in order to settle an issue with many contradictory opinions from experts at all levels, we will have to actually begin to measure how well risk analysis methods work.
- We assert that if firms are using cybersecurity risk‐analysis methods that cannot show a measurable improvement or, even worse, if they make risk assessment worse, then that is the single biggest risk in cybersecurity, and improving risk assessment will be the single most important risk management priority.
Measuring the methods themselves will be the basis of every recommendation in this book. Either we will propose risk analysis methods based on measurements that have already been done and published, or, if no such measurement has been done, we will propose a measurement that will eventually help identify a valid method. And while we describe how to measure the relative effectiveness of methods, we also need to explain how not to measure them.
By the end of this chapter we will see what published research has already measured about key pieces of the quantitative methods we proposed in Chapter 3. In the next chapter, we will also consider research showing that components of current popular risk‐assessment methods may do more harm than good. Now, let's look at why we need to base our methods on research in the first place as opposed to our expert opinion.
The Analysis Placebo: Why We Can't Trust Opinion Alone
The first principle is that you must not fool yourself, and you are the easiest person to fool.
—Richard P. Feynman, Nobel Prize–Winning Physicist
We often hear that a given method is “proven” and is a “best practice.” It may be touted as a “rigorous” and “formal” method—implying that this is adequate reason to believe that it improves estimates and decisions. Eventually it gets the title of “accepted standard.” Some satisfied users will even provide testimonials to the method's effectiveness.
But how often are these claims ever based on actual measurements of the method's performance? It is not as if large clinical trials were run with test groups and control groups. Estimates are rarely compared to actual outcomes, and costly cybersecurity breaches are almost never tracked over a large number of samples to see whether risk really changed as a function of which risk assessment and decision‐making methods are used. Unfortunately, the label of “best practice” does not mean it was measured and scientifically assessed to be the best performer among a set of practices. As Feynman's quote states, we are easy to fool. Perceived improvements may actually be a mirage. Even if a method does more harm than good, users may still honestly feel they see a benefit.
How is this possible? Blame an “analysis placebo”—the feeling that some analytical method has improved decisions and estimates even when it has not. The analogy to a placebo as it is used in medical research is a bit imprecise. In that case, there can actually be a positive physiological effect from a mere placebo beyond the mere perception of benefit. But when we use the term in this context, we mean there literally is no benefit other than the perception of benefits. Several studies in fields outside of cybersecurity have been done that show how spending effort on analysis improved confidence even when the actual performance was not improved at all. Here are a few examples that have also been mentioned in other books by Hubbard:
- Sports Picks: A 2008 study at the University of Chicago tracked probabilities of outcomes of sporting events as assigned by participants given varying amounts of information about the teams without being told the names of teams or players. As the fans were given more information about the teams in a given game, they would increase their confidence that they were picking a winner, even though the actual chance of picking the winner was nearly flat no matter how much information they were given.1
- Psychological Diagnosis: Another study showed how practicing clinical psychologists became more confident in their diagnosis and their prognosis for various risky behaviors by gathering more information about patients, and yet, again, the agreement with observed outcomes of behaviors did not actually improve.2
- Investments: A psychology researcher at MIT, Paul Andreassen, conducted several experiments in the 1980s showing that gathering more information about stocks in investment portfolios improved confidence but without any improvement in portfolio returns. In one study he showed how people tend to overreact to news and assume that the additional information is informative even though, on average, returns are not improved by these actions.3
- Collaboration on Sports Picks: In another study, sports fans were asked to collaborate with others to improve predictions. Again, confidence went up after collaboration, but actual performance did not. Indeed, the participants rarely even changed their views from before the discussions. The net effect of collaboration was to seek confirmation of what participants had already decided.4
- Collaboration on Trivia Estimates: Another study investigating the benefits of collaboration asked subjects for estimates of trivia from an almanac. It considered multiple forms of interaction including the Delphi technique, free‐form discussion, and other methods of collaboration. Although interaction did not improve estimates over simple averaging of individual estimates, the subjects did feel more satisfied with the results.5
- Lie Detection: A 1999 study measured the ability of subjects to detect lies in controlled tests involving videotaped mock interrogations of “suspects.” The suspects were actors who were incentivized to conceal certain facts in staged crimes to create real nervousness about being discovered. Some of the subjects reviewing the videos received training in lie detection and some did not. The trained subjects were more confident in judgments about detecting lies even though they were worse than untrained subjects at detecting lies.6
And these are just a few of many similar studies showing that we can engage in training, information gathering, and collaboration that improves confidence but not actual performance. Of course, these examples are from completely different types of problems than cybersecurity. But what is the basis for assuming that these same problems don't appear in cybersecurity? In the pharmaceutical industry, a new drug is effectively assumed to be a placebo until it is shown that the observed effect would be very unlikely if it were a placebo. The fact that a placebo exists in some areas means it could exist in other areas unless the data shows otherwise. With examples in problems as diverse as investments, horse racing, football games, and diagnosis of psychology patients, it would seem that the burden of proof is on the person claiming that some other area, such as cybersecurity, avoids these problems. So let's start by assuming that cybersecurity is not particularly immune to problems observed in so many other areas where humans have to make judgments.
What we will not do to measure the performance of various methods is rely on the proclamations of any expert regardless of his or her claimed level of knowledge or level of vociferousness. So even though the authors can fairly claim plenty of experience—cybersecurity in the case of Seiersen and quantitative risk analysis in general in the case of Hubbard—we will not rely on any appeals to our authority regarding what works and what does not. We see this as a shortcoming in many books on risk management and information security. Our arguments will be based on the published research from large experiments. Any mention of anecdotes or quotes from “thought leaders” will only be used to illustrate a point, never to prove it.
We don't think it is controversial to insist that reason and evidence are the way to reach reliable conclusions about reality. For “reason,” we include using math and logic to derive new statements from previously confirmed statements. For “evidence,” we don't include anecdotal or testimonial arguments. Any method, including astrology and pet psychics, can produce those types of “evidence.” The best source of evidence is large, random samples; clinical trials; unbiased historical data; and so on. The data should then be assessed with proper mathematical methods to make inferences.
How You Have More Data than You Think
What we need to do is define a scientifically sound way to evaluate methods and then look at how different methods compare based on that evaluation. But a common concern is that cybersecurity simply lacks sufficient data for proper, statistically valid measurements. Ironically, this claim is almost always made without doing any proper math.
Recall from Chapter 2 that if we can expand our horizons about what data could be informative, we really do have more data than we think. So here are some ways that we have more data than we think about the performance of cybersecurity risk assessment methods.
- We don't have to be limited by looking just at ourselves. Sure, each organization is unique, but that doesn't mean that we can't learn from different examples. Indeed, experience would mean nothing if we couldn't generalize from experiences that aren't identical. Using information from larger populations is how insurance companies estimate your health risk even though you never made a claim, or how a doctor believes a drug you never tried will work with you because he knows of a large experiment involving many other people.
- We can measure components as well as whole systems. We can measure the overall performance of an entire system, or we can measure individual components of the system. When an engineer predicts the behavior of a new system that has not yet been built, the engineer is using knowledge of the behavior of components and how they interact. It's easier to measure several components of risk assessment than it is to wait for rare events to happen. For example, tracking how well cybersecurity analysts estimate more frequent, small events is a measure of the “expert estimation component” in the risk management system.
- We can use published research. If we are willing to consider component ‐ level studies of larger populations outside of our own experience, then a lot more data becomes available. When you don't have existing data or outside research of any kind, it might be time to start gathering the data as part of a defined measurement process.
Understanding what data we can use to support measurements is ultimately the kind of “reference class” issue we discussed in the previous chapters. In a perfect world, your firm would have so much of its own data that it doesn't need to make inferences from a reference class consisting of a large population of other firms. You can measure the overall performance of a risk assessment system by measuring outcomes observed within your own firm. If the firm were large enough and willing to wait long enough, you could observe variations in major data breaches in different business units using different risk assessment methods. Better yet, industry‐wide experiments could expand the reference class to include many organizations and would produce a lot of data even about events that would be rare for a single firm.
Of course, multiyear, industry‐wide experiments would not be practical for several reasons, including the time it would take and the need to convince organizations to participate knowing they might be in the “placebo” group. (Which organizations would want to be in the “placebo” group using a fake method?) Not surprisingly, no such study has been published in peer‐reviewed literature by the date of this writing. So what can be done to compare different risk assessment methods in a scientifically rational way? The other measurement strategy dimensions we just mentioned give us some choices—some of which can give us immediate answers.
A more feasible answer for an initial measurement would be to experiment with larger populations but with existing research at the component level. Component testing is an approach many professionals in engineering and information technology are already familiar with. Components we could consider are the individual steps in risk assessment, the tools used, and the methods of collaboration. Even the act of simply putting a probability on a potential event is a component of the process we could test. In fact, a lot of research has already been done on this at a component level—including some studies that were very large, conducted over many decades by many separate researchers and published in leading, peer‐reviewed scientific journals.
If the individual components of a method are shown to be an improvement, then a method based entirely on these elements is much more likely to be effective than a method for which the components have no such evidence or, worse yet, have been shown to be flawed. This is no different than a designer of an oil refinery or rocket using established physical principles to evaluate components of a system and then calculating how those components would behave in the aggregate. There are many potential components to evaluate, so let's divide them into two broad categories that are or could be used in cybersecurity risk assessment:
- What is the relative performance of purely historical models in estimating uncertain outcomes as compared to experts?
- Where we use experts, what is the performance of the tools the experts use to assist in making estimates of outcomes?
When Algorithms Beat Experts
A key “component” we should consider in cybersecurity risk analysis is the performance of how information is synthesized to make estimates. Specifically, is it better to rely on experts to make a judgment or a statistical model? One particular area where research is plentiful is in the comparison of statistical models to human experts in the task of estimating uncertain outcomes of future events. This research generated one of the most consistently replicated and consequential findings of psychology: that even relatively naive statistical models seem to outperform human experts in a surprising variety of estimation and forecasting problems.
We should note here that while we promote quantitative methods (for good reasons we are about to explore), we aren't saying that we can entirely replace humans in risk assessment. We are simply looking at a few situations where objective, quantitative models were made and compared to expert intuition. We want to investigate the following question: If we could build a purely quantitative model on historical data, would that even be desirable?
As you read about this research, you may also want to know whether any of the research in other areas could even apply to cybersecurity. If you bear with us, we think you will agree that it does. In fact, like the placebo effect mentioned earlier, the studies are so numerous and varied it seems the burden of proof would be on the one arguing that cybersecurity somehow avoids these fundamental issues.
Some Research Comparing Experts and Algorithms
Some of this research started in a very different field and during a time before the concept of cybersecurity had even been imagined. As early as the 1950s, the American psychologist Paul Meehl proposed an idea that shook up the field of clinical psychology. He claimed that expert‐based clinical judgments about psychiatric patients might not be as good as simple statistical models. Meehl collected a large set of studies showing that statistical models based on medical records produced diagnoses and prognoses that at least matched but usually beat the judgment of trained clinicians. Meehl was able to show, for example, that personality tests were better than experts at predicting several behaviors regarding neurological disorders, juvenile delinquency, and addictive behaviors.
In 1954, he wrote the seminal book on the subject, Clinical versus Statistical Prediction. At the time of this initial research, he could already cite over 90 studies that challenged the assumed authority of experts.7 Researchers such as Robyn Dawes (1936–2010) of the University of Michigan were inspired to build on this body of research, and every new study that was generated only confirmed Meehl's findings, even as they expanded the scope to include experts outside of clinical diagnosis.8,9,10 The library of studies they compiled included findings predicting the GPAs of college freshmen and medical students, criminal recidivism, sporting events, and medical prognoses. After the studies had grown significantly in number, Meehl felt forced to conclude the following:
There is no controversy in social science which shows such a large body of qualitatively diverse studies coming out so uniformly in the same direction as this one. When you're pushing 90 investigations [now over 150], predicting everything from the outcome of football games to the diagnosis of liver disease and when you can hardly come up with a half dozen studies showing even a weak tendency in favor of the [human expert], it is time to draw a practical conclusion.11
The methods used in this research were straightforward. Ask experts to predict some objectively verifiable outcomes—such as whether a new business will fail or the effectiveness of chemotherapy for a cancer patient—then predict the same thing using an algorithm based only on historical data, then lastly track both over a large number of predictions, and see which method performs better.
Such conclusive findings as those of Meehl and his colleagues inevitably draw the interest of other researchers looking for similar phenomena in other fields. In one of the more recent examples, a study of oil exploration firms shows a strong relationship between the use of quantitative methods (including Monte Carlo simulations) to assess risks and a firm's financial performance.12,13 NASA has been applying Monte Carlo simulations based on historical data along with softer methods (based on subjective scales) to assess the risks of cost and schedule overruns and mission failures. The cost and schedule estimates from the quantitative methods had, on average, less than half the error of scientists and engineers using nonquantitative methods.14
In perhaps the most ambitious study of this kind, Philip Tetlock conducted an experiment over a 20‐year period and published it in his book Expert Political Judgment: How Good Is It? The title indicates a particular focus in politics, but he interpreted it broadly to include economics, military affairs, technology, and more. He tracked the probabilities of world events assigned by a total of 284 experts in their respective fields. By the conclusion of the study he had collected over 82,000 individual forecasts.15 (This puts Tetlock's data equal to or in excess of the largest phase III clinical drug trials published in scientific journals.) Based on this data, Tetlock was willing to make even stronger statements than Meehl and his colleagues:
It is impossible to find any domain in which humans clearly outperformed crude extrapolation algorithms, less still sophisticated statistical ones.
Why Does This Happen?
Robyn Dawes, Meehl's colleague whom we mentioned earlier, makes the case that poor performance by humans in forecasting and estimation tasks is partly due to inaccurate interpretations of probabilistic feedback.16 These researchers came to view the expert as a kind of imperfect mediator of input and output. Very few experts measure their performance over time, and they tend to summarize their memories with selected anecdotes. The expert then makes rough inferences from this selective memory, and according to the research published by Dawes, this can lead to an “illusion of learning.” That is, experts can interpret experience alone as evidence of performance. They believe years of experience should result in improved performance, so they assume that it does. But it turns out that we cannot take learning for granted no matter how many years of experience are gained.
Tetlock proposed in his book that “human performance suffers because we are, deep down, deterministic thinkers with an aversion to probabilistic strategies that accept the inevitability of error.” The math of dealing with error and uncertainty is the math of probabilities. If we can't get that math right in our heads, then we will have a lot of difficulty with probabilistic forecasting problems.
For example, if someone was not good at simple arithmetic, we wouldn't be surprised if that person was not very good at estimating, say, the costs and duration of a large, complex engineering project with many interrelated elements. Surely a person skilled at those estimates would know how to multiply the number of people involved in a task, their cost of labor, and the duration of the task in order to estimate the task's labor costs. He or she would also know how to total the costs of the separate tasks along with other project costs (e.g., materials, licenses, and equipment rental).
When an expert says that, based on some experience and data, one threat is a bigger risk than another, they are doing a kind of “mental math” whether intentional or not. We aren't saying they are literally trying to add numbers in their heads; rather, they are following an instinct for something that in many cases really could be computed. How well our intuition matches the math has also been measured by an impressive array of research including that of Daniel Kahneman, winner of the 2002 Nobel Prize in Economic Sciences, and his colleague Amos Tversky. They showed how even statistically sophisticated researchers will tend to greatly misestimate the odds that new data will confirm or contradict a previous experiment of a given sample size,17 and will incorrectly estimate expected variations in observations based on sample size.18 (This was briefly mentioned in Chapter 2.)
By “statistically sophisticated,” we mean that the subjects of this research were actual scientists published in respected, peer‐reviewed journals. As Kahneman and Tversky noted in this research, “It's not just that they should know the math, they did know the math.” Even for those who know the math, when they resort to their intuition, their intuition is wrong. For all of us, including trained scientists, various recurring—but avoidable—mathematical errors are just one of the challenges of trying to do math in our heads.
Even though all of this research is borrowed from fields outside of cybersecurity, the breadth of these findings in so many areas seems to demonstrate that they are fundamental and apply to any area of human judgment, including cybersecurity. But if the variety of findings in so many areas doesn't convince us that these same issues apply to cybersecurity, consider another argument made by Kahneman and another researcher in decision psychology, Gary Klein.
Kahneman and Klein point out three necessary conditions for experience to result in learning. First, there must be consistent feedback. The person must be given the information about past performance regularly, not rarely. Second, the feedback must be relatively immediate. If a person makes several forecasts for events that may happen years from now (which is often the case in a cost‐benefit analysis for some new investment in, say, technology, infrastructure, or new products), the delay in the feedback will make learning more difficult. Third, the feedback should be unambiguous. If the person simply says a cybersecurity project will be a “success” or that risk will be reduced, that may be open to interpretation. And when our past performance is left to interpretation, we are likely to interpret data in a way that would be flattering to ourselves. Unless we get regular, immediate, and unambiguous feedback, we are likely to have selective memory and interpret our experiences in the most flattering way.
So the uncomfortable question cybersecurity risk analysts must ask themselves is this: Does the experience of the cybersecurity expert actually meet those requirements? Do cybersecurity experts actually record all their estimates of probability and impact and then compare them to observation? Even assuming they did that, how long would they typically have to wait before they learned whether their estimate was correct? Even if estimates are recorded and we wait long enough for the event to occur, was it clear whether the original estimate was correct or the discrete event occurred or not? For example, if we say we lost reputation from a breach, how do we know that, and how did we actually validate—even approximately—the magnitude of the event as originally estimated?
Even if judgments of cybersecurity risk assessments were unambiguous and faithfully recorded, the delay of the feedback alone presents a major obstacle to learning. For example, suppose we have an event we assess as having a 10% chance of occurrence per year. We are considering a control to reduce this risk but have uncertainty about the control. If this control works, it doesn't eliminate the chance of the event, but it should reduce the annual likelihood of this event by half. Let's say the estimates so far are based on a lot of industry data except for whether the control will even work at all in our environment. To keep it simple, we'll assume that it either works or doesn't and we judge that there is a 50/50 chance the control will work and reduce the chance of occurrence by half (down to 5%). If it doesn't work, then the annual likelihood is still 10%.
If we observe this system long enough, we can update our judgment about whether the control is working. If we could observe this system over a very long time and maybe in a large number of organizations, we could detect a difference between a 10% and 5% annual probability faster. But suppose we limit our observations to the experience of one manager or risk analyst in one organization. If it doesn't happen in the first five years, that tells us very little about whether the control is working. That could easily be the same outcome if the control were effective or if the control were no better than wearing your lucky socks to work. In Chapter 8, we discuss Bayesian methods, which could be applied to solve this. For now, we'll just tell you the answer. If we don't observe the event after eight years, we can adjust our probability that the control is effective from 50% to just 60%. In other words, it could still easily be the case that the control was ineffective but we were just a bit lucky. If we waited 16 years and the event has not yet occurred, we would still only be 70% certain the control is working, and if we waited 30 years, it rises to about 84%. Even to learn at this slow rate assumes the original forecast was recalled accurately. How many of your forecasts from five years ago do you recall accurately today? How many did you even document?
Risk management also lacks another required component for learning. Kahneman and others pointed out that learning must be based on a “high validity” environment. This refers to the predictability of a system. In an environment where the outcomes are mostly random, learning becomes much more difficult. For example, you can watch a roulette table or coin flipping for many decades and not get any better at predicting outcomes. This would be a “low validity” environment. On the other hand, if you are watching moves in a chess game for that long, you will probably get better at estimating who will win well before the game ends. Risk management, by its nature, involves randomness and, consequently, it becomes very hard to learn from experience.
In cybersecurity, like many other fields, we cannot assume learning happens without deliberate processes to make sure that is the case. These findings are obvious to researchers such as Meehl:
The human brain is a relatively inefficient device for noticing, selecting, categorizing, recording, retaining, retrieving, and manipulating information for inferential purposes. Why should we be surprised at this?19
This does not mean that experts know very little about their fields. They have a lot of detailed technical knowledge. The performance of experts in the research mentioned so far relates only to the estimation of quantities based on subjective inferences from recalled experience. The problem is that experts often seem to conflate the knowledge of a vast set of details in their field with their skill at forecasting uncertain future events. A cybersecurity expert can become well versed in technical details such as conducting penetration tests, using encryption tools, setting up firewalls, using various types of cybersecurity software, and much more—and still be unable to realistically assess their own skills at forecasting future events.
Tools for Improving the Human Component
The research reviewed up to this point might make it look like there is little room for the expert in assessing risks. We are not making that case at all. When we can make sound mathematical models based on objective observations and historical data, we should do that. Still, we acknowledge that there are several tasks still left to the expert. The expert is a component of risk analysis we cannot remove but we can improve.
The expert must help define the problem in the first place. He or she must assess situations where the data is ambiguous or where conditions do not fit neatly into existing statistical data. The expert also must propose the solutions that must be tested.
In fact, our goal is to elevate the expert. We want to treat the cybersecurity expert as part of the risk assessment system. Like a race car or athlete, they need to be monitored and fine‐tuned for maximum performance. The expert is really a type of measurement instrument that can be “calibrated” to improve its output.
It is also worth noting that none of the challenges we are about to list are unique to the cybersecurity profession, but that profession does have some characteristics that put it among a set of professions susceptible to “uncalibrated” judgment. Cybersecurity can borrow from other, very technical engineering fields reliant on expert judgment that have specific methods in place to track and calibrate the judgments of experts. The Nuclear Regulatory Commission (NRC), for example, recognizes the need for expert input during several steps in the risk assessment process. An NRC report on the use and elicitation of expert judgment stated the following:
Expert judgments are both valid in their own right and comparable to other data. All data are imperfect representations of reality. The validity of expert judgment data, like any data, can vary based on the procedures used to collect it. So‐called “hard” data, such as data taken from instruments, cannot be considered to be perfect because of problems such as random noise, equipment malfunction, operator interference, data selection, or data interpretation. The validity of all data varies. The validity of expert judgment depends heavily on the quality of the expert's cognitive representation of the domain and ability to express knowledge. The elicitation of expert judgment is a form of data collection that can be scrutinized; the use of the judgments can, and should, also be scrutinized.20
We agree. We must scrutinize the expert as we would any other measurement instrument. We consider the cybersecurity expert to be an essential and ultimately irreplaceable component of any risk analysis. Even as new data sources emerge that will allow even more quantitative analysis of risks, cybersecurity will continue to rely on cybersecurity experts for the foreseeable future. It is because of the key role trained experts will have that we need to take special notice of their performance at various critical tasks. And just as we would not rely on only a measurement instrument to measure its own accuracy, we cannot rely on the experts themselves to evaluate their own performance.
As we did earlier, we will begin by looking at existing research on the topic. We want to consider the tools that experts use and whether they actually help or harm the value of their judgment.
The Subjective Probability Component
A critical component of risk analysis is cybersecurity experts’ assessment of the likelihoods of events, such as cybersecurity breaches, and the potential costs if those events occur. Whether they are using explicit probabilities or nonquantitative verbal scales, they need to judge whether one kind of threat is more likely than another. Since we will probably have to rely on the expert at some level for this task, we need to consider how the experts’ skill at this task can be measured and what those measurements show.
This is a well‐documented area of research based on recorded judgments of experts and nonexperts in many different fields. Every study takes a similar approach. Large numbers of estimates are collected from individuals and then compared to observed outcomes. The findings are conclusive and repeated by every study that looks at this issue:
- Without training or other controls, almost all of us would assign probabilities that deviate significantly from observed outcomes (e.g., of all the times we say we are 90% confident, the predicted outcome happens much less frequently than 90% of the time).
- There are methods, including training, that greatly improve the ability of experts to estimate subjective probabilities (e.g., when they say they are 90% confident, they turn out to be right about 90% of the time).
One example related to research in a different profession, that of corporate chief financial officer (CFO), illustrates the typical findings of these studies. Researchers in a 2010 study at the National Bureau of Economic Research asked CFOs to provide estimates of the annual returns on the S&P 500.21 These estimates were in the form of ranges—given as a lower bound and an upper bound—of values that were wide enough that the CFO believed they had an 80% chance that the range would contain the correct answer. We can refer to these as 80% confidence intervals (CI).22 By simply waiting, it was easy to confirm what the actual return was over a given period of time. Although the CFOs were extremely experienced and well educated for their positions, their 80% CIs actually contained the true answers only 33% of the time. They believed that they provided ranges that would not contain the correct answer only 20% of the time, but in fact the answers were outside of their bounds 67% of the time. This is a rate of “surprise” much higher than they expected.
This is a measure of overconfidence. The confidence of experts, in this case expressed in the width of an 80% CI, contained the correct answer much less often than the experts expected. In other words, they did not have the 80% chance they thought they had of the stated interval containing the eventually observed value. Unfortunately, this phenomenon is not limited to CFOs. Several studies over the last several decades confirm that overconfidence is a pervasive characteristic of nearly all of us. Calibrated probability assessments have been an area of investigation since the 1970s by a large body of published research, led at first by Daniel Kahneman and Amos Tversky.23 Their research showed that almost all people in many different professions are about as overconfident as the previously mentioned CFOs.
This research is not purely academic. It affects real‐world judgments and affects actions taken to solve real problems. One of the authors (Hubbard) has had the opportunity over the last 20 years to collect one of the largest data sets regarding this phenomenon. Hubbard has tested and trained over 2,000 individuals from several different industries, professions, and levels of management. As mentioned earlier, over 150 of the subjects in these studies were specifically in the field of cybersecurity at the time of this writing.
To measure how well experts assigned subjective probabilities, Hubbard gave them a series of tests similar to those in most other studies. In an initial benchmark test (conducted before any training meant to improve estimation skills), Hubbard would ask the participants their 90% CIs for estimates of general trivia knowledge (e.g., when was Isaac Newton born, how many meters tall is the Empire State Building, etc.). Most individuals provided ranges that only contained about 40% to 50% of the correct answers, similar to what the previously mentioned researchers had observed.24
Overconfidence is also observed when applying probabilities to discrete events—such as whether a cyberattack will result in a major data breach this year. Of course, the outcome of a single event is generally not a good indicator of how realistic a previously stated probability happens to be. If we say that an event is 25% likely to occur by the end of next year, whether it happens or not is not proof the probability was unrealistic. But if we track a number of experts making many probability assessments, then we can compare expectations to observations in a more valid manner.
Suppose, for example, a group of experts gives 1,000 estimates of probabilities of specifically defined events. These could be data breaches of a certain minimum size occurring during a defined period, the probability of loss greater than $10 million, and so on. Suppose for 100 of those estimates they said they were 90% certain of the outcome. Then the stated outcome should have happened about 90 out of 100 times. We would expect some variation just due to random luck, but we can compute (as we will show later) how much random error is acceptable. On the other hand, if they are right only 65 out of 100 times they said they were 90% confident, that result is a lot worse than what we would expect by just bad luck (if only bad luck were at play, there is only a 1 in 68.9 billion chance that they would be wrong that often). So the much more likely explanation would be that the experts are simply applying far too high a probability to events they should be less certain about. Fortunately, other researchers have run experiments showing that experts can be trained to be better at estimating probabilities by applying a battery of estimation tests, giving the experts a lot of quick, repetitive, clear feedback along with training in techniques for improving subjective probabilities.25 In short, researchers discovered that assessing uncertainty is a general skill that can be taught with a measurable improvement. That is, when calibrated cybersecurity experts say they are 85% confident that a major data breach will occur in their industry in the next 12 months, there really is an 85% chance it will occur.
Again, the breadth of different people that have been measured on this “component” includes not just CFOs but also physicians, engineers, intelligence analysts, students, scientists, project managers, and many more. So it is reasonable to say that these observations probably apply to everyone. Remember, just in case someone was to try to make the case that cybersecurity experts were different from all the other fields that have been measured, Hubbard's data does include over 150 cybersecurity experts from many industries. They do about as poorly as any other profession on the first test. We also observe that they improve dramatically during the training, just like those in every other field Hubbard has tested, and about the same share succeed in becoming calibrated by the end of the training (85% to 90% of experts become calibrated).
In Chapter 7, we will describe this training and its effects in more detail. We will explain how you can calibrate yourself with some practice and how you can measure your performance over time. This skill will be a starting point for developing more advanced quantitative models.
The Expert Consistency Component
Ultimately, testing subjective probabilities for calibration relative to overconfidence means waiting for observed outcomes to materialize. But another type of calibration can be observed very quickly and easily without necessarily waiting for the predicted outcomes to happen or not: we can measure the consistency of the expert. That is, independent of whether the judgment was accurate, we should also expect the expert to give the same answer consistently when given the exact same situation. Of course, consistent answers do not mean the answers are any good, but we know that two contradictory answers cannot both be correct. The amount of inconsistency must be at least a lower bound for estimation error. In one extreme, if “experts” give wildly different answers every time they look at the exact same issue, then this would be indistinguishable from someone who ignores the information they are given and randomly picks estimates from slips of paper in a bowl. We don't have to wait for predicted events to occur in order to evaluate the consistency of that expert. Likewise, even if researchers are perfectly consistent with their own previous judgments but give very different answers than other experts, again, we at least know they can't all be right (of course they could all be wrong). Fortunately, these components of expert performance have also been measured at length. Researchers in the 1960s have given names to both of these measures of consistency:26
- Stability: an expert's agreement with their own previous judgment of the identical situation (same expert, same data, different time);
- Consensus: an expert's agreement with other experts (same data, different experts).
In more recent work, Daniel Kahneman summarized research in this area in his book Noise: A Flaw in Human Judgment.27 He refers to the lack of stability as “occasion noise,” and he splits the lack of consensus into “level noise” and “pattern noise,” but otherwise the concepts and findings are consistent with the earlier research.
In every field tested so far, it has been observed that experts are highly inconsistent—both in stability and consensus—in virtually every area of judgment. This inconsistency applies whether it relates to project managers estimating costs, physicians diagnosing patients, or cybersecurity experts evaluating risks.
In an early twentieth‐century example of this expert consistency measurement, researchers gave several radiologists a stack of 96 x‐rays of stomach ulcers.28 Each radiologist was asked to judge whether the ulcer was a malignant tumor. A week later the same radiologists were given another set of 96 x‐rays to assess. Unbeknownst to the radiologists, they were actually the same x‐rays as before but in a different order. Researchers found that radiologists changed their answers 23% of the time.
If we ask an expert in such a situation whether the arbitrary order of the list should have any bearing on their judgments, they would all agree that it should not. And yet the research tells us that the arbitrary order of lists like this actually does affect their judgments.
A particular source of inconsistency appears in another common type of judgment. When estimating numbers, the expert can be influenced by an effect known as “anchoring.” Simply thinking of one number affects the value of a subsequent estimate even on a completely unrelated issue. Researchers showed how using arbitrary values, such as one's Social Security number or a randomly generated number, affects subsequent estimates of, for instance, the number of doctors in an area or the price of things on eBay.29,30
Why shouldn't random, irrelevant factors like anchoring also affect the judgment of cybersecurity experts? We've had a lot of opportunity to gather information on that point, and a summary of this data follows:
- In multiple separate projects by the time of this writing, Hubbard and his staff calibrated over 150 cybersecurity experts from over 20 organizations and asked them to estimate the probabilities of various types of cybersecurity events. The projects were for clients from six different industries: oil and gas, banking, higher education, insurance, retail, and health care. Each of these experts had previously completed calibrated probability‐assessment training.
- Each expert was given some descriptive data for 80 to 200 different systems or threat scenarios in the organization. The types of scenarios and the data provided varied among the clients, but it could include information about the type of data at risk, the operating systems involved, types of existing controls, the types and numbers of users, and so on.
- For each of these systems, scenarios, or controls, each expert was asked to assess the probabilities of up to six different types of events including confidentiality breaches, unauthorized editing of data, unauthorized transfer of funds, theft of intellectual property, availability outages, and how much a control might reduce a likelihood or impact.
- In total, for all of the experts surveyed assessing between two and six probabilities for each of 80 to 200 situations, we have more than 60,000 individual assessments of probabilities.
What the experts were not told at the time they were providing these estimates is that the list they were given included some duplicate pairs of scenarios. In other words, the data provided for the system in the ninth row of the list might be identical to the data provided in the ninety‐fifth row, the eleventh might be the same as the eighty‐first, and so on. Each expert had several duplicates in the list, totaling over 3,700 duplicate pairs by the time of this writing.
To measure inconsistency, we simply needed to compare the first estimate the expert provided with their second estimate for the identical scenario. Figure 4.1 shows how the first and second estimates of identical scenarios compare. To better display the concentration of a large number of points in the same locations of this chart, we added a bit of random noise around each point so that they don't all plot directly on top of one another. But the noise added is very small compared to the overall effect, and the noise is only for the display of this chart (it is not used in the statistical analysis of the results).
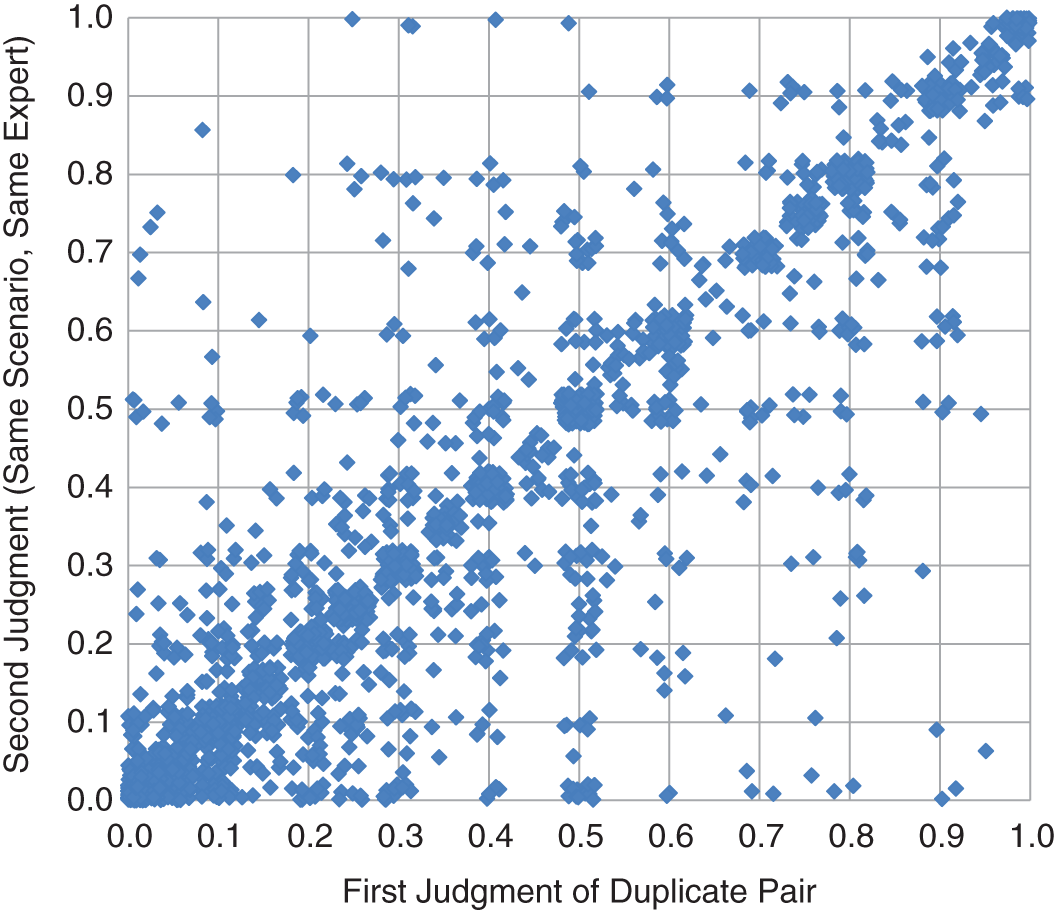
FIGURE 4.1 Duplicate Scenario Consistency: Comparison of First and Second Probability Estimates of Same Scenario by Same Judge
What we observe is that 26% of the time, there was a difference greater than 10 percentage points between the first and second estimate—for example, the first estimate was 15% and the second was 26%. Some differences were much more extreme. There were even 2.7% where the difference was greater than 50 percentage points. See Figure 4.2 for a summary of these response inconsistencies.
As inconsistent as this may seem, it's actually worse than it looks. We have to compare this inconsistency to the “discrimination” of the expert. That is, how much do the experts’ responses vary for a given type of event? The probabilities estimated varied substantially by the type of risk being assessed. For example, availability risk (a system going down) was generally given probabilities that were higher than an integrity risk where someone could actually steal funds with unauthorized transactions. If all of the responses of the expert only varied between, say, 2% and 15% for a given type of risk (say, the chance of a major data breach), then a 5 or 10 percentage point inconsistency would make up a large part of how much the judge varied their answers.
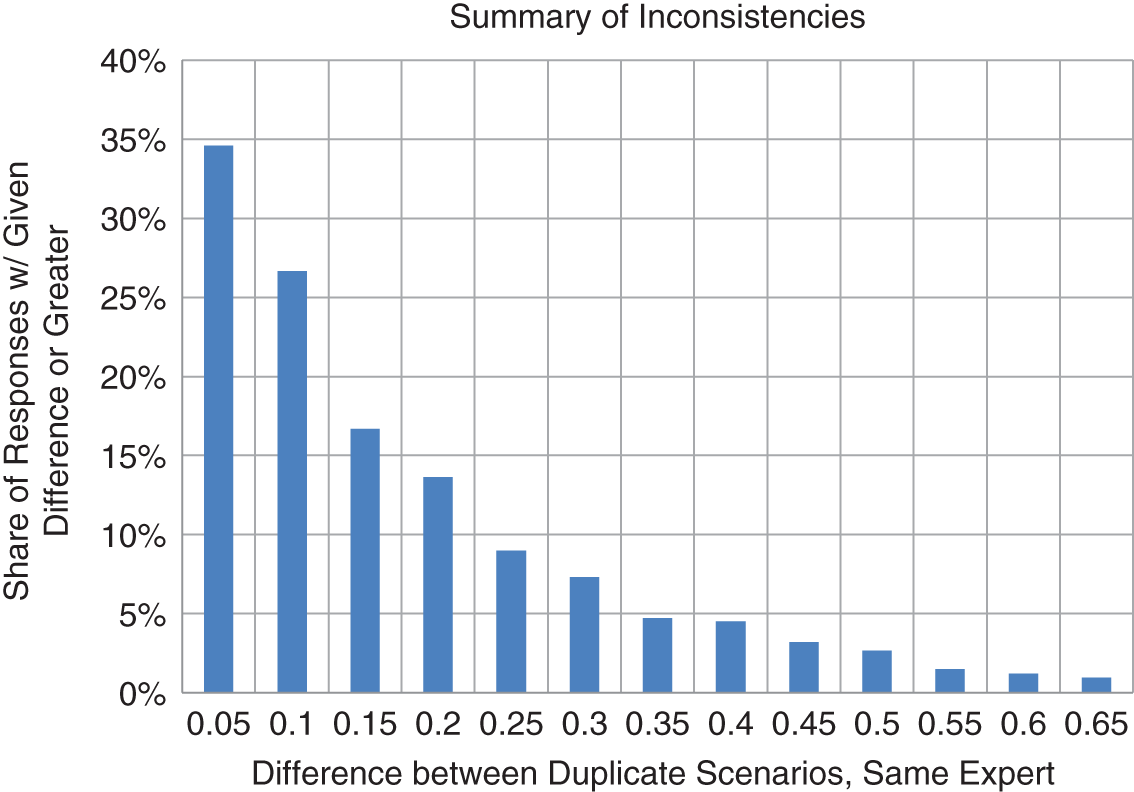
FIGURE 4.2 Summary of Distribution of Inconsistencies
Consistency is partly a measure of how diligently the expert is considering each scenario. For some of the experts, the inconsistency accounted for most of the discrimination. Note that if inconsistency equaled discrimination, this would be what we would observe if an expert were just picking probabilities at random regardless of the information provided. In our surveys, most judges appeared to at least try to carefully consider the responses with the information provided. Still, we see that inconsistency accounts for at least 21% of discrimination. That is a significant portion of the expert's judgment reflecting nothing more than personal inconsistency.
We should note that a small percentage of the duplicates were discovered by the participants. Some would send an email saying, “I think there is an error in your survey. These two rows have identical data.” But nobody who found a duplicate found more than two, and most people discovered none. More importantly, the discovery of some duplicates by the estimators would only serve to reduce the observed inconsistency. The fact that they happened to notice some duplicates means that their consistency was measured to be higher than it otherwise would have been. In other words, inconsistency is at least as high as we show, not lower.
Fortunately, we can also show that this inconsistency can be reduced, and this will result in improved estimates. We can statistically “smooth” the inconsistencies of experts using mathematical methods that reduce estimation error of experts. The authors have had the opportunity to apply these methods specifically in cybersecurity (the inconsistency data shown in Figure 4.1 were from real‐world projects where we applied these methods). We will describe these methods in more detail later in the book.
The Collaboration Component
We just saw that there is a lot of data about subjective judgments of individual experts, but there is also interesting research about how to combine the judgments of many experts. Perhaps the most common method of combining expert judgments is sometimes referred to in the US military as the “BOGSAT” method—that is, the “Bunch of Guys Sitting Around Talking” method (excuse the gender specificity). The experts meet in a room and talk about how likely an event would be, or what its impact would be if it occurred, until they reach a consensus (or at least until remaining objections have quieted down).
We can apply different mathematical methods for combining judgments and different ways to allow for interaction among the experts. So as we've done with the other component tests, we ask whether some methods are shown to measurably outperform others.
Some research, for example, shows that the random stability inconsistencies of individuals can be reduced by simply averaging several individuals together.31 Instead of meeting in the same room and attempting to reach consensus as a group, each expert produces their own estimate independently, and their estimates are averaged together.
This approach and some of the research behind it were explained in the book The Wisdom of Crowds by James Surowiecki.32 Surowiecki also described several other collaboration methods, such as “prediction markets,”33 which show a measurable improvement over the estimates of individual experts.
The same data that allowed Hubbard Decision Research to measure expert stability was also able to measure consensus. If judges were simply personally inconsistent—that is, they had low stability—we would expect disagreements between judges solely due to random personal inconsistency. However, the actual total disagreement between experts was more than could be accounted for by stability alone. In addition to being personally inconsistent, experts in the same organization also had systemic disagreements with each other about the importance of various factors and the overall risk of cybersecurity attacks.
It is interesting to note, however, that cybersecurity experts at a particular organization provided responses that were somewhat correlated with their peers at the same organization. One expert may have estimated the probability of an event to be consistently higher than their peers, but the same information that caused them to increase or decrease a probability also had the same effect on other experts. At least they were more or less in agreement “directionally.” So we do not observe that different experts behave as if they were just randomly picking answers. They agree with each other to some degree and, as the previous research shows, they can predict outcomes better if we can average several experts together.
In addition to simple averaging of multiple experts, there are some powerful methods that outperform averaging. In Chapter 7, we will discuss other various methods for combining estimates from multiple experts. Some “expert aggregation” methods are consistently better than averaging and even better than the best individual expert.
The Decomposition Component
We have already seen that experts don't perform as well as statistical models based on objective, historical data. But what about quantitative models that are still based on subjective estimates? Is it possible for experts to build models, using only their current knowledge, that outperform how they would have done without the quantitative models? The research says yes.
From the 1970s to the 1990s, decision science researchers Donald G. MacGregor and J. Scott Armstrong, both separately and together, conducted experiments about how much estimates can be improved by decomposition.34 For their various experiments, they recruited hundreds of subjects to evaluate the difficulty of estimates such as the circumference of a given coin or the number of pairs of men's pants made in the United States per year. Some of the subjects were asked to directly estimate these quantities, while a second group was instead asked to estimate decomposed variables, which were then used to estimate the original quantity. For example, for the question about pants, the second group would estimate the US population of men, the number of pairs of pants men buy per year, the percentage of pants made overseas, and so on. Then the first group's estimate (made without the benefit of decomposition) was compared to that of the second group.
Armstrong and MacGregor found that decomposition didn't help much if the estimates of the first group already had relatively little error—like estimating the circumference of a US 50‐cent coin in inches. But where the error of the first group was high—as they were with estimates for men's pants manufactured in the United States, or the total number of auto accidents per year—then decomposition was a huge benefit. They found that for the most uncertain variables, a simple decomposition—none of which was more than five variables—reduced error by a factor of as much as 10 or even 100. Imagine if this were a real‐world decision with big uncertainties. Decomposition itself is certainly worth the time.
Doing the math explicitly, even if the inputs themselves were subjective estimates, removes a source of error. If we want to estimate the monetary impact of a denial‐of‐service attack on a given system, we can estimate the duration, the number of people affected, and the cost per unit of time per person affected. Once we have these estimates, however, we shouldn't then just estimate the product of these values—we should compute the product. Since, as we have shown earlier, we tend to make several errors of intuition around such calculations, we would be better off just doing the math in plain sight. It seemed obvious to many of the researchers that we are better off doing whatever math we would have done in our heads explicitly. As Meehl mentioned in one of his papers:
“Surely, we all know that the human brain is poor at weighting and computing. When you check out at a supermarket, you don't eyeball the heap of purchases and say to the clerk, ‘Well it looks to me as if it's about $17.00 worth; what do you think?’ The clerk adds it up.”35
Still, not all decompositions are as informative. It is possible to “over‐decompose” a problem.36 The reason we decompose is that we have less uncertainty about some things than we do others, and we can compute the latter based on the former. If, however, we do not have less uncertainty about the variables we decompose the problem into, then we may not be gaining ground. In fact, a bad decomposition could make things worse. In Chapter 6, we will discuss what we call “uninformative decompositions” in more detail. Even assuming your decompositions are useful to you, there are several decomposition strategies to choose from, and we will start with no particular position about which of these decompositions are more informative. The best decomposition method may vary from one organization to the next as the information they have varies. But, as we will see in Chapter 6, there are some hard mathematical rules about whether a decomposition actually reduces uncertainty. We should use these rules as well as empirically measured performance to determine the best method of decomposition for a given organization.
Summary and Next Steps
“In my experience …” is generally the start of a sentence that should be considered with caution, especially when applied to evaluating the expert themselves. There are reasons why our experiences, even when they add up to many decades, may not be a trustworthy source of information on some topics. Because of the analysis placebo, we cannot evaluate ourselves in estimation tasks simply by whether we feel better about it. Evaluating experts and the methods they use will require that we look at the scientific research behind them. And the research clearly points to the following conclusions:
- Wherever possible, explicit, quantitative models based on objective historical data are preferred. The role of experts primarily would be to design and set up these models instead of being responsible for individual estimates.
- Where we need to estimate probabilities and other quantities, experts can be trained to provide subjective probabilities that can be compared to observed reality.
- The inconsistency of experts can be moderated with mathematical and collaborative methods to get an improvement in estimates. When using multiple experts, even simple averages of experts appear to be an improvement over individual experts.
- Decomposition improves estimates, especially when faced with very high uncertainty. Models that force calculations to be explicit instead of “in the head” of the expert avoid many of the inference errors that experts tend to make.
In this chapter, our measurements of different risk assessment methods have focused on previously published scientific research into individual components of risk assessment processes, including alternative tools for estimating probabilities (using experts or algorithms), how to control for inconsistencies, how to collaborate, and the effects of decomposition. We have focused entirely on components where we have research showing how alternative methods measurably improve results.
Every component of the methods we introduced in Chapter 3, and everything we introduce from this point forward, will be guided by this research. We are adopting no method component that doesn't have some research supporting it. Just as importantly, we are adopting no methods that have been shown to add error. The importance of cybersecurity risk assessment requires that we must continue to seek improvements in our methods. We must persist in the kind of skepticism that forces us to ask, “How do I know this works?”
Later, we will describe how to go beyond existing research to track your own data in a statistically sound manner that can further reduce uncertainty and allow you to continuously improve your risk assessment methods. In the next chapter we will continue with a component‐level analysis based on existing research, but we will focus on those methods that either show no improvement—or even make things worse. We need to do this because these components are actually part of the most widely used methods and standards in cybersecurity. So it is time we addressed these issues head on, along with responding to common objections to using the quantitative methods we just recommended.
Notes
- 1. C. Tsai, J. Klayman, and R. Hastie, “Effects of Amount of Information on Judgment Accuracy and Confidence,” Organizational Behavior and Human Decision Processes 107, no. 2 (2008): 97–105.
- 2. Stuart Oskamp, ”Overconfidence in Case‐Study Judgments,” Journal of Consulting Psychology 29, no. 3 (1965): 261–265, doi:10.1037/h0022125. Reprinted in Judgment under Uncertainty: Heuristics and Biases, eds. Daniel Kahneman, Paul Slovic, and Amos Tversky (Cambridge, UK: Cambridge University Press, 1982).
- 3. P. Andreassen, “Judgmental Extrapolation and Market Overreaction: On the Use and Disuse of News,” Journal of Behavioral Decision Making 3, no. 3 ( July–September 1990): 153–174.
- 4. C. Heath and R. Gonzalez, “Interaction with Others Increases Decision Confidence but Not Decision Quality: Evidence against Information Collection Views of Interactive Decision Making,” Organizational Behavior and Human Decision Processes 61, no. 3 (1995): 305–326.
- 5. D. A. Seaver, “Assessing Probability with Multiple Individuals: Group Interaction versus Mathematical Aggregation,” Report No. 78–3 (Los Angeles: Social Science Research Institute, University of Southern California, 1978).
- 6. S. Kassin and C. Fong, “I'm Innocent!: Effects of Training on Judgments of Truth and Deception in the Interrogation Room,” Law and Human Behavior 23 (1999): 499–516.
- 7. Paul E. Meehl, Clinical versus Statistical Prediction: A Theoretical Analysis and a Review of the Evidence (Minneapolis: University of Minnesota Press, 1954).
- 8. R. M. Dawes, D. Faust, and P. E. Meehl, “Clinical versus Actuarial Judgment,” Science (1989), doi:10.1126/science.2648573.
- 9. William M. Grove and Paul E. Meehl, “Comparative Efficiency of Informal (Subjective, Impressionistic) and Formal (Mechanical, Algorithmic) Prediction Procedures: The Clinical‐Statistical Controversy,” Psychology, Public Policy, and Law 2 (1996): 293–323.
- 10. William M. Grove et al., “Clinical versus Mechanical Prediction: A Meta‐Analysis,” Psychological Assessment 12, no. 1 (2000): 19–30.
- 11. Paul Meehl, “Causes and Effects of My Disturbing Little Book,” Journal of Personality Assessment 50 (1986): 370–375.
- 12. William Bailey et al., “Taking Calculated Risks,” Oilfield Review 12, no. 3 (Autumn 2000): 20–35.
- 13. G. S. Simpson et al., “The Application of Probabilistic and Qualitative Methods to Asset Management Decision Making,” presented at SPE Asia Pacific Conference on Integrated Modelling for Asset Management, April 25–26, 2000, Yokohama, Japan.
- 14. C. W. Freaner et al., “An Assessment of the Inherent Optimism in Early Conceptual Designs and Its Effect on Cost and Schedule Growth.” Paper presented at the Space Systems Cost Analysis Group/Cost Analysis and Forecasting/European Aerospace Cost Engineering Working Group 2008 Joint International Conference, European Space Research and Technology Centre, Noordwijk, The Netherlands, May 15–16, 2008, European Space Agency, Paris, France.
- 15. Philip E. Tetlock, Expert Political Judgment: How Good Is It? How Can We Know? (Princeton, NJ: Princeton University Press, 2005; Kindle edition, location 869).
- 16. Robyn Dawes, House of Cards: Psychology and Psychotherapy Built on Myth (New York: Simon & Schuster, 1996).
- 17. Amos Tversky and Daniel Kahneman, “Belief in the Law of Small Numbers,” Psychological Bulletin 76, no. 2 (1971): 105–110.
- 18. Daniel Kahneman and Amos Tversky, “Subjective Probability: A Judgment of Representativeness,” Cognitive Psychology 3 (1972): 430–454.
- 19. William M. Grove and Paul E. Meehl, “Comparative Efficiency of Informal (Subjective, Impressionistic) and Formal (Mechanical, Algorithmic) Prediction Procedures: The Clinical–Statistical Controversy,” Psychology, Public Policy, and Law 2 (1996), 293–323; #167.
- 20. Herren DeWispelare and Clemen Bonano, “Background Report on the Use and Elicitation of Expert Judgement,” prepared for Center for Nuclear Waste Regulatory Analyses under Contract NRC‐02–93–005, September 1994.
- 21. I. Ben‐David, J. R. Graham, and C. R. Harvey, Managerial Miscalibration (No. w16215) (Washington, DC: National Bureau of Economic Research, 2010).
- 22. Some authors would prefer that we distinguish a confidence interval computed from data from a subjectively estimated interval. They may use the terms “subjective confidence interval” or “a credible interval” for finer distinctions. We, however, will use the term “confidence interval” as an expression of uncertainty, whether that uncertainty is derived from expert opinion or from analysis of objective data.
- 23. D. Kahneman and A. Tversky, “Subjective Probability: A Judgment of Representativeness,” Cognitive Psychology 4 (1972): 430–454; D. Kahneman and A. Tversky, “On the Psychology of Prediction,” Psychological Review 80 (1973): 237–251.
- 24. This benchmark is based on only a sample size of 10 per person. Ten may sound like a small test to begin with, but if a person were well calibrated—such that there was actually a 90% chance that the correct value would fall within the stated ranges—there is only a 1 in 611 chance of getting 5 or fewer out of 10 questions with the answers in the stated range. In other words, the sample size is more than sufficient to detect the level of overconfidence that most professionals have.
- 25. Sarah Lichtenstein, Baruch Fischhoff, and Lawrence D. Phillips, “Calibration of Probabilities: The State of the Art to 1980,” in Judgement under Uncertainty: Heuristics and Biases, eds. Daniel Kahneman, Paul Slovic, and Amos Tversky (Cambridge, UK: Cambridge University Press, 1982).
- 26. L. Goldberg, “Simple Models or Simple Processes?: Some Research on Clinical Judgments,” American Psychologist 23, no. 7 ( July 1968).
- 27. Daniel Kahneman, Olivier Sibony, Cass R. Sunstein, Noise: A Flaw in Human Judgment (Little, Brown and Company. Kindle Edition, p. 73).
- 28. Paul J. Hoffman, Paul Slovic, and Leonard G. Rorer, “An Analysis‐of‐Variance Model for the Assessment of Configural Cue Utilization in Clinical Judgment,” Psychological Bulletin 69, no. 5 (1968): 338.
- 29. Amos Tversky and Daniel Kahneman, “Judgment under Uncertainty: Heuristics and Biases,” Science 185, no. 4157 (1974): 1124–1131.
- 30. D. Ariely et al., “Coherent Arbitrariness: Stable Demand Curves without Stable Preferences,” The Quarterly Journal of Economics 118, no. 1 (2003): 73–106.
- 31. R. Clemen and R. Winkler, “Combining Probability Distributions from Experts in Risk Analysis,” Risk Analysis 19 (1999): 187–203.
- 32. James Surowiecki, The Wisdom of Crowds (New York: Anchor, 2005).
- 33. In prediction markets, a large number of people can bid on a kind of coupon that pays off if a particular defined event occurs. The market price of the coupon reflects a kind of estimate of the event coming true, whether it is who will be the next US president or who wins the Oscars or World Cup. If the coupon pays one dollar if and when the event comes true and the current market price is 25 cents, then the market is behaving as if it believes the event has approximately a 25% chance of coming true. There are practical constraints on using something like this in cybersecurity (someone may be able to rig the market by bidding on coupons for an event they later cause themselves). But it shows how some forms of collaboration may outperform others.
- 34. Donald G. MacGregor and J. Scott Armstrong, “Judgmental Decomposition: When Does It Work?” International Journal of Forecasting 10, no. 4 (1994): 495–506.
- 35. Paul Meehl, “Causes and Effects of My Disturbing Little Book,” Journal of Personality Assessment 50 (1986): 370–375.
- 36. Michael Burns and Judea Pearl, “Causal and Diagnostic Inferences: A Comparison of Validity,” Organizational Behavior and Human Performance 28, no. 3 (1981): 379–394.
