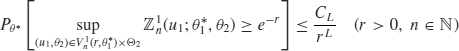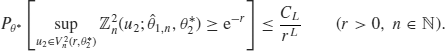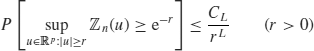4

Statistical Inference for Volatility and Related Limit Theorems

Nakahiro Yoshida

4.1 INTRODUCTION

This chapter provides a brief overview of some recent developments in statistical inference for stochastic processes from probabilistic and statistical aspects. We will discuss mainly three topics, that is, quasi likelihood analysis for semimartingales, nonsynchronous covariance estimation, and asymptotic expansion that can apply to finance.

In Sections 4.2 and 4.3, we will discuss quasi likelihood analysis (QLA) for semimartingales. In this article, the QLA means an asymptotic theory that provides asymptotic distribution of the quasi maximum likelihood and quasi Bayesian estimators (polynomial type), large deviation estimates for the quasi likelihood random field, and tail probability estimates for these estimators with their convergence of moments as a result. One cannot avoid such kinds of tail probability estimates when developing the very basic fields in standard theoretical statistics.

Section 4.4 is devoted to the problem of nonsynchronous covariance estimation. Statistical inference for stochastic processes under an irregular sampling scheme requires new developments in limit theorems. Among various irregularities, the nonsynchronicity gives challenging problems. Ad hoc interpolation causes bias in covariance estimation. The problem is how to construct a suitable estimator and to prove probabilistic performance of the estimator. Nonsynchronicity is not standard in stochastic analysis in which time related to measurability is rigid. However, the model is defined in terms of the stochastic analysis and we need it to address limit theorems under the nonsynchronicity. What is most important in the nonsynchronous estimation is that this concept has brought relativization of time. The concept of lead-lag can be treated thanks to the relativization.

In Section 4.5, we will briefly mention Project YUIMA II in order to develop an R-package YUIMA for statistical inference and simulation for stochastic differential equations.

An asymptotic expansion scheme gives a numerical method in option pricing. In Section 4.6, we will discuss this scheme. There are three approaches: martingale expansion (global approach), mixing expansion (local approach), and small σ expansion (perturbation method). The third method has already been applied to option pricing and implemented by the YUIMA package. Recently an essential progress was made for martingale expansion. The estimator of the volatility parameter has an asymptotically mixed normal distribution, in general. In order to go into a further approximation, we need a method that gives asymptotic expansion in the mixed normal limit. A new device is necessary since classical methods of asymptotic expansion cannot apply in this situation.

4.2 QLA FOR AN ERGODIC DIFFUSION PROCESS

Consider a d-dimensional stationary diffusion process satisfying the stochastic differential equation

Here wt is an r-dimensional standard Wiener process independent of the initial value x0, and and are unknown parameters with . The distribution of x0 possibly depends on the parameters. The true value of the unknown parameter will be denoted by .

We assume the following condition.

[D1]

In this section, we assume a mixing property for X.

[D2] There exists a positive constant a such that

where

In order to estimate the unknown parameters with the discrete-time observations , where ti=ih with h=hn depending on , we consider a quasi-likelihood function

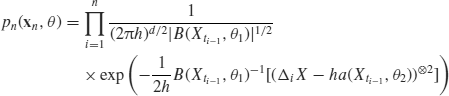
with .

For the sampling scheme, we will assume that , , and as . Moreover, we assume that for some positive constant , for large n.

The quasi log likelihood random field is defined by

(4.1)

The scaling limit of gives

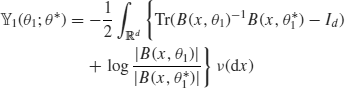
where ν is a unique invariant probability measure of X. The integrand on the right-hand side of the above equation is non-negative. An identifiability condition in the present situation is as follows:

Without this condition, we cannot expect the existence of a -consistent estimator of . A sufficient condition for [D3] is that the parametric model can be extended continuously to a compact set including and for .

The Ibragimov–Has'minskii–Kutoyants (Ibragimov and Has'minskii, 1972, 1973, 1981; Kutoyants (1984, 1994, 1998, 2004) program suggests that any asymptotic behavior of a QLA estimator is deduced from that of the statistical random field . Guided by this philosophy, we associate with the statistical random field

for . Let . Then the polynomial type large deviation (PLD) inequality (Yoshida, 2005) gives

(4.2)

for L>0, where CL is a constant depending on L.

Let us assume that can extend continuously to the boundary of . A typical estimator of the QLA is the quasi maximum likelihood estimator (QMLE) that maximizes in . Then as a consequence of (4.2), we obtain polynomial type large deviation estimates for the tail probability of . Indeed, if , then

and this event admits (4.2). In particular, this ensures the boundedness of the moments

for p>0. It should be noted that is any sequence of QMLEs.

Next, set

The scaling limit of yields

(4.3)

The identifiability of is as follows.

To deduce the properties of , we consider the statistical random field

for . The scaling is now . Let . Applying the PLD of Yoshida (2005) again, but this time for the statistical random fields , we obtain the PLD inequality

(4.4)

In quite the same way as for , Inequality (4.4) entails polynomial type large deviation estimates for the tail probability of , which corresponds to one of the maximizers of and equivalently the boundedness of the moments of the estimator:

for p>0.

Define random fields on by

where , and , . By the PLD inequalities, it is possible to extend to a random field on by a discounting factor and the extended random field becomes a random variable taking values in , the set of continuous functions that tends to 0 as . is a separable Banach space with uniform norm.

Set

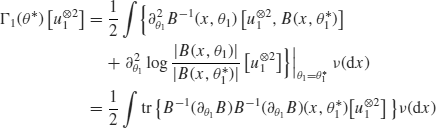
for , and

for .

Prepare random vectors (i=1, 2) such that and are independent. Define by

We denote by CR the space of continuous functions on {(u1, u2); and equip the uniform topology. It is easy to prove the weak convergence

(4.5)

in CR as for each R>0. In fact, the finite-dimensional convergence follows from a central limit theorem and tightness is easy to see on CR.1 Therefore, the PLD inequalities imply that the convergence (4.5) also takes place in . The convergence of follows from this convergence by the continuous mapping theorem. Since we already have the Lp-boundedness of the QMLE, we obtain the following theorem.

Theorem 1 For any sequence of the maximum likelihood type estimators for ,

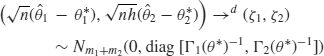
as . Moreover,

as for all continuous functions f of at most polynomial growth.

Prakasa Rao (1983, 1988) presented asymptotic results for an ergodic diffusion process under a sampling scheme. The joint weak convergence was presented in Yoshida (1992c) for a sampled diffusion process. Kessler (1997) applied a local Gaussian approximation with higher order correction terms to relax the rate of convergence of h to zero. Theorem 1 is from Yoshida (2005, 2006). Uchida (2010a) and Yoshida and Uchida (2010) proved convergence of moments of the adaptive quasi maximum likelihood estimators at a general sampling rate as well as the limit distribution. The tail probability estimate of polynomial type is inevitable for rigorously developing very basic asymptotic statistical theory, for example, prediction, model selection, asymptotic expansion, and higher-order decision theory among many fields involving such estimates. Uchida (2010b) proposed a contrast-based information criterion and proved its validity through technical arguments with the Malliavin calculus and the PLD. The PLD was applied in Masuda (2010) to drift estimation of a discretely observed Ornstein–Uhlenbeck process driven by a possibly heavy-tailed symmetric Lévy process with positive activity index.

The Ibragimov–Has'minskii–Kutoyants program applies to Bayesian type estimators for the diffusion process by the PLD. The adaptive Bayesian type estimator (ABE) is defined as follows. Here we only consider the quadratic loss function to make Bayesian estimators, for simplicity. Define a Bayesian type estimator by

where is a known dummy value of , and is a prior distribution of , bounded from below. Given the estimator for , we define a Bayesian type estimator by

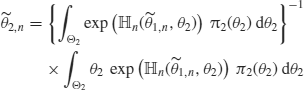
where is a prior distribution of , bounded from below. It is possible to replace by another suitable estimator of , in general, for our purpose. A simultaneous Bayesian type estimator can be defined. However, the ABE has a computational advantage because the dimension of integration is lower. It is crucial in practical applications.

By definition, we have

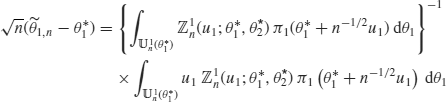
and a similar representation of . Since each Bayesian estimator consists of integrals of a random field and its asymptotic properties are available, we can investigate the asymptotic behavior of the Bayesian estimators.

Theorem 2 For the ABE for , it holds that

as . Moreover,

as for all continuous functions f of at most polynomial growth.

The adaptive Bayesian type estimator was defined in Yoshida (2005) and applied to the diffusion process. A simultaneous Bayesian type estimator was also treated. Ogihara and Yoshida (2011) proposed the QLA for the jump diffusion processes and proved limit theorems and convergence of moments for the ABE as well as the QMLE. The estimator that is characterized as a root of a random estimating equation, as it is often called a “Z-estimator”, is within our scope. Obviously, finding a root is reduced to a minimum/maximum optimization problem.

4.3 QLA FOR VOLATILITY IN THE FINITE TIME-HORIZON

Consider an m-dimensional Itô process satisfying the stochastic differential equation

(4.6)

where w is an r-dimensional standard Wiener process on some stochastic basis and b and X are progressively measurable processes with values in and , respectively. The process σ is an -valued function defined on , being a bounded domain in . For example, when bt=b(Yt, t) and Xt=(Yt, t), Y is a time-inhomogeneous diffusion process.

The unknown parameter θ will be estimated based on the data with tk=kh for h=hn=T/n. The process b is unobservable, completely unknown to the observer. Here T is fixed and consistent estimation of the drift term is impossible unless the diffusion is degenerate. This is a semiparametric estimation problem.

Asymptotic theory of estimation of the volatility parameter with high frequency data observed on a fixed interval has been developed. Dohnal (1987) showed the local asymptotic mixed normality (LAMN) property for the likelihood. Genon-Catalot and Jacod (1993, 1994) proposed contrast functions for diffusion processes, proving the asymptotic mixed normality of the minimum contrast estimator.

We will see the asymptotic mixed normality and convergence of moments of both the maximum likelihood type estimator and the Bayesian type estimator for a quasi-likelihood function. The Ibragimov–Has'minskii–Kutoyants scheme is applied. A key point is to obtain the polynomial type large deviation inequality for the statistical random field.

The quasi log likelihood function is given by

where , the nondegeneracy of which will be assumed. The unknown drift process b is not used.

The quasi maximum likelihood estimator is defined as

(4.7)

The quasi Bayesian estimator (QBE) for the prior density is defined by

(4.8)

We assume that is continuous and . The true value of θ is denoted by .

Let . Define the random field () by

Let

where with

and ζ is a -dimensional standard normal random variable independent of .

We need standard regularity conditions to derive asymptotic properties of the estimators though we do not write them here. See Uchida and Yoshida (2011) for details. That said, we should recall a problem of identifiability. A key index that evaluates the separation of statistical models is

where

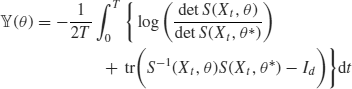
Naturally, the field came from . Differently from the ergodic case, is random since it involves Xt. A quantitative estimate of is necessary to construct a QLA that can catch more information about the estimators than just limit theorems. We set the following condition.2

Condition [H2] enables the PLD to be obtained for :

(4.9)

and the convergence

as for the extended , where ds means stable convergence (with respect to the original universe). Let ζ denote a -dimensional standard normal vector, on an extension of the original probability space, independent of .

In this way, we have for the QMLE

Theorem 3 (a) as . (b) For all continuous functions f of at most polynomial growth,

as .

For the QBE, by setting ,

(4.10)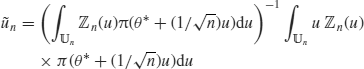

Let

(4.11)

Theorem 4 (a) as .(b) For all continuous functions f of at most polynomial growth,

as .

Condition [H2] implies the PLD inequality (4.9). The limit theorem with a mixed Gaussian limit and the tightness argument imply in for every R>0. The PLD plus implies the QLA in the above theorems. Hence, the problem is how to verify [H2]. A sufficient condition for [H2] is that

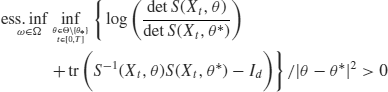
However, it is too naïve as it breaks, for example, in a simple model

This statistical model is completely degenerate at t=0. The state of separation between models strongly depends on randomness remaining in the limit. The existence of a local section of a certain tensor bundle validates [H2], even in such a nondegenerate case (Uchida and Yoshida, 2009, 2011).

For a concluding comment, there are still important questions related to QLA: jump diffusions in finite-time horizon, irregular sampling, nonsynchronous sampling, and inference under microstructure noise.

4.4 NONSYNCHRONOUS COVARIANCE ESTIMATION

4.4.1 Consistent estimator

Let be a two-dimensional Itô process defined on a stochastic basis with . A semiparametric problem is to estimate the (possibly random) “parameter” . If the two sequences of data are synchronously observed, the sum of products of increments of X and Y up to T

is a natural estimator of θ because it converges in probability to θ if the maximum lag of the time points tends to 0 in probability, as is well known. Indeed, we can regard RCOVT as a definition of [X, Y]T.

If the sampling times of X and Y are different, the estimation problem becomes nontrivial. In the nonsynchronous sampling scheme, we consider families and of partitions of the interval [0, T] corresponding to the observing times of X and Y, respectively.3 The increments are given by and .

If one wants to apply the “realized volatility” estimator to the nonsynchronous data, an interpolation such as previous-tick interpolation and linear interpolation will be necessary. However, it is known that such a naïve synchronization causes estimation bias. Nonsynchronicity causes the “Epps effect”.

For estimation of θ, Hayashi and Yoshida (2005) proposed

This estimator has some advantages. No interpolation is used so it does not depend on any tuning parameter such as the grid size. It is a finite sum and no cut-off number is involved. The summation is essentially one-dimensional. It attains asymptotically minimum variance.

Theoretical statistics requires some basic asymptotic properties: consistency of the estimator, asymptotic distribution of the error, efficiency and optimality, and precise approximation to the error distribution. The estimator is consistent: whenever (Hayashi and Yoshida, 2005; Hayashi and Kusuoka, 2008).

4.4.2 Functional limit theorem

We will discuss a limit theorem of the nonsynchronous covariance estimator. Suppose that (X, Y) satisfies the stochastic differential equations

on the stochastic basis . Here and are standard Wiener processes with correlation , and aX, aY, bX, bY, and are progressively measurable processes such that a.s. for every T>0.

Let and denote sampling times of X and Y, respectively. They are sequences of stopping times that are increasing a.s., and and S0=0, T0=0. We assume that the observation times depend on , e.g., Si=Si(n). We define a functional version of the nonsynchronous covariance process by

Write for an interval . The length of I is denoted by |I|. Let Ii=[Si−1, Si) and Jj=[Tj−1, Tj). We associate the sampling scheme {(Si), (Tj)} with the following nondecreasing functions:

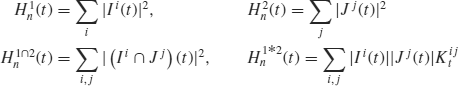
Assume that there exist positive numbers and random functions hk such that for every , as for , . Introducing a strong predictability of sampling times, Hayashi and Yoshida proved stable convergence of the nonsynchronous covariation process :

(4.12)

as , where is a Wiener process independent of and the process γ is given by

(4.13)

See Hayashi and Yoshida (2008a, 2008b, 2011) for details.

Example 1 (Poisson sampling) The partitions are given by independent Poisson random measures on [0, T] with intensities npi, i=1, 2. Suppose that is independent of (X, Y). If the functions , , and ρ are continuous, then the sequence converges in distribution to a centered Gaussian random variable with variance

For nonsynchronous covariance estimation, Malliavin and Mancino (2002) proposed a Fourier transform based estimator. Hoshikawa et al. (2008) compared the performance of various nonsynchronous covariance estimators. Mykland (2010) considered the HY-estimator from the aspect of Gaussian analysis. Bergomi (2010) pointed out the HY-estimator appears in the context of option pricing.

For nonsynchronicity with microstructure noise, Ubukata and Oya (2008) discussed detection of microstructure noise and estimation of the autocovariance. Robert and Rosenbaum (2010a, 2010b) gave a new insight into the nonsynchronous covariance estimator under microstructure noise, introducing the notion of the uncertainty zone. Recently, Bibinger (2011a, 2011b) proposed a rate-optimal estimator of a new version of the nonsynchronous covariance estimator to overcome the microstructure noise. There are many studies on variance estimation in the presence of microstructure noise. Among which are Zhou (1996), Bandi and Russell (2005), Bandi et al. (2008), Zhang et al. (2005), and Hansen and Lunde (2006).

As for the power and bipower variations, Barndorff-Nielsen and Shephard (2004) discussed robustness of the estimator. Barndorff-Nielsen et al. (2006) proved central limit theorems for power and bipower variations. Podolskij and Vetter (2009) provided a central limit theorem for the modulated bipower variation that has rate n1/4. Hayashi et al. (2008) proved asymptotic mixed normality for a general irregular sampling scheme.

It is possible to derive asymptotic expansion of the HY-estimator in the case without feedback to the diffusion coefficient, where the first order limit is central (Dalayan and Yoshida, 2011).

4.4.3 Application of YUIMA

In the R-package YUIMA (see Section 4.5), all simulation schemes, subsampling, and inference are designed to work on both regular or irregular sampling times. For an example, we apply YUIMA package to nonsynchronous covariance estimation. High frequency data consisting of nonsynchronously observed stock prices of four companies (“ba”, “ge”, “gm”, “cc”) were input and combined to make the YUIMA object “all.yuima”. We applied function “cce” to output covariance estimates for all pairs of companies, and obtained the table below.

4.4.4 Lead–lag estimation

What is most important in the nonsynchronous estimation is that this concept has brought relativization of time. If the observed multidimensional data had time lags between elements, the standard estimation methods for synchronously observed semimartingales would lose validity. Indeed, such a phenomenon is observed in high-frequency financial data. The lag estimation will be the first question in this situation.

Let and be Itô processes for a suitable filtration, and assume that is given by . Estimation of deserves investigation because it gives information of the leader/follower relation between two companies that is, when ; X is regarded as the leader and Y as the follower.

Suppose that X and Y are possibly nonsynchronously, randomly observed on the time interval [0, T] and write I and J for subintervals corresponding to two consecutive data of X and Y, respectively. Denote by the interval . Hoffmann et al. (2010) proposed the lead–lag estimator

where

We introduce parameter for asymptotic analysis. In typical examples, the intensities of the observation times on [0, T] are proportional to n. Write for . The intervals I and J form triangular arrays of sequences of subintervals depending on n. We can prove the consistency of with the rate of convergence.

Theorem 5 Under certain regularity conditions,

on the event for a sequence of positive constants tending to 0 as such that as . Here rn is the maximum length of the interarrival times of observations in [0, T].

The YUIMA package is equipped with the lead–lag estimator. We obtained lead–lag (s) and correlation between each pair of stock prices as follows.

ba-cc	1.4751087	0.2348809
ba-ge	−18.1460249	0.1311659
ba-gm	−4.1453611	0.1692068
cc-ge	−27.4679106	0.1760048
cc-gm	120.3912058	0.2170557
ge-gm	1.7497747	0.1282431

An extension to a multi-lag model is considered by Kato et al. (2011).

4.5 YUIMA II FOR STATISTICAL ANALYSIS AND SIMULATION FOR STOCHASTIC DIFFERENTIAL EQUATIONS

In modern finance, most of the theoretical results rely on the assumption that the underlying dynamics of asset prices, currencies exchange rates, interest rates, etc., are continuous time stochastic processes described by stochastic differential equations. Continuous time models are also at the basis of option pricing and this problem often requires Monte Carlo methods. Moreover, any computational method requires identification of a model by estimation or calibration in any case empirically from the real data. Most ready-to-use tools in computational finance rely on pure discrete time models, like ARCH, GARCH, etc., and very few examples of software handling continuous time processes in a general fashion are available also in the R community. There still exists a gap between what is going on in mathematical finance and applied finance. The YUIMA package is intended to fill this gap.

The Yuima II Project is an open source and collaborative effort of several mathematicians and statisticians aimed at developing the R package named YUIMA for inference and simulation of stochastic differential equations. The YUIMA package is an environment that follows the paradigm of methods and classes of the S4 system for the R language. The package can treat stochastic differential equations in a very general type, e.g., one or multidimensional, driven by Wiener process, fractional Brownian motion, and processes with or without jumps specified through Lévy processes.

The YUIMA package offers the infrastructure on which complex models and inference procedures can be built. In particular, the basic set of functions includes:

Proof-of-concept (but fully operational) examples of statistical procedures have been implemented, like change point analysis in volatility of stochastic differential equations, nonsynchronous covariance estimation, lead–lag estimation, various test statistics, and model selection. A preliminary version of YUIMA by Project YUIMA II is now available at R-forge https://r-forge.r-project.org/projects/yuima/.

A systematically constructed GUI facilitates data analysis and simulation for stochastic processes. NS Solutions Corporation and The Graduate School of Mathematical Sciences, University of Tokyo, are conducting a joint study (Azzurro Project) on “The Application of Advanced Mathematical Statistics Theories in the Financial Industry”. NS Solutions Corporation is developing financial software using a result of this study.

4.6 HIGHER ORDER ASYMPTOTICS AND FINANCE

4.6.1 Martingale expansion

For a process X=(Xt) defined by the stochastic integral equation

we consider a quadratic form of the increments of X with a strongly predictable kernel:

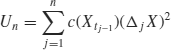
where and tj=j/n.

The asymptotic property is of interest as the realized volatility takes this form. For the normalized error

where , the limit theorem of mixed normal type is well known. Here we are interested in the second-order approximation of the distribution of Zn.

Zn admits the stochastic expansion

(4.14)

where

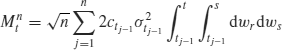
The expression of Nn is involved and omitted.

For a reference variable, we will consider the d1-dimensional random variable

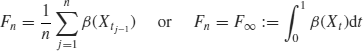
Asymptotic expansion of the distribution was presented by Yoshida (1997) for the variable (Zn, Fn) having the stochastic expansion (4.14) when . Joint distribution is inevitable in statistical applications. Related works are Mykland (1992, 1993). The expansion of Yoshida (1997) was applied to derive asymptotic expansion for an estimator of the linearly parameterized volatility. A distributional expansion was presented in Yoshida (2001) for martingales with jumps.

As mentioned above, the limit distribution of the realized volatility is mixed normal in general. This means that the statistics becomes “nonergodic”. The higher order inference theory in nonergodic statistics was not developed by lack of probabilistic devices. The classical methods for convergence to a process with independent increments do not work. Recently asymptotic expansion for a martingale with a mixed normal limit was obtained (Yoshida, 2008, 2010a).

Two random symbols and are used to describe the second order terms of asymptotic expansion. The adaptive random symbol corresponds to the classical second order term given in Yoshida (1997). The anticipative random symbol is new and it has a representation in terms of the Malliavin calculus. See Yoshida (2010a) or the site of Yoshida (2009, 2010b) for details. The full random symbol is given by

(4.15)

With this random symbol, the expansion formula is written by a certain adjoint operation:

(4.16)

where is Watanabe's delta function and rn=n−1/2 in the present case.

Theorem 6 Assume a certain nondegeneracy condition for (Zn, Fn). Then for any positive numbers M and γ,

as , where is the set of measurable functions satisfying for all .

While the formula (4.16) is general, the function pn(z, x) is very explicitly written in the present problem we started this section with. See the above mentioned papers.

It is possible to give the asymptotic expansion of the conditional law in the same framework we applied for the expansion of the joint law .

Statistical applications by the martingale expansion were presented in Yoshida (1997) and Sakamoto and Yoshida (1998a). Also see Fukasawa (2011) for finance. The martingale expansion is purely distributional; that is, the first order limit has a relationship to Zn only through distribution.

Another efficient but classical expansion of purely distributional type is mixing expansion in the central limit. There the underlying process is assumed to bear a mixing property. In this direction, see Kusuoka and Yoshida (2000) and Yoshida (2004) for asymptotic expansion of a functional of semimartingales. There are studies on this line (Sakamoto and Yoshida, 1998b, 2003, 2004, 2008, 2009, 2010; Uchida and Yoshida, 2001, 2006; Kutoyants and Yoshida, 2007). Masuda and Yoshida (2005) treated a stochastic volatility model.

4.6.2 Small σ expansion

Watanabe's theory (1987) was applied to statistical estimation problems for a stochastic differential equation with small perturbations (Yoshida, 1992b). Related studies are Yoshida (1993), Dermoune and Kutoyants (1995), Sakamoto and Yoshida (1996), Uchida and Yoshida (2004b), and Masuda and Yoshida (2004).

As for finance, this method was applied to option pricing in Yoshida (1992a) as a by-product of statistical applications. In this direction, there are many studies: Kunitomo and Takahashi (2001); Uchida and Yoshida (2004a); Takahashi and Yoshida (2004, 2005); Osajima (2006); Takahashi and Takehara (2009); Anderson and Hutchings (2009); Antonov and Misirpashaev (2009); Li (2010). A general asymptotic expansion formula for a functional of diffusion process is now available on YUIMA.

ACKNOWLEDGMENTS

This work was in part supported by Grants-in-Aid for Scientific Research No. 19340021; the Global COE program “The Research and Training Center for New Development in Mathematics” of the Graduate School of Mathematical Sciences, University of Tokyo; JST Basic Research Programs PRESTO; and by a Cooperative Research Program of the Institute of Statistical Mathematics. This chapter is a report for the author's talk at Asymptotic Statistics, Risk and Computation in Finance and Insurance, December 15, 2010. The author thanks the organizers of the conference for the opportunity to present the talk.

References

Andersen, L.B.G. and N.A. Hutchings (2009) Parameter Averaging of Quadratic SDES with Stochastic Volatility, Social Science Research Network.

Antonov, A. and T. Misirpashaev (2009) Projection on a Quadratic Model by Asymptotic Expansion with an Application to LMM Swaption, Social Science Research Network.

Bandi, F.M. and J.R. Russell (2005) Microstructure Noise, Realized Volatility, and Optimal Sampling.

Bandi, F.M., J.R. Russell and C. Yang (2008) Realized Volatility Forecasting and Option Pricing, Journal of Econometrics 147, 34–46.

Barndorff-Nielsen, O.E. and N. Shephard (2004) Power and Bipower Variation with Stochastic Volatility and Jumps, Journal of Financial Econometrics 2, 1–48.

Barndorff-Nielsen, O.E., S.E. Graversen, J. Jacod, M. Podolskij and N. Shephard (2006) A Central Limit Theorem for Realised Power and Bipower Variations of Continuous Semimartingales. In From Stochastic Calculus to Mathematical Finance, Springer, Berlin, pp. 33–68.

Bergomi, L. (2010) Correlations in Asynchronous Markets, Social Science Research Network, http://ssrn.com/abstract=1635866.

Bibinger, M. (2011a) Efficient Covariance Estimation for Asynchronous Noisy High-Frequency Data, Scandinavian Journal of Statistics 38, 23–45. DOI: 10.1111/j.1467-9469.2010.00712.x.

Bibinger, M. (2011b) An Estimator for the Quadratic Covariation of Asynchronously Observed Itô Processes with Noise: Asymptotic Distribution Theory, preprint.

Dalalyan A. and N. Yoshida (2011) Second-Order Asymptotic Expansion for a Non-synchronous Covariation Estimator, Annales de l'Institut Henri Poincaré, Probabilités et Statistiques 47(3), 748–789.

Dermoune, A. and Y. Kutoyants (1995) Expansion of Distribution of Maximum Likelihood Estimate for Misspecified Diffusion Type Observation, Stochastics Report 52(1–2), 121–145.

Dohnal, G. (1987) On Estimating the Diffusion Coefficient, Journal of Applied Probability 24(1), 105–114.

Fukasawa, M. (2011) Asymptotic Analysis for Stochastic Volatility: Martingale Expansion, Finance and Stochastics, 15(14), 635–654.

Genon-Catalot, V. and J. Jacod (1993) On the Estimation of the Diffusion Coefficient for Multidimensional Diffusion Processes. Annales de l'Institut Henri Poincaré, Probabilités et Statistiques 29(1), 119–151.

Genon-Catalot, V. and J. Jacod (1994) Estimation of the Diffusion Coefficient for Diffusion Processes: Random Sampling, Scandinavian Journal of Statistics 21(3), 193–221.

Hansen, P.R. and A. Lunde (2006) Realized Variance and Market Microstructure Noise, Journal of Business and Economic Statistics 24, 127–161.

Hayashi, T. and S. Kusuoka (2008) Consistent Estimation of Covariation Under Nonsynchronicity, Statistical Inference for Stochastic Processes 11, 93–106.

Hayashi, T. and N. Yoshida (2005) On Covariance Estimation of Non-synchronously Observed Diffusion Processes, Bernoulli Official Journal of the Bernoulli Society for Mathematical Statistics and Probability 11(2), 359–379.

Hayashi, T. and N. Yoshida (2008a) Asymptotic Normality of a Covariance Estimator for Nonsynchronously Observed Diffusion Processes, Annals of the Institute of Statistical Mathematics 60(2), 367–406.

Hayashi, T. and N. Yoshida (2008b) Nonsynchronous Covariance Estimator and Limit Theorem II, Institute of Statistical Mathematics, Research Memorandum 1067.

Hayashi, T. and N. Yoshida (2011) Nonsynchronous Covariance Process and Limit Theorems, Stochastic Processes and their Applications 121(10), 2416–2454.

Hayashi, T., J. Jacod and N. Yoshida (2008) Irregular Sampling and Central Limit Theorems for Power Variations: The Continuous Case, Preprint.

Hoffmann, M., M. Rosenbaum and N. Yoshida (2010) Estimation of the Lead–Lag Parameter From Non-Synchronous Data, to appear in Bernoulli.

Hoshikawa, T., K. Nagai, T. Kanatani and Y. Nishiyama (2008) Nonparametric Estimation Methods of Integrated Multivariate Volatilities, Econometric Reviews 27(1–3), 112–138.

Ibragimov, I.A. and R.Z. Has’minskii (1972) The asymptotic behavior of certain statistical estimates in the smooth case, I. Investigation of the likelihood ratio, Teor. Verojatnost. i Primenen 17, 469–486.

Ibragimov, I.A. and R.Z. Has’minskii (1973) Asymptotic behavior of certain statistical estimates, II. Limit theorems for a posteriori density and for Bayesian estimates, Teor. Verojatnost. i Primenen 18, 78–93.

Ibragimov, I.A. and R.Z. Has’minskii (1981) Statistical estimates, Applications of Mathematics, 16 (asymptotic theory, translated from the Russian by Samuel Kotz).

Kato, H., S. Sato and N. Yoshida (2011) Analysis of Foreign Exchange Data with the Lead–Lag Estimator (in Japanese), The 2011 Japanese Joint Statistical Meeting, 4–7 September 2011, Fukuoka.

Kessler, M. (1997) Estimation of an Ergodic Diffusion from Discrete Observations, Scandinavian Journal of Statistics 24(2), 211–229.

Kunitomo, N. and A. Takahashi (2001) The Asymptotic Expansion Approach to the Valuation of Interest Rate Contingent Claims, Mathematical Finance 11(1), 117–151.

Kusuoka, S. and N. Yoshida (2000) Malliavin Calculus, Geometric Mixing, and Expansion of Diffusion Functionals, Probabability Theory and Related Fields 116(4), 457–484.

Kutoyants, Y. (1994) Identification of dynamical systems with small noise, Mathematics and its Applications 300.

Kutoyants, Y.A. (1984) Parameter estimation for stochastic processes, Research and Exposition in Mathematics 6 (translated from the Russian and edited by B.L.S. Prakasa Rao).

Kutoyants, Y.A. (1998) Statistical inference for spatial Poisson processes, Lecture Notes in Statistics 134.

Kutoyants, Y.A. (2004) Statistical inference for ergodic diffusion processes, Springer Series in Statistics.

Kutoyants, Y.A. and N. Yoshida (2007) Moment estimation for ergodic diffusion processes, Bernoulli 13(4), 933–951.

Li, C. (2010) Managing Volatility Risk: Innovation of Financial Derivatives, Stochastic Models and Their Analytical Implementation, Columbia University.

Malliavin, P. and M.E. Mancino (2002) Fourier Series Method for Measurement of Multivariate Volatilities, Finance and Stochastics 6(1), 49–61.

Masuda, H. (2010) Approximate Self-Weighted LAD Estimation of Discretely Observed Ergodic Ornstein-Uhlenbeck Processes, Electronic Journal of Statistics 4, 525–565.

Masuda, H. and N. Yoshida (2004) An Application of the Double Edgeworth Expansion to a Filtering Model with Gaussian Limit, Statistical Probability Letters 70(1), 37–48.

Masuda, H. and N. Yoshida (2005) Asymptotic Expansion for Barndorff–Nielsen and Shephard's Stochastic Volatility Model, Stochastic Processes Application 115(7), 1167–1186.

Mykland, P. (2010) A Gaussian Calculus for Inference from High Frequency Data, Annals of Finance.

Mykland, P.A. (1992) Asymptotic Expansions and Bootstrapping Distributions for Dependent Variables: A Martingale Approach, Annals of Statistics 20(2), 623–654.

Mykland, P.A. (1993) Asymptotic Expansions for Martingales, Annals of Probability 21(2), 800–818.

Ogihara, T. and N. Yoshida (2011) Quasi-likelihood Analysis for the Stochastic Differential Equation with Jumps, Statistical Inference for Stochastic Processes 14, 189–229.

Osajima, Y. (2006) The Asymptotic Expansion Formula of Implied Volatility for Dynamic SABR Model and FX Hybrid Model, UTMS 2006-29.

Podolskij, M. and M. Vetter (2009) Estimation of Volatility Functionals in the Simultaneous Presence of Microstructure Noise and Jumps, Bernoulli Official Journal of the Bernoulli Society for Mathematical Statistics and Probability 15(3), 634–658.

Prakasa Rao, B.L.S. (1983) Asymptotic Theory for Nonlinear Least Squares Estimator for Diffusion Processes, Mathematische Operationsforschung und Statistik Series Statistics 14(2), 195–209.

Prakasa Rao, B.L.S. (1988) Statistical Inference from Sampled Data for Stochastic Processes. In Statistical Inference from Stochastic Processes, Ithaca, New York, 1987, American Mathematical Society, Providence, Rhode Island; also Contemporary Mathematics 80, 249–284.

Robert, C.Y. and M. Rosenbaum (2010a) A New Approach for the Dynamics of Ultra-High-Frequency Data: The Model With Uncertainty Zones, Journal of Financial Econometrics Advance Access 1–23.

Robert, C.Y. and M. Rosenbaum (2010b) Volatility and Covariation Estimation When Microstructure Noise and Trading Times are Endogenous, Mathematical Finance, DOI: 10.1111/j.1467-9965.2010.00454.x.

Sakamoto, Y. and N. Yoshida (1996) Expansion of Perturbed Random Variables Based on Generalized Wiener Functionals, Journal of Multivariate Analysis 59(1), 34–59.

Sakamoto, Y. and N. Yoshida (1998a) Asymptotic Expansion of M-Estimator Over Wiener Space, Statistical Inference of Stochastic Processes 1(1), 85–103.

Sakamoto, Y. and N. Yoshida (1998b) Third Order Asymptotic Expansion for Diffusion Process, Theory of Statistical Analysis and Its Applications 107, 53–60.

Sakamoto, Y. and N. Yoshida (2003) Asymptotic expansion under degeneracy, Journal of Japan Statistical Society 33(2), 145–156.

Sakamoto, Y. and N. Yoshida (2004) Asymptotic Expansion Formulas for Functionals of ε-Markov Processes with a Mixing Property, Annals of the Institute of Statistical Mathematics 56(3), 545–597.

Sakamoto, Y. and N. Yoshida (2008) Asymptotic Expansion for Stochastic Processes: An Overview and Examples, Journal of Japan Statistical Society 38(1), 173–185.

Sakamoto, Y. and N. Yoshida (2009) Third-Order Asymptotic Expansion of M-Estimators for Diffusion Processes, Annals of the Institute of Statistical Mathematics 61(3), 629–661.

Sakamoto, Y. and N. Yoshida (2010) Asymptotic Expansion for Functionals of a Marked Point Process, Communications in Statistics – Theory and Methods 39(8,9), 1449–1465.

Takahashi, A. and K. Takehara (2009) Asymptotic Expansion Approaches in Finance: Applications to Currency Options, Discussion Paper F Series, URL http://repository.dl.itc.u-tokyo.ac.jp/dspace/handle/2261/26663.

Takahashi, A. and N. Yoshida (2004) An Asymptotic Expansion Scheme for Optimal Investment Problems, Statistical Inference for Stochastic Processes 7, 153–188.

Takahashi, A. and N. Yoshida (2005) Monte Carlo Simulation with Asymptotic Method, Journal of Japan Statistical Society 35, 171–203.

Ubukata, M. and K. Oya (2008) A Test for Dependence and Covariance Estimator of Market Microstructure Noise, Discussion Papers In Economics and Business, 07-03, February 2007.

Uchida, M. (2010a) Adaptative Estimation of an Ergodic Diffusion Process Based on Sampled Data. In Proceedings of DYNSTOCH Meeting 2010, Angers, France, June 16–19, 2010.

Uchida, M. (2010b) Contrast-Based Information Criterion for Ergodic Diffusion Processes from Discrete Observations, Annals of the Institute of Statistical Mathematics 62(1), 161–187.

Uchida, M. and N. Yoshida (2001) Information Criteria in Model Selection for Mixing Processes, Statistical Inference for Stochastic Processes 4(1), 73–98.

Uchida, M. and N. Yoshida (2004a) Asymptotic Expansion for Small Diffusions Applied to Option Pricing, Statistical Inference for Stochastic Processes 7(3), 189–223.

Uchida, M. and N. Yoshida (2004b) Information Criteria for Small Diffusions via the Theory of Malliavin–Watanabe, Statistical Inference for Stochastic Processes 7(1), 35–67.

Uchida, M. and N. Yoshida (2006) Asymptotic Expansion and Information Criteria, SUT Journal of Mathematics 42(1), 31–58.

Uchida, M. and N. Yoshida (2009) Estimation of the Volatility for Stochastic Differential Equations. In Asymptotical Statistics of Stochastic Processes VII, LeMans, March 16–19, 2009.

Uchida, M. and N. Yoshida (2010) Adaptive Estimation of an Ergodic Diffusion Process Based on Sampled Data, Preprint.

Uchida, M. and N. Yoshida (2011) Nondegeneracy of Statistical Random Field and Quasi Likelihood Analysis for Diffusion, Institute of Statistical Mathematics, Research Memorandum 1149.

Watanabe, S. (1987) Analysis of Wiener Functionals (Malliavin Calculus) and Its Applications to Heat Kernels, Annals of Probability 15(1), 1–39.

Yoshida, N. (1992a) Asymptotic Expansion for Statistics Related to Small Diffusions, Journal of Japan Statistical Society 22(2), 139–159, URL http://www2.ms.u-tokyo.ac.jp/probstat/?page id=23.

Yoshida, N. (1992b) Asymptotic Expansions of Maximum Likelihood Estimators for Small Diffusions Via the Theory of Malliavin–Watanabe, Probability Theory and Related Fields 92(3), 275–311.

Yoshida, N. (1992c) Estimation for Diffusion Processes from Discrete Observation, Journal of Multivariate Analysis 41(2), 220–242.

Yoshida, N. (1993) Asymptotic Expansion of Bayes Estimators for Small Diffusions, Probability Theory and Related Fields 95(4), 429–450.

Yoshida, N. (1997) Malliavin Calculus and Asymptotic Expansion for Martingales, Probability Theory and Related Fields 109(3), 301–342.

Yoshida, N. (2001) Malliavin Calculus and Martingale Expansion, Bulletin of Scientific Mathematics 125(6–7), 431–456; also Rencontre Franco-Japonaise de Probabilités, Paris, 2000.

Yoshida, N. (2004) Partial Mixing and Conditional Edgeworth Expansion for Diffusions with Jumps, Probability Theory and Related Fields 129, 559–624.

Yoshida, N. (2005) Polynomial Type Large Deviation Inequality and Its Applications, Preprint.

Yoshida, N. (2006) Polynomial Type Large Deviation Inequalities and Convergence of Statistical Random Fields, The Institute of Statistical Mathematics Research Memorandum 1021.

Yoshida, N. (2008) Expansion of Asymptotically Conditionally Normal Law. In Finace and Related Mathematical and Statistical Issues, Kyoto Research Park, Kyoto, September 3–6, 2008.

Yoshida, N. (2009) Asymptotic Expansion for the Asymptotically Conditionally Normal Law. SAPS VII, March 16–19, 2009.

Yoshida, N. (2010a) Expansion of the Asymptotically Conditionally Normal Law, The Institute of Statistical Mathematics Research Memorandum 1125.

Yoshida, N. (2010b) Quasi-likelihood Analysis and Limit Theorems for Stochastic Differential Equations. In Market Microstructure, Confronting Many Viewpoints, Institut Louis Bachelier, Paris.

Zhang, L., P.A. Mykland and Y. Aät-Sahalia (2005) A Tale of Two Time Scales: Determining Integrated Volatility with Noisy High-Frequency Data, Journal of the American Statistical Association 100(472), 1394–1411.

Zhou, B. (1996) High-Frequency Data and Volatility in Foreign-Exchange Rates, Journal of Business and Economic Statistics 14, 45–52.

1. The pointwise convergence in particular means that is locally asymptotically normal (LAN) at if we abuse this terminology for the quasi likelihood.

2. We keep the same name for this condition as Uchida and Yoshida (2009, 2011).

3. It does not matter up to the first order asymptotic results whether the observations at T are available or not.