14.5 From Predicate Calculus to Logic Programming
14.5.1 Clausal Form
To prepare propositions in CNF for use in logic programming, we must further simplify their form, with the ultimate goal being to simplify the resolution process. Consider the following proposition expressed in CNF:
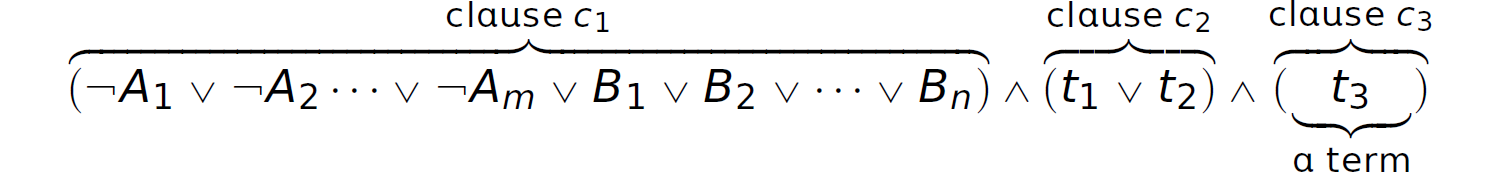
We convert each clause in this expression into clausal form, which is a standard and simplified syntactic form for propositions:
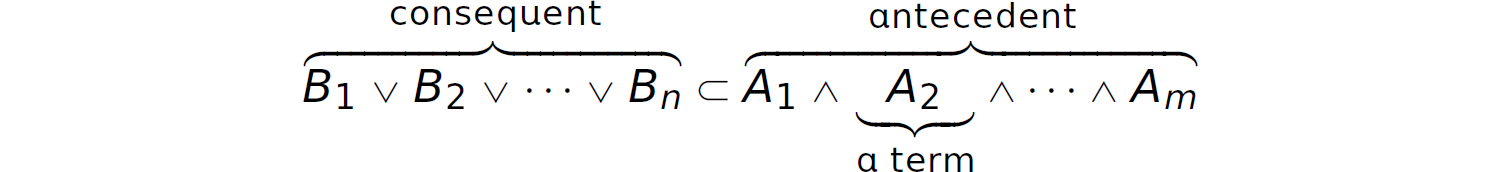
The As and Bs are called terms. The left-hand side (i.e., the expression before the ⊂ symbol) is called the consequent; the right-hand side (i.e., the expression after the ⊂ symbol) is called the antecedent. The intuitive interpretation of a proposition in clausal form is as follows: If all of the As are true, then at least one of the Bs must be true. When converting the individual clauses in an expression in CNF into clausal form, we introduce implication based on equivalence between ¬ p ∨ q and q ⊂ p. The clauses c1 and c2 given previously expressed in clausal form are
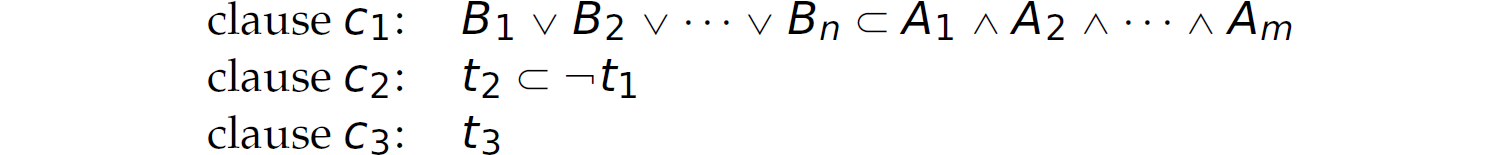
Thus, a single proposition expressed in CNF is converted into a set of propositions in clausal form. Notice that we used the DeMorgan Law ¬ p ∨ ¬ q ≡ ¬ (p ∧ q) to convert the (¬ A1 ∨ A2 … ∨ ¬ Am) portion of clause c2 to the antecedent of the proposition in clausal form. In particular,
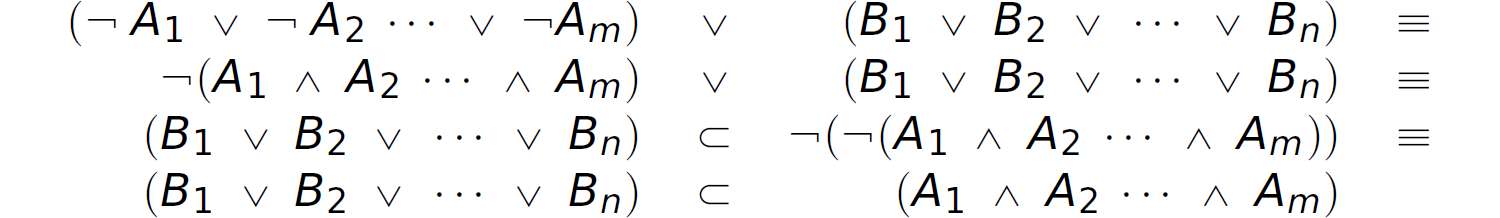
The first of the other clauses expressed in clausal form is
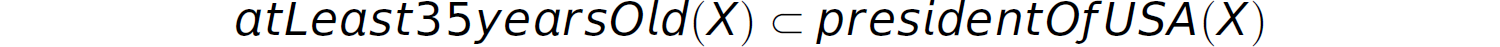
(If X is/was a president of the United States, then X is/was at least 35 years old.)
Examples of other propositions in clausal form follow:
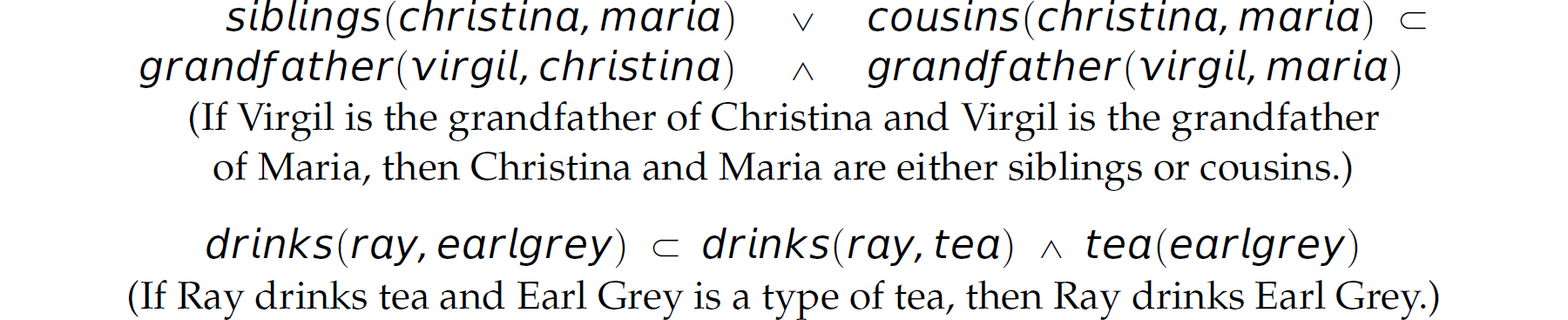
14.5.2 Horn Clauses
A restriction that can be applied to propositions in clausal form is to limit the right-hand side to at most one term. Propositions in clausal form adhering to this additional restriction are called Horn clauses. A Horn clause is a proposition with either exactly zero terms or one term in the consequent. Horn clauses conform to one of the three clausal forms shown in Table 14.8. A headless Horn clause is a proposition with no terms in the consequent (e.g., {} ⊂ p). A headed Horn clause is a proposition with exactly one atomic term in the consequent (e.g., q ⊂ p). The last preposition in clausal form in the prior subsection is a headed Horn clause. Table 14.8 provides examples of these types of Horn clauses.
Table 14.8 Types of Horn Clauses with Forms and Examples
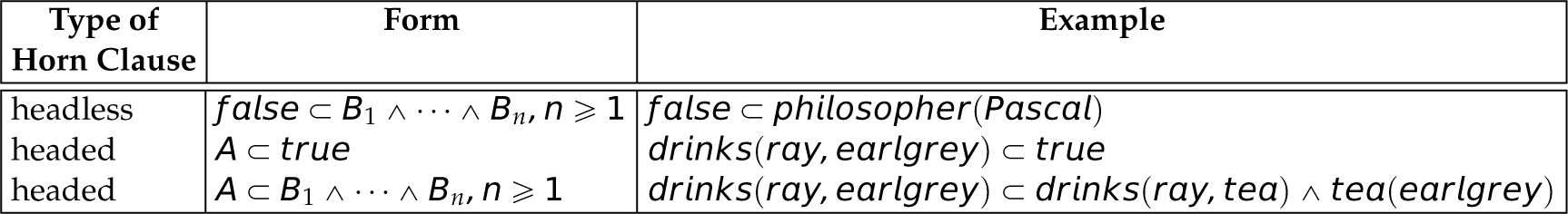
14.5.3 Conversion Examples
To develop an understanding of the representation of propositions in a variety of representations, including CNF and clausal form as Horn clauses, consider the following conversion examples.
Factorial
Natural language specification:
The factorial of zero is 1.
The factorial of a positive integer n is
n multiplied by the factorial of n – 1.
Predicate calculus:
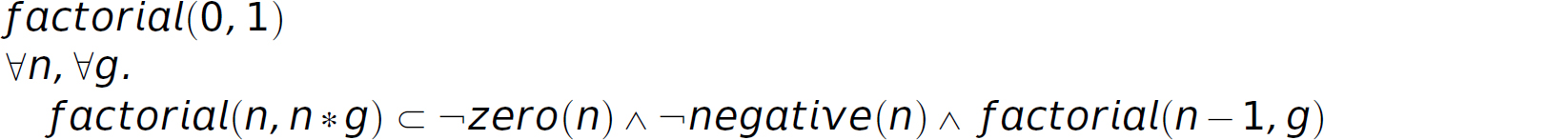
Description Conjunctive normal form:
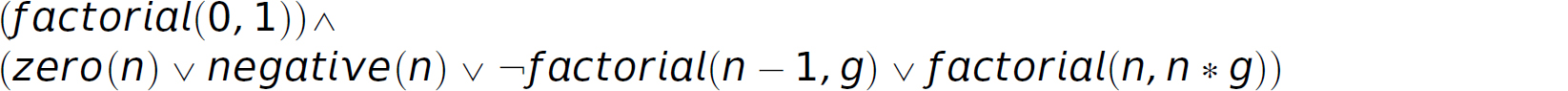
Description Horn clauses:
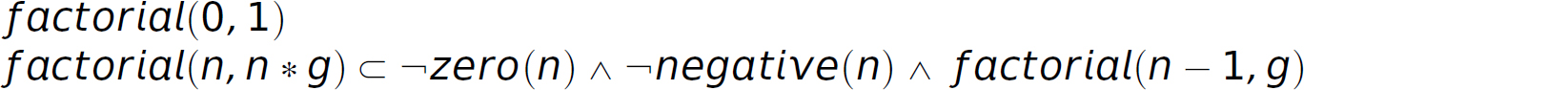
Description
Fibonacci
Natural language specification:
The first Fibonacci number is 0.
The second Fibonacci number is 1.
Any Fibonacci number n, except for the first and second, is the sum of the previous two Fibonacci numbers.
Predicate calculus:
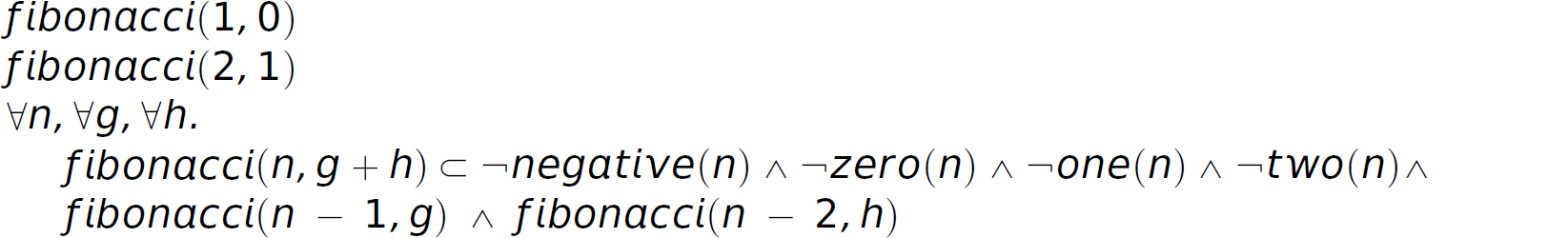
Description Conjunctive normal form:

Description Horn clauses:
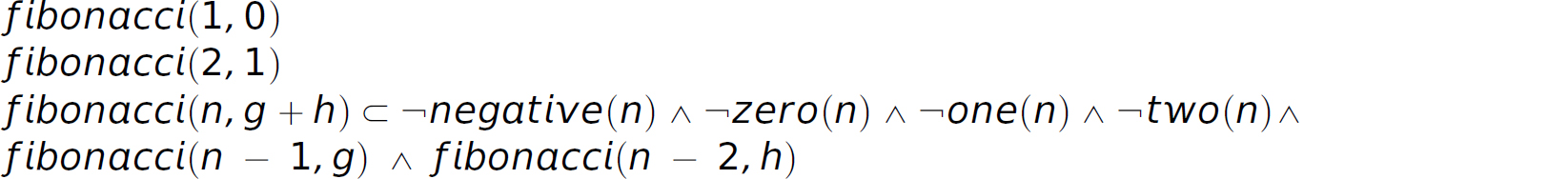
Description
Commuter
Natural language specification:
For all χ, if χ is a commuter, then χ rides either a bus or a train.
Predicate calculus:
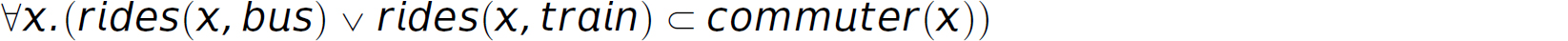
Description Conjunctive normal form:
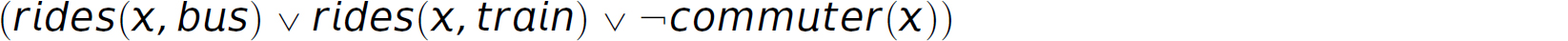
Description Horn clause:
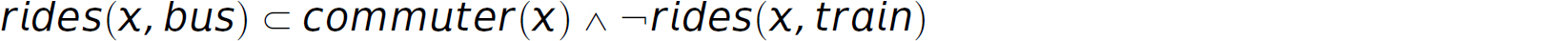
Description
Sibling relationship
Natural language specification:
χ is a sibling of y if χ and y have the same mother or the same father.
Predicate calculus:
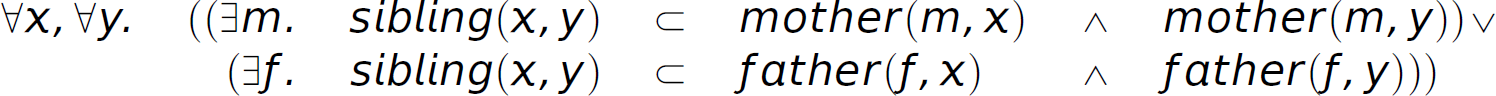
Description Conjunctive normal form:
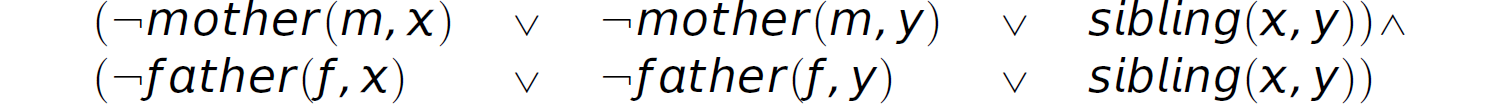
Description Horn clauses:
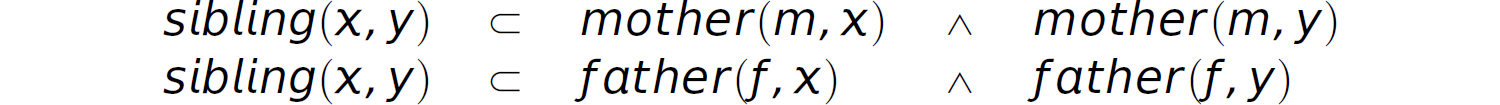
Description
Recall that the universal quantifier is implicit and the existential quantifier is not required in Horn clauses: All variables on the left-hand side (lhs) of the ⊂ operator are universally quantified and those on the right-hand side (which do not appear on the lhs) are existentially quantified.
In summary, to prepare the propositions in a knowledge base for use with Prolog, we must convert the wffs in the knowledge base to a set of Horn clauses:

We arrive at the final knowledge base of Horn clauses by applying the following conversion process on each wff in the original knowledge base:
Since more than one Horn clause may be required to represent a single wff, the number of propositions in the original knowledge base of wffs may not equal the number of Horn clauses in the final knowledge base.
14.5.4 Motif of Logic Programming
The purpose of expressing propositions as Horn clauses is to prepare them for use in a logic programming system like Prolog. Logic programs are composed as a set of facts and rules. A fact is an axiom that is asserted as true. A rule is a declaration expressed in the form of an if–then statement. A headless Horn clause is called a goal (called a hypothesis in Section 14.4.2). A headed Horn clause with an empty antecedence is called a fact, while a headed Horn clause with a non-empty antecedent is called a rule. Note that the headless Horn clause {} ⊂ philosopher(Pascal) representing a goal is the same as false ⊂ philosopher(Pascal); and the headed Horn clause weather(raining) ⊂ {} representing a fact is the same as weather(raining) ⊂ true.
In a logic programming system like Prolog the programmer declares/asserts facts and rules, and then asks questions or, in other words, pursues goals. For instance, to prove a given goal Q, the system must either
Find Q as a fact in the database, or
Find Q as the logical consequence of a sequence of propositions:
14.5.5 Resolution with Propositions in Clausal Form
Forward Chaining
To apply resolution to two propositions x and y represented in clausal form, take the disjunction of the consequences of x and y, take the conjunction of the antecedents of x and y, and cancel out the common terms on each side of the ⊂ symbol in the new proposition:
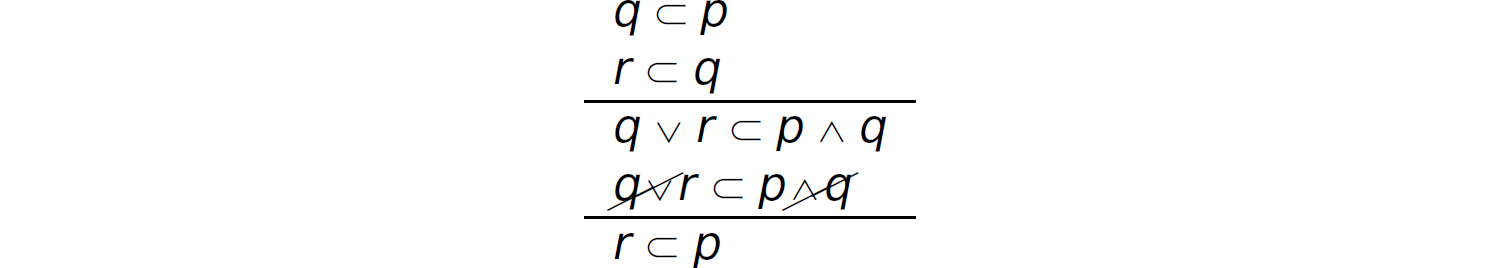
Thus, given q ⊂ p and r ⊂ q, we can infer r ⊂ p. Table 14.9 is an example of an application of resolution, where the propositions therein are represented in clausal form rather than CVF (using the example in Section 14.4.2). The new proposition inferred here indicates that “if Virgil is the grandfather of Christina and Maria, and Maria and Angela are siblings, then either Christina and Maria are cousins or Christina and Angela are siblings.”
Table 14.9 An Example Application of Resolution, Where the Propositions Therein Are Represented in Clausal Form

Restricting propositions in clausal form to Horn clauses further simplifies the rule of resolution, which can be restated as follows:
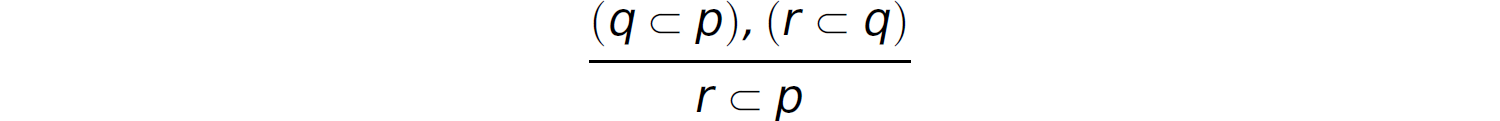
This rule indicates that if p implies q and q implies r, then p implies r. The mechanics of a resolution proof process over Horn clauses are slightly different than those for propositions expressed in CNF, as detailed in Section 14.4.2. In particular, given two Horn clauses x and y, if we can match the head of x with a term in the antecedent of clause y, then we can replace the matched head of x in the antecedent of y with the antecedent of x . Consider the following two Horn clauses x and y:
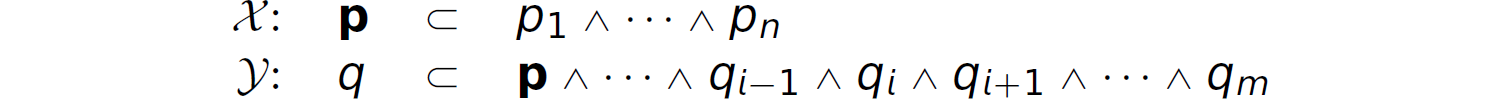
Since term p in the antecedent of clause y matches term p (i.e., the head of clause x), we can infer the following new proposition:
y′: q ⊂ q1 ∧ ∙∙∙ ∧ qi–1 ∧ p1 ∧ ∙∙∙ ∧ pn ∧ qi+1 ∧ ∙∙∙ ∧ qm
where p in the body of proposition y is replaced with p1 ∧ … ∧ pn from the body of proposition x to produce y′. Consider an application of resolution to two simple Horn clauses, q ⊂ p and r ⊂ q:
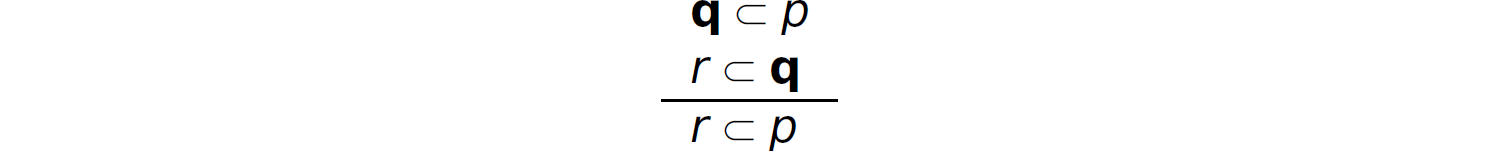
Thus, given q ⊂ p and r ⊂ q, we can infer r ⊂ p. Consider the following resolution example from Section 14.4.2, where the propositions are expressed as Horn clauses:
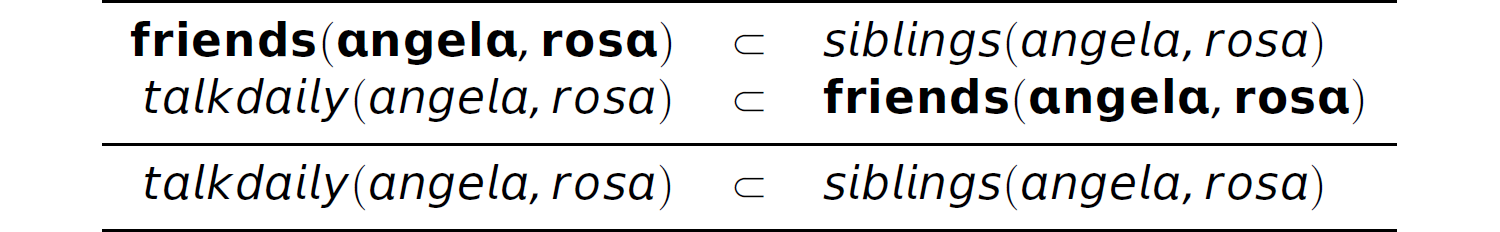
The structure of this resolution proof is the same as the structure of the prior example, but the propositions p, q, and r are represented as binary predicates. The proof indicates that
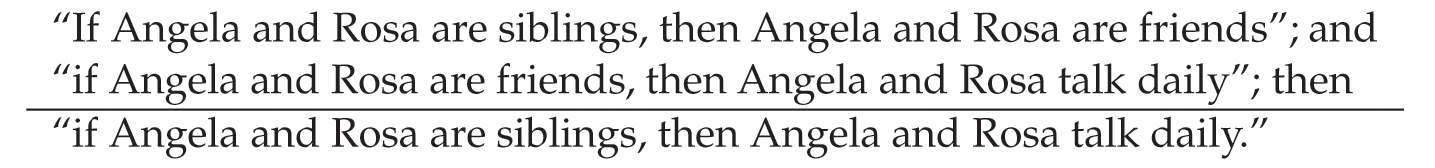
Backward Chaining
A goal in logic programming, which is called a hypothesis in Section 14.4.2, is expressed as a headless Horn clause and is similarly pursued through a resolution proof by contradiction: Assert the goal as a false fact in the database and then search for a contradiction. In particular, resolution searches the database of propositions for the head of the known Horn clause ![]() that unifies with a term in the antecedent of the headless Horn goal clause
that unifies with a term in the antecedent of the headless Horn goal clause ![]() representing the negated goal. If a match is found, the antecedent of the Horn clause
representing the negated goal. If a match is found, the antecedent of the Horn clause ![]() whose head matched a term in the antecedent of
whose head matched a term in the antecedent of ![]() is replaced with the unified term in
is replaced with the unified term in ![]() . This process continues until a contradiction is found:
. This process continues until a contradiction is found:
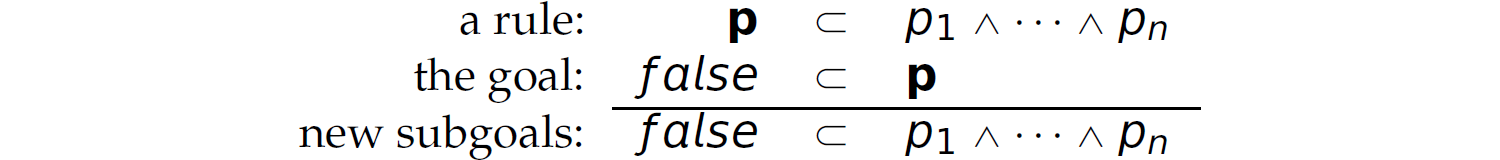
We unify the body of the goal with the head of one of the known clauses, and replace the matched goal with the antecedent of the clause, creating a new list of (sub-)goals. In this example, the resolution process replaces the original goal p with the subgoals p1 ∧ … ∧ pn. If, after multiple iterations of this process, a contradiction (i.e., true ⊂ false) is derived, then the goal is satisfied.
Consider a database consisting of only one fact: commuter (lucia) ⊂ true. To pursue the goal of determining if “Lucia is a commuter,” we add a negation of this proposition expressed as the headless Horn clause false ⊂ commuter(lucia) to the database and run the resolution algorithm:

This is a simple fact-checking example. Since the outcome of resolution is a contradiction, the goal ![]() commuter(lucia) is satisfied.
commuter(lucia) is satisfied.
In contrast to the application of resolution in a forward-chaining manner as demonstrated in Section 14.4.2, the resolution process here attempts to prove a goal by working backward from that goal—a process called backward chaining. Table 14.10 is a proof using this backward-chaining style of resolution to satisfy the goal false ⊂ rides(lucia, train), where the propositions therein are expressed as Horn clauses (from the example in Section 14.4.2). Since the outcome of resolution is a contradiction, the goal rides(lucia, train) is satisfied. Unlike the forward-chaining proof of rides(lucia, train) in Section 14.4.2, here we proved the goal rides(lucia, train) by reasoning from the goal backward toward a contradiction. Prolog uses backward chaining; CLIPS uses forward chaining (discussed in Section 14.10).
Table 14.10 An Example of a Resolution Proof Using Backward Chaining
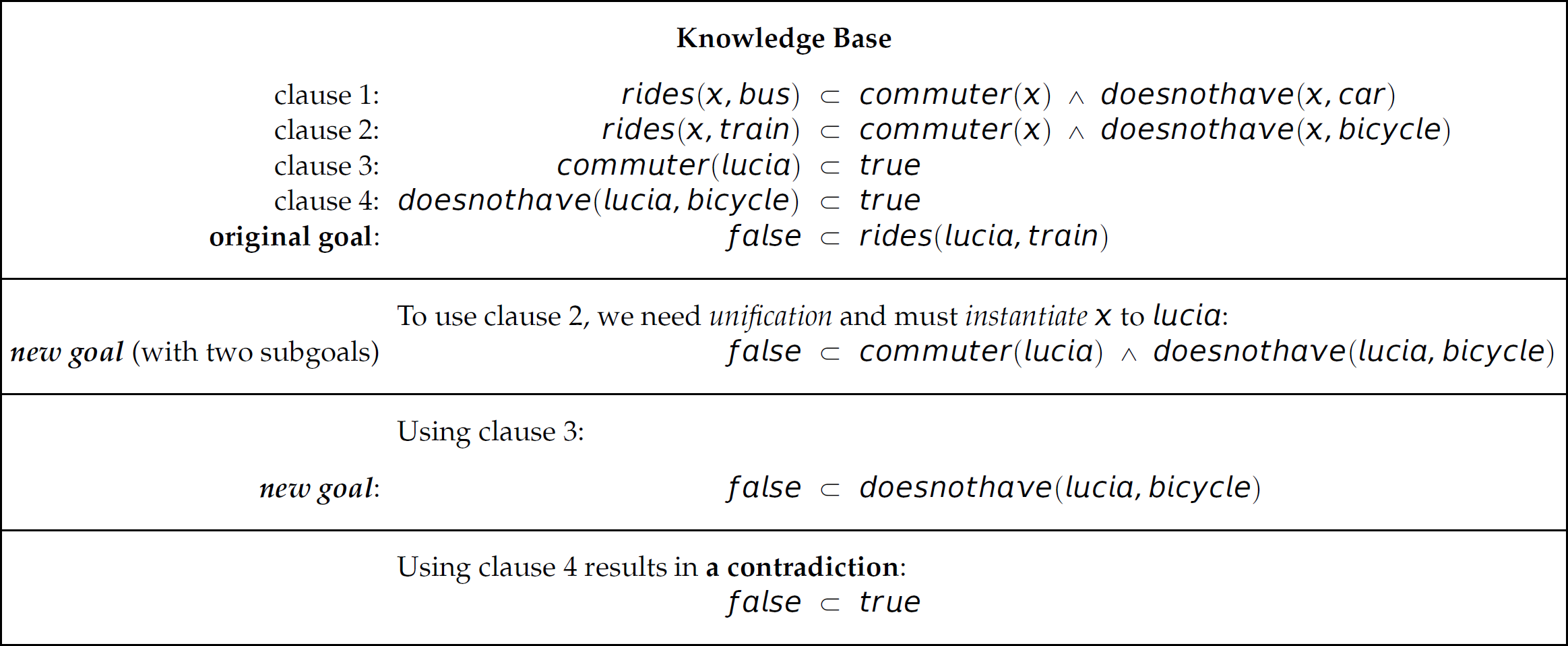
14.5.6 Formalism Gone Awry
The implementation of resolution in a computer system is problematic. Both the order in which to search the database (e.g., top-down, bottom-up, or other) and the order in which to prove subgoals (e.g., left-to-right, right-to-left, or other) during resolution is significant. For instance, consider that in our previous example, an attempt to prove the goal false ⊂ rides(lucia, train) led to the need to prove the two subgoals: false ⊂ commuter(χ) ∧ doesnothave(χ, bicycle). In this example, the end result of the proof (i.e., true) is the same if we attempt to prove the subgoal commuter(χ) first and the subgoal doesnothave(χ, bicycle) second, or vice versa. However, in other proofs, different orders can lead to different results (Section 14.7.1). Prolog searches its database and subgoals in a deterministic order during resolution, and programmers must be aware of the subtleties of the search process (Section 14.7.1). This violates a defining principle of declarative programming—that is, the programmer need only be concerned with the logic and leave the control (i.e., inference methods used to prove a hypothesis) up to the system. Kowalski (1979) captured the essence of logic programming with the following expression:

In this equation, the declaration of the facts and rules—the Logic—is independent of the Control. In other words, the construction of logic programs must be independent of program control. To be completely independent of control, predicates and the clauses therein must be evaluable either in any order or concurrently. The goal of logic programming is to make programming entirely an activity of specification, such that programmers should not have to impart control upon the program.
