![]()
Integers, Divisibility and Number Systems
2.1 Arithmetic Operations in MATLAB
Arithmetic operations in MATLAB are defined according to the standard mathematical conventions. MATLAB is an interactive program that allows you to perform a wide variety of mathematical operations. Furthermore, it has other properties that make it extremely versatile and complex, applicable to a broad range of subjects from more theoretical mathematics to the more applied.
One of the first applications of MATLAB is its use in realizing arithmetic operations as if it were a conventional calculator, but with one important difference: the precision of calculation. Operations are performed to the greatest accuracy required, or the user may specify the degree of precision in advance. This unlimited precision in calculation sets MATLAB apart from other numerical software, where the accuracy is determined by the word length of the computer, so it is essentially determined by the hardware and cannot be modified. This feature is one of the most important in symbolic calculation.
MATLAB assumes the usual arithmetic operations of sum, difference, product, division and power, with the usual hierarchy between them:
x + y sum
x - y difference
x * y or x y product
x/y division
x ^ y power
To add two numbers, simply enter the first number, type a plus sign (+) and then enter the second number. Spaces may be included before or after the plus sign to ease readability.
>> 53 + 78
ans =
131
We can perform the calculation of powers directly.
>> 34 ^ 56
ans =
5. 7919e + 085
Unlike a calculator, when working with integers, MATLAB displays the exact result even when you have more digits than would normally fit across the screen. Here MATLAB returns the exact value of 34 ^ 56.
>> vpa ' 34 ^ 56' 90
ans =
57918773205287127842044254126179599852840968492056164062843692360166371779746690236416.
These operations are used to perform calculations of varying degrees of complexity. When combining several operations in the same instruction, one must take into account the usual criteria of priority among them, which determine the order of evaluation of the expression. Consider the following example:
>> 2 * 3 ^ 2 + (5-2) * 3
ans =
27
Taking into account the usual order of priority of operators, the first to be evaluated is the power operation. The usual order of evaluation can be altered by grouping expressions in parentheses.
In addition to these arithmetic operators, MATLAB is equipped with a set of basic functions, and the user can also define their own functions. Both the embedded MATLAB functions and operators can be applied to symbolic or numeric constants.
EXERCISE 2-1
Perform the following operations:
(a) (-2 + 3 - 5) (4 - 3 + 2)/(15 + 4 - 21)
(b) [(2 - 3)(4 - 3 + 5)]3 [(3 - 2) + (6 - 8 - 5)]
(c) 5 - [4 - 3 + 2 * 7 + 5] + [(3 - 6)2 (7 - 9)2]
(d) 6 - 4 * 3/2 - 7 * 2 + 8 - 6/3 - 52 + 3
(e) [5 + 3 * 2/6 - 4].[4/2 - 3 + 6]/[7/2 - 8 - 2]2
We input the above operations in the following way:
>> ((-2 + 3 - 5)*(4 - 3 + 2))/(15 + 4 - 21)
ans =
6
>> ((2 - 3)*(4 - 3 + 5))^3 * (3 - 2 + 6 - 8 - 5)
ans =
1296
>> 5 - (4 - 3 + 2 * 7 + 5) + (3 - 6)^2 * (7 - 9)^2
ans =
21
>> 6 - (4 * 3)/2 - 7 * 2 + 8 - 6/3 - 5^2 + 3
ans =
-30
>> ((5 + (3*2)/6 - 4)*(4/2 - 3 + 6))/(7 - 8/2 - 2)^2
ans =
10
EXERCISE 2-2
Perform the following operations:
(a) 6 a b + 3a2 + 2 a b
(b) 6 a2 + 2 a - b2 + 3 a - 5 a2 + b2
(c) 6 a b - 2 a2 – 4 a b + 3 a2
We input the above operations in the following way:
>> syms a b
>> pretty(simplify(6*a*b + 3*a^2 + 2*a*b))
2
8 a b + 3 a
>> pretty(simplify( 6*a^2 + 2*a - b^2 + 3*a - 5*a^2 + b^2))
2
a + 5 a
>> pretty(simplify(6*a*b - 2*a^2 - 4*a*b + 3*a^2))
2
2 a b + a
The purpose of this exercise is to demonstrate the need to declare symbolic variables as such when they are part of non-numeric expressions.
EXERCISE 2-3
Where H = 3 a 2 – 2a + 7, F = 6 a3 - 5 a + 2 and G = 5 a2 + 4a -3, calculate:
a) H + F + G
b) H - F + G
c) H - F - G
We input the previous operations in the following way:
>> syms a
>> H = 3*a^2 - 2*a + 7, F = 6*a^3 - 5*a + 2, G = 5*a^2 + 4*a - 3
H =
3*a^2 - 2*a + 7
F =
6*a^3 - 5*a + 2
G =
5*a^2 + 4*a – 3
>> pretty(H+F+G)
2 3
8 a - 3 a + 6 + 6 a
>> pretty(H-F+G)
2 3
8 a + 7 a + 2 - 6 a
>> pretty(H-F-G)
2 3
- 2 a - a + 8 - 6 a
We can also perform these operations by using MATLAB’s specific symbolic computation command symop. In general, the command symop applies the specified operations (op) in quotation marks to the symbolic (sym) variables in the order presented.
>> pretty(symop(H,'+',F,'+',G))
2 3
8 a - 3 a + 6 + 6 a
>> pretty(symop(H,'-',F,'+',G))
2 3
8 a + 7 a + 2 - 6 a
>> pretty(symop(H,'-',F,'-',G))
2 3
- 2 a - a + 8 - 6 a
When it comes to symbolic operations, it is always possible to make use of the interrelationship between MATLAB and Maple.
>> pretty(sym(maple('3*a^2 - 2*a + 7 + 6*a^3 - 5*a + 2 + 5*a^2 + 4*a - 3')))
2 3
8 a - 3 a + 6 + 6 a
>> pretty(sym(maple('3*a^2 - 2*a + 7 - (6*a^3 - 5*a + 2) + 5*a^2 + 4*a - 3')))
2 3
8 a + 7 a + 2 - 6 a
>> pretty(sym(maple('3*a^2 - 2*a + 7 - (6*a^3 - 5*a + 2) - (5*a^2 + 4*a - 3)')))
2 3
- 2 a - a + 8 - 6 a
However, in this simple case it is not necessary to use Maple, because MATLAB already executes the operations correctly by introducing symbolic expressions between quotation marks.
>> syms a
>> pretty('3*a^2 - 2*a + 7 - (6*a^3 - 5*a + 2) - (5*a^2 + 4*a - 3)')
2 3
- 2 a - a + 8 - 6 a
2.2 Integers
The MATLAB program can work on different platforms. Depending on the power of the hardware and software, the program will work with greater or lesser precision. The precision with which MATLAB works means that there is virtually no limit to the maximum size of integers that it is capable of handling; the most typical limitation is the amount of computer memory available. Thus, all the usual operations with integers are exact, regardless of the size of the result.
If we want the result of an operation to appear on screen with a certain number of significant figures, we use the symbolic computation command vpa (variable precision arithmetic), whose syntax is:
vpa 'operation' no_of _ figures
For example, to calculate 7 to the power 400 to 500 significant figures we enter the following:
>> vpa '7 ^ 400' 500
ans =
109450060433611308542425445648666217529975487335970618633541940751543906316349209002147856846968715280739995373528253861552495710170702637728891720852868384710440066743972862761169960663579079291058878933088274875698178024977088223396398265555596916473536792437134632739719389969690630523317113111727683195819839003492006097994729312240001.
The result of the operation is accurate, always placing a point at the end of the result. In this case the result can be expressed in fewer than 500 figures, so the solution is exact. If you request a smaller number of significant figures than the exact result has, MATLAB will round the number to the appropriate multiple of a power of 10. For example, if we perform the above calculation only to 50 significant figures we get:
>> vpa ' 7 ^ 400' 50
ans =
1. 0945006043361130854242544564866621752997548733597e338
2.3 Divisibility
MATLAB provides multiple commands relating to divisibility. The program implements a variety of functions with integer arguments which will be presented below, most of which concern divisibility. Several of these functions are only available if you have installed the extended symbolic mathematics Toolbox. A group of the commands are accessible directly, another group first requires the command maple, and to gain access to the final group, it is necessary to load the Maple numtheory library with the command maple(‘with(numtheory)’).
Among the most typical functions with integer arguments are the following:
- rem(n,m): the remainder of the division of n by m (valid for real n and m)
- sign(n): the sign of n (1 if n > 0, - 1 if n < 0, n real)
- binomial(n,m): the binomial coefficient n choose m : n! / (m! (m-n)! )
- bernoulli(n): the nth Bernoulli number Bn: text/(et - 1) = Σ Bn(x) tn/n! n=0…∞
- euler(n) the nth Euler number En: 2/(et + e-t) = Σ En(x) tn/n! n=0…∞.
- max(n1,n2): the maximum of n1 and n2
- min(n1,n2): the minimum of n1 and n2
- gcd(n1,n2): the greatest common divisor of n1 and n2
- lcm(n1,n2): the least common multiple of n1 and n2
- maple(‘irem(n,m)’): the remainder of the division of n by m
- maple(‘igcd(n1,n2,…,nk)’): the greatest common divisor of k numbers
- maple(‘igcdex(n1,n2,…,nk)’): the greatest common divisor of k numbers using Euclid’s algorithm
- maple(‘ilcm(n1,n2,…,nk)’): the least common multiple of k numbers
- maple(‘max(n1,n2,…,nk)’): the maximum of k numbers
- maple(‘min(n1,n2,…,nk)‘): the minimum of k numbers
- maple(‘n!’): factorial n (n! = n(n-1) (n-2)…2.1)
- maple(‘ifactor(n)’) or factor(n): factorizes n
- maple(‘ithprime(k)’): returns the k-th prime
- maple(‘seq(ithprime(k),k = 1… n’) or primes(n): returns the first n primes
- maple(‘isprime(n)’) or isprime(n): determines whether n is prime or not
- maple(‘type(expr,prime)’): determines if the expression is a prime
- maple(‘type(expr,facint)’): determines if the given expression is completely factored or not
- maple(‘isqrt(n)’): determines if n is perfect square
- maple(‘nextprime(n)’): finds the smallest prime larger than n
- maple(‘prevprime(n)’): finds the largest prime less than n
Among the most typical functions with integer arguments for which it is necessary to previously load Maple’s numtheory library, we have the following:
- maple(‘with(numtheory)’) loads the numtheory library to be used before the following commands
- maple(‘issqr(n)’): determines if n is the square of an integer
- maple(‘issqrfree(n)’): determines if n is square-free
- maple(‘ifactors(n)’): returns the prime factors of n and their orders
- maple(‘factorset(n)’): returns the set of prime factors of n
- maple(‘splitters(n)’): returns a list of the divisors of n
- maple(‘sigma(n)’): returns the sum of the divisors of n
- maple(‘tau(n)’): returns the number of positive divisors of n
- maple(‘bigomega(n)’): returns the number of prime divisors of n
- maple(‘iroot(n,m)’): returns the integer part of n1/m
- maple(‘iquo(n1,n2)’): returns the integer part of the ratio n1/n2
- maple(‘b(n)’): returns the nth Bernoulli number Bn
- maple(‘fermat(n)’): returns the nth Fermat number: 2^(2^n)+1
Here are some examples:
Factorize the number 24:
>> maple ('ifactor(24)')
ans =
(2) ^ 3 * (3)
Factorize the number 999999999999:
>> maple ('ifactor(999999999999)')
ans =
(3) ^ 3 *(7) * (11) * (13) * (37) * (101) * (9901)
Find the remainder of the division of 17 by 3:
>> rem (17,3)
ans =
2
Find the remainder of division of 4.1 by 1.2:
>> rem (4.1,1.2)
ans =
0.5000
Find the remainder of the division of -4.1 by 1.2:
>> rem(-4.1,1.2)
ans =
-0.5000
Find the greatest common divisor of 1000, 500 and 625:
>> maple ('igcd (1000,500,625)')
ans =
125
Find the least common multiple of 1000, 500 and 625:
>> maple ('ilcm (1000,500,625)')
ans =
5000
Is 99991 a prime number?:
>> maple ('isprime (99991)')
ans =
true
Indeed, the number is prime.
Find the 100th prime number:
>> maple ('ithprime (100)')
ans =
541
Find the set of all numbers that divide 24:
>> maple('with(numtheory)');maple('divisors(24)')
ans =
{1, 2, 3, 4, 6, 8, 12, 24}
Find the prime factors of 12267845 together with their orders of multiplicity:
>> maple('with(numtheory)'); maple('ifactors(12267845)')
ans =
[1, [[5, 1], [113, 1], [21713, 1]]]
Find the set of prime factors of 135678743:
>> maple('with(numtheory)');maple('factorset(135678743)')
ans =
{135678743}
Logically, the above number has to be prime:
>> maple ('isprime (135678743)')
ans =
true
Find the set of prime factors of the number 135678742:
>> maple('with(numtheory)');maple('factorset(135678742)')
ans =
{2, 1699, 39929}
Find the list of divisors, the number of divisors and the sum of the divisors of 1000000:
>> maple('with(numtheory)');maple('divisors(1000000)')
ans =
{1, 2, 4, 5, 8, 10, 16, 20, 25, 32, 40, 50, 64, 80, 100, 125, 250000, 3125, 31250, 62500, 125000, 500000, 1000000, 12500, 625, 15625, 25000, 250, 6250, 1250, 500, 2500, 200, 1000, 5000, 400, 2000, 160, 800, 4000, 50000, 10000, 100000, 20000, 200000, 40000, 320, 1600, 8000}
>> maple('with(numtheory)');maple('tau(1000000)')
ans =
49
>> maple('with(numtheory)');maple('sigma(1000000)')
ans =
2480437
EXERCISE 2-4
Find the number of different ways of selecting 9 elements from 45 without repetition. Consider the same problem for three elements selected from n.
>> maple('binomial(45, 9)')
ans =
886163135
>> maple('expand(binomial(n, 3))')
ans =
1/6 * n ^ 3-1/2 * n ^ 2 + 1/3 * n
EXERCISE 2-5
Find the remainder of the division of 2134 by 3. Also find the smallest positive integer k such that k ≡ 12 mod 8.
>> rem(2^134,3)
ans =
1
>> maple('chrem([12],[8])')
ans =
4
The syntax of the function chrem will be presented in the next section.
EXERCISE 2-6
Find the prime factors and all the divisors of 18900. Also find the 189th prime number.
>> maple ('ifactor(18900)')
ans =
(2)^2*(3)^3*(5)^2*(7)
>> maple('with(numtheory)');maple('divisors(18900)')
ans =
{1, 2, 3, 4, 5, 6, 7, 9, 10, 12, 14, 15, 18, 20, 21, 25, 27, 28, 30, 35, 36, 42, 45, 50, 54, 60, 63, 70, 75, 84, 90, 100, 105, 108, 126, 135, 1050, 2700, 18900, 525, 1260, 180, 150, 225, 300, 450, 675, 900, 270, 1350, 540, 140, 175, 189, 210, 252, 315, 350, 378, 420, 630, 700, 756, 945, 1575, 2100, 3150, 4725, 6300, 1890, 9450, 3780}
>> maple('ithprime(189)')
ans =
1129
EXERCISE 2-7
Two books have 840 and 384 pages, respectively. If they are formed by sections of an equal number of pages (more than 18), calculate the number of pages per section.
>> gcd (840, 384)
ans =
24
EXERCISE 2-8
Find the smallest number N that when divided by 16, 24, 30 and 32 leaves the remainder 5.
N-5 will be a multiple of 16, 24, 30 and 32, and we are asked to calculate the least number, so N-5 will be the least common multiple of 16, 24, 30 and 32:
>> maple ('(16, 24, 30, 32) ilcm')
ans =
480
Therefore N = 480 + 5 = 485.
EXERCISE 2-9
Calculate the factorial of 2000.
We have here an example of the high-precision of MATLAB:
>> maple('2000!')
ans =
331627509245063324117539338057632403828111720810578039457193543706038077905600822400273230859
732592255402352941225834109258084817415293796131386633526343688905634058556163940605117252571
870647856393544045405243957467037674108722970434684158343752431580877533645127487995436859247
408032408946561507233250652797655757179671536718689359056112815871601717232657156110004214012
420433842573712700175883547796899921283528996665853405579854903657366350133386550401172012152
635488038268152152246920995206031564418565480675946497051552288205234899995726450814065536678
969532101467622671332026831552205194494461618239275204026529722631502574752048296064750927394
165856283531779574482876314596450373991327334177263608852490093506621610144459709412707821313
732563831572302019949914958316470942774473870327985549674298608839376326824152478834387469595
829257740574539837501585815468136294217949972399813599481016556563876034227312912250384709872
909626622461971076605931550201895135583165357871492290916779049702247094611937607785165110684
432255905648736266530377384650390788049524600712549402614566072254136302754913671583406097831
074945282217490781347709693241556111339828051358600690594619965257310741177081519922564516778
571458056602185654760952377463016679422488444485798349801548032620829890965857381751888619376
692828279888453584639896594213952984465291092009103710046149449915828588050761867924946385180
879874512891408019340074625920057098729578599643650655895612410231018690556060308783629110505
601245908998383410799367902052076858669183477906558544700148692656924631933337612428097420067
172846361939249698628468719993450393889367270487127172734561700354867477509102955523953547941
107421913301356819541091941462766417542161587625262858089801222443890248677182054959415751991
701271767571787495861619665931878855141835782092601482071777331735396034304969082070589958701
381980813035590160762908388574561288217698136182483576739218303118414719133986892842344000779
246691209766731651433494437473235636572048844478331854941693030124531676232745367879322847473
824485092283139952509732505979127031047683601481191102229253372697693823670057565612400290576
043852852902937606479533458179666123839605262549107186663869354766108455046198102084050635827
676526589492393249519685954171672419329530683673495544004586359838161043059449826627530605423
580755894108278880427825951089880635410567917950974017780688782869810219010900148352061688883
720250310665922068601483649830532782088263536558043605686781284169217133047141176312175895777
122637584753123517230990549829210134687304205898014418063875382664169897704237759406280877253
702265426530580862379301422675821187143502918637636340300173251818262076039747369595202642632
364145446851113427202150458383851010136941313034856221916631623892632765815355011276307825059
969158824533457435437863683173730673296589355199694458236873508830278657700879749889992343555
566240682834763784685183844973648873952475103224222110561201295829657191368108693825475764118
886879346725191246192151144738836269591643672490071653428228152661247800463922544945170363723
627940757784542091048305461656190622174286981602973324046520201992813854882681951007282869701
070737500927666487502174775372742351508748246720274170031581122805896178122160747437947510950
620938556674581252518376682157712807861499255876132352950422346387878954850885764466136290394
127665978044202092281337987115900896264878942413210454925003566670632909441579372986743421470
507213588932019580723064781498429522595589012754823971773325722910325760929790733299545056388
362640474650245080809469116072632087494143973000704111418595530278827357654819182002449697761
111346318195282761590964189790958117338627206088910432945244978535147014112442143055486089639
578378347325323595763291438925288393986256273242862775563140463830389168421633113445636309571
965978466338551492316196335675355138403425804162919837822266909521770153175338730284610841886
554138329171951332117895728541662084823682817932512931237521541926970269703299477643823386483
008871530373405666383868294088487730721762268849023084934661194260180272613802108005078215741
006054848201347859578102770707780655512772540501674332396066253216415004808772403047611929032
210154385353138685538486425570790795341176519571188683739880683895792743749683498142923292196
309777090143936843655333359307820181312993455024206044563340578606962471961505603394899523321
800434359967256623927196435402872055475012079854331970674797313126813523653744085662263206768
837585132782896252333284341812977624697079543436003492343159239674763638912115285406657783646
213911247447051255226342701239527018127045491648045932248108858674600952306793175967755581011
679940005249806303763141344412269037034987355799916009259248075052485541568266281760815446308
305406677412630124441864204108373119093130001154470560277773724378067188899770851056727276781
247198832857695844217588895160467868204810010047816462358220838532488134270834079868486632162
720208823308727819085378845469131556021728873121907393965209260229101477527080930865364979858
554010577450279289814603688431821508637246216967872282169347370599286277112447690920902988320
166830170273420259765671709863311216349502171264426827119650264054228231759630874475301847194
095524263411498469508073390080000000000000000000000000000000000000000000000000000000000000000
000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
000000000000000000000000000000000000000000000000000000000000000
EXERCISE 2-10
Calculate the number 2^115-1 and determine whether or not it is prime. If it is compound, break it down into its prime factors. Calculate the closest prime numbers greater than and less than 2^115-1. Verify that the largest of these two numbers is indeed prime.
>> 2 ^ 115-1
ans =
4. 1538e + 034
We can now calculate the exact value:
>> vpa ' 2 ^ 115-1' 100
ans =
41538374868278621028243970633760767
Now let’s check if it is prime:
>> maple ('isprime(2^115-1)')
ans =
false
Thus the number is not prime.
We find the decomposition into prime factors:
>> maple ('ifactor(2^115-1)')
ans =
(31) *(47) * (2646507710984041) *(4036961) * (178481) * (14951)
We now calculate the two prime numbers closest to the above number, one less than the number and the other greater than the number, and we see that the latter is indeed prime.
>> maple('prevprime(2^115-1)')
ans =
41538374868278621028243970633760701
>> maple('nextprime(2^115-1)')
ans =
41538374868278621028243970633760839
>> maple('isprime(nextprime(2^115-1))')
ans =
true
EXERCISE 2-11
Calculate the first 100 prime numbers.
>> maple('seq(ithprime(k),k=1..100)')
ans =
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541
EXERCISE 2-12
Given the number 51648597:
(a) Determine whether or not it is prime.
(b) If it is composite, break it down into prime factors.
(c) Calculate the set of its prime factors.
(d) Find its prime factors with their multiplicities.
(e) Find the set of its divisors.
(f) Find the sum of its divisors.
(g) Find the number of its divisors.
a)
>> maple ('isprime (51648597)')
ans =
false
Thus, it is not prime.
b)
>> maple('ifactor(51648597)')
ans =
(3)^4*(7)^3*(11)*(13)^2
c)
>> maple('with(numtheory)');maple('factorset(51648597)')
ans =
{3, 7, 11, 13}
d)
>> maple('with(numtheory)');maple('ifactors(51648597)')
ans =
[1, [[3, 4], [7, 3], [11, 1], [13, 2]]]
e)
>> maple('with(numtheory)');maple('divisors(51648597)')
ans =
{1, 3, 7, 9, 11, 13, 21, 27, 33, 39, 49, 63, 77, 81, 91, 99, 117, 819, 429, 297, 343, 351, 3972969, 11583, 4459, 14553, 3861, 1053, 231, 147, 1287, 441, 3003, 9009, 693, 51648597, 33957, 5733, 91091, 507, 305613, 120393, 273, 150579, 49049, 637637, 21021, 273273, 63063, 819819, 31941, 7371, 7007, 1565109, 95823, 51597, 24843, 74529, 117117, 81081, 1054053, 27027, 351351, 13377, 173901, 40131, 521703, 1911, 147147, 1912911, 361179, 4695327, 1324323, 17216199, 567567, 7378371, 17199, 223587, 39039, 10647, 13013, 13689, 16731, 50193, 57967, 3549, 4563, 5577, 637, 8281, 1001, 189189, 2459457, 441441, 5738733, 6237, 2079, 1183, 1521, 1859, 11319, 1029, 3087, 1323, 9261, 567, 3969, 27783, 539, 891, 3773, 1617, 4851, 101871, 43659, 169, 670761, 2457, 189, 143}
f)
>> maple('with(numtheory)');maple('sigma(51648597)')
ans =
106286400
g)
>> maple('with(numtheory)');maple('tau(51648597)')
ans =
120
2.4 Modular Arithmetic
MATLAB’s elementary number theoretic cababilities can be expanded via the numtheory library of the Extended Symbolic Math toolbox, which incorporates commands related to modular arithmetic. We have the following:
- maple(‘mroot(n1, n2, n3)’) is n11/n2 modulo n3
- maple(‘msrqt(n1,n2)’) is n11/2 modulo n2
- maple(‘nthpow(n1,n2)’) is the largest n such that n divides n1n2
- maple(‘chrem([n1…nx],[m1…mx])’) is the unique integer n such that n(mod mi) = ni i=1.....x
- maple(‘imagunit(n)’) gives √-1 modulo n
- maple(‘mlog(p,q,r)’) gives the logarithm of p to base q modulo r
- maple(‘phi(n)’) gives the number of positive integers less than or equal to n that are relatively prime with n
- maple(‘invphi(n)’) the inverse phi function (i.e. returns the set of positive integers k such that phi(k)=n)
- maple(‘jacobi(n1,n2)’) or maple(‘J(n1,n2)’) gives the Jacobi symbol of the integers n1 and n2, i.e. it returns 1 if n1 is relatively prime with n2 and n2 is positive and odd, n2 if n1 is not a positive odd integer, and -1 otherwise
- maple(‘legendre(n1,n2)’) or maple(‘L(n1,n2)’) gives the Legendre symbol of the integers n1 and n2, i.e. it returns 1 if n1 is a quadratic residue modulo n2, and -1 if it is not (n1 is a quadratic residue modulo n2 if there exists an integer m such that m2≡n1 (mod n2))
- maple(‘lambda(n)’) gives the size of the largest cyclic group generated by gi(mod n)
- maple(‘mersenne(n)’) or maple(‘M(n)’) returns 2n - 1 if it is prime, and if not, returns false
- maple(‘mcombine(n1,m1,n2,m2)’): gives an integer n such that n ≡ m1(mod n1) and n ≡ m2(mod n2). Returns FAIL if there is no such n
- maple(‘ mipolys(n,p)’) gives the number of monic univariate irreducible polynomials of degree n over Z (mod p)
- maple(‘mipolys(n,p,m)’) gives the number of monic univariate irreducible polynomials of degree n over the Galois field of order pm
- maple(‘mobius(n)’) gives the positive integer equal to the Möbius function of n
- maple(‘order(n1,n2)’) gives the order of the integer n1 in the multiplicative group modulo n2, i.e. gives the smallest positive integer m such that n1m ≡ 1(mod n2)
- maple(‘pprimroot(n)’) gives the smallest pseudo primitive root of the positive integer n, that is, the generator of the cyclic group under multiplication modulo n containing the integers relatively prime with n, and if it doesn’t exist, gives the least positive integer not exceeding n and relatively prime to n
- maple(‘pprimroot(n1,n2)’) gives the smallest pseudo primitive root of the positive integer n2 that is greater than n1
- maple(‘primroot(n)’) gives the smallest primitive root of the positive integer n, that is, the generator of the cyclic group under multiplication modulo n containing relatively prime integers with n
- maple(‘primroot(n1,n2)’) gives the smallest primitive root of the positive integer n2 that is greater than n1
- maple(‘quadres(n1,n2)’) determines if n1 is a quadratic residue modulo n2
- maple(‘rootsunity(p,n)’) give all p-th roots of unity modulo n
- maple(‘safeprime(n)’) calculates the smallest prime p greater than n such that (p-1) / 2 is also prime
Below are some examples:
To find the logarithm of 1000000 in base 8 and modulo 52 we do the following:
>> maple('with(numtheory)');maple('mlog(1000000,8,52)')
ans =
4
To find the fifth root of 1000000 modulo 52:
>> maple('with(numtheory)');maple('mroot(1000000,5,52)')
ans =
40
To find the square root of -1 modulo 5:
>> maple('with(numtheory)');maple('imagunit(5)')
ans =
2
To check if 24- 1 and 25- 1 are primes:
>> maple('with(numtheory)');maple('mersenne(4)')
ans =
false
>> maple('with(numtheory)');maple('mersenne(5)')
ans =
31
To find how many positive integers less than or equal to 15 are relatively prime with 15:
>> maple('with(numtheory)');maple('phi(15)')
ans =
8
EXERCISE 2-13
Find the largest integer n such that n3 divides 6561. Also find the square root of n modulo 7.
>> maple('with(numtheory)'); maple('nthpow (6561,3)')
ans =
(9)^3
>> maple('with(numtheory)');maple('msqrt(9,7)')
ans =
3
EXERCISE 2-14
Find the integer n that simultaneously satisfies the equations n ≡ 1000 (mod 37) and n ≡ 1500 (mod 53). Also find the integer n that simultaneously satisfies the equations n ≡ 500 (mod 3), n ≡ 600 (mod4) and n ≡ 700 (mod 5). Is there an integer m such that m2 ≡ 1000 (mod 37)? Finally, find the smallest integer k such that 1500k ≡ 1 (mod 53).
>> maple('with(numtheory)');
>> maple mcombine(37,1000,53,1500)
ans =
334
>> maple chrem([500,600,700],[3,4,5])
ans =
20
>> maple legendre(1000,37)
ans =
1
>> maple order (1500,53)
ans =
13
We therefore conclude that there is such an integer m.
EXERCISE 2-15
Find the number of monic irreducible univariate polynomials of degree 3 over the ring Z (mod 17). Find the number of monic univariate irreducible polynomials of degree 5 over the Galois field of order 711.
>> maple('with(numtheory)');
>> maple mipolys(3,17)
ans =
1632
>> maple mipolys(5,7,11)
ans =
6045360394355011189649410336790819322177683040
EXERCISE 2-16
Find the smallest generator of the cyclic group under multiplication modulo 1500 containing integers relatively prime with 1500. Find such a generator with the condition that it be greater than 11.
>> maple('with(numtheory)');
>> maple pprimroot(1500)
ans =
7
>> maple pprimroot(10,1500)
ans =
11
EXERCISE 2-17
Find the fifth roots of unity modulo 11. Also find the smallest prime p greater than 1000 such that (p-1)/2 is also prime.
>> maple('with(numtheory)');
>> maple rootsunity(5,11)
ans =
1, 3, 4, 5, 9
>> maple safeprime(1000)
ans =
1019
2.5 Divisibility in Z[√n]
Via the numtheory library of the Extended Symbolic Math toolbox, MATLAB allows you to perform divisibility tasks in the ring Z[√n], where n is any integer. In this regard, the program implements the following functions:
- maple(‘factorEQ(n,m)’) calculates the entire factorization of m in the Euclidean ring Z[n1/2]
- maple(‘sq2factor(n)’) gives the entire factorization of n in Z[√2]
- maple(‘sum2sqr(n)’) gives a list of pairs of numbers whose squares sum to n
EXERCISE 2-18
Factorize the following:
(a) 38477343 in the ring Z[√11]
(b) 38434 *√33 in the ring Z[√33]
(c) 408294234124-4242 *√29 in the ring Z[√29]
>> maple('with(numtheory)');
>> maple factorEQ(38477343,11)
ans =
(3) * (125 + 34 * 11 ^(1/2)) * (125-34 * 11 ^(1/2)) *(85 + 16 * 11 ^(1/2)) * (85-16 * 11 ^(1/2))
Written in radical form, this is:
![]()
>> maple factorEQ (38434 * sqrt (33), 33)
ans =
(33 ^(1/2)) * (- 23 + 4 * 33 ^(1/2)) * (5/2 + 1/2 * 33 ^(1/2)) * (5/2-1/2 * 33 ^(1/2)) * (11 + 2 * 33 ^(1/2)) ^ 2 * (58 + 7 * 33 ^(1/2)) * (58-7 * 33 ^(1/2))
Written in radical form, this is:

>> maple factorEQ (408294234124-4242 * sqrt (29), 29)
ans =
-(2) *(1/2 + 1/2 * 29 ^(1/2)) * (1/2-1/2 * 29 ^(1/2)) *(5/2-1/2 * 29 ^(1/2)) ^ 4 * (11 + 2 * 29 ^(1/2)) *(4 + 29 ^(1/2)) * (38 + 7 * 29 ^(1/2)) *(955872689/2 + 331629325/2 * 29 ^(1/2))
Written in radical form, this is:
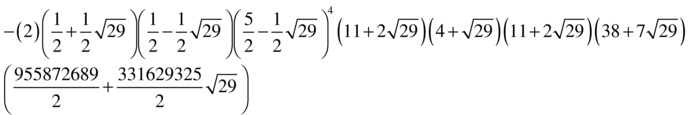
EXERCISE 2-19
Factorize the following in Z[√2]:
a) (1-√2)-4
b) 83424959
c) 9232-932*√2
>> maple('with(numtheory)');
>> maple sq2factor ((1-sqrt (2)) ^(-4))
ans =
(2 ^(1/2) + 1) ^ 4
Written in radical form, this is:
![]()
>> maple sq2factor (83424959)
ans =
(9503 + 1855 * 2 ^(1/2)) *(9503-1855 * 2 ^(1/2))
Written in radical form, this is:
![]()
>> maple sq2factor (9232-932 * sqrt (2))
ans =
(2 ^(1/2)) ^ 5 * (2-^(1/2)-1) * (1 + 3 * 2 ^(1/2)) * (5 + 2 ^(1/2)) * (17 + 59 * 2 ^(1/2))
Written in radical form, this is:
![]()
2.6 Diophantine Equations
Via the numtheory library of the Extended Symbolic Math toolbox, MATLAB can attempt to solve Diophantine equations, i.e., it can find integer solutions of certain equations, inequalities, systems of equations and systems of inequalities. In this regard, the program implements the following functions:
- maple(‘kronecker({ineq1,…,ineqx},{var1,1,…,var1,m},{var2,1,…,var2,n})’) gives the Diophantine approximation, in the inhomogeneous case, of the specified inequalities with respect to the given two sets of variables
- maple(‘minkowski({ineq1,…,ineqx},{var1,1,…,var1,m},{var2,1,…,var2,n})’) gives the Diophantine approximation, in the homogeneous case, of the specified inequalities with respect to the given two sets of variables
- maple(‘thue(f(x,y) = m,[x,y])’) solves the equation for f(x,y)∈Z[x, y] irreducible over Q[x,y] and integer m
- maple(‘thue(f(x,y)≤m, [x, y])’) solve the inequality for f(x,y)∈Z[x, y] irreducible over Q[x, y] and integer m
EXERCISE 2-20
Solve (integer solutions) the following equations and inequalities in Z[x,y]:
a) x2 + x y + y2= 19
b) abs(x3 + x2 y - 2 x y2 - y3)≤ 5
c) abs(x5 + x4 y - 4 x3 y2 - 3x2 y3 + 3x y4 + y5) ≤ 10
d) x3 + y3 = 5
a)
>> maple('with(numtheory)');
>> maple thue(x^2 + x*y + y^2 = 19,[x,y])
[x = 5, y = - 3], [x = - 2, y = - 3], [x = 2, y = - 5], [x = - 2, y = 5],
[x = - 5, y = 3], [x = 2, y = 3], [x = - 5, y = 2],
[x = - 3, y = - 2], [x = 5, y = - 2], [x = 3, y = 2],
[x = - 3, y = 5], [x = 3, y = - 5]
b)
>> maple thue(abs(x^3 + x^2*y-2*x*y^2-y^3) < = 5 [x, y])
[x = 0, y = 0], [x = 1, y = 0], [x = 1, y = 1], [x = 5, y = 4],
[x = - 5, y = - 4], [x = - 2, y = 1], [x = - 1, y = 0],
[x = - 1, y = 1], [x = - 1, y = 2], [x = - 1, y = - 1],
[x = 1, y = - 2], [x = 1, y = - 1], [x = - 4, y = 9], [x = 0, y = 1],
[x = 0, y = - 1], [x = 2, y = - 1], [x = 4, y = - 9,]
[x = - 9, y = 5], [x = 9, y = - 5]
c)
>> maple thue(abs(x^5 + x^4*y-4*x^3*y^2-3*x^2*y^3 + 3*x*y^4 + y^5) < = 10, [x, y])
[x = 0, y = 0], [x = 1, y = 0], [x = 1, y = 1], [x = - 1, y = 1],
[x = - 2, y = 1], [x = 0, y = 1], [x = 0, y = - 1],
[x = - 1, y = - 1], [x = - 1, y = 0], [x = 1, y = - 1],
[x = 2, y = - 1]
d)
>> maple thue(x^3 + y^3 =5,[x,y])
Error, (in thue) this binary form is not irreducible
EXERCISE 2-21
Solve the following Diophantine system in both homogeneous and inhomogeneous cases:
|ez1 + 21/2z2 - s1 | ≤ 10-2
|31/3 z1 + π z2 - s2 | ≤ 10 -4
>> maple('with(numtheory)');
>> maple minkowski ({abs (exp(1)*z1 + 2^(1/2)*z2 - s1 ) <=10^(-2),
abs (3^(1/3)*z1 + Pi*z2 - s2 ) <=10^(-4)}, {z1,z2},{s1,s2})
[z1 = 7484], [z2 = -2534], [s1 = 16760], [s2 = 2833]
>> maple kronecker ({abs (exp(1)*z1 + 2^(1/2)*z2 - s1 ) <=10^(-2),
abs (3^(1/3)*z1 + Pi*z2 - s2 ) <=10^(-4)}, {z1,z2},{s1,s2})
[z1 = - 1014], [z2 = 5300], [s1 = 4739], [s2 = 15188]
2.7 Number Systems
MATLAB allows you to work with number systems to any base, as long as the extended symbolic math Toolbox is available. It also allows you to express all kinds of numbers in different bases. The following functions are available:
- maple(‘convert(decimal,base,n_base)’) or dec2base(decimal,n_base) (base 10) converts the specified decimal number to the base n_base
- base2dec(number,B) converts the given number in base B to decimal
- maple(‘convert(decimal,binary)’) or dec2bin(decimal) converts the specified decimal number to base 2 (binary)
- maple(‘convert(decimal,octal)’) converts the specified decimal number to base 8 (octal)
- maple(‘convert(decimal,octal,n)’) or dec2hex(decimal) converts to base 8 (octal) the specified decimal number with n digits of precision
- maple(‘convert(decimal,hex)’) converts the decimal number specified to base 16 (hexadecimal)
- maple(‘convert(binary,decimal,binary)’) or bin2dec (binary) converts the specified binary number to decimal
- maple(‘convert(octal,decimal,octal)’) converts the octal number to decimal
- maple(‘convert(hexadecimal,decimal,hex)’) or hex2dec (hexadecimal) converts the specified base 16 number to decimal
- maple(‘convert([a,b,…,c],base,old_base,new_base)’) converts the number whose digits in the old base are: c… ba, to the new base. The result is a list with the figures placed in the reverse order to the usual ordering
- maple(‘convert(decimal,double,option)’) converts a decimal number to a double-precision hexadecimal according to the given option (ibm, mips and vax)
- maple(‘convert(hexad,double,maple,option)’) converts the given double-precision hexadecimal number to a Maple format hexadecimal according to the given option (ibm, mips and vax)
EXERCISE 2-22
Express the decimal number 2342424 in base 2. Also express the decimal number 242345341 in base 16.
>> maple ('convert(2342424,binary)')
ans =
1000111011111000011000
>> maple('convert(242345341,hex)')
ans =
E71E57D
EXERCISE 2-23
Express the binary number 100101 in base 10, and express in base 10 the hexadecimal number ffffaa00. Find in base 10 the result of the operation of hexadecimal numbers fffaa2 + ff – 1.
>> maple ('convert(100101,decimal,binary)') or base2dec('100101',2)
ans =
37
>> maple ('convert (FFFFAA0, decimal, hex)') or base2dec ('FFFFAA0', 16)
ans =
268434080
>> maple ('convert (FFFAA2, decimal, hex) + convert(FF,decimal,hex) - 1')
ans =
16776096
>> base2dec ('FFFAA2', 16) + base2dec('FF',16)-1
ans =
16776096
EXERCISE 2-24
Calculate in base 5 the results of the operation:
a25aaff616 + 6789aba12 + 11002218 + 356713 – 1250
We first convert the base 12 number 6789aba to decimal:
>> base2dec('6789aba',12)
ans =
19840750
or we can also use the function convert:
>> maple('convert([10,11,10,9,8,7,6],base,12,10)')
ans =
[0, 5, 7, 0, 4, 8, 9, 1]
Let us not forget that this form of the function convert returns the result with the figures in the reverse order to the usual ordering.
We now transform the base 3 number 1100221 to decimal:
>> base2dec('1100221',3)
ans =
997
We can also perform this operation as follows:
>> maple('convert([1,2,2,0,0,1,1],base,3,10)')
ans =
[7, 9, 9]
The number in base 10 is 997. Now we calculate the result of the entire operation in base 10:
>> maple ('convert(a25aaf6,decimal,hex) + 19840750 + convert(35671,decimal,octal) + 997-1250')
ans =
190096544
The same result is obtained directly as follows:
>> base2dec('a25aaf6',16) + base2dec('6789aba',12) + base2dec('35671',8) + base2dec('1100221',3)-1250
ans =
190096544
but we still need to convert this result to base 5:
>> maple('convert([4,4,5,6,9,0,0,9,1],base,10,5)')
ans =
[4, 3, 1, 2, 4, 0, 1, 3, 1, 2, 4, 3]
Thus, the final result of the operation in base 5 is 342131042134.
This last step could also have been determined as follows:
>> dec2base (190096544,5)
ans =
342131042134
EXERCISE 2-25
In base 13, find the result of the following operation:
(666551)4 (aa199800a)7 + (fffaaa125)11 / (33331 + 6)16
First of all, we convert all numbers to base 10:
>> maple('convert([1,5,5,6,6,6],base,7,10)')
ans =
[7, 8, 5, 7, 1, 1]
>> maple('convert([10,0,0,8,9,9,1,10,10],base,11,10)')
ans =
[7, 6, 9, 3, 2, 8, 1, 4, 3, 2]
>> maple ('convert (FFFAAA125, decimal, hex)')
ans =
68713881893
>> maple('convert([1,3,3,3,3],base,4,10)')
ans =
[1, 2, 0, 1]
Now we carry out the proposed calculations in base 10.
>> vpa ' 117587 * 2341823967 + 79 * 68713881893 /(1021+6)' 15
ans =
275373340490852
A more direct way of doing all of the above is:
>> base2dec('666551',7) * base2dec('aa199800a',11) + 79 * base2dec('fffaaa125',16) / (base2dec ('33331', 4) + 6)
ans =
275373340490852
We now transform the result gained into base 13.
>> maple('convert([2,5,8,0,9,4,0,4,3,3,7,3,5,7,2],base,10,13)')
ans =
[6, 9, 4, 1, 12, 3, 6, 9, 7, 6, 8, 10, 11]
Thus, the final result in base 13 is the number BA867963C1496.
This last conversion can also be done as follows:
>> dec2base (275373340490852,13)
ans =
BA867963C1496
EXERCISE 2-26
Convert the decimal 125.7864 to binary and convert the results of the decimal operation 8796.43 + 0.6789 - 4.25 to octal.
>> maple('convert(125.7864, binary)')
ans =
1111101.110010010
>> vpa '8796.43+0.6789-4.25'
ans =
8792.8589
>> maple('convert(8792.8589, octal)')
ans =
21130.66760336645
