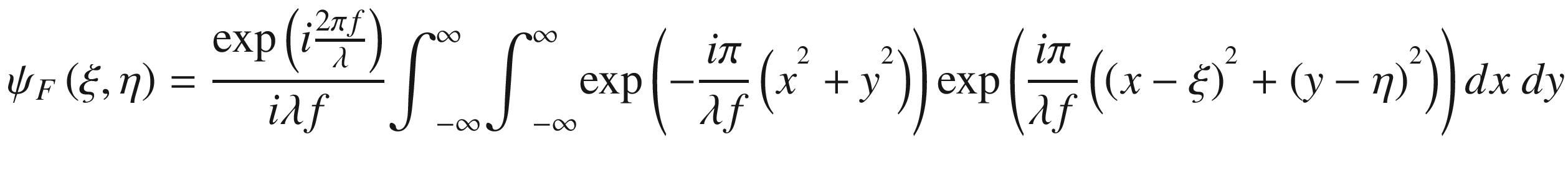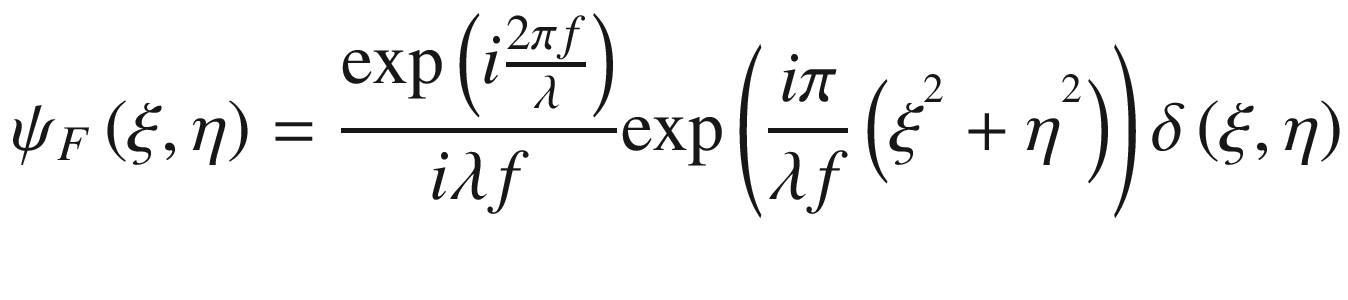In this chapter, we describe elements for plotting stereoscopic 3D cylindrical functions. For this purpose, we focus on the so-called aberrations of optical lenses, also referred to as Seidel aberrations .
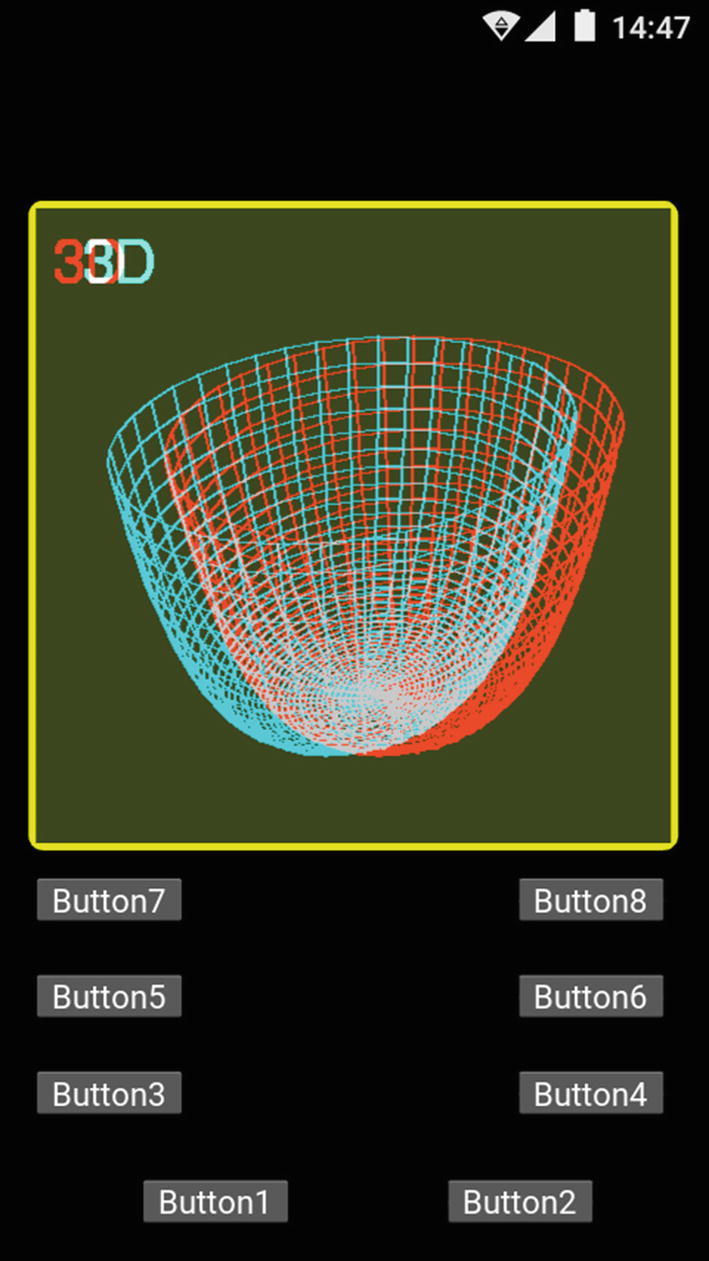
Screenshot of the program on an Android cell phone showing a plot of a spherical aberration term
The functionality of the buttons is the same as in previous chapters.
Seidel aberrations consist of algebraic terms, expressed as typical cylindrical coordinate functions, which can be obtained by expanding the transmittance phase function of an ideal lens by a Taylor series. According to the wave theory of light, in the process of focusing an illuminating light source by a lens, the interaction of the lens with the wavefronts of light prevents the lens from focusing on a single point, generating instead a spatial light distribution around the focal point. A precise analytical tool to calculate the spatial distribution of the focused profiles is given by the Fresnel diffraction integral , which allows one to introduce the concept of the phase transmittance function of a lens. In the next section, we provide an introductory analytical description of this subject.
15.1 Ideal Lens Focusing: The Fresnel Diffraction Integral
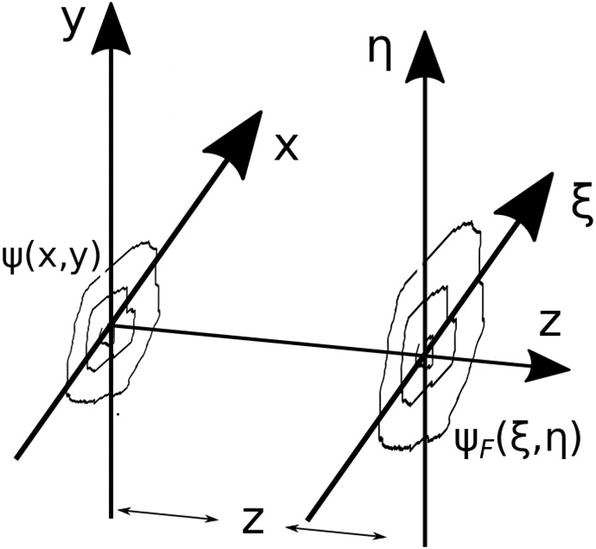
An initial field with amplitude distribution ψ(x, y) propagates a distance z toward an observation plane. The parameter ψF(ξ, η) represents the amplitude distribution at the plane of observation
![$$ {psi}_Fleft(xi, eta
ight)=frac{mathit{exp}left(ifrac{2pi z}{lambda}
ight)}{ilambda z}{int}_{-infty}^{infty }{int}_{-infty}^{infty}psi left(x,y
ight)mathit{exp}left[frac{ipi}{lambda z}left({left(x-xi
ight)}^{{}^2}+{left(y-eta
ight)}^{{}^2}
ight)
ight] dx dy $$](https://imgdetail.ebookreading.net/202109/3/9781484271131/9781484271131__9781484271131__files__images__510726_1_En_15_Chapter__510726_1_En_15_Chapter_TeX_Equ1.png)
For our program, we will apply the Fresnel diffraction integral to the case of an ideal lens. As is well known, a physical property that characterizes an ideal lens is its capability of focusing a spatially unlimited plane wave. Therefore, at the plane of observation, the focused light distribution should consist of an ideal geometrical point. Analytically, the corresponding equation of this point at the plane of observation is represented as δ(ξ, η). Here the δ symbol represents a Dirac delta function.

In Equation (15.2), ψ(x, y) represents the transmittance function of the ideal lens. In the exponential function with an imaginary argument, the quadratic expression is referred to as the phase of the lens. We will now see that this quadratic negative phase results in a convergent wavefront.
In Equation (15.3), we substituted z with f, the lens focal length.
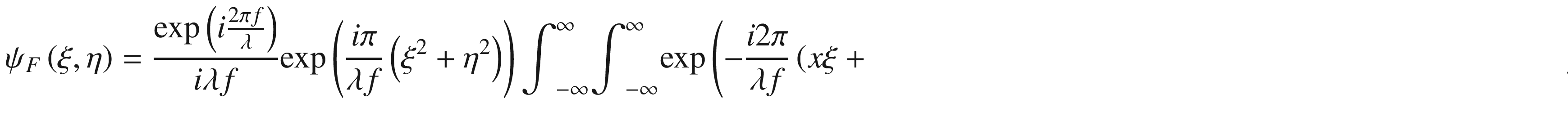

 property for λ > 0 and f > 0, which allows us to simplify Equation (15.6) as follows:
property for λ > 0 and f > 0, which allows us to simplify Equation (15.6) as follows: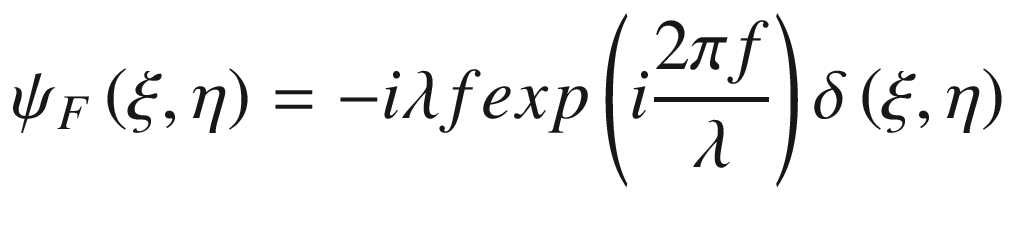
Equation (15.7) demonstrates that when an ideal lens is illuminated by a plane wave that propagates parallel to the optical axes, the lens concentrates (or focuses) the light precisely at the center of the observation plane. The focusing spot consists of an ideal geometrical point, provided that the plane of observation is placed precisely at a lens focal distance from the initial plane.
15.2 Departure from the Ideal Lens
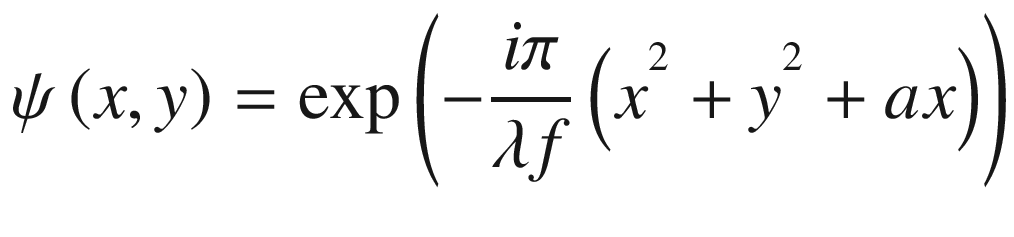
In Equation (15.8), the parameter a represents a constant term.
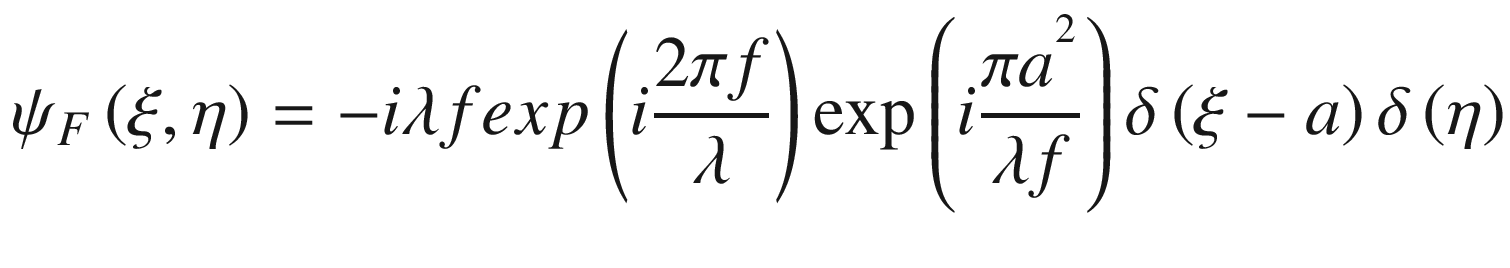
Equation (15.9) shows that the focused spot has been shifted from the origin in the x-direction, due to the linear term introduced in Equation (15.8). We conclude that the lens has tilted the wavefront with respect to the optical axes. An analog analysis applies to the y-direction.
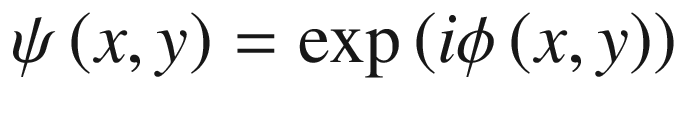
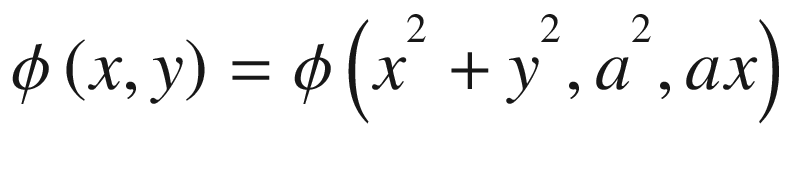
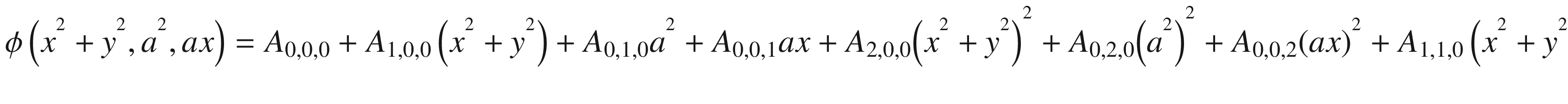
In Equation (15.12), each coefficient in the series has three sub-indexes. Each sub-index corresponds to the power of its corresponding expansion term. The first sub-index corresponds to the power of the term (x² + y²). The second sub-index corresponds to the power of a². Finally, the third sub-index corresponds to the power of ax. For example, A1, 0, 1 is the coefficient of the term of the products of (x² + y²)¹ by (a²)0 by (ax)¹.
15.3 The Wave Aberration Function in Cylindrical Coordinates

In Equation (15.13) the variables ρ and θ are, as usual, the radial and polar coordinates, respectively.
Note that there are other possible expressions for the coefficients.
Definition of Some Aberration Terms
Coefficient | Term | Typical Name |
|---|---|---|
A1, 0, 0 | ρ² | Focus |
A0, 1, 0 | a² | Piston |
A0, 0, 1 | aρcos(θ) | Tilt |
A2, 0, 0 | (ρ²)² | Spherical |
A0, 2, 0 | (a²)² | Piston |
A0, 0, 2 | (aρcos(θ))² | Astigmatism |
A1, 1, 0 | ρ²a² | Field curvature |
A1, 0, 1 | ρ²(aρcos(θ)) | Coma |
A0, 1, 1 | a²(aρcos(θ)) | Distortion |
In the following section, we describe the program that will stereoscopically plot the aberration terms in cylindrical coordinates.
15.4 Stereoscopic Plot of Wave Aberration Terms in Cylindrical Coordinates
We will place the plot of the aberration terms at the middle between the plane of projection and the screen, using the percentage variable P with a value of 0.5.
Creating the Mesh
As in previous chapters, the vertical heights are represented by the y-coordinate; x represents the horizontal coordinate and z represents the depth.
Creating and Filling the Radial and Polar Coordinates
The size of both arrays is N+1. The radial array, Rho, has N+1 entries, with entries ranging from 0 to 1. The polar array, Theta, stores values from 0 to 2π.
Creating the Mesh in the x-z Plane
Filling the Vertical Array
Code for the main.py File
Code for the file.kv File

Wavefront aberration terms corresponding to the coefficients A0, 0, 1, A0, 0, 2, A1, 0, 0, A1, 0, 1, and A2, 0, 0 of Equation (15.12), plotted with the program
15.5 Summary
In this chapter, we introduced elements for plotting stereoscopic 3D cylindrical functions. In particular, we presented working examples of Seidel aberrations. We provided a brief outline of the Fresnel diffraction integral and applied this integral to review the focusing properties of ideal lenses. We extended these concepts to lens aberrations, illustrating programming methods for plotting the aberration terms in stereoscopic views.