“I’ll Know It When I See It” Isn’t Enough

Making a set of raw data available to a person and expecting to get a complete and accurate set of outliers from it is typically a fool’s errand. Our processing capabilities are paradoxical: in some circumstances, we can easily discern a pattern or find an oddity in a sea of information, but even small datasets can be overwhelming to our brains without formal tools in place. Furthermore, many of the Gestalt insights we covered in the prior chapter have a learned aspect to them. For example, emergence occurs when the brain recognizes a pattern, meaningfulness applies to personally relevant scenes, and reification depends on our recognizing a thing. Two people who have different backgrounds and experiences may not find the same outliers in a given dataset for that reason. Because we cannot assume that all viewers will have the same backgrounds, experiences, and capabilities, handing data to viewers and expecting outputs is untenable.

Human Fallibility

This also leads into the next point: humans make mistakes. Our eyes are not perfect, and we do not always perfectly recall specific values, patterns, or concepts. Because we have a tendency to forget prior patterns, observe spurious or nonexistent patterns, and not observe patterns right in front of our faces, we aren’t perfectly reliable instruments for outlier detection.

I don’t want to oversell this point, however—humans are very good at the task and should be an important part of any anomaly detection system. At the very least, humans are necessary in order to convey significance to outliers and determine whether a given outlier is ultimately anomalous. Beyond that, humans can also provide some capability in finding outliers the machine or automated technique misses. Incidentally, this helps us get a feeling for how good an automated outlier detection process is—if humans are frequently finding anomalies that the process missed, that’s not a good sign!

Marginal Outliers

One class of human fallibility is the case of the marginal outlier. When looking at a graph, certain types of outliers are easy to spot. Figure 3-1 is a reproduction of an image we saw in Chapter 1, and it is easy to spot the two outliers in the example.

A scatterplot plot points scored versus passing yards. Estimated values are (160, 24), (290, 17), (310, 34), (340, 31), (380, 34), and (420, 44).

Those are easy to spot, but is the topmost point, in which a quarterback threw for approximately 415 yards and his team scored 44 points, an outlier? If not, what if his team scored 45 or 47 points? How many points would it take for that data point to become an outlier? Humans are great at spotting things that are quite different from the norm, but when it comes to noticing a very small difference, we tend not to be nearly as accurate. As a result, we can miss cases in which there was an outlier but it was just on the edge or add in cases that are actually inliers but are close to the edge.

The Limits of Visualization

Finally, humans do best when reviewing data in a visual form. Figures like 3-1 allow us to take advantage of our sensory perception capabilities much more efficiently than tables of numbers. Humans can do quite well managing a few variables, but the maximum number of variables the average person can deal with at a time is five: one each for the X, Y, and Z axes; one to represent the size of data points; and capturing a time measure by moving points across the chart in time. Even this may be pushing it in many circumstances, leaving us comfortable with no more than two or three variables.

What this tells us is that once things get complex and we need to look at relationships in higher and higher dimensional orders, Mark 1 eyeballs tend not to do so well. We can potentially use techniques such as dimensionality reduction to make the job easier for analysis, but even dimensionality reduction techniques like Principal Component Analysis (PCA) have their limits. In more complex scenarios, we may still not be able to get down to a small enough number of components to allow for easy visualization.

Distributions and Histograms

When looking at one-dimensional data, our focus is on the distribution of that data. A simple way to think of a distribution (or a statistical distribution) is the shape of the data. That is, how often do we see any particular value in the dataset? For one-dimensional data, we can create a plot called a histogram, which shows the frequency with which we see a value in our dataset.

Before we see a histogram in action, let’s briefly cover one property of variables, which is whether the variable is discrete or continuous. A discrete variable has a finite and known number of possible values. If I ask you to give a movie a number of stars ranging from 1 to 5, with 5 being the highest and no partial stars allowed, I have created a discrete variable that contains a set of responses ranging from 1 to 5, inclusive. By contrast, a continuous variable has an infinite number of possible values. In practice, though, “infinite” often means “a very large number” rather than truly infinite. If I asked a series of individuals how much money they made last year (translated to US dollars if necessary), I will get a wide variety of responses from people. Although there is a finite number of dollars and cents we could expect a single person to make in a single year—obviously, somewhere short of the combined GDP of all of the countries in the world last year—we consider this variable to be continuous in practice because we are likely to get a large number of unique responses.

Furthermore, when building a histogram from a continuous variable, we typically don’t care as much about the exact value of the variable but can make do instead with an approximation, allowing us to aggregate the values within a certain range and display them as a single group, which we call a bin. Figure 3-2 shows an example of one such histogram, containing the Earned Run Average (ERA) of all pitchers in Major League Baseball who threw at least 150 innings in a given season, giving us 4897 such entries. I generated this image using the ggplot2 library in R, which has a default of 30 bins.

A histogram plots the number of pitcher seasons versus E R A. Estimates values are (1, 10), (3, 450), (4, 490), (6, 10), and (7, 0).

Figure 3-3 shows the importance of bin selection, as we decrease the number of bins to 5.

A histogram plots the number of pitcher seasons versus E R A. Values are estimated. (1, 100), (2, 2400), (4, 2700), and (6, 250).

We lose a tremendous amount of fidelity in the data by dropping down to a mere five buckets. That said, there is no single “correct” number of buckets across all datasets. We typically use histograms to help understand the shape of the data, and so the “correct” number of bins is one that gives us information about the shape of the distribution without an excess of noise. Figure 3-4 shows an example of noise, as we increase the number of bins to 500.

A histogram plots the number of pitcher seasons versus E R A. Values are estimated. (1, 1), (3, 17), (4, 58), (4.5, 32), and (6, 1).

In this case, breaking the data into 500 bins hinders our understanding of its distribution; there are simply too many bins to make much sense of the resulting image. One rule of thumb when selecting bin counts is to decrease the number of bins until it stops looking spiky, as in Figure 3-4. With this example, that number is probably in the range of 30–50 bins, and the default was certainly good enough to give us an idea of the overall feel of our data.

Now that we have a basic idea of a distribution and know of one tool we can use to display the distribution of a univariate variable, let’s briefly cover the most famous of all distributions, as well as some of its relevant properties for anomaly detection.

The Normal Distribution

The normal or Gaussian distribution is easily the distribution with the greatest amount of name recognition. This distribution is one of the first any student learns in a statistics course and for good reason: it is easy to understand and has several helpful properties, and we see it often enough in practice to be interesting. Although there are other distributions that occur more frequently in nature—such as the log-normal distribution—let’s make like a statistics textbook and focus on the normal distribution first.

Figure 3-5 shows the probability density function (PDF) of the normal distribution.

A graph plots density versus value. Estimated values are (negative 4, 0.0), (0, 0.4), and (4, 0.0).

This image shows us two things: first, what is the likelihood that if we were to pick a point at random from the normal distribution, we would end up with a specific value. The probability that we would select a specific value from an infinitesimal range along the X axis is its height on the Y axis. This tells us that we are more likely to end up with values close to 0 than values far away from 0. Second, we can add up the area under the curve and gain a picture of how likely it is we will select a value less than or equal to (or greater than or equal to) a specific value along the X axis. For example, if we were to sum up the area along the curve up to the value –2, this equates to approximately 2.5% of the total area of the curve. That tells us that if we randomly select some point from the normal distribution, we have approximately a 2.5% chance of selecting a point less than or equal to –2.

These two properties apply to almost all of the distributions we will look at in Chapter 3. Now that we have a basic idea of distributions, let’s look at three measures that help us make sense of most distributions.

Mean, Variance, and Standard Deviation

The first measure of importance to us is the mean, one of the two terms (along with median) that we colloquially term “average.” We can calculate the mean of a collection of points as 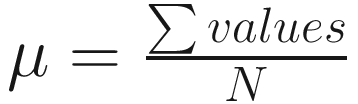. In other words, if we take the sum of values and divide by the count of values, we have the mean.

In the example of the normal distribution shown earlier, the mean is 0. Because the curve on a normal distribution is symmetrical and single peaked, the mean is easy to figure out from viewing the probability distribution function: it’s the peak. With other distributions, the mean is not necessarily quite as easy to find, as we’ll see in the following text.

Now that we have the mean figured out, the other key way of describing the normal distribution is the variance, or how spread out the curve is. The calculation of variance of a collection of points is a bit more complex than that of mean: 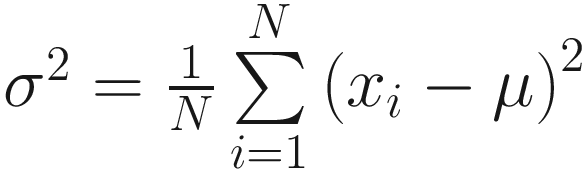. In other words, we sum up the square of the differences from the mean. Then, we divide that by the number of data points, and this gives us our calculation of variance.

Once you understand variance, standard deviation is easy: standard deviation is the square root of the variance. Standard deviation is a rather important measure for a normal distribution because there are certain rules of thumb around how likely we are to randomly draw a point some distance from the mean. Figure 3-6 shows this 68-95-99.7 rule.

A graph plots density versus value. Estimated values are (negative 4, 0.0), (0, 0.4), (4, 0.0). The values of rectangles are 68%, 95%, and 99.7%.

As we can see from Figure 3-6, the likelihood of drawing a value between –1 and 1 is approximately 68%. There’s a 95% chance we will draw a value between –2 and 2. Finally, there is approximately a 99.7% chance we will draw a value between –3 and 3. This leads us to our first technical definition of an outlier: a given point is an outlier if it is more than three standard deviations from the mean and we assume that the underlying distribution is a normal distribution. If the distribution is, in fact, normal, this means approximately 3 in 1000 points will fall outside the norm. The further from the mean a point is, the more likely it is to be anomalous. Suppose that we find a point six standard deviations from the mean. There is approximately a 1 in 500 million chance of finding a data point six standard deviations from the mean, so unless you process billions of rows of data, there’s a pretty good chance this point six standard deviations from the mean didn’t really come from our normal distribution and likely came from some other distribution instead. This is akin to saying, as we did in Chapter 1, that some other process likely generated that data point.

Before we close this section, let me differentiate the normal distribution from a normal distribution. The normal distribution is one with a mean of 0 and a variance of 1. Any other distribution that otherwise follows the properties of the normal distribution but has a mean other than 0 or variance other than 1 still operates like the normal distribution. The reason for that is we can perform equivalent operations on each point in our collection to get us to the normal distribution. What this means in practice is that we can apply the same set of tools to all of the distributions in Figure 3-7.

A graph plots density versus value. It has 3 normal curve of mean=0 S D=1, mean=0 S D=1, and mean=3 S D=0.6.

When the variance is not 1, we can multiply each point by some scaling factor to make the variance 1. When the mean is not 0, we can add some factor (positive or negative) to make the mean 0. Importantly, these operations do not affect the relationships between elements in the data, which allows us in practice to treat a distribution as normal even if its mean or variance differs from that of the normal distribution.

Additional Distributions

The normal distribution is the first distribution we reviewed because it has several nice properties and shows up often enough in practice. It is, however, certainly not the only relevant distribution for us. Let’s now look at three additional distributions, each of which adds its own nuances. Note that there are plenty of distributions we will not cover in this chapter due to time and scope. These distributions can still be important, so please do not consider this set comprehensive or covering all practical examples.

Log-Normal

The normal distribution shows up fairly frequently in our lives, but many important things are not normally distributed. For example, if you look at the population of towns in a given state, dollar amounts in line items for budgets, or net worth of all the people who live in a country, these datasets do not follow a normal distribution. Instead, they follow a log-normal distribution, which means that the logarithm of values will follow a normal distribution, not the values themselves. Figure 3-8 shows an example of a log-normal distribution vs. a normal distribution.

A graph plots density versus value. Log normal is a right-skewed curve and normal is a normal curve.

The normal distribution follows a symmetric “bell curve” shape, but the log-normal distribution has a “long tail,” meaning that you are more likely to see a value on the left-hand side of the peak than on the right-hand side. Another way to describe this is having skew, where one side of the curve stretches out significantly further than the other.

One other point to note is that because this is a logarithmic calculation, all values in your collection must be greater than zero as you cannot take the logarithm of a negative number or zero. If you have a phenomenon that cannot be negative (such as income earned over the past year), this is a tell that the distribution is more likely to be log-normal than normal.

If you assume a collection follows a normal distribution but it actually follows a log-normal distribution, you are likely to end up with a larger number of high-value outliers that turn out to be noise: that is, some people really are that wealthy or some cities really are that large.

Uniform

The uniform distribution is the easiest one to understand. If we have a uniform distribution over the range 0 to 9 inclusive, we are just as likely to get the value 0 as we are 9 as we are 5. Figure 3-9 shows an example of a uniform distribution.

A histogram plots count versus value. Estimated values are (0, 14900), (1, 15000), (3, 15100), (5, 15000), (7, 15100), and (9, 15000).

With a uniform distribution, we cannot call any single point an outlier, as every value is equally likely to happen. Instead, if we have reason to believe that the distribution should be uniform—such as when using the RAND() function in a database like SQL Server or the random() function in Python—we are going to need to observe a sequence of events and calculate the likelihood of this sequence occurring given a uniform distribution. To put this in concrete terms, rolling a 6 on a six-sided die is pretty common—in fact, it should happen 1/6 of the time. But rolling 20 consecutive 6s should bring into question whether that die is rigged.

Cauchy

The final distribution is a glorious and thankfully uncommon one. The Cauchy distribution looks a lot like a normal distribution, as we can see in Figure 3-10.

A graph plots density versus value. Estimated values are (negative 50, 0.0), (negative 8, 0.02), (0, 0.31), (8, 0.01), and (45, 0.0).

The key difference is that the Cauchy distribution has “fat tails” whereas the normal distribution does not. In other words, the normal distribution asymptotically approaches zero, meaning that you can realistically discount the likelihood of finding a point six or seven standard deviations from the mean and the further out you go, the more you can discount the likelihood. For a Cauchy distribution, however, there is always a realistic possibility of getting a point that looks 10 or 20 standard deviations from what you think is the mean. I needed to phrase the last sentence the way I did because a Cauchy distribution does not actually have a mean or variance. There is a point of highest probability that might look like a mean when looking at the probability distribution function, but because of the fat tails, we will never converge on a stable mean.

There are a few cases in which we see Cauchy distributions in nature, primarily in the field of spectroscopy. Fortunately, these occurrences are rare, as they make our job of figuring out whether something is an anomaly much harder!

The Susceptibility of Outliers

The biggest problem with using mean and standard deviation for anomaly detection is that they are sensitive to small numbers of outliers. Suppose that we have the following six data points in our collection: { 7.3, 8.2, 8.4, 9.1, 9.3, 9.6 }. Calculating the standard deviation of this collection, we get a value of 0.85. Calculating the mean of this collection, we get a value of 8.65. Assuming that this data comes from something approximating a normal distribution and using our first technical definition of an anomaly, we could consider a point to be anomalous if it is more than 3 * 0.85 away from 8.65 in either direction. In other words, our inliers should range between 6.1 and 11.2, based on what we see above.

Let’s now add one outlier value: 1.9. We can tell it is an outlier because it is well outside our expected range; thus, the system works. But now look what it does to our system: the standard deviation when you add in the value 1.9 becomes 2.67, and the mean drops to 7.69. Our range of acceptable values now becomes –0.32 up to 15.7, meaning that the item we just called an outlier would now become an inlier if it were to appear a second time!

The Median and “Robust” Statistics

This problem with mean and standard deviation led to the development of “robust” statistics, where robustness is defined as protecting against a certain number of outliers before the solution breaks down like the example shown previously. When calculating averages, we can switch from the nonrobust mean to the robust median. The median is the 50th percentile of a dataset, otherwise known as the midpoint of all values. In our previous example, the median of the set { 7.3, 8.2, 8.4, 9.1, 9.3, 9.6 } is 8.75. To determine this, we remove the smallest and largest values as pairs until we are left with either one or two remaining values. In this case, we remove 7.3 and 9.6, then 8.2 and 9.3. That leaves us with 8.4 and 9.1. Because we have two values remaining, we take the midpoint of those two values, which is 8.75.

From there, we can calculate Median Absolute Deviation, or MAD. MAD is another robust statistic, one that acts as a replacement for standard deviation. The formula for this is 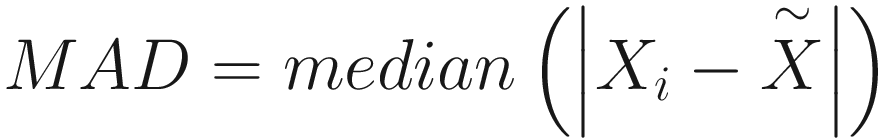. That is, we take the median of the absolute value of differences between individual values and the median of our set. Because our median is 8.75, we subtract 8.75 from each of the collection items and take its absolute value, leaving us with { 1.45, 0.55, 0.35, 0.35, 0.55, 0.85 }. The median of this collection is 0.55.

Applying a similar formula to before, we can call an outlier something that is more than three MAD away from the median. That is, if a value is more than 3 * 0.55 units distant from 8.75 (or outside the range of 7.1 to 10.4), we label the value an outlier. The value of 1.9 would certainly be an outlier here, but let’s see what it does to our next calculation.

The median of the set { 1.9, 7.3, 8.2, 8.4, 9.1, 9.3, 9.6 } is 8.4. This already lets us see the concept of robustness in action: we have an outlier and drop it immediately. It does push the median down but only to the next inlier point. Then, to calculate MAD, we need the median of the absolute value of differences from 8.4, which is { 6.5, 1.1, 0.2, 0, 0.7, 0.9, 1.2 }. Determining the median of this collection gives us a value of 0.9 for the MAD. This means that our range of acceptable values has expanded to 3 * 0.9 from 8.4, or 5.7 to 11.1. There is some expansion but not nearly as much as before—we would still catch 1.9 as an outlier even with this expanded set. Furthermore, MAD “recovers” from an outlier much faster than standard deviation does, meaning that our window of acceptable values opens more slowly and closes more quickly with a robust statistic than with a nonrobust statistic, making robust statistics much less likely to “hide” outliers if we happen to have several in our dataset.

Beyond the Median: Calculating Percentiles

We have already looked at one calculation of percentile: the median, or 50th percentile. There are other percentiles that we find useful in outlier detection, and one of the most useful visuals contains several of them: the box plot. Figure 3-11 shows an example of a box plot.

A box plot plots the number of invoices versus the year. It has eight boxes.

A box plot contains, at a minimum, five useful percentiles: the minimum value (0th percentile), maximum value (100th), median (50th percentile), and the 25th and 75th percentiles. The box itself is made up of the range between the 25th and 75th percentiles, which we call the interquartile range (IQR). We can see a line where the median is, giving us an idea of how skewed the data is (because data skewed in one direction will show a difference in size between the median and the outer percentile compared to its counterpart in the opposite direction). From there, we see “whiskers” stretching out from the box. The whiskers represent all data points within 1.5 * IQR units of the top or bottom of the box. Any points beyond this are outliers, giving us our third technical definition of an outlier: an outlier is any point more than 1.5 times the interquartile range below the 25th percentile or above the 75th percentile.

As we begin to collect some of these technical definitions of outliers, it is important to note that these definitions are not guaranteed to overlap, meaning that one process may call something an outlier but a second process may call it an inlier. We will deal with this complexity starting in Chapter 6.