Scalars, Vectors, and Spaces

Before we go any further, we need to define some basic concepts that underlie the rest of this book. A single numeric feature is also known as a scalar. An ordered list of scalars is known as a vector. Vectors sit within a vector space. In the vast majority of machine learning applications, the input to a model is usually represented as a numeric vector. The rest of this book will discuss best-practice strategies for converting raw data into a vector of numbers.

A vector can be visualized as a point in space. (Sometimes people draw a line or arrow from the origin to that point. In this book, we will mostly use just the point.) For instance, suppose we have a two-dimensional vector v = [1, –1]. The vector contains two numbers: in the first direction, d₁, the vector has a value of 1, and in the second direction, d₂, it has a value of –1. We can plot v in a 2D plot, as shown in Figure 2-1.

Figure 2-1. A single vector

In the world of data, an abstract vector and its feature dimensions take on actual meaning. For instance, a vector can represent a person’s preference for songs. Each song is a feature, where a value of 1 is equivalent to a thumbs-up, and –1 a thumbs-down. Suppose the vector v represents the preferences of a listener, Bob. Bob likes “Blowin’ in the Wind” by Bob Dylan and “Poker Face” by Lady Gaga. Other people might have different preferences. Collectively, a collection of data can be visualized in feature space as a point cloud.

Conversely, a song can be represented by the individual preferences of a group of people. Suppose there are only two listeners, Alice and Bob. Alice likes “Poker Face,” “Blowin’ in the Wind,” and “Hallelujah” by Leonard Cohen, but hates Katy Perry’s “Roar” and Radiohead’s “Creep.” Bob likes “Roar,” “Hallelujah,” and “Blowin’ in the Wind,” but hates “Poker Face” and “Creep.” Each song is a point in the space of listeners. Just like we can visualize data in feature space, we can visualize features in data space. Figure 2-2 shows this example.

Figure 2-2. Illustration of feature space versus data space

Dealing with Counts

In the age of Big Data, counts can quickly accumulate without bound. A user might put a song or a movie on infinite playback or use a script to repeatedly check for the availability of tickets for a popular show, which will cause the play count or website visit count to quickly rise. When data can be produced at high volume and velocity, it’s very likely to contain a few extreme values. It is a good idea to check the scale and determine whether to keep the data as raw numbers, convert them into binary values to indicate presence, or bin them into coarser granularity. To illustrate these ideas, let’s look at a few examples.

Binarization

The Echo Nest Taste Profile subset, the official user data collection for the Million Song Dataset, contains the full music listening histories of one million users on Echo Nest. Here are some relevant statistics about the dataset:

Suppose our task is to build a recommender to recommend songs to users. One component of the recommender might predict how much a user will enjoy a particular song. Since the data contains actual listen counts, should that be the target of the prediction? This would be the right thing to do if a large listen count means the user really likes the song and a low listen count means they’re not interested in it. However, the data shows that while 99% of the listen counts are 24 or lower, there are also some listen counts in the thousands, with the maximum being 9,667. (As Figure 2-3 shows, the histogram peaks in the bin closest to 0. But more than 10,000 triplets have greater counts, with a few in the thousands.) These values are anomalously large; if we were to try to predict the actual listen counts, the model would be pulled off course by these large values.

Figure 2-3. Histogram of listen counts in the Taste Profile subset of the Million Song Dataset—note that the y-axis is on a log scale

In the Million Song Dataset, the raw listen count is not a robust measure of user taste. (In statistical lingo, robustness means that the method works under a wide variety of conditions.) Users have different listening habits. Some people might put their favorite songs on infinite loop, while others might savor them only on special occasions. We can’t necessarily say that someone who listens to a song 20 times must like it twice as much as someone else who listens to it 10 times.

A more robust representation of user preference is to binarize the count and clip all counts greater than 1 to 1, as illustrated in Example 2-1. In other words, if the user listened to a song at least once, then we count it as the user liking the song. This way, the model will not need to spend cycles on predicting the minute differences between the raw counts. The binary target is a simple and robust measure of user preference.

Example 2-1. Binarizing listen counts in the Million Song Dataset

>>> import pandas as pd
>>> listen_count = pd.read_csv('millionsong/train_triplets.txt.zip',
...                            header=None, delimiter='	')
# The table contains user-song-count triplets. Only nonzero counts are
# included. Hence, to binarize the count, we just need to set the entire
# count column to 1.
>>> listen_count[2] = 1

This is an example where we engineer the target variable of the model. Strictly speaking, the target is not a feature because it’s not the input. But on occasion we do need to modify the target in order to solve the right problem.

Quantization or Binning

For this exercise, we take data from round 6 of the Yelp dataset challenge and create a much smaller classification dataset. The Yelp dataset contains user reviews of businesses from 10 cities across North America and Europe. Each business is labeled with zero or more categories.

Each business has a review count. Suppose our task is to use collaborative filtering to predict the rating a user might give to a business. The review count might be a useful input feature because there is usually a strong correlation between popularity and good ratings. Now the question is, should we use the raw review count or process it further? Figure 2-4, produced by Example 2-2, shows the histogram of all business review counts. We see the same pattern as in the listen counts in the previous example: most of the counts are small, but some businesses have reviews in the thousands.

Example 2-2. Visualizing business review counts in the Yelp dataset

>>> import pandas as pd
>>> import json

# Load the data about businesses
>>> biz_file = open('yelp_academic_dataset_business.json')
>>> biz_df = pd.DataFrame([json.loads(x) for x in biz_file.readlines()])
>>> biz_file.close()

>>> import matplotlib.pyplot as plt
>>> import seaborn as sns

# Plot the histogram of the review counts
>>> sns.set_style('whitegrid')
>>> fig, ax = plt.subplots()
>>> biz_df['review_count'].hist(ax=ax, bins=100)
>>> ax.set_yscale('log')
>>> ax.tick_params(labelsize=14)
>>> ax.set_xlabel('Review Count', fontsize=14)
>>> ax.set_ylabel('Occurrence', fontsize=14)

Raw counts that span several orders of magnitude are problematic for many models. In a linear model, the same linear coefficient would have to work for all possible values of the count. Large counts could also wreak havoc in unsupervised learning methods such as k-means clustering, which uses Euclidean distance as a similarity function to measure the similarity between data points. A large count in one element of the data vector would outweigh the similarity in all other elements, which could throw off the entire similarity measurement.

One solution is to contain the scale by quantizing the count. In other words, we group the counts into bins, and get rid of the actual count values. Quantization maps a continuous number to a discrete one. We can think of the discretized numbers as an ordered sequence of bins that represent a measure of intensity.

Figure 2-4. Histogram of business review counts in the Yelp reviews dataset—the y-axis is on a log scale

In order to quantize data, we have to decide how wide each bin should be. The solutions fall into two categories: fixed-width or adaptive. We will give an example of each type.

Fixed-width binning

With fixed-width binning, each bin contains a specific numeric range. The ranges can be custom designed or automatically segmented, and they can be linearly scaled or exponentially scaled. For example, we can group people into age ranges by decade: 0–9 years old in bin 1, 10–19 years in bin 2, etc. To map from the count to the bin, we simply divide by the width of the bin and take the integer part.

It’s also common to see custom-designed age ranges that better correspond to stages of life, such as:

• 0–12 years old

• 12–17 years old

• 18–24 years old

• 25–34 years old

• 35–44 years old

• 45–54 years old

• 55–64 years old

• 65–74 years old

• 75 years or older

When the numbers span multiple magnitudes, it may be better to group by powers of 10 (or powers of any constant): 0–9, 10–99, 100–999, 1000–9999, etc. The bin widths grow exponentially, going from O(10), to O(100), O(1000), and beyond. To map from the count to the bin, we take the log of the count. Exponential-width binning is very much related to the log transform, which we discuss in “Log Transformation”. Example 2-3 illustrates several of these binning methods.

Example 2-3. Quantizing counts with fixed-width bins

>>> import numpy as np

# Generate 20 random integers uniformly between 0 and 99
>>> small_counts = np.random.randint(0, 100, 20)
>>> small_counts
array([30, 64, 49, 26, 69, 23, 56,  7, 69, 67, 87, 14, 67, 33, 88, 77, 75,
       47, 44, 93])
# Map to evenly spaced bins 0-9 by division
>>> np.floor_divide(small_counts, 10)
array([3, 6, 4, 2, 6, 2, 5, 0, 6, 6, 8, 1, 6, 3, 8, 7, 7, 4, 4, 9], dtype=int32)

# An array of counts that span several magnitudes
>>> large_counts = [296, 8286, 64011, 80, 3, 725, 867, 2215, 7689, 11495, 91897, 
...                 44, 28, 7971, 926, 122, 22222]
# Map to exponential-width bins via the log function
>>> np.floor(np.log10(large_counts))
array([ 2.,  3.,  4.,  1.,  0.,  2.,  2.,  3.,  3.,  4.,  4.,  1.,  1.,
        3.,  2.,  2.,  4.])

Quantile binning

Fixed-width binning is easy to compute. But if there are large gaps in the counts, then there will be many empty bins with no data. This problem can be solved by adaptively positioning the bins based on the distribution of the data. This can be done using the quantiles of the distribution.

Quantiles are values that divide the data into equal portions. For example, the median divides the data in halves; half the data points are smaller and half larger than the median. The quartiles divide the data into quarters, the deciles into tenths, etc. Example 2-4 demonstrates how to compute the deciles of the Yelp business review counts, and Figure 2-5 overlays the deciles on the histogram. This gives a much clearer picture of the skew toward smaller counts.

Example 2-4. Computing deciles of Yelp business review counts

>>> deciles = biz_df['review_count'].quantile([.1, .2, .3, .4, .5, .6, .7, .8, .9])
>>> deciles
0.1     3.0
0.2     4.0
0.3     5.0
0.4     6.0
0.5     8.0
0.6    12.0
0.7    17.0
0.8    28.0
0.9    58.0
Name: review_count, dtype: float64

# Visualize the deciles on the histogram
>>> sns.set_style('whitegrid')
>>> fig, ax = plt.subplots()
>>> biz_df['review_count'].hist(ax=ax, bins=100)
>>> for pos in deciles:
...     handle = plt.axvline(pos, color='r')
>>> ax.legend([handle], ['deciles'], fontsize=14)
>>> ax.set_yscale('log')
>>> ax.set_xscale('log')
>>> ax.tick_params(labelsize=14)
>>> ax.set_xlabel('Review Count', fontsize=14)
>>> ax.set_ylabel('Occurrence', fontsize=14)

Figure 2-5. Deciles of the review counts in the Yelp reviews dataset—both the x- and y-axes are on a log scale

To compute the quantiles and map data into quantile bins, we can use the Pandas library, as shown in Example 2-5. pandas.DataFrame.quantile and pandas.Series.quantile compute the quantiles. pandas.qcut maps data into a desired number of quantiles.

Example 2-5. Binning counts by quantiles

# Continue example 2-3 with large_counts
>>> import pandas as pd

# Map the counts to quartiles
>>> pd.qcut(large_counts, 4, labels=False)
array([1, 2, 3, 0, 0, 1, 1, 2, 2, 3, 3, 0, 0, 2, 1, 0, 3], dtype=int64)

# Compute the quantiles themselves
>>> large_counts_series = pd.Series(large_counts)
>>> large_counts_series.quantile([0.25, 0.5, 0.75])
0.25     122.0
0.50     926.0
0.75    8286.0
dtype: float64

Log Transformation

In the previous section, we briefly introduced the notion of taking the logarithm of the count to map the data to exponential-width bins. Let’s take a closer look at that now.

The log function is the inverse of the exponential function. It is defined such that log_a(a^x) = x, where a is a positive constant, and x can be any positive number. Since a⁰ = 1, we have log_a(1) = 0. This means that the log function maps the small range of numbers between (0, 1) to the entire range of negative numbers (–∞, 0). The function log₁₀(x) maps the range of [1, 10] to [0, 1], [10, 100] to [1, 2], and so on. In other words, the log function compresses the range of large numbers and expands the range of small numbers. The larger x is, the slower log(x) increments.

This is easier to digest by looking at a plot of the log function (see Figure 2-6). Note how the horizontal x values from 100 to 1,000 get compressed into just 2.0 to 3.0 in the vertical y range, while the tiny horizontal portion of x values less than 100 are mapped to the rest of the vertical range.

Figure 2-6. The log function compresses the high numeric range and expands the low range

The log transform is a powerful tool for dealing with positive numbers with a heavy-tailed distribution. (A heavy-tailed distribution places more probability mass in the tail range than a Gaussian distribution.) It compresses the long tail in the high end of the distribution into a shorter tail, and expands the low end into a longer head. Figure 2-7 compares the histograms of Yelp business review counts before and after log transformation (see Example 2-6). The y-axes are now both on a normal (linear) scale. The increased bin spacing in the bottom plot between the range of (0.5, 1] is due to there being only 10 possible integer counts between 1 and 10. Notice that the original review counts are very concentrated in the low count region, with outliers stretching out above 4,000. After log transformation, the histogram is less concentrated in the low end and more spread out over the x-axis.

>>> fig, (ax1, ax2) = plt.subplots(2,1)
>>> biz_df['review_count'].hist(ax=ax1, bins=100)
>>> ax1.tick_params(labelsize=14)
>>> ax1.set_xlabel('review_count', fontsize=14)
>>> ax1.set_ylabel('Occurrence', fontsize=14)

>>> biz_df['log_review_count'].hist(ax=ax2, bins=100)
>>> ax2.tick_params(labelsize=14)
>>> ax2.set_xlabel('log10(review_count))', fontsize=14)
>>> ax2.set_ylabel('Occurrence', fontsize=14)

Figure 2-7. Comparison of Yelp business review counts before (top) and after (bottom) log transformation

As another example, let’s consider the Online News Popularity dataset from the UC Irvine Machine Learning Repository (Fernandes et al., 2015).

Our goal is to use these features to predict the popularity of the articles in terms of the number of shares on social media. In this example, we’ll focus on only one feature—the number of words in the article. Figure 2-8 shows the histograms of the feature before and after log transformation (see Example 2-7). Notice that the distribution looks much more Gaussian after log transformation, with the exception of the burst of number of articles of length zero (no content).

>>> fig, (ax1, ax2) = plt.subplots(2,1)
>>> df['n_tokens_content'].hist(ax=ax1, bins=100)
>>> ax1.tick_params(labelsize=14)
>>> ax1.set_xlabel('Number of Words in Article', fontsize=14)
>>> ax1.set_ylabel('Number of Articles', fontsize=14)

>>> df['log_n_tokens_content'].hist(ax=ax2, bins=100)
>>> ax2.tick_params(labelsize=14)
>>> ax2.set_xlabel('Log of Number of Words', fontsize=14)
>>> ax2.set_ylabel('Number of Articles', fontsize=14)

Figure 2-8. Comparison of word counts in Mashable news articles before (top) and after (bottom) log transformation

Log Transform in Action

Let’s see how the log transform performs for supervised learning. We’ll use both of the previous datasets here. For the Yelp reviews dataset, we’ll use the number of reviews to predict the average rating of a business (see Example 2-8). For the Mashable news articles, we’ll use the number of words in an article to predict its popularity. Since the outputs are continuous numbers, we’ll use simple linear regression as the model. We use scikit-learn to perform 10-fold cross validation of linear regression on the feature with and without log transformation. The models are evaluated by the R-squared score, which measures how well a trained regression model predicts new data. Good models have high R-squared scores. A perfect model gets the maximum score of 1. The score can be negative, and a bad model can get an arbitrarily low negative score. Using cross validation, we obtain not only an estimate of the score but also a variance, which helps us gauge whether the differences between the two models are meaningful.

Example 2-8. Using log transformed Yelp review counts to predict average business rating

>>> import pandas as pd
>>> import numpy as np
>>> import json
>>> from sklearn import linear_model
>>> from sklearn.model_selection import cross_val_score

# Using the previously loaded Yelp reviews DataFrame,
# compute the log transform of the Yelp review count.
# Note that we add 1 to the raw count to prevent the logarithm from
# exploding into negative infinity in case the count is zero.
>>> biz_df['log_review_count'] = np.log10(biz_df['review_count'] + 1)

# Train linear regression models to predict the average star rating of a business,
# using the review_count feature with and without log transformation.
# Compare the 10-fold cross validation score of the two models.
>>> m_orig = linear_model.LinearRegression()
>>> scores_orig = cross_val_score(m_orig, biz_df[['review_count']], 
...                               biz_df['stars'], cv=10)
>>> m_log = linear_model.LinearRegression()
>>> scores_log = cross_val_score(m_log, biz_df[['log_review_count']], 
...                              biz_df['stars'], cv=10)
>>> print("R-squared score without log transform: %0.5f (+/- %0.5f)"
...       % (scores_orig.mean(), scores_orig.std() * 2))
>>> print("R-squared score with log transform: %0.5f (+/- %0.5f)"
...       % (scores_log.mean(), scores_log.std() * 2))
R-squared score without log transform: -0.03683 (+/- 0.07280)
R-squared score with log transform: -0.03694 (+/- 0.07650)

Judging by the output of the experiment, the two simple models (with and without log transform) are equally bad at predicting the target, with the log transformed feature performing slightly worse. How disappointing! It’s not surprising that neither of them are very good, given that they both use just one feature, but one would have hoped that the log transformed feature might have performed better.

Now let’s look at how the log transform does on the Online News Popularity dataset (Example 2-9).

Example 2-9. Using log transformed word counts in the Online News Popularity dataset to predict article popularity

# Download the Online News Popularity dataset from UCI, then use
# Pandas to load the file into a DataFrame.
>>> df = pd.read_csv('OnlineNewsPopularity.csv', delimiter=', ')

# Take the log transform of the 'n_tokens_content' feature, which 
# represents the number of words (tokens) in a news article.
>>> df['log_n_tokens_content'] = np.log10(df['n_tokens_content'] + 1)

# Train two linear regression models to predict the number of shares
# of an article, one using the original feature and the other the
# log transformed version.
>>> m_orig = linear_model.LinearRegression()
>>> scores_orig = cross_val_score(m_orig, df[['n_tokens_content']],
...                               df['shares'], cv=10)
>>> m_log = linear_model.LinearRegression()
>>> scores_log = cross_val_score(m_log, df[['log_n_tokens_content']],
...                              df['shares'], cv=10)
>>> print("R-squared score without log transform: %0.5f (+/- %0.5f)"
...       % (scores_orig.mean(), scores_orig.std() * 2))
>>> print("R-squared score with log transform: %0.5f (+/- %0.5f)"
...       % (scores_log.mean(), scores_log.std() * 2))
R-squared score without log transform: -0.00242 (+/- 0.00509)
R-squared score with log transform: -0.00114 (+/- 0.00418)

The confidence intervals still overlap, but the model with the log transformed feature is doing better than the one without. Why is the log transform so much more successful on this dataset? We can get a clue by looking at the scatter plots (Example 2-10) of the input feature and target values. As can be seen in the bottom panel of Figure 2-9, the log transform reshaped the x-axis, pulling the articles with large outliers in the target value (>200,000 shares) further out toward the righthand side of the axis. This gives the linear model more “breathing room” on the low end of the input feature space. Without the log transform (top panel), the model is under more pressure to fit very different target values under very small changes in the input.

Example 2-10. Visualizing the correlation between input and output in the news popularity prediction problem

>>> fig2, (ax1, ax2) = plt.subplots(2,1)
>>> ax1.scatter(df['n_tokens_content'], df['shares'])
>>> ax1.tick_params(labelsize=14)
>>> ax1.set_xlabel('Number of Words in Article', fontsize=14)
>>> ax1.set_ylabel('Number of Shares', fontsize=14)

>>> ax2.scatter(df['log_n_tokens_content'], df['shares'])
>>> ax2.tick_params(labelsize=14)
>>> ax2.set_xlabel('Log of the Number of Words in Article', fontsize=14)
>>> ax2.set_ylabel('Number of Shares', fontsize=14)

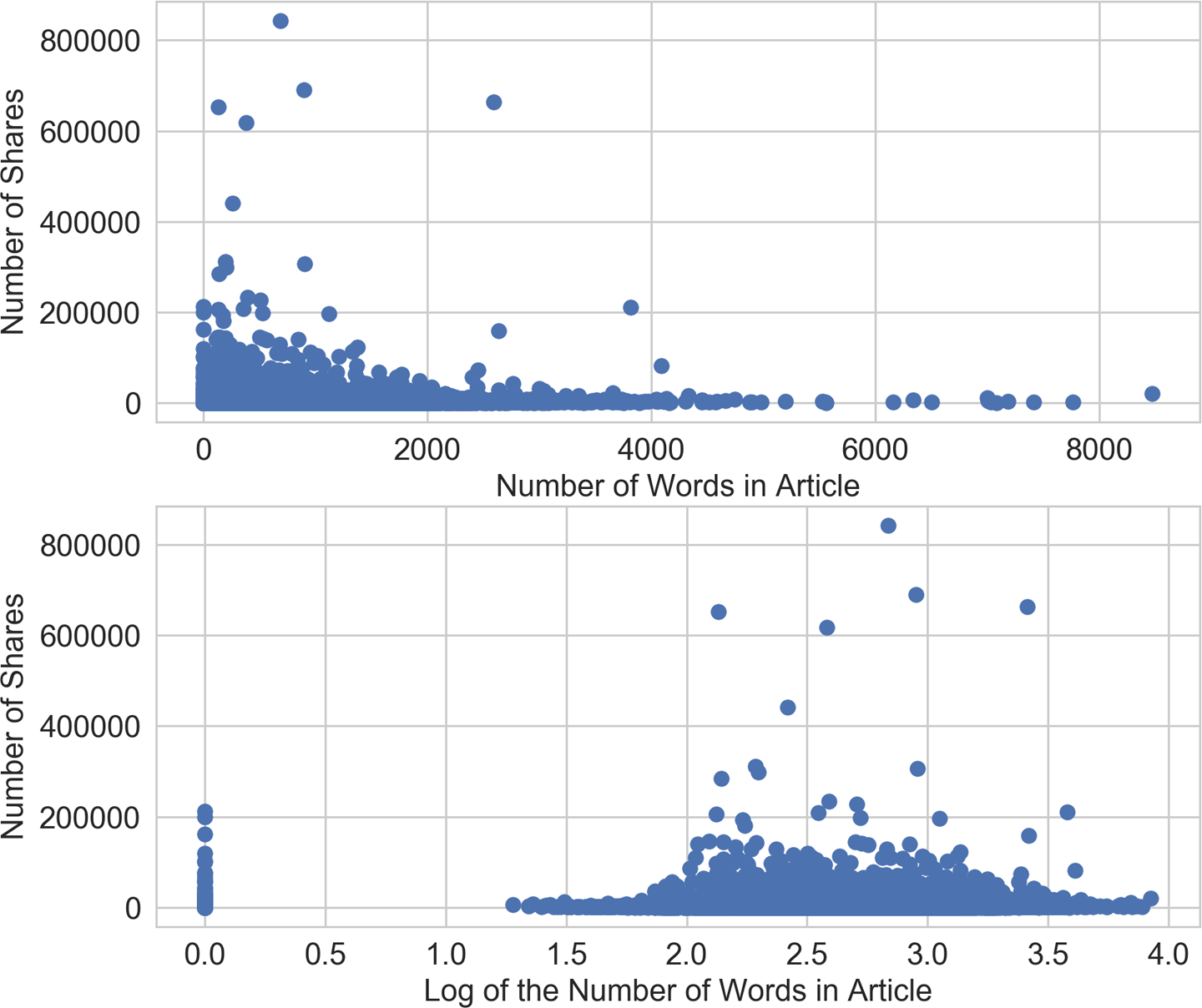
Figure 2-9. Scatter plots of number of words (input) versus number of shares (target) in the Online News Popularity dataset—the top plot visualizes the original feature, and the bottom plot shows the scatter plot after log transformation

Compare this with the same scatter plot applied to the Yelp reviews dataset (Example 2-11). Figure 2-10 looks very different from Figure 2-9. The average star rating is discretized in increments of half-stars ranging from 1 to 5. High review counts (roughly >2,500 reviews) do correlate with higher average star ratings, but the relationship is far from linear. There is no clear way to draw a line to predict the average star rating based on either input. Essentially, the plot shows that review count and its logarithm are both bad linear predictors of average star rating.

Example 2-11. Visualizing the correlation between input and output in Yelp business review prediction

>>> fig, (ax1, ax2) = plt.subplots(2,1)
>>> ax1.scatter(biz_df['review_count'], biz_df['stars'])
>>> ax1.tick_params(labelsize=14)
>>> ax1.set_xlabel('Review Count', fontsize=14)
>>> ax1.set_ylabel('Average Star Rating', fontsize=14)

>>> ax2.scatter(biz_df['log_review_count'], biz_df['stars'])
>>> ax2.tick_params(labelsize=14)
>>> ax2.set_xlabel('Log of Review Count', fontsize=14)
>>> ax2.set_ylabel('Average Star Rating', fontsize=14)

The Importance of Data Visualization

The comparison of the effect of the log transform on two different datasets illustrates the importance of visualizing the data. Here, we intentionally kept the input and target variables simple so that we can easily visualize the relationship between them. Plots like those in Figure 2-10 immediately reveal that the chosen model (linear) cannot possibly represent the relationship between the chosen input and target. On the other hand, one could convincingly model the distribution of review count given the average star rating. When building models, it is a good idea to visually inspect the relationships between input and output, and between different input features. 

Figure 2-10. Scatter plots of review counts (input) versus average star rating (target) in the Yelp reviews dataset—the top panel plots the original review count, and the bottom panel plots the review count after log transformation

Power Transforms: Generalization of the Log Transform

The log transform is a specific example of a family of transformations known as power transforms. In statistical terms, these are variance-stabilizing transformations. To understand why variance stabilization is good, consider the Poisson distribution. This is a heavy-tailed distribution with a variance that is equal to its mean: hence, the larger its center of mass, the larger its variance, and the heavier the tail. Power transforms change the distribution of the variable so that the variance is no longer dependent on the mean. For example, suppose a random variable X has the Poisson distribution. If we transform X by taking its square root, the variance of $\tilde{X}=\sqrt{X}$ is roughly constant, instead of being equal to the mean.

Figure 2-11 illustrates λ, which represents the mean of the distribution. As λ increases, not only does the mode of the distribution shift to the right, but the mass spreads out and the variance becomes larger.

Figure 2-11. A rough illustration of the Poisson distribution, an example distribution where the variance increases along with the mean

A simple generalization of both the square root transform and the log transform is known as the Box-Cox transform:

$$\tilde{x}=\left\{\begin{array}{ll}\frac{x^{\lambda }–1}{\lambda }& \text{if}\lambda \ne 0,\\ \ln \left(x\right)& \text{if}\lambda =0.\end{array}\right.$$

Figure 2-12 shows the Box-Cox transform for λ = 0 (the log transform), λ = 0.25, λ = 0.5 (a scaled and shifted version of the square root transform), λ = 0.75, and λ = 1.5. Setting λ to be less than 1 compresses the higher values, and setting λ higher than 1 has the opposite effect.

Figure 2-12. Box-Cox transforms for different values of λ

The Box-Cox formulation only works when the data is positive. For nonpositive data, one could shift the values by adding a fixed constant. When applying the Box-Cox transformation or a more general power transform, we have to determine a value for the parameter λ. This may be done via maximum likelihood (finding the λ that maximizes the Gaussian likelihood of the resulting transformed signal) or Bayesian methods. A full treatment of the usage of Box-Cox and general power transforms is outside the scope of this book. Interested readers may find more information on power transforms in Econometric Methods by Johnston and DiNardo (1997). Fortunately, SciPy’s stats package contains an implementation of the Box-Cox transformation that includes finding the optimal transform parameter. Example 2-12 demonstrates its use on the Yelp reviews dataset.

Example 2-12. Box-Cox transformation of Yelp business review counts

>>> from scipy import stats

# Continuing from the previous example, assume biz_df contains
# the Yelp business reviews data.
# The Box-Cox transform assumes that input data is positive. 
# Check the min to make sure.
>>> biz_df['review_count'].min()
3

# Setting input parameter lmbda to 0 gives us the log transform (without 
# constant offset)
>>> rc_log = stats.boxcox(biz_df['review_count'], lmbda=0)
# By default, the scipy implementation of Box-Cox transform finds the lambda
# parameter that will make the output the closest to a normal distribution
>>> rc_bc, bc_params = stats.boxcox(biz_df['review_count'])
>>> bc_params
-0.4106510862321085

Figure 2-13 provides a visual comparison of the distributions of the original and transformed counts (see Example 2-13).

Example 2-13. Visualizing the histograms of original, log transformed, and Box-Cox transformed counts

>>> fig, (ax1, ax2, ax3) = plt.subplots(3,1)
# original review count histogram
>>> biz_df['review_count'].hist(ax=ax1, bins=100)
>>> ax1.set_yscale('log')
>>> ax1.tick_params(labelsize=14)
>>> ax1.set_title('Review Counts Histogram', fontsize=14)
>>> ax1.set_xlabel('')
>>> ax1.set_ylabel('Occurrence', fontsize=14)

# review count after log transform
>>> biz_df['rc_log'].hist(ax=ax2, bins=100)
>>> ax2.set_yscale('log')
>>> ax2.tick_params(labelsize=14)
>>> ax2.set_title('Log Transformed Counts Histogram', fontsize=14)
>>> ax2.set_xlabel('')
>>> ax2.set_ylabel('Occurrence', fontsize=14)

# review count after optimal Box-Cox transform
>>> biz_df['rc_bc'].hist(ax=ax3, bins=100)
>>> ax3.set_yscale('log')
>>> ax3.tick_params(labelsize=14)
>>> ax3.set_title('Box-Cox Transformed Counts Histogram', fontsize=14)
>>> ax3.set_xlabel('')
>>> ax3.set_ylabel('Occurrence', fontsize=14)

Figure 2-13. Box-Cox transformation of Yelp business review counts (bottom), compared to original (top) and log transformed (middle) histograms

A probability plot, or probplot, is an easy way to visually compare an empirical distribution of data against a theoretical distribution. This is essentially a scatter plot of observed versus theoretical quantiles. Figure 2-14 shows the probplots of original and transformed Yelp review counts data against the normal distribution (see Example 2-14). Since the observed data is strictly positive and the Gaussian can be negative, the quantiles could never match up on the negative end. Thus, our focus is on the positive side. On this front, the original counts are obviously much more heavy-tailed than a normal distribution. (The ordered values go up to 4,000, whereas the theoretical quantiles only stretch to 4.) Both the plain log transform and the optimal Box-Cox transform bring the positive tail closer to normal. The optimal Box-Cox transform deflates the tail more than the log transform, as is evident from the fact that the tail flattens out under the red diagonal equivalence line.

Example 2-14. Probability plots of original and transformed counts against the normal distribution

>>> fig2, (ax1, ax2, ax3) = plt.subplots(3,1)
>>> prob1 = stats.probplot(biz_df['review_count'], dist=stats.norm, plot=ax1)
>>> ax1.set_xlabel('')
>>> ax1.set_title('Probplot against normal distribution')
>>> prob2 = stats.probplot(biz_df['rc_log'], dist=stats.norm, plot=ax2)
>>> ax2.set_xlabel('')
>>> ax2.set_title('Probplot after log transform')
>>> prob3 = stats.probplot(biz_df['rc_bc'], dist=stats.norm, plot=ax3)
>>> ax3.set_xlabel('Theoretical quantiles')
>>> ax3.set_title('Probplot after Box-Cox transform')

Figure 2-14. Comparing the distribution of raw and transformed review counts against the normal distribution

Feature Scaling or Normalization

Some features, such as latitude or longitude, are bounded in value. Other numeric features, such as counts, may increase without bound. Models that are smooth functions of the input, such as linear regression, logistic regression, or anything that involves a matrix, are affected by the scale of the input. Tree-based models, on the other hand, couldn’t care less. If your model is sensitive to the scale of input features, feature scaling could help. As the name suggests, feature scaling changes the scale of the feature. Sometimes people also call it feature normalization. Feature scaling is usually done individually to each feature. Next, we will discuss several types of common scaling operations, each resulting in a different distribution of feature values.

Min-Max Scaling

Let x be an individual feature value (i.e., a value of the feature in some data point), and min(x) and max(x), respectively, be the minimum and maximum values of this feature over the entire dataset. Min-max scaling squeezes (or stretches) all feature values to be within the range of [0, 1]. Figure 2-15 demonstrates this concept. The formula for min-max scaling is:

$$\tilde{x}=\frac{x–\min \left(x\right)}{\max \left(x\right)–\min \left(x\right)}$$

Figure 2-15. Illustration of min-max scaling

Standardization (Variance Scaling)

Feature standardization is defined as:

$$\tilde{x}=\frac{x–\mathrm{mean}\left(x\right)}{\mathrm{sqrt}\left(\mathrm{var}\right(x\left)\right)}$$

It subtracts off the mean of the feature (over all data points) and divides by the variance. Hence, it can also be called variance scaling. The resulting scaled feature has a mean of 0 and a variance of 1. If the original feature has a Gaussian distribution, then the scaled feature does too. Figure 2-16 is an illustration of standardization.

Figure 2-16. Illustration of feature standardization

Don’t “Center” Sparse Data!

Use caution when performing min-max scaling and standardization on sparse features. Both subtract a quantity from the original feature value. For min-max scaling, the shift is the minimum over all values of the current feature; for standardization, it is the mean. If the shift is not zero, then these two transforms can turn a sparse feature vector where most values are zero into a dense one. This in turn could create a huge computational burden for the classifier, depending on how it is implemented (not to mention that it would be horrendous if the representation now included every word that didn’t appear in a document!). Bag-of-words is a sparse representation, and most classification libraries optimize for sparse inputs.

ℓ² Normalization

This technique normalizes (divides) the original feature value by what’s known as the ℓ² norm, also known as the Euclidean norm. It’s defined as follows:

$$\tilde{x}=\frac{x}{{\parallel x\parallel }_2}$$

The ℓ² norm measures the length of the vector in coordinate space. The definition can be derived from the well-known Pythagorean theorem that gives us the length of the hypotenuse of a right triangle given the lengths of the sides:

$${\parallel x\parallel }_2=\sqrt{x_1^2+x_2^2+\dots +x_m^2}$$

The ℓ² norm sums the squares of the values of the features across data points, then takes the square root. After ℓ² normalization, the feature column has norm 1. This is also sometimes called ℓ² scaling. (Loosely speaking, scaling means multiplying by a constant, whereas normalization could involve a number of operations.) Figure 2-17 illustrates ℓ² normalization.

Figure 2-17. Illustration of ℓ² feature normalization

Data Space Versus Feature Space

Note that the illustration in Figure 2-17 is in data space, not feature space. One can also do ℓ² normalization for the data point instead of the feature, which will result in data vectors with unit norm (norm of 1). See the discussion in “Bag-of-Words” about the complementary nature of data vectors and feature vectors.

No matter the scaling method, feature scaling always divides the feature by a constant (known as the normalization constant). Therefore, it does not change the shape of the single-feature distribution. We’ll illustrate this with the online news article token counts (see Example 2-15).

Example 2-15. Feature scaling example

>>> import pandas as pd
>>> import sklearn.preprocessing as preproc

# Load the Online News Popularity dataset
>>> df = pd.read_csv('OnlineNewsPopularity.csv', delimiter=', ')

# Look at the original data - the number of words in an article
>>> df['n_tokens_content'].as_matrix()
array([ 219.,  255.,  211., ...,  442.,  682.,  157.])

# Min-max scaling
>>> df['minmax'] = preproc.minmax_scale(df[['n_tokens_content']])
>>> df['minmax'].as_matrix()
array([ 0.02584376,  0.03009205,  0.02489969, ...,  0.05215955,
        0.08048147,  0.01852726])

# Standardization - note that by definition, some outputs will be negative
>>> df['standardized'] = preproc.StandardScaler().fit_transform(df[['n_tokens_content']])
>>> df['standardized'].as_matrix()
array([-0.69521045, -0.61879381, -0.71219192, ..., -0.2218518 ,
        0.28759248, -0.82681689])

# L2-normalization
>>> df['l2_normalized'] = preproc.normalize(df[['n_tokens_content']], axis=0)
>>> df['l2_normalized'].as_matrix()
array([ 0.00152439,  0.00177498,  0.00146871, ...,  0.00307663,
        0.0047472 ,  0.00109283])

We can also visualize the distribution of data with different feature scaling methods (Figure 2-18). As Example 2-16 shows, unlike the log transform, feature scaling doesn’t change the shape of the distribution; only the scale of the data changes.

Example 2-16. Plotting the histograms of original and scaled data

>>> fig, (ax1, ax2, ax3, ax4) = plt.subplots(4,1)
>>> fig.tight_layout()
>>> df['n_tokens_content'].hist(ax=ax1, bins=100)
>>> ax1.tick_params(labelsize=14)
>>> ax1.set_xlabel('Article word count', fontsize=14)
>>> ax1.set_ylabel('Number of articles', fontsize=14)

>>> df['minmax'].hist(ax=ax2, bins=100)
>>> ax2.tick_params(labelsize=14)
>>> ax2.set_xlabel('Min-max scaled word count', fontsize=14)
>>> ax2.set_ylabel('Number of articles', fontsize=14)

>>> df['standardized'].hist(ax=ax3, bins=100)
>>> ax3.tick_params(labelsize=14)
>>> ax3.set_xlabel('Standardized word count', fontsize=14)
>>> ax3.set_ylabel('Number of articles', fontsize=14)

>>> df['l2_normalized'].hist(ax=ax4, bins=100)
>>> ax4.tick_params(labelsize=14)
>>> ax4.set_xlabel('L2-normalized word count', fontsize=14)
>>> ax4.set_ylabel('Number of articles', fontsize=14)

Figure 2-18. Original and scaled news article word counts—note that only the scale of the x-axis changes; the shape of the distribution stays the same with feature scaling

Feature scaling is useful in situations where a set of input features differs wildly in scale. For instance, the number of daily visitors to a popular ecommerce site might be a hundred thousand, while the actual number of sales might be in the thousands. If both of those features are thrown into a model, then the model will need to balance its scale while figuring out what to do. Drastically varying scale in input features can lead to numeric stability issues for the model training algorithm. In those situations, it’s a good idea to standardize the features. Chapter 4 goes into detail about feature scaling in the context of handling natural text, including usage examples.

Interaction Features

A simple pairwise interaction feature is the product of two features. The analogy is the logical AND. It expresses the outcome in terms of pairs of conditions: “the purchase is coming from zip code 98121” AND “the user’s age is between 18 and 35.” Decision tree–based models get this for free, but generalized linear models often find interaction features very helpful.

A simple linear model uses a linear combination of the individual input features x₁, x₂, ... x_n to predict the outcome y:

An easy way to extend the linear model is to include combinations of pairs of input features, like so:

This allows us to capture interactions between features, and hence these pairs are called interaction features. If x₁ and x₂ are binary, then their product x₁x₂ is the logical function x₁ AND x₂. Suppose the problem is to predict a customer’s preference based on their profile information. In our example, instead of making predictions based solely on the age or location of the user, interaction features allow the model to make predictions based on the user being of a certain age AND at a particular location.

In Example 2-17, we use pairwise interaction features from the UCI Online News Popularity dataset to predict the number of shares for each news article. As the results show, interaction features result in some lift in accuracy above singleton features. Both perform better than Example 2-9, which used as a single predictor the number of words in the body of the article (with or without a log transform).

>>> from sklearn import linear_model
>>> from sklearn.model_selection import train_test_split
>>> import sklearn.preprocessing as preproc

# Assume df is a Pandas DataFrame containing the UCI Online News Popularity dataset
>>> df.columns
Index(['url', 'timedelta', 'n_tokens_title', 'n_tokens_content',
       'n_unique_tokens', 'n_non_stop_words', 'n_non_stop_unique_tokens',
       'num_hrefs', 'num_self_hrefs', 'num_imgs', 'num_videos',
       'average_token_length', 'num_keywords', 'data_channel_is_lifestyle',
       'data_channel_is_entertainment', 'data_channel_is_bus',
       'data_channel_is_socmed', 'data_channel_is_tech',
       'data_channel_is_world', 'kw_min_min', 'kw_max_min', 'kw_avg_min',
       'kw_min_max', 'kw_max_max', 'kw_avg_max', 'kw_min_avg', 'kw_max_avg',
       'kw_avg_avg', 'self_reference_min_shares', 'self_reference_max_shares',
       'self_reference_avg_sharess', 'weekday_is_monday', 'weekday_is_tuesday',
       'weekday_is_wednesday', 'weekday_is_thursday', 'weekday_is_friday',
       'weekday_is_saturday', 'weekday_is_sunday', 'is_weekend', 'LDA_00',
       'LDA_01', 'LDA_02', 'LDA_03', 'LDA_04', 'global_subjectivity',
       'global_sentiment_polarity', 'global_rate_positive_words',
       'global_rate_negative_words', 'rate_positive_words',
       'rate_negative_words', 'avg_positive_polarity', 'min_positive_polarity',
       'max_positive_polarity', 'avg_negative_polarity',
       'min_negative_polarity', 'max_negative_polarity', 'title_subjectivity',
       'title_sentiment_polarity', 'abs_title_subjectivity',
       'abs_title_sentiment_polarity', 'shares'],
      dtype='object')

# Select the content-based features as singleton features in the model,
# skipping over the derived features
>>> features = ['n_tokens_title', 'n_tokens_content',
...             'n_unique_tokens', 'n_non_stop_words', 'n_non_stop_unique_tokens',
...             'num_hrefs', 'num_self_hrefs', 'num_imgs', 'num_videos',
...             'average_token_length', 'num_keywords', 'data_channel_is_lifestyle',
...             'data_channel_is_entertainment', 'data_channel_is_bus',
...             'data_channel_is_socmed', 'data_channel_is_tech',
...             'data_channel_is_world']

>>> X = df[features]
>>> y = df[['shares']]

# Create pairwise interaction features, skipping the constant bias term
>>> X2 = preproc.PolynomialFeatures(include_bias=False).fit_transform(X)
>>> X2.shape
(39644, 170)

# Create train/test sets for both feature sets
>>> X1_train, X1_test, X2_train, X2_test, y_train, y_test = 
...     train_test_split(X, X2, y, test_size=0.3, random_state=123)                                                             

>>> def evaluate_feature(X_train, X_test, y_train, y_test):
...     """Fit a linear regression model on the training set and 
...     score on the test set"""
...     model = linear_model.LinearRegression().fit(X_train, y_train)
...     r_score = model.score(X_test, y_test)
...     return (model, r_score)

# Train models and compare score on the two feature sets
>>> (m1, r1) = evaluate_feature(X1_train, X1_test, y_train, y_test)
>>> (m2, r2) = evaluate_feature(X2_train, X2_test, y_train, y_test)
>>> print("R-squared score with singleton features: %0.5f" % r1)
>>> print("R-squared score with pairwise features: %0.10f" % r2)
R-squared score with singleton features: 0.00924
R-squared score with pairwise features: 0.0113276523

Interaction features are very simple to formulate, but they are expensive to use. The training and scoring time of a linear model with pairwise interaction features would go from O(n) to O(n²), where n is the number of singleton features.

There are a few ways around the computational expense of higher-order interaction features. One could perform feature selection on top of all of the interaction features. Alternatively, one could more carefully craft a smaller number of complex features.

Both strategies have their advantages and disadvantages. Feature selection employs computational means to select the best features for a problem. (This technique is not limited to interaction features.) However, some feature selection techniques still require training multiple models with a large number of features.

Handcrafted complex features can be expressive enough that only a small number of them are needed, which reduces the training time of the model—but the features themselves may be expensive to compute, which increases the computational cost of the model scoring stage. Good examples of handcrafted (or machine-learned) complex features may be found in Chapter 8. Let’s now look at some feature selection techniques.

Feature Selection

Feature selection techniques prune away nonuseful features in order to reduce the complexity of the resulting model. The end goal is a parsimonious model that is quicker to compute, with little or no degradation in predictive accuracy. In order to arrive at such a model, some feature selection techniques require training more than one candidate model. In other words, feature selection is not about reducing training time—in fact, some techniques increase overall training time—but about reducing model scoring time.

Roughly speaking, feature selection techniques fall into three classes:

Filtering

Filtering techniques preprocess features to remove ones that are unlikely to be useful for the model. For example, one could compute the correlation or mutual information between each feature and the response variable, and filter out the features that fall below a threshold. Chapter 3 discusses examples of these techniques for text features. Filtering techniques are much cheaper than the wrapper techniques described next, but they do not take into account the model being employed. Hence, they may not be able to select the right features for the model. It is best to do prefiltering conservatively, so as not to inadvertently eliminate useful features before they even make it to the model training step.

Wrapper methods

These techniques are expensive, but they allow you to try out subsets of features, which means you won’t accidentally prune away features that are uninformative by themselves but useful when taken in combination. The wrapper method treats the model as a black box that provides a quality score of a proposed subset for features. There is a separate method that iteratively refines the subset.

Embedded methods

These methods perform feature selection as part of the model training process. For example, a decision tree inherently performs feature selection because it selects one feature on which to split the tree at each training step. Another example is the ${\ell }^1$ regularizer, which can be added to the training objective of any linear model. The ${\ell }^1$ regularizer encourages models that use a few features as opposed to a lot of features, so it’s also known as a sparsity constraint on the model. Embedded methods incorporate feature selection as part of the model training process. They are not as powerful as wrapper methods, but they are nowhere near as expensive. Compared to filtering, embedded methods select features that are specific to the model. In this sense, embedded methods strike a balance between computational expense and quality of results.

A full treatment of feature selection is outside the scope of this book. Interested readers may refer to the survey paper by Guyon and Elisseeff (2003).

Summary

This chapter discussed a number of common numeric feature engineering techniques, such as quantization, scaling (a.k.a. normalization), log transforms (a type of power transform), and interaction features, and gave a brief summary of feature selection techniques, necessary for handling large quantities of interaction features. In statistical machine learning, all data eventually boils down to numeric features. Therefore, all roads lead to some kind of numeric feature engineering technique at the end. Keep these tools handy for the end game of feature engineering!

Bibliography

Bertin-Mahieux, Thierry, Daniel P.W. Ellis, Brian Whitman, and Paul Lamere. “The Million Song Dataset.” Proceedings of the 12th International Society for Music Information Retrieval Conference (2011): 591–596.

Fernandes, K., P. Vinagre, and P. Cortez. “A Proactive Intelligent Decision Support System for Predicting the Popularity of Online News.” Proceedings of the 17th Portuguese Conference on Artificial Intelligence (2015): 535–546.

Guyon, Isabell, and André Elisseeff. “An Introduction to Variable and Feature Selection.” Journal of Machine Learning Research Special Issue on Variable and Feature Selection 3 (2003): 1157–1182.

Johnston, Jack, and John DiNardo. Econometric Methods. 4th ed. New York: McGraw Hill, 1997.