The machine learning models that we have discussed so far in the previous two chapters share one common characteristic: they require training data containing ground truth. This implies a dataset containing true values of the predicate or dependent variable that is often manually labeled. Such machine learning where the algorithm is trained using labeled data is called supervised learning. This type of machine learning gives a very good performance in terms of accuracy of prediction. It is, in fact, the de facto method used in most industrial systems using machine learning. However, the drawback of this method is that, when one wants to train a model with large datasets, it would be difficult to get the labeled data. This is particularly relevant in the era of Big Data as a lot of data is available for organizations from various logs, transactions, and interactions with consumers; organizations want to gain insight from this data and make predictions about their consumers' interests.
In unsupervised methods, no labeled data is required for learning. The process of learning happens through identifying dominant patterns and correlations present in the dataset. Some common examples of unsupervised learning are clustering, association rule mining, density estimation, and dimensional reduction. In clustering, naturally occurring groups in data are identified using a suitable algorithm that makes use of some distance measure between data points. In association rule mining, items that frequently occur together in a transaction are identified from a transaction dataset. In dimensional reduction techniques such as principal component analysis, the original dataset containing a large number of variables (dimensions) is projected down to a lower dimensional space where the maximum information in the data is present. Though unsupervised learning doesn't require labeled training data, one would need a large amount of data to learn all the patterns of interest and often the learning is more computationally intensive.
In many practical cases, it would be feasible to create a small amount of labeled data. The third type of learning, semi-supervised learning, is a method that makes use of this small labeled dataset and propagates labels to the rest of the unlabeled training data using suitable algorithms. In this chapter, we will cover Bayesian approaches for unsupervised learnings. We will discuss in detail two important models: Gaussian mixture models for clustering and Latent Dirichlet allocation for topic modeling.
In general, a mixture model corresponds to representing data using a mixture of probability distributions. The most common mixture model is of the following type:

Here, ![]() is a probability distribution of X with parameters
is a probability distribution of X with parameters ![]() , and
, and ![]() represents the weight for the kth component in the mixture, such that
represents the weight for the kth component in the mixture, such that ![]() . If the underlying probability distribution is a normal (Gaussian) distribution, then the mixture model is called a
Gaussian mixture model (GMM). The mathematical representation of GMM, therefore, is given by:
. If the underlying probability distribution is a normal (Gaussian) distribution, then the mixture model is called a
Gaussian mixture model (GMM). The mathematical representation of GMM, therefore, is given by:

Here, we have used the same notation, as in previous chapters, where X stands for an N-dimensional data vector ![]() representing each observation and there are M such observations in the dataset.
representing each observation and there are M such observations in the dataset.
A mixture model such as this is suitable for clustering when the clusters have overlaps. One of the applications of GMM is in computer vision. If one wants to track moving objects in a video, it is useful to subtract the background image. This is called background subtraction or foreground detection. GMMs are used for this purpose where the intensity of each pixel is modeled using a mixture of Gaussian distributions (reference 1 in the References section of this chapter).
The task of learning GMMs corresponds to learning the model parameters ![]() and mixture weights
and mixture weights ![]() for all the components
for all the components ![]() . The standard approach for learning GMMs is by using the
maximum likelihood method. For a dataset consisting of M observations, the logarithm of the likelihood function is given by:
. The standard approach for learning GMMs is by using the
maximum likelihood method. For a dataset consisting of M observations, the logarithm of the likelihood function is given by:

Unlike a single Gaussian model, maximizing the log-likelihood with respect to parameters ![]() cannot be done in a straightforward manner in GMM. This is because there is no closed-form expression for the derivative in this case, since it is difficult to compute the logarithm of a sum. Therefore, one uses what is called an
expectation-maximization (EM) algorithm to maximize the log-likelihood function. The EM algorithm is an iterative algorithm, where each iteration consists of two computations: expectation and maximization. The EM algorithm proceeds as follows:
cannot be done in a straightforward manner in GMM. This is because there is no closed-form expression for the derivative in this case, since it is difficult to compute the logarithm of a sum. Therefore, one uses what is called an
expectation-maximization (EM) algorithm to maximize the log-likelihood function. The EM algorithm is an iterative algorithm, where each iteration consists of two computations: expectation and maximization. The EM algorithm proceeds as follows:
-
Initialize parameters
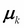 ,
,  , and
, and  and evaluate the initial value of log-likelihood.
and evaluate the initial value of log-likelihood.
-
In the expectation step, evaluate mixture components
 from log-likelihood using the current parameter values
from log-likelihood using the current parameter values 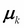 and
and  .
.
-
In the maximization step, using the values of
 computed in step 2, estimate new parameter values
computed in step 2, estimate new parameter values 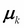 and
and  by the maximization of log-likelihood.
by the maximization of log-likelihood.
-
Compute a new value of the log-likelihood function using the estimated values of
 ,
, 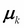 , and
, and  from steps 2 and 3.
from steps 2 and 3.
- Repeat steps 2-4 until the log-likelihood function is converged.
In the Bayesian treatment of GMM, the maximization of log-likelihood is simplified by introducing a latent variable Z. Let Z be a K-dimensional binary random variable having only one element 1, and the rest of the K – 1 elements are 0. Using Z, one can write the joint distribution of X and Z as follows:
Here:

And:

Therefore:

And:

The advantage of introducing a latent variable Z in the problem is that the expression for log-likelihood is simplified, where the logarithm directly acts on the normal distribution as in the case of a single Gaussian model. Therefore, it is straightforward to maximize P(X, Z). However, the problem that still remains is that we don't know the value of Z! So, the trick is to use an EM-like iterative algorithm where, in the E-step, the expectation value of Z is estimated and in the M-step, using the last estimated value of Z, we find the parameter values of the Gaussian distribution. The Bayesian version of the EM algorithm for GMM proceeds as follows:
-
Initialize parameters
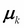 ,
,  , and
, and  and evaluate the initial value of log-likelihood.
and evaluate the initial value of log-likelihood.
-
In the expectation step, use these values to compute the expectation value
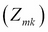 .
.
-
In the maximization step, using
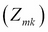 fixed, estimate
fixed, estimate 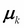 and
and  by maximizing
by maximizing  .
.
- Compute the new likelihood function.
- Repeat steps 2-4 until convergence.
A more detailed treatment of the Bayesian version of the EM algorithm and GMM can be found in the book by Christopher M. Bishop (reference 2 in the References section of this chapter). Here, we leave the theoretical treatment of the Bayesian GMM and proceed to look at its R implementation in the bgmm package.
The bgmm package was developed by Przemyslaw Biecek and Ewa Szczurek for modeling gene expressions data (reference 3 in the References section of this chapter). It can be downloaded from the CRAN website at http://cran.r-project.org/web/packages/bgmm/index.html. The package contains not only an unsupervised version of GMM but fully supervised and semi-supervised implementations as well. The following are the different models available in the bgmm package:
- Fully supervised GMM: This is the labeled data available for all records in a training set. This includes the following:
- The
supervised( )function
- The
- Semi-supervised GMM: This is the labeled data available for a small subset of all records in a training set. This includes the following
- The
semisupervised( )function
- The
- Partially supervised GMM: This is the labeled data available for a small subset of all records, but these labels are uncertain. The values of labels are given with some probability. There are two functions in the package for partially supervised GMM. This includes the following::
-
The
belief( )function: The uncertainty of labels is expressed as a probability distribution over its components. For the first m observations, a belief matrix B of dimensions m x k is given as input where the matrix entry denotes the probability that the ith record has the jth label.
denotes the probability that the ith record has the jth label.
-
The
soft( )function: In this approach, a plausibility matrix of dimension M x k is defined across all records in the training set of size M. The matrix element is interpreted as the weight of the prior probability that the ith record has the jth label. If there is no particular information about labels of any records, they can be given equal weights. For the purpose of implementation, a constraint is imposed on the matrix elements:
is interpreted as the weight of the prior probability that the ith record has the jth label. If there is no particular information about labels of any records, they can be given equal weights. For the purpose of implementation, a constraint is imposed on the matrix elements:  .
.
-
The
- Unsupervised GMM: This labeled data is not available for any records. This includes the following:
The typical parameters that are passed to these functions are as follows:
- X: This is a data.frame with the unlabelled X data.
- knowns: This is a data.frame with the labeled X data.
- B: This is a belief matrix that specifies the distribution of beliefs for the labeled records. The number of rows of B should be the same as that of knowns.
- P: This is a matrix of weights of prior probabilities (plausibilities).
- class: This is a vector of classes or labels for the labeled records.
- k: This is the number of components or columns of the B matrix.
- init.params: These are the initial values for the estimates of model parameters.
The difference between the belief( ) and soft( ) functions is that, in the first case, the input is a matrix containing prior probability values for each possible label, whereas in the second case, the input is a matrix containing weights for each of the priors and not the prior probability itself. For more details, readers are requested to read the paper by Przemyslaw Biecek et.al (reference 3 in the References section of this chapter).
Now, let's do a small illustrative example of using bgmm. We will use the ADL dataset from the UCI Machine Learning repository. This dataset contains acceleration data from wrist-worn accelerometers from 16 volunteers. The dataset and metadata details can be found at https://archive.ics.uci.edu/ml/datasets/Dataset+for+ADL+Recognition+with+Wrist-worn+Accelerometer. The research work on ADL monitoring systems, where this dataset was generated, is published in the two papers by Bruno B. et.al. (reference 4 and reference 5 in the References section of this chapter).
For the example of bgmm, we will only use one folder in the dataset directory, namely Brush_teeth. Firstly, we will do a small amount of preprocessing to combine data from the different volunteers into a single file. The following R script does this job:
>#Set working directory to folder containing files (provide the correct path)
>setwd("C:/…/ADL_Dataset/HMP_Dataset/Brush_teeth")
>flist <- list.files(path = "C:/../ADL_Dataset/HMP_Dataset/Brush_teeth",pattern = "*.txt")
>all.data <- lapply(flist,read.table,sep = " ",header = FALSE)
>combined.data <- as.data.frame(do.call(rbind,all.data))
>combined.data.XZ <- combined.data[,c(1,3)]The last step is to select the X and Z components of acceleration to create a two-dimensional dataset.
The following R script calls the bgmm function and performs clustering. A simple scatter plot of the data suggests that there could be four clusters in the dataset and choosing k = 4 would be sufficient:
>modelbgmm <- unsupervised(combined.data.XZ,k=4) >summary(modelbgmm) >plot.mModel(modelbgmm)
The clusters generated by bgmm can be seen in the following figure; there are four clusters whose centers are represented by the four color dots and their respective Gaussian densities are represented by the ellipses:

