As we have seen in the Chapter 1, Introduction to Practical Machine Learning Using Python, unsupervised learning is designed to provide insightful information on data unlabeled date. In many cases, a large dataset (both in terms of number of points and number of features) is unstructured and does not present any information at first sight, so these techniques are used to highlight hidden structures on data (clustering) or to reduce its complexity without losing relevant information (dimensionality reduction). This chapter will focus on the main clustering algorithms (the first part of the chapter) and dimensionality reduction methods (the second part of the chapter). The differences and advantages of the methods will be highlighted by providing a practical example using Python libraries. All of the code will be available on the author's GitHub profile, in the https://github.com/ai2010/machine_learning_for_the_web/tree/master/chapter_2/ folder. We will now start describing clustering algorithms.
Clustering algorithms are employed to restructure data in somehow ordered subsets so that a meaningful structure can be inferred. A cluster can be defined as a group of data points with some similar features. The way to quantify the similarity of data points is what determines the different categories of clustering.
Clustering algorithms can be divided into different categories based on different metrics or assumptions in which data has been manipulated. We are going to discuss the most relevant categories used nowadays, which are distribution methods, centroid methods, density methods, and hierarchical methods. For each category, a particular algorithm is going to be presented in detail, and we will begin by discussing distribution methods. An example to compare the different algorithms will be discussed, and both the IPython notebook and script are available in the my GitHub book folder at https://github.com/ai2010/machine_learning_for_the_web/tree/master/chapter_2/.
These methods assume that the data comes from a certain distribution, and the expectation maximization algorithm is used to find the optimal values for the distribution parameters. Expectation maximization and the mixture of Gaussian clustering are discussed hereafter.
This algorithm is used to find the maximum likelihood estimates of parameter distribution models that depend on hidden (unobserved) variables. Expectation maximization consists of iterating two steps: the E-step, which creates the log-likelihood function evaluated using the current values of the parameters, and the M-step, where the new parameters' values are computed, maximizing the log-likelihood of the E-step.
Consider a set of N elements, {x(i)}i = 1,…,N, and a log-likelihood on the data as follows:

Here, θ represents the set of parameters and z(i) are the so-called hidden variables.
We want to find the values of the parameters that maximize the log-likelihood without knowing the values of the z(i) (unobserved variables). Consider a distribution over the z(i), and Q(z(i)), such as ![]() . Therefore:
. Therefore:

This means Q(z(i)) is the posterior distribution of the hidden variable, z(i), given x(i) parameterized by θ. The expectation maximization algorithm comes from the use of Jensen's inequality and it ensures that carrying out these two steps:
The log-likelihood converges to the maximum, and so the associated θ values are found.
This method models the entire dataset using a mixture of Gaussian distributions. Therefore, the number of clusters will be given as the number of Gaussians considered in the mixture. Given a dataset of N elements, {x(i)}i = 1,…,N, where each ![]() is a vector of d-features modeled by a mixture of Gaussian such as the following:
is a vector of d-features modeled by a mixture of Gaussian such as the following:

Where:
 is a hidden variable that represents the Gaussian component each x(i) is generated from
is a hidden variable that represents the Gaussian component each x(i) is generated from represents the set of mean parameters of the Gaussian components
represents the set of mean parameters of the Gaussian components represents the set of variance parameters of the Gaussian components
represents the set of variance parameters of the Gaussian components
 is the mixture weight, representing the probability that a randomly selected x(i) was generated by the Gaussian component k, where
is the mixture weight, representing the probability that a randomly selected x(i) was generated by the Gaussian component k, where  , and
, and  is the set of weights
is the set of weights
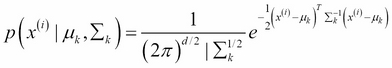 is the Gaussian component k with parameters
is the Gaussian component k with parameters  associated with the point x(i)
associated with the point x(i)
The parameters of our model are thus φ, µ and ∑. To estimate them, we can write down the log-likelihood of the dataset:

In order to find the values of the parameters, we apply the expectation maximization algorithm explained in the previous section where ![]() and
and ![]() .
.
After choosing a first guess of the parameters, we iterate the following steps until convergence:
Note that the expectation maximization algorithm is needed because the hidden variables z(i) are unknown. Otherwise, it would have been a supervised learning problem, where z(i) is the label of each point of the training set (and the supervised algorithm used would be the Gaussian discriminant analysis). Therefore, this is an unsupervised algorithm and the goal is also to find z(i), that is, which of the K Gaussian components each point x(i) is associated with. In fact, by calculating the posterior probability ![]() for each of the K classes, it is possible to assign each x(i) to the class k with the highest posterior probability. There are several cases in which this algorithm can be successfully used to cluster (label) the data.
for each of the K classes, it is possible to assign each x(i) to the class k with the highest posterior probability. There are several cases in which this algorithm can be successfully used to cluster (label) the data.
A possible practical example is the case of a professor with student grades for two different classes but not labeled per class. He wants to split the grades into the original two classes assuming that the distribution of grades in each class is Gaussian. Another example solvable with the mixture of the Gaussian approach is to determine the country of each person based on a set of people's height values coming from two different countries and assuming that the distribution of height in each country follows Gaussian distribution.
This class collects all the techniques that find the centers of the clusters, assigning the data points to the nearest cluster center and minimizing the distances between the centers and the assigned points. This is an optimization problem and the final centers are vectors; they may not be the points in the original dataset. The number of clusters is a parameter to be specified a priori and the generated clusters tend to have similar sizes so that the border lines are not necessarily well defined. This optimization problem may lead to a local optimal solution, which means that different initialization values can result in slightly different clusters. The most common method is known as k-means (Lloyd's algorithm), in which the distance minimized is the Euclidean norm. Other techniques find the centers as the medians of the clusters (k-medians clustering) or impose the center's values to be the actual data points. Furthermore, other variations of these methods differ in the choice that the initial centers are defined (k-means++ or fuzzy c-means).
This algorithm tries to find the center of each cluster as the mean of all the members that minimize the distance between the center and the assigned points themselves. It can be associated with the k-nearest-neighbor algorithm in classification problems, and the resulting set of clusters can be represented as a Voronoi diagram (a method of partitioning the space in regions based on the distance from a set of points, in this case, the clusters' centers). Consider the usual dataset, ![]() . The algorithm prescribes to choose a number of centers K, assign the initial mean cluster centers
. The algorithm prescribes to choose a number of centers K, assign the initial mean cluster centers ![]() to random values, and then iterate the following steps until convergence:
to random values, and then iterate the following steps until convergence:
-
For each data point i, calculate the Euclidean square distances between each point i and each center j and find the center index di, which corresponds to the minimum of these distances:
 .
.
-
For each center j, recalculate its mean value as the mean of the points that have d_i j equal to j (that is, points belonging to the cluster with mean
 ):
It is possible to show that this algorithm converges with respect to the function given by the following function:
):
It is possible to show that this algorithm converges with respect to the function given by the following function:

It decreases monotonically with the number of iterations. Since F is a nonconvex function, it is not guaranteed that the final minimum will be the global minimum. In order to avoid the problem of a clustering result associated with the local minima, the k-means algorithm is usually run multiple times with different random initial center's means. Then the result associated with the lower F value is chosen as the optimal clustering solution.
These methods are based on the idea that sparse areas have to be considered borders (or noise) and high-density zones should be related to the cluster's centers. The common method is called density-based spatial clustering of applications with noise (DBSCAN), which defines the connection between two points through a certain distance threshold (for this reason, it is similar to hierarchical algorithms; see Chapter 3, Supervised Machine Learning). Two points are considered linked (belonging to the same cluster) only if a certain density criterion is satisfied—the number of neighboring points has to be higher than a threshold value within a certain radius. Another popular method is mean-shift, in which each data point is assigned to the cluster that has the highest density in its neighborhood. Due to the time-consuming calculations of the density through a kernel density estimation, mean-shift is usually slower than DBSCAN or centroid methods. The main advantages of this class of algorithms are the ability to define clusters with arbitrary shapes and the ability to determine the best number of clusters instead of setting this number a priori as a parameter, making these methods suitable to cluster datasets in which it is not known.
Mean-shift is nonparametric algorithm that finds the positions of the local maxima in a density kernel function defined on a dataset. The local maxima found can be considered the centers of clusters in a dataset ![]() , and the number of maxima is the number of clusters. In order to be applied as a clustering algorithm, each point
, and the number of maxima is the number of clusters. In order to be applied as a clustering algorithm, each point ![]() has to be associated with the density of its neighborhood:
has to be associated with the density of its neighborhood:
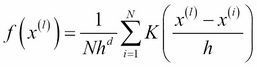
Here, h is the so-called bandwidth; it estimates the radius of the neighborhood in which the points affect the density value f(x(l)) (that is, the other points have negligible effect on ![]() ). K is the kernel function that satisfies these conditions:
). K is the kernel function that satisfies these conditions:
Typical examples of K(x(i)) are the following functions:
 : Gaussian kernel
: Gaussian kernel
 : Epanechnikov kernel
: Epanechnikov kernel
The mean-shift algorithm imposes the maximization of f(x(l)), which translates into the mathematical equation (remember that in function analysis, the maximum is found by imposing the derivative to 0):

Here, K' is derivative of the kernel density function K.
Therefore, to find the local maxima position associated with the feature vector x(l), the following iterative equation can be computed:

Here, ![]() is called the mean-shift vector. The algorithm will converge when at iteration t=a, the condition
is called the mean-shift vector. The algorithm will converge when at iteration t=a, the condition  is satisfied.
is satisfied.
Supported by the equation, we can now explain the algorithm with the help of the following figure. At the first iteration t=0, the original points ![]() (red) are spread on the data space, the mean shift vector
(red) are spread on the data space, the mean shift vector ![]() is calculated, and the same points are marked with a cross (x) to track their evolution with the algorithm. At iteration 1, the dataset will be obtained using the aforementioned equation, and the resulting points
is calculated, and the same points are marked with a cross (x) to track their evolution with the algorithm. At iteration 1, the dataset will be obtained using the aforementioned equation, and the resulting points ![]() are shown in the following figure with the (+) symbol:
are shown in the following figure with the (+) symbol:

Sketch of the mean-shift evolution through iterations
In the preceding figure, at iteration 0 the original points are shown in red (cross), at iteration 1 and K the sample points (symbols + and * respectively) move towards the local density maxima indicated by blue squares.
Again, at iteration K, the new data points ![]() are computed and they are shown with the * symbol in the preceding figure. The density function values
are computed and they are shown with the * symbol in the preceding figure. The density function values ![]() associated with
associated with ![]() are larger than the values in the previous iterations since the algorithm aims to maximize them. The original dataset is now clearly associated with points
are larger than the values in the previous iterations since the algorithm aims to maximize them. The original dataset is now clearly associated with points ![]() , and they converge to the locations plotted in blue squares in the preceding figure. The feature vectors
, and they converge to the locations plotted in blue squares in the preceding figure. The feature vectors ![]() are now collapsing to two different local maxima, which represent the centers of the two clusters.
are now collapsing to two different local maxima, which represent the centers of the two clusters.
In order to properly use the method, some considerations are necessary.
The only parameter required, the bandwidth h, needs to be tuned cleverly to achieve good results. In fact, too low value of h may result in a large number of clusters, while a large value of h may merge multiple distinct clusters. Note also that if the number d of feature vector dimensions is large, the mean-shift method may lead to poor results. This is because in a very-high-dimensional space, the number of local maxima is accordingly large and the iterative equation can easily converge too soon.
The class of hierarchical methods, also called connectivity-based clustering, forms clusters by collecting elements on a similarity criteria based on a distance metric: close elements gather in the same partition while far elements are separated into different clusters. This category of algorithms is divided in two types: divisive clustering and agglomerative clustering. The divisive approach starts by assigning the entire dataset to a cluster, which is then divided in two less similar (distant) clusters. Each partition is further divided until each data point is itself a cluster. The agglomerative method, which is the most often employed method, starts from the data points, each of them representing a cluster. Then these clusters are merged by similarity until a single cluster containing all the data points remains. These methods are called hierarchical because both categories create a hierarchy of clusters iteratively, as the following figure shows. This hierarchical representation is called a dendrogram. On the horizontal axis, there are the elements of the dataset, and on the vertical axis, the distance values are plotted. Each horizontal line represents a cluster and the vertical axis indicates which element/cluster forms the related cluster:

In the preceding figure, agglomerative clustering starts from many clusters as dataset points and ends up with a single cluster that contains the entire dataset. Vice versa, the divisive method starts from a single cluster and finishes when all clusters contain a single data point each.
The final clusters are then formed by applying criteria to stop the agglomeration/division strategy. The distance criteria sets the maximum distance above which two clusters are too far away to be merged, and the number of clusters criteria sets the maximum number of clusters to stop the hierarchy from continuing to merge or split the partitions.
An example of agglomeration is given by the following algorithm:
-
Assign each element i of the dataset
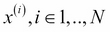 to a different cluster.
to a different cluster.
- Calculate the distances between each pair of clusters and merge the closest pair into a single cluster, reducing the total number of clusters by 1.
- Calculate the distances of the new cluster from the others.
- Repeat steps 2 and 3 until only a single cluster remains with all N elements.
Since the distance d(C1,C2) between two clusters C1, C2, is computed by definition between two points ![]() and each cluster contains multiple points, a criteria to decide which elements have to be considered to calculate the distance is necessary (linkage criteria). The common linkage criteria of two clusters C1 and C2 are as follows:
and each cluster contains multiple points, a criteria to decide which elements have to be considered to calculate the distance is necessary (linkage criteria). The common linkage criteria of two clusters C1 and C2 are as follows:
- Single linkage: The minimum distance among the distances between any element of C1 and any element of C2 is given by the following:

- Complete linkage: The maximum distance among the distances between any element of C1 and any element of C2 is given by the following:

- Unweighted pair group method with arithmetic mean (UPGMA) or average linkage: The average distance among the distances between any element of C1 and any element of C2 is
 , where
, where  are the numbers of elements of C1 and C2, respectively.
are the numbers of elements of C1 and C2, respectively.
- Ward algorithm: This merges partitions that do not increase a certain measure of heterogeneity. It aims to join two clusters C1 and C2 that have the minimum increase of a variation measure, called the merging cost
 , due to their combination. The distance in this case is replaced by the merging cost, which is given by the following formula:
Here,
, due to their combination. The distance in this case is replaced by the merging cost, which is given by the following formula:
Here,
 are the numbers of elements of C1 and C2, respectively.
are the numbers of elements of C1 and C2, respectively.
There are different metrics d(c1,c2) that can be chosen to implement a hierarchical algorithm. The most common is the Euclidean distance:

Note that this class of method is not particularly time-efficient, so it is not suitable for clustering large datasets. It is also not very robust towards erroneously clustered data points (outliers), which may lead to incorrect merging of clusters.
To compare the clustering methods just presented, we need to generate a dataset. We choose the two dataset classes given by the two two-dimensional multivariate normal distributions with means and covariance equal to ![]() and
and  , respectively.
, respectively.
The data points are generated using the NumPy library and plotted with matplotlib:
from matplotlib import pyplot as plt import numpy as np np.random.seed(4711) # for repeatability c1 = np.random.multivariate_normal([10, 0], [[3, 1], [1, 4]], size=[100,]) l1 = np.zeros(100) l2 = np.ones(100) c2 = np.random.multivariate_normal([0, 10], [[3, 1], [1, 4]], size=[100,]) #add noise: np.random.seed(1) # for repeatability noise1x = np.random.normal(0,2,100) noise1y = np.random.normal(0,8,100) noise2 = np.random.normal(0,8,100) c1[:,0] += noise1x c1[:,1] += noise1y c2[:,1] += noise2 fig = plt.figure(figsize=(20,15)) ax = fig.add_subplot(111) ax.set_xlabel('x',fontsize=30) ax.set_ylabel('y',fontsize=30) fig.suptitle('classes',fontsize=30) labels = np.concatenate((l1,l2),) X = np.concatenate((c1, c2),) pp1= ax.scatter(c1[:,0], c1[:,1],cmap='prism',s=50,color='r') pp2= ax.scatter(c2[:,0], c2[:,1],cmap='prism',s=50,color='g') ax.legend((pp1,pp2),('class 1', 'class2'),fontsize=35) fig.savefig('classes.png')
A normally distributed noise has been added to both classes to make the example more realistic. The result is shown in the following figure:

Two multivariate normal classes with noise
The clustering methods have been implemented using the sklearn and scipy libraries and again plotted with matplotlib:
import numpy as np from sklearn import mixture from scipy.cluster.hierarchy import linkage from scipy.cluster.hierarchy import fcluster from sklearn.cluster import KMeans from sklearn.cluster import MeanShift from matplotlib import pyplot as plt fig.clf()#reset plt fig, ((axis1, axis2), (axis3, axis4)) = plt.subplots(2, 2, sharex='col', sharey='row') #k-means kmeans = KMeans(n_clusters=2) kmeans.fit(X) pred_kmeans = kmeans.labels_ plt.scatter(X[:,0], X[:,1], c=kmeans.labels_, cmap='prism') # plot points with cluster dependent colors axis1.scatter(X[:,0], X[:,1], c=kmeans.labels_, cmap='prism') axis1.set_ylabel('y',fontsize=40) axis1.set_title('k-means',fontsize=20) #mean-shift ms = MeanShift(bandwidth=7) ms.fit(X) pred_ms = ms.labels_ axis2.scatter(X[:,0], X[:,1], c=pred_ms, cmap='prism') axis2.set_title('mean-shift',fontsize=20) #gaussian mixture g = mixture.GMM(n_components=2) g.fit(X) pred_gmm = g.predict(X) axis3.scatter(X[:,0], X[:,1], c=pred_gmm, cmap='prism') axis3.set_xlabel('x',fontsize=40) axis3.set_ylabel('y',fontsize=40) axis3.set_title('gaussian mixture',fontsize=20) #hierarchical # generate the linkage matrix Z = linkage(X, 'ward') max_d = 110 pred_h = fcluster(Z, max_d, criterion='distance') axis4.scatter(X[:,0], X[:,1], c=pred_h, cmap='prism') axis4.set_xlabel('x',fontsize=40) axis4.set_title('hierarchical ward',fontsize=20) fig.set_size_inches(18.5,10.5) fig.savefig('comp_clustering.png', dpi=100)
The k-means function and Gaussian mixture model have a specified number of clusters (n_clusters =2,n_components=2), while the mean-shift algorithm has the bandwidth value bandwidth=7. The hierarchical algorithm is implemented using the ward linkage and the maximum (ward) distance, max_d, is set to 110 to stop the hierarchy. The fcluster function is used to obtain the predicted class for each data point. The predicted classes for the k-means and the mean-shift method are accessed using the labels_ attribute, while the Gaussian mixture model needs to employ the predict function. The k -means, mean-shift, and Gaussian mixture methods have been trained using the fit function, while the hierarchical method has been trained using the linkage function. The output of the preceding code is shown in the following figure:

IClustering of the two multivariate classes using k-means, mean-shift, Gaussian mixture model, and hierarchical ward method
The mean-shift and hierarchical methods show two classes, so the choice of parameters (bandwidth and maximum distance) is appropriate. Note that the maximum distance value for the hierarchical method has been chosen looking at the dendrogram (the following figure) generated by the following code:
from scipy.cluster.hierarchy import dendrogram fig = plt.figure(figsize=(20,15)) plt.title('Hierarchical Clustering Dendrogram',fontsize=30) plt.xlabel('data point index (or cluster index)',fontsize=30) plt.ylabel('distance (ward)',fontsize=30) dendrogram( Z, truncate_mode='lastp', # show only the last p merged clusters p=12, leaf_rotation=90., leaf_font_size=12., show_contracted=True, ) fig.savefig('dendrogram.png')
The truncate_mode='lastp' flag allows us to specify the number of last merges to show in the plot (in this case, p=12). The preceding figure clearly shows that when the distance is between 100 and 135, there are only two clusters left:

IHierarchical clustering dendrogram for the last 12 merges
In the preceding figure on the horizontal axis, the number of data points belonging to each cluster before the last 12 merges is shown in brackets ().
Apart from the Gaussian mixture model, the other three algorithms misclassify some data points, especially k-means and hierarchical methods. This result proves that the Gaussian mixture model is the most robust method, as expected, since the dataset comes from the same distribution assumption. To evaluate the quality of the clustering, scikit-learn provides methods to quantify the correctness of the partitions: v-measure, completeness, and homogeneity. These methods require the real value of the class for each data point, so they are referred to as external validation procedures. This is because they require additional information not used while applying the clustering methods. Homogeneity, h, is a score between 0 and 1 that measures whether each cluster contains only elements of a single class. Completeness, c, quantifies with a score between 0 and 1 whether all the elements of a class are assigned to the same cluster. Consider a clustering that assigns each data point to a different cluster. In this way, each cluster will contains only one class and the homogeneity is 1, but unless each class contains only one element, the completeness is very low because the class elements are spread around many clusters. Vice versa, if a clustering results in assigning all the data points of multiple classes to the same cluster, certainly the completeness is 1 but homogeneity is poor. These two scores have a similar formula, as follows:

Here:
 is the conditional entropy of the classes Cl, given the cluster assignments
is the conditional entropy of the classes Cl, given the cluster assignments 
 is the conditional entropy of the clusters, given the class membership
is the conditional entropy of the clusters, given the class membership 
- H(Cl) is the entropy of the classes:

- H(C) is the entropy of the clusters:

- Npc is the number of elements of class p in cluster c, Np is the number of elements of class p, and Nc is the number of elements of cluster c
The v-measure is simply the harmonic mean of the homogeneity and the completeness:

These measures require the true labels to evaluate the quality of the clustering, and often this is not real-case scenario. Another method only employs data from the clustering itself, called silhouette, which calculates the similarities of each data point with the members of the cluster it belongs to and with the members of the other clusters. If on average each point is more similar to the points of its own cluster than the rest of the points, then the clusters are well defined and the score is close to 1 (it is close to -1, otherwise). For the formula, consider each point i and the following quantities:
- ds(i) is the average distance of the point i from the points of the same cluster
- drest(i) is the minimum distance of point i from the rest of the points in all other clusters
The silhouette can be defined as
 , and the silhouette score is the average of s(i) for all data points.
, and the silhouette score is the average of s(i) for all data points.
The four clustering algorithms we covered are associated with the following values of these four measures calculated using sklearn (scikit-learn):
from sklearn.metrics import homogeneity_completeness_v_measure from sklearn.metrics import silhouette_score res = homogeneity_completeness_v_measure(labels,pred_kmeans) print 'kmeans measures, homogeneity:',res[0],' completeness:',res[1],' v-measure:',res[2],' silhouette score:',silhouette_score(X,pred_kmeans) res = homogeneity_completeness_v_measure(labels,pred_ms) print 'mean-shift measures, homogeneity:',res[0],' completeness:',res[1],' v-measure:',res[2],' silhouette score:',silhouette_score(X,pred_ms) res = homogeneity_completeness_v_measure(labels,pred_gmm) print 'gaussian mixture model measures, homogeneity:',res[0],' completeness:',res[1],' v-measure:',res[2],' silhouette score:',silhouette_score(X,pred_gmm) res = homogeneity_completeness_v_measure(labels,pred_h) print 'hierarchical (ward) measures, homogeneity:',res[0],' completeness:',res[1],' v-measure:',res[2],' silhouette score:',silhouette_score(X,pred_h) The preceding code produces the following output: kmeans measures, homogeneity: 0.25910415428 completeness: 0.259403626429 v-measure: 0.259253803872 silhouette score: 0.409469791511 mean-shift measures, homogeneity: 0.657373750073 completeness: 0.662158204648 v-measure: 0.65975730345 silhouette score: 0.40117810244 gaussian mixture model measures, homogeneity: 0.959531296098 completeness: 0.959600517797 v-measure: 0.959565905699 silhouette score: 0.380255218681 hierarchical (ward) measures, homogeneity: 0.302367273976 completeness: 0.359334499592 v-measure: 0.32839867574 silhouette score: 0.356446705251
As expected from the analysis of the preceding figure, the Gaussian mixture model has the best values of the homogeneity, completeness, and v-measure measures (close to 1); mean-shift has reasonable values (around 0.5); while k-means and hierarchical methods result in poor values (around 0.3). The silhouette score instead is decent for all the methods (between 0.35 and 0.41), meaning that the clusters are reasonably well defined.





