Dimensionality reduction, which is also called feature extraction, refers to the operation to transform a data space given by a large number of dimensions to a subspace of fewer dimensions. The resulting subspace should contain only the most relevant information of the initial data, and the techniques to perform this operation are categorized as linear or non-linear. Dimensionality reduction is a broad class of techniques that is useful for extracting the most relevant information from a large dataset, decreasing its complexity but keeping the relevant information.
The most famous algorithm, Principal Component Analysis (PCA), is a linear mapping of the original data into a subspace of uncorrelated dimensions, and it will be discussed hereafter. The code shown in this paragraph is available in IPython notebook and script versions at the author's GitHub book folder at https://github.com/ai2010/machine_learning_for_the_web/tree/master/chapter_2/.
The principal component analysis algorithm aims to identify the subspace where the relevant information of a dataset lies. In fact, since the data points can be correlated in some data dimensions, PCA will find the few uncorrelated dimensions in which the data varies. For example, a car trajectory can be described by a series of variables such as velocity in km/h or m/s, position in latitude and longitude, position in meters from a chosen point, and position in miles from a chosen point. Clearly, the dimensions can be reduced because the velocity variables and the position variables give the same information (correlated variables), so the relevant subspace can be composed of two uncorrelated dimensions (a velocity variable and a position variable). PCA finds not only the uncorrelated set of variables but also the dimensions where the variance is maximized. That is, between the velocity in km/h and miles/h, the algorithm will select the variable with the highest variance, which is trivially represented by the line between the two axes given by the function velocity[km/h]=3.6*velocity[m/s] (typically closer to the km/h axis because 1 km/h = 3.6 m/s and the velocity projections are more spread along the km/h axis than the m/s axis):

The linear function between the velocity in m/s and km/h
The preceding figure represents the linear function between the velocity in m/s and km/h. The projections of the points along the km/h axis have a large variance, while the projections on the m/s axis have a lower variance. The variance along the linear function velocity[km/h]=3.6*velocity[m/s] is larger than both axes.
Now we are ready to discuss the method and its features in detail. It is possible to show that finding the uncorrelated dimensions in which the variance is maximized is equivalent to computing the following steps. As usual, we consider the feature vectors ![]() :
:
-
The average of the dataset:

-
The mean shifted dataset:

-
The rescaled dataset, in which each feature vector component
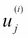 has been divided by the standard deviation,
has been divided by the standard deviation,  , where
, where 
-
The sample covariance matrix:

-
The k largest eigenvalues,
 , and their associated eigenvectors,
, and their associated eigenvectors, 
- Projected feature vectors on the subspace of the k eigenvectors
 , where
, where  is the matrix of the eigenvectors with N rows and k columns
is the matrix of the eigenvectors with N rows and k columns
The final feature's vectors (principal components), ![]() lie on a subspace Rk, which still retain the maximum variance (and information) of the original vectors.
lie on a subspace Rk, which still retain the maximum variance (and information) of the original vectors.
Note that this technique is particularly useful when dealing with high-dimensional datasets, such as in face recognition. In this field, an input image has to be compared with a database of other images to find the right person. The PCA application is called Eigenfaces, and it exploits the fact that a large number of pixels (variables) in each image are correlated. For instance, the background pixels are all correlated (the same), so a dimensionality reduction can be applied, and comparing images in a smaller subspace is a faster approach that gives accurate results. An example of implementation of Eigenfaces can be found on the author's GitHub profile at https://github.com/ai2010/eigenfaces.
As an example of the usage of PCA as well as the NumPy library discussed in Chapter 1, Introduction to Practical Machine Learning using Python we are going to determine the principal component of a two-dimensional dataset distributed along the line y=2x, with random (normally distributed) noise. The dataset and the corresponding figure (see the following figure) have been generated using the following code:
import numpy as np from matplotlib import pyplot as plt #line y = 2*x x = np.arange(1,101,1).astype(float) y = 2*np.arange(1,101,1).astype(float) #add noise noise = np.random.normal(0, 10, 100) y += noise fig = plt.figure(figsize=(10,10)) #plot plt.plot(x,y,'ro') plt.axis([0,102, -20,220]) plt.quiver(60, 100,10-0, 20-0, scale_units='xy', scale=1) plt.arrow(60, 100,10-0, 20-0,head_width=2.5, head_length=2.5, fc='k', ec='k') plt.text(70, 110, r'$v^1$', fontsize=20) #save ax = fig.add_subplot(111) ax.axis([0,102, -20,220]) ax.set_xlabel('x',fontsize=40) ax.set_ylabel('y',fontsize=40) fig.suptitle('2 dimensional dataset',fontsize=40) fig.savefig('pca_data.png')
The following figure shows the resulting dataset. Clearly there is a direction in which the data is distributed and it corresponds to the principal component ![]() that we are going to extract from the data.
that we are going to extract from the data.

A two-dimensional dataset. The principal component direction v1 is indicated by an arrow.
The algorithm calculates the mean of the two-dimensional dataset and the mean shifted dataset, and then rescales with the corresponding standard deviation:
mean_x = np.mean(x) mean_y = np.mean(y) u_x = (x- mean_x)/np.std(x) u_y = (y-mean_y)/np.std(y) sigma = np.cov([u_x,u_y])
To extract the principal component, we have to calculate the eigenvalues and eigenvectors and select the eigenvector associated with the largest eigenvalue:
eig_vals, eig_vecs = np.linalg.eig(sigma) eig_pairs = [(np.abs(eig_vals[i]), eig_vecs[:,i]) for i in range(len(eig_vals))] eig_pairs.sort() eig_pairs.reverse() v1 = eig_pairs[0][1] print v1 array([ 0.70710678, 0.70710678]
To check whether the principal component lies along the line as expected, we need to rescale back its coordinates:
x_v1 = v1[0]*np.std(x)+mean_x y_v1 = v1[1]*np.std(y)+mean_y print 'slope:',(y_v1-1)/(x_v1-1) slope: 2.03082418796
The resulting slope is approximately 2, which agrees with the value chosen at the beginning. The scikit-learn library provides a possible ready-to-use implementation of the PCA algorithm without applying any rescaling or mean shifting. To use the sklearn module, we need to transform the rescaled data into a matrix structure in which each row is a data point with x, y coordinates:
X = np.array([u_x,u_y]) X = X.T print X.shape (100,2)
The PCA module can be started now, specifying the number of principal components we want (1 in this case):
from sklearn.decomposition import PCA pca = PCA(n_components=1) pca.fit(X) v1_sklearn = pca.components_[0] print v1_sklearn [ 0.70710678 0.70710678]
The principal component is exactly the same as the one obtained using the step-by-step approach,[ 0.70710678 0.70710678], so the slope will also be the same. The dataset can now be transformed into the new one-dimensional space with both approaches:
#transform in reduced space X_red_sklearn = pca.fit_transform(X) W = np.array(v1.reshape(2,1)) X_red = W.T.dot(X.T) #check the reduced matrices are equal assert X_red.T.all() == X_red_sklearn.all(), 'problem with the pca algorithm'
The assert exception is not thrown, so the results show a perfect agreement between the two methods.
