5
Copredication and Individuation
Copredication (Pustejovsky 1995) is the phenomenon where more than one predicate (verb or adjective) that require different types of arguments are used in coordination and applied to the “same” common noun (CN) argument:
(5.1) John picked up and mastered the book.
Individuation, on the other hand, is the process by which objects in a particular collection are distinguished from one another. Individuation provides us with the means that enables us to count individual objects, e.g. cats, dogs or any other type of object, and differentiate among them. At the same time, individuation also provides one with an identity criterion (IC), i.e. a way to decide whether two members of a particular collection are the same or not. Copredication interacts with individuation in a number of interesting and challenging ways. Most specifically, copredication, when combined with quantification, provides compelling examples supporting the idea that CN have their own ICs. The idea of CNs involving their own ICs was first discussed by Geach (1962) and was further studied later on by other researchers including, for example, the second author (Luo 2012a) on the CNs-as-types paradigm within the semantic framework based on MTTs.
In this chapter, we study copredication and individuation in MTT-semantics. In section 5.1, some introductory explanations on copredication and its interaction with quantification are given, where we also illustrate why a formal treatment of copredication in the CNs-as-predicates tradition is problematic. Then, in section 5.2, we revisit the dot-types, particularly its formal inference rules, developed by the second author (Luo 2009c, 2012b) to model copredication in MTT-semantics. When both copredication and quantification are involved, CNs are not just types but should better be interpreted as types associated with their own ICs, formally called setoids in type theory (Luo 2012a; Chatzikyriakidis and Luo 2018).1 When copredication interacts with quantification, ICs play an essential role in giving a proper treatment of both individuation and counting and, hence, constructing appropriate semantics to facilitate reasoning correctly. We will argue, and hopefully convincingly show, that the dot-type approach (Luo 2009c) provides an adequate theory for copredication in general and for copredication involving quantification in particular.
5.1. Copredication and individuation: an introduction
To appreciate the nature of the issues, consider again (5.1). In this example, the predicates “pick up” and “master” require physical and informational objects as their respective arguments. Formally, their domains are PHY and INFO, the types of physical and informational objects, respectively. However, they manage to be applied in coordination to the argument “the book”. What goes on in this example is that “book” is used in its physical sense with respect to the predicate “picked up” and in its informational sense with respect to the predicate “mastered”.
The term copredication was first coined by Pustejovsky (1995), according to whom lexical items like “book” in (5.1) are complex and have more than one sense, to be chosen appropriately according to the context. The topic has since been studied by many researchers and different attempts to account for copredication have been proposed in various semantic frameworks. Besides Pustejovsky’s initial proposal (Pustejovsky 1995), these include, to mention a few among many: Asher (2012) using type composition logic, Gotham (2014, 2017) using a mereological theory, Bassac et al. (2010) using the second-order λ-calculus and Cooper (2011) using type theory with records (TTR).2
Most of the above approaches have been studied in the Montagovian setting where, in particular, CNs are interpreted as predicates. This has raised a challenge to the researchers because a formal modeling of copredication in such a setting meets with a problem, pointed out by the second author in Luo (2009c, 2012b): the CNs-as-predicates paradigm is incompatible with the subtyping relations used in an intended analysis. Let us use a simple example to illustrate. Consider how to interpret the phrase “heavy book”, where “book” is assumed to be of a complex type having two aspects, one informational and other physical. Then, the adjective “heavy” is a predicate, a function from physical objects to truth values, and “book” is a predicate over some dot-type PHY • INFO, where PHY and INFO are the subtypes of e of physical and informational objects, respectively.3 In symbols, we have:
(5.2) heavy : PHY → t and book : PHY • INFO → t
With these assumptions in line, the account will not work. Here is why: ideally, what we want to get is a predicate of the following form:
(5.3) ![]()
However, this predicate (5.3) is not well-typed on the assumption that the dot-type is a subtype of its constituent types, in our case PHY • INFO ≤ PHY. To the contrary, in order for typing to work in the above example, and given the CNs as predicates approach, what we need is the subtyping relation PHY ≤ PHY • INFO. Of course, an assumption like this is totally counterintuitive and formally untenable. Assuming a higher order type for the adjective “heavy” will not work either, but we leave the details of this to the interested reader to work out (or one can find out the details in Luo (2012b)).
MTT-semantics, different from the Montague semantics, adopts the CNs-as-types paradigm and this makes a real difference in formalizing dot-types for a treatment of copredication: one does not get the problem of incompatibility with subtyping anymore. Recognizing this, the second author has proposed the introduction of dot-types in MTTs for the semantic study of copredication (Luo 2009c, 2012b). The idea is that, the phenomenon of the single occurrence of “book” being able to be used in both physical and informational senses can be captured by stipulating that the type Book, that interprets “book”, be a subtype of the dot-type of those of physical and informational objects:
The copredication phenomenon as exhibited in (5.1) can then be dealt with straightforwardly: the predicates “pick up” and “master” can be applied in coordination to the argument “the book” because they are both of type
Book → Prop under the usual subtyping laws (see section 5.2 for a more detailed description of dot-types and their use for copredication).
In order to give an adequate account of copredication, we need to take care of a more advanced issue as well – the involvement of quantification. In (5.4), taken from Asher (2012), copredication and quantification interact:
(5.4) John picked up and mastered three books.
The above sentence involves a number of different things that need to be taken care of in order to get a proper semantic analysis: individuation and counting with numerical quantifiers in copredication. An adequate account of copredication must take into consideration all these parameters and make sure that when combined, they produce the correct semantic interpretations. The crucial question is then, what is needed for such an adequate account? In order to answer this question, let us first start by considering the following simpler sentences that do not involve copredication:
(5.5) John picked up three books.
(5.6) John mastered three books.
(5.5) is true in case John picked up three distinct physical objects. Thus, it is compatible with a situation where John picked up three copies of a book that are informationally identical as long as three distinct physical copies are picked up. Similarly, example (5.6) is true in case three distinct informational objects are mastered, but it does not impose any restrictions on whether these three informational objects should be different physical objects or not.4 A more explicit way of explaining this is that, intuitively, the following entailments should be the case:
(5.7) John picked up three books ⇒ John picked up three physical objects.
(5.8) John mastered three books ⇒ John mastered three informational objects.
At first appearance, the above examples may be puzzling. The books John picked up and the books he mastered must have different individuation criteria – being physically identical is different from being informationally identical. Are they the same books? Actually, they are not. The collection of books with being physically the same as its IC (call it =p) is different from the collection of books with being informationally the same as its IC (call it =i). In other words, ICs play a crucial role in fixing collections of objects represented by CNs, although they are not made explicit in NL sentences. “Books” in (5.5) and (5.7) refer to those with IC =p, while “books” in (5.6) and (5.8) refer to those with IC =i. Note that it is the predicates (“pick up” and “master”) that determine which IC should be: in (5.5), the domain of “picked up” is the type PHY of physical objects, and the IC for books is =p (being physically the same); and in (5.6), the domain of “master” is the type INFO of informational objects, and the IC for books is =i (being informationally the same).
Now, a further complication arises in cases like (5.4), where copredication and quantification interact and, therefore, in its semantic analysis, both ICs have to be used, i.e. we have to consider both collections of books: one with being physically the same as its IC and the other with being informationally the same as its IC. Giving semantics properly, we should be able to get the following entailment:
(5.9) John picked up and mastered three books ⇒ John picked up three physical objects and mastered three informational objects.
Here, there is some sort of double distinctness that should be accounted for, involving both ICs. Any adequate theory of copredication should not only account for (5.7) and (5.8), but also for (5.9), dealing with counting and individuation correctly. In order to provide such an account, we further develop the idea on ICs for CNs, initially studied for MTT-semantics by the second author in (Luo 2012a). We propose that, in general, CNs are interpreted as types associated with their ICs, i.e. they are setoids. A setoid is a pair (A, =), where A is a type (domain of the setoid) and = is an equivalence relation on A (equality of the setoid). If a setoid interprets a CN, its domain interprets that of the CN and its equality gives the IC for the CN. For example, “books” in (5.7) refer to those in the collection of books whose IC is =p (being physically the same), while “books” in (5.8) refer to those in the collection of books whose IC is =i (being informationally the same). They are books with different ICs; or put in a better way, they belong to different collections of books whose ICs are different. In the CNs-as-setoids setting, it is shown that dot-types offer a proper treatment of copredication, including the sophisticated cases involving both copredication and quantification.
At this point, one might want to ask: why do people working in MTT-semantics usually say that, in MTT-semantics, CNs are interpreted as types and do not pay attention to their ICs? The answer is rather simple. This is because most of the cases are not as sophisticated as those cases where copredication interacts with quantification and as such, in these less sophisticated cases, the related CNs usually have essentially the “same” IC. For example, type Man inherits its IC from type Human: two men are the same if and only if they are the same as humans. This explains why we usually consider the entailment below induced by the subtyping relationship Man ≤ Human as “straightforward” without the need to mention, or explicitly flesh out, their:
(5.10) Three men talk ⇒ Three humans talk
In other words, when interpreting a CN, its IC can usually be safely ignored. Of course, this is not always the case: “books” in (5.5) and (5.6) are referring to different collections of books that have different ICs and, in (5.4) where both copredication and quantification are involved, more than one ICs will be involved in constructing appropriate semantics. In other words, in general, CNs are setoids but, in the usual cases, their IC can be safely ignored and they are just types.
5.2. Dot-types for copredication: a brief introduction
Dot-types in MTT-semantics were introduced by the second author (Luo 2009c, 2012b) to model copredication. In what follows, we shall first present the basic ideas behind this approach and then explain the rules for dot-types. Consider the copredication example (5.1), repeated below:
(5.11) John picked up and mastered the book.
Let PHY and INFO represent the types of physical and informational objects, respectively, and further assume that the interpretations of “pick up” and “master” have the following types:
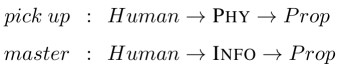
In (5.11), “pick up” and “master” are applied in coordination to “the book”. In order for such coordination to happen, the two verbs must be of the same type.5 Our question is: given the above typing, can both of them be of the same type? The introduction of dot-types make this happen naturally. Let us informally start with the dot-type PHY • INFO. PHY•INFO is the dot-type that satisfies the following property: it is a subtype of both PHY and INFO. So far, so good. Now, we need to account for the assumption that books have both a physical and an informational aspect. This can be easily captured using subtyping, i.e. by assuming that Book is a subtype of PHY • INFO:

Given that subtyping is contravariant for function types, i.e. if A ≤ B, then B → Type ≤ A → Type (informally, subtyping goes the other way around), the following holds:

In other words, pick up and master can be both considered of type Human → Book → Prop given subtyping and, therefore, the coordination in (5.11) and its interpretation can proceed straightforwardly as intended.
With this taken care of, let us dig a little bit deeper on what dot-types are and how they are introduced in MTT-semantics. In order to get there, we need first to mention that one of the basic features of dot-types: their formation. To form a dot-type A • B, its constituent types A and B should not share common parts. This is what Pustejovsky calls inherent polysemy, as witnessed by the passage below:
Dot objects have a property that I will refer to as inherent polysemy. This is the ability to appear in selectional contexts that are contradictory in type specification. (Pustejovsky 2005)
Thus, a dot-type A • B can only be formed if the types A and B do not share any components. Consider the following:
- – PHY • PHY should not be a dot-type because its constituent types are the of same type PHY.
- – PHY • (PHY • INFO) should not be a dot-type because its constituent types PHY and PHY • INFO share the component PHY.
To rephrase what we have just said, given types A and B, we can form the dot-type A • B just in case that A and B do not share common parts (formally called components). For instance, PHY • INFO is a legitimate dot-type, while PHY • (PHY • INFO) is not, because in the latter, the constituent types PHY and PHY •INFO share the common part PHY. Furthermore, as already mentioned, a dot-type A • B is a subtype of both of its constituent types A and B. Note also that the whole dot-type formation is based on the notion of component. Its definition is as follows:
DEFINITION 5.1 (components).– Let T : Type be a type in the empty context. Then, C(T), the set of components of T , is defined as:

where SUP(T) = {T′ | T ≤ T′}. □
Note that because of the non-sharing requirement for components and the subtyping relationships with its component types, a dot-type is not an ordinary type (like an inductive type) already available in MTTs, but we still specify them by means of formation, introduction, elimination and computation rules, with suitable conditions and some extra coercive subtyping rules to stipulate that the elimination/projection operators are coercions. The rules for dot-types can be found in Appendix 6. Here, we will have a look at some of them four of these rules, starting with the formation rule of dot-types, which basically is the rule that takes care of the formation of dot-types based on what we just been discussing:
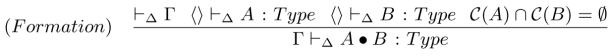
What this rule intuitively says is that if types A and B do not share any components, the dot-type A • B can be formed. The important point here that we need to stress again is the non-sharing of components. Thus, given the types INFO and PHY, we can form the dot-type PHY • INFO, but not the dot-type PHY • PHY since the two types are identical (PHY and PHY) and thus do not obey the non-sharing components restriction. The next rule is the introduction rule:

Intuitively, the introduction rule says that given an element a of type A, b of type B and the dot-type A • B, the pair ![]() a, b
a, b![]() is of type A. The next rule is the elimination rule:
is of type A. The next rule is the elimination rule:

This rule gives us a way to access the components of a dot-type via its two projections. Given a : A • B, we can use projections p1 and p2 to access the two components of c of type A and B, respectively. The last rule we want to have a look at is the projections as coercions rule:

These two rules simply say that in case we have a dot-type A • B : B, its projections p1 and p2 are declared as coercions, i.e. the dot-type is a subtype of its constituent types. For example, PHY • INFO (the dot-type) is a subtype of its constituent types PHY and INFO, i.e. PHY • INFO ≤ PHY, INFO.
Let us use again example (5.11) repeated below as (5.12), but this time with more explanations given and referral to the relevant rules used when needed:
(5.12) John picked up and mastered the book.
Let us repeat the types involved:

The first thing to note is that PHY • INFO is a well-formed dot-type, since PHY and INFO do not share any components. This means that we can find elements of that type, e.g. the_book : Book. Now in order to compose picked up, on the one hand, and master, on the other hand, with the_book, we need to use the projections as coercions rule. In the first instance, we use the p1 to extract the PHY component of the_book, while in the second case p2 to extract the INFO component. Because of the subtyping declarations Book ≤ PHY • INFO ≤ PHY and Book ≤ PHY• INFO ≤ INFO, as well as the contravariance of subtyping for function types, i.e. PHY → Prop ≤ PHY • INFO → Prop ≤ Book → Prop and INFO → Prop ≤ PHY • INFO → Prop ≤ Book → Prop, we are able to do the composition. This concerns the individual cases of putting together the individual predicates with the argument the_book. We are in a coordination environment however. This is how we coordinate: we take the A argument needed by the typing of and to be Book → Prop. Both the typings of the two predicates are subtypes of that type, thus they can be coordinated and together applied to the argument the_book. We can also access the individual components of the dot-type. For example, we can access the informational component of the the_book in mastered(John, the_book) using the second elimination rule.
With this brief introduction to dot-types in place, there is a remark that should be made concerning these types. As already extensively discussed in this book, in MTT-semantics, CNs are interpreted as types (rather than predicates): for instance, the CNs “table” and “man” can be interpreted as types Table and Man, respectively. However, there is something that needs to be stressed: even though every CN corresponds to a type, the opposite relation does not hold, i.e. not every type represents a CN. Dot-types are a good example of this: dot-types such as Table • Man do not represent any CNs in natural language, at least to the extent that we know. The way we see it is that dot-types are useful type theoretical constructions that help us in getting from natural language to logical form in a way that corresponds to the intuitions with regard to copredication.
5.3. Identity criteria: individuation and CNs as setoids
As already mentioned in the introduction, individuation is the process by which objects in a particular collection are distinguished from one another. The discussion on individuation goes back to at least Aristotle (Cohen 1984) and has been the subject of enquiry of great philosophers in both the continental as well as the analytical tradition. However, it is outside the scope of the present chapter to present an overview of individuation from a philosophical point of view. Our point of departure will be individuation as discussed in the philosophy of language and the linguistic semantics tradition.
In linguistic semantics, individuation is very much related to the idea that a CN may have its own IC for individuation, an idea already discussed in (Geach 1962). In mathematical terms, the idea amounts to the association of an equivalence relation (the IC) to each CN. In fact, in the tradition of constructive mathematics, a set or a type is indeed a collection of objects together with an equivalence relation that serves as an IC of that collection.6 For CNs in MTT-semantics, this is the same as saying that a CN should in general be interpreted as a setoid – a type associated with an equivalence relation over the type.
In our discussions of MTT-semantics, the author of this book have been extensively discussing and endorsing the view that CNs are better treated as types rather than predicates. In doing so, we have been skipping some detail for the sake of simplicity.
These details will now become significant, as well as handy, when discussing the issue of individuation concerning CNs. Put it in another way, these details we have been skipping are now crucial in giving an account of individuation and correct predictions in complex cases involving dot-types and counting like (5.7), (5.8) and dot-types, counting and copredication in cases like (5.9), where individuation, and the derived issue of counting, becomes significant and cannot be ignored anymore.
The crucial detail that has been mostly ignored so far in this book is embodied in the proposal put forward by the second author in Luo (2012a), according to which the interpretation of a CN is not just a type, but rather a type associated with an IC for that specific CN. In other words, a CN is in general interpreted as a setoid, i.e. a pair
(5.13) (A, =), where A is a type and = : A → A → Prop is an equivalence relation over A.
The notion of setoids is not new in type theory and in constructive mathematics, and reflects the view that a type is basically a setoid, meaning that it is composed of a type plus an equivalence relation on this type. We want to pursue the same idea in linguistic semantics and assume that CNs are more nuanced with respect to ICs: two CNs may have the same base type, but their IC can be different and, if so, they are different CNs.
To see how this proposal works, let us first consider some simple examples for illustration purposes. In a simplified view, one would only interpret a CN as a type: for instance, “human” would be interpreted as a type Human, as in (5.14). However, in the elaborate view, CNs are interpreted as setoids, i.e. pairs of the form (5.13) and, therefore the CN “human” is now interpreted as in 5.15:
(5.14) [human] = Human : Type (CNs-as-types view)
(5.15) [human] = (Human, =h), where =h : Human → Human → Prop is the equivalence relation that represents the identity criterion for humans (CNs-as-setoids view)
Interpreting CNs as setoids makes explicit the individuation criteria (or their ICs) of CNs. This idea seems to be on the correct track in order to deal with copredication properly, i.e. in order to take care of the more fine-grained cases where there is interaction of copredication with numerical quantification. Indeed, this is what we are going to show, i.e. the dot-type as introduced in the previous section in conjunction with the CNs-as-setoids view, is adequate to deal with cases of copredication that also involve numerical quantification (see section 5.3.3). Let us now have a look at simple cases of individuation that do not involve copredication and the ICs of related CNs are essentially the same – inherited from supertypes.
5.3.1. Inheritance of identity criteria: usual cases of individuation
Consider the following sentences (5.16) and (5.17) and their formal interpretations (5.18) and (5.19), respectively:7
(5.16) A man talks.
(5.17) A human talks.
(5.18) ∃m : Man.talk(m)
(5.19) ∃h : Human.talk(h)
where “talk” is interpreted as a predicate of type Human → Prop.
Then, the following inference should hold:
This is true and we can easily prove (5.20). It is worth noting that analyzing the above example, we did not need to consider the IC of “man” and “human” at all, simply because for the simple sentences like (5.16) and (5.17), these are not needed in order to get the correct semantics. However, this is not the case anymore if we consider sentences (5.21) and (5.22) and their corresponding semantics, (5.23) and (5.24), respectively:
(5.21) Three men talk.
(5.22) Three humans talk.
(5.23) ![]()
(5.24) ![]()
where MAN = (Man, =M) and HUMAN = (Human, =H) are setoids and the IC for men and that for humans are used in (5.23) and (5.24), respectively, to express that x, y and z are distinct from each other.
The difference between (5.21)/(5.22) and the earlier examples (5.16)/(5.17) is the presence of quantifier “three” (a numerical quantifier bigger than one), which makes it necessary to consider the individuation criteria explicitly by using the ICs =M and =H . The relationship between the setoids MAN and HUMAN is not just that the domain of the former is a subtype of that of the latter (Man ≤ Human). Their ICs are also essentially the same: the IC for men is the restriction of the IC for humans to the domain of men. Put in another way, the IC for men is inherited from that for humans: two men are the same if, and only if, they are the same as human beings. In symbols, we have:
(5.25) (=M) = (=H)|Man
One may wonder how =M and =H may be specified so that (5.25) is true. For example, if Man and Human are both base types with assumed coercion c such that Man ≤c Human, then given =H, we can define ![]() Then, (5.25) is true. Another possibility is that, in the case that the type of men is defined to be the type of humans who are male – formally, Man = Σx : Human.male(x), we can then define
Then, (5.25) is true. Another possibility is that, in the case that the type of men is defined to be the type of humans who are male – formally, Man = Σx : Human.male(x), we can then define ![]() as π1(m) =H π1(m′), where π1 is the operator for the first projection. With this, (5.25) is true as well. Because of the subtyping relation Man ≤ Human and (5.25), we have the following result as expected, which would not be provable if we only had the subtyping relation but not (5.25):
as π1(m) =H π1(m′), where π1 is the operator for the first projection. With this, (5.25) is true as well. Because of the subtyping relation Man ≤ Human and (5.25), we have the following result as expected, which would not be provable if we only had the subtyping relation but not (5.25):
It is important to notice that, in usual non-copredication cases, the relationship between related CNs is like the one between “man” and “human”: one of the domains is a subtype of the other (e.g. Man ≤ Human). Thus, one of the CNs inherits the IC of the other, in the same sense =M (the IC for CN “man”) inherits =H (the IC for CN “human”). Such an inheritance relationship occurs in many cases. Examples of such pairs include “man” and “human”, “red table” and “table”, and many others. It may be useful to provide a name for this relation. The following definition does exactly the same.
DEFINITION 5.2 (Sub-setoid).– We say that a setoid A = (A, =A) is a sub-setoid of B = (B, =B), notation A ![]() B, if A ≤ B and =A is the same as (=B)|A (the restriction of =B over A). We often write =B for (=B)|A, omitting the restriction operator. □
B, if A ≤ B and =A is the same as (=B)|A (the restriction of =B over A). We often write =B for (=B)|A, omitting the restriction operator. □
For example, besides MAN ![]() HUMAN, we also have (RTable, =t)
HUMAN, we also have (RTable, =t) ![]() (Table, = t), where RTable is the type Σx : Table.red(x) representing the domain of red tables and =t is the equivalence relation representing the IC for tables (and inherited for red tables). Note that, in the restricted domain like Man or RTable, the ICs coincide with those for Human and Table and, in such a case, they are essentially the same and we can safely ignore them in studying relevant examples that make use of them.
(Table, = t), where RTable is the type Σx : Table.red(x) representing the domain of red tables and =t is the equivalence relation representing the IC for tables (and inherited for red tables). Note that, in the restricted domain like Man or RTable, the ICs coincide with those for Human and Table and, in such a case, they are essentially the same and we can safely ignore them in studying relevant examples that make use of them.
Of course, there are more sophisticated cases where ICs are not inherited, i.e. they are in fact rather different. The cases we are mainly interested in this chapter, i.e. cases where there an interaction between copredication and numerical quantification exists, constitute such examples. This is what we will try to capture in section 5.3.3. But before we do that, we will first have to discuss the generic semantics of numerical quantifiers like “three”.
5.3.2. Generic semantics of numerical quantifiers
Another way to consider the semantic interpretations of (5.21) and (5.22) is to define a generic semantics of numeral quantifiers such as “three” and then define the semantics using the generic operator. In the following, we shall use “three” as an example of a numerical quantifier to show how to give generic semantics to them. A first attempt to define the semantics of “three” is to consider the following definition for it:
DEFINITION 5.3 (Three0).– For any setoid B = (B, =B), and any predicate P : B → Prop:
(5.27) Three0(B, P) = ∃x, y, z : B. D[B](x, y, z) ∧ P(x) ∧ P(y) ∧ P(z)
![]() □
□
Using Three0, the semantics of (5.23) and (5.24) can be rewritten as (5.28) and (5.29), respectively:
(5.28) Three0(MAN, talk)
(5.29) Three0(HUMAN, talk)
And, similarly, we can express the semantics of (5.30) as (5.31), which is (5.32) after Three0 is expanded, and where PHY = (PHY, =p) is the setoid for the collection of physical objects and pick up : PHY → Prop:
(5.30) John picked up three physical objects.
(5.31) Three0(PHY, pick up)
(5.32) ∃x, y, z : PHY. D[PHY](x, y, z) ∧ pick up(x) ∧ pick up(y) ∧ pick up(z)
A common feature of examples (5.21), (5.22) and (5.30) is that the verb’s domain is the same as that of the object CN: for example, in (5.30), the domain of “pick up” is the same as PHY, the type of physical objects. Because of this restriction, the operator Three0 is not generic enough: it does not cover semantics of sentences with reference to more general situations, including (5.33):
(5.33) John picked up three pens.
In (5.33), the verb is first applied to a CN whose domain is more restricted (but not the same): “pick up” can be applied to any physical object, not just pens; second, the IC of the object CN is inherited from that for the domain of the verb (two pens are the same if, and only if, they are the same as physical objects). The IC for pens inherits that for physical objects and can be determined from the contextual information in the sentence, more specifically, from the verb “pick up”: only physical objects can be picked up (the semantic type of pick up is PHY → Prop). The semantics of the CN “pen” is the setoid (Pen, =p), whose IC comes (is inherited) from the setoid of physical objects. In general, the ICs are determined by those of the verbs or adjectives applied to them. This leads us to the following generic definition for “three”:
DEFINITION 5.4 (Three).– Let A be a type and B = (B, =B) a setoid such that A ≤ B, and P : B → Prop a predicate over B. Then, we define the generic semantics of “three” as follows:
(5.34) Three(A, B, P) = ∃x, y, z : A. D[B](x, y, z) ∧ P (x) ∧ P (y) ∧ P (z).
where D[B](x, y, z) = x ≠ B y ∧ y ≠B z ∧ x ≠B z. □
Among Three’s arguments, the type A and the domain B of setoid B are related in one of the following manners (all of them satisfy that A is a subtype of B):
1) B = A: in this case, Three(A, B, P) is just Three0(B, P). In other words, Three0 is a special case of Three. For example, the semantics of (5.30) can be re-written as Three(PHY, pick up).
2) B is different from A, but it is not a dot-type. An example of this is (5.33) whose semantics can be given as 5.35, which is (5.36) when Three is expanded:
(5.35) Three(Pen, PHY, pick up)
(5.36) ∃x, y, z : P en. D[PHY](x, y, z) ∧ pick up(x) ∧ pick up(y) ∧ pick up(z)
3) B is different from A, but it is a dot-type – we shall discuss this in section 5.3.3.
When the setoid B interprets a CN, the predicate P is usually the interpretation of a verb phrase or an adjective. We usually require that such a predicate respects the ICs in the sense that, if x =B y, P (x) ⇐⇒ P (y) (see, footnote 7 on p. 110.). Sometimes, B does not interpret a CN; an example is when B is a dot-type, which represents a typical case of copredication, to be discussed in the next section.
5.3.3. Copredication with quantification
When both copredication and quantification are involved, the situation becomes more sophisticated and requires special treatment in order to give proper semantics with respect to the setoids concerned. Dot-types in MTTs, as already mentioned, have been developed for copredication in linguistic semantics (Luo 2009c, 2012b). The basic idea and formal rules are sketched in section 5.2, with the simple example of (5.11), repeated below as (5.37), which involves copredication, but no quantification. This is different in (5.4), repeated here as (5.38), where copredication interacts with quantification manifested in the numerical quantifier “three”.
(5.37) John picked up and mastered the book.
(5.38) John picked up and mastered three books.
In cases like (5.38) where both copredication and quantification are involved, a proper semantic treatment becomes more sophisticated and requires more careful consideration. Let us first start by considering the simpler subcases (5.39) and (5.40), which do not involve copredication.
(5.39) John picked up three books.
(5.40) John mastered three books.
First, it is not difficult to realize that (5.39) is not much different than (5.33), if we replace “pens” by “books”. Thus, they should receive similar semantics. Actually, they do, the semantics of (5.39) and (5.40) are (5.41) and (5.42), respectively:
(5.41) Three(Book, PHY, pick up)
(5.42) Three(Book, INFO, master)where PHY = (PHY, =p) and INFO = (INFO, =i). However, it is important to note that the CN “book” in (5.39) refers to a different collection from that referred to by “book” in (5.40): for the collection of books in (5.39), two books are the same if they are physically the same, while for that in (5.40), two books are the same if they are informationally the same. Put in another way, although they share the same domain Book, their ICs are different and, therefore, they are different collections. This is reflected in their semantics: to compare books, =p is used in (5.41) and =i in (5.42). So, the CN “book” in (5.39) stand for a collection of books that is different from that in (5.40), represented by the setoids BOOK1 and BOOK2 as follows:
At this point, a question that naturally arises is how the ICs for “books” are determined: why do we use =p in (5.41) and =i in (5.42)? The answer is that it is the verb (and its semantics) that determines the IC of the CN. In (5.39), the verb is “pick up”, whose semantic domain PHY has determined that it is =p, the identity between physical objects, that should be used for the books; and in (5.40), the verb is “master”, whose semantic domain INFO has determined that it is =i, the identity between informational objects, that should be used for the books. In general, we may express this as follows: given a predicate V : Dom(V) → Prop that interprets the verb, the IC of the CN N (“book” in the above examples) to which the verb is applied is determined by the domain of the predicate: in case Dom(V) ∈ {PHY, INFO},
What the above does not cover, however, is the case of copredication, for example, coordination of verbs “pick up” and “master” in (5.37). In order for such a coordination to happen, the two verbs must be of the same type, but the originally given types to “picked up” and “mastered” are different: Human → PHY → Prop and Human → INFO → Prop, respectively. As explained in section 5.2, the introduction of the dot-type PHY • INFO and the subtyping in (5.46) make both verbs be of the same type and, hence, the two verbs can be coordinated.
(5.46) Book ≤ PHY • INFO
When copredication interacts with quantification, as illustrated by (5.38), the situation becomes more complex. However, we can still give a generic semantics for quantifiers such as the numeric quantifier “three”. Unlike the operator Three defined in definition 5.4, we need a similar but more general operator: specifically, its second argument is not necessarily a setoid anymore, since it needs to be applied to the corresponding setoid-like structure of the dot-type, rather than the setoid structure of a CN. This has led us to introduce the notion of pre-setoid and, in particular, the specific pre-setoid corresponding to a dot-type given as follows.
DEFINITION 5.5 (Pre-setoids for dot-types).–
![]()
![]()
A • B = (A • B, κA•B)
![]() □
□
Then, we can define the generic operator THREE for the numerical quantifier “three” by means of the definition below. Compared with Three defined in definition 5.4, THREE is more general: the second argument for THREE is not required to be a setoid anymore – it can be any pre-setoid.
DEFINITION 5.6 (THREE).– Let A be a type, B = (B, κB) a pre-setoid such that A ≤ B, and P : B → Prop. Then, we define the generic semantics of “three” as follows:
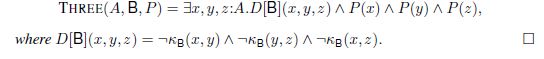
Note that the disjunction connective ∨ is used in definition 5.5(2). This is mainly because, with this definition, the generic semantics THREE of the numerical quantifier is exactly what we want. For instance, the semantics for (5.38) is (5.47), where pm : Human → PHY • INFO → Prop is the interpretation of “pick up and master”. Note that this is achieved through defining the relation κA•B by means of disjunction of the constituent relations κA and κB. As a result, we obtain double distinctness by negating the sentence formed by disjunction: for example, after expansion of THREE, we obtain (5.48), which is recognized more easily as the intended semantic interpretation of (5.38), saying that books x, y and z picked up and mastered are different both physically and informationally.
(5.47) THREE(Book, PHY • INFO, pm(j))
(5.48) ∃x, y, z : Book.
D[PHY](x, y, z) ∧ D[INFO](x, y, z) ∧ pm(j, x) ∧ pm(j, y) ∧ pm(j, z)
REMARK.– Note that the definition of THREE covers all pre-setoids, including setoids as well. For THREE(A, B, P), B can be any pre-setoid, including those A • A’ corresponding to dot-types. As explained above, this captures the semantics with double distinctness correctly. We may ask a subtler and possibly deeper question: is the definition of A • B appropriate? Instead of answering this question directly, let us discuss two related issues that we hope would clear away some misunderstandings that may be behind asking this question and clarify the issues at hand. The first issue concerns the relationship between dot-types and linguistic entities like CNs. Although CNs can be interpreted as types, there is no CN that can be interpreted as a dot-type. In particular, the relation associated with a dot-type does not represent any IC – a dot-type is not an interpretation of a CN. That is why we have been careful in not calling the relation κA•B an IC – it is simply not an IC.
The other related issue is more general than the first: we think that unlike other data types in MTTs (e.g. the type of natural numbers), a dot-type A • B is not a representation of a collection of objects, although its constituent types A and B may be. Therefore, in a pre-setoid whose domain is a dot-type, its associated relation is not supposed to be the equality for a collection. This explains the flexibility we have in defining the associated relation for dot-types. In fact, as far as correctness is concerned, as long as it is a reflexive and symmetric relation, it would do – our definition by means of disjunction does result in such a relation. □
5.3.4. Verbs plus adjectives: more on copredication with quantification
Consider the following example:
(5.49) John mastered three heavy books.
In interpreting the above sentence, we need to capture that John mastered three informational objects that are also heavy as physical objects. In effect, both the verb and the adjective have a word on the decision concerning the involved in interpreting this sentence. Formally, we have:
(5.51) master(j) : INFO → Prop
More specifically, both ICs for physical/informational objects are at play. This is a more sophisticated copredication phenomenon. Let us divide the problem into two parts: first we look at the adjectival modification “heavy books” and the result of “three” quantifying over it, and, then, at the application of mastered(j) to the whole quantified NP “three heavy books”. The interpretation of the adjectival modification, as usual, is taken to be a Σ-type: “heavy book” will be interpreted as (5.52), which is a subtype of Book as shown in (5.53):8
(5.52) H Book = Σ(Book, heavy)
(5.53) H Book ≤ Book ≤ PHY • INFO
The interpretation we get for the whole sentence (5.49) is (5.54), which is (5.55) when THREE is expanded:
(5.54) THREE(H Book, PHY • INFO, master(j))
(5.55) ∃x, y, z : H Book
D[PHY](x, y, z) ∧
D[INFO](x, y, z) ∧ master(j, x) ∧ master(j, y) ∧ master(j, z)
What is important to note here is that the information regarding x, y and z being heavy is contained in the Σ-type H Book. More specifically, the second projection (p2) of the Σ will contain the information that the property heavy holds for x, y and z. The account can also be extended to the case when a noun is modified by more than one adjective that may induce different ICs , such as (5.56):
(5.56) John mastered three heavy informative books.
In such a case, what we need to capture is the fact that John mastered three informational objects that are heavy as physical objects but informative as informational objects. Let us see how this works. We first form the Σ-type in a nested manner,9 and we have similar subtyping relationships (5.59):
(5.57) I Book = Σ(Book, informative), where informative : INFO → Prop.
(5.58) H I Book = Σ(I Book, heavy), where heavy : PHY → Prop.
(5.59) H I Book ≤ I Book ≤ Book ≤ PHY • INFO.
The interpretation we get for the whole sentence (5.56) is as follows:
(5.60) THREE(H I Book, PHY • INFO, master(j))
What is obvious from the above examples is that the way the ICs are decided are a little bit more complicated, given that we might have cases where both a verb and an adjective play a role in this decision.
Another related issue is how many ICs can be used. In all our examples, the maximum number is two. This is not an accident as it basically represents the ability of a CN to be associated with ICs . This is true for CN like “book” that are associated with two aspects: in the case of book, a physical and an informational one. Whether we have cases where more than three ICs are involved for the same CN boils down to the question of whether CN with that many aspects can be found. One such case is “newspaper”: it is associated with three senses: (1) physical, (2) informational, and (3) institutional. However, rather interestingly, only two of the three senses can appear together. More specifically, Antunes and Chaves (2003) argue that, whereas senses (1) and (2) can appear together in a coordinated structure, sense (3) cannot appear with any of the other two:10
(5.61) # That newspaper is owned by a trust and is covered with coffee.
(5.62) # The newspaper fired the reporter and fell off the table.
(5.63) # John sued and ripped the newspaper.
In Chatzikyriakidis and Luo (2015), we have argued that one can find cases where the two senses are actually coordinated:
(5.64) The newspaper you are reading is being sued by Mia.
Whatever the data are, however, there are no cases where all three senses are coordinated nor we know of any other CN that allows this kind of situation. This means that an account of individuation can be reduced to dot-types with two senses, not more than that, even though in principle the account presented here, as well as other accounts like the one proposed by Gotham (2017), could easily be generalized for n senses if there is a need to do so.
5.4. Concluding remarks and related work
The introduction of dot-types in MTTs offers an adequate formal account of copredication in general. In combination with the formal treatment of CNs as setoids, dot-types provide a proper treatment of the more sophisticated cases in copredication where its interaction with quantification is involved. In particular, in this chapter we have shown that such notoriously problematic double distinctness cases are also correctly captured within our account, once CNs are interpreted as setoids, rather than just types.
In this section, we shall give a review of some of the related work on copredication and individuation, especially about identity criteria for CNs. As far as we know (see section 3.2.1), the origin of the notion of identity criteria can at least be traced back to Frege (1884) and it was Geach (1962) who first connected ICs with CNs in linguistic semantics. Subsequent studies include Gupta (1980), Baker (2003), Barker (2008) and Luo (2012a), among others. As mentioned in footnote 1 on p. 100, studying the issues of copredication with quantification in (Chatzikyriakidis and Luo 2015), we failed to properly acknowledge the necessity of considering ICs for these cases, although it was already recognized in Luo (2012a). The issue has been taken up again in (Chatzikyriakidis and Luo 2018) and expanded here, providing an account, which is capable of dealing with ICs under copredication with quantification. The same problem, under the name of individuation, was studied by Asher (2008, 2012) and Gotham (2017), among others.11 In particular, Gotham (2017), starting from his PhD thesis (Gotham 2014), gives a first thorough account of the individuation problem discussed in section 5.3 in a mereological setting, as related to Link (1983) among others. In the following, besides giving a more detailed summary of Gotham’s work, we shall also discuss a recent very interesting paper by Liebesman and Magidor (2017) that studies copredication from a philosophical point of view.
Gotham (2014, 2017). The first account to deal in depth with the problems discussed in section 5.3 is given in (Gotham 2014, 2017). Gotham has managed to provide a compositional account of copredication that derives the correct ICs in the cases where double distinctness is needed. Gotham also provides a comprehensive critique and discussion of a number of the previous accounts, most importantly Asher (2012), Cooper (2011) and Chatzikyriakidis and Luo (2015), showing their inefficiency to derive the correct individuation criteria in quantified copredication cases. He then moves on to propose his account that tackles the issues correctly.
Gotham manages to provide a compositional account of co-predication that derives the correct ICs in the cases where double distinctness is needed. The main components of the account are as follows:
1) Both complex and plural objects exist
- – complex objects are denoted with the + operator while plural objects with the ⊕ operator (assumes a join semilattice ála Link (1983));
- – any property that holds of p holds of p + i, and likewise any property that holds of i also holds of p + i.
2) Lexical entries for CI and verbs are more complex than what is traditionally assumed in Montague Grammar. They do not only decide extensions, but they further specify a distinctness criterion.
3) Different objects have different distinctness criteria. Gotham calls these individuation relations. They are two-place predicates of the following form:
- a) PHY = λx, y : e.phys-equiv(x)(y)
- b) INFO = λx, y : e.equiv(x)(y)
4) A non-compressibility statement denoting that no two members of a plurality stand to a relation R. This basically is the way to ensure that members of the plurality do not bear any relation to each other (see Gotham (2014) for the formal definition of compressibility).
5) A further assumption that verbs also somehow point to the individuation criteria that have to be used.
6) Finally, operator, called Ω, is used that helps in choosing the individuation criteria for each of the argument.12
Putting all these assumptions together, Gotham manages to get the correct ICs for the different cases interested. But before we present you with an example, some notes are presented on the Ω operator. First of all, it must be already clear to the reader that the type of CNs according to Gotham departs from the classic conception of CNs as being predicates (or sets if you wish). The first proposal involves the type e → (t × R), where (t × R) is a product type with t a truth value and R the type of relations, basically an abbreviation for e → e → t. The second and final proposal takes CNs like “book” to involve the type e → (t × ((e → R) → t)), which Gotham abbreviates to e → T. The second projection p2 is now a set of functions that map the type e argument, say x, to a relation of type e → R, where R ![]() Rcn, and where Rcn is taken to be the individuation relation given by the noun or the predicate. For example, the entry for book is now as follows (where ∗Pd means that the predicate P is a set of pluralities):
Rcn, and where Rcn is taken to be the individuation relation given by the noun or the predicate. For example, the entry for book is now as follows (where ∗Pd means that the predicate P is a set of pluralities):
Assuming such an entry for a CN, the function Ω computes the least upper bound of the set of relations R. In the case of books, this is (PHYS INFO), for master it is (INFO), and so on.13 The end result of the semantics of the sentence “John picked up and mastered three books” is shown below:
This gives the correct ICs for the double distinctness cases. To put it in words: the formula talks of a plurality of three objects that are books, that are all picked up and mastered and that are neither informationally nor physically compressible (thus distinct). The second projection just gives the ICs for the arguments, PHYS ![]() INFO for the object and ANI for the subject. There are a number of similarities between Gotham’s account and the one proposed in this chapter. First of all, both of them make the claim that the definition of CNs has to be extended with a notion of ICs. For Gotham, this amounts to extending the traditional notion of predicates as sets to a considerably more complex type. For our account, the idea is that CNs are not just types anymore, but rather setoids, with their second component being an equivalence relation on the type, i.e. its IC. Gotham also assumes individuation relations. With regard deciding the ICs for verbs or adjectives, Gotham uses the Ω function. For our account, the ICs criteria for the arguments of the verb are decided by the type of the argument and whether it is a complex object or not. Furthermore, Gotham uses a mereological account to capture the individuation criteria, but makes an additional crucial assumption that, as far as we know, is not found in standard mereological studies. This is the introduction of the + operator and the introduction of the following axiom:
INFO for the object and ANI for the subject. There are a number of similarities between Gotham’s account and the one proposed in this chapter. First of all, both of them make the claim that the definition of CNs has to be extended with a notion of ICs. For Gotham, this amounts to extending the traditional notion of predicates as sets to a considerably more complex type. For our account, the idea is that CNs are not just types anymore, but rather setoids, with their second component being an equivalence relation on the type, i.e. its IC. Gotham also assumes individuation relations. With regard deciding the ICs for verbs or adjectives, Gotham uses the Ω function. For our account, the ICs criteria for the arguments of the verb are decided by the type of the argument and whether it is a complex object or not. Furthermore, Gotham uses a mereological account to capture the individuation criteria, but makes an additional crucial assumption that, as far as we know, is not found in standard mereological studies. This is the introduction of the + operator and the introduction of the following axiom:
for any predicate P. This is crucial for the account to work and pretty much plays the role of the definition we have for setoids of dot-types in section 5.3.3. We can question its naturalness, as Gotham (2017) seems to be doing in footnote 2, where he says:
One can imagine other ways of implementing this mereological approach to copredication, both in terms of what composite objects there are and in terms of what their properties are. That in turn would require a revision to the definition of compressibility in Section 3.1.1. The approach adopted in this article is adequate for criteria of individuation to be determined compositionally, and can be adapted if revisions of this kind turn out to be necessary (Gotham 2017, footnote 2).
One of the interesting connections of Gotham’s work with ours concerns with double distinctness. In Gotham’s work, this is reflected in its basic assumption that (5.67) is true for every predicate, which can be found in the first paragraph of section 2 of Gotham (2017). Although the two formal frameworks are completely different, this is informally related to our notion of pre-setoids for semantic interpretations of dot-types. However, there seems to be a potential problem with the formalization in Gotham (2017): consider the following predicate P :
(5.68) P (p) = true, if p = a + x;
P (p) = false, otherwise.
Then, according to (5.67), P(a) is false and P(a + x) is true, and thus P does not satisfy (5.67). We do not know how serious of a flaw this is and whether a straightforward fixing can be obtained for an amendment.
Liebesman and Magidor (2017). Here, we want to discuss an interesting account of copredication from a more philosophical point of view, that of Liebesman and Magidor (2017). In this paper, the authors claim that copredication does not pose any problems for traditional referential semantics and no extra work needs to be done in formal semantics or in terms of metaphysics to account for them. According to Liebesman and Magidor (2017), “book” involves one sense that designates both informational and physical books, instead of two senses. One of the examples they use to prove this is as follows: there is a bookshelf that has two copies of the French translation of “Naming and Necessity”, and one copy of the Hebrew translation. Given this situation, consider the following sentences:
(5.69) One book is on the shelf.
(5.70) Two books are on the shelf.
(5.71) Three books are on the shelf.
They expand the true readings for each of the sentences:
(5.72) One book is on the shelf: Naming and Necessity.
(5.73) Two books are on the shelf: the Hebrew translation of Naming and Necessity and the French translation of Naming and Necessity.
(5.74) Three books are on the shelf: the one on the left, the one in the middle, and the one on the right.
Liebesman and Magidor (2017) argue that in the dot-type approach, we will have to stipulate at least three senses for “book”, one for physical books, one for informational books that different translations do not count as different informational objects and one where different translations matter. We do not have to posit three senses, but rather to allow the informational sense to have different individuation criteria in different contexts. For example, for a given speaker or a given situation the IC for the informational sense might not distinguish between translations of the same book, and for other speakers or given contexts it can. This is something that is afforded by the theory proposed here by making use of local coercions already discussed in section 3.2.2.
Consider another example by Liebesman and Magidor (2017):
(5.75) Each week, you will be assigned a single book, on which you will be required to submit a report: on odd weeks, your book will be a theoretical book on the history of book making, while on even weeks, our special collections librarian will assign you a volume from our historical collection to examine.
Liebesman and Magidor (2017) state with respect to that example:
“Book” ranges over both physical and informational books: the books the students are mastering on odd weeks are informational books, while the ones they are mastering on even weeks are physical books. (Liebesman and Magidor 2017, p. 136).
However, this is hardly a problem in the account we have presented so far. Volume is a dot-type. In the case of “assign”, its PHY sense is used, and in the case of “examine” its INFO sense is used. On this assumption, the problem vanishes. In general, the problem that is dubbed Univocity by Liebesman and Magidor (2017) does not seem to be a real problem, at least for our account.
Another problem that the authors identify with respect to accounts that posit different senses for elements like “book” is what they name inheritance. In the authors’ words:
In particular, the key challenge raised by copredication arises from the supposition that the properties ascribed in copredicational sentences cannot be instantiated by both. For instance, physical books can be heavy but not informative and informational books can be informative but not heavy. (Liebesman and Magidor 2017, p. 137).
The authors provide the following example as a counterexample to approaches like the approach described in this chapter. Imagine a case where there are three copies of “War and Peace” on the shelf. Even in that case, the following seems to have a true reading the authors claim:
(5.76) One book is on the top shelf.
Since what is quantified here is a single entity, the authors conclude that this single entity cannot be a physical, but rather an informational object. The authors take this to be an argument that accounts like the one put forth in this example are wrong. But there is nothing problematic with these examples. Let us take the elaborated versions of the examples, given by the authors to further prove their point:
(5.77) One book is on the top shelf: War and Peace, and it is 587,287 words long.
(5.78) (#) One book is on the top shelf: War and Peace, and it is worn out.
Some typing:14

Now, the interpretations (5.77) and (5.78) are:
(5.79) ∃b : Book. OT S(b) ∧ WaP = b ∧ XW L(b)
(5.80) ∃b : Book. OT S(b) ∧ WaP = b ∧ WO(b)
We strongly disagree with Liebesman and Magidor (2017) that (5.78) is an infelicitous example. It is a perfectly good example given the context, and should be captured in giving a formal semantics account. Consider the following:
(5.81) One book is on the top shelf: War and Peace, and it is worn out. All three copies.
This example shows that there is nothing wrong with 5.78 in the first place. In sum, the problems raised in Liebesman and Magidor (2017) do not seem to apply to our account. To the contrary, the account proposed in Liebesman and Magidor (2017) cannot deal with the double distinctness cases, as the authors themselves note. They claim that they are not sure that double distinctness actually exists. We are not going to get into this discussion. What we are going to say is that the accounts as given in the formal semantics literature have the double distinctness cases at their center and are evaluated as to whether they can capture these cases or not. Our account does not really suffer from the problems that Liebesman and Magidor (2017) identify, and furthermore, it also captures the double distinctness cases. For us, this is a gain compared to what Liebesman and Magidor (2017) propose.
REMARK.– While finalizing the book, two relevant papers came to our attention: one by Mery et al. (2018) and another by Ortega-Andrés and Vicente (2019). In Mery et al. (2018), the authors, as they say, attempt to solve the quantification in copredication problem. The idea is to connect Retore’s Montagovian Generative Lexicon Retoré (2013) with discourse representation theory. In essence, the authors consider the problem of counting to be a discourse-related problem. The example they concentrate on is as follows:
(5.82) Oliver stole the books and read them.
In the above example, “the books” are individuated physically in the first instance and informationally in the second instance. The authors present a partial implementation of this sentence, going from the actual utterance (parsing) to logical form. What the authors do not seem to notice is that the counting problem is not an anaphoric problem, or it may not need be so. The most important issue in individuation in copredication cases, and the most difficult to tackle, concerns cases where a numerical quantifier is involved (like “three”), i.e. the double distinctness cases we have been discussing. These cases are not brought up by the authors, and as far as we can see, it is not clear how these cases are going to be handled with the system Mery et al. (2018) propose.
Ortega-Andrés and Vicente (2019) is a different line of work that concentrates on the question of why some groups of senses (the components of the dot-type in our case) allow for copredication and why some others do not. They present interesting cross-linguistic data that can be further elaborated in fully understanding the nature of copredication and explain why some cases like “newspaper” present restrictions of the type we have discussed. The argument is that the legit copredication cases are possible because the senses in question are accessible by the time the speaker/hearer has to retrieve them. They present and discuss interesting data from the psycholinguistics literature to support this claim. This discussion, albeit extremely interesting, has no effect on our account whatsoever (even though a complete account of copredication needs to be informed from these results). Our account is agnostic to the discussion, in the sense that it operates as soon as the legit and illicit copredication senses are decided. Simply put, formal semantics accounts like the account proposed here or any formal semantics account proposed in the literature do not have anything to say on why some senses can appear in copredication and some others do not. □
- 1 The current authors have considered the issue of dealing with cases where copredication interacts with numerical quantification in (Chatzikyriakidis and Luo 2015) where, however, the necessity of considering ICs formally was not taken seriously and, realising this, we have studied the CNs-as-setoids approach in depth in (Chatzikyriakidis and Luo 2018).
- 2 Note that copredication has not only been dealt with within the formal semantics community. Some other researchers have claimed that dot-types are not needed to account for copredication: Falkum (2011) argues that copredication is a pragmatic phenomenon, while Liebesman and Magidor (2017) argue that copredication does not even pose a problem for classical referential semantics. It is worth noting that copredication is one of the classic examples used by generative syntacticians, for example Chomsky et al. (2000), to argue against any kind of referential semantics. Furthermore, the account by Liebesman and Magidor (2017) will be discussed in section 5.4.
- 3 Note that, here, this notion of “dot-type” is only considered informally. Asher (2008) has analyzed the notion of dot-type. Although the authors do not completely agree with all the arguments there, the analysis is very informative and worth reading. For example, in the paper, Asher gave convincing examples to argue that a dot-type should not be an “intersection” of the constituent types.
- 4 We adopt the view that two physically identical books can be informationally different, as assumed by Asher (2012) and Gotham (2014). However, the authors are actually inclined to believe that, in reality, if two books are physically identical, they cannot be informationally different. For example, Asher considers the example of several books in one volume, thinking that the same volume is involved. We do not think that volume and the books are comparable in such an example. But, as we said, we will still adopt Asher/Gotham’s view partly because this would make it easier for us to compare our account with theirs.
- 5 The conjunction “and” can be given a polymorphic type ΠA : LTYPE.A → A → A, where LTYPE is the universe of linguistic types. See section 2.3.2 for more details on polymorphic conjunction as well as LTYPE.
- 6 For this idea, the interested reader may consult classic research in constructive mathematics including, just to mention two of them, Bishop (1967) and Beeson (1985). The idea that sets/types may have different ICs is fundamentally different from that in classical mathematics where a universal equality relation between all objects of the formal theory (say, set theory) exists.
- 7 When CNs are interpreted as setoids, the interpretations of verbs/adjectives should be IC-respecting predicates: for example, for talk : Human → Prop, talk(h1) ⇔ talk(h2) if h1 =h h2.
- 8 (5.52) is just another notation for Σx : Book.heavy(x), the type of books which are heavy.
- 9 We note that there is another interpretation of the adjective modification: heavy informative books is seen as heavy and informative books. Then, a similar but slightly different analysis would follow.
- 10 See also the discussion in the notes on p. 125 of this chapter.
- 11 There are many studies on copredication, but they usually do not consider the advanced cases where individuation plays a crucial role in getting the counting facts right. Such work includes papers using type theories (Bassac et al. 2010; Kinoshita et al. 2016). At this point, let us also make some brief comments on Bahramian et al. (2017), an unpublished paper that proposes an approach to use identity types in Homotopy Type Theory (HoTT 2013) to model CNs and to deal with copredication. However, when studying the proposal carefully, one would realize that the basic idea of “common nouns as identifications” is flawed and problematic, and furthermore, even if the approach worked (which, unfortunately, does not), the proposal does not make use of the univalence axiom or higher inductive types in any essential way, so the claim that this is using HoTT is also misleading.
- 12 Please check (Gotham 2014) for the formal definition.
- 13 Please consult (Gotham 2014, 2017) for more details on the formalization.
- 14 OTS = on the shelf, WO = worn out, XWL = x words long and WaP = War and Peace.


