Chapter 4
Control of the Double-star Synchronous Machine Supplied by PWM Inverters 1
4.1. Introduction
In high-power applications, such as naval propulsion, the constraints of power segmentation, reliability and safety of functioning have led to the development of specific electrical actuators created by associating machines with a high number of phases with static converters. Thus, during the 1980s, the double-star synchronous machine with two current commutators was used for the electrical propulsion systems of ships [BEN 98, KET 95, KHE 95, KOT 96]. This supply mode, with thyristor current commutators, ensured the simplicity and reliability of the electrical actuator. However the supply of the machine with pulses of currents rich in harmonics led to ripples in the electromagnetic torque. A shift of 30° between the two stars of the machine stator reduced these torque ripples [KHE 95, WER 84]. The use of the smoothing inductance necessary to manufacture the direct current (DC) source supplying the commutator, and thyristor type semi-conductor components decreased the performance of the electrical actuator in dynamic state.
Since the end of the 1990s, thanks to progress made in the field of power electronics and industrial computer science, a new power electronic converter – the double star synchronous machine – is being investigated. The supply of double star synchronous machines with PWM inverters produces sinusoidal currents in the machine windings [ABB 84, NEL 73, SIN 02] that considerably decrease the torque ripples. Furthermore, the vectorial control algorithms that are well known for the three phase synchronous machine [LEO 96, LOU 95, VAS 94] can be extended to the double-star synchronous machine to improve the performance in static and dynamic states.
This chapter is devoted to the vectorial control of the double-star synchronous machine supplied with two PWM inverters. The control strategy is similar to that of a three-phase synchronous machine; an internal loop to control the torque and an external loop to control the speed. Usually for a three-phase machine, control of the torque requires control of currents in reference frame dq linked to the rotor and the management of specific problems, such as the coupling between axes d and q [LOU 10a, LOU 10b]. As for the three-phase synchronous machine, the control algorithm of the double-star synchronous machine is closely linked to the dynamic model of the machine. Two modeling approaches can be distinguished. The first considers the machine as two three-phase machines that are magnetically coupled [TER 00]. In this case, we apply the classic Concordia and then Park transformations a [LOU 04a, LOU 04b] to each star and manage the magnetic coupling between the two stars. The control algorithm of the total torque controls the torques produced by the two stars in a way similar to that of a classical three-phase machine and manages the new coupling introduced by the two stars. The second approach consists of managing the coupling at the modeling level [MER 05]. In this context, the machine is described on an orthonormal basis whose dimension is identical to that of the initial basis. The modeling principle requires us to generalize the vectorial formalism developed for polyphase machines with equally distributed phases [SEM 00, SEM 10] in the case of double-star or even multi-star machines [BEN 04]. Hence, the current vector is projected in an orthonormal space with six dimensions. All currents are decoupled. The first two components of current vector are equivalent to those of the classical triphase machine in Concordia’s frame. Then, the application of the usual Park’s transformation introduces the classical coupling. The other four currents are non-sequential ones and remain decoupled from the two currents in Park’s frame.
Briefly, the problem with the control of a double-star synchronous machine control is linked to the dynamic modeling of the machine. Thus, after a quick description of the electrical actuator and a reminder of the basic matricial electrical equations of the machine, we explain the dynamic models of the machine. The last part of this chapter is dedicated to the specific problems linked to control, such as the management of decoupling and the generation of references in relation to control.
4.2. Description of the electrical actuator
Each star of the machine is supplied with its own three-phase PWM inverter. The two inverters can be supplied with the same DC bus or with two different DC buses. In this study, we consider the most general case, illustrated in Figure 4.1. It consists of supplying each inverter with its own DC voltage source. We assume that the two DC buses have the same amplitude.
Figure 4.1. Supply structure of the double-star synchronous machine

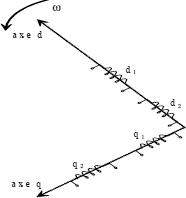
Figure 4.2. Distribution of statoric phases of the double-star synchronous machine

Like every rotating electrical machine, the double-star synchronous machine consists of a stator and a rotor. The machine considered is a salient pole synchronous machine. The stator illustrated in Figure 4.2 has two three-phase windings shifted by an angle γ generally equal to 30°. The rotor is identical to a classical synchronous machine. It can be with permanent magnets or a coiled rotor. In the latter case it includes an inductor winding supplied with DC and damper windings modeled by two windings in short-circuit: one on the direct axis of the rotor; and the other on the quadrature axis. The inductor winding is supplied with a DC voltage Vf via a current-controlled chopper.
4.3. Basic equations
4.3.1. Voltage equations
The models developed from now on are based on the following hypotheses:
– the two three-phase windings making the stator are identical, electrically insulated and shifted by an angle γ;
– the magnetomotive forces have a sinusoidal distribution;
– only the first space harmonics are considered and the mutual inductances are characterized by their fundamental component alone; and
– the magnetic saturation is disregarded.
The electrical equations of the machine are written in the following general matricial form:
[4.1] 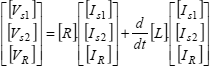
The current and voltage vectors are defined as follows:

The resistance matrix is diagonal and the terms in it are the values of the resistances of the different windings:
The inductance matrix can be broken down on its diagonal according to the self-inductance matrices of the different winding systems: the first star, the second star and the rotor. The other inductance matrices are introduced by the magnetic coupling between the winding systems:
[4.3] 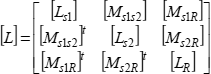
Matrices [Ls1] and [Ls2] represent the inductance matrices of the first and second star, respectively. Each of them is broken down as the sum of a constant matrix and of a matrix varying as a function of the rotor position reflecting the saliency of the machine:
with:

Angle ![]() x depends on electric position
x depends on electric position ![]() and on the given star (x = 1, 2):
and on the given star (x = 1, 2):
The magnetic coupling between the two stars of the stator is characterized by inductance matrix [Ms1s2], which is put in the following form:
with:

Matrix [Mss0] is a constant matrix; it depends on the shift angle of the two stars equal to π/6. Matrix [Mss(![]() )] cancels out in the case of a machine with smooth poles.
)] cancels out in the case of a machine with smooth poles.
Self-inductance Ls can be written as the sum of an inductance of statoric leaks and inductance Mss.
The coupling between the stator and rotor is characterized by two matrices [Ms1r] and [Ms2r]:
with: x = 1, 2
Since the rotor is identical to that of a classic three-phase machine, the rotor inductance matrix remains unchanged. It is written as:
4.3.2. Equation of the electromagnetic torque
The general expression of the torque can be inferred from the derivative of the coenergy:
from which:
[4.11] 
4.4. Dynamic models of the double-star synchronous machine
With the natural basis, as shown by the voltage equations of the double-star synchronous machine in equation [4.1], the inductance matrix of the stator (equation [4.3]) is full. When we are interested in establishing a model to control or study transient states, it is usual to look for a referential in which the inductance matrix is diagonal and the state variables are continuous variables. To achieve this, in the case of classic three-phase machines, electrical engineers have defined transformation matrices to change the referential. These transformations are the Concordia and Park matrices. The aim of this section, as in the case of three-phase machines, is to look for a new basis and define transformations to switch from the natural basis to this new basis. These transformations, which are in fact changes of reference point, form the basic tools for establishing dynamic models that aim to control double star-machines. Two modeling approaches can be distinguished. The first considers the machine as two three-phase systems. The machine is represented by two coupled submachines in the Park reference system. The second approach takes advantage of the symmetry property of the inductance matrix and considers the double-star machine to be a polyphase machine. It is important to underline, however, that contrary to a polyphase winding, with three-phase double winding the six phases are identical but are not equally distributed.
4.4.1. Dynamic model in referential d1q1d2q2
4.4.1.1. Definition of the transformations
As shown in Figure 4.2, the three-phase double winding constituting the stator consists of two three-phase windings shifted by an angle equal to π/6.
Figure 4.3. Transformation of the three-phase double system into a two-phase double system

The transformation from a three-phase double system to two two-phase orthonormal systems [MOU 99, TER 00] is illustrated in Figure 4.3. It consists of performing the following two steps:
a) applying the Concordia transformation to each three-phase system forming a star. This operation allows us to transform the two three-phase systems into two two-phase systems:
[4.12] 
with:

b) apply a rotation of angle π/6 for the second two-phase system. This operation allows us to minimize the coupling between the two two-phase systems. In fact only the equivalent phases according to the same ![]() or
or ![]() axis show a magnetic coupling.
axis show a magnetic coupling.
[4.13] 
with:

By assuming that the neutral points of the two stars are not linked to the sources supplying the inverters, we suppress the homopolar components and keep just the variables following referentials (![]() 1,
1, ![]() 1) and
1) and ![]() . In the same way as the three-phase synchronous machine, we apply the rotation of angle
. In the same way as the three-phase synchronous machine, we apply the rotation of angle ![]() to the two two-phase systems:
to the two two-phase systems:
[4.14] 
The model of the machine in Park referential (d,q) linked to the rotor is shown in Figure 4.4:
Figure 4.4. Representation of the machine in referential dq

4.4.1.2. Voltage equations in referential d1q1d2q2
By applying the transformations defined in equations [4.12], [4.13] and [4.14] to voltage equations [4.1], we can infer the electrical model of the synchronous machine with salient poles written in referential dq, or more precisely in referential d1q1d2q2:
[4.15] 
where:

Each matrix is defined as follows:
with:
By emphasizing the leakage inductances, the expressions of inductances given above become:
By emphasizing the coupling inductances between the stars in their respective Park referentials, we can rewrite the inductances according to axes d and q in the following form:
4.4.1.3. Expression of the electromagnetic torque in referential d1q1d2q2
By applying the transformations defined in equations [4.12], [4.13] and [4.14] to the general expression of torque [4.11], we infer the expression of torque in this referential. It is put in the form:
[4.20] ![]()
By emphasizing the contribution of each star and the interaction between the two, expression [4.20] of torque can be rewritten as the sum of three terms:
[4.21] ![]()
with:

In the case of a machine with smooth poles and without damper, the expression of torque is directly inferred from expression [4.21]:
We get a result similar to that of a three-phase synchronous machine with smooth poles. Only the currents following the quadrature axis generate torque. In fact, by replacing the sum of the two currents following axis q with the quadrature current in the case of a three-phase machine, we obtain the classic expression of torque in a three-phase machine in the Park referential.
4.4.2. Dynamic model in referential dqz1z2 z3z4
In this context, we do not separate the two stars and attempt to establish a completely decoupled dynamic model. This model can be obtained in two different ways: either by taking advantage of the analysis and then using the dynamic model developed in section 4.4.1.2, or by rewriting the model on an orthonormal basis. In the latter case, we first need to establish the change of basis matrices.
4.4.2.1. Voltage equations in referential d+q+d-q
Relationship [4.20] shows that the electromagnetic torque depends on the sum of currents in axis d or q [MER 05, MOU 99]. This remark leads us to define new state variables that are the sum of currents following the same axis (id1+id2, iq1+iq2). For reasons of bijectivity and to keep the initial dimension of the state vector, the differences between the respective currents following the same axis must appear in the state vector. From now on, the new state vector becomes:
The dynamic model of the machine will then be expressed in a new referential, written (d+, q+, O+, d-, q-, O-). It is obtained from the model by respectively calculating the sums and differences of equations according to the different axes. In order to keep the norm of the current vector, we use the following normalized transformation:
[4.24] 
Starting from voltage equation [4.15], by introducing the variable change defined above we establish the new dynamic model:
[4.25] 
with:
![]()
This dynamic model (equation [4.25]) consists of two completely decoupled sub-systems (d+q+) and (d-q-). The first sub-system (d+q+) is similar to that of a three-phase machine described in the Park referential (dq). The second sub-system (d-q) is described by two decoupled passive circuits whose inductance is that of leakage. It is important to underline that in the framework of the sinusoidal distribution hypotheses, only the first system contributes to the electromechanical conversion of energy.
4.4.2.2. Voltage equations in referential 
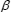 z1z2 z3z4
z1z2 z3z4
Using the approach developed above, it takes several steps to obtain a friendly work referential d+,q+,d-,q-. After applying the classic Concordia and Park transformations to each three-phase star of the double-star machine, the equations of the machine were still coupled. An analysis of the model obtained allowed us to define a third simple transformation (equation [4.24]) defining a new basis by which to describe the double-star machine using a dynamic model. Another modeling approach based on generalizing the vectorial formalism established for polyphase systems or the projection of different vectors in a six-dimensional orthonormal space leads to a decoupled dynamic model.
4.4.2.2.1. Generalization of the vectorial formalism
This approach exploits the symmetry property of inductance matrices of the windings that make up the stator. This property [BAS 95] implies that the inductance matrix is diagonalizable and that an orthogonal basis for eigenvectors exists. As a consequence, we know that there is a referential in which the equations of the machine are decoupled.
In [SEM 00], this basis has been obtained in the case of a machine whose phases are regularly distributed (the statoric windings are dephased by 2π/n for a winding with n phases). Yet, in the case of a double-star machine, as shown in Figure 4.2, the six phases are not regularly distributed. It is necessary to extrapolate the vectorial formalism to this type of machine. The dephasing between the two stars is 30°, as shown in Figure 4.5, so the equivalent polyphase machine has 12 phases that are regularly distributed [MAD 04].
Figure 4.5. Transformation of double-star winding into a 12-phase winding

Knowing that the currents going through real phases (ia1, ia2, ib1, ib2, ic1, ic2) are linear combinations of the currents going through the fictitious phases (ia, ib, ic, id, ie,if, ig,ih, ii, ij), we infer matrix [C12x6], allowing the transformation of a double-star system into an equivalent 12-phase system:
with:

Thanks to this matrix, [C12x6], we can transform the six-dimensional natural basis into a 12-dimensional basis. The matrix of inverse transformation is given by the following relationship:
We refer to [T12] as the generalized Concordia matrix, allowing us to transform this new 12-dimensional basis into an orthonormal basis of the same dimension [BEN 04]:
The first two lines of [T12]t correspond to the first two lines of the generalized Concordia matrix. They allow us to obtain the usual components according to axes ![]() and
and ![]() . The last two lines correspond to the homopolar and quasi-homopolar components, respectively. The other components are called non-sequential components. These are perpendicular to the first components.
. The last two lines correspond to the homopolar and quasi-homopolar components, respectively. The other components are called non-sequential components. These are perpendicular to the first components.
Finally, the matrix transforming the initial six-dimensional basis into an orthonormal basis is done via the [T12, 6]t matrix, which is equal to the product of the two matrices, [T12]t and [c12x6]. If we keep the non-zero vectors resulting from this matricial product [BEN 04], the dimension of the transformation matrix is reduced to six.
Given the fact that the matrix resulting from the product of matrices [C6x12] and [C12x6] is not normalized, the transformation matrix is not normalized either.
By exploiting these different properties, and by taking into account the normalization factor of the matricial product [C6x12] and [C12x6], we can infer the matrix of the transformation of the initial double-star basis into the six-dimensional orthonormal basis:
[4.29] 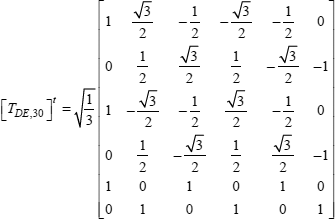
This matrix diagonalizes the inductance matrix of a double three-phase winding where the two windings are shifted by 30°.
4.4.2.2.2. Projection of vectors on a six-dimensional orthonormal basis
It is clear that there is no single approach to follow to define transformation matrix [4.29]. Lipo and his co-authors [ZHA 96] have proposed an algorithm to establish this diagonalization matrix of the inductance matrix. Other similar algorithms have been established by other authors [ABB 84, BEN 03, HAD 01]. With this goal in mind, they define an orthonormal work basis. The corresponding work space is broken down in two orthogonal subspaces.
The first two-dimensional subspace is known by plane (![]() ,
,![]() ) of Concordia. It corresponds to the plane of electromechanical conversion of energy for electrical machines with sinusoidal distribution. As shown in Figure 4.2, axis
) of Concordia. It corresponds to the plane of electromechanical conversion of energy for electrical machines with sinusoidal distribution. As shown in Figure 4.2, axis ![]() is collinear with the axis of phase a1. The components of physical variable x in this plane are obtained by the projection of the vector components of this variable according to these axes
is collinear with the axis of phase a1. The components of physical variable x in this plane are obtained by the projection of the vector components of this variable according to these axes ![]() and
and ![]() :
:
The second subspace is four-dimensional. The different axes defining it (z1, z2, z3, z4) are orthogonal to each other and to the Concordia plane. A trivial solution takes the two homopolar vectors of the two stars as a solution for components z3 and z4. The other two components, z1 and z2, called non-sequential components, are inferred from solving the following system of equations:
[4.31] 
Thus, after solving the system of equations [4.31] and taking the normalization criterion into account [MER 05], we get the transform matrix of the original initial basis into the new orthonormal basis (![]()
![]() z1 z2 z3 z4):
z1 z2 z3 z4):
[4.32] 
It is important to underline that this solution is not unique.
4.4.2.2.3. Comments
Admittedly, the two approaches shown above lead to similar transformation matrices. The two transformations [T6]t and [TDE,30]t are identical. The first approach is based on linear algebra arguments. The expressions of eigenvalues can easily be generalized. However, the first approach requires the use of the equivalent polyphase machine with phases that are regularly distributed and disregard the variable reluctance of the machine in the first step. The second approach is easier. It is based on the projection of initial vectors on a new orthonormal basis. It is not based on restrictive hypotheses, such as geometrical isotropy and regularity of the phase distribution. It does, however, require the calculation of eigenvalues on a case-by-case basis and solving the [4.31] system of equations is not straightforward.
4.4.2.2.4. Voltage equations in space 
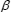 z1z2z3z4
z1z2z3z4
Establishing voltage equations in the ![]()
![]() z1z2z3z4 space requires us to consider the stator winding as a six-phase winding rather than as two three-phase windings. The basic matricial voltage equation [4.1] remains identical but they need to be reordered:
z1z2z3z4 space requires us to consider the stator winding as a six-phase winding rather than as two three-phase windings. The basic matricial voltage equation [4.1] remains identical but they need to be reordered:
[4.33] ![]()
with:

The inductance matrix [L] is written in the form:
In this case, the inductance matrix of the stator is defined as follows:
where:

The stator-rotor mutual inductance matrix is given by:
By applying the basic transformation defined by relationship [4.32] to the systems of equations [4.33], we can infer the voltage equations in orthonormal basis (![]()
![]() z1z2 z3z4):
z1z2 z3z4):
[4.37] 
where:

System of equations [4.37] shows that the electrical equations describing the stator are completely decoupled. In fact, the equations according to plane (![]() ,
,![]() ) are completely decoupled from the equations according to space (z1z2z3z4). And the four equations in space z1z2z3z4 are decoupled.
) are completely decoupled from the equations according to space (z1z2z3z4). And the four equations in space z1z2z3z4 are decoupled.
4.4.2.2.5. Voltage equations in space dqz1z2z3z4
The voltage equations of the double-star machine in space ![]()
![]() z1z2z3z4 are equivalent to that of the three-phase machine in space
z1z2z3z4 are equivalent to that of the three-phase machine in space ![]()
![]() z. We can apply the classic Park rotation transformation to the statoric variables according to plane (
z. We can apply the classic Park rotation transformation to the statoric variables according to plane (![]() ,
,![]() ) to infer the dynamic model of the machine in plane dq. This model is put in the following form:
) to infer the dynamic model of the machine in plane dq. This model is put in the following form:
[4.38] 
with:
![]()
Comparison of relationships [4.25] and [4.38] shows that the two dynamic models are identical. Referential d+q+ is the classic Park referential dq.
4.4.2.3. Expression of electromagnetic torque in referential dqz1z2 z3z4
Starting from general torque expression [4.11] and applying the matrix of referential change from the initial basis to the orthonormal basis [4.32], then Park rotation, we get the expression of the torque:
[4.39] ![]()
with:

The same result can be obtained quickly by analyzing the system of equations [4.38]. In fact, the electromotive forces (emfs) according to space z1z2z3z4 are 0. The only currents in the Park referential therefore contribute to the electromechanical conversion of energy. We notice that according to plane (d,q), the model of the machine is equivalent to that of the three-phase synchronous machine in plane (d,q), provided that we replace the different and mutual inductances and their counterparts with stars.
4.5. Control of the double-star synchronous machine
In this context, we assume that the excitation current is kept constant and that it is not disrupted by the other currents. We disregard the effect of the dampers. Figures 4.6 and 4.7 illustrate the principle diagrams for control of the double-star synchronous machine in referentials d1q1d2q2 and dqz1z2z3z4, respectively. The difference between the two lies chiefly in the generation of reference currents from the reference torque generated by the speed regulator, and the control loops of reference currents. The latter referentials are broken down into two: the control blocks of the currents and the decoupling blocks. In the rest of this section we will focus on problems specific to the double-star synchronous machine. These are the decoupling algorithms in each of the two referentials and the generation of reference currents from a reference torque.
Figure 4.6. Control structure of double-star synchrone machine (DSSM) in referential d1q1d2q2

Figure 4.7. Control structure of double-star synchrone machine in referential dqz1z2z3z4

4.5.1. Control in referential d1q1d2q2
4.5.1.1. Decoupling algorithm
4.5.1.1.1. Principle of the decoupling approach
By disregarding the effect of dampers and assuming that the excitation current is regulated and kept constant, the machine, as shown in Figure 4.8, is replaced with an equivalent with four windings distributed two-by-two according to axes d and q in Park referential.
By arranging the components of the current vector according to the adequate order [Id1, Id2, Iq1, Iq2], the electrical equations given by the relationships [4.15] can be rewritten in the following matricial form:
[4.40] ![]()
with:
![]()

Figure 4.8. Equivalent windings in referential (d, q).
Equation [4.40] shows that there are two types of coupling between the state variables. The first coupling is between the state variables of axes d and q due to the rotation term introduced by the Park transformation. The second is due to the mutual inductance effect (Ldm and Lqm) between the windings of the same axis.
The perturbation terms introduced by the components of emf vector [E] can be compensated for in a traditional way, as in the case of a DC motor or a three-phase synchronous motor.
The decoupling principle consists of bringing back the real system, representing the electrical actuator initially with fourth-order multivariables in an equivalent fictitious system where each state variable is decoupled with respect to the others. Initial input vector [V] becomes [V'] by means of a decoupling algorithm. As shown in Figure 4.9, the new system is equivalent to four independent monovariable subsystems from the point of view of the regulators. As a consequence, all the problems now lie in the establishment of a decoupling algorithm [BEN 04, TER 00].
Figure 4.9. Decoupling principle

After factorization and introduction of Laplace operator p, equation [4.40] is put in the following form:
where:
[U ] = [V] −[E] and [Id]4x4 is the fourth-order identity matrix.
We define a transfer matrix H, linking input vector [U] to state vector [I]:
[4.42] ![]()
with:
Given the existence of coupling between the state variables, matrix [H] is not diagonal. Furthermore, since this matrix depends on the speed, the system is then in non-steady state. As a consequence, without being cautious, every attempt to establish the transfer matrix from Laplace operator p would be wrong.
However, for such a motor, the dynamic of the mechanical mode is much slower than that of the electrical mode. Thus, the speed evolution is so weak with respect to electrical variables that the speed can be considered constant piecewise, making the diagonalization of the transfer matrix possible.
Two solutions can be considered according to the evolution of the speed. In the case of steady-state systems, the rotational speed of the motor can be assumed to be constant. The problem amounts to diagonalizing the transfer matrix. In the case of quasi-steady-state systems, the speed evolves but with very weak dynamic with respect to the electrical variables. The solution considered consists of combining the method of diagonalization and static compensation of the terms introduced by the rotational speed. The first method is referred to as complete diagonalization and the second as partial diagonalization.
4.5.1.1.2. Complete diagonalization
In accordance with Figure 4.9, control vector [U] is then replaced with a new vector, [U']. The system described by relationship [4.42] becomes:
Where [Hdiag] is a diagonal matrix equal to the product of the desired decoupling matrix and the transfer matrix:
In this new system, the control vector is:
The matrix of change of basis [M] representing the decoupling algorithm depends on the transfer matrix “imposed” by the system and on the diagonalization matrix [Hdiag] chosen:
[4.47] ![]()
From now on, the solution is not unique. The heart of the problem lies in the judicious choice of transfer matrix [Hdiag]. The former allows us to impose the dynamics of the system in open loop.
The evolution of each state variable linked to a winding di or qi is ruled by an equation in the form:
with:
![]()
ex is a perturbation term for state variable ix. Generally it reproduces the coupling terms with the other windings for axis d or q as well as it does the windings of quadrature axis q or d.
Given that the aim of decoupling is to make the evolution of each state variable ![]() independent of the others, it appears to be relevant for each variable ix to keep its own time constant:
independent of the others, it appears to be relevant for each variable ix to keep its own time constant:
By taking into account these different criteria, we can define the diagonalization matrix:
By replacing [Hdiag] with its expression in relationship [4.47], we get the matrix of change of basis:
[4.51] 
Figure 4.10 illustrates the final structure of the block describing the decoupling algorithm. The inputs of this block are the outputs of the regulators of current vectors [idq1] and [idq2], and the outputs of the block are the control voltage vectors in referential d1q1d2q2 ![]() and
and ![]() . The two blocks of demultiplexing and multiplexing only allow us to reorder the input and output vectors:
. The two blocks of demultiplexing and multiplexing only allow us to reorder the input and output vectors:
Figure 4.10. Decoupling structure following the complete diagonalization approach

4.5.1.1.3. Partial diagonalization
As shown in by relationship [4.51], the matrix of the change of basis M depends on the rotational speed. In order to free ourselves from the presence of rotational speed ![]() in the transfer matrix, the two axes are initially decoupled by compensation of the terms depending on
in the transfer matrix, the two axes are initially decoupled by compensation of the terms depending on ![]() . It leads to two independent subsystems – one for each axis. The two subsystems obtained are linear and steady state, so it is possible to diagonalize the transfer matrix of each by introducing two matrices of change of basis [MD] and [MQ], respectively, for axes d and q. This decoupling process, combining the compensation and diagonalization methods of each axis, is called the partial diagonalization method.
. It leads to two independent subsystems – one for each axis. The two subsystems obtained are linear and steady state, so it is possible to diagonalize the transfer matrix of each by introducing two matrices of change of basis [MD] and [MQ], respectively, for axes d and q. This decoupling process, combining the compensation and diagonalization methods of each axis, is called the partial diagonalization method.
Electrical equations [4.40] can be put in the form of two subsystems of equations:
We define the two decoupling matrices [MD] and [MQ] for the two subsystems. By following the same approach as in the previous section, we get:
The new structure describing the decoupling algorithm is given in Figure 4.11.
Figure 4.11. Decoupling structure following the partial diagonalization approach

4.5.1.1.4. Validation of decoupling algorithms [TER 00]
As we have seen previously, the model in referential d1q1d2q2 is characterized by two types of coupling: one between the state variables according to the same axis, d or q; and the other between variables according to axis d and state variables according to axis q.
When stationary, only the couplings between the state variables according to the same axis remain. Figures 4.12 and 4.13 show the efficiency of the two decoupling algorithms, complete and partial diagonalization. A step variation of one current (id1 or id2) along the d axis introduced a very weak disturbance of 0.5% on the other current of the same axis (id2 or id1). The same remarks can be said when applying a step variation along the q axis. Since the speed is 0, the state variables according to the other axis are unaffected.
Figure 4.12. Validation of the decoupling algorithm by complete diagonalization when stationary

Figure 4.13. Validation of the decoupling algorithm by partial diagonalization when stationary

Figures 4.14 and 4.15 show the decoupling efficiency at non-zero speed (when the machine is in motion). In fact, at a rotational speed of 100 rpm, two tests have been performed for the two decoupling algorithms. The first test (left column) varies the reference currents according to axis q, a level of iq1 at 0.5 s and a level of iq2 at 0.15 s. The second test (right column) measures the reference current variations according to axis d, a level of id1 at 0.5 s and a level of id2 at 0.15 s. The results obtained confirm those measured when stationary and show the very weak perturbation due to a state variable on axis (d or q) compared to the variables of the other axis (q or d).
Figure 4.14. Validation of the decoupling algorithm by complete diagonalization at a speed of 100 rpm

Figure 4.15. Validation of the decoupling algorithm by partial diagonalization at a speed of 100 rpm

4.5.1.2. Generation of current references
If we do not take the effects of the dampers into account, the expression of torque [4.20] becomes:
[4.56] ![]()
In the case of the machine with smooth poles and without dampers, the expression of torque is directly inferred from expression [4.21]:
[4.57] ![]()
Relationship [4.56] shows that the torque in referential d1q1d2q2 depends on currents idi and iqi (i = 1,2) and the inductor current. Relationship [4.57] shows that in the case of a machine with smooth poles, the expression of torque is simplified and no longer depends on the two currents according to axis q. The reference currents according to axis d are kept constant and equal to 0. In the most general case, by referring to the case of a DC machine, to have a torque that is directly proportional to the currents according to axis q, we set the currents to 0 according to axis d:
Since the two stars are identical, the reference torque is equally distributed between the two stars. The two reference currents according to axis q are equal and defined by the following relationship:
We notice that we again find the results known for torque control of a three-phase synchronous machine. Each star is equivalent to a three-phase machine.
4.5.2. Control in referential dqz1z2z3z4
4.5.2.1. Decoupling algorithm
As shown by the voltage equations in this referential [4.38], the dynamic model of the double-star synchronous machine is made of two systems, dq and z1z2z3z4, that are completely decoupled. The equations describing subsystem dq are equivalent to that of a three-phase synchronous machine in Park referential. The control algorithm is then identical to that of a three-phase machine. Sub-system z1z2z3z4 is described by four identical and completely decoupled first-order equations whose current control is easy.
4.5.2.2. Generation of current references
If we do not take the effects of dampers into account, the expression of torque [4.39] becomes:
[4.60a] ![]()
In the case of the machine with smooth poles, the expression of torque is simplified and becomes:
The former relationship [4.60a] shows that within the framework of our hypotheses, which consider the sinusoidal distribution machine, the torque in plane dqz1z2z3z4 does not depend on sequential currents (iz1, iz2, iz3 and iz4). Knowing that iz3 and iz4 correspond to homopolar currents of the machine and that each star has a non-linked neutral point, these two currents have a value of 0. Furthermore, since currents iz1 and iz2 do not contribute to the development of torque, they are set to 0:
We notice that the expression of torque for the machine in this referential is equivalent to that of the three-phase synchronous machine in Park referential. We therefore adopt the same torque control strategy as that of a three-phase machine [LOU 10b]. Thus, in the case of the machine with smooth poles, the reference current according to axis d is kept constant and equal to 0. In the most general case, by referring to the DC machine to have a torque that is directly proportional to the current according to axis q we keep the current at 0 according to axis d. We again find the expressions of reference currents in the Park referential of a three-phase machine:
4.6. Bibliography
[ABB 84] ABBAS M.A., CHRISTEN R., JAHNS T.M., “Six-phase voltage source inverter driven induction motor”, IEEE Transactions on Industry Applications, vol. 1A-20, no. 5, 1984.
[BAS 95] BASILI B., PESKINE C. “Algèbre”, in: Bibliothèque des Sciences, Diderot Editeur Paris, 1995.
[BEN 03] BENKHORIS M.F., MERABTÈNE M., MEIBODYTABAR F., DAVAT B., SEMAIL E., “Approches de modélisation de la MSDE alimentée par des onduleurs de tension en vue de la commande” Revue Internationale de Génie Electrique RS série RIGE, vol. 6, no. 5, pp 579-608, 2003.
[BEN 04] BENKHORIS M.F., Modélisation dynamique et commande des systèmes convertisseurs - machines complexes, habilitation à diriger des recherches, University of Nantes, March 2004.
[HAD 01] HADIOUCHE D., Contribution à l’étude de la machine asynchrone double étoile : modélisation, alimentation et structure, PhD thesis, Henri Poincaré university, Nancy1, December 2001.
[KET 95] KETTELER K.H., “Multisystem propulsion concept on the double star circuit”, EPE, 1995, pp.159-166, 1995.
[KHE 95] KHELOUI A., MEIBODY-TABAR F., DAVAT B., “Current commutation analysis in self-controlled double star synchronous machine taking into account saturation effect” Electric Machines and Power Systems, vol. 23, issue 5, pp. 557-569, 1995.
[KOT 96] KOTNY J.L., ROGER D., ROMARY R., “Analytical determination of the double star synchronous machine commutating reactance”, 6th International Conference on Power Electronics and Variable Speed Drives (PEVD96), IEE, pp. 306-310, 1996.
[LEO 96] LEONHARD W., Control of Electrical Drives, Springer, 1996.
[LOU 95] LOUIS J.-P., Bergmann C. “Commande numérique des machines – Evolution des commandes”, Techniques de l’Ingénieur, D3644, vol. DAB, pp. 3640-3644, 1995.
[LOU 04a] LOUIS J.-P. (ed.), Modélisation des machines électriques en vue de leur commande, Concepts généraux, Traité EGEM, Série Génie Électrique, Hermès-Lavoisier, Paris, 2004.
[LOU 04b] LOUIS J.-P. (ed.), Modèles pour la commande des actionneurs électriques, Traité EGEM, Série Génie Électrique, Hermès-Lavoisier, Paris, 2004.
[LOU 11a] LOUIS J.-P. (ed.), Control of Synchronous Motors, ISTE Ltd, London and John Wiley and Sons, New York, 2011.
[LOU 11b] LOUIS J.-P., FLIELLER, D., NGUYEN N. K., STURTZER G., “Optimal supplies and synchronous motors torque controls. Design in the d-q reference frame”, Chapter 3 in LOUIS J.-P., Control of Synchronous Motors, ISTE Ltd., London and John Wiley and Sons, New York, 2011.
[MAD 04] MADANI N., Commande à structure variable d'une machine asynchrone double étoile, alimentée par deux onduleurs MLI, modélisation dynamique, alimentation et validation expérimentale, PhD thesis, University of Nantes, Saint-Nazaire, December 2004.
[MER 05] MERABTENE M., Modélisation dynamique et commande d’une machine synchrone double étoile alimentée par des onduleurs ML. Fonctionnement en mode normal et dégradé, PhD thesis, University of Nantes, Saint-Nazaire, July 2005.
[MOU 98] MOUBAYED N., MEIBODY-TABAR F., DAVAT B., “Alimentation par des onduleurs de tension d’une machine synchrone double étoile”, Revue Internationale de Génie Electrique, vol. 1, no. 4, pp.457-470, 1998.
[MOU 99] MOUBAYED N., Alimentation par onduleurs de tension des machines multi-étoiles, PhD thesis, INP Lorraine, Nancy, 1999.
[NEL 73] NELSON R.H., KRAUSE P.C., “Induction machine analysis for arbitrary displacement between multiple winding set”, IEEE Industry Application Society, Milwaukee, USA, pp. 841-848, October 1973.
[SEM 00] SEMAIL E., Outils et méthodologie d’étude des systèmes électriques polyphasés. Généralisation de la méthode des vecteurs d’espace, PhD thesis, University of Lille, June 2000.
[SEM 11] SEMAIL E., KESTELYN X., “Modélisation vectorielle et commande de machines polyphasées à pôles lisses alimentées par onduleur de tension”, Chapter 5 in LOUIS J.-P., Commandes d’actionneurs électriques synchrones et spéciaux, Traité EGEM, Série Génie Électrique, Hermès-Lavoisier, Paris, 2011.
[SIN 02] SINGH G.K., “Multi-phase induction machine drive research-a survey”, Electric Power Systems Research, vol. 61, pp. 139-147, 2002.
[TER 99] TERRIEN F., BENKHORIS M.F., “Analysis of double star motor drives for electrical propulsion”, IEE, Elect Mach and Drives, London, pp. 90-94, September 1-3, 1999.
[TER 00] TERRIEN F., Commande d’une machine synchrone double étoile alimentée par des onduleurs MLI, modélisation, simulation et prototype expérimental, PhD thesis, University of Nantes, Saint-Nazaire, December 2000.
[VAS 94] VAS P. Vector Control of AC Machines, Clarendon Press Oxford, 1994.
[WER 84] WERREN L., “Synchronous machine with 2 three-phase windings, spatially displaced by 30°el. Commutation reactance and model for converter-performance simulation”, ICEM 84, Lausanne, Switzerland, vol. 2, pp 781-784, September 1984.
[ZHA 95] ZHAO Y., LIPO T.A., “Space vector PWM control of dual three phase induction machine using vector space decomposition”, IEEE Trans. Ind. Appl., vol. 31, no. 5, pp. 1100-1109, 1995.
1 Chapter written by Mohamed Fouad BENKHORIS.













