3Data preprocessing and model evaluation
This chapter covers the following items:
–Data preprocessing, data cleaning, data integration, data reduction and data transformation
–Attribute subset selection: normalization
–Classification of data
–Model evaluation and selection
Today, owing to their large sizes and heterogeneous sources, real-world datasets are prone to noisy, inconsistent data and missing data. For high-quality mining, it is vital that data are of high quality. Several data preprocessing techniques exist so as to enhance the quality of data, which result in mining. For example, data cleaning is applied for the removal of noise and correction of data inconsistency. Data integration unites data that come from varying sources, making them integrated into coherent store like data dataset. Normalization is an example of data transformation, which is applied to improve the efficiency and accuracy of mining algorithms that include distance measurements. Such techniques can be applied together. For example, transformation procedures are applied in data cleaning so as to correct the wrong data. For this, all entries in a field are transformed to a common format. In Chapter 2, we have gone through different types of attributes. These can also prove to be helpful to identify the wrong values and outliers. Such identification is of help for steps pertaining to data cleaning and integration. The following parts shed light on data cleaning, data integration, data reduction as well as data transformation [1–5].
In this chapter, fundamental concepts of data preprocessing are introduced (see Section 3.2). The data preprocessing methods are categorized as follows: data cleaning (Section 3.2.1), data integration (Section 3.2.3), data reduction (Section 3.5) and data transformation (Section 3.6).
This chapter presents an overall picture of data preprocessing. Section 3.1 discusses many elements that define data quality. This provides a reason behind data preprocessing. In Section 3.2, the most important tasks involved in data preprocessing are discussed.
3.1Data quality
It is considered that if data can fulfill the requirements of intended use, then it is of quality. This also refers to validity of data, enabling it to be used for intended purposes. Certain factors indicate data quality; these being accurate, consistent, complete, reliable and interpretable [6]. Accuracy refers to yielding correct attribute values. Consistency refers to the process of keeping information uniform as it progresses along a network and/ or between various applications. Consistent data do not contain discrepancies. Completeness refers to not having any lacking attribute values. Reliability refers to yielding the same results when different applications or practices are performed. Interpretability refers to how easy the data are understood. Following these brief explanations, let us, at this point, provide a real-world example: let’s say you are asked to analyze patients’ data but you have discovered that some information has not been recorded. In addition, you may notice some data having inconsistencies or reported errors for some patient characteristics. All these indicate that the data you are asked to analyze through data mining techniques are not complete, which means they do not have attribute values or certain attributes that may be of interest to you. Sometimes data may be unavailable for the access of the researcher. It can also be said that the data are noisy or inaccurate, which refers to the fact that the data have errors or may have values that deviate from the expected. Data containing discrepancies are said to be inconsistent. In theory, everything about data may seem clear-cut and organized; however, as you may see in the future or you have already experienced, real world is not as smooth as the theory suggests. For this reason, we should have the required tools in our toolbox so that we can be equipped with sorting out problems related to inconsistent, inaccurate or disorganized data [7, 8].
3.2Data preprocessing: Major steps involved
This section explains the major steps involved in data preprocessing and relevant methods for each. Major steps under discussion for data preprocessing are data cleaning, integration, data reduction and data transformation as shown in Figure 3.1.

3.2.1Data cleaning and methods
Routines involved in data cleaning literally clean the data. In order to do that, noisy data are smoothed, missing values are filled in, outliers are either identified or removed, finally inconsistencies, if there are any, are solved. If a researcher thinks that the data are dirty, he/ she knows that it is not trustworthy. In addition, another disadvantage that dirty data can cause is that it may confuse the mining procedure, which in the end results in unreliable outputs. As for the basic methods used for data cleaning, we can talk about certain steps for dealing with missing values . Reminding ourselves of the real-life example, you may need to analyze the data of multiple sclerosis (MS) patients in a clinic. You see that some magnetic resonance (MR) image processing data for some patients are missing. How can one proceed covering those missing values for this attribute (MR data)? To sort out this problem, you need to follow certain methods. The first of which is ignoring these ordered list of elements in the dataset. This is usually followed if the class label is not present. It is considered that this method is not very effective if the dataset does not contain several attributes that have missing values . This might mean adopting a pragmatic attitude, using what works and what is available. Another method involved is missing the value manually [9]. This method also has drawbacks: one of which is that it takes time and it may not be applicable if large dataset with numerous values that are missing is at stake. The third method for data cleaning is using a global constant to cover the missing value. In this method, all missing attribute values are replaced with the same constant by a label unknown This method is not complicated. It is simple, but it is with foolproof since when missing values are replaced by the label unknown, then the mining program may by mistake consider that they form an interesting concept with a value in common that is unknown. Another method we can speak of at this point is using a measure of central tendency for the attribute (e.g., the mean or median) to cover the missing value. Central tendency indicates the middle value of a data distribution. The mean can be used for normal (symmetric) data distributions, whereas median is a better choice to be employed by skewed data distribution. The fifth method is using the attribute mean or median for all samples that belong to the same class. For example, the distribution of data in the gross domestic product (GDP) per capita for the economy of U.N.I.S. (USA, New Zealand, Italy, Sweden) countries is symmetrical with a mean value of 29,936 (according to Table 2.8). This value is valued to replace the missing value for income. The last method to be used for data cleaning is to use the most likely value to fill in the missing value. This can be found out by regression, an inference-based tool using Bayesian type of formalism, or decision tree induction. This method is considered to be a popular strategy using most of the information from the present data so that the researcher can predict the values that are missing. Overall, in a good design pertaining to dataset, data entry helps to find the number of missing values, thereby minimizing errors initially while one is trying to do his/ her best to clean the data after having it seized [10–12].
3.2.2Data cleaning as a process
Missing values, inconsistencies and noise lead to inaccurate data. Data cleaning is an important and big task; hence, it is a process. The first step for the data cleaning process is discrepancy detection. Discrepancies can emerge due to several factors such as designed data entry forms that are poorly designed including many optional fields, human error in data entry, intentional errors (respondents being unwilling to give information about themselves) and data decay (outdated email address). Discrepancies may also be brought about by inconsistent use of codes and inconsistent data representations. Other sources of discrepancies involve system errors and errors in instrumentation devices recording data. Errors may occur when the data are inadequately used for intentions aside from the ones originally aimed at. For discrepancy detection, one may use any knowledge he/she has already had as to the properties of the data. This kind of knowledge is known as metadata (“data about data”). Knowledge on attributes can be of help at this stage. Ask yourself the questions: “what are the data type and domain of each attribute?” and “what are the acceptable values for each attribute?” to understand data trends and identify the anomalies. Finding the mean, median and mode values are useful, which will help you find out if the data are skewed or symmetric, what the range of values is or if all values belong to the expected range or not [13].
Field overloading [14] is another source of error that occurs when developers crowd new attribute definitions into unused (bit) portions of attributes that are already defined. The data should be examined for unique rules, consecutive rules and null rules. A unique rule suggests that all values of the given attribute have to differ from all the other values for that attribute. A consecutive rule suggests that there cannot be any missing values between the minimum and maximum values for the attribute, with all values being unique (as given in Table 2.12, the ID of the individuals). A null rule postulates the use of special characters, punctuation symbols such as blanks or other strings that show the null condition (in cases where a value for a given attribute is not available) and the way these values are to be handled. The null rule should show us to be able to indicate the procedure of recording the null condition. A number of different commercial tools exist for helping the discrepancy detection step. Relying on fuzzy matching and parsing techniques while cleaning data from various sources, data scrubbing tools utilize simple domain knowledge (knowledge of postal addresses and spell-checking) to find errors and make the required corrections in the data. Data auditing tools can also identify discrepancies by making the analysis of data to find out relationships and rules, thus data are detected violating these conditions. These are variants for data mining tools. For instance, statistical analysis can be utilized for the purpose of finding correlations or clustering for the identification of the outliers. Basic statistical data descriptions presented in Section 2.4 can also be used. In addition to these mentioned earlier, it is also possible to correct some of the data inconsistencies manually by using external references. Errors at the data entry can be corrected by carrying out a paper trace. Most errors, nevertheless, require the preference of data transformations. Once discrepancies are found, transformations are used for definition and application for the purpose of correction.
There exist some commercial tools that can be of help for the data transformation step. Data migration tools can ensure simple transformations by replacing the string gender with sex. Extraction/transformation/loading tools [15] render users to identify changes through a graphical user interface. Such tools assist only a limited set of transforms, though. For this reason, it is also possible to prefer writing custom scripts for this particular step of the data cleaning process.
There are novel approaches employed for data cleaning, and emphasis is placed for an increased sort of interactivity. Users progressively build a sequence of transformations by creating and debugging discrete transformations on a spreadsheet-like interface. The transformations can be displayed in a graphic format or through coming up with examples. Results are displayed straightaway on the records that are visible on the screen. The user can prefer undoing the transformations as well for the erasing of additional errors. The tool automatically conducts checking of discrepancies in the background on the latest transformed view of the data. Users can in this way develop and also refine transformations gradually as the discrepancies are detected. This procedure can ensure a data cleaning process to be more effective and efficient.
Developing declarative languages for the arrangement of data transformation operator is acknowledged as another approach for augmented interactivity in data cleaning. Such efforts are oriented toward the definition of powerful extensions to Structured Query Language (SQL) and algorithms that allow users to state data cleaning specifications more competently.
If one discovers further regarding the data, it is important that he/she keeps updating the metadata to reveal this knowledge, which will certainly be helpful for speeding up data cleaning for the future versions of the same data store.
3.2.3Data integration and methods
Data integration is required for the purpose of data mining. This involves the incorporation of multiple datasets, data cubes or flat files into a coherent data store. The structure of data and semantic heterogeneity pose challenges in data integration process. In some cases, we come across a situation where some attributes represent a given concept that may have different name(s) in different datasets. Such a situation would lead to inconsistency and redundancy for sure. For example, the attribute for patient names may be referred to as individual (ID) in one data store and individual (ID) in another one. The same naming inconsistency may also occur in attribute values. For instance, the same first name could be recorded as “Donald” in one dataset, “Michael” in another one and “D.” in the third. If you have a large amount of redundant data in your cases, the knowledge discovery process may be slowed down or may lead to confusion. Besides data cleaning, it is important to take steps to assist in avoiding redundancies throughout data integration [16]. Generally, data integration and data cleaning are conducted as a preprocessing step while one is preparing data for a data dataset. Further data cleaning can be carried out to find out and eliminate redundancies that could have been a result of data integration.
Entity identification problem is an issue related to data integration. For this reason, one should be particularly attentive to the structure of the data while matching attributes from one dataset to another one. Redundancy is another noteworthy issue in data integration. If you can derive an attribute from another attribute or set of attributes, such an attribute is known to be redundant. Some redundancies can be found out through correlation analysis. Based on the available data, this analysis can quantify how effectively one attribute infers the other attribute. For nominal data, the x2 (chi-square) test is administered. As for numeric attributes, the correlation coefficient and covariance are often opted for. Thus, it becomes possible to access how the value of one attribute differs from that of the other.
3.2.3.1x2 correlation test for nominal data
A correlation relationship between two attributes, A and B, can be found out by x 2 (chi-square) test for nominal data as mentioned earlier. Let’s say A has c distinct values, which are a1, a2, ..., ar. B has r distinct values, which are b1, b2, ..., br. The described datasets A and B can be presented as a contingency table, ( with c )values of A constituting the columns and r values of B constituting the rows. Ai, Bj shows the joint event ( with attribute )A assuming the ( value )ai and attribute B taking on the value bj, where A = ai, B = bj . Each possible Ai, Bj joint event has its own cell (or slot) in the table [16]. The x2 value (also referred to as the Pearson x2 statistic) is calculated in the following manner:
where oij is the observed frequency ( ()i.e., actual count of the joint event ( Ai, Bj )) and eij is the expected regularity of Ai, Bj , which is calculated as follows:
where n is the frequency observed for the dataset, count(A = ai) is the number of datasets that have the value ai for A and count (B = bj) is the number of datasets with the value bj for B. The sum in eq. (3.2) is calculated for all r × c cells. The cells that have the most contribution to the x2 value are the ones and regarding these the actual count highly differs from the one expected [17].
The hypothesis that A and B are independent is verified by the x2 statistic. This indicates that no correlation exists between them. The test is based on a significance level, which shows (r −1) × (c − 1) degrees of freedom. Example 3.1 presents the use of this statistic. If it is possible to reject the hypothesis, then it is said that A and B are statistically correlated.
Example 3.1 Correlation analyses of nominal attributes with x2 being used.
Consider that the sum of the expected frequencies in any row must be equal to the total frequency observed for that row. The sum of the expected frequencies in the columns must be equal to the total frequency observed for the column (Table 3.1).
Table 3.1: 2 × 2 contingency table for Table 2.19.

Note: Are gender and psychological_analysis correlated?
For x2 when eq. (3.1) is used,
For this 2 × 2 table, the degrees of freedom are (2 − 1) (2 − 1) = 1. For 1 degree of freedom, x2 value needed to discard the hypothesis at the 0.001 significance level is 10.828, which is obtained from the table of upper percentage points of the x2 distribution. Course books provide this distribution. As the value calculated is above this, the hypothesis that health status and gender are independent is rejected. As such, it can be concluded that both attributes have (strong) correlation for the particular group of people.
3.2.3.2x2 correlation test for numeric data
As mentioned earlier, the correlation between two attributes, A and B, can be evaluated by calculating the correlation coefficient (also referred to as Pearson’s product moment coefficient [18], named after its inventor, Karl Pearson) for numeric attributes. The formula for this calculation is
where n is the number of datasets, ai and bi are the particular values of A and B in i, Ā and B̄ are the corresponding mean values of A and B, σA and σB are the corresponding standard deviations of A and B. is the sum of the AB cross-product (i.e., for each dataset, the value of A is multiplied by the value of B in that dataset). Note that − 1 ≤ rA, B ≤ + 1. If rA, B is higher than 0, A and B have positive correlation, which means that as the values of A go up so do the values of B. The higher the value is, the stronger the correlation will be. Thus, a higher value can also suggest that A (or B) may be deleted as a redundancy.
In a case when the result value equals to 0, A and B are independent and they have no correlation that exists. In cases where the resulting value is lower than 0, A and B have negative correlation between them, and the values of one attribute go up as the values of the other attribute go down, which means that each attribute dejects the other. It is also possible to use scatter plots if one wishes to view the correlations between attributes.
3.2.3.3Covariance of numeric data
Correlation and covariance are two similar measures employed in probability theory and statistics – the evaluation of what extent two attributes alter together. Let’s say A and B are two numeric attributes. In a set of n observations {(a1, b1), ..., (an, bn)}, the mean values of A and B, in that order, are also regarded as the expected values on A and B based on formulas
and
between A and B, and the covariance is characterized as
By comparing eq. (3.3) for rA, B (correlation coefficient) with eq. (3.4) for covariance, it can be seen that
where σA and σB are the standard deviations of A and B in the relevant order. It is also possible to show that
This equation may render the calculations more simplified.
Let’s say that A and B, as two attributes, are likely to change together. We mean that if A is larger than Ā (the expected value of A), B is likely to be larger than B̄ (the expected value of B). For this reason, the covariance between A and B is said to be positive. Alternatively, if one attribute is prone to be higher than its expected value when the other attribute is below its expected value, in this case the A and B covariance is said to be negative.
In a case where A and B are independent (they are not correlated), we can say that E(A ᐧ B) = E(A) ᐧ E(B).
In such a case, the covariance is Yet, the converse does not hold either [12–14].
Some random variable (attribute) pairs may have 0 covariance but they are not independent. They are said to be independent only under some additional assumptions.
Example 3.2 (Covariance analysis of numeric attributes). Considering Table 3.2 for the economy, data analysis, tax payments and GDP per capita attributes with the disorder definition will be analyzed for four countries’ economy on which U.N.I.S. economy data were administered.
Table 3.2: Sample result for tax payments and GDP per capita as per Table 2.8.
| Tax payments | GDP percapita |
| 1 | 0.4712 |
| 1 | 0.4321 |
| 2 | 0.4212 |
| 3 | 0.3783 |
| 4 | 0.3534 |
Thus using eq. (3.6), the following is calculated:
Cov(tax payments; GDP per capita)
As a result, given the negative covariance.
Example 3.3 (Covariance analysis of numeric attributes). Considering Table 3.3 for the psychiatric analysis, three-dimensional ability and numbering attributes with the disorder definition will be analyzed for five individuals on whom WAIS-R test was administered.
Table 3.3: Sample result for three-dimensional ability and numbering as per Table 2.19.
| Individual(ID) | Three-dimensional ability | Numbering |
| 1 | 9 | 11 |
| 2 | 17 | 13 |
| 3 | 1 | 2 |
| 4 | 8 | 13 |
| 5 | 10 | 11 |
and
Thus using eq. (3.6), the following is calculated:
As a result, given the positive covariance it can be said that three-dimensional ability and numbering are the attributes concerned with the diagnosis of mental disorder.
3.3Data value conflict detection and resolution
Among data integration procedures, the detection and resolution of data value conflicts is also worthy of being mentioned. For instance, in real-world instances, attribute values that originate from different sources may vary from one another. This is because of the differences in scaling, representation or even encoding. For example, a weight attribute may be recorded in metric units in a system, and it may be recorded in another kind of unit in a different system. Education-level codification or naming or university grading systems can also differ from one country to another or even from one institution to another. For this reason, an exact course-to-grade transformation rules between two universities could be highly difficult, which makes information exchange difficult as a result. The discrepancy detection issue is described further in Section 3.2.2 [15].
In brief, a meticulous combination can be of help for the reduction and avoiding of inconsistencies and redundancies in the resulting dataset, which will in return improve both the speed and the accuracy of the following data mining process.
3.4Data smoothing and methods
Before discussing the data smoothing issue, let us focus on noisy data. Noise is defined as a random error or variance in a variable measured. Chapter 2 provided some ways as to how some basic statistical description techniques (boxplots and scatter plots) along with methods of data visualization can be utilized so as to detect outliers that might signify noise. Speaking of a numeric attribute such as age, how would it be possible to smooth out the data for the purpose of removing the noise? The answer to such question leads us to analyze data smoothing techniques as provided below.
Binning methods are used for smoothing a sorted data value by referring to its “neighborhood,” which refers to the values around it. The arranged values are distributed into a number of buckets or, in other words, bins. Binning methods perform local smoothing because the neighborhood of values is consulted. Figure 3.2 presents some of the relevant binning techniques. The data for age are first assorted, and then partitioned into equal-frequency bins of size 3. Each bin includes three values. In smoothing by bin means, one replaces each value in a bin by mean value of the bin. The mean of the values 15, 17 and 19 in bin 1 is 17. Thus, each original value in this bin is substituted by 17 as the value. Correspondingly, leveling by bin medians can be used. Each bin value is substituted by the bin median. In smoothing by bin boundaries, the lowest and highest values in a given bin are recognized as the bin boundaries [16].

Arranged data for age (WAIS-R dataset, see Table 2.19): 15, 17, 19, 22, 23, 24, 30, 30, 33.
Each bin value is substituted by the boundary value that closes. The greater the width is, the bigger the effect of smoothing is. Bins may have equal width and the interval range of values in each bin is constant. It is also known that binning is used as a discretization technique (to be discussed in Section 3.6).
There are several data smoothing methods used for data discretization which is known to be a form of data reduction and data transformation. For instance, the binning techniques diminish the number of distinct values for each attribute. These act as a procedure of data reduction for logic-based data mining methods such as decision tree induction. With this, value comparisons on arranged data are made repetitively. As a form of data discretization, we can give concept hierarchies as an example also being employed for data smoothing.
Another technique used for data smoothing is regression, which accords data values to a function. Linear regression includes spotting the “best” line to fit two attributes in order that one attribute can be utilized for the prediction of other attribute. Extrapolating linear regression in multiple linear regression, there are more than two attributes, where data are being fit into a surface that is multidimensional. Regression is described in Section 3.5.
In outlier analysis, outliers can be identified by clustering, which suggests that you organize the similar values into groups or “clusters.” Naturally, values falling outside of the group of clusters can be regarded as outliers (Figure 3.3).

3.5Data reduction
Data reduction attains a lessened representation of the dataset smaller in volume. Nevertheless, either the same or almost the same analytical results are yielded. Data reduction techniques can be implemented to obtain a reduced representation of the dataset that is smaller in volume, but one that keeps original data’s integrity. Dimensionality reduction, numerosity reduction and data compression are among the data reduction strategies [16]. In dimensionality reduction, data encoding schemes are applied in order that one can obtain a “compressed” representation of the original data. This process is a reducing process of the number of random attributes or variables at stake. Data compression techniques are wavelet transforms and principal components analysis, attribute subset selection (removing irrelevant attributes) and attribute construction (a small set of more useful attributes is obtained from the original set). Numerosity reduction techniques replace the original data volume through alternative and smaller forms of data representation. Through this strategy, alternative smaller representations replace the data. And during this process, parametric models are used. Some examples of parametric models are regression or log-linear models, or nonparametric models such as histograms, clusters, sampling or data aggregation can also be employed. It is also preferred to use a distance-based mining algorithm for analyses using nearest neighbor classifiers and neural networks [15, 16]. These methods yield more accurate results if the data to be analyzed have been normalized, or in other words, mounted to a smaller range of [0.0, 1.0]. Data compression transformations are implemented to get a reduced or “compressed” original data representation. If it is possible to reconstruct the original data from the compressed data without being subjected to information loss, then we can call such a data reduction lossless. However, if only an estimate of the original data can be reconstructed, the data reduction would be named lossy. Several lossless algorithms exist for string compression; yet they permit only limited data manipulation. Numerosity reduction and dimensionality reduction techniques can also be considered as forms of data compression. Some other ways also exist for methods of data reduction organization. The calculation time that allocated for data reduction should not be greater than or “erase” the time saved by mining on a reduced dataset size [17].
3.6Data transformation
Concept hierarchy generation and discretization can also be useful. Raw data values for attributes are substituted by ranges or higher conceptual levels [16, 17]. For instance, raw values for Expanded Disability Status Scale (EDSS) score may be substituted by higher level concepts, such as relapsing remitting multiple sclerosis (RRMS), secondary progressive multiple sclerosis (SPMS) and primary progressive multiple sclerosis (PPMS). Concept hierarchy generation and discretization are prevailing tools for data mining since they ensure data mining at multiple abstraction levels. Data discretization, normalization and concept hierarchy generation are forms of data transformation.
To recap, as we have mentioned earlier, data in the real world tend to be incomplete, inconsistent and noisy. For this reason, data preprocessing techniques help us to render us to improve data quality, which in return helps us improve the efficiency and accuracy of the mining process as the next level. Since quality decisions are to be reliant on quality data, finding out data anomalies, correcting them promptly and decreasing the data to be analyzed can contribute to significant benefits for us in decision making.
3.7Attribute subset selection
Datasets as to analysis may include a high number of attributes and some of which could be redundant or irrelevant for the mining procedure. Eliminating relevant attributes or keeping the irrelevant ones may have detrimental effects because this leads to misunderstanding for the mining algorithm used. This could bring about revealed patterns of poor quality. Moreover, a further volume with redundant or irrelevant attributes may cause a slowdown in the mining process.
Attribute subset selection [15, 16, 19] is recognized as feature subset selection in machine learning and it decreases the dataset size by removing the redundant or irrelevant attributes. Here the aim is to find a minimum set of attributes so that the resulting probability distribution of the data classes will be close to the original distribution derived by using all attributes as much as possible. Mining on a reduced set of attributes offers an extra benefit since it curtails the number of attributes that appear in the patterns discovered, which makes the patterns easier to comprehend. For n attributes, there are 2n possible subsets when one wants to find a good subset of the original attributes. A comprehensive search for the optimal subset of attributes can be costly as n and the number of data classes increases. For this very reason, heuristic methods exploring a reduced search space are generally used for the selection of attribute subset. These methods are generally known to be greedy since they always make what seems to be the best choice when looking for through attribute space. This strategy lends itself to make an optimal choice that is local for an optimal solution that is global. These greedy methods are known to be effective in real life and practice. In addition, it may be close to an estimation regarding an optimal solution.
Generally speaking, the “best” (and “worst”) attributes are identified by employing tests regarding statistical significance. This suggests that the attributes are independent of each other. Many other evaluation measures for attributes can be used. The information gain measure can be used in building decision trees for the purpose of classification. (The details of the information gain measure are provided in Chapter 6.)
There are basic heuristic methods of attribute subset selection which encompass certain techniques as described in Figure 3.4.
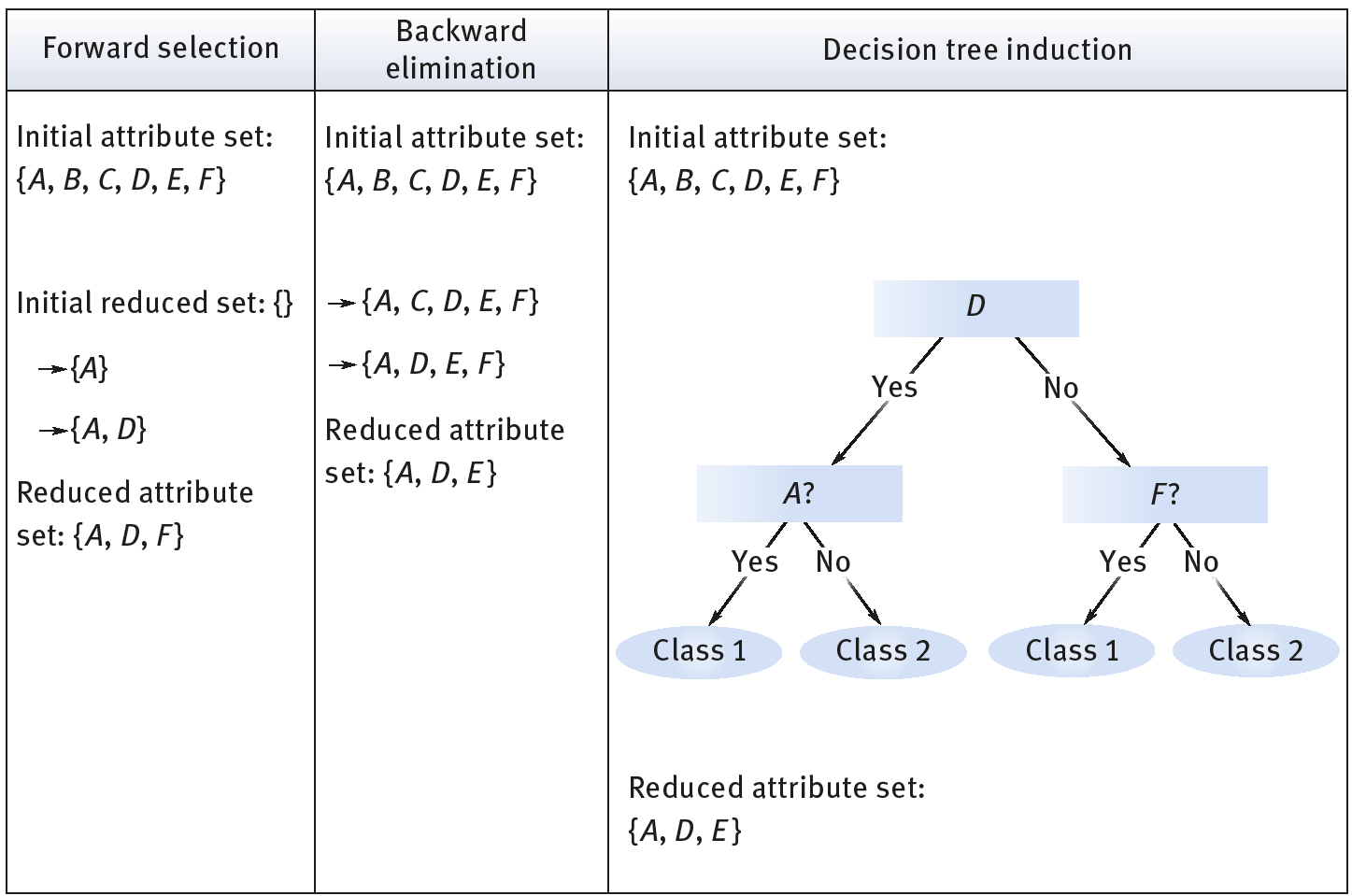
- Stepwise forward selection: The procedure begins with an empty set of attributes, which make up the reduced set. Among the original attributes, the best are determined and included in the reduced set. At each next step or iteration, the best of the original attributes that remain are added into the set.
- Stepwise backward elimination: The procedure begins with the complete set of attributes. The worst attribute remaining in the set is eliminated in each step.
- Combination of forward selection and backward elimination: It is possible to merge the methods such as the stepwise backward elimination and forward selection. In this way, the best attribute is selected by the procedure and the worst among the remaining attributes is discarded accordingly.
- Decision tree induction: Decision tree algorithms such as ID3, C4.5 and CART were originally intended for the purpose of classification. Decision tree induction forms a structure like a flowchart. Here, each internal node or nonleaf shows a test on an attribute and each branch corresponds to a test outcome and each external node or leaf represents a class prediction. The algorithm chooses the best attribute to divide the data into separate classes. A tree is formed based on the given data when decision tree induction is implemented for attribute subset selection. All attributes not seen in the tree are said to be unrelated. The set of attributes that appear in the tree constitutes the reduced subset of attributes.
Stopping criteria for the methods might change. A threshold on the measure may be used by the procedure so as to determine when the attribute selection process is to be stopped.
In some cases, new attributes based on others can be formed. Such attribute construction can be of help to increase accuracy and comprehension of structure in data. For instance, attribute marital status based on the attributes married, single and divorced may be added. Attribute construction can spot the missing information about the relationships between data attributes through combining attributes, which can be helpful for the discovery of knowledge.
Data normalization in which the attribute data are scaled to be able to fall within a smaller range could be −1.0 to 1.0, or 0.0 to 1.0.
The measurement unit that has been used can have an effect on the data analysis. The data should be normalized or standardized to avoid dependence on the choice of measurement units. In this process, transforming the data to fall within a smaller or common range such as [−1, 1] or [0.0, 1.0] is at question. If the data are normalized, this will give all attributes an equal weight. Normalization is a procedure which proves to be useful for classifying algorithms that involve neural networks or distance measurements (e.g., the nearest neighbor classification and clustering). If one uses the neural network backpropagation algorithm for classification mining (Chapter 10), normalizing the input values for each attribute measured in the training dataset will make the learning phase faster. In distance-based methods, normalization is also helpful in preventing attributes that have initially large ranges (e.g., GDP per capita) from outweighing attributes that have initially smaller ranges (e.g., binary attributes). This could help in cases when no prior knowledge of the data is available [16].
There exist several ways of data normalization. Let us assume that minA and maxA are the minimum and maximum values of an attribute, A. Min–max normalization plots a value, vi, of A to in the range [new minA, new maxA], hence, one calculates:
The relationships among the original data values are persevered by min–max normalization. It may face an “out-of-bounds” error if a future input case for normalization lies outside the original data range for A [16, 17].
Example 3.4 (Min–max normalization). Let us assume that the minimum and maximum values for the attribute deposits are $24,000 and $96,000. GDP per capita can be mapped to the range [0.0, 1.0]. By min–max normalization, a value of $51,200 for deposit is changed into
As for z-score normalization (zero-mean normalization), the values of an attribute A are normalized relying on the mean (average) and standard deviation of A. A value vi of A is normalized to by calculating
In this denotation, Ā and σA are the standard deviation and mean of attribute A, respectively. The mean and standard deviation have been discussed in Section 2.4.
and σA are computed as the square root of the variance of A (see eq. (2.8)). This normalization method proves to be of use when the actual minimum and maximum of attribute A are not known or in cases when there are outliers that dominate the min–max normalization.
Example 3.5 (z-Score normalization). Let us suppose that the mean and standard deviation of the values for the attribute income are 190 and mean (μ) of 150 and a standard deviation (σ) of 25, respectively. With z-score normalization, 190 – 150/25 = 1.6.
A variation of this z-score normalization takes the place of the standard deviation of eq. (3.9) by the mean absolute deviation of A [16, 17]. The mean absolute deviation of A, shown by sA, is
Accordingly, z-score normalization that uses the mean absolute deviation is
The mean absolute deviation, sA, is stronger to outliers than the standard deviation, σA. When you calculate the mean absolute deviation, you do not square the deviations from the mean For this very reason, the effect of outliers is reduced to some extent.
Another method for data normalization is normalization by decimal scaling. The normalization takes place by moving the decimal point of values of attribute A. Moreover, the number of decimal points that is moved is based on the maximum absolute value of A. A value, vi, of A is normalized to by doing the following calculation [16]:
