7.1.2 Algorithms for the analysis of multiple sclerosis

Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

Here, in order to calculate the conditional probability of $P (X | C l a s s) P (S w e d e n)$ $P (X | C l a s s) P (S w e d e n)$ calculations are done distinctively for the X = {x1, x2, . . . , xn} values.

\begin{array}{l} P (N e t D o m e s t i c C r e d i t = (% o f G D P) = 49, 000 | C l a s s = S w e d e n) = 1 \\ P (T a x R e v e n u e = (% o f G D P) [1, 000 - 3, 000] C l a s s = S w e d e n) = 0 \\ P (Y e a r = [2003 - 2005] | C l a s s = S w e d e n) = \frac{1}{5} \end{array}

$\begin{array}{l} P (N e t D o m e s t i c C r e d i t = (% o f G D P) = 49, 000 | C l a s s = S w e d e n) = 1 \\ P (T a x R e v e n u e = (% o f G D P) [1, 000 - 3, 000] C l a s s = S w e d e n) = 0 \\ P (Y e a r = [2003 - 2005] | C l a s s = S w e d e n) = \frac{1}{5} \end{array}$

Table 7.4: Sample Economy (U.N.I.S.) Dataset conditional probabilities.

Thus, using eq. (7.3), the following equation is obtained:

P (X | C l a s s = S w e d e n) = (\frac{2}{3}) (0) (\frac{1}{5}) = 0

$P (X | C l a s s = S w e d e n) = (\frac{2}{3}) (0) (\frac{1}{5}) = 0$

On the other hand, we have to calculate the probability of $P (C l a s s = S w e d e n) = \frac{2}{6}$ $P (C l a s s = S w e d e n) = \frac{2}{6}$ as well.

Thus,

P (X | C l a s s = S w e d e n) P (C l a s s = S w e d e n) = (0) (\frac{2}{6}) = 0

$P (X | C l a s s = S w e d e n) P (C l a s s = S w e d e n) = (0) (\frac{2}{6}) = 0$

It has been identified that an economy with the

x1 :Net Domestic Credit = 49, 000 (Current LCU),

x2 :Tax Revenue = 2, 934(% of GDP), x3 :Year = 2003 attributes has a probability result of 0 about belonging to Sweden class.

Step (8–9) Maximum posterior probability conditioned on X. According to maximum posterior probability method, $\underset{C_{i}}{\arg \max} {P (X | C_{i}) P (C_{i})}$ $\underset{C_{i}}{\arg \max} {P (X | C_{i}) P (C_{i})}$ value is calculated.

Maximum probability value is taken from the results obtained in Step (2–7).

\begin{array}{l} \underset{C_{i}}{\arg \max} {P (X | C_{i}) P (C_{i})} = \max {0.111, 0, 0, 0} = 0.111 \\ x_{i} : N e t D o m e s t i c C r e d i t (C u r r e n t ​ L C U) = 49, 000 \\ x_{2} : T a x R e v e n u e (% o f G D P) = 2, 934 \\ x_{3} : Y e a r = 2003 \end{array}

$\begin{array}{l} \underset{C_{i}}{\arg \max} {P (X | C_{i}) P (C_{i})} = \max {0.111, 0, 0, 0} = 0.111 \\ x_{i} : N e t D o m e s t i c C r e d i t (C u r r e n t L C U) = 49, 000 \\ x_{2} : T a x R e v e n u e (% o f G D P) = 2, 934 \\ x_{3} : Y e a r = 2003 \end{array}$

It has been identified that an economy has a probability of 0.111. It has been identified that an economy with the attributes given above has a probability result of 0.111 about belonging to USA class.

As a result, the data in the Economy (U.N.I.S.) with 33.33% portion allocated for the test procedure and classified as USA, New Zealand, Italy and Sweden have been classified with an accuracy rate of 41.18% based on Bayesian classifier algorithm.

7.1.2Algorithms for the analysis of multiple sclerosis

As presented in Table 2.12, multiple sclerosis dataset has data from the following groups: 76 samples belonging to RRMS, 76 samples to SPMS, 76 samples to PPMS, 76 samples belonging to healthy subjects of control group. The attributes of the control group are data regarding brain stem (MRI 1), corpus collasum periventricular (MRI 2), upper cervical (MRI 3) lesion diameter size (milimetric [mm]) in the MR image and EDSS score. Data are made up of a total of 112 attributes. It is known that using these attributes of 304 individuals the data if they belong to the MS subgroup or healthy group is known. How can we make the classification as to which MS patient belongs to which subgroup of MS, including healthy individuals and those diagnosed with MS (based on the lesion diameters (MRI 1, MRI 2, MRI 3), number of lesion size for (MRI 1, MRI 2, MRI 3) as obtained from MRI images and EDSS scores)? D matrix has a dimension of (304 × 112). This means D matrix includes the MS dataset of 304 individuals along with their 112 attributes (see Table 2.12 for the MS dataset. For the classification of D matrix through Naive Bayesian algorithm the first-step training procedure is to be employed. For the training procedure, 66.66% of the D matrix can be split for the training dataset (203 × 112) and 33.33% as the test dataset (101 × 112). For MS Dataset, we would like to develop a linear model for MS patients and healthy individuals whose data are available. Following the classification of the training dataset being trained with Naive Bayesian algorithm, we can do the classification of the test dataset.

The procedural steps of the algorithm may seem complicated initially. Yet, the only thing one will have to do is to focus on the steps and comprehend them. For this purpose, we can inquire into the steps presented in Figure 7.4.

In order to be able to do classification through Bayesian classifier algorithm, the test data has been selected randomly from the MS Dataset.

Let us now think for a while about how to classify the MS dataset provided in Table 2.12 in accordance with the steps of Bayesian classifier algorithm (Figure 7.3.)

Based Figure 7.4, let us calculate the analysis of MS Dataset according to Bayesian classifier step by step in Example 7.4.

Example 7.3 Our sample dataset (see Table 7.3 below) has been chosen from MS dataset (see Table 2.12). Let us calculate the probability as to which class (RRMS, SPMS, PPMS, Healthy) an individual (with x1 = EDSS: 6, x2 = MRI 2 2 : 4, x3 = Gender: Female on Table 7.5) will fall under Naive Bayesian classifier algorithm.

Solution 7.3 In order to calculate the probability as to which class (RRMS, SPMS, PPMS, Healthy) an individual (with the following attributes [with x1 = EDSS: 6, x2 = MRI 2: 4, x3 = Gender: Female]) attributes will belong to, let us apply the Naive Bayes algorithm in Figure 7.4.

Step (1) Let us calculate the probability of which class (RRMS, SPMS, PPMS and Healthy) the individuals with EDSS, MRI 2 and Gender attributes in MS sample dataset in Table 7.6 will belong to.

The probability of class to belong to for each attribute is calculated in Table 7.6. Classification of the individuals is labeled as C1 = RRMS, C2 = SPMS, C3 = PPMS, C4= (Healthy on Number, Gender) belonging to which class (RRMS, SPMS, PPMS, Healthy has been calculated through $P (X | C_{1}) P (C_{1}), P (X | C_{2}) P (C_{2}), P (X | C_{3}) P (C_{3}),$ $P (X | C_{1}) P (C_{1}), P (X | C_{2}) P (C_{2}), P (X | C_{3}) P (C_{3}),$ $P (X | C_{4}) P (C_{4})$ $P (X | C_{4}) P (C_{4})$ (see eq. 7.2). The steps for this probability can be found as follows:

Figure 7.4: Naive Bayesian classifier algorithm for the analysis of the MS Dataset.

Table 7.5: Selected sample from the MS Dataset.

(a) P(X|RRMS)P(RRMS) calculation of the conditional probability

Here, in order to calculate the conditional probability of $(X | C l a s s = R R M S),$ $(X | C l a s s = R R M S),$ the probability calculations are done distinctively for the $X = {x_{1}, x_{2}, ..., x_{n}}$ $X = {x_{1}, x_{2}, ..., x_{n}}$ values.

\begin{array}{l} P (E D S S = (S c o r e) 7 | C l a s s = R R M S) = \frac{1}{2} \\ P (M R I 2 = (N u m b e r) [3 - 10] | C l a s s = R R M S) = \frac{1}{2} \\ P (G e n d e r = F e m a l e | C l a s s = R R M S) = \frac{1}{2} \end{array}

$\begin{array}{l} P (E D S S = (S c o r e) 7 | C l a s s = R R M S) = \frac{1}{2} \\ P (M R I 2 = (N u m b e r) [3 - 10] | C l a s s = R R M S) = \frac{1}{2} \\ P (G e n d e r = F e m a l e | C l a s s = R R M S) = \frac{1}{2} \end{array}$

Thus, using eq. (7.3) the following result is obtained:

P (X | C l a s s = R R M S) = (\frac{1}{2}) (\frac{1}{2}) (\frac{2}{4}) = \frac{1}{8}

$P (X | C l a s s = R R M S) = (\frac{1}{2}) (\frac{1}{2}) (\frac{2}{4}) = \frac{1}{8}$

Now let us also calculate $(C l a s s = R R M S) = \frac{2}{8}$ $(C l a s s = R R M S) = \frac{2}{8}$ (probability.

Thus, following equation is obtained:

P (X | C l a s s = R R M S) P (C l a s s = R R M S) = (\frac{1}{8}) (\frac{2}{8}) ≅ 0.031

$P (X | C l a s s = R R M S) P (C l a s s = R R M S) = (\frac{1}{8}) (\frac{2}{8}) ≅ 0.031$

The probability of an individual with x1 = EDSS: 6, x2 = MRI 2: 4, x3 = Gender: Female attributes to belong to SPMS class has been obtained as approximately 0.031.

(b) P(X|SPMS)P(SPMS) calculation of conditional probability:

Here, in order to calculate the conditional probability of (X|Class = RRMS), the probability calculations are done distinctively for the X = {x1, x2, . . . , xn} values.

\begin{array}{l} P (E D S S = 7 | C l a s s = S P M S) = \frac{1}{3} \\ P (M R I 2 = (R a n g e) [3 - 10] | C l a s s = S P M S) = \frac{1}{4} \\ P (G e n d e r = F e m a l e | C l a s s = S P M S) = \frac{1}{4} \end{array}

$\begin{array}{l} P (E D S S = 7 | C l a s s = S P M S) = \frac{1}{3} \\ P (M R I 2 = (R a n g e) [3 - 10] | C l a s s = S P M S) = \frac{1}{4} \\ P (G e n d e r = F e m a l e | C l a s s = S P M S) = \frac{1}{4} \end{array}$

Thus, using eq. (7.3) following result is obtained:

P (X | C l a s s = S P M S) = (\frac{1}{3}) (\frac{1}{4}) (\frac{1}{4}) = \frac{1}{48}

$P (X | C l a s s = S P M S) = (\frac{1}{3}) (\frac{1}{4}) (\frac{1}{4}) = \frac{1}{48}$

Now let us also calculate $(C l a s s = S P M S) = \frac{3}{8}$ $(C l a s s = S P M S) = \frac{3}{8}$ probability.

Thus, following equation is obtained:

Table 7.6: Sample MS Dataset conditional probabilities.

P (X | C l a s s = S P M S) P (C l a s s = S P M S) = (\frac{1}{48}) (\frac{3}{8}) ≅ 0.002

$P (X | C l a s s = S P M S) P (C l a s s = S P M S) = (\frac{1}{48}) (\frac{3}{8}) ≅ 0.002$

The probability of an individual with the

x1 = EDSS: 6, x2 = MRI 2: 4, x3 = Gender: Female attributes to belong to SPMS class has been obtained as approximately 0.002.

(c)The conditional probability for PPMS class P(X|PPMS)P(PPMS) has been obtained as 0.

(d)The conditional probability for Healthy class P(X|Healthy)P(Healthy) has been obtained as 0.

Maximum probability value is taken from the results obtained in Step (2–7).

\begin{array}{l} \underset{C_{i}}{\arg \max} {P (X | C_{i}) P (C_{i})} = \max {0.031, 0.002, 0} = 0.031 \\ x_{1} = E D S S : 6 \\ x_{2} = M R I 2 : 4 \\ x_{3} = G e n d e r : F e m a l e \end{array}

$\begin{array}{l} \underset{C_{i}}{\arg \max} {P (X | C_{i}) P (C_{i})} = \max {0.031, 0.002, 0} = 0.031 \\ x_{1} = E D S S : 6 \\ x_{2} = M R I 2 : 4 \\ x_{3} = G e n d e r : F e m a l e \end{array}$

It has been identified that an individual (with the attributes given above) with an obtained probability result of 0.031 belongs to RRMS class.

As a result, the data in the MS Dataset with 33.33% portion allocated for the test procedure and classified as RRMS, SPMS, PPMS and Healthy have been classified with an accuracy rate of 52.95% based on Bayesian classifier algorithm.

7.1.3Naive Bayesian classifier algorithm for the analysis of mental functions

As presented in Table 2.19, the WAIS-R dataset has 200 data belonging to patient and 200 samples belonging to healthy control group. The attributes of the control group are data on School Education, Age, Gender and D.M. Data comprised a total of 21 attributes. The data on the group they belong to (patient or healthy group) is known using these attributes of 400 individuals. Given this, how would it be possible for us to make the classification as to which individual belongs to which patient or healthy individuals and ones diagnosed with WAIS-R test (based on the School Education, Age, Gender and D.M)? D matrix dimension is 400 × 21. This means D matrix consists of the WAIS-R dataset with 400 individuals as well as their 21 attributes (see Table 2.19) for the WAIS-R dataset. For the classification of D matrix through Bayesian algorithm, the first step in the training procedure is made use of 66.66% of the D matrix can be split for the training dataset (267 × 21), and 33.33% as the test dataset (133 × 21) for the training procedure.

Following the classification of the training dataset being trained with Bayesian algorithm, we classify the test dataset. As mentioned above, the steps about the procedures of the algorithm may seem complicated at first hand; however, it would be of help to concentrate on the steps and develop an understanding of them. Let us look into the steps elicited in Figure 7.5.

Although the procedural steps of the algorithm may seem complicated at first glance. The only thing you have to do is to concentrate on the steps and grasp them. For this, let us have a close look at the steps provided in Figure 7.5.

Let us do the WAIS-R Dataset analysis step by step analysis according to Bayesian classifier in Example 7.4 as based on Figure 7.5.

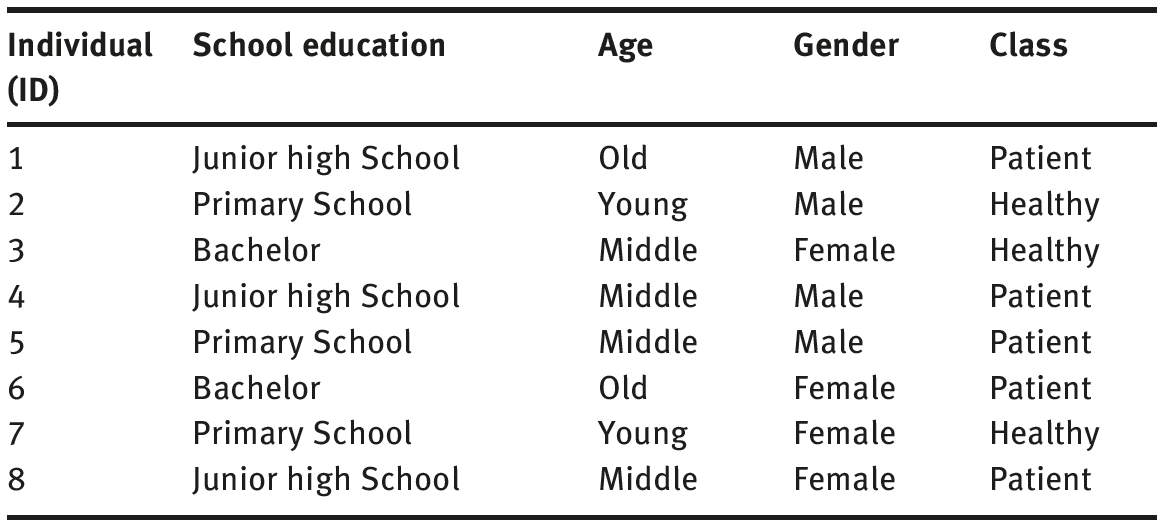
Example 7.4 Our sample dataset (see Table 7.7 below) has been chosen from WAIS-R Dataset (see Table 2.19). Let us calculate the probability as to which class (Patient, Healthy) an individual with

x1 : School education = Primary School, x2 : Age = Old, x3 : Gender = Male attributes (Table 7.7) will fall under Naive Bayes classifier algorithm.

Solution 7.4 In order to calculate the probability as to which class (Patient, Healthy) an individual with the following attributes

x1 : School Education = Primary School, x2 : Age = Old, x3 : Gender : Male will belong to, let us apply the Naive Bayes algorithm in Figure 7.5.

Step (1) Let us calculate the probability of which class (Patient, Healthy) the individuals with School education, Age, Gender attributes in WAIS-R sample dataset in Table 7.2 will belong to.

The probability of class to belong to for each attribute is calculated in Table 7.2. Classification of the individuals is labeled as C1 = Patient, C2 = Healthy. The probability for each attribute (School education, Age, Gender) belonging to which class (Patient, Healthy) has been calculated through P(x|C1)P(C1) and P(X|C2)P(C2), (see eq. 7.2). The steps for this probability can be found as follows:

Step (2–7) (a) P(X|Patient)P(Patient), (b) P (X|Healthy)P(Healthy) calculation for the probability:

(a) P(X|Patient)P(Patient) calculation of conditional probability:

Here, in order to calculate the conditional probability of (X|Class = Patient), the probability calculations are done distinctively for the X = {x1, x2, . . . , xn} values.

P (S c h o o l e d u c a t i o n = P r i m a r y S c h o o l | C l a s s = P a t i e n t) = \frac{1}{5}

$P (S c h o o l e d u c a t i o n = P r i m a r y S c h o o l | C l a s s = P a t i e n t) = \frac{1}{5}$

Table 7.7: Selected sample from the Economy Dataset.

Figure 7.5: Naïve Bayesian classifier algorithm for the WAIS-R Dataset analysis.

\begin{array}{l} P (A g e = O l d | C l a s s = P a t i e n t) = \frac{2}{5} \\ P (G e n d e r = M a l e | C l a s s = P a t i e n t) = \frac{3}{5} \end{array}

$\begin{array}{l} P (A g e = O l d | C l a s s = P a t i e n t) = \frac{2}{5} \\ P (G e n d e r = M a l e | C l a s s = P a t i e n t) = \frac{3}{5} \end{array}$

Thus, using eq. (7.3) following result is obtained:

P (X | C l a s s = P a t i e n t) = (\frac{1}{5}) (\frac{2}{5}) (\frac{3}{5}) = \frac{6}{125}

$P (X | C l a s s = P a t i e n t) = (\frac{1}{5}) (\frac{2}{5}) (\frac{3}{5}) = \frac{6}{125}$

Now, let us calculate $P (C l a s s = P a t i e n t) = \frac{5}{8}$ $P (C l a s s = P a t i e n t) = \frac{5}{8}$ probability as well.

Thus, the following result is obtained:

P (X | C l a s s = P a t i e n t) P (C l a s s = P a t i e n t) = (\frac{6}{125}) (\frac{5}{8}) ≅ 0.03

$P (X | C l a s s = P a t i e n t) P (C l a s s = P a t i e n t) = (\frac{6}{125}) (\frac{5}{8}) ≅ 0.03$

It has been identified that an individual with the

x1 : School education = Primary School, x2 : Age = Old, x3 : Gender: Male attributes has a probability result of about 0.03 belonging to Patient class.

(b) P(X|Healthy)P(Healthy) calculation of conditional probability:

Here, in order to calculate the conditional probability of (X|Class = Healthy), the probability calculations are done distinctively for the X = {x1, x2, . . . , xn} values.

\begin{array}{l} P (S c h o o l E d u c a t i o n = P r i m a r y S c h o o l | C l a s s = H e a l t h y) = \frac{2}{3} \\ P (A g e = O l d | C l a s s = H e a l t h y) = 0 \\ P (G e n d e r = M a l e | C l a s s = H e a l t h y) = \frac{1}{3} \end{array}

$\begin{array}{l} P (S c h o o l E d u c a t i o n = P r i m a r y S c h o o l | C l a s s = H e a l t h y) = \frac{2}{3} \\ P (A g e = O l d | C l a s s = H e a l t h y) = 0 \\ P (G e n d e r = M a l e | C l a s s = H e a l t h y) = \frac{1}{3} \end{array}$

Thus, using eq. (7.3) the following result is obtained:

P (X < C l a s s = H e a l t h y) = (\frac{2}{3}) (0) (\frac{1}{3}) = 0

$P (X < C l a s s = H e a l t h y) = (\frac{2}{3}) (0) (\frac{1}{3}) = 0$

Now, let us calculate $P (C l a s s = H e a l t h y) = \frac{3}{8}$ $P (C l a s s = H e a l t h y) = \frac{3}{8}$ probability as well.

Thus, the following result is obtained:

P (X | C l a s s = H e a l t h y) P (C l a s s = H e a l t h y) = (0) (\frac{3}{8}) = 0

$P (X | C l a s s = H e a l t h y) P (C l a s s = H e a l t h y) = (0) (\frac{3}{8}) = 0$

It has been identified that an individual with the

x1 : School education = Primary School, x2 : Age = Old, x3 : Gender : Male attributes has a probability result of about 0 belonging to Healthy class.

Maximum probability value is taken from the results obtained in Step (2–7).

\begin{array}{l} \underset{C_{i}}{\arg \max} {P (X | C_{i}) P (C_{i})} = \max {0.03, 0} = 0.003 \\ x_{i} : S c h o o l e d u c a t i o n = P r i m a r y S c h o o l \end{array}

$\begin{array}{l} \underset{C_{i}}{\arg \max} {P (X | C_{i}) P (C_{i})} = \max {0.03, 0} = 0.003 \\ x_{i} : S c h o o l e d u c a t i o n = P r i m a r y S c h o o l \end{array}$

\begin{array}{l} x_{2} : A g e = o l d \\ x_{3} : G e n d e r = M a l e \end{array}

$\begin{array}{l} x_{2} : A g e = o l d \\ x_{3} : G e n d e r = M a l e \end{array}$

It has been identified that an individual (with the attributes given above) with an obtained probability result of 0.03 belongs to Patient class.

How can we classify the WAIS-R Dataset in Table 2.19 in accordance with the steps of Bayesian classifier algorithm (Figure 7.5).

As a result, the data in the WAIS-R dataset with 33.33% portion allocated for the test procedure and classified as patient and healthy have been classified with an accuracy rate of 56.93% based on Bayesian classifier algorithm.

References

[1]Kelleher JD, Brian MN, D’Arcy A. Fundamentals of machine learning for predictive data analytics: Algorithms, worked examples, and case studies. USA: MIT Press, 2015.

[2]Hristea, FT. The Naïve Bayes Model for unsupervised word sense disambiguation: Aspects concerning feature selection. Berlin Heidelberg: Springer Science&Business Media, 2012.

[3]Huan L, Motoda H. Computational methods of feature selection. USA: CRC Press, 2007.

[4]Aggarwal CC, Chandan KR. Data clustering: Algorithms and applications. USA: CRC Press, 2013.

[5]Nolan D, Duncan TL. Data science in R: A case studies approach to computational reasoning and problem solving. USA: CRC Press, 2015.

[6]Han J, Kamber M, Pei J, Data mining Concepts and Techniques. USA: The Morgan Kaufmann Series in Data Management Systems, Elsevier, 2012.

[7]Kubat M. An Introduction to Machine Learning. Switzerland: Springer International Publishing, 2015.

[8]Stone LD, Streit RL, Corwin TL, Bell KL. Bayesian multiple target tracking. USA: Artech House, 2013.

[9]Tenenbaum J. B., Thomas LG. Generalization, similarity, and Bayesian inference. Behavioral and Brain Sciences, USA, 2001, 24(4), 629–640.

[10]Spiegelhalter D, Thomas A, Best N, Gilks W, BUGS 0.5: Bayesian inference using Gibbs sampling. MRC Biostatistics Unit, Institute of Public Health, Cambridge, UK, 1996, 1–59.

[11]Simovici D, Djeraba C. Mathematical Tools for Data Mining. London: Springer, 2008.

[12]Carlin BP, Thomas AL. Bayesian empirical Bayes methods for data analysis. USA: CRC Press, 2000.

[13]Hamada MS, Wilson A, Reese SC, Martz H. Bayesian Reliability. New York: Springer Science & Business Media, 2008.

[14]Carlin BP, Thomas AL. Bayesian methods for data analysis. USA: CRC Press, 2008.

[15]http://www.worldbank.org/

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 7.1.2 Algorithms for the analysis of multiple sclerosis

Create new playlist

Sign In

Sign Up

7.1.2Algorithms for the analysis of multiple sclerosis

7.1.3Naive Bayesian classifier algorithm for the analysis of mental functions

References

Table of Contents for
7.1.2 Algorithms for the analysis of multiple sclerosis