4
Regular Expression
4.1 BASICS OF REGULAR EXPRESSION
Q. What is Regular Expression?
Ans. A regular expression can be defined as a language or string accepted by a finite automata.
We know that a finite automata consists of five touples {Q, Σ, δ, q0, F}. Among them a Regular Expression is a string on Σ, i.e. it will consist only with input alphabets.
In short a Regular Expression is written as RE.
Q. Give some formal recursive definition of Regular Expression
Ans.
(i) Any terminals, i.e. the symbols belong to Σ are Regular Expression. Null string(Λ) and Null set(Φ) are also Regular Expression.
(ii) If P and Q are two Regular Expressions then the union of the two Regular Expressions denoted by P + Q is also a Regular Expression.
(iii) If P and Q are two Regular Expressions then their concatenation denoted by PQ is also a Regular Expression.
(iv) If P is a Regular Expression then the iteration (repetition or closure) denoted by P* is also a Regular Expression.
(v) If P is a Regular Expression then (P) is a Regular Expression.
(vi) The expressions got by repeated application of the rules from (i) to (v) over Σ are also Regular Expression.
Q. Describe three basic operations on Regular Expression.
Ans. Three basic operations are Union, Concatenation and closure.
Operation of union on Regular Expression: If R1 and R2 are two Regular Expression s over Σ then L(R1 ![]() R2) is denoted by L(R1 + R2).
R2) is denoted by L(R1 + R2).
L(R1 ![]() R2) is a string from R1 or a string from R2.
R2) is a string from R1 or a string from R2.
L(R1 + R2) = L(R1) ![]() L(R2).
L(R2).
Operation of Concatenation on Regular Expression: If R1 and R2 are two Regular Expression s over Σ then L(R1 ![]() R2) is denoted by L(R1R2).
R2) is denoted by L(R1R2).
L(R1 ![]() R2) is a string from R1 followed by a string from R2.
R2) is a string from R1 followed by a string from R2.
L(R1R2) = L(R1)L(R2).
Operation of Closure on Regular Expression: If R1 and R2 are two Regular Expressions over Σ then L(R*) is a string obtained by concatenating n elements for n ≥ 0.
Q. Define Kleene's Closure with example. What is the difference with Closure?
Ans.
Kleene's Closure: It is defined as a set of all strings including null (Λ) obtained from the alphabets of the set Σ. It is denoted as Σ*.
If ![]()
If Σ = {0, 1}, then Σ* = {Λ, 0, 1, 01, 00, 11, 010, 011, 100 }.
Difference
(i) Closure is nothing but iteration of 0 to ∞ times, but Kleene's Closure is set including Λ.
(ii) Closure is applied on Regular Expression, but Kleene's Closure is applied on Σ
(iii) If R = 01, then Closure on R denoted by R* are Λ, 01, 0101, 010101 ,…, etc., i.e. iteration of the same string 01.
If Σ = {0, 1} then Kleene's Closure denoted
by Σ* = {Λ, 0, 1, 01, 00, 11, 010, 011, 100,…}, i.e. set of any combinations of 0 and 1 including Λ.
Q. Describe the following REs in English language.
![]()
Ans.
(i) The strings that we get from the Regular Expression 10*1 are {11, 101, 1001, 10001,…}. From the set we can conclude that the strings that are generated from the Regular Expression s are beginning with 1 and ending with 1. In between 1 and 1 there are any numbers of 0.
So we can describe in English like this:
Set of all strings, beginning and ending with 1 with any number of 0 in between two 1.
(ii) The strings that we get from the Regular Expression a*b* are a*.b*, i.e. {Λ, a, aa, aaa,…}.{Λ, b, bb, bbb,…} = {Λ, a, b, aa, bb, ab, abb, aab,…} from the set we can conclude that the strings that are generated from the Regular Expression, contain any number of ‘a’ followed by any number of ‘b’,
so we can describe in English like this:
Set of all strings of ‘a’ and ‘b’ containing any number of ‘a’ followed by any number of ‘b’.
(iii) The strings that we get from the Regular Expression (ab)* are {Λ, ab, abab, ababab,…}.
In English it can be said as:
Set of all string of a and b with equal number of a and b containing ‘ab’ as repetition.
(iv) (a* + b*) means any combination of a or any combination of b. The c* means any combination of c, which is concatenated with (a* + b*).
In English it can be described as
Any combination of ‘a’ or any combination of ‘b’ followed by any combination of ‘c’.
(v) The strings that we get, from the Regular Expression (00)*(11)*1, are {1, 001, 111, 00111,…}. In the string there are always odd number of 1 and even number of 0.
In English it can be described as:
Set of all strings of ‘0’ and ‘1’ with even number 0 followed by odd number of 1.
Q. Construct Regular Expression from the description given below.
(i) A Regular Expression consists of any combination of a and b; beginning with a, and ending with b.
(ii) A language of any combination of a and b containing abb as a substring.
(iii) Regular Expression of a and b containing at least 2 ‘a’s.
(iv) Write Regular Expression for the language L = {anbm | where m + n is even}.
(v) A Regular Expression of a and b, having exactly one ‘a’.
Ans.
(i) The Regular Expression consists of any combination of a and b, i.e. (a + b)*. But the Regular Expression starts with a and ends with b. In between a and b any combination of a and b occurs. So the Regular Expression is
L = a(a + b)*b.
(ii) In the Regular Expression abb occurs as a substring. The R.E. consists of any combination of a and b. The substring abb may occur at the beginning, at the middle, or at the last. If abb occurs at the beginning then after abb there is any combination of a and b. If abb occurs at the middle then before and after abb there are any combination of a and b. If abb occurs at the last then before abb there is any combination of a and b.
So the Regular Expression is L = (a + b)*abb(a + b)*.
(iii) The expression consists of a and b and it contains atleast two a. There may be more than two a. So any combination of ‘a’ and ‘b’ can occur before the first ‘a’, before the second ‘a’, i.e. after the first ‘a’ and after the second ‘a’.
So the Regular Expression will be L = (a + b)*a(a + b)* a(a + b)*
(iv) The Regular Expression consists of n number of ‘a’ followed by m number of ‘b’. However, m + n is always even. This is possible if
(a) m and n both are even or (b) m and n both are odd.
If m and n are both even then the expression will be (aa)*(bb)*.
If m and n are both odd then the expression will be (aa)*a(bb)*b
By combining these two the Regular Expression will be
L = (aa)*(bb)* + (aa)*a(bb)*b.
(v) In the Regular Expression there is exactly one ‘a’. Before and after a there is any combination of b.
Hence the Regular Expression will be L = b*ab*.
Q. Mention the identities of Regular Expression.
Ans. We all know that by using two points one and only one straight line can be drawn. This statement is taken as a true and based on that the Geometry stands. This cannot be proved. This is taken as a universal truth. This type of statements is called Identities.
For Regular Expression there are also some identities.
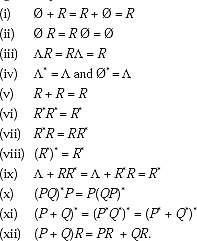
Q. From the Identities of Regular Expression prove that
(1 + 100*) + (1 + 100*)(0 + 10*)(0 + 10*)* = 10 (0 + 10*)*.
Ans. LHS
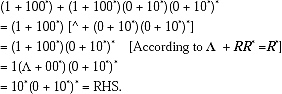
Q. From the Identities of Regular Expression prove that
![]()
Ans. Take 1*(011)* as P then the LHS becomes
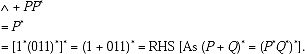
Q. From the Identities of Regular Expression prove that![]()
Ans.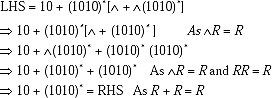
4.2 ARDEN THEOREM
Q. State and prove Arden's theorem.
Ans.
Arden's Theorem:
Statement: Let P and Q be two Regular Expression s over Σ. If P does not contain Λ, then for the equation
R = Q + RP has a unique (one and only one) solution R = QP*.
Proof:
Now point out the statements in Arden's Theorem in General form.
(i) P and Q are two Regular Expressions.
(ii) P does not contain Λ symbol.
(iii) R = Q + RP has a solution, i.e. R = QP*
(iv) This solution is the one and only one solution of the equation.
If R = QP* is a solution of the equation R = Q + RP then by putting the value of R in the equation we shall get the value ‘0’.
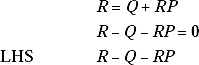
(Putting the value of R in the LHS we get)
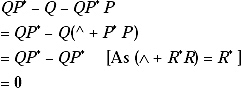
So from here it is proved that R = QP* is a solution of the equation R = Q + RP.
Now we have to prove that R = QP* is the one and only one solution of the equation R = Q + RP.
As R = Q + RP, so put the value of R again and again in the RHS of the equation.
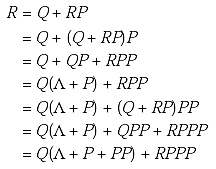
After several steps we shall get
![]()
Now let a string w belongs to R. If w is a Λ string then in which part the Λ will belong?
This string will belong to either in ![]() part or in RPn + 1 part. However, according to point number (ii) P does not contain Λ, so the string w does not belong to RPn + 1 . So it will obviously belong to
part or in RPn + 1 part. However, according to point number (ii) P does not contain Λ, so the string w does not belong to RPn + 1 . So it will obviously belong to ![]() which is nothing but QP*. [(Λ + P + P + P3 + ---- Pn ) is any combination of P including Λ].
which is nothing but QP*. [(Λ + P + P + P3 + ---- Pn ) is any combination of P including Λ].
As this string belongs only in one part so R and QP* represents the same set. That means R = QP* is the unique solution of the equation R = Q + RP.
Q. How Regular Expression can be constructed from Finite Automata by Algebraic Method using Arden's Theorem.
Ans.
There are some assumptions:
(i) In the transitional graph there will be no Λ-move.
(ii) In the Finite Automata there will be only one initial state.
For the Finite Automata given above there is no Λ-move. And it has only one initial state.
Now we have to construct equations for all the three states. There will be n number of equations if there are n-states.
For any Finite Automata these equations will be constructed in the following way.
<State Name> = Σ[<State Name from which inputs are coming>.<input>]
For the beginning state there is an arrow at the beginning coming from no state. Therefore, a Λ will be added with the equation of beginning state.
Then these equations have to be solved by the Identities of Regular Expression. The expression consists of only the input symbols of Σ, for the final state is the Regular Expression for the Finite Automata.
Q. Construct a Regular Expression from the given Finite Automata by Algebraic Method using Arden's Theorem
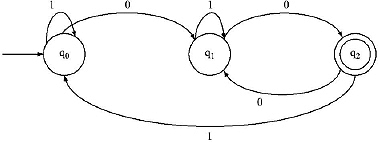
Ans.
For the above given Finite Automata the equations will be
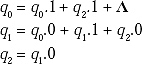
Put the value of q2 in equation no. (ii)
![]()
This equation is in the form R = Q + RP where R = q1 , Q = q0.0 and P = (1 + 0.0)
So the solution of the equation will be R = QP*, i.e. q1 = q0.0. (1 + 0.0)*
Put the value q2 = q1.0 in equation no. (i).
We will get
q0 = q0.1 + q1.0.1 + Λ
Again put the value of q1 in the above equation, we will get
![]()
This equation is in the form R = Q + RP, where R = q0, Q = Λ and P = (1 + 0.(1 + 0.0)*.0.1). So the solution of the equation:
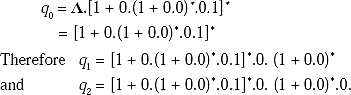
As q2 is the final state of the Finite automata so all strings will halt on this state. So the Regular Expression will be [1 + 0.(1 + 0.0)*.0.1]*.0. (1 + 0.0)*.0 accepting the Finite Automata.
Q. Construct a Regular Expression from the given Finite Automata by Algebraic Method using Arden's Theorem
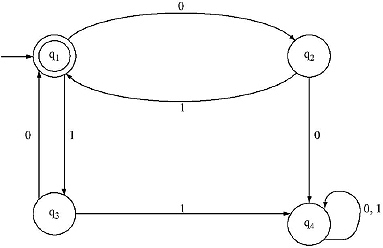
Ans.
For the above given Finite Automata the equations will be

Solution:
Substituting the value of q2 and q3 in q1 we get.
![]()
If q1 is treated as R, Λ as Q and (01 + 10) as P then the equation will become R = Q + RP
The solution for the equation will be R = QP*.
Therefore ![]()
As q1 is the only final state so the string accepted by the Finite Automata is (01 + 10)*
[We are seeing that we do not need the equation (iv), i.e. the equation for q4 in the solution process. Here equation (iv) is redundant.]
Q. Construct a Regular Expression from the given Finite Automata by Algebraic Method using Arden's Theorem
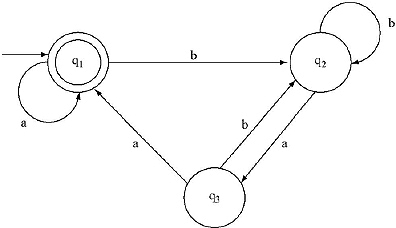
Ans. For the given Finite Automata the equations:

Solution:
q3 = q2.a, replace this in equation (ii). The equation will become
q2 = q2.b + q2a.b + q1.b,
= q2(b + a.b) + q1.b.
The equation is in the format of R = Q + RP, q2[R] = q2[R](b + a.b)[P] + q1.b [Q].
The solution will be R = QP* i.e. q2 = q1b.(b + ab)*.
Replace the value of q2 in equation (iii).
![]()
Replace the value of q3 in equation (i),
![]()
The equation is in the format of R = Q + RP, q1[R] = q1[R].[a + b.(b + ab)*.a.a][P] + Λ[Q]. The solution of the equation will be R = QP*, i.e. q1 = Λ[a + b.(b + ab)*.a.a]*,
i.e. q1 = [a + b.(b + ab)*.a.a]* [According to ΛR = RΛ = R]
q1 is the final state, so the Regular Expression accepting the Finite Automata is
[a + b.(b + ab)*.a.a]*.
4.3 CONSTRUCTION OF FINITE AUTOMATA EQUIVALENT TO A REGULAR EXPRESSION
Q. What is the process of construction of Finite Automata equivalent to a Regular Expression?
Ans. The Regular Expression is the language format of finite automata. There are two steps for making a finite automata from an Regular Expression.
Step I: From the given Regular Expression an equivalent transitional system (Finite Automata) with Λ move has to be constructed.
Step II: From the transitional system with Λ moves a DFA need to be constructed.
For constructing Step I again there are several steps.
(i) Take two states one is Beginning state and another is Final state. Make a transition from Beginning state to Final state and place the Regular Expression in between the beginning and final state.

(ii) If in the Regular Expression there is a ‘ + ’ (union) sign, then there are parallel paths between the two states.
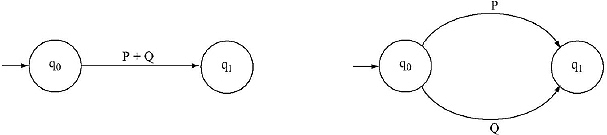
(iii) If in the Regular Expression there is a ‘.’ (dot) sign, then one extra state will be added between the two states.

(iv) If in the Regular Expression there is a ‘*’ (closure) sign, then a loop will be added to the next state putting label Λ between the two states.
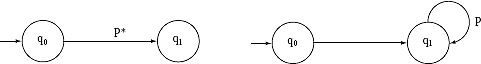
Q. Construct Finite Automata equivalent the Regular Expression.
![]()
Ans.
I. Two states are taken. One is beginning state and another is final state. The Regular Expression is placed between the two states with a transition from beginning state to final state.
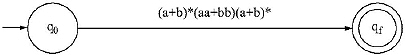
II. In the Regular Expression there are two ‘.’ (Concatenation), between (a + b)* and (aa + bb), and (aa + bb) and (a + b)*, two extra states will be added between q0 and qf .
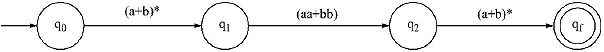
III. In aa and bb there is a ‘ + ’ (Union) sign. Therefore between q1 and q2 there will be parallel paths.
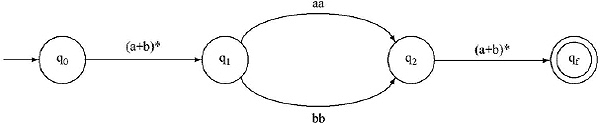
IV. There are two ‘*’ (Closure) signs between q0 and q1, and q2 and qf . So, loop with label a + b will be added to q1 and qf, making transitions between q0, q1 and q2, qf with label Λ.
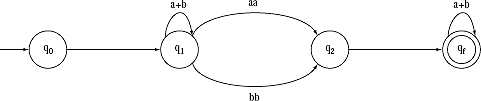
V. Removing ‘ + ’ (Union) and ‘.’(Concatenation) the final Finite Automata with Λ transitions will be.
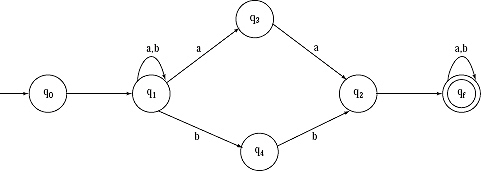
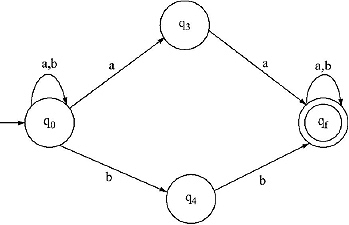
VI. Between q0, q1 and q2, qf there is a label Λ. It means from q0 by getting no input it can reach to q1, same thing is for q2 and qf. So q0 and q1 may be treated as same state, same for q2 and qf. The transitions from q1 and qf will be added with q0 and q2, respectively with same label.
By removing the Λ transactions the Finite Automata will be
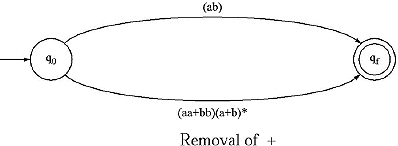
Q. Construct Finite Automata equivalent to the Regular Expression.
![]()
Ans.
I.
II.
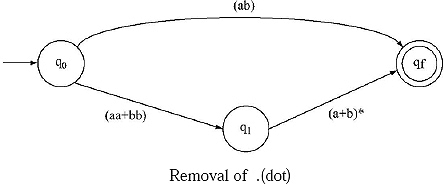
III.
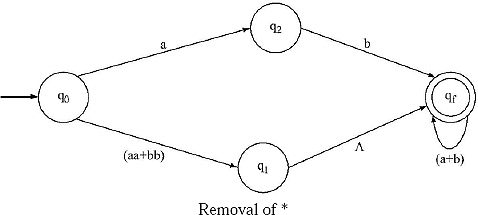
IV.
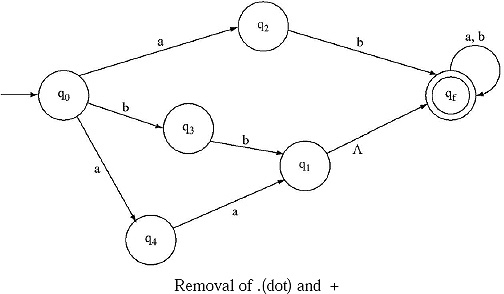
V.
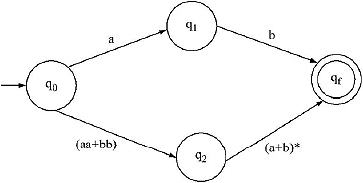
Q. Construct Finite Automata equivalent the Regular Expression.
![]()
Ans. Step I: Take a beginning state q0 and a final state qf .Between the beginning and final state place the Regular Expression.
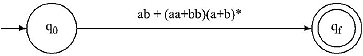
Step II: Between ab and (aa + bb)(a + b)* there is a + sign, so there will be parallel edges between q0 and qf.
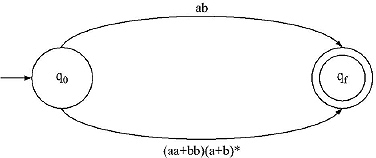
Step III: Between ‘a’ and ‘b’ there is a ‘.’ (dot), so extra state will be added. Between (aa + bb) and (a + b)* another extra state will also be added.

Step IV: In aa + bb there is a + ,so there will be parallel edges between q0 and q2 and in (a + b)* there is a*. So between q2 and qf there will be L and loop will be on qf with label (a + b).
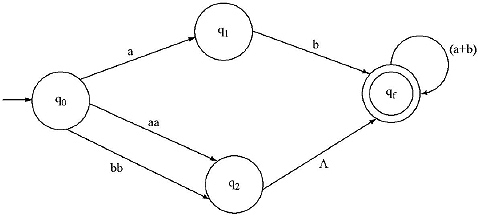
Step V: aa and bb there is .(dot). So, two extra states will be added between q0 and q2 [one for aa and another bb]. (a + b) on qf will be made loop with label a,b. Between q2 and qf there is a L, that is with no input, control can go to q2 to qf. So, q2 and qf are equivalent state. The final finite automata for the given Regular Expression will be.
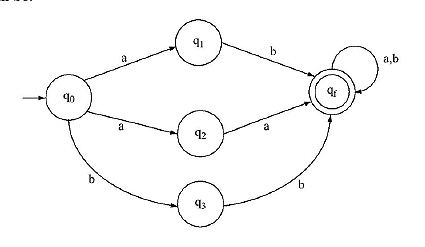
4.4 NFA WITH ![]() MOVE AND CONVERSION TO DFA BY
MOVE AND CONVERSION TO DFA BY ![]() - CLOSURE METHOD
- CLOSURE METHOD
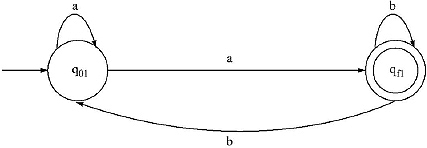
Q. What do you mean by NFA with ![]() moves? Give an example. Why is it called NFA?
moves? Give an example. Why is it called NFA?
Ans.
If any Finite Automata contains any ![]() (null) move or transaction then that Finite Automata is called NFA with
(null) move or transaction then that Finite Automata is called NFA with ![]() moves. As an example
moves. As an example
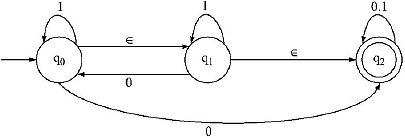
The previous Finite Automata contain two null moves. So the previous FA is NFA with null move.
From the definition of NFA we know for a NFA from a single state for a single input the machine can go to more than one state, i.e. Q X Σ → 2Q, Where 2Q is the power set of Q.
From a state by getting ![]() input the machine is confined into that state. A Finite Automata with null move must contain at least one
input the machine is confined into that state. A Finite Automata with null move must contain at least one ![]() move. For this type of Finite Automata for input
move. For this type of Finite Automata for input ![]() the machine can go to more than one state. (One is that same state and another state is the
the machine can go to more than one state. (One is that same state and another state is the ![]() - transaction next state). So a Finite Automata with
- transaction next state). So a Finite Automata with ![]() move can be called as a NFA.
move can be called as a NFA.
For the previous Finite Automata
![]()
A NFA with ![]() move can be defined as
move can be defined as
![]()
Where Σ: Set of input alphabets including ![]() . and
. and
δ is a transitional function mapping Q X Σ → 2Q 2Q is the power set of Q.
Q. Define ![]() closure. Clarify it by a suitable example.
closure. Clarify it by a suitable example.
Ans. ![]() - closure of a state is defined as the set of all states S, such that it can reach from that state to all the states in S with input
- closure of a state is defined as the set of all states S, such that it can reach from that state to all the states in S with input ![]() (i.e. with no input).
(i.e. with no input).
Example: Consider the following NFA with ![]() moves.
moves.
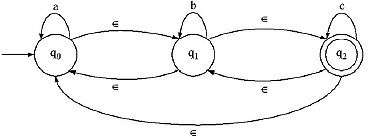
From state q0 by input ![]() (i.e. with no input) we can reach to state q1 and q2. With no input we can reach to the same state, i.e. q0. Therefore, we can write
(i.e. with no input) we can reach to state q1 and q2. With no input we can reach to the same state, i.e. q0. Therefore, we can write
![]() -closure (qo) = {q0 q1 q2}
-closure (qo) = {q0 q1 q2}
Same like ![]() -closure(q1) = {q0, q1, q2}
-closure(q1) = {q0, q1, q2}
![]() -closure (q2) = {q0, q1, q2} (From q1 with no input we can reach to q0, from q2 with no input we can reach to q1, so from q2 with no input we can reach to q0)
-closure (q2) = {q0, q1, q2} (From q1 with no input we can reach to q0, from q2 with no input we can reach to q1, so from q2 with no input we can reach to q0)
Q. How to convert a NFA with ![]() move to a DFA?
move to a DFA?
Ans. Step I: Find ![]() -closure of all the states.
-closure of all the states.
Step II: Construct transitional function δ' for the beginning state for all inputs. The function δ'; will be calculated like the following
![]()
Let ![]() -closure(A) = {q1, q2, q3} = Q, Therefore the previous equation will become
-closure(A) = {q1, q2, q3} = Q, Therefore the previous equation will become
![]()
Step III: First find ![]() -closure of the initial state. Rename the set of states as a new state. Then find function δ' of that state for all inputs. If δ' of that state for all inputs is constructed then it is called that the state is marked (Fully Traversed for all the inputs). If any new combinations of state, other than the marked state appear in the process of marking then rename that as a new state.
-closure of the initial state. Rename the set of states as a new state. Then find function δ' of that state for all inputs. If δ' of that state for all inputs is constructed then it is called that the state is marked (Fully Traversed for all the inputs). If any new combinations of state, other than the marked state appear in the process of marking then rename that as a new state.
Step IV: Repeat step III for all new unmarked states. If no the new state appears, then stop construction.
Step V: In this process the states which contain final state as entry are final state of the constructed new DFA.
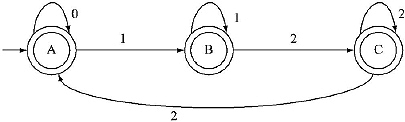
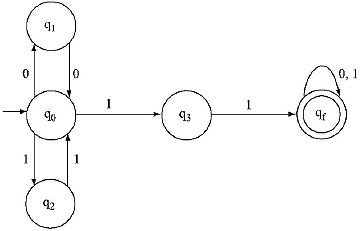
Q. Convert the following NFA with ![]() -move to an equivalent DFA.
-move to an equivalent DFA.

Ans.
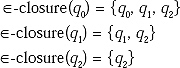
![]() -closure(q0) = {q0, ql, q2}. Let rename this state as A. Then construct δ' function for the new unmarked state A for input 0, 1 and 2.
-closure(q0) = {q0, ql, q2}. Let rename this state as A. Then construct δ' function for the new unmarked state A for input 0, 1 and 2.

As it is new combination of state other than A so rename it as B.
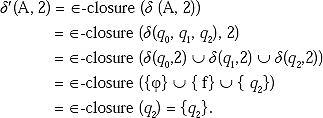
As it is new combination of state other than A and B so rename it as C.
As δ' is constructed for all inputs on A so A is marked.
B is till unmarked.
Then construct δ' function for the new unmarked state B for input 0, 1 and 2.

As δ' is constructed for all inputs on B so B is marked.
C is till unmarked.
Then construct δ' function for the new unmarked state C for input 0, 1 and 2.

As A, B and C all contain q2, which is final state, so A, B, C all are final states.
The equivalent DFA
Q. Convert the following NFA with ![]() - move to an equivalent DFA.
- move to an equivalent DFA.
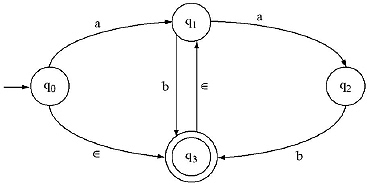
Ans.
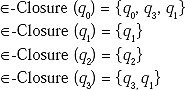
![]() -closure(q0) = {q0, q1, q3}. Lets rename this state as A. Then construct δ' function for the new unmarked state A for input ‘ a and ‘ b'.
-closure(q0) = {q0, q1, q3}. Lets rename this state as A. Then construct δ' function for the new unmarked state A for input ‘ a and ‘ b'.
Then construct δ function for the new unmarked state A for input ‘a’ and ‘b’.
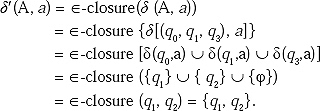
As it is new combination of state other than A so rename it as B.
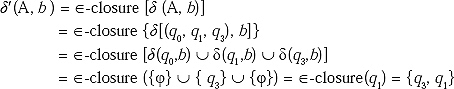
As it is new combination of state other than A and B so rename it as C.
As δ' is constructed for all inputs on A so A is marked.
B is till unmarked.
Then construct δ' function for the new unmarked state B for input ‘a’ and ‘b’.
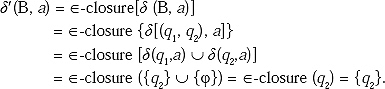
As it is a new combination of state other than A, B and C so rename it as D.
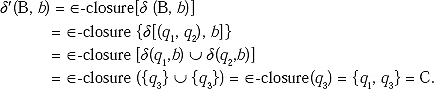
As δ' is constructed for all inputs on B so B is marked.
C is till unmarked.
Then construct δ' function for the new unmarked state C for input ‘a’ and ‘b’.

As δ' is constructed for all inputs on C so C is marked.
The D is still unmarked.
Then construct δ' function for the new unmarked state D for input ‘a’ and ‘b'.

As the state C contains q3 so it is final state.
The equivalent DFA is
4.5 EQUIVALENCE OF TWO FINITE AUTOMATA AND TWO REGULAR EXPRESSIONS
Q. What are the steps to declare two Finite Automata equivalents?
Ans. Let there are two Finite Automata M and M' where number of input symbols are the same.
(i) Make a comparison table with n + 1 columns, where n is the number of input symbols.
(ii) In the first column there will be pair of vertices (q, q') where q ![]() M and q'
M and q' ![]() M'. The first pair of vertices will be the initial states of the two machines M and M'. Second column consists of (qa, qa'). Where qa is reachable from the initial state of the machine M for the first input, and q'a is reachable from the initial state of the machine M' for the first input. The other n–2 columns consist of pair of vertices from M and M' for n–1 inputs, where n = 2, 3,…n–1.
M'. The first pair of vertices will be the initial states of the two machines M and M'. Second column consists of (qa, qa'). Where qa is reachable from the initial state of the machine M for the first input, and q'a is reachable from the initial state of the machine M' for the first input. The other n–2 columns consist of pair of vertices from M and M' for n–1 inputs, where n = 2, 3,…n–1.
(iii) If any new pair of States appears in any of the n―1 next state columns, which were not taken in the First column; take that pair in the present state column and construct subsequent column elements like the first row.
(iv) If a pair of states (q, q') appear in any of the n columns for a pair of states in the present state column, where q is the final state of M and q is the non-final state of M' or vice versa, terminate the construction and conclude that M and M' are not equivalent.
(v) If no new pair of states appears, which were not taken in the First Column and step (iv) does not hold stop construction and declare M and M' are equivalent.
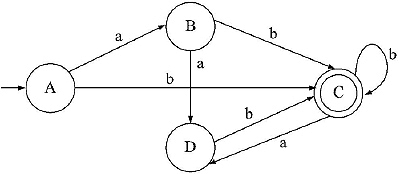
Q. Find whether the two DFAs are equivalent or not.
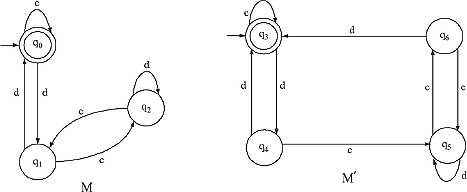
Ans.
In the previous two DFAs number of input is two, c and d. Therefore in the comparison table there will be three columns. The beginning state pair is (q0, q3). From there for input c we are getting (q0, q3) and for input d we are getting (q1, q4). Among them (q1, q4) is the new combination of states which has not appeared yet in the present state column. Hence take it in the present state column and construct next state pairs for input c and d.

After the fourth step no new state combinations have appeared. Hence further construction is stopped. In the whole table no such type of combination of states appears where one state is Final state of one machine and other is the non-final state of another machine.
Therefore, two DFAs are equivalent.
Q. Find whether the two DFAs are equivalent or not.
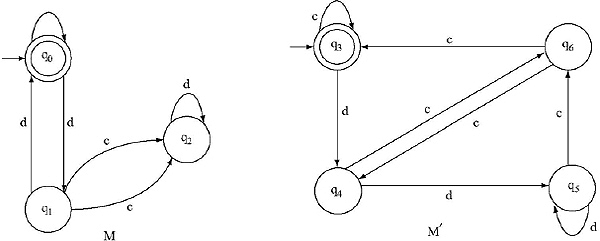
In the previous two DFAs number of input is two c and d. Hence in the comparison table there will be three columns. The beginning state pair is (q0, q3).

(q0, q5) is a combination of states where q0 is the Final state of the machine M and q5 is the Non-Final state of the machine M'. Hence we shall stop construction declaring two machines are not equivalent.
Q. How will you prove that two Regular Expressions are equivalent?
Ans. For every Regular Expression there is an accepting Finite Automata. If the finite automata constructed from both of the Regular Expressions are same, then we can say that two Regular Expressions are equivalent.
Q. Prove that the following Regular Expressions are Equivalent.
L1 = (a + b)* L2 = a*(b*a)*
Ans.The Finite Automata for L1 is
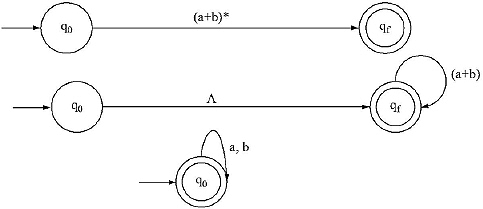
Finite Automata for L2 is
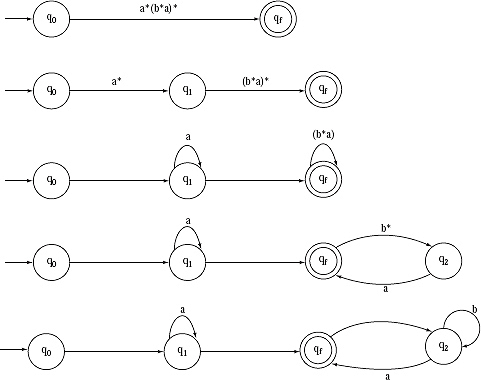
We are seeing the Finite Automata Generated by two Regular Expressions, L1 and L2 are same. Hence we can decide that the two Finite Automata are Equivalent.
4.6 CONSTRUCTION OF REGULAR GRAMMAR FROM A REGULAR EXPRESSION
Q. What is the process of generating a Regular Grammar from a Regular Expression?
Ans. From a Regular Expression the Regular grammar for the Regular Expression can be made.
Step I: Construct the equivalent FA for the given Regular Expression (Eliminate all null moves).
Step II: Number of Non-terminals of the grammar will be equal to the number of states of the FA.
Step III: For all transitional functions in the form ![]() the production rules will be in the form A→aA1. If Q2 is a final state then for the transitional function δ(Q1,a>→Q2 the production rules will be A→aA1 and A→a. The start symbol will be the symbol representing the initial state of the FA.
the production rules will be in the form A→aA1. If Q2 is a final state then for the transitional function δ(Q1,a>→Q2 the production rules will be A→aA1 and A→a. The start symbol will be the symbol representing the initial state of the FA.
Q. Construct Regular Grammar for the Regular Expressions.
(i) a*(a + b)b*
(ii) ab(a + b)*
(iii) 10 + (0 + 11)0*1
Ans.
(i) The Deterministic Finite Automata for the string a*(a + b)b* is?
Number of states of the Finite Automata is 2. Hence there will be two non-terminals in the Grammar for the Regular Expression. Lets consider them as A [For q0] and B [For q1].
For the transitional function δ(q0,a)→q0 the production rule will be A → aA. For the transitional function δ(q0, a) → ql the production rule will be A → aB. As ql is a final state so there will be another production rule A → a
δ(q0, b) → q1 : A → bB and A → b (As q1 is a final state),
δ(q1, a) → q1 : B → aB and B → a (As q1 is a final state),
δ(q1, b) → q1 : B → bB and B → b (As q1 is a final state).
Start symbol will be A as q0 is the beginning state.
The grammar G for the Regular Expression a*(a + b)b* { VN, Σ, P, S} where
VN = {A,B},
Σ = {a,b},
P: {A → aA/ bB/a/b, B → aB/bB/a/b},
S: {A},
(ii) The DFA for the string ab(a + b)* is
There are three states in the DFA. Number of Non-terminals for the Grammar of the Regular Expression will be 3. Let take them as A (For q0), B(For q1) and C (For q2).
For the transitional function δ(q0, a) → ql the production rule will be A → aB
δ(q1, b) → q2:B → bC and B → b[As q2 is final state],
δ(q2, a) → q2 : C → aC and C → a [As q21 is final state],
δ(q2, b) → q2 : C → bC and C → b [As q21 is final state].
Start symbol will be A as q0 is the beginning state.
The grammar G for the Regular Expression ab(a + b)* is {VN, Σ, P, s}, where
VN = {A, B, C},
Σ = {a, b},
P: {A → aB, B → bC/b, C → aC/ bC/ a/ b},
S: {A}.
(iii) The NFA without null move for the Regular Expression 10 + (0 + 11)0*1 is
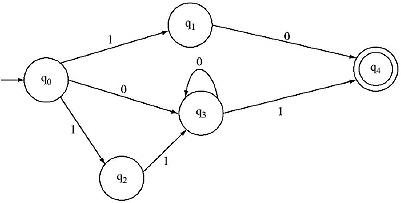
The equivalent DFA for the above NFA will is
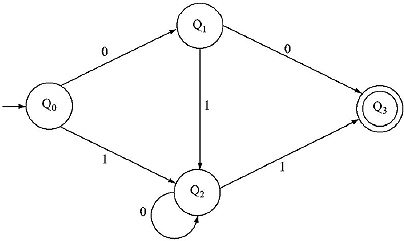
There are four states of the DFA for the Regular Expression 10 + (0 + 11)0*1. Hence for the Grammar of the Regular Expression there will be four non-terminals. Lets consider them as A [For Q0], B [For Q1], C [For Q2] and D [For Q3].
Now we have to construct the Production rules of the Grammar.
For the transitional function S(Q0, 0) → Qì , the production rule will be A → 0B
Same like.
δ(Q0, 1) → Q2, the production rule will be A → 1C,
δ(QV 0) → Q3 the production rule will be B → 0D and B → 0 (As Q3 is final state), S(Q1, 1) → Q2, the production rule will be B → 1C, S(Q2, 0) → Q2, the production rule will be C → 0C,
δ(Q2, 1) → Q3, the production rule will be C → 1D and C → 1 (As Q3 is final state). Start symbol will be A as Q0 is the beginning state.
The grammar G for the Regular Expression 10 + (0 + 11)0*1 is {VN, Σ, P, S}, where
VN = {A,B,C,D},
Σ ={0,1},
P: {A → 0B/ 1C, B → 0D/ 1C/ 0 , C → 0C/ 1D/ 1},
S: {A}.
(N.B. From NFA without ![]() move the Regular Grammar can not be constructed. We can do this by constructing the equivalent DFA)
move the Regular Grammar can not be constructed. We can do this by constructing the equivalent DFA)
Q. Define Left-Linear and Right-Linear Grammar. What is the relation between these two forms of grammar? Describe with an example.
Left-Linear Grammar: In a grammar if all productions are in the form A → Bα or A → α then that grammar is called left-linear grammar. Here A and B are non-terminals and α is a string of terminals.
Right-Linear Grammar: In a grammar if all productions are in the form A → αB or A → α then that grammar is called right-linear grammar. Here A and B are non-terminals and α is a string of terminals.
Left-Linear grammar is the reverse of Right-Linear grammar and vice versa. Let there is a regular grammar A → aA/ bB/ b, B → aB/ bB/ a/ b. The grammar is Right-Linear Grammar. The Left-Linear form of the grammar is the reverse of Right-Linear Form.
A → Aa/ Bb/ b, B → Ba/ Bb/ a/b.
4.7 PUMPING LEMMA AND ITS APPLICATION
Q. What is Pumping Lemma for Regular Expression? What is the application of it?
Ans. There is a necessary condition for an input string to belong to a Regular set. This necessary condition is the Pumping Lemma. Pumping means generating. This lemma is called Pumping Lemma because it gives a method of generating many input strings from a given string.
As Pumping lemma is a necessary condition for a string belongs to a Regular set, it is used to prove that certain sets are not regular. If any set fulfills all the conditions of Pumping Lemma it cannot be said confirm that the set is regular.
But the reverse is true, i.e. if any set breaks the conditions of Pumping Lemma it can be said confirm that the set is not regular. So Pumping Lemma is used to prove that certain sets are not regular.
Q. State and prove Pumping Lemma for Regular Expression.
Ans. Pumping Lemma: Let M = {Q, Σ, δ, q0, F} is a Finite Automata with n number of states. Let L is a Regular Set accepted by M. Let w is a string belongs to the set L and w|≥ m. If m≥ n, i.e. length of the string is greater than or equal to the number of states, then there exists x, y, z such that w = xyz, where|xy| ≤ n,|y| > 0 and xyiz ![]() L for each i ≥ 0.
L for each i ≥ 0.
[It needs some clarification, after we shall go to the proof section of it.
Lets consider the following Finite Automata. Here from q0 by getting a it goes to q1 and from q1 by getting b it goes to q2, which is the Final state. The Finite Automata consists of three states, q0, q1, q2. The string that is accepted by the Finite Automata is ba. Length of the string is 2 which is less than the number of states of the Finite Automata.

Here from a state by getting a single input it goes to a single distinct state. But if the length of the string is equal or greater than the number of states of the Finite Automata, then from a state by getting single input it is not possible to get all single distinct states. There must be repetition of at least a single state. This can be described by the following diagrams.
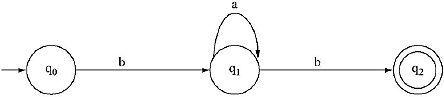
The Regular Expression accepted by the Automata is ba*b. The expression can be divided into three parts x, y, z where y is the looping portion, x is the portion before looping and z is the portion after the looping portion.]
Proof:
Let w be a string of length m, where m is greater that n, the number of state of the finite automata accepting the string w.
![]()
Starting from the beginning state q0, by getting the string w as input the machine will go to the final state.
In general
![]()

The set of the states followed by the string w in the transitional path from beginning state to final state are Qn = {q0, q1, q2…qm}. Number of states in the set is m.
But number of states of the Finite Automata accepting the string w is n. As m ≥n so at least two states in the set Qn must coincide.
Take two integers j and k, where 0 ≤ j< k ≤ n. Among the various pairs of repeated states, take a pair qj, qk. The string w can be decomposed into three substrings a1a2…… aj, aj+1……1 ak and akak+1…… am Lets denote them as x, y, and z, respectively. As k≤ n so length of the string a1…ak is ≤ n, i.e. |xy| ≤ n and w = xyz.

The automaton starts from the initial state q0. On applying the string x it reaches to the state qj. On applying the string y it comes back to qj as qj = qk. So on applying the string y, i number of times (where i≤ >0) on qj, it will be in the same state qj. On applying z on qj the automaton will reach to the final state. Hence the string xyizwith i≥ 0 belongs to the language set L, i.e. xyiz![]() L.
L.
Q. How Pumping Lemma can be applied to prove that certain sets are not regular?
Ans. Pumping lemma is used to prove that certain sets are not regular. This needs certain steps.
Step I: Assume the set L is regular. Let n be the number of states of the finite automata accepting L.
Step II: Choose a string w (wЄ L) such that | w| ≥ n. By using pumping lemma we can write w = xyz, with |xy| ≤ n and |y| > 0.
Step III: Find a suitable integer i such that xyiz ∉ L. This will contradict our assumption. From here L will be declared as not regular.
Q. Show that L = {ai2 |i ≥ 1} is not regular.
Ans.
Step I: Assume the set L is regular. Let n be the number of states of the finite automata accepting the set L.
Step II: Let w = an2. |w| = nw2 which is greater than n, the number of states of the finite automata accepting L. By using pumping lemma, we can write w = xyz with |xy| < n and |y| > 0.
Step III: Take i = 2. Hence the string will become xy2z.
![]()
From step II we know |w| = |xyz| = |x| + |y| + |z| = n2.
So |xy2Z| > n2
Again |xy2z|= |x| + 2|y + |z| = |x| + |y| + |z| + |y| = n2 + |y|
As |xyj| ≤ n so, |y| ≤ n
Therefore xy2z| ≤ n2 + n
From the previous derivations we can write
![]()
Hence |xy2z| lies between n2 and (n + 1)2. They are square of two consecutive positive integers. In between square of two consecutive positive integers no square of positive integer belongs. But ai2 where i ≥ 1 is a perfect square of an integer. Hence the string derived from it, i.e. |xy2z| is also a square of an integer, which lies between square of two consecutive positive integers. This is not possible.
So xy2z ∉ L. This is a contradiction.
So, L={ai2 |i ≥ 1} is not regular.
Q. Show that L = {ap|p is prime} is not regular.
Ans.
Step I: Assume the set L is regular. Let n be the number of states in the finite automaton accepting L.
Step II: Let p is a prime number which is greater than n. Let the string w = ap, w ∉ L. By using Pumping lemma we can write w = xyz with |xy| ≤ n and |y| > 0. As the string w consists of only 'a so x, y, and z are also string of ‘a’s. Let y = am for some m with 1 ≤ m ≤ n.
Step III: Let take i = p + 1. |xy1z| will be |xyz| + |yi-1|
![]()
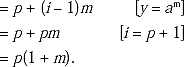
p(1 + m) is not a prime number as it has factors p and (1 + m) including 1 and p(1 + m). Hence, xyiz ∉ L. This is a contradiction.
Therefore L = {ap | p is prime} is not regular.
Q. Show that L={an3 | i ≥ 1} is not regular.
Ans.
Step I: Assume the set L is regular. Let n be the number of states of the finite automata accepting the set L.
Step II: Let L = an3. The |w| = n3 which is greater than n, the number of states of the finite automata accepting L. By using pumping lemma, we can write w = xyz with |xy| ≤ n and |y| > 0.
Step III: Consider i = 3. Therefore the string will become xy3z.
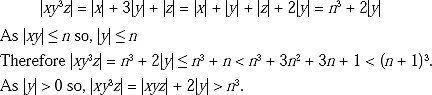
We can write
n3 < |xy3z| < (n + 1)3
xy3z is a perfect cube which lies between n3 and (n + 1)3, i.e. two consecutive perfect cube numbers. In between cube of two consecutive positive integers no cube of positive integer belongs. But ai3 where i≥ 1 is a perfect cube of an integer. Hence the string derived from it, i.e. xy3z is also a cube of an integer, which lies between cube of two consecutive positive integers. This is not possible. Therefore xy3z ∉ L. This is a contradiction. So, L={ai3 |i ≥ 1} is not regular.
Q. Show that L={anbn where n ≥ 1} is not regular.
Ans.
Step I: Suppose the set L is regular. Let n be the number of states of the finite automata accepting L.
Step II: Let w = anbn, |w| = 2n > n. By pumping lemma we can write w = xyz with |xy| ≤ n and |y> 0.
Step III: We want to find a suitable i so that xyiz ∉ L . The string y can be of any of the following:
(i) y is a string of only ‘a’, i.e. y = ak for some k ≥ 1
(ii) y is a string of only ‘b’, i.e. y = bk for some k ≥ 1
(iii) y is a string of both ‘a’, and ‘b’, i.e. y = akb1 for some k, l ≥ 1
For Case (i) ![]()
![]()
For Case (ii) ![]()
![]()
For Case (iii) ![]()
![]()
an-kak b1 ak b1 bn-k = anb1akbn, which is not in the form anbn. So xy2z ∉ L
For all the three cases we are getting contradiction. Therefore L is not regular.
Q. Show that L = palindrome over {a,b} is not regular.
Ans.
Step I: Suppose the set L is regular. Let n be the number of states of the finite automata accepting L.
Step II: Let w = anban, |w| = (2n + 1) > n. By pumping lemma we can write w = xyz with |xy| ≤ n and |y| > 0.
Step III: We want to find a suitable i so that xyiz ∉ L. The string y may consists of only ‘a’ let aj where j > 0. Let take i = 0. xyz = anban = an-jaj ban. Therefore xy0z = an-Jban.
As j > 0, n - j ≠ n. So an-jban; is not a palindrome.
So xy0z ≠ L. Hence it is proved that L is not Regular.
Q. Show that L = { ww, where w ∈ (a,b)*} is not regular Ans.
Step I: Let consider the set L is regular. Let n be the number of states of the finite automata accepting L.
Step II: Let ww = anbanb ∉ L, so |ww| = 2(n + 1) > n. By applying pumping lemma we can write w = xyz with |xy| ≤ n and |y| > 0.
Step III: We want to find a suitable i so that xyiz ∉ L. The string consist of ‘a’ and ‘b’. Therefore y can be of any of these
(i) y has no ‘b’, i.e. y = ak.
(ii) y has only one ‘ b' (because the string is anbanb).
Let take i = 0 in case I. If i = 0, then xy0z = xz and it is in the form an-kbanb or anban-kb.
This is not in the form ww, i.e. xz ∉ L. Hence L is not regular.
In case II, if we take i = 0 then xy0z = xz which contain only one ‘b’. Which is not in the form ww, i.e. xz ∉ L. Hence L is not regular.
Q. Show that L = {anban, where n ≥ 1} is not regular.
Ans.
Step I: Assume that L is regular. Let n be the number of states of the finite automata accepting L.
Step II: Let w = anban. Hence |w| = 2n + 1 > n. According to pumping lemma we can write w = xyz, with w = xyz with |xy| ≤ n and |y| > 0.
Step III: We want to find a suitable i so that xyiz ∉ L. The string consist of ‘a’ and ‘b’. So y can be of any of these:
(i) y has no ‘b’, i.e. y = ak
(ii) y has only one ‘b’ [because the string is anban]
For Case I take i = 2.
The string xyz = an-k akban or anbakan-k
Therefore, xy2z=an-ka2kban=an + kban or anba2kan-k=anban + k.
As k ≠ 0, (n + k) ≠ n. Therefore xy2z ∉ L.
This is a contradiction so L is not regular.
For Case II let take i = k. So xykz = anbkan. This is not in the form anban. Therefore xykz ∉ L.
This is a contradiction so L is not regular.
Q. Show that L = {anbnabn+1} is not regular.
Ans.
Step I: Assume that L is regular. Let n be the number of states of the finite automata accepting L.
Step II: Let w = anbnabn+1, so |w| = (3n + 2) > n. By using pumping lemma we can write w = xyz, with w = xyz with |xy| ≤ n and |y| > 0.
Step III: We want to find a suitable i so that xyiz ∉ L. The string consist of ‘a’ and ‘ b’. Hence y can be of any of these
(a) y contain only ‘a’, let y = ak.
(b) y contain only ‘b’, let y = b1
(c) y contain ‘a’ and ‘b’ both, let y = bka.
For case I, take i = 0.
w = xyz = (an-k )(ak )(bnabn+1)
xy°z = an-k bnabn+1 which is not in the form anbnabn+1.
For case II take i = 0
w = xyz = (an-k)knbnabn+1
xy0z = anbn-1 abn+1 which is not in the form anbnabn+1.
For case III, take i = 2
w = xyz = anbn-k(bka)2 bn+1
= anbna bkabn+1, which is not in the form anbnabn+1.
In all the three cases there are contradiction, hence the language is not regular.
Q. Show that the language containing the set of all balanced parenthesis is not regular.
Ans.
Step I: Assume that L is regular. Let n be the number of states of the finite automata accepting L.
Step II: Let w = (((….()….))) = (n)n . |w| = 2n > n. By using pumping lemma we can write w = xyz, with w = xyz with |xy| ≤ n and |y| > 0.
Step III: We want to find a suitable i so that xyiz ∉ L. The string consists of ‘(’ and ‘)’. So y can be of any of these
(a) y consists of only ‘(’ let y = (k
(b) y consists of only ‘)’, let y = )k
(c) y consists of both ‘(’ and ‘)’, let y = (k)k
For case I, take i =0.
w = xyz = (n-k ( k)n
xy0z = (n-k)n which is not set of all balanced parenthesis.
For case II, take i = 0.
w = xyz = (n ) k)n-k
xy0z = (n)n-k which is not set of all balanced parenthesis.
For case III, take i = 2.
w = xyz = (n-k(k)k)n-k
xy2z = (n)k(k)n which is not set of all balanced parenthesis.
In all the three cases there are contradiction, hence the language is not regular.
Regular Expression
Q. Show that L = {0n12n, where n > 1 } is not regular.
Ans
Step I: Assume that L is regular. Let n be the number of states of the finite automata accepting L.
Step II: Let w = 0“12”, where n3 1. |w| = 3n > n. By using pumping lemma we can write w = xyz, with |xy| , n and |y| - 0.
Step III: We want to find a suitable i so that xy'z ∉ L. The string consists of ‘0' and ‘1'. y can be any of the following forms
y consists of only ‘0', let y = 0k
y consists of only ‘1', let y = 1k
y consists of both ‘0' and ‘1'. Let y = 0k1k
For case I, take i = 0.
![]()
For case II, take i = 0.
![]()
For case III, take i=2.
![]()
For all the three cases we are getting contradiction, therefore L is not regular.
4.8 CLOSURE PROPERTIES OF REGULAR SET
Q. What do you mean by closure property? Give an example.
Ans. A set is closed (under an operation) if and only if the operation on two elements of the set produces another element of the set. If an element outside the set is produced, then the operation is not closed. Closure is a property which describes when we combine any two elements of the set; the result is also included in the set.
If we multiply two real numbers, we will get another real number. Since this process is always true, it is said that the real numbers are “closed under the operation of multiplication”. There is simply no way to escape the set of real numbers when multiplying.
Let S = {1,2,3,4,5,6,7,8,9,10,…} is a set of real numbers.
1 × 2 = 2,
2 × 3 = 6,
5 × 2 = 10.
All are included in the set of real numbers.
Therefore we can say real numbers are closed under the operation of multiplication.
Q. Prove that two Regular Expressions Ll and L2 over Σ are closed under union operation.
Ans. We have to prove that if L1 and L2 are regular over Σ, then their union, i.e. L1 ∪ L2 will be also regular.
As L1 and L2 are regular over Σ, there must exist finite automata M1 = (Q1, Σ, δ1, q01, F1) and M2 = (Q2, Σ, δ2, q02, F2) such that L1 ∈ M1 and L2 ∈ M2
Assume that there is no common states between Q1 and Q2, i.e. Q1 ∩ Q2 = ∧.
Define another Finite Automata M3 = (Q, Σ, δ, q0, F), where
(i) Q = Q1 ∪ Q2 ∪ {q0}, where q0 is a new state g Q1 ∪ Q2
(ii) F = F1 ∪ F2
(iii) Transitional function δ is defined as δ(q , e) → {q01, q02} and δ(q, Σ) δ1(q, Σ) if q ∈ Q1
δ(q, Σ) → δ2{q, Σ)if q ∈ Q2
It is clear from the previous discussion that from q0 we can reach to either initial state q1 of M1 or initial state q2 of M2.
Transitions for the new Finite Automata M are same like the transitions of M1 and M2. As F = F1 ∪ F2 so any string accepted by M1 or M2 will also be accepted by M Therefore L1 ∪ L2 is also regular.
Example:
![]()
The Finite Automata M1 accepting L1 is
The Finite Automata M2 accepting L2 is

The machine M produced by combining M1 and M2 is

It accepts L1 u L,
Q. Prove that complement of a Regular Expression is also regular.
Ans. If L is regular we have to prove that LT is also Regular.
As L is Regular there must be a Finite Automata M = (Q, Σ, δ, q0 , F) accepting L. M is a Finite Automata, so M has a transitional system.
Let construct another transitional system M' with the state diagram of M but reversing the direction of the directed edges. M' can be designed as follows
(i) set of states of M' is same as M
(ii) set of input symbols of M' is same as M
(iii) Initial state of M' is same as Final state of M [M' is reverse direction of M]
(iv) Final state of M' is same as initial state of M [M' is reverse direction of M]
Let a string w belongs to L, i.e. w ∈ M. Therefore, there is a path from q0 to F with path value w. By reversing the edges we get a path from F to q0 (Beginning and Final state of M’) in M'. The path value is reverse of w, i.e. wT. Therefore wT ∈ M'.
so the reverse of the string w is regular.
Let L = ab(a+b)*
The Finite Automata M accepting L is

The reverse of The fi nite automata accepting Lc is

M' accepts (a+b)*ba which is reverse of L.
Therefore w ∈ L, i.e. Σ* - LL. However, Σ* - L is accepted by M' which is a Finite Automata.
Replace this by Σ* - L ≠ L
Q. If L is regular and L is a subset of Σ*, prove that Σ* - L is also a regular set.
Ans. As L is Regular there must be a Finite Automata M = (Q, Σ, δ, q0, F) accepting L. Let construct another DFA M' = (Q, Σ, δ, q0, F’), where F' = Q-F. Therefore two DFA differ only in their final states. A final state of M is a nonfinal state of M' and vice versa.
Let take a string w which is accepted by M'. Therefore Σ^0, w) e F', i.e. Σ^0, w) e (Q - F).
The string w cannot be accepted by M, because Σ^0, w) g F[As F does not belong to (Q - F)].
Therefore w g L, i.e. Σ* - L Σ L. However, Σ* - L is accepted by M' which is a Finite Automata.
Therefore Σ* - L is a regular set
Q. Prove that two Regular Expressions L1 and L2 over Σ are closed under intersection operation.
Ans. From D'Morgan's theorem we know
![]()
We know if Ll and L2 are regular then LlC and L2C are also regular.
As LlC and L2C are regular, LlC ![]() L2C is also regular (Regular Expression are closed under union operation.)
L2C is also regular (Regular Expression are closed under union operation.)
As LlC ![]() L2C is regular so their complement (LlC
L2C is regular so their complement (LlC ![]() L2C)C is also regular.
L2C)C is also regular.
So Ll![]() L2 is also regular, i.e. the regular sets are closed under intersection.Σ
L2 is also regular, i.e. the regular sets are closed under intersection.Σ
WHAT WE HAVE LEARNED SO FAR
1. A Regular Expression can be defined as a language or string accepted by a Finite Automata.
2. Any terminal symbols, null string (Σ), null set (Σ) are Regular Expression.
3. Union, Concatenation, Iteration of two Regular Expressions or any combination of them are also Regular Expression.
4. Arden's Theorem states that if P and Q be two Regular Expressions over Σ. If P does not contain Σ, then for the equation R=Q + RP has a unique (one and only one) solution R=QP*.
5. Arden's Theorem is used to construct Regular Expression from a given Finite Automata by Algebraic Method.
6. If any Finite Automata contains any e (null) move or transaction then that Finite Automata is called NFA with e moves.
7. e - closure of a state is defined as the set of all states s, such that it can reach from that state to all the states in s with input e (i.e. with no input).
8. Pumping Lemma for Regular Expression is used to prove that certain sets are not regular.
9. A set is closed (under an operation) if and only if the operation on two elements of the set produces another element of the set.
10. Closure is a property which describes when we combine any two elements of the set; the result is also included in the set.
11. Regular Expressions are closed under Union, Complementation, and Intersection operation.
SOLVED PROBLEMS
1. Describe the following Regular Expressions in English Language.
(i) a(a + b)*b
(ii) (a + b)*aba(a + b)*
(iii) (0 + 1)*1(0 + 1)*0(0 + 1)*
Ans. (i) The language starts with 'a and ends with 'b'. In the middle of 'a and 'b' there is any combination of 'a and ‘b'. Hence the Regular Expression described in English language
{set of any combination of ‘a' and ‘b' beginning with ‘a' and ending with ‘b'}
(ii) The expression is divided into three parts (a + b)*, aba, and (a + b)*. In each element of the language set there is aba as substring. In English language, the Regular Expression is described as
{set of any combination of ‘a' and ‘b' containing ‘aba' as substring}
(iii) The expression is divided into five parts (0 + 1)*, 1, (0 + 1)*, 0 and (0 + 1)*. In each element of the language set there is 1 and 0, where 1 appears first. In English language the Regular Expression is described as
{set of any combination of ‘0' and ‘1' containing atleast one 1 and one 0}.
2. Find Regular Expression for the following:
(a) Set of Languages of any combination of ‘a' and ‘b' beginning with ‘a'.
(b) Set of languages of any combination of ‘0' and ‘1' containing atleast one double symbol.
(c) Set of languages of any combination of ‘0' and ‘1' containing no double symbol
Ans. (a) Set of any combination of 'a and 'b' is denoted by (a + b)*. The Regular Expression is
L = a(a + b)*.
(b) The language consists of two symbols ‘0' and ‘l'. Double [same] symbol means either 00 or ll. Part of the language containing atleast one double symbol is denoted by (00 + ll). Therefore the language of any combination of ‘0' and ‘l' containing atleast one double symbol is expressed as L = (0 + 1)* (00 + 11) (0 + 1)*.
(c) The language consists of two symbols ‘0' and ‘l'. Double [same] symbol means either 00 or ll. According to the condition, in the language 00 or ll will not appear. The language may start with ‘0' or start with ‘l'. The language start with ‘0' with no double symbol is (0l)*. The language start with ‘l' with no double symbol is (l0)*.
The expression is L = (01)* + (10)*
3. Construct a Regular Expression from the given Finite Automata by Algebraic Method using Arden's Theorem.
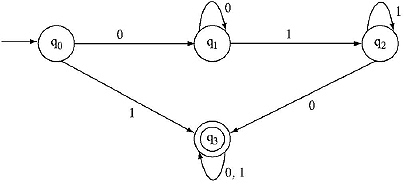
Ans. For the above given Finite Automata the equations
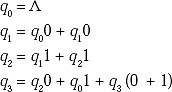
Put the value of q0 in equation ql. ql = 0 + ql0. The equation is in the form R = Q + RP, where R = ql, Q = 0 and P = 0. By Arden theorem the solution of the equation is R = QP* i.e.
ql = 00*.
Substituting the value ql in equation (3) we get q2 = 00*l + q2l.
The equation is in the form R = Q + RP, where R = q2, Q = 00*1 and P = 1. By Arden theorem the solution of the equation is R = QP* i.e.
q2 = 00*11*.
Substituting the value of q, and q0 in equation (4) we get
q3 = (00*11*0 + 1) + q3 (0 + 1).
The equation is in the form R = Q + RP, where R = q3, Q = (00*11*0 + 1) and P = (0 + 1). By Arden theorem the solution of the equation is R = QP* i.e.
q3 = (00*11*0 + 1) (0 + 1)*.
As q3 is the final state so the Regular Expression generated from the given Finite Automata is (00*11*0 + 1) (0+ 1)*.
4. Construct a Regular Expression from the given Finite Automata by Algebraic Method using Arden's Theorem.

Ans. For the above given Finite Automata the equations will be
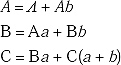
The equation (1) is in the form R = Q + RP, where R = A, Q = Σ and P = b. According to Arden's Theorem, the solution for the equation is R = QP*.
Therefore, A = Σ^ = b' [As ΣR = R Σ = R].
Substituting the value of A in equation (2) we get
B = b'a + Bb
The equation is in the format R = Q + RP, where R = B, Q = b'a, and P = b. According to Arden's Theorem, the solution for the equation is R = QP*.
Therefore, B = b* ab*.
Substituting the value of B in equation (3) we get
C = b'ab'a + C(a + b).
The equation is in the format R = Q + RP, where R = C, Q = b'ab'a and P = (a + b). According to Arden's Theorem, the solution for the equation is R = QP*.
So C = b*ab*a(a + b)*.
As C is the final state so the Regular Expression accepted by the finite automata is b*ab*a(a + b)*
5. Construct a Regular Expression from the given Finite Automata by Algebraic Method using Arden's Theorem.
Ans. For the above given Finite Automata the equations will be

The equation (1) is in the form R = Q + RP, where R = A, Q = Σ, and P = a. According to Arden's Theorem, the solution for the equation is R = QP*.
Therefore ![]()
substituting the value of A in equation (2) we get
![]()
substituting the value of B in equation (3) we get
![]()
This is in the format R = Q + RP, where R = C, Q = a*bb, and P = b. According to Arden's Theorem, the solution for the equation is R = QP*.
C = a*bbb*.
substituting the value of B and C in equation (4) we get
D = a*ba + a*bbb*a + D(a + b).
This is in the format R = Q + RP, where R = D, Q = a*ba + a*bbb*a and P = a + b. According to Arden's Theorem, the solution for the equation is R = QP*.
![]()
In the finite automata there are two final states B and D. Therefore, the Regular Expression accepted by the finite automata:
![]()
6. Construct Finite Automata equivalent to the Regular Expression.
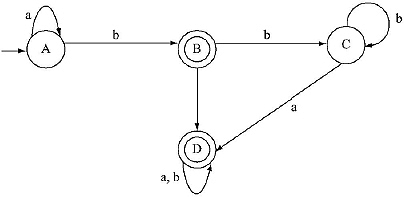
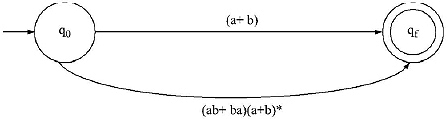
L = (a + b) + (ab + ba)(a + b)*
Ans. Step I: Take a beginning state q0 and a final state qf. Between the beginning and fi nal state place the Regular Expression.
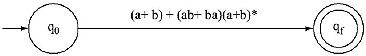
Step II: Between (a + b) and (ab + ba)(a + b)* there is a ‘ + ’ sign, so there will be parallel edges between q0 and qf.
Step III: Between (ab + ba) and (a + b)* there is a ‘.' (dot) sign, so a extra state is added between q0 and qf.
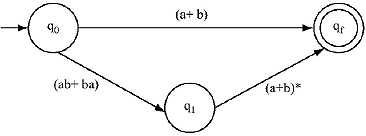
Step IV: Between ab and ba there is ‘ + ’ sign, so there will be parallel edges between q0 and ql.
Step V: Between ‘a’ and b there is ‘ + ’ sign. Therefore, between q0 and qf there is parallel edge. As there is a ‘*’ in (a + b), hence a loop is added on qf and an ∈ is added between ql and qf.
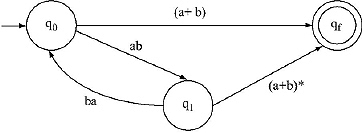
Step VI: Between ‘a’ and ‘b’ and between ‘b’ and ‘a’ there are ‘.’(dot). Therefore, two extra states are added between q0 and q1.
Step VII: Between ql and qf there is an ![]() . To remove that
. To remove that ![]() , merge ql and qf. Now two transition from q2 and q3 is added on qf.
, merge ql and qf. Now two transition from q2 and q3 is added on qf.
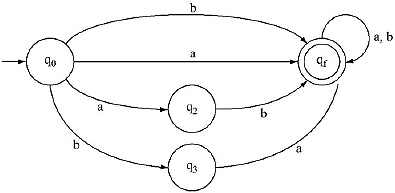
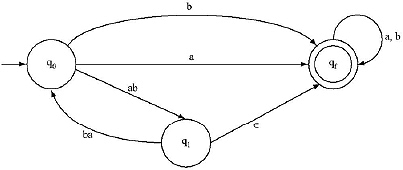
7. Construct Finite Automata equivalent to the Regular Expression.
L = (00 + 11)* 11 (0 + 1)*
Ans.
Step I: Take a beginning state q0 and a final state qf. Between the beginning and final state place the Regular Expression.
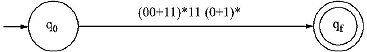
Step II: There are three ‘.’ (dot) in between (00 + 11)* and 1, 1 and 1, and 1 and (0 + 1)*. So three extra states are added in between q0 and qf.

Step III: There are two * in the Regular Expression. Hence, there will be self loop on q1 and qf. And ![]() transition will be in between q0 and q1, and q3 and qf.
transition will be in between q0 and q1, and q3 and qf.

Step IV: There is a ‘ + ‘ sign between 00 and 11, hence there will be parallel edges. And two ‘.'(dot) sign (between 0, 0 and 1,1) Hence two extra states are added.
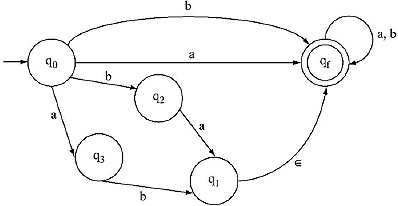
Step V: Removing ![]() , the final automata becomes
, the final automata becomes
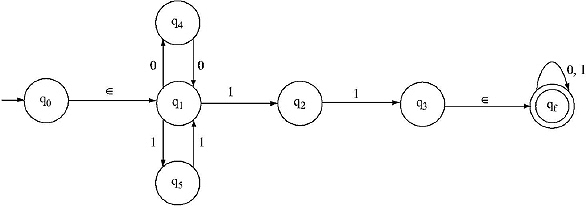
8. Convert the following NFA with ∈ -move to an equivalent DFA.
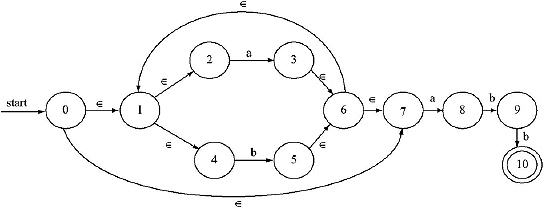
Ans.
![]() -closure (0) = {0,1,2,4,7}
-closure (0) = {0,1,2,4,7}
![]() -closure (1) = {1, 2, 4, 5}.
-closure (1) = {1, 2, 4, 5}.
![]() -closure (2) = {2}
-closure (2) = {2}
![]() -closure (9) = {9}
-closure (9) = {9}
![]() -closure (3) = {1, 2, 3, 4, 6, 7}
-closure (3) = {1, 2, 3, 4, 6, 7}
![]() -closure (4) = {4}
-closure (4) = {4}
![]() -closure (5) = {1, 2, 4, 5, 6, 7}
-closure (5) = {1, 2, 4, 5, 6, 7}
![]() -closure (10) = {10}
-closure (10) = {10}
![]() -closure (6) = {1, 2, 4, 6, 7}
-closure (6) = {1, 2, 4, 6, 7}
![]() -closure (7) = {7}
-closure (7) = {7}
![]() -closure (8) = {8}
-closure (8) = {8}
As 0 is the beginning state so start with ![]() -closure(0) = {0,1,2,4,7}. Let rename it as A.
-closure(0) = {0,1,2,4,7}. Let rename it as A.
A is till unmarked.
Then construct δ' function for the new unmarked state A for input a and b.

New state so rename it as B.
New state so rename it as C.
B is till unmarked.
Then construct δ' function for the new unmarked state B for input a and b.

New state so rename it as D.
C is till unmarked.
Then construct δ' function for the new unmarked state C for input a and b.

D is till unmarked.
Then construct δ' function for the new unmarked state D for input a and b.

New state so rename it as E.

Here final state is E.
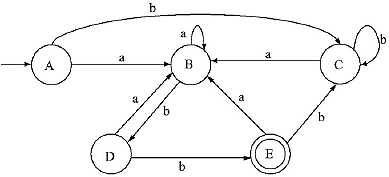
The equivalent DFA:
9. Construct Regular Grammar for the Regular Expression L = (a + b)*(aa + bb)(a + b)*
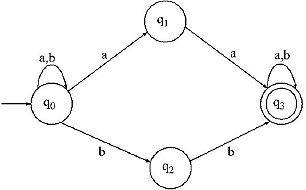
Ans. The NFA for the Regular Expression
There are four states in the finite automata. Therefore, in the regular grammar there are four nonterminals.
Lets consider them as A [For q0], B [For q1, C [For q2] and D [For q3].
Now we have to construct the Production rules of the Grammar.
For the state q0 the production rules are
A → aA, A → bA, A → aB, A → bC.
For the state q1 the production rules are
B → aD, B → a [As D is final state].
For the state q3 the production rules are
C → bD, C → b [As D is final state].
For the state q4 the production rules are
D → aD, D → bD, D → a/b
The grammar = {VN, S, P, S}
VN = {A, B, C, D} S ={a, b}

MULTIPLE CHOICE QUESTIONS
1. Machine format of Regular Expression is
(a) Finite Automata
(b) Push Down Automata
(c) Turing Machine
(d) All of the above.Σ
2. Regular Expression is accepted by
(a) Finite Automata
(b) Push Down Automata
(c) Turing Machine
(d) All of the above.
3. The language of all words with atleast 2 a's can be described by the Regular Expression (a) (ab)*a
(b) (a + b)*ab*a(a + b)*
(c) b*ab*a(a + b)*
(d) All of the above
4. Which type of language is Regular Expression?
(a) Type 0
(b) Type 1
(c) Type 2
(d) Type 3.
5. Which of the following Regular Expression over {0,1} denotes set of all strings not containing 100 as substring?
(a) (1 + 0)*0*
(b) 0*1010*
(c) 0*1*01
(d) All of the above.
6. Σ + RR* = ?
(a) R
(b) R*
(c) R +
(d) Σ.
7. What is the solution for the equation R = Q + RP (If P and Q are Regular Expression and P does not contain ∧)
(a) R = QP*
(b) R = QP
(c) R = PQ* (d) R = P*Q*.
8. Which is true for e -closure of a state.
(a) All the states reachable from the state with input null excluding the state
(b) The state only
(c) All the other states
(d) All the states reachable from the state with input null.
9. Pumping lemma for Regular Expression is used to prove that
(a) Certain sets are Regular
(b) Certain Sets are not Regular
(c) Certain Regular Grammar produce Regular Expression
(d) Certain Regular Grammar does not produce Regular Expression
10. Regular sets are closed under
(a) Union
(b) Concatenation
(c) Kleene Closure
(d) All of the above.
Ans. 1. a 2. d 3. b 4. d 5. c 6. b 7. a 8. d 9. b 10. d.
EXERCISES
1. Prove that (0 + 011*) + (0 + 011*)(01 + 0100*)(01 + 0100*)* = 01*(010*)*.
2. Find Regular Expression for the followings
(a) Set of all strings over (a, b) containing exactly one a
(b) Set of all strings over (a, b) containing atleast two a's
(c) Set of all strings over (0, 1) containing exactly two a's
(d) Set of all strings over (a, b) beginning and ending with b.Σ
(e) Set of all strings over (0, 1) containing 010 as substring
(f) Set of all strings over (0, 1) not containing substring 00.
3. Describe the following Regular Expressions in English language
(a) b'ab'
(b) (a + b)* aba(a + b)'
(c) a(a + b)*ab
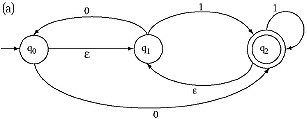
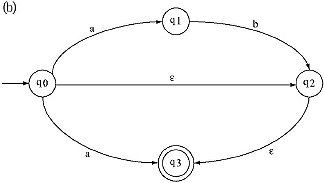
4. Find Regular Expressions corresponding to the automaton generated by the following Finite Automata.
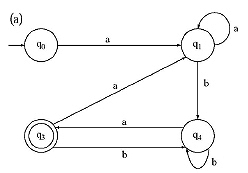

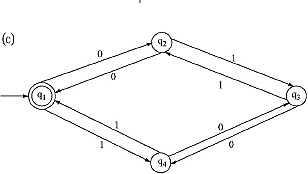
5. Convert the following NFA with null move to an equivalent DFA by ![]() closure method.
closure method.
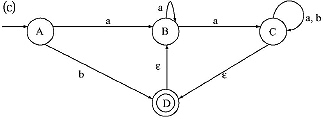
6. Develop Finite Automata for the following Regular Expressions
(a) (a*ab + ba)*a*
(b) (ab + a)*(aa + b)
(c) 10 + (0 + 11)0*1
7. Construct Regular Grammar for the following Finite Automata.
(a) ab + (aa + bb)(a + b)*
(b) 01(00 + 11)*11*
(c) a*(aa + bb)* + b*(ab + ba)*
8. Using Pumping Lemma show that following sets are not regular.
(a) L = {anbm, where 0 < n < m}
(b) L = {anbn + 1, where n > 0}
(c) L = {aibjck, where i,j,k > 0}
FILL IN THE BLANKS
1. Regular Expression is a string on_______among {Q, Σ, δ, q0, F}
2. If R is a Regular Expression then Λ + RR* =_______.
3. According to Arden's Theorem the solution of the equation R=Q+RP is_______.
4. Set of all states that can be reached from that state to all the states with input ![]() is called_______
is called_______
5. For the following NFA with ![]() move
move ![]() closure of ql is_______
closure of ql is_______
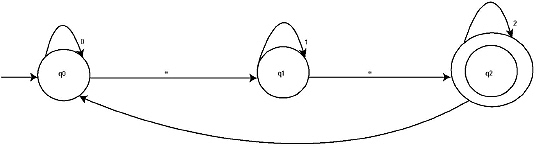
6. A grammar where all productions are in the form A → Ba or A → a then that grammar is called_______
7. A grammar where all productions are in the form A → aB or A → a then that grammar is called_______
8. Pumping Lemma for Regular Expression is used to prove that certain sets are not_______
9. The property which describes when we combine any two elements of the set; the result is also included in the set is called_______
10. If any Finite Automata contains any ![]() (null) move or transaction then that Finite Automata is called_______.
(null) move or transaction then that Finite Automata is called_______.
11. Machine format of Regular Expression is_______
ANSWERS
1. Σ
2. R*
3. R = QP*
4. ![]() closure
closure
5. q0, q1, q2
6. left linear grammar
7. right linear grammar
8. Regular
9. Closure property
10. NFA with ![]() moves
moves
11. Finite Automata
