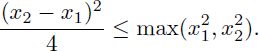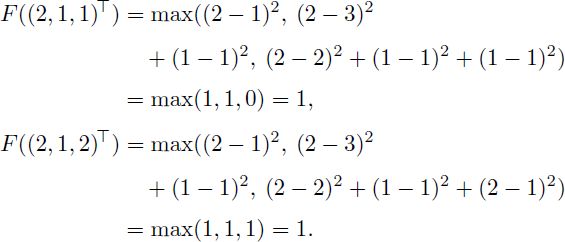Solutions to exercises from Chapter 1

Solution to Exercise 1.1. Let us establish existence and uniqueness of the point of minimum.

1. 1) Existence of the point of minimum follows from section 1.4, because the particular form of the kernel z(t, s) was never used in the proof.
2. 2) Similarly, uniqueness can be obtained in the same way as it was done in section 1.6. However, we put a short proof of uniqueness here.

Note that f(a) ≥ 0 for all a ∈ L₂([0,1]). Hence, the functionals f(a) and (f(a))² reach their minima on the same set of points.

Suppose that f(a) reaches minimum at points a₁ and a₀ with essentially different functions a₁ and a₀, which means that ||a₁ — a₀|| > 0; here, all norms are in L₂([0, 1]). Then, and (min f)².

If is easy to show that f²(a) is a convex function of a, and z(1, •)||² is a strictly convex function of a. The convexity of f²(a) follows from the facts that square function is convex and increasing in the range of f(a) and the functional f(a) is convex due to Lemma 1.4. The strict convexity of follows from Remark 1.8.

From the convexity and strong convexity, it follows that for any point a_t = t_a1 + (1 — t)a₀, t ∈ (0, 1), we have

whence

Thus, for every point a_t, t ∈ (0,1), the function f reaches its minimum at a_t while . This is contrary to the assumption that for every function a where f(a) reaches minimum, g_a(1) = f(a).

Solution to Exercise 1.2. We give the solution only for the second statement.

1. 2) Note that the kernel of the Riemann–Liouville process is (β—1)-homogeneous, namely for any c > 0

Let us establish that our kernel satisfies the assumption of Exercise 1.1. Suppose that the functional f reaches minimum at some point a ∈ L₂([0,1]). So, we need to check that g_a(1) = f(a). Suppose the opposite is true, g_a(1) < f(a), and try to obtain a contradiction. To this end, extend the function a from [0, 1] to [0, +∞), by adding it as follows:

This allows us to consider g_a(t) for t > 1. Prove the following property of semicontinuity:

[s.1]

Indeed, for t > 0

Due to the mean-square continuity of the Riemann–Liouville process, tends to 0 as t → 1. Hence

whence [S.1] follows.

Recall our assumption g_a(1) < f(a). Since

which holds true due to [S.1], and

which is the definition of f(a), c > 1 exists such that

[s.2]

Define a function

Then

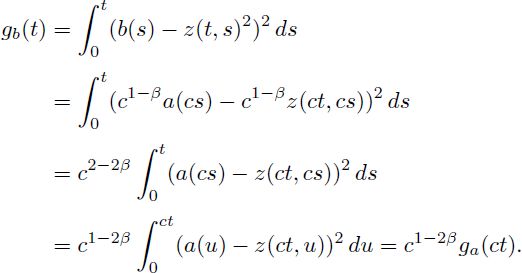
With [S.2], we have

However, the functional f reaches its minimal value at point a. Hence

[s.3]

Since f(a) ≥ 0 and c^1−2β < 0, inequality [S.3] is possible only if f(a) = 0. However, as g_a(1) ≥ 0, this contradicts to assumption g_a(1) < f(a).

We have verified the assumption from item 2 of Exercise 1.1. Now, apply Exercise 1.1 to prove the desired uniqueness.

REMARK S.1.– In the solution above, the function g_a(t) is in fact continuous on [0, +∞).

Solution to Exercise 1.3. First, let us prove the inequality

[s.4]

Indeed, apply inequality [1.15]:

Now, for N = 3, create a matrix

[s.5]

and verify that the functional F reaches its minimum at multiple points. Hence, let us prove that

Indeed, for every

Thus, 1 is a lower bound for F(a):

[s.6]

Now evaluate f(a) for a = (2,1,1)^⊤ and for a = (2, 1, 2)^⊤:

[s.7]

From [S.6] and [S.7], it follows that . Finally,

and the minimum of F is reached at two different points.

REMARK S.2.– For the matrix K defined in [S.5], the set of all points, where the minimum of F is reached, is a line segment in :

REMARK S.3.– The N × N matrix K for which the functional F reaches minimum at multiple points can be constructed for any N ≥ 3.

For N =1, the minimum of F is reached at the unique point a = (k₁₁).

For N = 2, the minimum of F is reached at the unique point

Solutions to exercises from Chapter 2

Solution to Exercise 2.6. We have obvious inequalities

On the left-hand side, the minimum is reached for (see the proof of Theorem 2.7). The right-hand side is equal to . Thus,

In section 2.1.6.2, we showed that if . In this case

and inequality [2.83] becomes

Solutions to exercises from Chapter 3

Solution to Exercise 3.3. By Stirling’s formula [3.51],

since and . Now the required result follows from the representation

see [A1.18].