The IsoMap algorithm is based on the manifold projection technique. In mathematics, the manifold is a topological space (which is, in general, a set of points with their neighbors) that locally resembles the Euclidian space near each point. For example, one-dimensional manifolds include lines and circles but not figures with self-intersections. Two-dimensional manifolds are called surfaces; for example, they can be a sphere, a plane, or a torus, but these surfaces can't have self-intersection. For example, a circle is a one-dimensional manifold embedded into a two-dimensional space. Here, each arc of the circle locally resembles a straight line segment. A 3D curve can also be a manifold if it can be divided into straight-line segments that can be embedded in 3D space without self-intersections. A 3D shape can be a manifold if its surface can be divided into flat plane patches without self-intersections.
The basics of applying manifold projection techniques are to search for a manifold that is close to the data, project the data onto the manifold, and then unfold it. The most popular technique that's used to find the manifold is to build a graph based on information about data points. Usually, these data points are placed into the graph nodes, and the edges simulate the relationships between the data points.
The IsoMap algorithm depends on two parameters:
- The number of neighbors,
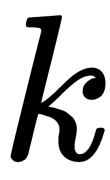, used to search for geodetic distances - The dimension of the final space,
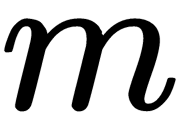
In brief, the IsoMap algorithm follows these steps:
- First, it constructs a graph representing geodesic distances. For each point, we search the
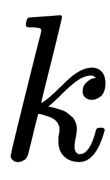nearest neighbors and construct a weighted, undirected graph from the distances to these nearest neighbors. The edge weight is the Euclidean distance to the neighbor.
- Using an algorithm to find the shortest distance in the graph, for example, Dijkstra's algorithm, we need to find the shortest distance between each pair of vertices. We can consider this distance as a geodesic distance on a manifold.
- Based on the matrix of pairwise geodesic distances we obtained in the previous step, train the MDS algorithm.
- The MDS algorithm associates a set of points in the
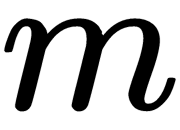-dimensional space with the initial set of distances.