The stochastic neighbor embedding (SNE) problem is formulated as follows: we have a dataset with points described by a multidimensional variable with a dimension of space substantially higher than three. It is necessary to obtain a new variable that exists in a two-dimensional or three-dimensional space that would maximally preserve the structure and patterns in the original data. The difference between t-SNE and the classic SNE lies in the modifications that simplify the process of finding the global minima. The main modification is replacing the normal distribution with the Student's t-distribution for low-dimensional data. SNE begins by converting the multidimensional Euclidean distance between points into conditional probabilities that reflect the similarity of points. Mathematically, it looks like this:

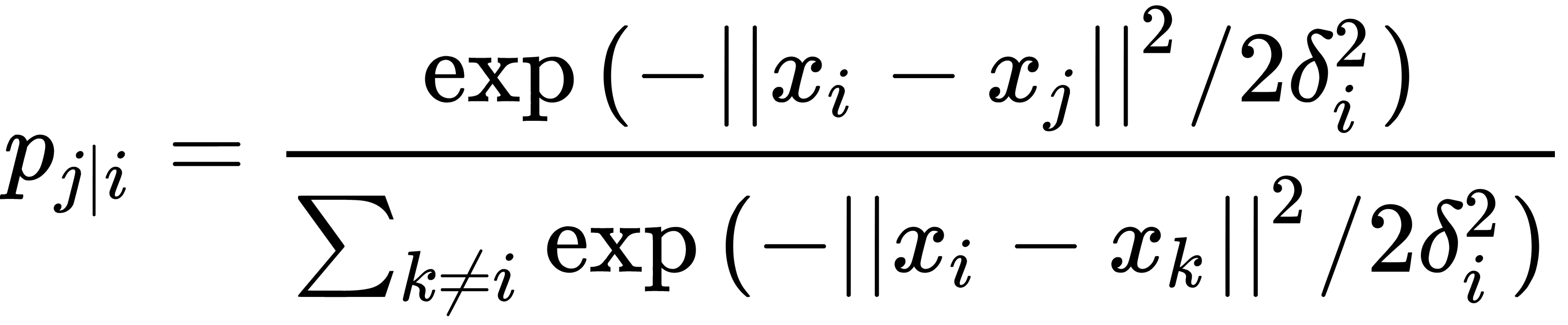
This formula shows how close the point 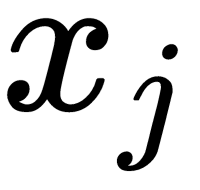 lies to the point  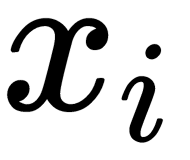with a Gaussian distribution around 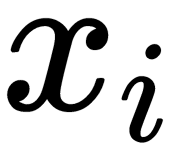, with a given deviation of 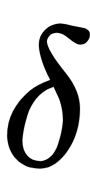.  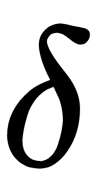is different for each point. It is chosen so that the points in areas with higher density have less variance than others.

Let's denote two-dimensional or three-dimensional mappings of the (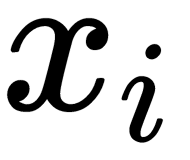, 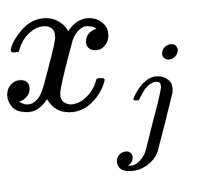) pair as the (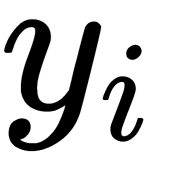, 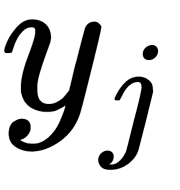) pair. It is necessary to estimate the conditional probability using the same formula. The standard deviation is :

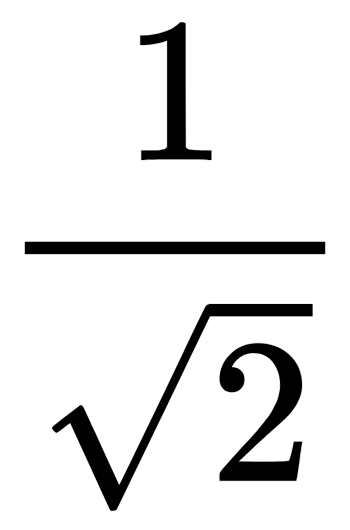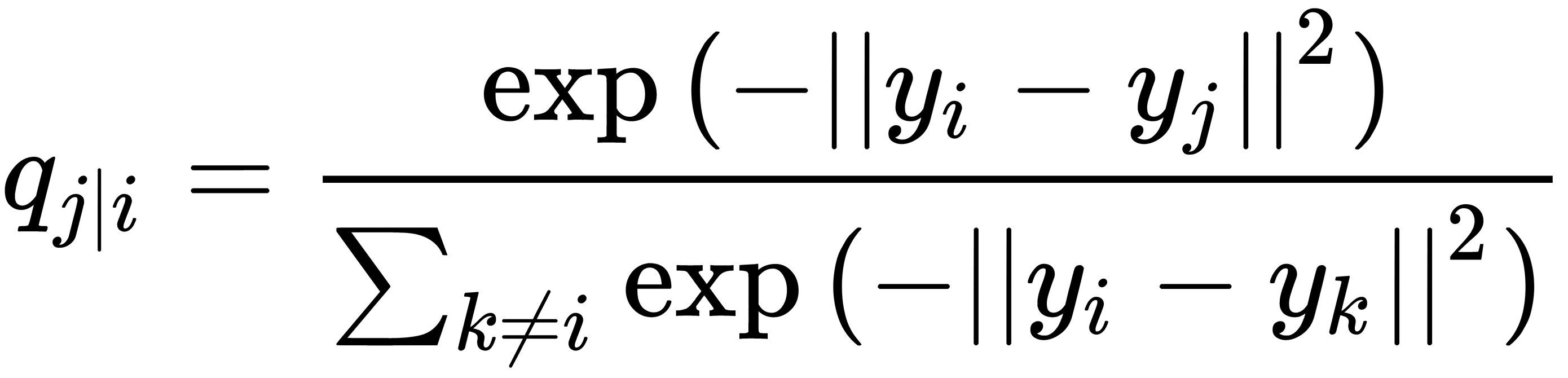
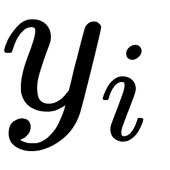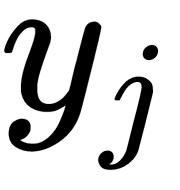If the mapping points,  and , correctly simulate the similarity between the original points of the higher dimension,  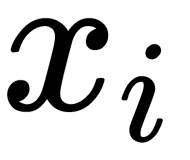and 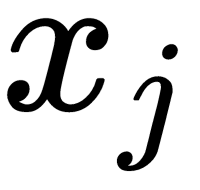, then the corresponding conditional probabilities,  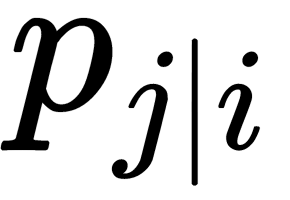and 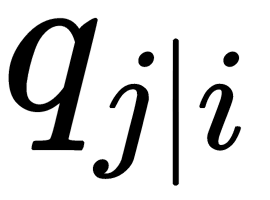, will be equivalent. As an obvious assessment of the quality of how  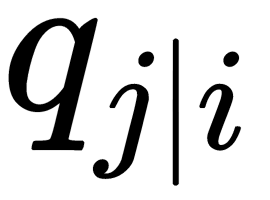reflects 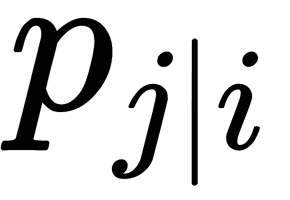, divergence, or the Kullback-Leibler distance, is used. SNE minimizes the sum of such distances for all mapping points using gradient descent. The following formula determines the loss function for this method:

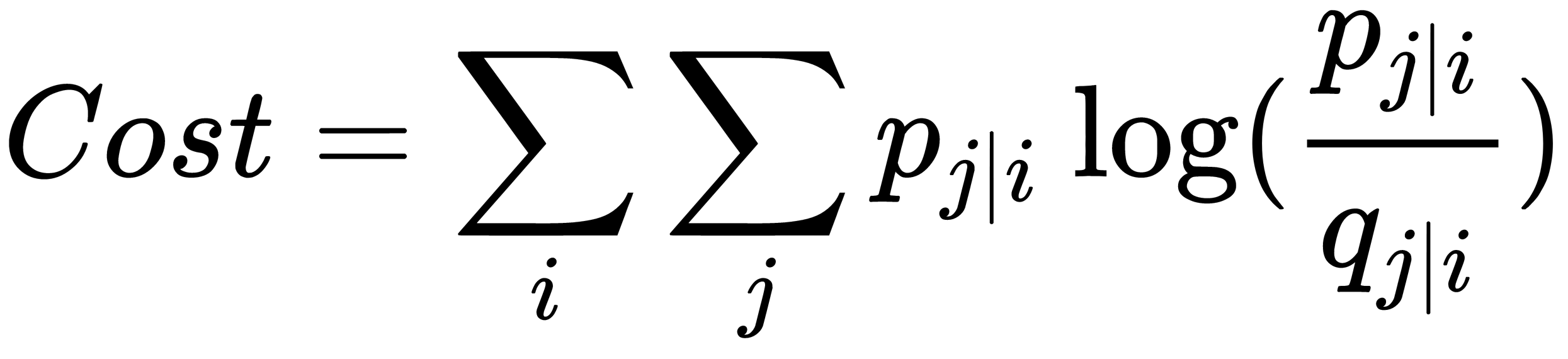
It has the following gradient:

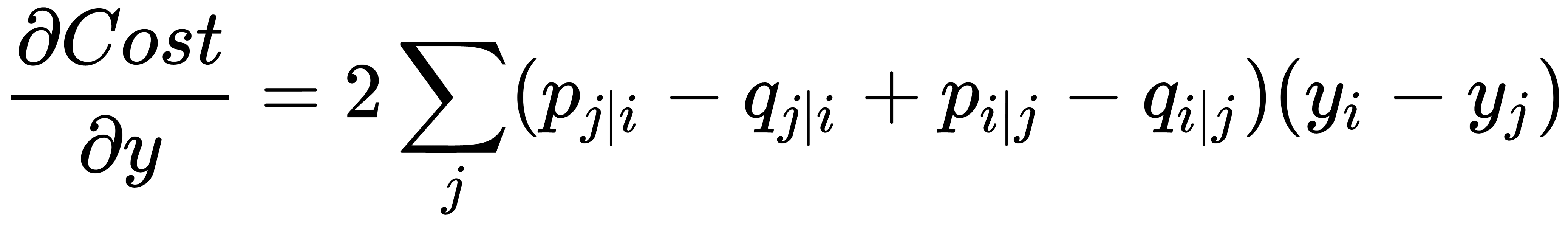
The authors of this problem proposed the following physical analogy for the optimization process. Let's imagine that springs connect all the mapping points. The stiffness of the spring connecting points 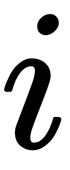 and 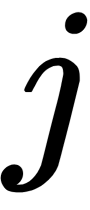 depends on the difference between the similarity of two points in a multidimensional space and two points in a mapping space. In this analogy, the gradient is the resultant force that acts on a point in the mapping space. If we let the system go, after some time, it results in balance, and this is the desired distribution. Algorithmically, it searches for balance while taking the following moments into account:

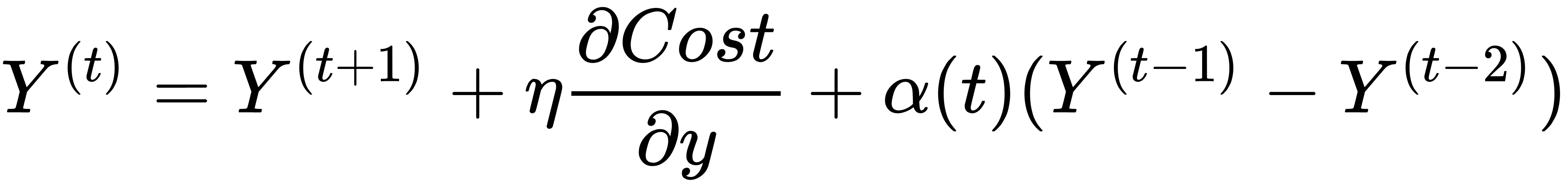
Here, 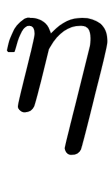 is the learning rate and  is the coefficient of inertia. Classic SNE also allows us to get good results but can be associated with difficulties when optimizing the loss function and the crowding problem. t-SNE doesn't solve these problems in general, but it makes them much more manageable.

The loss function in t-SNE has two principal differences from the loss function of the classic SNE. The first one is that it has a symmetric form of similarity in a multidimensional space and a simpler gradient version. Secondly, instead of using a Gaussian distribution for points from the mapping space, the t-distribution (Student) is used.