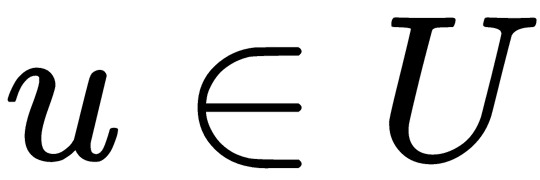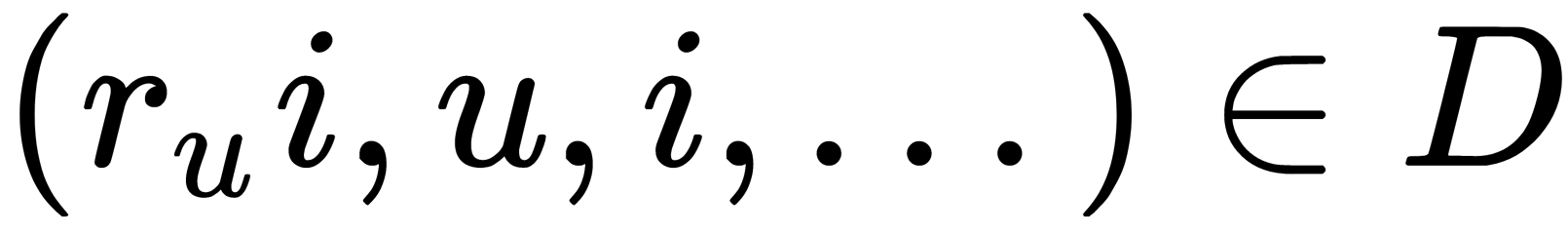In this section, let's formalize the recommender system problem. We have a set of users, , a set of items,  (movies, tracks, products, and so on), and a set of estimates, . Each estimate is given by user , object 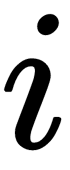, its result 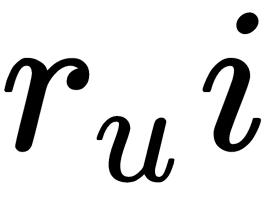, and, possibly, some other characteristics.

We are required to predict preference as follows:

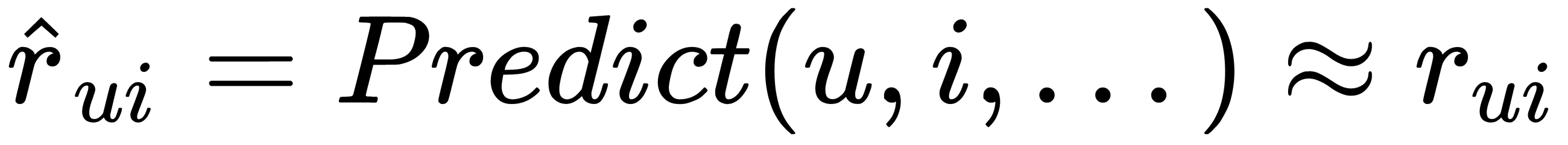
We are required to predict personal recommendations as follows:

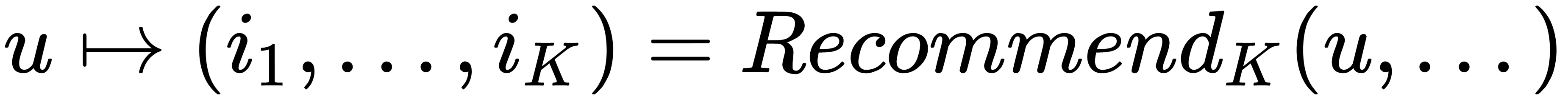
We are required to predict similar objects as follows:

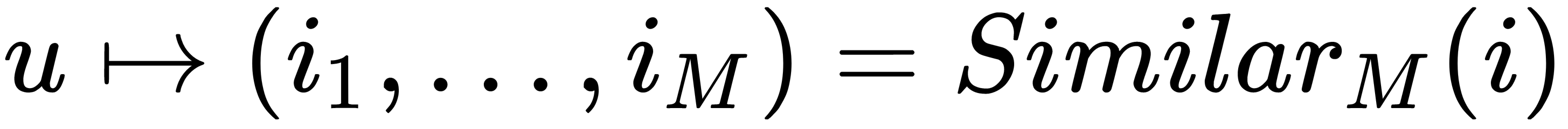
Remember—the main idea behind collaborative filtering is that similar users usually like similar objects. Let's start with the simplest method, as follows:

• Select some conditional measures of similarity of users according to their history of 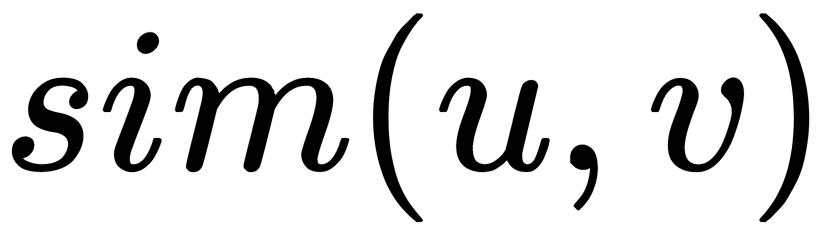ratings.
• Unite users into groups (clusters) so that similar users will end up in the same cluster: _.
• Predict the item's user rating as the cluster's average rating for this object:

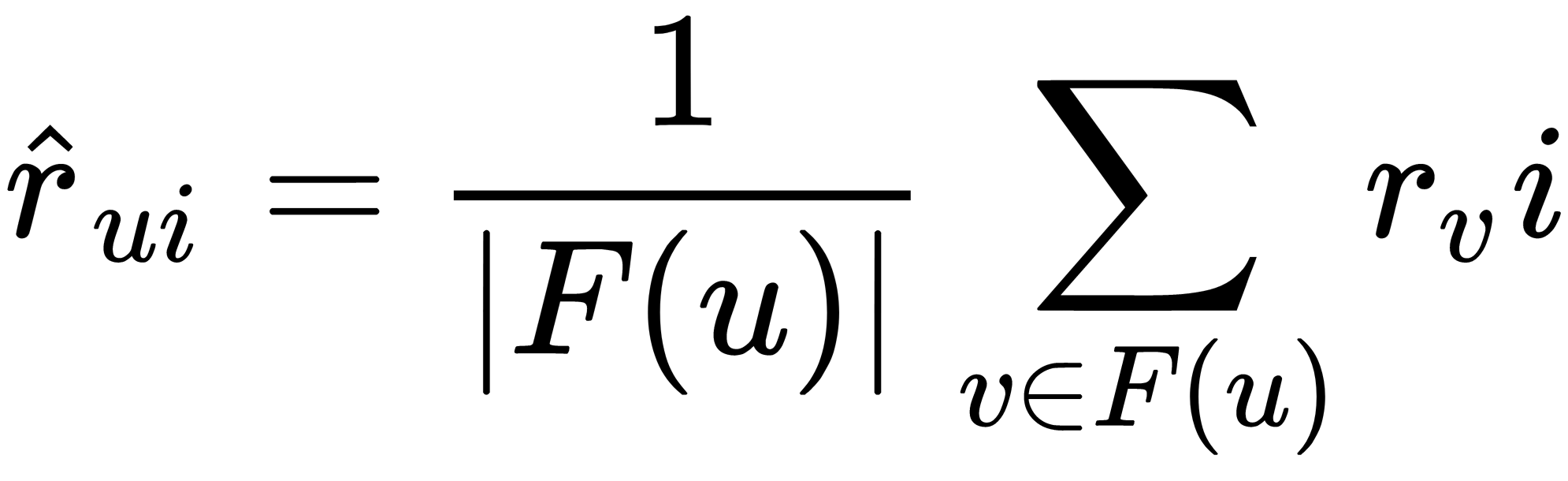
This algorithm has several problems, detailed as follows:

• There is nothing to recommend to new or atypical users. For such users, there is no suitable cluster with similar users.
• It ignores the specificity of each user. In a sense, we divide all users into classes (templates).
• If no one in the cluster has rated the item, the prediction will not work.

We can improve this method and replace hard clustering with the following formula:

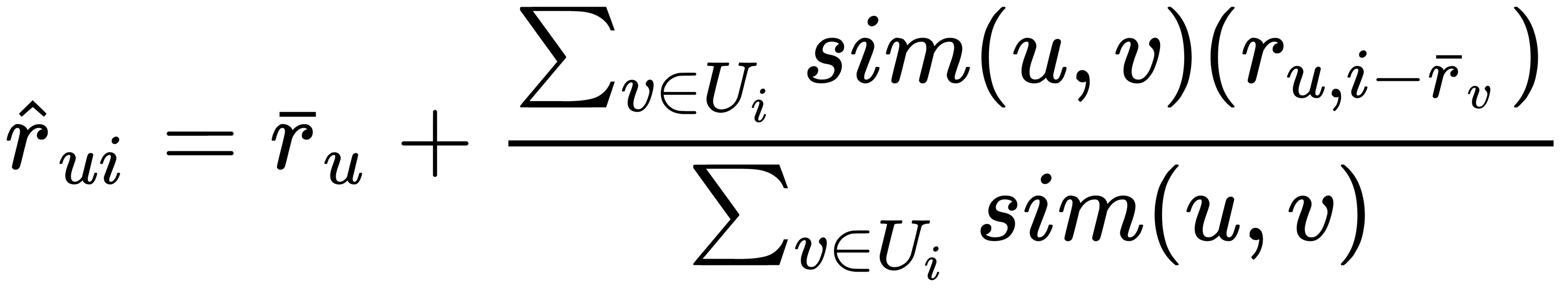
For an item-based version, the formula will be symmetrical, as follows:

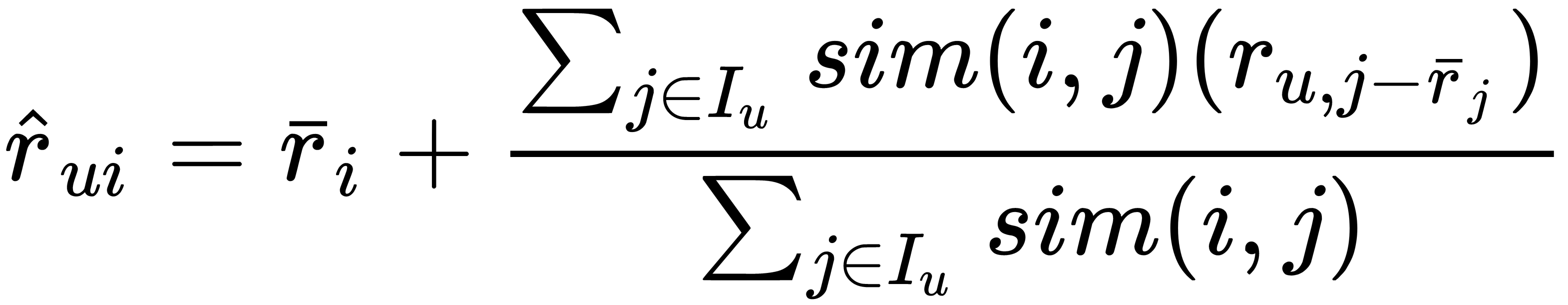
These approaches have the following disadvantages:

• Cold start problem
• Bad predictions for new and atypical users or items
• Trivial recommendations
• Resource intensity calculations

To overcome these problems, you can use the SVD. The preference (ratings) matrix can be decomposed into the product of three matrices 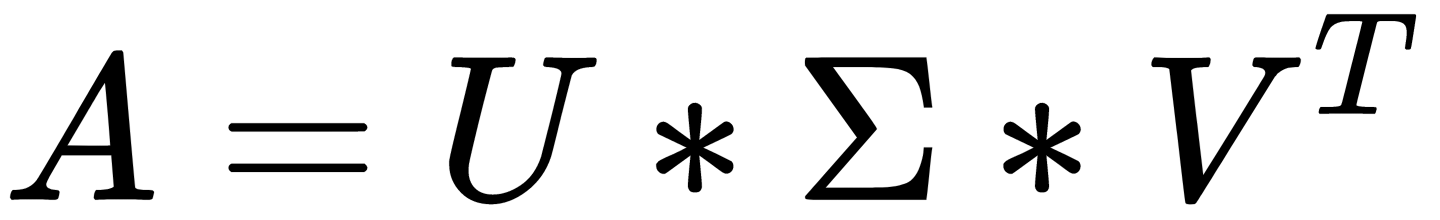. Let's denote the product of the first two matrices for one matrix, , where R is the matrix of preferences, U is the matrix of parameters of users, and V is the matrix of parameters of items.

To predict the user U rating for an item, 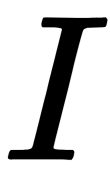, we take vector 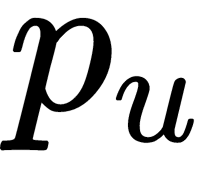(parameter set) for a given user and a vector for a given item, 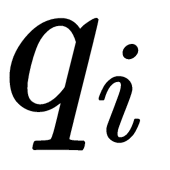. Their scalar product is the prediction we need: 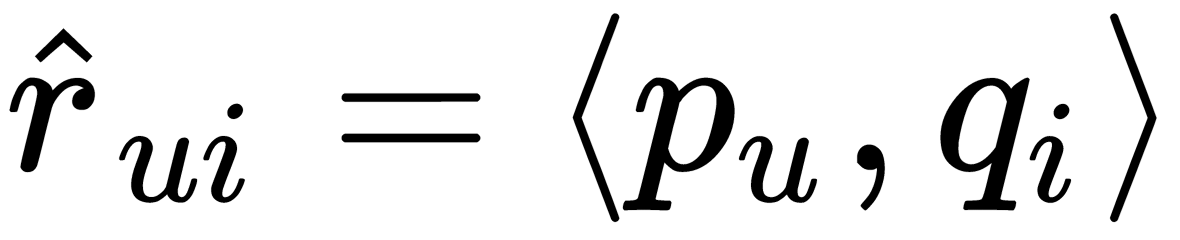. Using this approach, we can identify the hidden features of items and user interests by user history. For example, it may happen that at the first coordinate of the vector, each user has a number indicating whether the user is more likely to be a boy or a girl, and the second coordinate is a number reflecting the approximate age of the user. In the item, the first coordinate shows whether it is more interesting to boys or girls, and the second one shows the age group of users this item appeals to.

However, there are also several problems. The first one is the preferences matrix R which is not entirely known to us, so we cannot merely take its SVD decomposition. Secondly, the SVD decomposition is not the only one, so even if we find at least some decomposition, it is unlikely that it is optimal for our task.

Here, we need machine learning. We cannot find the SVD decomposition of the matrix since we do not know the matrix itself. But we can take advantage of this idea and come up with a prediction model that works like SVD. Our model depends on many parameters—vectors of users and items. For the given parameters, to predict the estimate, we take the user vector, the vector of the item, and get their scalar product, 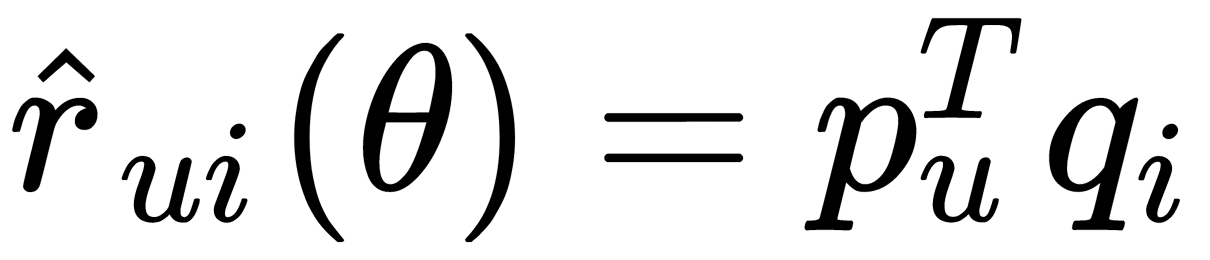. But since we do not know vectors, they still need to be obtained. The idea is that we have user ratings with which we can find optimal parameters so that our model can predict these estimates as accurately as possible using the following equation: 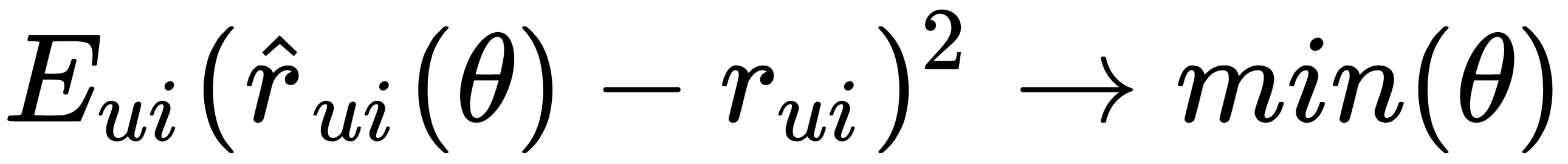. We want to find such parameters' θ so that the square error is as small as possible. We also want to make fewer mistakes in the future, but we do not know what estimates we need. Accordingly, we cannot optimize parameters' θ. We already know the ratings given by users, so we can try to choose parameters based on the estimates we already have to minimize the error. We can also add another term, the regularizer, shown here:

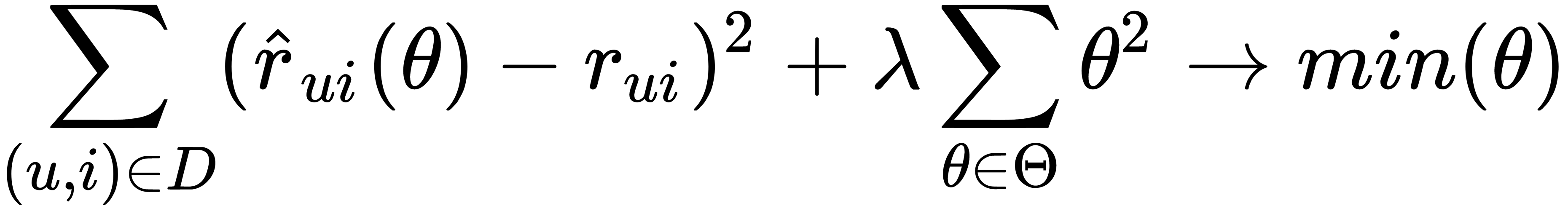
Regularization is needed to combat overfitting. To find the optimal parameters, you need to optimize the following function:

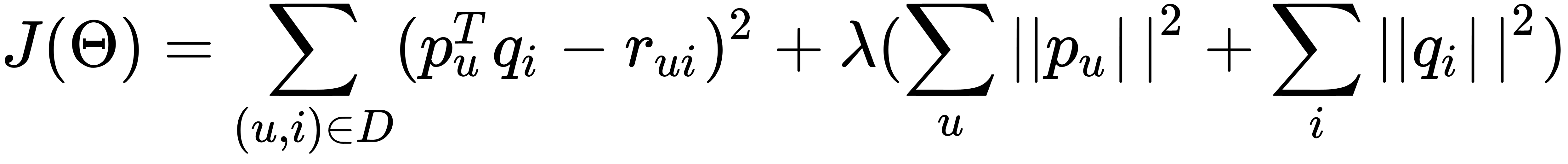
There are many parameters: for each user, for each item, we have our vector that we want to optimize. The most well-known method for optimizing functions is gradient descent (GD). Suppose we have a function of many variables, and we want to optimize it. We take an initial value, and then we look where we can move to minimize this value. The GD method is an iterative algorithm: it repeatedly takes the parameters of a certain point, looks at the gradient, and steps against its direction, as shown here:

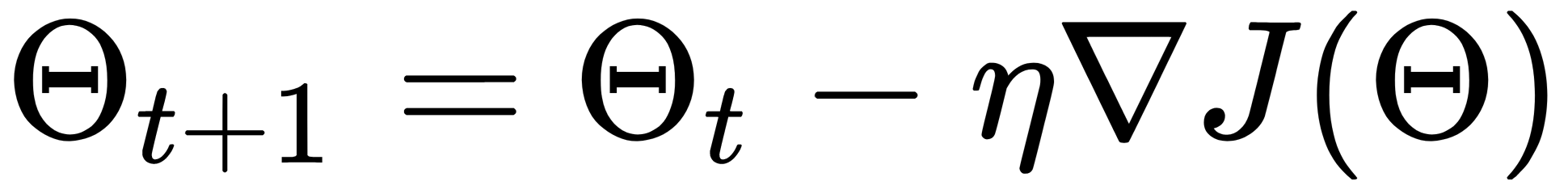
There are problems with this method: firstly, it works very slowly; and secondly, it finds local, rather than global, minima. The second problem is not so bad for us because in our case, the value of the function in local minima is close to the global optimum.

However, the GD method is not always necessary. For example, if we need to calculate the minimum for a parabola, there is no need to act by this method, as we know precisely where its minimum is. It turns out that the functionality that we are trying to optimize—the sum of the squares of errors plus the sum of the squares of all the parameters—is also a quadratic functional, which is very similar to a parabola. For each specific parameter, if we fix all the others, it is just a parabola. For those, we can accurately determine at least one coordinate. The ALS method is based on this assumption. We alternately accurately find minima in either one coordinate or another, as shown here:

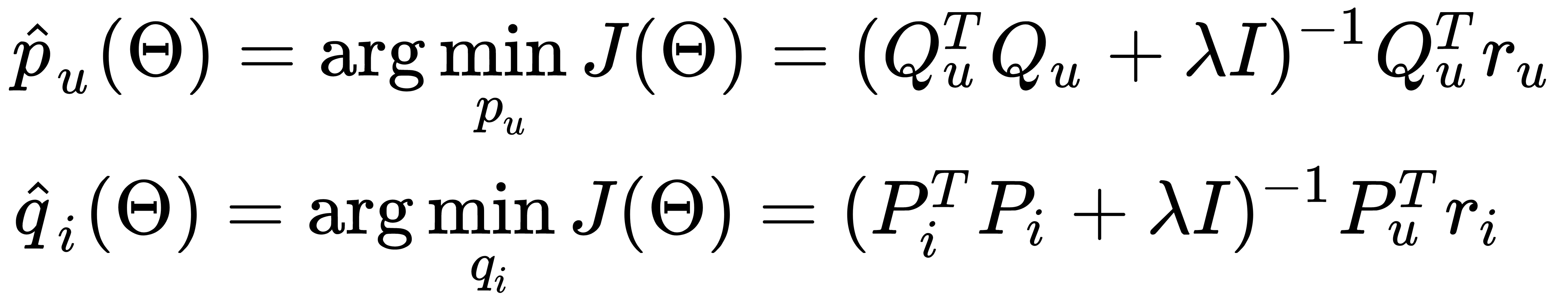
We fix all the parameters of the items, optimize the parameters of users, fix the parameters of users, and then optimize the parameters of items. We act iteratively, as shown here:

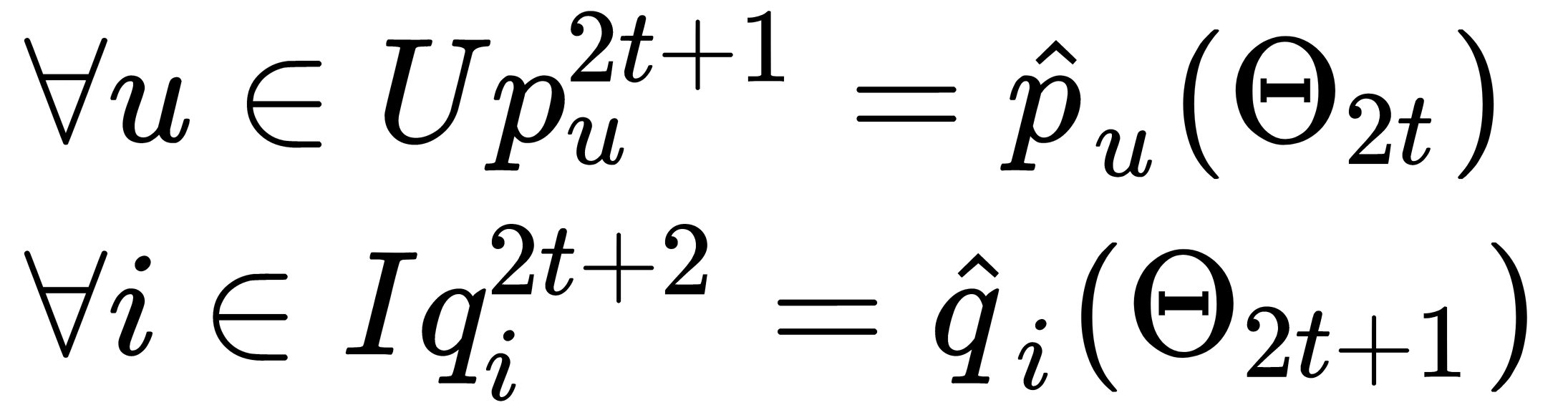
This method works reasonably quickly, and you can parallelize each step. However, there's still a problem with implicit data because we have neither full user data nor full item data. So, we can penalize the items that do not have ratings in the update rule. By doing so, we depend only on the items that have ratings from the users and do not make any assumption around the items that are not rated. Let's define a weight matrix 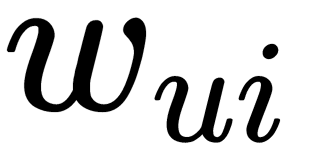as such, as follows:

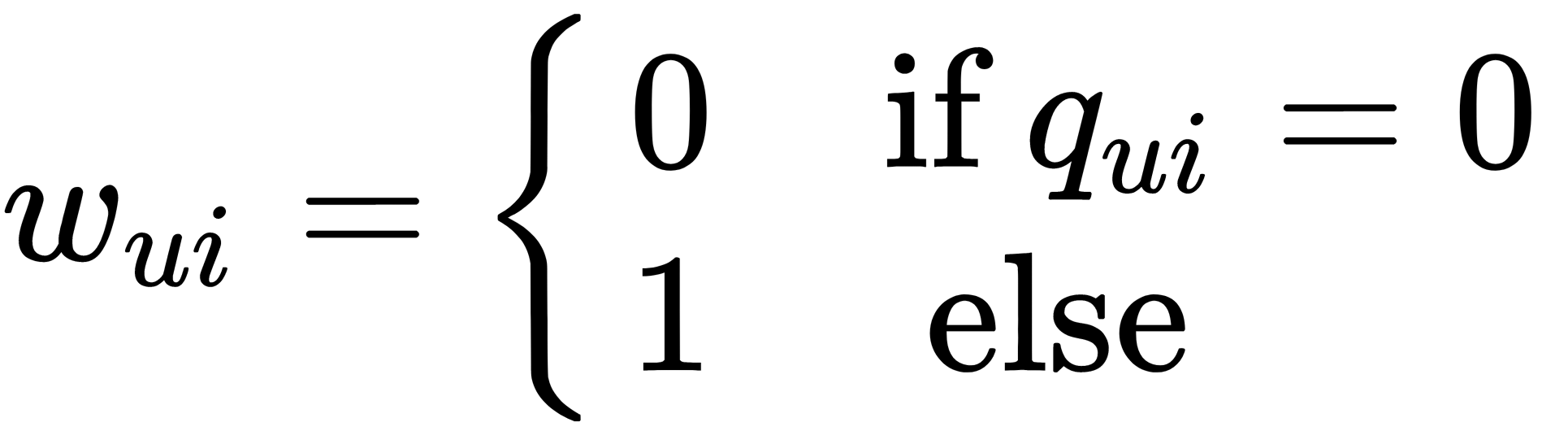
The cost functions that we are trying to minimize look like the following:

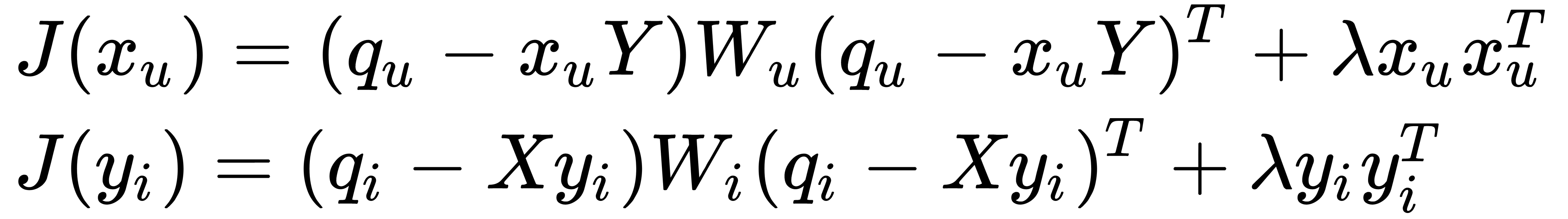
Note that we need regularization terms to avoid overfitting the data. Solutions for factor vectors are as follows:

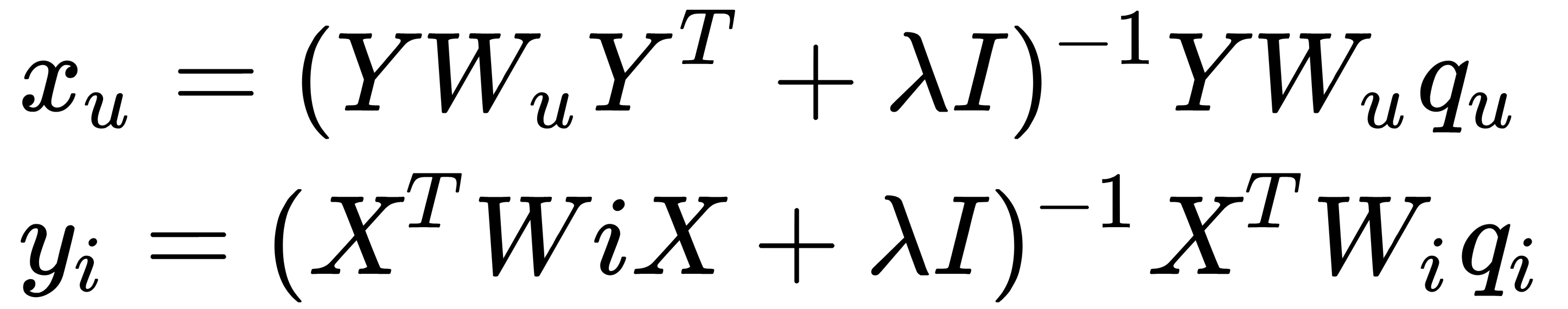
Here, 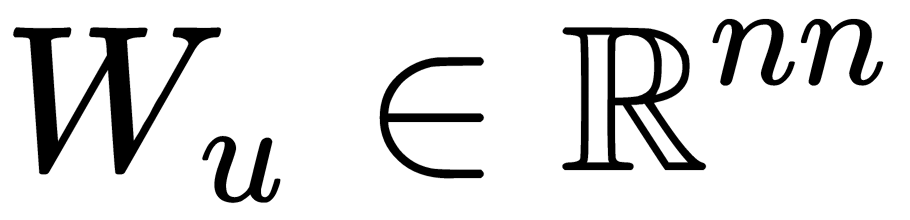 and 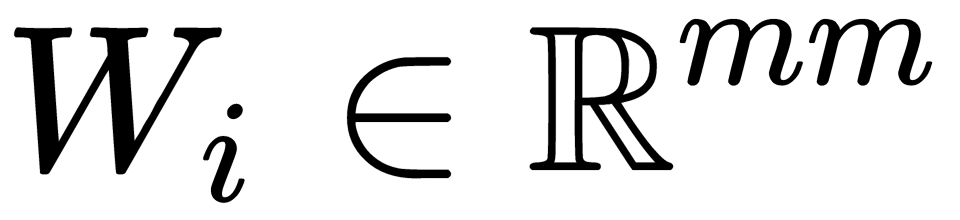are diagonal matrices.

Another approach for dealing with implicit data is to introduce confidence levels. Let's define a set of binary observation variables, as follows:

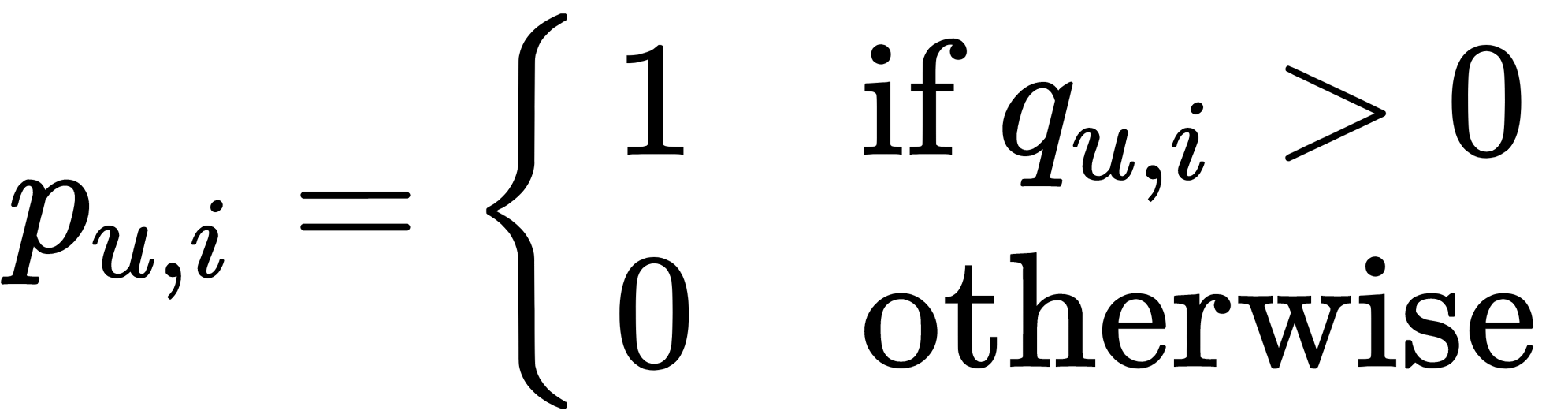
Now, we define confidence levels for each 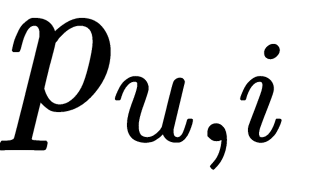. When 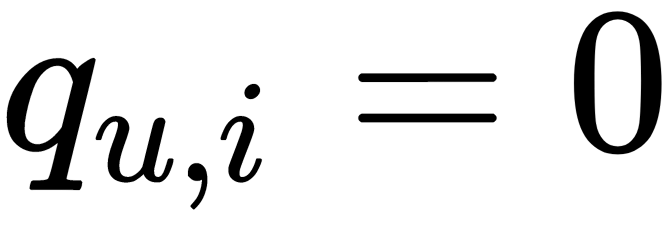, we have low confidence. The reason can be that the user has never been exposed to that item or it may be unavailable at the time. For example, it could be explained by the user buying a gift for someone else. Hence, we would have low confidence. When 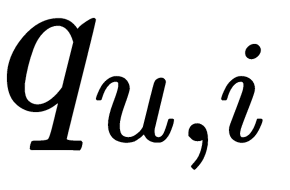is larger, we should have much more confidence. For example, we can define confidence as follows:

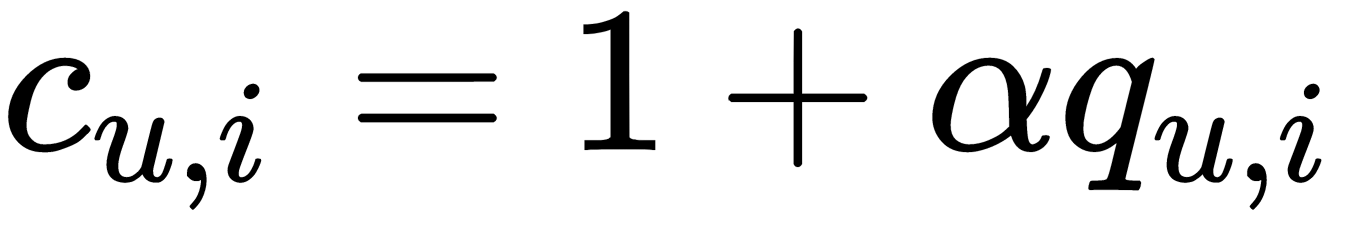
Here,  is a hyperparameter, which should be tuned for a given dataset. The updated optimization function is as follows:

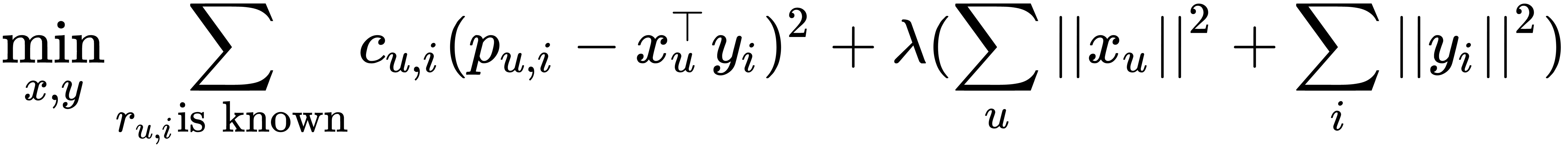
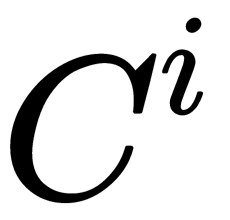is a diagonal matrix with values 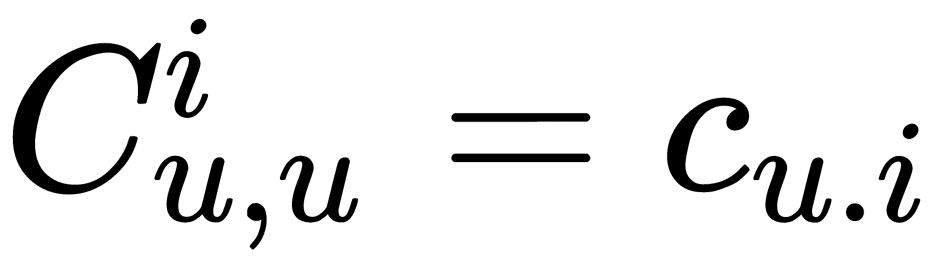. Solutions for user and item ratings are as follows:

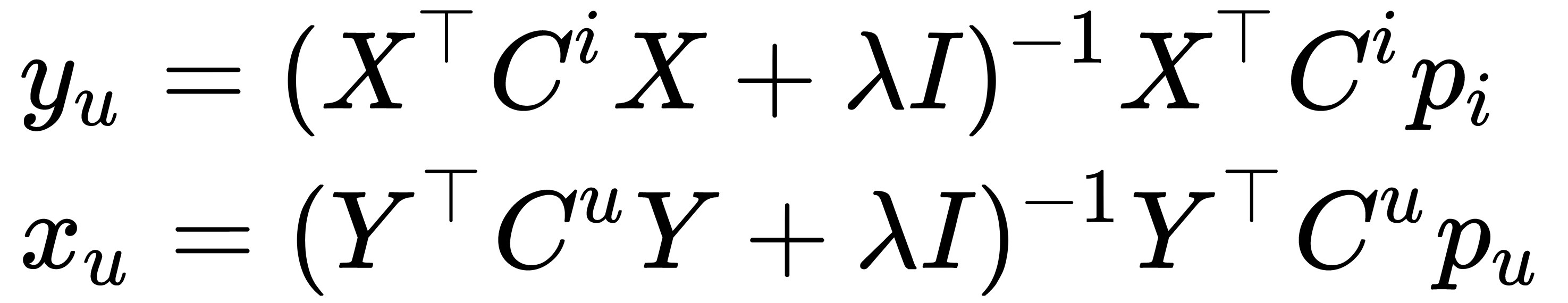
However, it is an expensive computational problem to calculate the 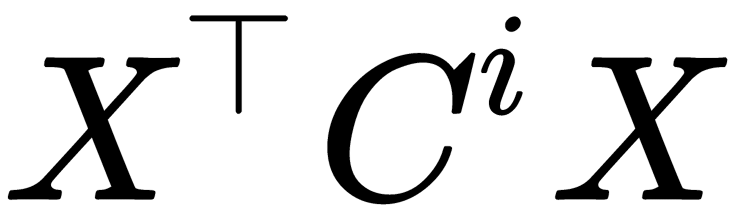expression. However, it can be optimized in the following way: .

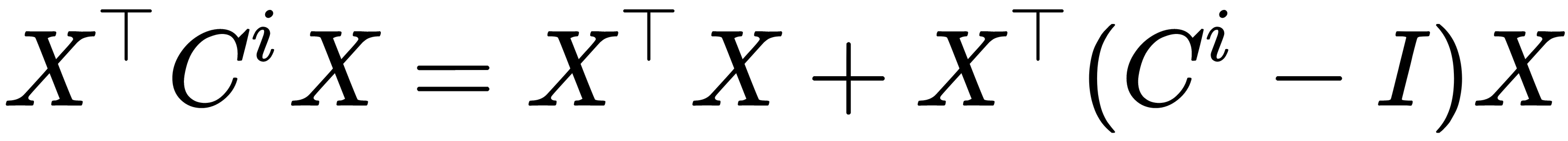This means that 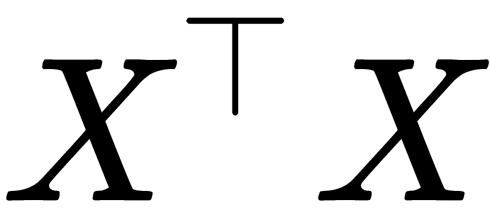 can be precomputed at each of the steps, and 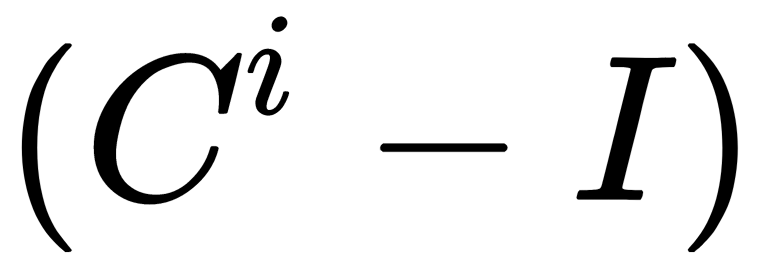has the non-zero entries only where 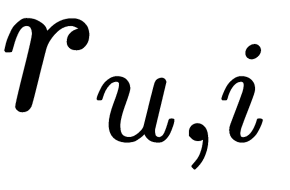was non-zero. Now that we have learned about the collaborative filtering method in detail, let's further understand it practically by considering a few examples about how to implement a collaborative filtering recommender system in the following section.

In the following sections, we will look at how to use different C++ libraries for developing recommender systems.