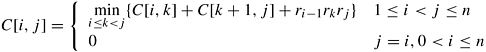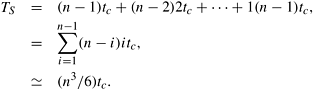Dynamic programming (DP) is a commonly used technique for solving a wide variety of discrete optimization problems such as scheduling, string-editing, packaging, and inventory management. More recently, it has found applications in bioinformatics in matching sequences of amino-acids and nucleotides (the Smith-Waterman algorithm). DP views a problem as a set of interdependent subproblems. It solves subproblems and uses the results to solve larger subproblems until the entire problem is solved. In contrast to divide-and-conquer, where the solution to a problem depends only on the solution to its subproblems, in DP there may be interrelationships across subproblems. In DP, the solution to a subproblem is expressed as a function of solutions to one or more subproblems at the preceding levels.
We start our discussion with a simple DP algorithm for computing shortest paths in a graph.
Example 12.1 The shortest-path problem
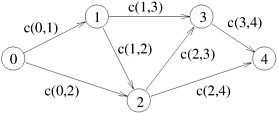
Consider a DP formulation for the problem of finding a shortest (least-cost) path between a pair of vertices in an acyclic graph. (Refer to Section 10.1 for an introduction to graph terminology.) An edge connecting node i to node j has cost c(i, j). If two vertices i and j are not connected then c(i, j) = ∞. The graph contains n nodes numbered 0, 1, ..., n − 1, and has an edge from node i to node j only if i < j. The shortest-path problem is to find a least-cost path between nodes 0 and n − 1. Let f (x) denote the cost of the least-cost path from node 0 to node x. Thus, f (0) is zero, and finding f (n − 1) solves the problem. The DP formulation for this problem yields the following recursive equations for f (x):
As an instance of this algorithm, consider the five-node acyclic graph shown in Figure 12.1. The problem is to find f (4). It can be computed given f (3) and f (2). More precisely,
Therefore, f (2) and f (3) are elements of the set of subproblems on which f (4) depends. Similarly, f (3) depends on f (1) and f (2),and f (1) and f (2) depend on f (0). Since f (0) is known, it is used to solve f (1) and f (2), which are used to solve f (3). ▪
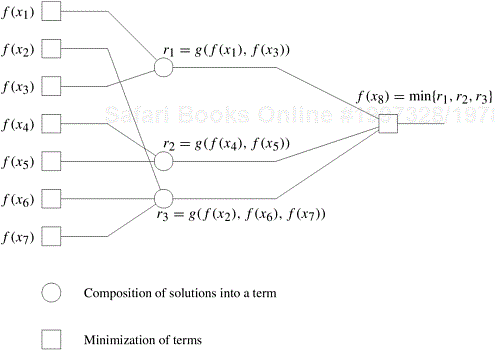
In general, the solution to a DP problem is expressed as a minimum (or maximum) of possible alternate solutions. Each of these alternate solutions is constructed by composing one or more subproblems. If r represents the cost of a solution composed of subproblems x1, x2, ..., xl, then r can be written as
The function g is called the composition function, and its nature depends on the problem. If the optimal solution to each problem is determined by composing optimal solutions to the subproblems and selecting the minimum (or maximum), the formulation is said to be a DP formulation. Figure 12.2 illustrates an instance of composition and minimization of solutions. The solution to problem x8 is the minimum of the three possible solutions having costs r1, r2, and r3. The cost of the first solution is determined by composing solutions to subproblems x1 and x3, the second solution by composing solutions to subproblems x4 and x5, and the third solution by composing solutions to subproblems x2, x6, and x7.
DP represents the solution to an optimization problem as a recursive equation whose left side is an unknown quantity and whose right side is a minimization (or maximization) expression. Such an equation is called a functional equation or an optimization equation. In Equation 12.1, the composition function g is given by f (j) + c(j, x). This function is additive, since it is the sum of two terms. In a general DP formulation, the cost function need not be additive. A functional equation that contains a single recursive term (for example, f (j)) yields a monadic DP formulation. For an arbitrary DP formulation, the cost function may contain multiple recursive terms. DP formulations whose cost function contains multiple recursive terms are called polyadic formulations.
The dependencies between subproblems in a DP formulation can be represented by a directed graph. Each node in the graph represents a subproblem. A directed edge from node i to node j indicates that the solution to the subproblem represented by node i is used to compute the solution to the subproblem represented by node j. If the graph is acyclic, then the nodes of the graph can be organized into levels such that subproblems at a particular level depend only on subproblems at previous levels. In this case, the DP formulation can be categorized as follows. If subproblems at all levels depend only on the results at the immediately preceding levels, the formulation is called a serial DP formulation; otherwise, it is called a nonserial DP formulation.
Based on the preceding classification criteria, we define four classes of DP formulations: serial monadic, serial polyadic, nonserial monadic, and nonserial polyadic. These classes, however, are not exhaustive; some DP formulations cannot be classified into any of these categories.
Due to the wide variety of problems solved using DP, it is difficult to develop generic parallel algorithms for them. However, parallel formulations of the problems in each of the four DP categories have certain similarities. In this chapter, we discuss parallel DP formulations for sample problems in each class. These samples suggest parallel algorithms for other problems in the same class. Note, however, that not all DP problems can be parallelized as illustrated in these examples.
We can solve many problems by using serial monadic DP formulations. This section discusses the shortest-path problem for a multistage graph and the 0/1 knapsack problem. We present parallel algorithms for both and point out the specific properties that influence these parallel formulations.
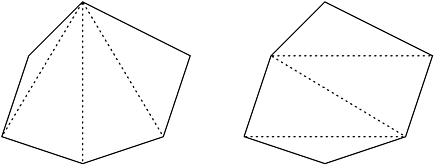
Consider a weighted multistage graph of r + 1 levels, as shown in Figure 12.3. Each node at level i is connected to every node at level i + 1. Levels zero and r contain only one node, and every other level contains n nodes. We refer to the node at level zero as the starting node S and the node at level r as the terminating node R. The objective of this problem is to find the shortest path from S to R. The ith node at level l in the graph is labeled ![]() . The cost of an edge connecting
. The cost of an edge connecting ![]() to node
to node ![]() is labeled
is labeled ![]() . The cost of reaching the goal node R from any node
. The cost of reaching the goal node R from any node ![]() is represented by
is represented by ![]() . If there are n nodes at level l, the vector
. If there are n nodes at level l, the vector ![]() is referred to as Cl. The shortest-path problem reduces to computing C0. Since the graph has only one starting node,
is referred to as Cl. The shortest-path problem reduces to computing C0. Since the graph has only one starting node, ![]() . The structure of the graph is such that any path from
. The structure of the graph is such that any path from ![]() to R includes a node
to R includes a node ![]() (0 ≤ j ≤ n − 1). The cost of any such path is the sum of the cost of the edge between
(0 ≤ j ≤ n − 1). The cost of any such path is the sum of the cost of the edge between ![]() and
and ![]() and the cost of the shortest path between
and the cost of the shortest path between ![]() and R (which is given by
and R (which is given by ![]() ). Thus,
). Thus, ![]() , the cost of the shortest path between
, the cost of the shortest path between ![]() and R, is equal to the minimum cost over all paths through each node in level l + 1. Therefore,
and R, is equal to the minimum cost over all paths through each node in level l + 1. Therefore,
Figure 12.3. An example of a serial monadic DP formulation for finding the shortest path in a graph whose nodes can be organized into levels.
Since all nodes ![]() have only one edge connecting them to the goal node R at level r, the cost
have only one edge connecting them to the goal node R at level r, the cost ![]() is equal to
is equal to ![]() . Hence,
. Hence,
Because Equation 12.2 contains only one recursive term in its right-hand side, it is a monadic formulation. Note that the solution to a subproblem requires solutions to subproblems only at the immediately preceding level. Consequently, this is a serial monadic formulation.
Using this recursive formulation of the shortest-path problem, the cost of reaching the goal node R from any node at level l (0 < l < r − 1) is
Now consider the operation of multiplying a matrix with a vector. In the matrix-vector product, if the addition operation is replaced by minimization and the multiplication operation is replaced by addition, the preceding set of equations is equivalent to
where Cl and Cl+1 are n × 1 vectors representing the cost of reaching the goal node from each node at levels l and l + 1, and Ml,l+1 is an n × n matrix in which entry (i, j) stores the cost of the edge connecting node i at level l to node j at level l + 1. This matrix is
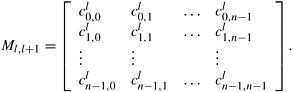
The shortest-path problem has thus been reformulated as a sequence of matrix-vector multiplications. On a sequential computer, the DP formulation starts by computing Cr −1 from Equation 12.3, and then computes Cr −k−1 for k = 1, 2, ..., r −2 using Equation 12.4. Finally, C0 is computed using Equation 12.2.
Since there are n nodes at each level, the cost of computing each vector Cl is Θ(n2). The parallel algorithm for this problem can be derived using the parallel algorithms for the matrix-vector product discussed in Section 8.1. For example, Θ(n) processing elements can compute each vector Cl in time Θ(n) and solve the entire problem in time Θ(rn). Recall that r is the number of levels in the graph.
Many serial monadic DP formulations with dependency graphs identical to the one considered here can be parallelized using a similar parallel algorithm. For certain dependency graphs, however, this formulation is unsuitable. Consider a graph in which each node at a level can be reached from only a small fraction of nodes at the previous level. Then matrix Ml,l+1 contains many elements with value ∞. In this case, matrix M is considered to be a sparse matrix for the minimization and addition operations. This is because, for all x, x + ∞ = ∞, and min{x, ∞} = x. Therefore, the addition and minimization operations need not be performed for entries whose value is ∞. If we use a regular dense matrix-vector multiplication algorithm, the computational complexity of each matrix-vector multiplication becomes significantly higher than that of the corresponding sparse matrix-vector multiplication. Consequently, we must use a sparse matrix-vector multiplication algorithm to compute each vector.
A one-dimensional 0/1 knapsack problem is defined as follows. We are given a knapsack of capacity c and a set of n objects numbered 1, 2, ..., n. Each object i has weight wi and profit pi. Object profits and weights are integers. Let v = [v1, v2, ..., vn] be a solution vector in which vi = 0 if object i is not in the knapsack, and vi = 1 if it is in the knapsack. The goal is to find a subset of objects to put into the knapsack so that
(that is, the objects fit into the knapsack) and
is maximized (that is, the profit is maximized).
A straightforward method to solve this problem is to consider all 2n possible subsets of the n objects and choose the one that fits into the knapsack and maximizes the profit. Here we provide a DP formulation that is faster than the simple method when c = O (2n /n). Let F [i, x] be the maximum profit for a knapsack of capacity x using only objects {1, 2, ..., i}. Then F [n, c] is the solution to the problem. The DP formulation for this problem is as follows:
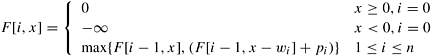
This recursive equation yields a knapsack of maximum profit. When the current capacity of the knapsack is x, the decision to include object i can lead to one of two situations: (i) the object is not included, knapsack capacity remains x , and profit is unchanged; (ii) the object is included, knapsack capacity becomes x − wi, and profit increases by pi. The DP algorithm decides whether or not to include an object based on which choice leads to maximum profit.
The sequential algorithm for this DP formulation maintains a table F of size n × c. The table is constructed in row-major order. The algorithm first determines the maximum profit by using only the first object with knapsacks of different capacities. This corresponds to filling the first row of the table. Filling entries in subsequent rows requires two entries from the previous row: one from the same column and one from the column offset by the weight of the object. Thus, the computation of an arbitrary entry F [i, j] requires F [i − 1, j] and F [i − 1, j − wi]. This is illustrated in Figure 12.4. Computing each entry takes constant time; the sequential run time of this algorithm is Θ(nc).
![Computing entries of table F for the 0/1 knapsack problem. The computation of entry F[i, j] requires communication with processing elements containing entries F[i − 1, j] and F[i − 1, j − wi].](http://imgdetail.ebookreading.net/software_development/21/0201648652/0201648652__introduction-to-parallel__0201648652__graphics__12fig23.gif)
Figure 12.4. Computing entries of table F for the 0/1 knapsack problem. The computation of entry F[i, j] requires communication with processing elements containing entries F[i − 1, j] and F[i − 1, j − wi].
This formulation is a serial monadic formulation. The subproblems F [i, x] are organized into n levels for i = 1, 2, ..., n. Computation of problems in level i depends only on the subproblems at level i − 1. Hence the formulation is serial. The formulation is monadic because each of the two alternate solutions of F [i, x] depends on only one subproblem. Furthermore, dependencies between levels are sparse because a problem at one level depends only on two subproblems from previous level.
Consider a parallel formulation of this algorithm on a CREW PRAM with c processing elements labeled P0 to Pc−1. Processing element Pr −1 computes the rth column of matrix F. When computing F [j, r] during iteration j, processing element Pr −1 requires the values F [j − 1, r] and F [j − 1, r − wj]. Processing element Pr −1 can read any element of matrix F in constant time, so computing F [j, r] also requires constant time. Therefore, each iteration takes constant time. Since there are n iterations, the parallel run time is Θ(n). The formulation uses c processing elements, hence its processor-time product is Θ(nc). Therefore, the algorithm is cost-optimal.
Let us now consider its formulation on a distributed memory machine with c-processing elements. Table F is distributed among the processing elements so that each processing element is responsible for one column. This is illustrated in Figure 12.4. Each processing element locally stores the weights and profits of all objects. In the jth iteration, for computing F [j, r] at processing element Pr −1, F [j − 1, r] is available locally but F [j − 1, r − wj] must be fetched from another processing element. This corresponds to the circular wj -shift operation described in Section 4.6. The time taken by this circular shift operation on p processing elements is bounded by (ts + twm) log p for a message of size m on a network with adequate bandwidth. Since the size of the message is one word and we have p = c, this time is given by (ts + tw) log c. If the sum and maximization operations take time tc, then each iteration takes time tc + (ts + tw) log c. Since there are n such iterations, the total time is given by O (n log c). The processor-time product for this formulation is O (nc log c); therefore, the algorithm is not cost-optimal.
Let us see what happens to this formulation as we increase the number of elements per processor. Using p-processing elements, each processing element computes c/p elements of the table in each iteration. In the jth iteration, processing element P0 computes the values of elements F [j, 1], ..., F [j, c/p], processing element P1 computes values of elements F [j, c/p + 1], ..., F [j, 2c/p], and so on. Computing the value of F [j, k], for any k, requires values F [j − 1, k] and F [j − 1, k − wj]. Required values of the F table can be fetched from remote processing elements by performing a circular shift. Depending on the values of wj and p, the required nonlocal values may be available from one or two processing elements. Note that the total number of words communicated via these messages is c/p irrespective of whether they come from one or two processing elements. The time for this operation is at most (2ts + twc/p) assuming that c/p is large and the network has enough bandwidth (Section 4.6). Since each processing element computes c/p such elements, the total time for each iteration is tcc/p + 2ts + twc/p. Therefore, the parallel run time of the algorithm for n iterations is n(tcc/p + 2ts + twc/p). In asymptotic terms, this algorithm’s parallel run time is O (nc/p). Its processor-time product is O (nc), which is cost-optimal.
There is an upper bound on the efficiency of this formulation because the amount of data that needs to be communicated is of the same order as the amount of computation. This upper bound is determined by the values of tw and tc (Problem 12.1).
The DP algorithm for determining the longest common subsequence of two given sequences can be formulated as a nonserial monadic DP formulation.
Given a sequence A = <a1, a2, ..., an>, a subsequence of A can be formed by deleting some entries from A. For example, <a, b, z> is a subsequence of <c, a, d, b, r, z>, but <a, c, z> and <a, d, l> are not. The longest-common-subsequence (LCS) problem can be stated as follows. Given two sequences A = <a1, a2, ..., an> and B = <b1, b2, ..., bm>, find the longest sequence that is a subsequence of both A and B. For example, if A = <c, a, d, b, r, z> and B = <a, s, b, z>, the longest common subsequence of A and B is <a, b, z>.
Let F [i, j] denote the length of the longest common subsequence of the first i elements of A and the first j elements of B. The objective of the LCS problem is to determine F [n, m]. The DP formulation for this problem expresses F [i, j] in terms of F [i − 1, j − 1], F [i, j − 1], and F [i − 1, j] as follows:
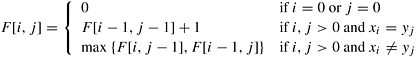
Given sequences A and B , consider two pointers pointing to the start of the sequences. If the entries pointed to by the two pointers are identical, then they form components of the longest common subsequence. Therefore, both pointers can be advanced to the next entry of the respective sequences and the length of the longest common subsequence can be incremented by one. If the entries are not identical then two situations arise: the longest common subsequence may be obtained from the longest subsequence of A and the sequence obtained by advancing the pointer to the next entry of B; or the longest subsequence may be obtained from the longest subsequence of B and the sequence obtained by advancing the pointer to the next entry of A. Since we want to determine the longest subsequence, the maximum of these two must be selected.
The sequential implementation of this DP formulation computes the values in table F in row-major order. Since there is a constant amount of computation at each entry in the table, the overall complexity of this algorithm is Θ(nm). This DP formulation is nonserial monadic, as illustrated in Figure 12.5(a). Treating nodes along a diagonal as belonging to one level, each node depends on two subproblems at the preceding level and one subproblem two levels earlier. The formulation is monadic because a solution to any subproblem at a level is a function of only one of the solutions at preceding levels. (Note that, for the third case in Equation 12.5, both F [i, j − 1] and F [i − 1, j] are possible solutions to F [i, j], and the optimal solution to F [i, j] is the maximum of the two.) Figure 12.5 shows that this problem has a very regular structure.

Figure 12.5. (a) Computing entries of table F for the longest-common-subsequence problem. Computation proceeds along the dotted diagonal lines. (b) Mapping elements of the table to processing elements.
Example 12.2 Computing LCS of two amino-acid sequences
Let us consider the LCS of two amino-acid sequences H E A G A W G H E E and P A W H E A E. For the interested reader, the names of the corresponding amino-acids are A: Alanine, E: Glutamic acid, G: Glycine, H: Histidine, P: Proline, and W: Tryptophan. The table of F entries for these two sequences is shown in Figure 12.6. The LCS of the two sequences, as determined by tracing back from the maximum score and enumerating all the matches, is A W H E E. ▪
To simplify the discussion, we discuss parallel formulation only for the case in which n = m. Consider a parallel formulation of this algorithm on a CREW PRAM with n processing elements. Each processing element Pi computes the ith column of table F. Table entries are computed in a diagonal sweep from the top-left to the bottom-right corner. Since there are n processing elements, and each processing element can access any entry in table F, the elements of each diagonal are computed in constant time (the diagonal can contain at most n elements). Since there are 2n − 1 such diagonals, the algorithm requires Θ(n) iterations. Thus, the parallel run time is Θ(n). The algorithm is cost-optimal, since its Θ(n2) processor-time product equals the sequential complexity.
This algorithm can be adapted to run on a logical linear array of n processing elements by distributing table F among different processing elements. Note that this logical topology can be mapped to a variety of physical architectures using embedding techniques in Section 2.7.1. Processing element Pi stores the (i + 1)th column of the table. Entries in table F are assigned to processing elements as illustrated in Figure 12.5(b). When computing the value of F [i, j], processing element Pj −1 may need either the value of F [i − 1, j − 1] or the value of F [i, j − 1] from the processing element to its left. It takes time ts + tw to communicate a single word from a neighboring processing element. To compute each entry in the table, a processing element needs a single value from its immediate neighbor, followed by the actual computation, which takes time tc. Since each processing element computes a single entry on the diagonal, each iteration takes time (ts + tw + tc). The algorithm makes (2n − 1) diagonal sweeps (iterations) across the table; thus, the total parallel run time is
Since the sequential run time is n2tc, the efficiency of this algorithm is
A careful examination of this expression reveals that it is not possible to obtain efficiencies above a certain threshold. To compute this threshold, assume it is possible to communicate values between processing elements instantaneously; that is, ts = tw = 0. In this case, the efficiency of the parallel algorithm is
Thus, the efficiency is bounded above by 0.5. This upper bound holds even if multiple columns are mapped to a processing element. Higher efficiencies are possible using alternate mappings (Problem 12.3).
Note that the basic characteristic that allows efficient parallel formulations of this algorithm is that table F can be partitioned so computing each element requires data only from neighboring processing elements. In other words, the algorithm exhibits locality of data access.
Floyd’s algorithm for determining the shortest paths between all pairs of nodes in a graph can be reformulated as a serial polyadic DP formulation.
Consider a weighted graph G, which consists of a set of nodes V and a set of edges E. An edge from node i to node j in E has a weight ci, j. Floyd’s algorithm determines the cost di, j of the shortest path between each pair of nodes (i, j) in V (Section 10.4.2). The cost of a path is the sum of the weights of the edges in the path.
Let ![]() be the minimum cost of a path from node i to node j, using only nodes v0, v1, ..., vk−1. The functional equation of the DP formulation for this problem is
be the minimum cost of a path from node i to node j, using only nodes v0, v1, ..., vk−1. The functional equation of the DP formulation for this problem is
Since ![]() is the shortest path from node i to node j using all n nodes, it is also the cost of the overall shortest path between nodes i and j . The sequential formulation of this algorithm requires n iterations, and each iteration requires time Θ(n2). Thus, the overall run time of the sequential algorithm is Θ(n3).
is the shortest path from node i to node j using all n nodes, it is also the cost of the overall shortest path between nodes i and j . The sequential formulation of this algorithm requires n iterations, and each iteration requires time Θ(n2). Thus, the overall run time of the sequential algorithm is Θ(n3).
Equation 12.6 is a serial polyadic formulation. Nodes ![]() can be partitioned into n levels, one for each value of k. Elements at level k + 1 depend only on elements at level k. Hence, the formulation is serial. The formulation is polyadic since one of the solutions to
can be partitioned into n levels, one for each value of k. Elements at level k + 1 depend only on elements at level k. Hence, the formulation is serial. The formulation is polyadic since one of the solutions to ![]() requires a composition of solutions to two subproblems
requires a composition of solutions to two subproblems ![]() and
and ![]() from the previous level. Furthermore, the dependencies between levels are sparse because the computation of each element in
from the previous level. Furthermore, the dependencies between levels are sparse because the computation of each element in ![]() requires only three results from the preceding level (out of n2).
requires only three results from the preceding level (out of n2).
A simple CREW PRAM formulation of this algorithm uses n2 processing elements. Processing elements are organized into a logical two-dimensional array in which processing element Pi,j computes the value of ![]() for k = 1, 2, ..., n. In each iteration k, processing element Pi,j requires the values
for k = 1, 2, ..., n. In each iteration k, processing element Pi,j requires the values ![]() ,
, ![]() , and
, and ![]() . Given these values, it computes the value of
. Given these values, it computes the value of ![]() in constant time. Therefore, the PRAM formulation has a parallel run time of Θ(n). This formulation is cost-optimal because its processor-time product is the same as the sequential run time of Θ(n3). This algorithm can be adapted to various practical architectures to yield efficient parallel formulations (Section 10.4.2).
in constant time. Therefore, the PRAM formulation has a parallel run time of Θ(n). This formulation is cost-optimal because its processor-time product is the same as the sequential run time of Θ(n3). This algorithm can be adapted to various practical architectures to yield efficient parallel formulations (Section 10.4.2).
As with serial monadic formulations, data locality is of prime importance in serial polyadic formulations since many such formulations have sparse connectivity between levels.
In nonserial polyadic DP formulations, in addition to processing subproblems at a level in parallel, computation can also be pipelined to increase efficiency. We illustrate this with the optimal matrix-parenthesization problem.
Consider the problem of multiplying n matrices, A1, A2, ..., An, where each Ai is a matrix with ri −1 rows and ri columns. The order in which the matrices are multiplied has a significant impact on the total number of operations required to evaluate the product.
Example 12.3 Optimal matrix parenthesization
Consider three matrices A1, A2, and A3 of dimensions 10 × 20, 20 × 30, and 30 × 40, respectively. The product of these matrices can be computed as (A1 × A2) × A3 or as A1 × (A2 × A3). In (A1 × A2) × A3, computing (A1 × A2) requires 10 × 20 × 30 operations and yields a matrix of dimensions 10 × 30. Multiplying this by A3 requires 10 × 30 × 40 additional operations. Therefore the total number of operations is 10 × 20 × 30 + 10 × 30 × 40 = 18000. Similarly, computing A1 × (A2 × A3) requires 20 × 30 × 40 + 10 × 20 × 40 = 32000 operations. Clearly, the first parenthesization is desirable. ▪
The objective of the parenthesization problem is to determine a parenthesization that minimizes the number of operations. Enumerating all possible parenthesizations is not feasible since there are exponentially many of them.
Let C [i, j] be the optimal cost of multiplying the matrices Ai ,..., Aj. This chain of matrices can be expressed as a product of two smaller chains, Ai, Ai +1,..., Ak and Ak+1 ,..., Aj. The chain Ai, Ai +1 ,..., Ak results in a matrix of dimensions ri −1 × rk, and the chain Ak+1 ,..., Aj results in a matrix of dimensions rk × rj. The cost of multiplying these two matrices is ri −1rk rj. Hence, the cost of the parenthesization (Ai, Ai +1 ,..., Ak)( Ak+1 ,..., Aj) is given by C [i, k] + C [k + 1, j] + ri −1rk rj. This gives rise to the following recurrence relation for the parenthesization problem:
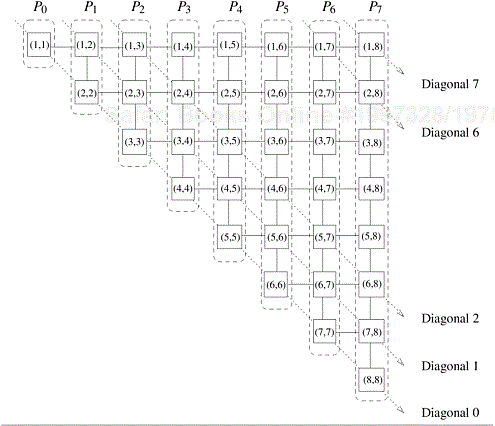
Given Equation 12.7, the problem reduces to finding the value of C [1, n]. The composition of costs of matrix chains is shown in Figure 12.7. Equation 12.7 can be solved if we use a bottom-up approach for constructing the table C that stores the values C [i, j]. The algorithm fills table C in an order corresponding to solving the parenthesization problem on matrix chains of increasing length. Visualize this by thinking of filling in the table diagonally (Figure 12.8). Entries in diagonal l corresponds to the cost of multiplying matrix chains of length l + 1. From Equation 12.7, we can see that the value of C [i, j] is computed as min{C [i, k]+C [k +1, j]+ri −1rk rj}, where k can take values from i to j −1. Therefore, computing C [i, j] requires that we evaluate (j − i) terms and select their minimum. The computation of each term takes time tc, and the computation of C [i, j] takes time (j − i)tc. Thus, each entry in diagonal l can be computed in time ltc.
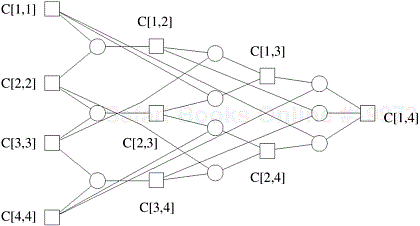
Figure 12.7. A nonserial polyadic DP formulation for finding an optimal matrix parenthesization for a chain of four matrices. A square node represents the optimal cost of multiplying a matrix chain. A circle node represents a possible parenthesization.
In computing the cost of the optimal parenthesization sequence, the algorithm computes (n − 1) chains of length two. This takes time (n − 1)tc. Similarly, computing (n − 2) chains of length three takes time (n − 2)2tc. In the final step, the algorithm computes one chain of length n. This takes time (n − 1)tc. Thus, the sequential run time of this algorithm is
The sequential complexity of the algorithm is Θ(n3).
Consider the parallel formulation of this algorithm on a logical ring of n processing elements. In step l, each processing element computes a single element belonging to the lth diagonal. Processing element Pi computes the (i + 1)th column of Table C. Figure 12.8 illustrates the partitioning of the table among different processing elements. After computing the assigned value of the element in table C, each processing element sends its value to all other processing elements using an all-to-all broadcast (Section 4.2). Therefore, the assigned value in the next iteration can be computed locally. Computing an entry in table C during iteration l takes time ltc because it corresponds to the cost of multiplying a chain of length l + 1. An all-to-all broadcast of a single word on n processing elements takes time ts log n + tw(n − 1) (Section 4.2). The total time required to compute the entries along diagonal l is ltc + ts log n + tw(n − 1). The parallel run time is the sum of the time taken over computation of n − 1 diagonals.
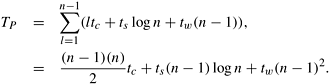
The parallel run time of this algorithm is Θ(n2). Since the processor-time product is Θ(n3), which is the same as the sequential complexity, this algorithm is cost-optimal.
When using p processing elements (1 ≤ p ≤ n) organized in a logical ring, if there are n nodes in a diagonal, each processing element stores n/p nodes. Each processing element computes the cost C [i, j] of the entries assigned to it. After computation, an all-to-all broadcast sends the solution costs of the subproblems for the most recently computed diagonal to all the other processing elements. Because each processing element has complete information about subproblem costs at preceding diagonals, no other communication is required. The time taken for all-to-all broadcast of n/p words is ts log p + twn(p − 1)/p ≈ ts log p + twn. The time to compute n/p entries of the table in the lth diagonal is ltcn/p. The parallel run time is
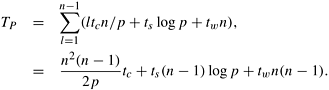
In order terms, TP = Θ(n3/p) + Θ(n2). Here, Θ(n3/p) is the computation time, and Θ(n2) the communication time. If n is sufficiently large with respect to p, communication time can be made an arbitrarily small fraction of computation time, yielding linear speedup.
This formulation can use at most Θ(n) processing elements to accomplish the task in time Θ(n2). This time can be improved by pipelining the computation of the cost C [i, j] on n(n + 1)/2 processing elements. Each processing element computes a single entry c(i, j) of matrix C. Pipelining works due to the nonserial nature of the problem. Computation of an entry on a diagonal t does not depend only on the entries on diagonal t − 1 but also on all the earlier diagonals. Hence work on diagonal t can start even before work on diagonal t − 1 is completed.
This chapter provides a framework for deriving parallel algorithms that use dynamic programming. It identifies possible sources of parallelism, and indicates under what conditions they can be utilized effectively.
By representing computation as a graph, we identify three sources of parallelism. First, the computation of the cost of a single subproblem (a node in a level) can be parallelized. For example, for computing the shortest path in the multistage graph shown in Figure 12.3, node computation can be parallelized because the complexity of node computation is itself Θ(n). For many problems, however, node computation complexity is lower, limiting available parallelism.
Second, subproblems at each level can be solved in parallel. This provides a viable method for extracting parallelism from a large class of problems (including all the problems in this chapter).
The first two sources of parallelism are available to both serial and nonserial formulations. Nonserial formulations allow a third source of parallelism: pipelining of computations among different levels. Pipelining makes it possible to start solving a problem as soon as the subproblems it depends on are solved. This form of parallelism is used in the parenthesization problem.
Note that pipelining was also applied to the parallel formulation of Floyd’s all-pairs shortest-paths algorithm in Section 10.4.2. As discussed in Section 12.4, this algorithm corresponds to a serial DP formulation. The nature of pipelining in this algorithm is different from the one in nonserial DP formulation. In the pipelined version of Floyd’s algorithm, computation in a stage is pipelined with the communication among earlier stages. If communication cost is zero (as in a PRAM), then Floyd’s algorithm does not benefit from pipelining.
Throughout the chapter, we have seen the importance of data locality. If the solution to a problem requires results from other subproblems, the cost of communicating those results must be less than the cost of solving the problem. In some problems (the 0/1 knapsack problem, for example) the degree of locality is much smaller than in other problems such as the longest-common-subsequence problem and Floyd’s all-pairs shortest-paths algorithm.
Dynamic programming was originally presented by Bellman [Bel57] for solving multistage decision problems. Various formal models have since been developed for DP [KH67, MM73, KK88b]. Several textbooks and articles present sequential DP formulations of the longest-common-subsequence problem, the matrix chain multiplication problem, the 0/1 knapsack problem, and the shortest-path problem [CLR90, HS78, PS82, Bro79].
Li and Wah [LW85, WL88] show that monadic serial DP formulations can be solved in parallel on systolic arrays as matrix-vector products. They further present a more concurrent but non-cost-optimal formulation by formulating the problem as a matrix-matrix product. Ranka and Sahni [RS90b] present a polyadic serial formulation for the string editing problem and derive a parallel formulation based on a checkerboard partitioning.
The DP formulation of a large class of optimization problems is similar to that of the optimal matrix-parenthesization problem. Some examples of these problems are optimal triangularization of polygons, optimal binary search trees [CLR90], and CYK parsing [AU72]. The serial complexity of the standard DP formulation for all these problems is Θ(n3). Several parallel formulations have been proposed by Ibarra et al. [IPS91] that use Θ(n) processing elements on a hypercube and that solve the problem in time Θ(n2). Guibas, Kung, and Thompson [GKT79] present a systolic algorithm that uses Θ(n2) processing cells and solves the problem in time Θ(n). Karypis and Kumar [KK93] analyze three distinct mappings of the systolic algorithm presented by Guibas et al. [GKT79] and experimentally evaluate them by using the matrix-multiplication parenthesization problem. They show that a straightforward mapping of this algorithm to a mesh architecture has an upper bound on efficiency of 1/12. They also present a better mapping without this drawback, and show near-linear speedup on a mesh embedded into a 256-processor hypercube for the optimal matrix-parenthesization problem.
Many faster parallel algorithms for solving the parenthesization problem have been proposed, but they are not cost-optimal and are applicable only to theoretical models such as the PRAM. For example, a generalized method for parallelizing such programs is described by Valiant et al. [VSBR83] that leads directly to formulations that run in time O (log2 n) on O (n9) processing elements. Rytter [Ryt88] uses the parallel pebble game on trees to reduce the number of processing elements to O (n6/log n) for a CREW PRAM and O (n6) for a hypercube, yet solves this problem in time O (log2 n). Huang et al. [HLV90] present a similar algorithm for CREW PRAM models that run in time O (![]() log n) on O (n3.5 log n) processing elements. DeMello et al. [DCG90] use vectorized formulations of DP for the Cray to solve optimal control problems.
log n) on O (n3.5 log n) processing elements. DeMello et al. [DCG90] use vectorized formulations of DP for the Cray to solve optimal control problems.
As we have seen, the serial polyadic formulation of the 0/1 knapsack problem is difficult to parallelize due to lack of communication locality. Lee et al. [LSS88] use specific characteristics of the knapsack problem and derive a divide-and-conquer strategy for parallelizing the DP algorithm for the 0/1 knapsack problem on a MIMD message-passing computer (Problem 12.2). Lee et al. demonstrate experimentally that it is possible to obtain linear speedup for large instances of the problem on a hypercube.
12.1 Consider the parallel algorithm for solving the 0/1 knapsack problem in Section 12.2.2. Derive the speedup and efficiency for this algorithm. Show that the efficiency of this algorithm cannot be increased beyond a certain value by increasing the problem size for a fixed number of processing elements. What is the upper bound on efficiency for this formulation as a function of tw and tc?
12.2 [LSS88] In the parallel formulation of the 0/1 knapsack problem presented in Section 12.2.2, the degree of concurrency is proportional to c, the knapsack capacity. Also this algorithm has limited data locality, as the amount of data to be communicated is of the same order of magnitude as the computation at each processing element. Lee et al. present another formulation in which the degree of concurrency is proportional to n, the number of weights. This formulation also has much more data locality. In this formulation, the set of weights is partitioned among processing elements. Each processing element computes the maximum profit it can achieve from its local weights for knapsacks of various sizes up to c. This information is expressed as lists that are merged to yield the global solution. Compute the parallel run time, speedup, and efficiency of this formulation. Compare the performance of this algorithm with that in Section 12.2.2.
12.3 We noticed that the parallel formulation of the longest-common-subsequence problem has an upper bound of 0.5 on its efficiency. It is possible to use an alternate mapping to achieve higher efficiency for this problem. Derive a formulation that does not suffer from this upper bound, and give the run time of this formulation.
Hint: Consider the blocked-cyclic mapping discussed in Section 3.4.1.
12.4 [HS78] The traveling salesman problem (TSP) is defined as follows: Given a set of cities and the distance between each pair of cities, determine a tour through all cities of minimum length. A tour of all cities is a trip visiting each city once and returning to the starting point. Its length is the sum of distances traveled. This problem can be solved using a DP formulation. View the cities as vertices in a graph G(V, E). Let the set of cities V be represented by {v1, v2, ..., vn} and let S ⊆ {v2, v3, ..., vn}. Furthermore, let ci,j be the distance between cities i and j. If f (S, k) represents the cost of starting at city v1, passing through all the cities in set S, and terminating in city k, then the following recursive equations can be used to compute f (S, k):
Based on Equation 12.9, derive a parallel formulation. Compute the parallel run time and the speedup. Is this parallel formulation cost-optimal?
12.5 [HS78] Consider the problem of merging two sorted files containing O (n) and O (m) records. These files can be merged into a sorted file in time O (m + n). Given r such files, the problem of merging them into a single file can be formulated as a sequence of merge operations performed on pairs of files. The overall cost of the merge operation is a function of the sequence in which they are merged. The optimal merge order can be formulated as a greedy problem and its parallel formulations derived using principles illustrated in this chapter.
Write down the recursive equations for this problem. Derive a parallel formulation for merging files using p processing elements. Compute the parallel run time and speedup, and determine whether your parallel formulation is cost-optimal.
12.6 [HS78] Consider the problem of designing a fault-tolerant circuit containing n devices connected in series, as shown in Figure 12.9(a). If the probability of failure of each of these devices is given by fi, the overall probability of failure of the circuit is given by
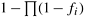 . Here,
. Here, 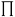 represents a product of specified terms. The reliability of this circuit can be improved by connecting multiple functional devices in parallel at each stage, as shown in Figure 12.9(b). If stage i in the circuit has ri duplicate functional units, each with a probability of failure given by fi , then the overall probability of failure of this stage is reduced to
represents a product of specified terms. The reliability of this circuit can be improved by connecting multiple functional devices in parallel at each stage, as shown in Figure 12.9(b). If stage i in the circuit has ri duplicate functional units, each with a probability of failure given by fi , then the overall probability of failure of this stage is reduced to 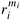 and the overall probability of failure of the circuit is given by
and the overall probability of failure of the circuit is given by 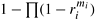 . In general, for physical reasons, the probability of failure at a particular level may not be
. In general, for physical reasons, the probability of failure at a particular level may not be 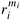 , but some function ϕi (ri, mi). The objective of the problem is to minimize the overall probability of failure of the circuit,
, but some function ϕi (ri, mi). The objective of the problem is to minimize the overall probability of failure of the circuit, 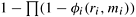 .
.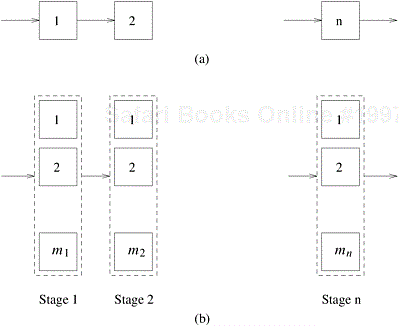
Figure 12.9. (a) n devices connected in a series within a circuit. (b) Each stage in the circuit now has mi functional units. There are n such stages connected in the series.
Construction cost adds a new dimension to this problem. If each of the functional units used at stage i costs ci then due to cost constraints, the overall cost
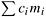 should be less than a fixed quantity c.
should be less than a fixed quantity c.The problem can be formally defined as
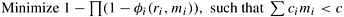
where mi > 0 and 0 < i ≤ n.
Let fi (x) represent the reliability of a system with i stages of cost x. The optimal solution is given by fn (c). The recursive equation for fi (x) is as follows:
Classify this formulation into one of the four DP categories, and derive a parallel formulation for this algorithm. Determine its parallel run time, speedup, and isoefficiency function.
12.7 [CLR90] Consider the simplified optimal polygon-triangulation problem. This problem can be defined as follows. Given a simple polygon, break the polygon into a set of triangles by connecting nodes of the polygon with chords. This process is illustrated in Figure 12.10. The cost of constructing a triangle with nodes vi, vj, and vk is defined by a function f (vi, vj, vk). For this problem, let the cost be the total length of the edges of the triangle (using Euclidean distance). The optimal polygon-triangulation problem breaks up a polygon into a set of triangles such that the total length of each triangle (the sum of the individual lengths) is minimized. Give a DP formulation for this problem. Classify it into one of the four categories and derive a parallel formulation for p processing elements. Determine its parallel run time, speedup, and isoefficiency function.
Hint: This problem is similar to the optimal matrix-parenthesization problem.