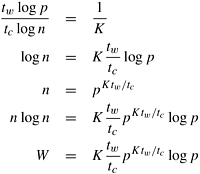The discrete Fourier transform (DFT) plays an important role in many scientific and technical applications, including time series and waveform analysis, solutions to linear partial differential equations, convolution, digital signal processing, and image filtering. The DFT is a linear transformation that maps n regularly sampled points from a cycle of a periodic signal, like a sine wave, onto an equal number of points representing the frequency spectrum of the signal. In 1965, Cooley and Tukey devised an algorithm to compute the DFT of an n-point series in Θ(n log n) operations. Their new algorithm was a significant improvement over previously known methods for computing the DFT, which required Θ(n2) operations. The revolutionary algorithm by Cooley and Tukey and its variations are referred to as the fast Fourier transform (FFT). Due to its wide application in scientific and engineering fields, there has been a lot of interest in implementing FFT on parallel computers.
Several different forms of the FFT algorithm exist. This chapter discusses its simplest form, the one-dimensional, unordered, radix-2 FFT. Parallel formulations of higher-radix and multidimensional FFTs are similar to the simple algorithm discussed in this chapter because the underlying ideas behind all sequential FFT algorithms are the same. An ordered FFT is obtained by performing bit reversal (Section 13.4) on the output sequence of an unordered FFT. Bit reversal does not affect the overall complexity of a parallel implementation of FFT.
In this chapter we discuss two parallel formulations of the basic algorithm: the binary-exchange algorithm and the transpose algorithm. Depending on the size of the input n, the number of processes p, and the memory or network bandwidth, one of these may run faster than the other.
Consider a sequence X = <X [0], X [1], ..., X [n − 1]> of length n. The discrete Fourier transform of the sequence X is the sequence Y = <Y [0], Y [1], ..., Y [n − 1]>, where
In Equation 13.1, ω is the primitive nth root of unity in the complex plane; that is, ![]() , where e is the base of natural logarithms. More generally, the powers of ω in the equation can be thought of as elements of the finite commutative ring of integers modulo n. The powers of ω used in an FFT computation are also known as twiddle factors.
, where e is the base of natural logarithms. More generally, the powers of ω in the equation can be thought of as elements of the finite commutative ring of integers modulo n. The powers of ω used in an FFT computation are also known as twiddle factors.
The computation of each Y [i] according to Equation 13.1 requires n complex multiplications. Therefore, the sequential complexity of computing the entire sequence Y of length n is Θ(n2). The fast Fourier transform algorithm described below reduces this complexity to Θ(n log n).
Assume that n is a power of two. The FFT algorithm is based on the following step that permits an n-point DFT computation to be split into two (n/2)-point DFT computations:
Let ![]() ; that is,
; that is, ![]() is the primitive (n/2)th root of unity. Then, we can rewrite Equation 13.2 as follows:
is the primitive (n/2)th root of unity. Then, we can rewrite Equation 13.2 as follows:
In Equation 13.3, each of the two summations on the right-hand side is an (n/2)-point DFT computation. If n is a power of two, each of these DFT computations can be divided similarly into smaller computations in a recursive manner. This leads to the recursive FFT algorithm given in Algorithm 13.1. This FFT algorithm is called the radix-2 algorithm because at each level of recursion, the input sequence is split into two equal halves.
Example 13.1. The recursive, one-dimensional, unordered, radix-2 FFT algorithm. Here ![]() .
.
1. procedure R_FFT(X, Y, n, ω) 2. if (n = 1) then Y[0] := X[0] else 3. begin 4. R_FFT(<X[0], X[2], ..., X[n − 2]>, <Q[0], Q[1], ..., Q[n/2]>, n/2, ω2); 5. R_FFT(<X[1], X[3], ..., X[n − 1]>, <T[0], T[1], ..., T[n/2]>, n/2, ω2); 6. for i := 0 to n − 1 do 7. Y[i] :=Q[i mod (n/2)] + ωi T[i mod (n/2)]; 8. end R_FFT
Figure 13.1 illustrates how the recursive algorithm works on an 8-point sequence. As the figure shows, the first set of computations corresponding to line 7 of Algorithm 13.1 takes place at the deepest level of recursion. At this level, the elements of the sequence whose indices differ by n/2 are used in the computation. In each subsequent level, the difference between the indices of the elements used together in a computation decreases by a factor of two. The figure also shows the powers of ω used in each computation.
The size of the input sequence over which an FFT is computed recursively decreases by a factor of two at each level of recursion (lines 4 and 5 of Algorithm 13.1). Hence, the maximum number of levels of recursion is log n for an initial sequence of length n. At the mth level of recursion, 2m FFTs of size n/2m each are computed. Thus, the total number of arithmetic operations (line 7) at each level is Θ(n) and the overall sequential complexity of Algorithm 13.1 is Θ(n log n).
The serial FFT algorithm can also be cast in an iterative form. The parallel implementations of the iterative form are easier to illustrate. Therefore, before describing parallel FFT algorithms, we give the iterative form of the serial algorithm. An iterative FFT algorithm is derived by casting each level of recursion, starting with the deepest level, as an iteration. Algorithm 13.2 gives the classic iterative Cooley-Tukey algorithm for an n-point, one-dimensional, unordered, radix-2 FFT. The program performs log n iterations of the outer loop starting on line 5. The value of the loop index m in the iterative version of the algorithm corresponds to the (log n − m)th level of recursion in the recursive version (Figure 13.1). Just as in each level of recursion, each iteration performs n complex multiplications and additions.
Algorithm 13.2 has two main loops. The outer loop starting at line 5 is executed log n times for an n-point FFT, and the inner loop starting at line 8 is executed n times during each iteration of the outer loop. All operations of the inner loop are constant-time arithmetic operations. Thus, the sequential time complexity of the algorithm is Θ(n log n). In every iteration of the outer loop, the sequence R is updated using the elements that were stored in the sequence S during the previous iteration. For the first iteration, the input sequence X serves as the initial sequence R. The updated sequence X from the final iteration is the desired Fourier transform and is copied to the output sequence Y.
Example 13.2. The Cooley-Tukey algorithm for one-dimensional, unordered, radix-2 FFT. Here ![]() .
.
1. procedure ITERATIVE_FFT(X, Y, n) 2. begin 3. r := log n; 4. for i := 0 to n − 1 do R[i] := X[i]; 5. for m := 0 to r − 1 do /* Outer loop */ 6. begin 7. for i := 0 to n − 1 do S[i]:= R[i]; 8. for i := 0 to n − 1 do /* Inner loop */ 9. begin /* Let (b0b1 ··· br −1) be the binary representation of i */ 10. j := (b0...bm−10bm+1···br −1); 11. k := (b0...bm−11bm+1···br −1); 12.13. endfor; /* Inner loop */ 14. endfor; /* Outer loop */ 15. for i := 0 to n − 1 do Y[i] := R[i]; 16. end ITERATIVE_FFT
Line 12 in Algorithm 13.2 performs a crucial step in the FFT algorithm. This step updates R[i] by using S[j] and S[k]. The indices j and k are derived from the index i as follows. Assume that n = 2r. Since0 ≤ i < n, the binary representation of i contains r bits. Let (b0b1 ···br −1) be the binary representation of index i. In the mth iteration of the outer loop (0 ≤ m < r), index j is derived by forcing the mth most significant bit of i (that is, bm) to zero. Index k is derived by forcing bm to 1. Thus, the binary representations of j and k differ only in their mth most significant bits. In the binary representation of i, bm is either 0 or 1. Hence, of the two indices j and k, one is the same as index i, depending on whether bm = 0 or bm = 1. In the mth iteration of the outer loop, for each i between 0 and n − 1, R[i] is generated by executing line 12 of Algorithm 13.2 on S[i] and on another element of S whose index differs from i only in the mth most significant bit. Figure 13.2 shows the pattern in which these elements are paired for the case in which n = 16.
This section discusses the binary-exchange algorithm for performing FFT on a parallel computer. First, a decomposition is induced by partitioning the input or the output vector. Therefore, each task starts with one element of the input vector and computes the corresponding element of the output. If each task is assigned the same label as the index of its input or output element, then in each of the log n iterations of the algorithm, exchange of data takes place between pairs of tasks with labels differing in one bit position.
In this subsection, we describe the implementation of the binary-exchange algorithm on a parallel computer on which a bisection width (Section 2.4.4) of Θ(p) is available to p parallel processes. Since the pattern of interaction among the tasks of parallel FFT matches that of a hypercube network, we describe the algorithm assuming such an interconnection network. However, the performance and scalability analysis would be valid for any parallel computer with an overall simultaneous data-transfer capacity of O (p).
We first consider a simple mapping in which one task is assigned to each process. Figure 13.3 illustrates the interaction pattern induced by this mapping of the binary-exchange algorithm for n = 16. As the figure shows, process i (0 ≤ i < n) initially stores X [i] and finally generates Y [i]. In each of the log n iterations of the outer loop, process Pi updates the value of R[i] by executing line 12 of Algorithm 13.2. All n updates are performed in parallel.
To perform the updates, process Pi requires an element of S from a process whose label differs from i at only one bit. Recall that in a hypercube, a node is connected to all those nodes whose labels differ from its own at only one bit position. Thus, the parallel FFT computation maps naturally onto a hypercube with a one-to-one mapping of processes to nodes. In the first iteration of the outer loop, the labels of each pair of communicating processes differ only at their most significant bits. For instance, processes P0 to P7 communicate with P8 to P15, respectively. Similarly, in the second iteration, the labels of processes communicating with each other differ at the second most significant bit, and so on.
In each of the log n iterations of this algorithm, every process performs one complex multiplication and addition, and exchanges one complex number with another process. Thus, there is a constant amount of work per iteration. Hence, it takes time Θ(log n) to execute the algorithm in parallel by using a hypercube with n nodes. This hypercube formulation of FFT is cost-optimal because its process-time product is Θ(n log n), the same as the complexity of a serial n-point FFT.
We now consider a mapping in which the n tasks of an n-point FFT are mapped onto p processes, where n > p. For the sake of simplicity, let us assume that both n and p are powers of two, i.e., n = 2r and p = 2d. As Figure 13.4 shows, we partition the sequences into blocks of n/p contiguous elements and assign one block to each process.

Figure 13.4. A 16-point FFT on four processes. Pi denotes the process labeled i. In general, the number of processes is p = 2d and the length of the input sequence is n = 2r.
An interesting property of the mapping shown in Figure 13.4 is that, if (b0b1 ··· br −1) is the binary representation of any i, such that 0 ≤ i < n, then R[i] and S[i] are mapped onto the process labeled (b0···bd−1). That is, the d most significant bits of the index of any element of the sequence are the binary representation of the label of the process that the element belongs to. This property of the mapping plays an important role in determining the amount of communication performed during the parallel execution of the FFT algorithm.
Figure 13.4 shows that elements with indices differing at their d (= 2) most significant bits are mapped onto different processes. However, all elements with indices having the same d most significant bits are mapped onto the same process. Recall from the previous section that an n-point FFT requires r = log n iterations of the outer loop. In the mth iteration of the loop, elements with indices differing in the mth most significant bit are combined. As a result, elements combined during the first d iterations belong to different processes, and pairs of elements combined during the last (r − d) iterations belong to the same processes. Hence, this parallel FFT algorithm requires interprocess interaction only during the first d = log p of the log n iterations. There is no interaction during the last r − d iterations. Furthermore, in the i th of the first d iterations, all the elements that a process requires come from exactly one other process – the one whose label is different at the i th most significant bit.
Each interaction operation exchanges n/p words of data. Therefore, the time spent in communication in the entire algorithm is ts log p + tw(n/p) log p. A process updates n/p elements of R during each of the log n iterations. If a complex multiplication and addition pair takes time tc, then the parallel run time of the binary-exchange algorithm for n-point FFT on a p-node hypercube network is
The process-time product is tcn log n + ts p log p + twn log p. For the parallel system to be cost-optimal, this product should be O (n log n) – the sequential time complexity of the FFT algorithm. This is true for p ≤ n.
The expressions for speedup and efficiency are given by the following equations:
From Section 13.1, we know that the problem size W for an n-point FFT is
Since an n-point FFT can utilize a maximum of n processes with the mapping of Figure 13.3, n ≥ p or n log n ≥ p log p to keep p processes busy. Thus, the isoefficiency function of this parallel FFT algorithm is Ω(p log p) due to concurrency. We now derive the isoefficiency function for the binary exchange algorithm due to the different communication-related terms. We can rewrite Equation 13.5 as
In order to maintain a fixed efficiency E , the expression (ts p log p)/(tcn log n) + (twlog p)/(tc log n) should be equal to a constant 1/K, where K = E/(1 − E). We have defined the constant K in this manner to keep the terminology consistent with Chapter 5. As proposed in Section 5.4.2, we use an approximation to obtain closed expressions for the isoefficiency function. We first determine the rate of growth of the problem size with respect to p that would keep the terms due to ts constant. To do this, we assume tw = 0. Now the condition for maintaining constant efficiency E is as follows:
Equation 13.7 gives the isoefficiency function due to the overhead resulting from interaction latency or the message startup time.
Similarly, we derive the isoefficiency function due to the overhead resulting from tw. We assume that ts = 0; hence, a fixed efficiency E requires that the following relation be maintained:
If the term Ktw/tc is less than one, then the rate of growth of the problem size required by Equation 13.8 is less than Θ(p log p). In this case, Equation 13.7 determines the overall isoefficiency function of this parallel system. However, if Ktw/tc exceeds one, then Equation 13.8 determines the overall isoefficiency function, which is now greater than the isoefficiency function of Θ(p log p) given by Equation 13.7.
For this algorithm, the asymptotic isoefficiency function depends on the relative values of K, tw, and tc. Here, K is an increasing function of the efficiency E to be maintained, tw depends on the communication bandwidth of the parallel computer, and tc depends on the speed of the computation speed of the processors. The FFT algorithm is unique in that the order of the isoefficiency function depends on the desired efficiency and hardware-dependent parameters. In fact, the efficiency corresponding to Ktw/tc = 1(i.e.,1/(1 − E) = tc/tw, or E = tc/(tc + tw)) acts as a kind of threshold. For a fixed tc and tw, efficiencies up to the threshold can be obtained easily. For E ≤ tc/(tc + tw), the asymptotic isoefficiency function is Θ(p log p). Efficiencies much higher than the threshold tc/(tc + tw) can be obtained only if the problem size is extremely large. The reason is that for these efficiencies, the asymptotic isoefficiency function is Θ![]() . The following examples illustrate the effect of the value of Ktw/tc on the isoefficiency function.
. The following examples illustrate the effect of the value of Ktw/tc on the isoefficiency function.
Example 13.1 Threshold effect in the binary-exchange algorithm
Consider a hypothetical hypercube for which the relative values of the hardware parameters are given by tc = 2, tw = 4, and ts = 25. With these values, the threshold efficiency tc/(tc + tw) is 0.33.
Now we study the isoefficiency functions of the binary-exchange algorithm on a hypercube for maintaining efficiencies below and above the threshold. The isoefficiency function of this algorithm due to concurrency is p log p. From Equations 13.7 and 13.8, the isoefficiency functions due to the ts and tw terms in the overhead function are K (ts/tc) p log p and ![]() log p, respectively. To maintain a given efficiency E (that is, for a given K), the overall isoefficiency function is given by:
log p, respectively. To maintain a given efficiency E (that is, for a given K), the overall isoefficiency function is given by:
Figure 13.5 shows the isoefficiency curves given by this function for E = 0.20, 0.25, 0.30, 0.35, 0.40, and 0.45. Notice that the various isoefficiency curves are regularly spaced for efficiencies up to the threshold. However, the problem sizes required to maintain efficiencies above the threshold are much larger. The asymptotic isoefficiency functions for E = 0.20, 0.25, and 0.30 are Θ(p log p). The isoefficiency function for E = 0.40 is Θ(p1.33 log p), and that for E = 0.45 is Θ(p1.64 log p).

Figure 13.5. Isoefficiency functions of the binary-exchange algorithm on a hypercube with tc = 2, tw = 4, and ts = 25 for various values of E.
Figure 13.6 shows the efficiency curve of n-point FFTs on a 256-node hypercube with the same hardware parameters. The efficiency E is computed by using Equation 13.5 for various values of n, when p is equal to 256. The figure shows that the efficiency initially increases rapidly with the problem size, but the efficiency curve flattens out beyond the threshold. ▪
Example 13.1 shows that there is a limit on the efficiency that can be obtained for reasonable problem sizes, and that the limit is determined by the ratio between the CPU speed and the communication bandwidth of the parallel computer being used. This limit can be raised by increasing the bandwidth of the communication channels. However, making the CPUs faster without increasing the communication bandwidth lowers the limit. Hence, the binary-exchange algorithm performs poorly on a parallel computer whose communication and computation speeds are not balanced. If the hardware is balanced with respect to its communication and computation speeds, then the binary-exchange algorithm is fairly scalable, and reasonable efficiencies can be maintained while increasing the problem size at the rate of Θ(p log p).
Now we consider the implementation of the binary-exchange algorithm on a parallel computer whose cross-section bandwidth is less than Θ(p). We choose a mesh interconnection network to illustrate the algorithm and its performance characteristics. Assume that n tasks are mapped onto p processes running on a mesh with ![]() rows and
rows and ![]() columns, and that
columns, and that ![]() is a power of two. Let n = 2r and p = 2d. Also assume that the processes are labeled in a row-major fashion and that the data are distributed in the same manner as for the hypercube; that is, an element with index (b0b1···br −1) is mapped onto the process labeled (b0 ··· bd−1).
is a power of two. Let n = 2r and p = 2d. Also assume that the processes are labeled in a row-major fashion and that the data are distributed in the same manner as for the hypercube; that is, an element with index (b0b1···br −1) is mapped onto the process labeled (b0 ··· bd−1).
As in case of the hypercube, communication takes place only during the first log p iterations between processes whose labels differ at one bit. However, unlike the hypercube, the communicating processes are not directly linked in a mesh. Consequently, messages travel over multiple links and there is overlap among messages sharing the same links. Figure 13.7 shows the messages sent and received by processes 0 and 37 during an FFT computation on a 64-node mesh. As the figure shows, process 0 communicates with processes 1, 2, 4, 8, 16, and 32. Note that all these processes lie in the same row or column of the mesh as that of process 0. Processes 1, 2, and 4 lie in the same row as process 0 at distances of 1, 2, and 4 links, respectively. Processes 8, 16, and 32 lie in the same column, again at distances of 1, 2, and 4 links. More precisely, in log ![]() of the log p steps that require communication, the communicating processes are in the same row, and in the remaining log
of the log p steps that require communication, the communicating processes are in the same row, and in the remaining log ![]() steps, they are in the same column. The number of messages that share at least one link is equal to the number of links that each message traverses (Problem 13.9) because, during a given FFT iteration, all pairs of nodes exchange messages that traverse the same number of links.
steps, they are in the same column. The number of messages that share at least one link is equal to the number of links that each message traverses (Problem 13.9) because, during a given FFT iteration, all pairs of nodes exchange messages that traverse the same number of links.

Figure 13.7. Data communication during an FFT computation on a logical square mesh of 64 processes. The figure shows all the processes with which the processes labeled 0 and 37 exchange data.
The distance between the communicating processes in a row or a column grows from one link to ![]() links, doubling in each of the log
links, doubling in each of the log ![]() iterations. This is true for any process in the mesh, such as process 37 shown in Figure 13.7. Thus, the total time spent in performing rowwise communication is
iterations. This is true for any process in the mesh, such as process 37 shown in Figure 13.7. Thus, the total time spent in performing rowwise communication is ![]() . An equal amount of time is spent in columnwise communication. Recall that we assumed that a complex multiplication and addition pair takes time tc. Since a process performs n/p such calculations in each of the log n iterations, the overall parallel run time is given by the following equation:
. An equal amount of time is spent in columnwise communication. Recall that we assumed that a complex multiplication and addition pair takes time tc. Since a process performs n/p such calculations in each of the log n iterations, the overall parallel run time is given by the following equation:
The speedup and efficiency are given by the following equations:
The process-time product of this parallel system is ![]() . The process-time product should be O (n log n) for cost-optimality, which is obtained when
. The process-time product should be O (n log n) for cost-optimality, which is obtained when ![]() , or p = O (log2 n). Since the communication term due to ts in Equation 13.9 is the same as for the hypercube, the corresponding isoefficiency function is again Θ(p log p) as given by Equation 13.7. By performing isoefficiency analysis along the same lines as in Section 13.2.1, we can show that the isoefficiency function due to the tw term is
, or p = O (log2 n). Since the communication term due to ts in Equation 13.9 is the same as for the hypercube, the corresponding isoefficiency function is again Θ(p log p) as given by Equation 13.7. By performing isoefficiency analysis along the same lines as in Section 13.2.1, we can show that the isoefficiency function due to the tw term is ![]() (Problem 13.4). Given this isoefficiency function, the problem size must grow exponentially with the number of processes to maintain constant efficiency. Hence, the binary-exchange FFT algorithm is not very scalable on a mesh.
(Problem 13.4). Given this isoefficiency function, the problem size must grow exponentially with the number of processes to maintain constant efficiency. Hence, the binary-exchange FFT algorithm is not very scalable on a mesh.
The communication overhead of the binary-exchange algorithm on a mesh cannot be reduced by using a different mapping of the sequences onto the processes. In any mapping, there is at least one iteration in which pairs of processes that communicate with each other are at least ![]() links apart (Problem 13.2). The algorithm inherently requires Θ(p) bisection bandwidth on a p-node ensemble, and on an architecture like a 2-D mesh with Θ
links apart (Problem 13.2). The algorithm inherently requires Θ(p) bisection bandwidth on a p-node ensemble, and on an architecture like a 2-D mesh with Θ![]() bisection bandwidth, the communication time cannot be asymptotically better than
bisection bandwidth, the communication time cannot be asymptotically better than ![]() as discussed above.
as discussed above.
So far, we have described a parallel formulation of the FFT algorithm on a hypercube and a mesh, and have discussed its performance and scalability in the presence of communication overhead on both architectures. In this section, we discuss another source of overhead that can be present in a parallel FFT implementation.
Recall from Algorithm 13.2 that the computation step of line 12 multiplies a power of ω (a twiddle factor) with an element of S. For an n-point FFT, line 12 executes n log n times in the sequential algorithm. However, only n distinct powers of ω (that is, ω0, ω1, ω2, ..., ωn−1) are used in the entire algorithm. So some of the twiddle factors are used repeatedly. In a serial implementation, it is useful to precompute and store all n twiddle factors before starting the main algorithm. That way, the computation of twiddle factors requires only Θ(n) complex operations rather than the Θ(n log n) operations needed to compute all twiddle factors in each iteration of line 12.
In a parallel implementation, the total work required to compute the twiddle factors cannot be reduced to Θ(n). The reason is that, even if a certain twiddle factor is used more than once, it might be used on different processes at different times. If FFTs of the same size are computed on the same number of processes, every process needs the same set of twiddle factors for each computation. In this case, the twiddle factors can be precomputed and stored, and the cost of their computation can be amortized over the execution of all instances of FFTs of the same size. However, if we consider only one instance of FFT, then twiddle factor computation gives rise to additional overhead in a parallel implementation, because it performs more overall operations than the sequential implementation.
As an example, consider the various powers of ω used in the three iterations of an 8-point FFT. In the mth iteration of the loop starting on line 5 of the algorithm, ωl is computed for all i (0 ≤ i < n), such that l is the integer obtained by reversing the order of the m + 1 most significant bits of i and then padding them by log n − (m + 1) zeros to the right (refer to Figure 13.1 and Algorithm 13.2 to see how l is derived). Table 13.1 shows the binary representation of the powers of ω required for all values of i and m for an 8-point FFT.
If eight processes are used, then each process computes and uses one column of Table 13.1. Process 0 computes just one twiddle factor for all its iterations, but some processes (in this case, all other processes 2–7) compute a new twiddle factor in each of the three iterations. If p = n/2 = 4, then each process computes two consecutive columns of the table. In this case, the last process computes the twiddle factors in the last two columns of the table. Hence, the last process computes a total of four different powers – one each for m = 0 (100) and m = 1 (110), and two for m = 2 (011 and 111). Although different processes may compute a different number of twiddle factors, the total overhead due to the extra work is proportional to p times the maximum number of twiddle factors that any single process computes. Let h(n, p) be the maximum number of twiddle factors that any of the p processes computes during an n-point FFT. Table 13.2 shows the values of h(8, p) for p = 1, 2, 4, and 8. The table also shows the maximum number of new twiddle factors that any single process computes in each iteration.
Table 13.1. The binary representation of the various powers of ω calculated in different iterations of an 8-point FFT (also see Figure 13.1). The value of m refers to the iteration number of the outer loop, and i is the index of the inner loop of Algorithm 13.2.
|
i | ||||||||
|---|---|---|---|---|---|---|---|---|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 | |
|
m = 0 |
000 |
000 |
000 |
000 |
100 |
100 |
100 |
100 |
|
m = 1 |
000 |
000 |
100 |
100 |
010 |
010 |
110 |
110 |
|
m = 2 |
000 |
100 |
010 |
110 |
001 |
101 |
011 |
111 |
Table 13.2. The maximum number of new powers of ω used by any process in each iteration of an 8-point FFT computation.
|
p = 1 |
p = 2 |
p = 4 |
p = 8 | |
|---|---|---|---|---|
|
m = 0 |
2 |
1 |
1 |
1 |
|
m = 1 |
2 |
2 |
1 |
1 |
|
m = 2 |
4 |
4 |
2 |
1 |
|
Total = h(8, p) |
8 |
7 |
4 |
3 |
The function h is defined by the following recurrence relation (Problem 13.5):

The solution to this recurrence relation for p > 1 and n ≥ p is
Thus, if it takes time ![]() to compute one twiddle factor, then at least one process spends time
to compute one twiddle factor, then at least one process spends time ![]() log p computing twiddle factors. The total cost of twiddle factor computation, summed over all processes, is
log p computing twiddle factors. The total cost of twiddle factor computation, summed over all processes, is ![]() log p. Since even a serial implementation incurs a cost of
log p. Since even a serial implementation incurs a cost of ![]() in computing twiddle factors, the total parallel overhead due to extra work (
in computing twiddle factors, the total parallel overhead due to extra work (![]() ) is given by the following equation:
) is given by the following equation:

This overhead is independent of the architecture of the parallel computer used for the FFT computation. The isoefficiency function due to ![]() is Θ(p log p). Since this term is of the same order as the isoefficiency terms due to message startup time and concurrency, the extra computations do not affect the overall scalability of parallel FFT.
is Θ(p log p). Since this term is of the same order as the isoefficiency terms due to message startup time and concurrency, the extra computations do not affect the overall scalability of parallel FFT.
The binary-exchange algorithm yields good performance on parallel computers with sufficiently high communication bandwidth with respect to the processing speed of the CPUs. Efficiencies below a certain threshold can be maintained while increasing the problem size at a moderate rate with an increasing number of processes. However, this threshold is very low if the communication bandwidth of the parallel computer is low compared to the speed of its processors. In this section, we describe a different parallel formulation of FFT that trades off some efficiency for a more consistent level of parallel performance. This parallel algorithm involves matrix transposition, and hence is called the transpose algorithm.
The performance of the transpose algorithm is worse than that of the binary-exchange algorithm for efficiencies below the threshold. However, it is much easier to obtain efficiencies above the binary-exchange algorithm’s threshold using the transpose algorithm. Thus, the transpose algorithm is particularly useful when the ratio of communication bandwidth to CPU speed is low and high efficiencies are desired. On a hypercube or a p-node network with Θ(p) bisection width, the transpose algorithm has a fixed asymptotic isoefficiency function of Θ(p2 log p). That is, the order of this isoefficiency function is independent of the ratio of the speed of point-to-point communication and the computation.
The simplest transpose algorithm requires a single transpose operation over a two-dimensional array; hence, we call this algorithm the two-dimensional transpose algorithm.
Assume that ![]() is a power of 2, and that the sequences of size n used in Algorithm 13.2 are arranged in a
is a power of 2, and that the sequences of size n used in Algorithm 13.2 are arranged in a ![]() two-dimensional square array, as shown in Figure 13.8 for n = 16. Recall that computing the FFT of a sequence of n points requires log n iterations of the outer loop of Algorithm 13.2. If the data are arranged as shown in Figure 13.8, then the FFT computation in each column can proceed independently for log
two-dimensional square array, as shown in Figure 13.8 for n = 16. Recall that computing the FFT of a sequence of n points requires log n iterations of the outer loop of Algorithm 13.2. If the data are arranged as shown in Figure 13.8, then the FFT computation in each column can proceed independently for log ![]() iterations without any column requiring data from any other column. Similarly, in the remaining log
iterations without any column requiring data from any other column. Similarly, in the remaining log ![]() iterations, computation proceeds independently in each row without any row requiring data from any other row. Figure 13.8 shows the pattern of combination of the elements for a 16-point FFT. The figure illustrates that if data of size n are arranged in a
iterations, computation proceeds independently in each row without any row requiring data from any other row. Figure 13.8 shows the pattern of combination of the elements for a 16-point FFT. The figure illustrates that if data of size n are arranged in a ![]() array, then an n-point FFT computation is equivalent to independent
array, then an n-point FFT computation is equivalent to independent ![]() -point FFT computations in the columns of the array, followed by independent
-point FFT computations in the columns of the array, followed by independent ![]() -point FFT computations in the rows.
-point FFT computations in the rows.

Figure 13.8. The pattern of combination of elements in a 16-point FFT when the data are arranged in a 4 × 4 two-dimensional square array.
If the ![]() array of data is transposed after computing the
array of data is transposed after computing the ![]() -point column FFTs, then the remaining part of the problem is to compute the
-point column FFTs, then the remaining part of the problem is to compute the ![]() -point columnwise FFTs of the transposed matrix. The transpose algorithm uses this property to compute the FFT in parallel by using a columnwise striped partitioning to distribute the
-point columnwise FFTs of the transposed matrix. The transpose algorithm uses this property to compute the FFT in parallel by using a columnwise striped partitioning to distribute the ![]() array of data among the processes. For instance, consider the computation of the 16-point FFT shown in Figure 13.9, where the 4 × 4 array of data is distributed among four processes such that each process stores one column of the array. In general, the two-dimensional transpose algorithm works in three phases. In the first phase, a
array of data among the processes. For instance, consider the computation of the 16-point FFT shown in Figure 13.9, where the 4 × 4 array of data is distributed among four processes such that each process stores one column of the array. In general, the two-dimensional transpose algorithm works in three phases. In the first phase, a ![]() -point FFT is computed for each column. In the second phase, the array of data is transposed. The third and final phase is identical to the first phase, and involves the computation of
-point FFT is computed for each column. In the second phase, the array of data is transposed. The third and final phase is identical to the first phase, and involves the computation of ![]() -point FFTs for each column of the transposed array. Figure 13.9 shows that the first and third phases of the algorithm do not require any interprocess communication. In both these phases, all
-point FFTs for each column of the transposed array. Figure 13.9 shows that the first and third phases of the algorithm do not require any interprocess communication. In both these phases, all ![]() points for each columnwise FFT computation are available on the same process. Only the second phase requires communication for transposing the
points for each columnwise FFT computation are available on the same process. Only the second phase requires communication for transposing the ![]() matrix.
matrix.
In the transpose algorithm shown in Figure 13.9, one column of the data array is assigned to one process. Before analyzing the transpose algorithm further, consider the more general case in which p processes are used and 1 ≤ p ≤ ![]() . The
. The ![]() array of data is striped into blocks, and one block of
array of data is striped into blocks, and one block of ![]() rows is assigned to each process. In the first and third phases of the algorithm, each process computes
rows is assigned to each process. In the first and third phases of the algorithm, each process computes ![]() FFTs of size
FFTs of size ![]() each. The second phase transposes the
each. The second phase transposes the ![]() matrix, which is distributed among p processes with a one-dimensional partitioning. Recall from Section 4.5 that such a transpose requires an all-to-all personalized communication.
matrix, which is distributed among p processes with a one-dimensional partitioning. Recall from Section 4.5 that such a transpose requires an all-to-all personalized communication.
Now we derive an expression for the parallel run time of the two-dimensional transpose algorithm. The only inter-process interaction in this algorithm occurs when the ![]() array of data partitioned along columns or rows and mapped onto p processes is transposed. Replacing the message size m by n/p – the amount of data owned by each process – in the expression for all-to-all personalized communication in Table 4.1 yields ts (p − 1) + twn/p as the time spent in the second phase of the algorithm. The first and third phases each take time
array of data partitioned along columns or rows and mapped onto p processes is transposed. Replacing the message size m by n/p – the amount of data owned by each process – in the expression for all-to-all personalized communication in Table 4.1 yields ts (p − 1) + twn/p as the time spent in the second phase of the algorithm. The first and third phases each take time ![]() . Thus, the parallel run time of the transpose algorithm on a hypercube or any Θ(p) bisection width network is given by the following equation:
. Thus, the parallel run time of the transpose algorithm on a hypercube or any Θ(p) bisection width network is given by the following equation:
The expressions for speedup and efficiency are as follows:
The process-time product of this parallel system is tcn log n + ts p2 + twn. This parallel system is cost-optimal if n log n = Ω(p2 log p).
Note that the term associated with tw in the expression for efficiency in Equation 13.12 is independent of the number of processes. The degree of concurrency of this algorithm requires that ![]() because at most
because at most ![]() processes can be used to partition the
processes can be used to partition the ![]() array of data in a striped manner. As a result, n = Ω(p2), or n log n = Ω(p2 log p). Thus, the problem size must increase at least as fast as Θ(p2 log p) with respect to the number of processes to use all of them efficiently. The overall isoefficiency function of the two-dimensional transpose algorithm is Θ(p2 log p) on a hypercube or another interconnection network with bisection width Θ(p). This isoefficiency function is independent of the ratio of tw for point-to-point communication and tc. On a network whose cross-section bandwidth b is less than Θ(p) for p nodes, the tw term must be multiplied by an appropriate expression of Θ(p/b) in order to derive TP, S, E, and the isoefficiency function (Problem 13.6).
array of data in a striped manner. As a result, n = Ω(p2), or n log n = Ω(p2 log p). Thus, the problem size must increase at least as fast as Θ(p2 log p) with respect to the number of processes to use all of them efficiently. The overall isoefficiency function of the two-dimensional transpose algorithm is Θ(p2 log p) on a hypercube or another interconnection network with bisection width Θ(p). This isoefficiency function is independent of the ratio of tw for point-to-point communication and tc. On a network whose cross-section bandwidth b is less than Θ(p) for p nodes, the tw term must be multiplied by an appropriate expression of Θ(p/b) in order to derive TP, S, E, and the isoefficiency function (Problem 13.6).
A comparison of Equations 13.4 and 13.11 shows that the transpose algorithm has a much higher overhead than the binary-exchange algorithm due to the message startup time ts, but has a lower overhead due to per-word transfer time tw. As a result, either of the two algorithms may be faster depending on the relative values of ts and tw. If the latency ts is very low, then the transpose algorithm may be the algorithm of choice. On the other hand, the binary-exchange algorithm may perform better on a parallel computer with a high communication bandwidth but a significant startup time.
Recall from Section 13.2.1 that an overall isoefficiency function of Θ(p log p) can be realized by using the binary-exchange algorithm if the efficiency is such that Ktw/tc ≤ 1, where K = E /(1 − E). If the desired efficiency is such that Ktw/tc = 2, then the overall isoefficiency function of both the binary-exchange and the two-dimensional transpose algorithms is Θ(p2 log p). When Ktw/tc > 2, the two-dimensional transpose algorithm is more scalable than the binary-exchange algorithm; hence, the former should be the algorithm of choice, provided that n ≥ p2. Note, however, that the transpose algorithm yields a performance benefit over the binary-exchange algorithm only if the target architecture has a cross-section bandwidth of Θ(p) for p nodes (Problem 13.6).
In the two-dimensional transpose algorithm, the input of size n is arranged in a ![]() two-dimensional array that is partitioned along one dimension on p processes. These processes, irrespective of the underlying architecture of the parallel computer, can be regarded as arranged in a logical one-dimensional linear array. As an extension of this scheme, consider the n data points to be arranged in an n1/3 × n1/3 × n1/3 three-dimensional array mapped onto a logical
two-dimensional array that is partitioned along one dimension on p processes. These processes, irrespective of the underlying architecture of the parallel computer, can be regarded as arranged in a logical one-dimensional linear array. As an extension of this scheme, consider the n data points to be arranged in an n1/3 × n1/3 × n1/3 three-dimensional array mapped onto a logical ![]() two-dimensional mesh of processes. Figure 13.10 illustrates this mapping. To simplify the algorithm description, we label the three axes of the three-dimensional array of data as x, y, and z. In this mapping, the x-y plane of the array is checkerboarded into
two-dimensional mesh of processes. Figure 13.10 illustrates this mapping. To simplify the algorithm description, we label the three axes of the three-dimensional array of data as x, y, and z. In this mapping, the x-y plane of the array is checkerboarded into ![]() parts. As the figure shows, each process stores
parts. As the figure shows, each process stores ![]() columns of data, and the length of each column (along the z-axis) is n1/3. Thus, each process has
columns of data, and the length of each column (along the z-axis) is n1/3. Thus, each process has ![]() elements of data.
elements of data.

Figure 13.10. Data distribution in the three-dimensional transpose algorithm for an n-point FFT on p processes ![]() .
.
Recall from Section 13.3.1 that the FFT of a two-dimensionally arranged input of size ![]() can be computed by first computing the
can be computed by first computing the ![]() -point one-dimensional FFTs of all the columns of the data and then computing the
-point one-dimensional FFTs of all the columns of the data and then computing the ![]() -point one-dimensional FFTs of all the rows. If the data are arranged in an n1/3 × n1/3 × n1/3 three-dimensional array, the entire n-point FFT can be computed similarly. In this case, n1/3-point FFTs are computed over the elements of the columns of the array in all three dimensions, choosing one dimension at a time. We call this algorithm the three-dimensional transpose algorithm. This algorithm can be divided into the following five phases:
-point one-dimensional FFTs of all the rows. If the data are arranged in an n1/3 × n1/3 × n1/3 three-dimensional array, the entire n-point FFT can be computed similarly. In this case, n1/3-point FFTs are computed over the elements of the columns of the array in all three dimensions, choosing one dimension at a time. We call this algorithm the three-dimensional transpose algorithm. This algorithm can be divided into the following five phases:
In the first phase, n1/3-point FFTs are computed on all the rows along the z-axis.
In the second phase, all the n1/3 cross-sections of size n1/3 × n1/3 along the y-z plane are transposed.
In the third phase, n1/3-point FFTs are computed on all the rows of the modified array along the z-axis.
In the fourth phase, each of the n1/3 × n1/3 cross-sections along the x-z plane is transposed.
In the fifth and final phase, n1/3-point FFTs of all the rows along the z-axis are computed again.
For the data distribution shown in Figure 13.10, in the first, third, and fifth phases of the algorithm, all processes perform ![]() FFT computations, each of size n1/3. Since all the data for performing these computations are locally available on each process, no interprocess communication is involved in these three odd-numbered phases. The time spent by a process in each of these phases is
FFT computations, each of size n1/3. Since all the data for performing these computations are locally available on each process, no interprocess communication is involved in these three odd-numbered phases. The time spent by a process in each of these phases is ![]() . Thus, the total time that a process spends in computation is tc(n/p) log n.
. Thus, the total time that a process spends in computation is tc(n/p) log n.
Figure 13.11 illustrates the second and fourth phases of the three-dimensional transpose algorithm. As Figure 13.11(a) shows, the second phase of the algorithm requires transposing square cross-sections of size n1/3 × n1/3 along the y-z plane. Each column of ![]() processes performs the transposition of
processes performs the transposition of ![]() such cross-sections. This transposition involves all-to-all personalized communications among groups of
such cross-sections. This transposition involves all-to-all personalized communications among groups of ![]() processes with individual messages of size n/p3/2. If a p-node network with bisection width Θ(p) is used, this phase takes time
processes with individual messages of size n/p3/2. If a p-node network with bisection width Θ(p) is used, this phase takes time ![]() . The fourth phase, shown in Figure 13.11(b), is similar. Here each row of
. The fourth phase, shown in Figure 13.11(b), is similar. Here each row of ![]() processes performs the transpose of
processes performs the transpose of ![]() cross-sections along the x-z plane. Again, each cross-section consists of n1/3 × n1/3 data elements. The communication time of this phase is the same as that of the second phase. The total parallel run time of the three-dimensional transpose algorithm for an n-point FFT is
cross-sections along the x-z plane. Again, each cross-section consists of n1/3 × n1/3 data elements. The communication time of this phase is the same as that of the second phase. The total parallel run time of the three-dimensional transpose algorithm for an n-point FFT is

Figure 13.11. The communication (transposition) phases in the three-dimensional transpose algorithm for an n-point FFT on p processes.
Having studied the two- and three-dimensional transpose algorithms, we can derive a more general q-dimensional transpose algorithm similarly. Let the n-point input be arranged in a logical q-dimensional array of size n1/q × n1/q ×···×n1/q (a total of q terms). Now the entire n-point FFT computation can be viewed as q subcomputations. Each of the q subcomputations along a different dimension consists of n(q−1)/q FFTs over n1/q data points. We map the array of data onto a logical (q − 1)-dimensional array of p processes, where p ≤ n(q−1)/q, and p = 2(q−1)s for some integer s. The FFT of the entire data is now computed in (2q − 1) phases (recall that there are three phases in the two-dimensional transpose algorithm and five phases in the three-dimensional transpose algorithm). In the q odd-numbered phases, each process performs n(q−1)/q/p of the required n1/q-point FFTs. The total computation time for each process over all q computation phases is the product of q (the number of computation phases), n(q−1)/q/p (the number of n1/q-point FFTs computed by each process in each computation phase), and tcn1/q log(n1/q) (the time to compute a single n1/q-point FFT). Multiplying these terms gives a total computation time of tc(n/p) log n.
In each of the (q − 1) even-numbered phases, sub-arrays of size n1/q × n1/q are transposed on rows of the q-dimensional logical array of processes. Each such row contains p1/(q−1) processes. One such transpose is performed along every dimension of the (q − 1)-dimensional process array in each of the (q − 1) communication phases. The time spent in communication in each transposition is ts(p1/(q−1) − 1) + twn/p. Thus, the total parallel run time of the q-dimensional transpose algorithm for an n-point FFT on a p-node network with bisection width Θ(p) is
Equation 13.14 can be verified by replacing q with 2 and 3, and comparing the result with Equations 13.11 and 13.13, respectively.
A comparison of Equations 13.11, 13.13, 13.14, and 13.4 shows an interesting trend. As the dimension q of the transpose algorithm increases, the communication overhead due to tw increases, but that due to ts decreases. The binary-exchange algorithm and the two-dimensional transpose algorithms can be regarded as two extremes. The former minimizes the overhead due to ts but has the largest overhead due to tw. The latter minimizes the overhead due to tw but has the largest overhead due to ts . The variations of the transpose algorithm for 2 < q < log p lie between these two extremes. For a given parallel computer, the specific values of tc, ts , and tw determine which of these algorithms has the optimal parallel run time (Problem 13.8).
Note that, from a practical point of view, only the binary-exchange algorithm and the two- and three-dimensional transpose algorithms are feasible. Higher-dimensional transpose algorithms are very complicated to code. Moreover, restrictions on n and p limit their applicability. These restrictions for a q-dimensional transpose algorithm are that n must be a power of two that is a multiple of q, and that p must be a power of 2 that is a multiple of (q − 1). In other words, n = 2qr, and p = 2(q−1)s, where q, r, and s are integers.
Example 13.2 A comparison of binary-exchange, 2-D transpose, and 3-D transpose algorithms
This example shows that either the binary-exchange algorithm or any of the transpose algorithms may be the algorithm of choice for a given parallel computer, depending on the size of the FFT. Consider a 64-node version of the hypercube described in Example 13.1 with tc = 2, ts = 25, and tw = 4. Figure 13.12 shows speedups attained by the binary-exchange algorithm, the 2-D transpose algorithm, and the 3-D transpose algorithm for different problem sizes. The speedups are based on the parallel run times given by Equations 13.4, 13.11, and 13.13, respectively. The figure shows that for different ranges of n, a different algorithm provides the highest speedup for an n-point FFT. For the given values of the hardware parameters, the binary-exchange algorithm is best suited for very low granularity FFT computations, the 2-D transpose algorithm is best for very high granularity computations, and the 3-D transpose algorithm’s speedup is the maximum for intermediate granularities. ▪
Due to the important role of Fourier transform in scientific and technical computations, there has been great interest in implementing FFT on parallel computers and on studying its performance. Swarztrauber [Swa87] describes many implementations of the FFT algorithm on vector and parallel computers. Cvetanovic [Cve87] and Norton and Silberger [NS87] give a comprehensive performance analysis of the FFT algorithm on pseudo-shared-memory architectures such as the IBM RP-3. They consider various partitionings of data among memory blocks and, in each case, obtain expressions for communication overhead and speedup in terms of problem size, number of processes, memory latency, CPU speed, and speed of communication. Aggarwal, Chandra, and Snir [ACS89c] analyze the performance of FFT and other algorithms on LPRAM – a new model for parallel computation. This model differs from the standard PRAM model in that remote accesses are more expensive than local accesses in an LPRAM. Parallel FFT algorithms and their implementation and experimental evaluation on various architectures have been pursued by many other researchers [AGGM90, Bai90, BCJ90, BKH89, DT89, GK93b, JKFM89, KA88, Loa92].
The basic FFT algorithm whose parallel formulations are discussed in this chapter is called the unordered FFT because the elements of the output sequence are stored in bit-reversed index order. In other words, the frequency spectrum of the input signal is obtained by reordering the elements of the output sequence Y produced by Algorithm 13.2 in such a way that for all i, Y [i] is replaced by Y [j], where j is obtained by reversing the bits in the binary representation of i. This is a permutation operation (Section 4.6) and is known as bit reversal. Norton and Silberger [NS87] show that an ordered transform can be obtained with at most 2d + 1 communication steps, where d = log p. Since the unordered FFT computation requires only d communication steps, the total communication overhead in the case of ordered FFT is roughly double of that for unordered FFT. Clearly, an unordered transform is preferred where applicable. The output sequence need not be ordered when the transform is used as a part of a larger computation and as such remains invisible to the user [Swa87]. In many practical applications of FFT, such as convolution and solution of the discrete Poisson equation, bit reversal can be avoided [Loa92]. If required, bit reversal can be performed by using an algorithm described by Van Loan [Loa92] for a distributed-memory parallel computer. The asymptotic communication complexity of this algorithm is the same as that of the binary-exchange algorithm on a hypercube.
Several variations of the simple FFT algorithm presented here have been suggested in the literature. Gupta and Kumar [GK93b] show that the total communication overhead for mesh and hypercube architectures is the same for the one- and two-dimensional FFTs. Certain schemes for computing the DFT have been suggested that involve fewer arithmetic operations on a serial computer than the simple Cooley-Tukey FFT algorithm requires [Nus82, RB76, Win77]. Notable among these are computing one-dimensional FFTs with radix greater than two and computing multidimensional FFTs by transforming them into a set of one-dimensional FFTs by using the polynomial transform method. A radix-q FFT is computed by splitting the input sequence of size n into q sequences of size n/q each, computing the q smaller FFTs, and then combining the result. For example, in a radix-4 FFT, each step computes four outputs from four inputs, and the total number of iterations is log4 n rather than log2 n. The input length should, of course, be a power of four. Despite the reduction in the number of iterations, the aggregate communication time for a radix-q FFT remains the same as that for radix-2. For example, for a radix-4 algorithm on a hypercube, each communication step now involves four processes distributed in two dimensions rather than two processes in one dimension. In contrast, the number of multiplications in a radix-4 FFT is 25% fewer than in a radix-2 FFT [Nus82]. This number can be marginally improved by using higher radices, but the amount of communication remains unchanged.
13.1 Let the serial run time of an n-point FFT computation be tcn log n. Consider its implementation on an architecture on which the parallel run time is (tcn log n)/p + (twn log p)/p. Assume that tc = 1and tw = 0.2.
Write expressions for the speedup and efficiency.
What is the isoefficiency function if an efficiency of 0.6 is desired?
How will the isoefficiency function change (if at all) if an efficiency of 0.4 is desired?
Repeat parts 1 and 2 for the case in which tw = 1 and everything else is the same.
13.2 [Tho83] Show that, while performing FFT on a square mesh of p processes by using any mapping of data onto the processes, there is at least one iteration in which the pairs of processes that need to communicate are at least
 links apart.
links apart.13.3 Describe the communication pattern of the binary-exchange algorithm on a linear array of p processes. What are the parallel run time, speedup, efficiency, and isoefficiency function of the binary-exchange algorithm on a linear array?
13.4 Show that, if ts = 0, the isoefficiency function of the binary-exchange algorithm on a mesh is given by
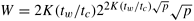
Hint: Use Equation 13.10.
13.5 Prove that the maximum number of twiddle factors computed by any process in the parallel implementation of an n-point FFT using p processes is given by the recurrence relation given in Section 13.2.3.
13.6 Derive expressions for the parallel run time, speedup, and efficiency of the two-dimensional transpose algorithm described in Section 13.3.1 for an n-point FFT on a p-node two-dimensional mesh and a linear array of p nodes.
13.7 Ignoring ts, by what factor should the communication bandwidth of a p-node mesh be increased so that it yields the same performance on the two-dimensional transpose algorithm for an n-point FFT on a p-node hypercube?
13.8 You are given the following sets of communication-related constants for a hypercube network: (i) ts = 250, tw = 1, (ii) ts = 50, tw = 1, (iii) ts = 10, tw =1, (iv) ts = 2, tw =1, and (v) ts = 0, tw = 1.
Given a choice among the binary-exchange algorithm and the two-, three-, four-, and five-dimensional transpose algorithms, which one would you use for n = 215 and p = 212 for each of the preceding sets of values of ts and tw?
Repeat part 1 for (a) n = 212, p = 26, and (b) n = 220, p = 212.
13.9 [GK93b] Consider computing an n-point FFT on a
 mesh. If the channel bandwidth grows at a rate of Θ(px) (x > 0) with the number of nodes p in the mesh, show that the isoefficiency function due to communication overhead is Θ(p0.5−x22(tw/tc)p0.5−x) and that due to concurrency is Θ(p1+x log p). Also show that the best possible isoefficiency for FFT on a mesh is Θ(p1.5 log p), even if the channel bandwidth increases arbitrarily with the number of nodes in the network.
mesh. If the channel bandwidth grows at a rate of Θ(px) (x > 0) with the number of nodes p in the mesh, show that the isoefficiency function due to communication overhead is Θ(p0.5−x22(tw/tc)p0.5−x) and that due to concurrency is Θ(p1+x log p). Also show that the best possible isoefficiency for FFT on a mesh is Θ(p1.5 log p), even if the channel bandwidth increases arbitrarily with the number of nodes in the network.