Appendix D Complex Numbers
For the purposes of algebra, the field of real numbers is not sufficient, for there are polynomials of nonzero degree with real coefficients that have no zeros in the field of real numbers (for example, ). It is often desirable to have a field in which any polynomial of nonzero degree with coefficients from that field has a zero in that field. It is possible to “enlarge” the field of real numbers to obtain such a field.
Definitions.
A complex number is an expression of the form , where a and b are real numbers called the real part and the imaginary part of z, respectively.
The sum and product of two complex numbers and (where a, b, c, and d are real numbers) are defined, respectively, as follows:
and
Example 1
The sum and product of and are, respectively,
and
Any real number c may be regarded as a complex number by identifying c with the complex number , that is, treating them as identical. Observe that this correspondence preserves sums and products; that is,
Any complex number of the form , where b is a nonzero real number, is called imaginary. The product of two imaginary numbers is real since
In particular, for , we have .
The observation that provides an easy way to remember the definition of multiplication of complex numbers: simply multiply two complex numbers as you would any two algebraic expressions, and replace by . Example 2 illustrates this technique.
Example 2
The product of and is
The real number 0, regarded as a complex number, is an additive identity element for the complex numbers since
Likewise the real number 1, regarded as a complex number, is a multiplicative identity element for the set of complex numbers since
Every complex number a + bi has an additive inverse, namely . But also each complex number except 0 has a multiplicative inverse. In fact,
In view of the preceding statements, the following result is not surprising.
Theorem D.1.
The set of complex numbers with the operations of addition and multiplication previously defined is a field.
Proof.
Exercise.
Definition.
The (complex) conjugate of a complex number is the complex number . We denote the conjugate of the complex number z by .
Example 3
The conjugates of , and 6 are, respectively,
The next theorem contains some important properties of the conjugate of a complex number.
Theorem D.2.
Let z and w be complex numbers. Then the following statements are true.
if
z is a real number if and only if .
Proof.
We leave the proofs of (a), (d), and (e) to the reader.
(b) Let and , where a, b, c, . Then
(c) For z and w, we have
For any complex number is real and nonnegative, for
This fact can be used to define the absolute value of a complex number.
Definition.
Let , where a, . The absolute value (or modulus) of z is the real number . We denote the absolute value of z by .
Observe that . The fact that the product of a complex number and its conjugate is real provides an easy method for determining the quotient of two complex numbers; for if , then
Example 4
To illustrate this procedure, we compute the quotient :
The absolute value of a complex number has the familiar properties of the absolute value of a real number, as the following result shows.
Theorem D.3.
Let z and w denote any two complex numbers. Then the following statements are true.
.
if .
.
.
Proof.
(a) By Theorem D.2, we have
proving (a).
(b) For the proof of (b), apply (a) to the product .
(c) For any complex number , where , observe that
Thus is real and satisfies the inequality . Taking , we have, by Theorem D.2 and (a),
Using Theorem D.2 again gives
By taking square roots, we obtain (c).
(d) From (a) and (c), it follows that
So
proving (d).
It is interesting as well as useful that complex numbers have both a geometric and an algebraic representation. Suppose that , where a and b are real numbers. We may represent z as a vector in the complex plane (see Figure D.1(a)). Notice that, as in , there are two axes, the real axis and the imaginary axis. The real and imaginary parts of z are the first and second coordinates, and the absolute value of z gives the length of the vector z. It is clear that addition of complex numbers may be represented as in using the parallelogram law.
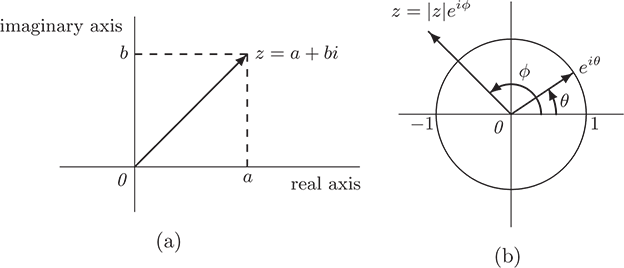
Figure D.1
In Section 2.7 (p.133), we introduce Euler’s formula. The special case is of particular interest. Because of the geometry we have introduced, we may represent the vector as in Figure D.1(b); that is, is the unit vector that makes an angle with the positive real axis. From this figure, we see that any nonzero complex number z may be depicted as a multiple of a unit vector, namely, , where is the angle that the vector z makes with the positive real axis. Thus multiplication, as well as addition, has a simple geometric interpretation: If and are two nonzero complex numbers, then from the properties established in Section 2.7 and Theorem D.3, we have
So zw is the vector whose length is the product of the lengths of z and w, and makes the angle with the positive real axis.
Our motivation for enlarging the set of real numbers to the set of complex numbers is to obtain a field such that every polynomial with nonzero degree having coefficients in that field has a zero. Our next result guarantees that the field of complex numbers has this property.
Theorem D.4 (The Fundamental Theorem of Algebra).
Suppose that is a polynomial in P(C) of degree . Then p(z) has a zero.
The following proof is based on one in the book Principles of Mathematical Analysis 3d., by Walter Rudin (McGraw-Hill Higher Education, New York, 1976).
Proof.
We want to find in C such that . Let m be the greatest lower bound of . For , we have
Because the last expression approaches infinity as s approaches infinity, we may choose a closed disk D about the origin such that if z is not in D. It follows that m is the greatest lower bound of . Because D is closed and bounded and p(z) is continuous, there exists in D such that . We want to show that . We argue by contradiction.
Assume that . Let . Then q(z) is a polynomial of degree n, , and for all z in C. So we may write
where . Because has modulus one, we may pick a real number such that , or . For any , we have
Choose r small enough so that . Then
Now choose r even smaller, if necessary, so that the expression within the brackets is positive. We obtain that . But this is a contradiction.
The following important corollary is a consequence of Theorem D.4 and the division algorithm for polynomials (Theorem E.1).
Corollary.
If is a polynomial of degree with complex coefficients, then there exist complex numbers (not necessarily distinct) such that
Proof.
Exercise.
A field is called algebraically closed if it has the property that every polynomial of positive degree with coefficients from that field factors as a product of polynomials of degree 1. Thus the preceding corollary asserts that the field of complex numbers is algebraically closed.
