6.3 Non-Fragile H∞ Controller Design for Continuous-Time Systems
In this section, the non-fragile dynamic output feedback H∞ controller design for continuous-time systems with the interval type of gain variations is considered.
Consider a continuous-time linear time-invariant model described by
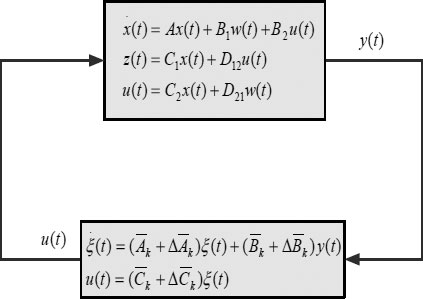
˙x(t)=Ax(t)+B1ω(t)+B2u(t),z(t)=C1x(t)+D12u(t),y(t)=C2x(t)+D12ω(t), |
(6.38) |
where x(t) ∈ Rn is the state, u(t) ∈ Rm is the control input, y(t) ∈ Rp is the measured output, ω(t) ∈ Rr is the disturbance input, z(t) ∈ Rq is the regulated output, and A, B1, B2, C1, C2, D12, and D21 are known constant matrices of appropriate dimensions.
And for system (6.38), consider a dynamic output feedback controller with gain variations of the following form:
˙ξ(t)=(Ak+ΔAk)ξ(t)+(Bk+ΔBk)y(t),u(t)=(Ck+ΔCk)ξ(t), |
(6.39) |
where ξ(t) ∈ Rn is the controller state, and Ak, Bk, and Ck are controller gain matrices of appropriate dimensions to be designed. ΔAk, ΔBk, and ΔCk represent the additive gain variations of the interval type (6.3).
6.3.2 Non-Fragile H∞ Controller Design Methods
Note that the proofs of the main results are similar to those of discrete-time systems, so here we only give the main results for continuous-time systems without proofs.
First, we give the design method of the initial controller gain Ck, which will be used in the non-fragile H∞ controller design.
Consider the controller (6.39) with ΔAk = 0 and ΔBk = 0, which is described by
˙ξ(t)=Akξ(t)+Bky(t)u(t)=(Ck+ΔCk)ξ(t), |
(6.40) |
where ΔCk is with the norm-bounded form as in the discrete-time case of the former section.
Combining the controller (6.40) with the system (6.38), we obtain the following closed-loop system:
˙xe(t)=Aedcxe(t)+Bedcω(t)z(t)=Cexe(t), |
(6.41) |
Then the following theorem gives a design method of the initial controller gain Ck.
Theorem 6.4 Consider system (6.38), where γ > 0 and θa > 0 are constants. If there exist matrices ˆA, ˆB, ˆC, X > 0,
where Σ1=AX+B2ˆC+XAT+ˆCTBT2 and Σ2=YA+ˆBC2+ATY+CT2ˆBT,
Ak=(X−1−Y)−1(ˆA−YAX−ˆBC2X−YB2ˆC)X−1,Bk=(X−1−Y)−1ˆB, Ck=ˆCX−1 |
(6.43) |
solves the non-fragile H∞ control problem for system (6.38).
Then, with the initial controller gain Ck designed above, we give the non-fragile dynamic output feedback H∞ controller design methods in the following.
Theorem 6.5 Consider the plant (6.38), where γ > 0 and θa > 0 are given constants, and the gain matrix Ck is given. If there exist matrices FA, FB, Sa > 0, Na < 0, such that the following LMIs hold:
M0(ΔAk,ΔBk,ΔCk)<0,θaij,θbit,θclj∈{−θa,θa},i,j=1,⋯,n; t=1,⋯,p; l=1,⋯,m, |
(6.44) |
then the controller (6.39) with additive uncertainty described by (6.3), Ck, and
(6.45) |
solves the non-fragile H∞ control problem for system (6.38), where
M0(ΔAk,ΔBk,ΔCk)=[M0a+MT0aM0bMT0c∗−γ2I0∗∗−I], |
(6.46) |
with
M0a=[SaA+SaB2(Ck+ΔCk)Φ1+(Sa−Na)A+FBC2+NaΔBkC2 SaA(Sa−Na)A+FBC2+NaΔBkC2],
M0b=[SaB1(Sa−Na)B1+FBD21+NaΔBkD21],
M0c=[C1+D12(Ck+ΔCk)C1],
and Φ1 = FA + NaΔAk + (Sa – Na)B2(Ck + ΔCk).
Similar to the discrete-time case, it should be noted that the number of LMIs involved in (6.44) is 2n2 + np + nq, which results in the difficulty of implementing the LMI constraints in computation. To overcome the difficulty arising from implementing the design condition given in Theorem 6.5, the following method is developed.
Denote
Fa1=[fa11fa12⋯fa1la],Fa2=[fTa21fTa22⋯fTa2la]T |
(6.47) |
where la = n2 + np + nm, and
fa1k=[01×n(Naei)T01×r01×q]T,fa2k=[eTi01×n01×r01×q],for k=(i−1)n+j,i,j=1,⋯,n.fa1k=[01×n(Naei)T01×r01×q]T,fa2k=[hTjC2hTjC2hTjD2101×q],for k=n2+(i−1)p+j, i=1,⋯,n,j=1,⋯,p.fa1k=[(SaB2gi)T[(Sa−Na)B2gi]T01×r(D12gi)T]T,fa2k=[eTj01×n01×r01×q],for k=n2+np+(i−1)n+j, i=1,⋯,m,j=1,⋯,n.
Let k0, k1, …, kSa be integers satisfying
(6.48) |
and matrix Σ have the following structure,
∑=[diag[σ111⋯σsa11]diag[σ112⋯σsa12]diag[σ112⋯σsa12]diag[σ122⋯σsa22]], |
(6.49) |
where σi11,σi12,
Theorem 6.6 Consider the plant (6.38), where γ > 0, θa > 0, and sa > 0 are given constants, and the gain matrix Ck is given. If there exist matrices FA, FB, Sa > 0, Na < 0, and symmetric matrix Σ with the structure described by (6.49) such that the following LMIs hold:
[QFa1FTa10]+[Fa200I]T∑[Fa200I]<0, |
(6.50) |
where
with Φ3 = FA + (Sa – Na)B2Ck.
Then (6.39) with additive uncertainty described by (6.3), Ck, and the controller gain parameters given by (6.45) solve the non-fragile H∞ control problem for system (6.38).
Remark 6.7 In Theorem 6.6, in some cases, the magnitude of the designed Ak (Bk) may be too large to be applied in practice. For solving the problem, in Theorem 6.6, by adding the following constraints
(6.53) |
then the magnitude of Ak can be reduced. In fact, by Ak=N−1aFA and (6.53), it follows that
‖AF‖<1/α‖FA‖≤√β/α.
The same method can be applied for the gain Bk.
In the following, we will introduce the result of non-fragile H∞ controller design with norm-bounded gain variations with the form (6.29), and the relationship with our result is discussed.
Noting that the problem of non-fragile dynamic output feedback H∞ controller design with norm-bounded gain variations is also a non-convex problem, and similar to Theorem 6.6, when the controller gain Ck is known it is converted to a convex one. First, assume Ck is known. Then, by using the method in Yang, Wang, and Lin [149] and Mahmoud [103], the non-fragile H∞ controller design with norm-bounded gain variations is reduced to solve the following LMI:
(6.54) |
with Sa > 0 and Na < 0, where Q is defined by (6.52) with known Ck, ε > 0 is a given scalar, and
Ma1=[SaB2Mc0000NaMaNaMbSaB2Mc00000000 00−NaB2Mc0000D12Mc],
Ma2=[Ec000Ea000EbC2EbC2EbD210Ec000Ec000Ec000].
The following lemma will show the relationship between condition (6.54) and the condition for designing non-fragile H∞ controllers given in Theorem 6.6.
Lemma 6.3 Consider the system (6.38). If condition (6.54) is feasible, then the condition for designing non-fragile H∞ controllers given in Theorem 6.6 is feasible.
Combining the results in Theorem 6.4 and Theorem 6.6, we have the following algorithm.
Algorithm 6.2
Step 1. Minimize γ subject to X > 0, Y > 0, and LMI (6.42). Denote the optimal solutions as X = Xopt and ˆC=ˆCopt Then by (6.43), Ckopt=ˆCoptX−1opt
Step 2. Let Ck = Ckopt, minimize γ subject to FA, FB, Na > 0, Sa > 0, and LMIs (6.50) and (6.51). Denote the optimal solutions as Na = Naopt, FA = FAopt, and FB = FBopt. Then according to (6.45), we obtain Ak=N−1aFAopt, Bk=N−1aFBopt. The resulting Ak, Bk, and Ck will form the non-fragile dynamic output feedback H∞ controller gains.
In Theorem 6.6, we restrict the Lyapunov function matrix P with the structure (2.14) for obtaining the convex design condition, which may result in more conservative evaluation of the H∞ performance index bound. So, in this section, for a designed controller, the Lyapunov matrix P without the restriction is exploited for obtaining less conservative evaluation of the H∞ performance index bound.
When the controller parameter matrices Ak, Bk, and Ck are known, the problem of minimizing γ subject to (6.3) for a given θa > 0 and ‖ TZeω‖< γ can be converted into the one: minimize γ2 subject to the following LMIs:
[PAe+ATePPBeCTe∗−γ2I0∗∗−I]<0,θaij,θbit,θclj∈{−θa,θa},i,j=1,⋯,n; t=1,⋯,p; l=1,⋯,m. |
(6.55) |
Similar to the design condition given in Theorem 6.5, the above optimization problem is also with the numerical computational problem, to solve the problem, the following lemma provides a solution using the structured vertex separator approach.
Denote
(6.56) |
where
ga1k=[[01×neTi]P01×r01×q]T,ga2k=[01×neTj01×r01×q],for k=(i−1)n+j, i,j=1,⋯,n.ga1k=[[01×neTi]P01×r01×q]T,ga2k=[hTjC201×nhTjD2101×q],for k=n2+(i−1)p+j, i=1,⋯,n,j=1,⋯,p.ga1k=[[(B2gi)T01×n]P01×n01×r(D12gi)T]T,ga2k=[01×neTj01×r01×q]for k=n2+np+(i−1)n+j, i=1,⋯,m,j=1,⋯,n.
Then we have the following lemma.
Lemma 6.4 Consider the system (6.38). Let γ > 0 and θa > 0 be constants, and let controller parameter matrices Ak, Bk, and Ck be given. Then ‖ Tzω ‖< γ holds for all θaij, θbit, and θclj satisfying (6.3), if there exist matrices P > 0 and symmetric matrix Σ with the structure described by (6.49) such that (6.51) and the following LMI hold:
(6.57) |
where
Qs=[P[AB2CkBkC2Ak]+[AB2CkBkC2Ak]TP∗∗ P[B1BkD21][CT1(D12Ck)T]−γ2I0∗−I]. |
(6.58) |
Remark 6.8 For evaluating the H∞ performance bound of the transfer function from ω to z, the condition given in Lemma 6.4 usually is less conservative than that given in Theorem 6.6 because no structure constraint on the Lyapunov function matrix in Lemma 6.4 is imposed.
To illustrate the effectiveness of the proposed non-fragile H∞ controller, an example is given to provide a comparison between the proposed non-fragile H∞ controller design method and the existing non-fragile H∞ controller design method with the norm-bounded gain variations. Consider a linear system of the form (6.38) with
A=[0100−1−101−1],B1=[−101010],B2=[12−2],C1=[2−1−2000],C2=[−22−1],D21=[00.5],D12=[01].
By the standard H∞ controller design method [113], we obtain the optimal H∞ performance index for the system as γopt = 2.7069.
On the other hand, assume that the designed controller is in the form of (6.40). Let θa = 0.05, then by Theorem 6.3 with εc = 0.0023, we obtain
Ckini=[−3.0525 0.0998 1.3036].
Here, εc is obtained by searching such that the H∞ performance index is optimal. The value for θa is chosen appropriately large such that the designed Ckini can guarantee that Step 2 is feasible.
In the following, we design an H∞ controller by condition (6.54) with Ck = Ckini
Assume that the designed controller is with norm-bounded additive uncertainties described by (6.29), by applying condition (6.54) with θa = 0.02 and εc = 0.0040 to design a non-fragile controller. The obtained gains are given by
AKnm=108×[−2.02202.0588−0.9508−0.94350.9607−0.44361.0268−1.04550.4828],BKnm=108×[−1.0030−0.46800.5093]T,
and the H∞ performance index of the obtained non-fragile controller is 3.3719. Note that the εc used here is obtained by the searching method to guarantee the H∞ performance index is optimal.
Notice that the gains of the above controller are too large to be applied in practice. As indicated in Remark 6.7, applying condition (6.54) with (6.53), and with α = 0.4 and β = 1000000, the controller gains are reduced as:
AKnm=[−93.703093.1259−41.7578−45.861239.1903−16.476848.3981−42.388316.5820],BKnm=[−45.0240−19.306921.1626]T,
and the H∞ performance index is 3.4514.
Then, we design an H∞ controller by Theorem 6.6 with Ck = Ckini.
Assume that the designed controller is with the additive interval type of uncertainties described by (6.3). For this case with Ck = Ckini, it is difficult to apply Theorem 6.5 to design a non-fragile H∞ controller because the number of the LMI constraints involved in (6.44) is 215. However, Theorem 6.6 is applicable for solving this problem. By applying Theorem 6.6 with θa = 0.02 and ki = i, i = 1, …, 15, that is, sa = 15 as well as ki = 3i, i = 1, …, 5, that is, sa = 5 to design a non-fragile controller, the obtained gains are as follows.
For sa = 15,
AK=107×[−9.50289.4661−4.4679−3.39943.3863−1.59836.2383−6.21422.9330],Bk=107×[−4.6909−1.67813.0794]T.
For sa = 5,
AK=108×[−4.77444.7522−2.2444−1.70671.69888−0.80233.1388−3.12431.4755],Bk=108×[−2.3556−0.84211.5487]T.
Correspondingly, the H∞ performance indexes of the obtained non-fragile controllers are γ = 3.0598 and γ = 3.0578, respectively.
Similarly, the gains of the above two controllers are too large to be applied in practice. Applying Theorem 6.6 with (6.53), and with α = 0.4 and β = 1000000, the controller gains are reduced as follows.
For sa = 15,
Ak=[−83.105381.2701−37.0045−31.408824.1061−9.597256.8175−50.194720.7228],Bk=[−39.8799−12.112925.4119]T.
For sa = 5,
Ak=[−82.981881.1005−36.9408−31.358024.0411−9.572456.7847−50.129720.7037],Bk=[−39.8034−12.083825.3848]T.
The H∞ performance indices of the obtained non-fragile controllers are γ = 3.0913 and γ = 3.0898, respectively. Compared with the above design without (6.53), the design results in a slight performance degradation, but the magnitude of Ak and Bk has been significantly reduced.
In the following part, for the above designed controllers, Lemma 6.4 can give better evaluations of the H∞ performance index bounds.
First, to facilitate the presentation, denote the controller designed by condition (6.54) with (6.53) as Knmαβ, while denoting the controllers designed by Theorem 6.6 with (6.53) as Kin15αβ (sa = 15) and Kin5αβ (sa = 5).
By Lemma 6.4, the H∞ performance indices of the controller Knmαβ are γ = 3.2945 (sa = 15) and γ = 3.2940 (sa = 5), while the H∞ performance indices of the controllers Kin15αβ and Kin5αβ are γ = 3.0872 (sa = 15) and γ = 3.0849 (sa = 5), respectively.
Then, tables are given to provide a comparison between the two methods.
First, Table 6.3 shows the H∞ performance indices achieved by the designs directly.
From Table 6.3, it is easy to see that compared with the optimal H∞ performance index bound γopt = 2.7069, the performance index of the controller designed by condition (6.54) is degraded 24.57%. The performance indices of the controllers designed by Theorem 6.6 are degraded 13.04% (sa = 15) and 12.96% (sa = 5), which are much more improved than 24.57%.
TABLE 6.3
Performance Index by Design with θa = 0.02
Condition (6.54) |
Theorem 6.6 (sa = 15) |
Theorem 6.6 (sa = 5) |
|
γ |
3.3719 |
3.0598 |
3.0578 |
TABLE 6.4
Performance Index by Design with θa = 0.02, α = 0.4, β = 1000000
Condition (6.54) |
Theorem 6.6 (sa = 15) |
Theorem 6.6 (sa = 5) |
|
γ |
3.4514 |
3.0913 |
3.0898 |
Then, Table 6.4 shows the H∞ performance indices achieved by the design conditions with (6.53).
We can see from Table 6.4 that compared with γopt = 2.7069, the performance index of the controller designed by (6.54) with (6.53) is degraded 27.51%. The performance indices of the controllers designed by Theorem 6.6 with (6.53) are degraded 14.20% (sa = 15) and 14.15% (sa = 5).
Finally, for the designed non-fragile controllers, Lemma 6.4 gives better performance indices, shown in Table 6.5.
Obviously, compared with γopt = 2.7069, by using Lemma 6.4, the H∞ performance indices of the controller Knmαβ are degraded 21.71% for sa = 15 and 21.69% for sa = 5. Correspondingly, the performance indices for the controllers Kin15αβ and Kin5αβ are degraded 14.05% for sa = 15 and 13.96% for sa = 5, respectively. The result shows the advantage of the new proposed method.
In this part, we will give a simulation to illustrate the effectiveness of the presented design method. Let x(0)=[−0.10.6−0.2], ξ(0)=[−0.10.50.5] And let the disturbance ω(t) be
ω(t)={0.5,15≤t≤25(second)0otherwise.
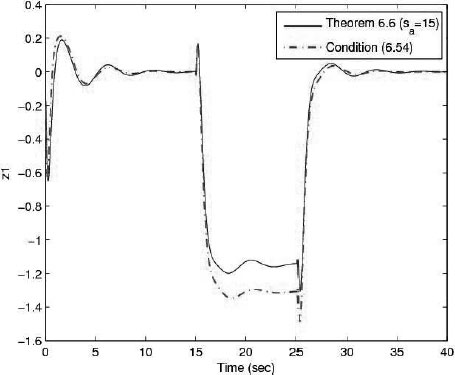
Then Figure 6.3 shows the regulated output responses of z1 controlled by the non-fragile controllers designed by condition (6.54) with (6.53) and Theorem 6.6 with (6.53), and with α = 0.4, β = 1000000. The responses of z2 controlled by the two non-fragile controllers are the same, and omitted here.
TABLE 6.5
Performance Evaluation by Lemma 6.4 with θa = 0.02
Knmαβ |
Kinαβ |
Kinαβ |
|
γ(sa = 15) |
3.2945 |
3.2945 |
— |
γ(sa = 5) |
3.2940 |
— |
3.0849 |
FIGURE 6.3
Comparison of the regulated output responses of z1(t) with θa = 0.02.
From this example, we can see that the worst case (sa = 15) of Theorem 6.6 also is more effective than the non-fragile H∞ controller existence condition (6.54).
6.4 Non-Fragile H∞ Controller Designs with Sparse Structures
In this section, we define a class of sparse structures for controllers to be designed.
For system (6.38), consider the dynamic output feedback controller described as:
(6.59) |
where ξ(t) ∈ Rn is the controller state, and Ak, Bk, and Ck are gain matrices of appropriate dimensions.
Then, a method for finding a class of feasible sparse structures from a given fully parameterized H∞ controller is presented as follows.
By Lemma 2.7, without loss of generality, we may assume that Ak, Bk, and Ck satisfy the following assumption:
Assumption 6.1 There exists a symmetric matrix P > 0 with the structure P=[YNN−N] such that
(6.60) |
Moreover, for the designed fully parameterized H∞ controller gains Ak, Bk, and Ck, the characteristic polynomial of Ak is described as
(6.61) |
where α0, α1,…, αn–1 are scalars. Assume there exists a row vector c such that Q=[(cAn−1k)T⋯(cAk)TcT]T is nonsingular. Construct the following transformation matrix:
(6.62) |
Then we have that ˉAK,ˉBk, and ˉCk are with the following sparse structured form
(6.63) |
where
(6.64) |
Hereafter, a controller described by
(6.65) |
with structure (6.63) is said to be a sparse structured controller.
Remark 6.9 When the gain matrices ˉAK,ˉBk, and ˉCk have the structure of (6.63), the nontrivial elements are only present in fK,ˉBk, and ˉCk So the number of additive uncertain parameters in the controller gains with any of the two structures is reduced from n2+np+mn for full parameterized controller (6.59) to n + np + mn for the sparse structured controller (6.65). Especially, when the vector c in the matrix Q is chosen from a row of Ck, denoted as Cki, then ˉCki=eTn, that is, the elements of the ith row of ˉCk become trivial.
Consider a sparse structured controller with gain variations described as:
(6.66) |
where ˉξ(t) ∈ Rn is the controller state, and ˉAK,ˉBk, and ˉCk are with the structure described by (6.63). The additive gain variations ΔˉAK,ΔˉBk, and ΔˉCk are with the following form:
ΔˉAk=ΔˉAka=[θaˉai]n×1v,|θaˉai|≤θa,i=1,⋯,n,ΔˉBk=ΔˉBka=EBadiag[θaˉb1,⋯,θaˉbrB]EBa,|θaˉbi|≤θa,i=1,⋯,rB,ΔˉCk=ΔˉCka=ECadiag[θaˉc1,⋯,θaˉcrC]ECa,|θaˉci|≤θa,i=1,⋯,rC |
(6.67) |
where EBa, EBb, ECa, and ECb are constant matrices.
Remark 6.10 For the additive case, the description of the gain variations in ˉBk ˉCk given by (6.67) can cover the cases where ˉBk and ˉCk are with or without trivial elements.
Applying controller (6.66) to system (6.38), the closed-loop system is illustrated by Figure 6.4 and given by
(6.68) |
where ˉxe(t)=[x(t)T,ˉξ(t)T]T, and
ˉAe=[AB2(ˉCk+ΔˉCk)(ˉBk+ΔˉBk)C2ˉAk+ΔˉAk],ˉBe=[B1(ˉBk+ΔˉBk)D21],ˉCe=[C1D12((ˉCk+ΔˉCk))]. |
(6.69) |
FIGURE 6.4
Control block diagram for Equation (6.68).
The transfer function matrix of the closed-loop system (6.68) from ω to z is given by
ˉTzω=ˉCe(sI−ˉAe)−1ˉBe.
Then the problem under consideration in this chapter is as follows.
Non-fragile H∞ control problem with sparse structure: Given positive constants γ and θa, design a controller described by (6.66) with additive gain variations of form (6.67) such that the resulting system (6.68) is asymptotically stable and ‖ˉTzω‖<γ.
The following preliminaries and lemmas are required in this chapter.
Lemma 6.5 Let the controller gain matrices Ak, Bk, and Ck satisfy Assumption 6.1, and T is defined by (6.62), then there exists a symmetric matrix ˉP>0 with ˉP=[ˉYˉNˉN−ˉN] such that
(6.70) |
where
ˉAe0=[ˉAˉB2ˉCkˉBkˉC2ˉAk] ,ˉBe0=[ˉB1ˉBkˉD21], ˉCe0=[ˉC1ˉD12ˉCk] , |
(6.71) |
with ˉAK,ˉBk, and ˉCk given by (6.63), and
ˉA=TAT−1,ˉB1=TB1,ˉB2=TB2ˉC1=C1T−1,ˉC2=C2T−1,ˉD21=D21ˉD12=D12. |
(6.72) |
Proof 6.6 By Assumption 6.1, it follows that there exists a symmetric matrix P > 0 with P=[YNN−N] such that (6.60) holds. Let
P=diag[T−1T−1]TP diag[T−1T−1],
then from (6.60), it follows that
ˉATe0ˉP+ˉPˉAe0+1γ2ˉPˉBe0ˉBTe0ˉP+ˉCTe0ˉCe0=diag[T−1T−1]TΨ1diag[T−1T−1]<0,
where Ψ1=ATe0P+PAe0+1γ2PBe0BTe0P+CTe0Ce0.
Thus, the proof is complete.
Lemma 6.6 Let γ and θa be given positive constants. If there exists a symmetric matrix ˉP>0 with ˉP=[ˉYˉNˉN−ˉN] such that
(6.73) |
holds for all ΔˉAK,ΔˉBk, and ΔˉCk satisfying form (6.67), where
ˉAea=[ˉAˉB2(ˉCk+ΔˉCk)(ˉBk+ΔˉBk)ˉC2ˉAk+ΔˉAk],ˉBea=[ˉB1(ˉBk+ΔˉBk)ˉD21], ˉCea=[ˉC1ˉD12(ˉCk+ΔˉCk)], |
(6.74) |
ˉA, ˉB1, ˉB2, ˉC1, ˉC2, ˉD12, and ˉD21 are defined by (6.72). Then the controller-described by (6.66) with additive gain variations (6.67) solves the non-fragile H∞ control problem with sparse structure for system (6.38).
Proof 6.7 Let ˉPs=diag[TI]TˉPdiag[TI]. According to (6.71), (6.72), (6.73), (6.74), it follows that
ˉATeˉPs+ˉPsˉAe+1γ2ˉPsˉBeˉBTeˉPs+ˉCTeˉCe=diag[TI]TΨ2diag[TI]<0,
where Ψ2=ˉATeaˉP+ˉPˉAea+1γ2ˉPˉBeaˉBTeaˉP+ˉCTeaˉCeaandˉAe,ˉBe,ˉCe are defined by (6.69). Then, by Lemma 2.6, the conclusion follows.
6.4.2 Sparse Structured Controller Design
In this section, a three-step procedure for designing non-fragile H∞ controllers with the sparse structure with respect to additive gain uncertainties is presented.
First, we will give a method for designing a non-fragile H∞ controller with a sparse structure (6.63) and with additive gain variations (6.67) under the assumption that the controller gain ˉCk is known.
To facilitate the presentation of Theorem 6.7, we denote
(6.75) |
where
M0as=[ˉSa(ˉA+ˉB2eeTn)+ˉSaˉB2r(ˉCkr+ΔˉCkr)(ˉSa−ˉNa)(ˉA+ˉB2eeTn)+(ˉFB+ˉNaΔˉBk)ˉC2+Φ1ˉSaˉA(ˉSa−ˉNa)ˉA+(ˉFB+ˉNaΔˉBk)ˉCk],
M0bs=[ˉSaˉB1(ˉSa−ˉNa)ˉB1+(ˉFB+ˉNaΔˉBk)ˉD21],
M0cs=[ˉC1+ˉD12eeTn+ˉD12rˉCkr+ˉD12rΔˉCkrˉC1].
Here, Φ1=ˉNaAkc+(ˉFA+ˉNaΔfA)ϕ+(ˉSa−ˉNa)ˉB2r(ˉCkr+ΔˉCkr)andˉA, ˉB1, ˉB2, ˉC1, ˉC2, ˉD12, and ˉD21 are defined by (6.72) with T defined by (6.62).
Then, by using Lemma 6.6, the following theorem presents a sufficient condition for the solvability of the non-fragile H∞ control problem with sparse structure (6.63).
Theorem 6.7 Consider system (6.38). Let γ > 0 and θa > 0 be given constants. If there exist matrices ˉFA,ˉFB,ˉSa>0,andˉNa<0 such that the following condition holds:
M0s(ΔˉAka,ΔˉBka,ΔˉCka)<0for all θaˉai,θaˉbj,θaˉcr∈{−θa,θa},i=1,⋯,n;j=1,⋯,rB,r=1,⋯,rc |
(6.76) |
then controller (6.66) with the gain variations described by (6.67), and
(6.77) |
solves the non-fragile H∞ control problem with sparse structure for system (6.38).
Proof 6.8 By Lemma 6.6, it is sufficient to show that there exists a symmetric matrix ˉP>0 with structure (2.14), namely ˉP = [ˉYˉNaˉNa−ˉNa] such that
(6.78) |
holds for all gain variations satisfying (6.67), where ˉAea,ˉBea, and¯ Cea are defined by (6.74). Denote ˉSa=ˉY+ˉNa,Γ1=[III0], then ˉP>0 with the structure described by (2.14) is equivalent to ˉSa>0 and ˉNa<0. Furthermore, Γ1 is nonsingular for I > 0, and (6.78) is equivalent to
(6.79) |
where
M2a=[ˉSaˉA+ˉSaˉB2eeTn+ˉSaˉB2r(ˉCkr+ΔˉCkr)ˉNa(ˉBk+ΔˉBk)ˉC2+(ˉSa−ˉNa)ˉA+Φ2ˉSaˉA(ˉSa−ˉNa)ˉA+ˉNa(ˉBk+ΔˉBk)ˉC2],
M2b=[ˉSaˉB1(ˉSa−ˉNa)ˉB1+ˉNa(ˉBk+ΔˉBk)ˉD21],
M2c=[ˉC1+ˉD12eTn+ˉD12r(ˉCkr+ΔˉCkr)ˉC1]
with Φ2=ˉNaAkc+fAϕ+ΔfAϕ+(ˉSa−ˉNa)ˉB2eeTn(ˉSa+ˉNa)ˉB2r(ˉCkr+ΔˉCkr).
Then, by (6.75), (6.77), and the Schur complement, it follows that (6.79) is equivalent to (6.76) with respect to additive gain variations (6.67). Thus, the proof is complete.
Remark 6.11 In Theorem 6.7, convex sufficient conditions for the solvability of the non-fragile H∞ control problem with sparse structure (6.63) are given in terms of solutions to a set of LMIs. In fact, the result provides an LMI-based method for designing nan-fragile H∞ controllers with the sparse structure from a given fully parameterized H∞ controller. When the designed controller contains no gain variations, from Lemma 2.7, it follows that the design condition given in Theorem 6.7 reduces to a necessary and sufficient condition for the standard H∞ control problem, which means that the structure constraint (2.14) on Lyapunov function matrices does not result in any conservativeness for the standard H∞ controller design.
Here, we will show that the problem of the special case of single-input–single-output (SISO) is a convex one.
Consider the designed controller with gain matrices described by (6.63) and with additive gain variations (6.67).
To facilitate the presentation, denote
(6.80) |
where
Moas=[ˉSaˉA+ˉSaˉB2(ˉCk+ΔˉCk)(ˉSa−ˉNa)ˉA+(ˉFB+ˉNaΔˉBk)ˉC2+Φ1ˉSaˉA(ˉSa−ˉNa)ˉA+(ˉFB+ˉNaΔˉBk)ˉC2],
Mobs=[ˉSaˉB1(ˉSa−ˉNa)ˉB1+(ˉFB+ˉNaΔˉBk)ˉD21],
Mocs=[ˉC1+ˉD12(ˉCk+ΔˉCk)ˉC1.],
Here, Φ1=ˉNaAkc+(ˉFA+ˉNaΔfA)ϕ+(ˉSa−ˉNa)ˉB2(ˉCk+ΔˉCk)andˉA,ˉB1,ˉB2,ˉC1, ˉC2,ˉD12, andˉD21 are defined by (6.72) with T defined by (6.62).
Then, according to Theorem 6.7, the following corollary presents a sufficient condition for the solvability of the non-fragile H∞ control problem with the sparse structure (6.63).
Corollary 6.1 Consider system (6.38). Let γ > 0 and θa > 0 be given constants. If there exist matrices ˉFA,ˉFB,ˉSa>0, and ˉNa<0 such that the following conditions hold:
Mos(ΔˉAka,ΔˉBka,ΔˉCka,)<0,for all θaˉai,θaˉbj∈{−θa,θa},i=1,⋯,n; j=1,⋯,rB, |
(6.81) |
then the controller (6.66) with the gain variations described by form (6.67), and
(6.82) |
solves the non-fragile H∞ control problem with sparse structure for system (6.38).
Remark 6.12 For SISO systems, the problem of non-fragile dynamic output feedback H∞ controller design with the sparse structure can be converted to a convex one. In fact, if we construct the transformation matrix T by using Ak and Ck, we can obtain the sparse structured controller with ˉCk=[10…0], namely, ˉCk is known. So, by Theorem 6.7, the design conditions are given directly.
Due to the fact that the design method given by Theorem 6.7 is based on Assumption 6.1, we need to give methods for designing H∞ controllers satisfying Assumption 6.1. First, the following standard H∞ controller design method [113] is introduced.
Lemma 6.7 [113] Consider system (6.38). Let γ > 0 be a given scalar. If there exist matrices ˆA, ^ B, ˆC,X>0, and Y > 0 such that the following LMI holds:
[AX+XAT+B2ˆC+(B2ˆC)TˆAT+A*ATY+YA+ˆBC2+(ˆBC2)T****B1(C1X+D12ˆC)TYB1+ˆBD21CT1−γ2I0*−I]<0, |
(6.83) |
then controller (6.59) with
(6.84) |
(2.19) holds, where MNT = I – XY.
Then, by using Lemma 6.6, we present a design method to design H∞ controllers satisfying Assumption 6.1.
Lemma 6.8 In Lemma 6.6, let M = X, then controller (6.59) with
Ak=(X−1−Y)−1(ˆA−YAX−ˉBC2X−YB2ˆC)X−1,Bk=(X−1−Y)−1ˆB, Ck=ˆCX−1, |
(6.85) |
(6.60) holds with P = [YX−1−YX−1−Y−(X−1−Y)].
Proof 6.9 Let M = X, then, by using the arguments developed in Scherer, Gahinet, and Chilali [113], the conclusion follows.
Remark 6.13 Lemma 6.8 presents a method of designing H∞ controllers for satisfying Assumption 6.1, which is the initial step for the following algorithm.
Based on Lemma 6.7 and Lemma 6.8, the following algorithm is presented to solve the non-fragile H∞ control problem with sparse structures described by (6.63).
Algorithm 6.3 Let γ > 0 be a given scalar.
Step 1. Minimize γ subject to LMIs X > 0, Y > 0, and (6.83). Denote the optimal solutions as X = Xopt, Y = Yopt, ˆA=ˆAopt,ˆB=ˆBopt, and ˆC=ˆCopt. Substitute the matrices (Xopt,Yopt,ˆAopt,ˆBopt,ˆCopt) to (6.85), compute
Ak=(X−1opt−Yopt)−1(ˆA−YoptAXopt−ˆBoptC2Xopt−YoptB2ˆCopt)X−1opt,Bk=(X−1opt−Yopt)−1ˆBopt, Ck=ˆCoptX−1opt,
then go to Step 2.
Step 2. Combining Ak with the a row vector c (it can be a row vector Cki of Ck) such that Q=[(cAn−1k)T⋯(cAk)TcT]T is nonsingular, by using (6.62), we construct a transformation matrix T. Then, compute ˉA,ˉB,ˉB,ˉC1,ˉC2,ˉD12,andˉD21 according to (6.72), and go to Step 3.
Step 3. Let ˉCk = CkT–1. Minimize γ subject to ˉFA,ˉFB,ˉNa<0,ˉSa>0, and LMI (6.76) for additive gain variations. Denote the optimal solutions as ˉNa=ˉNaopt,FA=FAopt,, and FB = FBopt. Then, according to (6.77),
ˉAk=Akc+ˉN−1aoptˉFAoptϕ,ˉBk=ˉN−1aoptˉFBopt,ˉCk=ˉCk.
The resulting ˉAk,ˉBk, and¯ Ck form the sparse structured non-fragile H∞ controller gains.
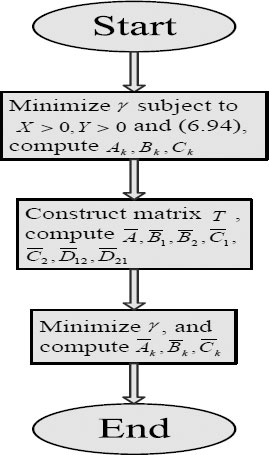
Remark 6.14 Algorithm 6.3 gives a method of designing the non-fragile H∞ controller with sparse structure described by (6.63). In Step 1, an H∞ controller satisfying Assumption 6.1 is designed, followed by determining the sparse structure, and then a non-fragile H∞ controller with the sparse structure is obtained. In order to clarify the algorithm, Figure 6.5 is given to illustrate the flowchart of Algorithm 6.3.
For obtaining the convex design conditions, we restrict the Lyapunov function matrix P with structure (2.14) in Theorem 6.7, which may result in a more conservative evaluation of the H∞ performance bounds. So, in this section, for a designed controller with the sparse structure, the Lyapunov matrix P without the restriction is exploited for obtaining a less conservative evaluation of the H∞ performance bounds.
When the controller parameter matrices ˉAk,ˉBk, and ˉCk are known, the following lemma presents sufficient conditions for measuring the non-fragile H∞ performance of system (6.68).
Denote
(6.86) |
where ˉAe,ˉBe, and ˉCe are defined by (6.69).
FIGURE 6.5
Flowchart of Algorithm 6.3.
Lemma 6.9 Consider system (6.38). Let γ > 0, θa > 0 be constants, and let controller parameter matrices ˉAk,ˉBk, andˉCk be given. Then ‖ Tzω ‖< γ holds for all gain variations described by (6.67), if there exists a symmetric matrix P > 0 such that the following condition holds:
Moss(ΔˉAka,ΔˉBka,ΔˉCka)<0for all θaˉai,θaˉbj,∈{−θa,θa}i=1,⋯,n; j=1,⋯,rB. |
(6.87) |
In this section, we will illustrate the effectiveness of our design methods of the non-fragile H∞ controller with the sparse structure.
Example 6.1 Consider a linear system of form (6.38) with
Ak=[0100−1−101−1],B1=[−100.501.50],B2=[12−2.5],C1=[1−1−3000],C2=[−32−1],D21=[00.5],D12=[01]T.
First, by Step 1 of Algorithm 6.3, we obtain the H∞ controller Kso with gains as
Ak=[−20.050313.3586−2.7130−4.92111.30244.816826.2416−14.4317−1.8096],Bk=[−6.0622−0.42467.2303]T,Ck=[−1.72410.61652.9546],
and the optimal H∞ performance is γopt = 2.9246.
It is easy to see that the matrix Q=[(CkAn−1k)T ⋯ (CkAk)T CTk]T is nonsingular, so in Step 2 of Algorithm 6.3, let the row vector c = Ck. The transformation matrix is obtained as
To=[65.4937137.854367.806773.6172−52.190563.0340−1.72410.61652.9543].
Then, by Step 3, when the designed sparse structured controller is assumed to be with additive uncertainties described by (6.67), by solving (6.76) with θa = 0.65, the non-fragile sparse structured H∞ controller Knoa is obtained with gains as:
ˉAk=[0056.881110−261.355401−40.7364], ˉCk=[001],ˉBk=[42.652637.219933.9007]T,
and the H∞ performance index is 3.4547.
On the other hand, for the designed controller Kso in Step 1 with the optimal H∞ performance γopt = 2.9246, according to (6.63) and transforming ksowith the transformation matrix To, we obtain the sparse structured H∞ controller Kso1 directly with the gains as
ˉAk=[00123.084010−214.259801−20.5575], ˉCk=[001],
TABLE 6.6
Performance Evaluation of Lemma 6.9 with θa = 0.65
Controller |
Knoa |
Kso1 |
γ |
3.2643 |
4.2225 |
TABLE 6.7
H∞ Performance Level for Variant Values of θa
![]()
ˉBk=[34.693931.632131.5505]T.
In this part, for the above designed controllers, Lemma 6.9 gives better evaluations of the H∞ performance index bounds, which are compared and shown in the above tables.
For the sparse structured controllers Knoa (obtained by our design Algorithm 6.3) and Kso1 (obtained by transformation with To directly), with θa = 0.65, Lemma 6.9 gives better evaluations shown in Table 6.6.
Obviously, compared with γopt = 2.9246, the H∞ performance index of the controller Knoa is degraded 11.62%, while the performance index of the controller Kso1 is degraded 44.38%.
Then, a simulation is given to illustrate the effectiveness of the design method. Let x(0)=[0.8 -0.6 0.4]T,ξ(0)=[0.3 -0.5 0.8]TAnd let the disturbance ω(t) be
ω(t)={[11],40≤t≤40.5 (second),0,otherwise.
Then Figure 6.6 shows the regulated output responses of z1 controlled by the sparse structured controller Kso1 (obtained by transformation with To directly) and the non-fragile sparse structured controller Knoa (obtained by our design Algorithm 6.3) with θa = 0.65, respectively. The responses of z2 controlled by the two controllers with θa = 0.65 are shown in Figure 6.7. From the two figures, we can see the superiority of our proposed methods.
In the following, for variant values of θa, we obtain variant H∞ performance levels by using our proposed design method as shown in Table 6.7. Figure 6.8 further presents the relationship between the H∞ a clearly. It can be seen that, the larger the value of θa is, the worse the H∞ performance level is.
FIGURE 6.6
Responses of z1(t) with θa = 0.65.
FIGURE 6.7
Responses of z2(t) with θa = 0.65.
FIGURE 6.8
Response of H∞ performance (γ) with respect to θa.
The full parameterized and sparse structured non-fragile H∞ controller design problems have been investigated in this chapter. The controller to be designed is assumed to be with the additive gain variations of interval type, which are due to the FWL effects when the controller is implemented. For the full parameterized controller design problem, we consider the discretetime and continuous-time systems, respectively. And a two-step procedure is adopted to solve this non-convex problem. In addition, the notion of a structured vertex separator is proposed to approach the numerical computational problem resulting from the interval type of gain uncertainties, and exploited to develop sufficient conditions for the non-fragile H∞ controller design in terms of solutions to a set of LMIs. For the sparse structured controller design problem, a class of sparse structures is specified. Then, a three-step procedure for non-fragile H∞ controller design under the restriction of the sparse structure is provided. The contribution of this method is that it not only reduces the number of nontrivial parameters but also designs the sparse structured controllers with non-fragility. The resulting designs of the two cases guarantee that the closed-loop system is asymptotically stable and the H∞ performance from the disturbance to the regulated output is less than a prescribed level. Numerical examples are given to illustrate the effectiveness of the proposed design methods.