7
Advanced Discrete Distributions
7.1 Compound Frequency Distributions
A larger class of distributions can be created by the processes of compounding any two discrete distributions. The term compounding reflects the idea that the pgf of the new distribution, 
, is written as
where 
and 
are called the primary and secondary distributions, respectively.
The compound distributions arise naturally as follows. Let N be a counting random variable with pgf 
. Let 
be i.i.d. counting random variables each with pgf 
. Assuming that the 
s do not depend on N, the pgf of the random sum 
(where 
implies that 
) is 
. This is shown as follows:
In insurance contexts, this distribution can arise naturally. If N represents the number of accidents arising in a portfolio of risks and 
represents the number of claims (injuries, number of cars, etc.) from the accidents, then S represents the total number of claims from the portfolio. This kind of interpretation is not necessary to justify the use of a compound distribution. If a compound distribution fits data well, that may be enough justification itself. Also, there are other motivations for these distributions, as presented in Section 7.5.
The probability of exactly k claims can be written as
Letting 
, 
, and 
, this is rewritten as
where 
, is the “n-fold convolution” of the function 
, that is, the probability that the sum of n random variables which are each i.i.d. with probability function 
will take on value k.
When 
is chosen to be a member of the 
class,
then a simple recursive formula can be used. This formula avoids the use of convolutions and thus reduces the computations considerably.
In order to use (7.5), the starting value 
is required and is given in Theorem 7.3. If the primary distribution is a member of the 
class, the proof must be modified to reflect the fact that the recursion for the primary distribution begins at 
. The result is the following.
The method used to obtain 
applies to any compound distribution.
Note that the secondary distribution is not required to be in any special form. However, to keep the number of distributions manageable, secondary distributions are selected from the 
or the 
class.
Example 7.5 shows that the Poisson–logarithmic distribution does not create a new distribution beyond the 
and 
classes. As a result, this combination of distributions is not useful to us. Another combination that does not create a new distribution beyond the 
class is the compound geometric distribution, where both the primary and secondary distributions are geometric. The resulting distribution is a zero-modified geometric distribution, as shown in Exercise 7.2. The following theorem shows that certain other combinations are also of no use in expanding the class of distributions through compounding. Suppose that 
as before. Now, 
can always be written as
where 
is the pgf of the conditional distribution over the positive range (in other words, the zero-truncated version).
This shows that adding, deleting, or modifying the probability at zero in the secondary distribution does not add a new distribution because it is equivalent to modifying the parameter 
of the primary distribution. Thus, for example, a Poisson primary distribution with a Poisson, zero-truncated Poisson, or zero-modified Poisson secondary distribution will still lead to a Neyman Type A (Poisson–Poisson) distribution.
7.1.1 Exercises
- 7.1 Do all the members of the
class satisfy the condition of Theorem 7.4? For those that do, identify the parameter (or function of its parameters) that plays the role of 
in the theorem. - 7.2 Show that the following three distributions are identical: (1) geometric–geometric, (2) Bernoulli–geometric, and (3) zero-modified geometric. That is, for any one of the distributions with arbitrary parameters, show that there is a member of the other two distribution types that has the same pf or pgf.
- 7.3 Show that the binomial–geometric and negative binomial–geometric (with negative binomial parameter r a positive integer) distributions are identical.
7.2 Further Properties of the Compound Poisson Class
Of central importance within the class of compound frequency models is the class of compound Poisson frequency distributions. Physical motivation for this model arises from the fact that the Poisson distribution is often a good model to describe the number of claim-causing accidents, and the number of claims from an accident is often itself a random variable.There are numerous convenient mathematical properties enjoyed by the compound Poisson class. In particular, those involving recursive evaluation of the probabilities were also discussed in Section 7.1. In addition, there is a close connection between the compound Poisson distributions and the mixed Poisson frequency distributions that is discussed in Section 7.3.2. Here, we consider some other properties of these distributions. The compound Poisson pgf may be expressed as
where 
is the pgf of the secondary distribution.
We can compare the skewness (third moment) of these distributions to develop an appreciation of the amount by which the skewness and, hence, the tails of these distributions can vary even when the mean and variance are fixed. From (7.9) (see Exercise 7.5) and Definition 3.2, the mean and second and third central moments of the compound Poisson distribution are
where 
is the jth raw moment of the secondary distribution. The coefficient of skewness is
For the Poisson–binomial distribution, with a bit of algebra (see Exercise 7.6), we obtain
Carrying out similar exercises for the negative binomial, Polya–Aeppli, Neyman Type A, and Poisson–ETNB distributions yields
For the Poisson–ETNB distribution, the range of r is 
, 
. The other three distributions are special cases. Letting 
, the secondary distribution is logarithmic, resulting in the negative binomial distribution. Setting 
defines the Polya–Aeppli distribution. Letting 
, the secondary distribution is Poisson, resulting in the Neyman Type A distribution.
Note that for fixed mean and variance, the third moment only changes through the coefficient in the last term for each of the five distributions. For the Poisson distribution, 
, and so the third term for each expression for 
represents the change from the Poisson distribution. For the Poisson–binomial distribution, if 
, the distribution is Poisson because it is equivalent to a Poisson–zero-truncated binomial as truncation at zero leaves only probability at 1. Another view is that from (7.11) we have
which reduces to the Poisson value for 
when 
. Hence, it is necessary that 
for non-Poisson distributions to be created. Then, the coefficient satisfies
For the Poisson–ETNB, because 
, the coefficient satisfies
noting that when 
this refers to the negative binomial distribution. For the Neyman Type A distribution, the coefficient is exactly 1. Hence, these three distributions provide any desired degree of skewness greater than that of the Poisson distribution.
A very useful property of the compound Poisson class of probability distributions is the fact that it is closed under convolution. We have the following theorem.
One main advantage of this result is computational. If we are interested in the sum of independent compound Poisson random variables, then we do not need to compute the distribution of each compound Poisson random variable separately (i.e. recursively using Example 7.3), because Theorem 7.5 implies that a single application of the compound Poisson recursive formula in Example 7.3 will suffice. The following example illustrates this idea.
In various situations, the convolution of negative binomial distributions is of interest. The following example indicates how this distribution may be evaluated.
It is not hard to see that Theorem 7.5 is a generalization of Theorem 6.1, which may be recovered with 
for 
. Similarly, the decomposition result of Theorem 6.2 may also be extended to compound Poisson random variables, where the decomposition is on the basis of the region of support of the secondary distribution. For further details, see Panjer and Willmot [100, Sec. 6.4] or Karlin and Taylor [67, Sec. 16.9].
7.2.1 Exercises
- 7.4 For
let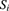 
have independent compound Poisson frequency distributions with Poisson parameter 
and a secondary distribution with pgf 
. Note that all n of the variables have the same secondary distribution. Determine the distribution of 
. - 7.5 Show that, for any pgf,
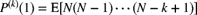provided that the expectation exists. Here, 
indicates the kth derivative. Use this result to confirm the three moments as given in (7.10). - 7.6 Verify the three moments as given in (7.11).
7.3 Mixed-Frequency Distributions
7.3.1 The General Mixed-Frequency Distribution
Many compound distributions can arise in a way that is very different from compounding. In this section, we examine mixture distributions by treating one or more parameters as being “random” in some sense. This section expands on the ideas discussed in Section 6.3 in connection with the gamma mixture of the Poisson distribution being negative binomial.
We assume that the parameter is distributed over the population under consideration and that the sampling scheme that generates our data has two stages. First, a value of the parameter is selected. Then, given that parameter value, an observation is generated using that parameter value.
In automobile insurance, for example, classification schemes attempt to put individuals into (relatively) homogeneous groups for the purpose of pricing. Variables used to develop the classification scheme might include age, experience, a history of violations, accident history, and other variables. Because there will always be some residual variation in accident risk within each class, mixed distributions provide a framework for modeling this heterogeneity.
Let 
denote the pgf of the number of events (e.g. claims) if the risk parameter is known to be 
. The parameter, 
, might be the Poisson mean, for example, in which case the measurement of risk is the expected number of events in a fixed time period.
Let 
be the cdf of 
, where 
is the risk parameter, which is viewed as a random variable. Then, 
represents the probability that, when a value of 
is selected (e.g. a driver is included in our sample), the value of the risk parameter does not exceed 
. Let 
be the pf or pdf of 
. Then,
is the unconditional pgf of the number of events (where the formula selected depends on whether 
is discrete or continuous). The corresponding probabilities are denoted by
The mixing distribution denoted by 
may be of the discrete or continuous type or even a combination of discrete and continuous types. Discrete mixtures are mixtures of distributions when the mixing function is of the discrete type; similarly for continuous mixtures. This phenomenon was introduced for continuous mixtures of severity distributions in Section 5.2.4 and for finite discrete mixtures in Section 4.2.3.
It should be noted that the mixing distribution is unobservable because the data are drawn from the mixed distribution.
Many mixed models can be constructed beginning with a simple distribution. Two examples are given here.
7.3.2 Mixed Poisson Distributions
If we let 
in (7.13) have the Poisson distribution, this leads to a class of distributions with useful properties. A simple example of a Poisson mixture is the two-point mixture.
This example illustrates two important points about finite mixtures. First, the model is probably oversimplified in the sense that risks (e.g. drivers) probably exhibit a continuum of risk levels rather than just two. The second point is that finite mixture models have a lot of parameters to be estimated. The simple two-point Poisson mixture has three parameters. Increasing the number of distributions in the mixture to r will then involve r−1 mixing parameters in addition to the total number of parameters in the r component distributions. Consequently, continuous mixtures are frequently preferred.
The class of mixed Poisson distributions has some interesting properties that are developed here. Let 
be the pgf of a mixed Poisson distribution with arbitrary mixing distribution 
. Then (with formulas given for the continuous case), by introducing a scale parameter 
, we have
where 
is the mgf of the mixing distribution.
Therefore, 
and with 
we obtain 
, where N has the mixed Poisson distribution. Also, 
, implying that 
and, therefore,
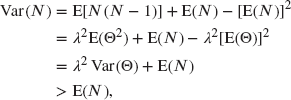
and thus for mixed Poisson distributions the variance is always greater than the mean.
Most continuous distributions in this book involve a scale parameter. This means that scale changes to distributions do not cause a change in the form of the distribution, but only in the value of its scale parameter. For the mixed Poisson distribution, with pgf (7.14), any change in 
is equivalent to a change in the scale parameter of the mixing distribution. Hence, it may be convenient to simply set 
where a mixing distribution with a scale parameter is used.
Douglas [29] proves that for any mixed Poisson distribution, the mixing distribution is unique. This means that two different mixing distributions cannot lead to the same mixed Poisson distribution and this allows us to identify the mixing distribution in some cases.
There is also an important connection between mixed Poisson distributions and compound Poisson distributions.
In other words, taking the 
power of the characteristic function still results in a characteristic function. The characteristic function is defined as follows.
In Definition 7.6, “characteristic function” could have been replaced by “moment generating function” or “probability generating function,” or some other transform. That is, if the definition is satisfied for one of these transforms, it will be satisfied for all others that exist for the particular random variable. We choose the characteristic function because it exists for all distributions, while the moment generating function does not exist for some distributions with heavy tails. Because many earlier results involved probability generating functions, it is useful to note the relationship between it and the characteristic function.
The following distributions, among others, are infinitely divisible: normal, gamma, Poisson, and negative binomial. The binomial distribution is not infinitely divisible because the exponent m in its pgf must take on integer values. Dividing m by 
will result in nonintegral values. In fact, no distributions with a finite range of support (the range over which positive probabilities exist) can be infinitely divisible. Now to the important result.
A proof can be found in Feller [37, Chapter 12]. If we choose any infinitely divisible mixing distribution, the corresponding mixed Poisson distribution can be equivalently described as a compound Poisson distribution. For some distributions, this is a distinct advantage when carrying out numerical work, because the recursive formula (7.5) can be used in evaluating the probabilities once the secondary distribution is identified. For most cases, this identification is easily carried out. A second advantage is that, because the same distribution can be motivated in two different ways, a specific explanation is not required in order to use it. Conversely, the fact that one of these models fits well does not imply that it is the result of mixing or compounding. For example, the fact that claims follow a negative binomial distribution does not necessarily imply that individuals have the Poisson distribution and the Poisson parameter has a gamma distribution.
To obtain further insight into these results, we remark that if a counting distribution with pgf 
is known to be of compound Poisson form (or, equivalently, is an infinitely divisible pgf), then the quantities 
and 
in Theorem 7.9 may be expressed in terms of 
. Because 
, it follows that 
or, equivalently,
Thus, using (7.15),
The following examples illustrate the use of these ideas.
It is not difficult to see that, if 
is the pf for any discrete random variable with pgf 
, then the pgf of the mixed Poisson distribution is 
, a compound distribution with a Poisson secondary distribution.
A further interesting result obtained by Holgate [57] is that, if a mixing distribution is absolutely continuous and unimodal, then the resulting mixed Poisson distribution is also unimodal. Multimodality can occur when discrete mixing functions are used. For example, the Neyman Type A distribution can have more than one mode. You should try this calculation for various combinations of the two parameters. The relationships between mixed and compound Poisson distributions are given in Table 7.2.
Table 7.2 Pairs of compound and mixed Poisson distributions.
| Name | Compound secondary distribution | Mixing distribution |
| Negative binomial | Logarithmic | Gamma |
| Neyman–Type A | Poisson | Poisson |
| Poisson–inverse Gaussian | ETNB  |
Inverse Gaussian |
In this chapter, we focus on distributions that are easily handled computationally. Although many other discrete distributions are available, we believe that those discussed form a sufficiently rich class for most problems.
7.3.3 Exercises
- 7.7 Show that the negative binomial–Poisson compound distribution is the same as a mixed Poisson distribution with a negative binomial mixing distribution.
- 7.8 For
let 
have a mixed Poisson distribution with parameter 
. Let the mixing distribution for 
have pgf 
. Show that 
has a mixed Poisson distribution and determine the pgf of the mixing distribution. - 7.9 Let N have a Poisson distribution with (given that
) parameter 
. Let the distribution of the random variable 
have a scale parameter. Show that the mixed distribution does not depend on the value of 
. - 7.10 Let N have a Poisson distribution with (given that
) parameter 
. Let the distribution of the random variable 
have pdf 
. Determine the pf of the mixed distribution. In addition, show that the mixed distribution is also a compound distribution. - 7.11 Consider the mixed Poisson distribution
where the pdf
is that of the positive stable distribution (see, e.g. Feller [38, pp. 448, 583]) given by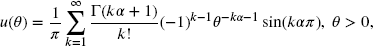
where
. The Laplace transform is 
. Prove that 
is a compound Poisson distribution with Sibuya secondary distribution (this mixed Poisson distribution is sometimes called a discrete stable distribution). - 7.12 Consider the Poisson–inverse Gaussian distribution (Example 7.16) with pgf
Use the results of Exercise 5.20(g) to prove that
and, for
,
- 7.13 Let N have a Poisson distribution with mean
, where 
has the reciprocal inverse Gaussian distribution with mgf [from Exercise 5.20(d)] given by
- Derive the pgf of N and explain in words what type of distribution has this pgf.
- Express the pgf in (a) in compound Poisson form, identifying the Poisson parameter and the secondary distribution.
- 7.14 Suppose the following:
is a random variable with support on the positive real numbers.
is a Poisson random variable with mean 
and N has pgf 
.
, where 
is constant.
is a Poisson random variable with mean 
.
- Prove that the pgf of
is
and explain in words what type of distribution has this pgf.
- Assume
has an inverse Gaussian distribution. Describe carefully how you could recursively calculate the probabilities of the compound distribution with pgf 
, where 
is itself a pgf.
7.4 The Effect of Exposure on Frequency
Assume that the current portfolio consists of n entities, each of which could produce claims. Let 
be the number of claims produced by the jth entity. Then, 
. If we assume that the 
are independent and identically distributed, then
Now suppose that the portfolio is expected to expand to 
entities with frequency 
. Then,
Thus, if N is infinitely divisible, the distribution of 
will have the same form as that of N, but with modified parameters.
For the 
class, all members except the binomial have this property. For the 
class, none of the members do. For compound distributions, it is the primary distribution that must be infinitely divisible. In particular, compound Poisson and compound negative binomial (including the geometric) distributions will be preserved under an increase in exposure. Earlier, some reasons were given to support the use of zero-modified distributions. If exposure adjustments are anticipated, it may be better to choose a compound model, even if the fit is not quite as good. It should be noted that compound models have the ability to place large amounts of probability at zero.
7.5 An Inventory of Discrete Distributions
We have introduced the simple 
class, generalized to the 
class, and then used compounding and mixing to create a larger class of distributions. Calculation of the probabilities of these distributions can be carried out by using simple recursive procedures. In this section, we note that there are relationships among the various distributions similar to those of Section 5.3.2. The specific relationships are given in Table 7.3.
Table 7.3 Relationships among discrete distributions.
| Distribution | Is a special case of | Is a limiting case of |
| Poisson | ZM Poisson | Negative binomial |
| Poisson–binomial | ||
| Poisson–inverse Gaussian | ||
| Polya–Aepplia | ||
| Neyman–Type Ab | ||
| ZT Poisson | ZM Poisson | ZT negative binomial |
| ZM Poisson | ZM negative binomial | |
| Geometric | Negative binomial, ZM geometric | Geometric–Poisson |
| ZT geometric | ZT negative binomial | |
| ZM geometric | ZM negative binomial | |
| Logarithmic | ZT negative binomial | |
| ZM logarithmic | ZM negative binomial | |
| Binomial | ZM binomial | |
| Negative binomial | ZM negative binomial, Poisson–ETNB | |
| Poisson–inverse Gaussian | Poisson–ETNB | |
| Polya–Aeppli | Poisson–ETNB | |
| Neyman–Type A | Poisson–ETNB | |
| a Also called Poisson–geometric. bAlso called Poisson–Poisson. |
||
It is clear from earlier developments that members of the 
class are special cases of members of the 
class and that zero-truncated distributions are special cases of zero-modified distributions. The limiting cases are best discovered through the probability generating function, as was done in Section 6.3 where the Poisson distribution is shown to be a limiting case of the negative binomial distribution.
We have not listed compound distributions where the primary distribution is one of the two-parameter models, such as the negative binomial or Poisson–inverse Gaussian. They are excluded because these distributions are often themselves compound Poisson distributions and, as such, are generalizations of distributions already presented. This collection forms a particularly rich set of distributions in terms of shape. However, many other distributions are also possible and are discussed in Johnson, Kotz, and Kemp [65], Douglas [29], and Panjer and Willmot [100].
7.5.1 Exercises
- 7.15 Calculate
, 
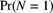, and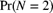 
for each of the following distributions:
- Poisson(
) - Geometric(
) - Negative binomial(
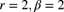) - Binomial(
) - Logarithmic(
) - ETNB(
) - Poisson–inverse Gaussian(
) - Zero-modified geometric(
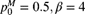) - Poisson–Poisson(Neyman Type A)(
) - Poisson–ETNB(
) - Poisson–zero-modified geometric (
)
- Poisson(
- 7.16 A frequency model that has not been mentioned up to this point is the zeta distribution. It is a zero-truncated distribution with
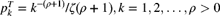. The denominator is the zeta function, which must be evaluated numerically as 
. The zero-modified zeta distribution can be formed in the usual way. More information can be found in Luong and Doray [84]. Verify that the zeta distribution is not a member of the 
class. - 7.17 For the discrete counting random variable N with probabilities
, let 
.
- Demonstrate that
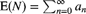. - Demonstrate that
and 
are related by 
. What happens as 
? - Suppose that N has the negative binomial distribution
where r is a positive integer. Prove that
- Suppose that N has the Sibuya distribution with pgf
Prove that
and that
- Suppose that N has the mixed Poisson distribution with
where
is a cumulative distribution function. Prove that
- Demonstrate that