16
Introduction To Limited Fluctuation Credibility
16.1 Introduction
Credibility theory is a set of quantitative tools that allows an insurer to perform prospective experience rating (adjust future premiums based on past experience) on a risk or group of risks. If the experience of a policyholder is consistently better than that assumed in the underlying manual rate (sometimes called the pure premium, then the policyholder may demand a rate reduction.
The policyholder's argument is as follows. The manual rate is designed to reflect the expected experience (past and future) of the entire rating class and implicitly assumes that the risks are homogeneous. However, no rating system is perfect, and there always remains some heterogeneity in the risk levels after all the underwriting criteria are accounted for. Consequently, some policyholders will be better risks than that assumed in the underlying manual rate. Of course, the same logic dictates that a rate increase should be applied to a poor risk, but in this situation the policyholder is certainly not going to ask for a rate increase! Nevertheless, an increase may be necessary, due to considerations of equity and the economics of the situation.
The insurer is then forced to answer the following question: How much of the difference in experience of a given policyholder is due to random variation in the underlying claims experience and how much is due to the fact that the policyholder really is a better or worse risk than average? In other words, how credible is the policyholder's own experience? Two facts must be considered in this regard:
- The more past information the insurer has on a given policyholder, the more credible is the policyholder's own experience, all else being equal. In the same manner, in group insurance the experience of larger groups is more credible than that of smaller groups.
- Competitive considerations may force the insurer to give full (using the past experience of the policyholder only and not the manual rate) or nearly full credibility to a given policyholder in order to retain the business.
Another use for credibility is in the setting of rates for classification systems. For example, in workers compensation insurance, there may be hundreds of occupational classes, some of which may provide very little data. To accurately estimate the expected cost for insuring these classes, it may be appropriate to combine the limited actual experience with some other information, such as past rates, or the experience of occupations that are closely related.
From a statistical perspective, credibility theory leads to a result that would appear to be counterintuitive. If experience from an insured or group of insureds is available, our statistical training may convince us to use the sample mean or some other unbiased estimator. But credibility theory tells us that it is optimal to give only partial weight to this experience and give the remaining weight to an estimator produced from other information. We will discover that what we sacrifice in terms of bias, we gain in terms of reducing the average (squared) error.
Credibility theory allows an insurer to quantitatively formulate the problem of combining data with other information, and this part provides an introduction to this theory. This chapter deals with limited fluctuation credibility theory, a subject developed in the early part of the twentieth century. This theory provides a mechanism for assigning full (Section 16.3) or partial (Section 16.4) credibility to a policyholder's experience. The difficulty with this approach is the lack of a sound underlying mathematical theory to justify the use of these methods. Nevertheless, this approach provided the original treatment of the subject and is still in use today.
A classic paper by Bühlmann in 1967 [19] provides a statistical framework within which credibility theory has developed and flourished. While this approach, termed greatest accuracy credibility theory,1 was formalized by Bühlmann, the basic ideas had been around for some time. This approach is introduced in Chapter 17. The simplest model, that of Bühlmann [19], is discussed in Section 17.5. Practical improvements were made by Bühlmann and Straub in 1970 [21]. Their model is discussed in Section 17.6. The concept of exact credibility is presented in Section 17.7.
Practical use of the theory requires that unknown model parameters be estimated from data. Chapter 18 covers two estimation approaches. Nonparametric estimation (where the problem is somewhat model free and the parameters are generic, such as the mean and variance) is considered in Section 18.2. Semiparametric estimation (where some of the parameters are based on assuming particular distributions) is covered in Section 18.3.
We close this introduction with a quote from Arthur Bailey in 1950 [9, p. 8] that aptly summarizes much of the history of credibility. We, too, must tip our hats to the early actuaries, who, with unsophisticated mathematical tools at their disposal, were able to come up with formulas that not only worked but also were very similar to those that we carefully develop in this part:
It is at this point in the discussion that the ordinary individual has to admit that, while there seems to be some hazy logic behind the actuaries' contentions, it is too obscure for him to understand. The trained statistician cries “Absurd! Directly contrary to any of the accepted theories of statistical estimation.” The actuaries themselves have to admit that they have gone beyond anything that has been proven mathematically, that all of the values involved are still selected on the basis of judgment, and that the only demonstration they can make is that, in actual practice, it works. Let us not forget, however, that they have made this demonstration many times. It does work!
16.2 Limited Fluctuation Credibility Theory
This branch of credibility theory represents the first attempt to quantify the credibility problem. This approach was suggested in the early 1900s in connection with workers compensation insurance. The original paper on the subject was by Mowbray in 1914 [42]. The problem may be formulated as follows. Suppose that a policyholder has experienced ![]() claims or losses2 in past experience period j, where
claims or losses2 in past experience period j, where ![]() . Another view is that
. Another view is that ![]() is the experience from the jth policy in a group or from the jth member of a particular class in a rating scheme. Suppose that
is the experience from the jth policy in a group or from the jth member of a particular class in a rating scheme. Suppose that ![]() , that is, the mean is stable over time or across the members of a group or class.3 This quantity would be the premium to charge (net of expenses, profits, and a provision for adverse experience) if only we knew its value. Also suppose that
, that is, the mean is stable over time or across the members of a group or class.3 This quantity would be the premium to charge (net of expenses, profits, and a provision for adverse experience) if only we knew its value. Also suppose that ![]() , again, the same for all j. The past experience may be summarized by the average
, again, the same for all j. The past experience may be summarized by the average ![]() . We know that
. We know that ![]() , and if the
, and if the ![]() are independent,
are independent, ![]() . The insurer's goal is to decide on the value of
. The insurer's goal is to decide on the value of ![]() . One possibility is to ignore the past data (no credibility) and simply charge M, a value obtained from experience on other similar, but not identical, policyholders. This quantity is often called the manual premium because it would come from a book (manual) of premiums. Another possibility is to ignore M and charge
. One possibility is to ignore the past data (no credibility) and simply charge M, a value obtained from experience on other similar, but not identical, policyholders. This quantity is often called the manual premium because it would come from a book (manual) of premiums. Another possibility is to ignore M and charge ![]() (full credibility). A third possibility is to choose some combination of M and
(full credibility). A third possibility is to choose some combination of M and ![]() (partial credibility).
(partial credibility).
From the insurer's standpoint, it seems sensible to “lean toward” the choice ![]() if the experience is more “stable” (less variable,
if the experience is more “stable” (less variable, ![]() small). Stable values imply that
small). Stable values imply that ![]() is of more use as a predictor of next year's results. Conversely, if the experience is more volatile (variable), then
is of more use as a predictor of next year's results. Conversely, if the experience is more volatile (variable), then ![]() is of less use as a predictor of next year's results and the choice of M makes more sense.
is of less use as a predictor of next year's results and the choice of M makes more sense.
Also, if we have an a priori reason to believe that the chances are great that this policyholder is unlike those who produced the manual premium M, then more weight should be given to ![]() because, as an unbiased estimator,
because, as an unbiased estimator, ![]() tells us something useful about
tells us something useful about ![]() while M is likely to be of little value. In contrast, if all of our other policyholders have similar values of
while M is likely to be of little value. In contrast, if all of our other policyholders have similar values of ![]() , there is no point in relying on the (perhaps limited) experience of any one of them when M is likely to provide an excellent description of the propensity for claims or losses.
, there is no point in relying on the (perhaps limited) experience of any one of them when M is likely to provide an excellent description of the propensity for claims or losses.
While reference is made to policyholders, the entity contributing to each ![]() could arise from a single policyholder, a class of policyholders possessing similar underwriting characteristics, or a group of insureds assembled for some other reason. For example, for a given year j,
could arise from a single policyholder, a class of policyholders possessing similar underwriting characteristics, or a group of insureds assembled for some other reason. For example, for a given year j, ![]() could be the number of claims filed in respect of a single automobile policy in one year, the average number of claims filed by all policyholders in a certain ratings class (e.g. single, male, under age 25, living in an urban area, driving over 7,500 miles per year), or the average amount of losses per vehicle for a fleet of delivery trucks owned by a food wholesaler.
could be the number of claims filed in respect of a single automobile policy in one year, the average number of claims filed by all policyholders in a certain ratings class (e.g. single, male, under age 25, living in an urban area, driving over 7,500 miles per year), or the average amount of losses per vehicle for a fleet of delivery trucks owned by a food wholesaler.
We first present one approach to decide whether to assign full credibility (charge ![]() ), and then we present an approach to assign partial credibility if there is evidence that full credibility is inappropriate.
), and then we present an approach to assign partial credibility if there is evidence that full credibility is inappropriate.
16.3 Full Credibility
One method of quantifying the stability of ![]() is to infer that
is to infer that ![]() is stable if the difference between
is stable if the difference between ![]() and
and ![]() is small relative to
is small relative to ![]() with high probability. In statistical terms, stability can be defined by selecting two numbers
with high probability. In statistical terms, stability can be defined by selecting two numbers ![]() and
and ![]() (with r close to 0 and p close to 1, common choices being
(with r close to 0 and p close to 1, common choices being ![]() and
and ![]() ) and assigning full credibility if
) and assigning full credibility if
It is convenient to restate (16.1) as

Now let ![]() be defined by
be defined by
That is, ![]() is the smallest value of y that satisfies the probability statement in braces in (16.2). If
is the smallest value of y that satisfies the probability statement in braces in (16.2). If ![]() has a continuous distribution, the “≥” sign in (16.2) may be replaced by an “=” sign, and
has a continuous distribution, the “≥” sign in (16.2) may be replaced by an “=” sign, and ![]() satisfies
satisfies
Then, the condition for full credibility is ![]() ,
,
where ![]() . Condition (16.4) states that full credibility is assigned if the coefficient of variation
. Condition (16.4) states that full credibility is assigned if the coefficient of variation ![]() is no larger than
is no larger than ![]() , an intuitively reasonable result.
, an intuitively reasonable result.
Also of interest is that (16.4) can be rewritten to show that full credibility occurs when
Alternatively, solving (16.4) for n gives the number of exposure units required for full credibility, namely
In many situations, it is reasonable to approximate the distribution of ![]() by a normal distribution with mean
by a normal distribution with mean ![]() and variance
and variance ![]() . For example, central limit theorem arguments may be applicable if n is large. In that case,
. For example, central limit theorem arguments may be applicable if n is large. In that case, ![]() has a standard normal distribution. Then, (16.3) becomes (where Z has a standard normal distribution and
has a standard normal distribution. Then, (16.3) becomes (where Z has a standard normal distribution and ![]() is its cdf)
is its cdf)

Therefore, ![]() , and
, and ![]() is the
is the ![]() percentile of the standard normal distribution.
percentile of the standard normal distribution.
For example, if ![]() , then standard normal tables give
, then standard normal tables give ![]() . If, in addition,
. If, in addition, ![]() , then
, then ![]() and (16.6) yields
and (16.6) yields ![]() . Note that this answer assumes we know the coefficient of variation of
. Note that this answer assumes we know the coefficient of variation of ![]() . It is possible that we have some idea of its value, even though we do not know the value of
. It is possible that we have some idea of its value, even though we do not know the value of ![]() (remember, that is the quantity we want to estimate).
(remember, that is the quantity we want to estimate).
The important thing to note when using (16.6) is that the coefficient of variation is for the estimator of the quantity to be estimated. The right-hand side gives the standard for full credibility when measuring it in terms of exposure units. If some other unit is desired, it is usually sufficient to multiply both sides by an appropriate quantity. Finally, any unknown quantities will have be to estimated from the data, which implies that the credibility question can be posed in a variety of ways. The following examples cover the most common cases.
![]()
In the next example, it is further assumed that the observations are from a particular type of distribution.
![]()
In these examples, the standard for full credibility is not met, and so the sample means are not sufficiently accurate to be used as estimates of the expected value. We need a method for dealing with this situation.
16.4 Partial Credibility
If it is decided that full credibility is inappropriate, then for competitive reasons (or otherwise), it may be desirable to reflect the past experience ![]() in the net premium as well as the externally obtained mean, M. An intuitively appealing method for combining the two quantities is through a weighted average, that is, through the credibility premium
in the net premium as well as the externally obtained mean, M. An intuitively appealing method for combining the two quantities is through a weighted average, that is, through the credibility premium
where the credibility factor ![]() needs to be chosen. There are many formulas for Z that have been suggested in the actuarial literature, usually justified on intuitive rather than theoretical grounds. (We remark that Mowbray [92] considered full but not partial credibility.) One important choice is
needs to be chosen. There are many formulas for Z that have been suggested in the actuarial literature, usually justified on intuitive rather than theoretical grounds. (We remark that Mowbray [92] considered full but not partial credibility.) One important choice is
where k needs to be determined. This particular choice will be shown to be theoretically justified on the basis of a statistical model to be presented in Chapter 17. Another choice, based on the same idea as full credibility (and including the full-credibility case ![]() ), is now discussed.
), is now discussed.
A variety of arguments have been used for developing the value of Z, many of which lead to the same answer. All of them are flawed in one way or another. The development we have chosen to present is also flawed but is at least simple. Recall that the goal of the full-credibility standard is to ensure that the difference between the net premium we are considering ![]() and what we should be using
and what we should be using ![]() is small with high probability. Because
is small with high probability. Because ![]() is unbiased, achieving this standard is essentially (and exactly if
is unbiased, achieving this standard is essentially (and exactly if ![]() has the normal distribution) equivalent to controlling the variance of the proposed net premium,
has the normal distribution) equivalent to controlling the variance of the proposed net premium, ![]() , in this case. We see from (16.5) that there is no assurance that the variance of
, in this case. We see from (16.5) that there is no assurance that the variance of ![]() will be small enough. However, it is possible to control the variance of the credibility premium,
will be small enough. However, it is possible to control the variance of the credibility premium, ![]() , as follows:
, as follows:

Thus ![]() , provided that it is less than 1, which can be expressed using the single formula
, provided that it is less than 1, which can be expressed using the single formula
One interpretation of (16.9) is that the credibility factor Z is the ratio of the coefficient of variation required for full credibility ![]() to the actual coefficient of variation. For obvious reasons, this formula is often called the square-root rule for partial credibility, regardless of what is being counted.
to the actual coefficient of variation. For obvious reasons, this formula is often called the square-root rule for partial credibility, regardless of what is being counted.
While we could do the algebra with regard to (16.9), it is sufficient to note that it always turns out that Z is the square root of the ratio of the actual count to the count required for full credibility.
![]()
![]()
Earlier, we mentioned a flaw in the approach. Other than assuming that the variance captures the variability of ![]() in the right way, all of the mathematics is correct. The flaw is in the goal. Unlike
in the right way, all of the mathematics is correct. The flaw is in the goal. Unlike ![]() ,
, ![]() is not an unbiased estimator of
is not an unbiased estimator of ![]() . In fact, one of the qualities that allows credibility to work is its use of biased estimators. But for biased estimators the appropriate measure of its quality is not its variance, but its MSE. However, the MSE requires knowledge of the bias and, in turn, that requires knowledge of the relationship of
. In fact, one of the qualities that allows credibility to work is its use of biased estimators. But for biased estimators the appropriate measure of its quality is not its variance, but its MSE. However, the MSE requires knowledge of the bias and, in turn, that requires knowledge of the relationship of ![]() and M. However, we know nothing about that relationship, and the data we have collected are of little help. As noted in Section 16.5, this is not only a problem with our determination of Z; it is a problem that is characteristic of the limited fluctuation approach. A model for this relationship is introduced in Chapter 17.
and M. However, we know nothing about that relationship, and the data we have collected are of little help. As noted in Section 16.5, this is not only a problem with our determination of Z; it is a problem that is characteristic of the limited fluctuation approach. A model for this relationship is introduced in Chapter 17.
This section closes with a few additional examples. In the first two examples, ![]() is used.
is used.
![]()
![]()
![]()
16.5 Problems with the Approach
While the limited fluctuation approach yields simple solutions to the problem, there are theoretical difficulties. First, there is no underlying theoretical model for the distribution of the ![]() and, thus, no reason why a premium of the form (16.7) is appropriate and preferable to M. Why not just estimate
and, thus, no reason why a premium of the form (16.7) is appropriate and preferable to M. Why not just estimate ![]() from a collection of homogeneous policyholders and charge all policyholders the same rate? While there is a practical reason for using (16.7), no model has been presented to suggest that this formula may be appropriate. Consequently, the choice of Z (and hence
from a collection of homogeneous policyholders and charge all policyholders the same rate? While there is a practical reason for using (16.7), no model has been presented to suggest that this formula may be appropriate. Consequently, the choice of Z (and hence ![]() ) is completely arbitrary.
) is completely arbitrary.
Second, even if (16.7) were appropriate for a particular model, there is no guidance for the selection of r and p.
Finally, the limited fluctuation approach does not examine the difference between ![]() and M. When (16.7) is employed, we are essentially stating that the value of M is accurate as a representation of the expected value, given no information about this particular policyholder. However, it is usually the case that M is also an estimate and, therefore, unreliable in itself. The correct credibility question should be “how much more reliable is
and M. When (16.7) is employed, we are essentially stating that the value of M is accurate as a representation of the expected value, given no information about this particular policyholder. However, it is usually the case that M is also an estimate and, therefore, unreliable in itself. The correct credibility question should be “how much more reliable is ![]() compared to M?” and not “how reliable is
compared to M?” and not “how reliable is ![]() ?”
?”
In the next chapter, a systematic modeling approach is presented for the claims experience of a particular policyholder that suggests that the past experience of the policyholder is relevant for prospective rate making. Furthermore, the intuitively appealing formula (16.7) is a consequence of this approach, and Z is often obtained from relations of the form (16.8).
16.6 Notes and References
The limited fluctuation approach is discussed by Herzog [52] and Longley-Cook [83]. See also Norberg [94].
16.7 Exercises
- 16.1 An insurance company has decided to establish its full-credibility requirements for an individual state rate filing. The full-credibility standard is to be set so that the observed total amount of claims underlying the rate filing would be within 5% of the true value with probability 0.95. The claim frequency follows a Poisson distribution and the severity distribution has pdf

Determine the expected number of claims necessary to obtain full credibility using the normal approximation.
- 16.2 For a particular policyholder, the past total claims experience is given by
 , where the
, where the 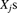 are i.i.d. compound random variables with Poisson parameter
are i.i.d. compound random variables with Poisson parameter  and gamma claim size distribution with pdf
and gamma claim size distribution with pdf

You also know the following:
- The credibility factor based on number of claims is 0.9.
- The expected claim size
 .
. - The credibility factor based on total claims is 0.8.
Determine
 and
and 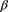 .
. - 16.3 For a particular policyholder, the manual premium is 600 per year. The past claims experience is given in Table 16.1. Assess whether full or partial credibility is appropriate and determine the net premium for next year's claims assuming the normal approximation. Use
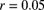 and
and  .
.
Table 16.1 The data for Exercise 16.3.
Year 1 2 3 Claims 475 550 400 - 16.4 Redo Example 16.2 assuming that
 is a compound negative binomial distribution rather than compound Poisson.
is a compound negative binomial distribution rather than compound Poisson. - 16.5 (*) The total number of claims for a group of insureds is Poisson with mean
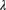 . Determine the value of
. Determine the value of  such that the observed number of claims will be within 3% of
such that the observed number of claims will be within 3% of  with a probability of 0.975 using the normal approximation.
with a probability of 0.975 using the normal approximation. - 16.6 (*) An insurance company is revising rates based on old data. The expected number of claims for full credibility is selected so that observed total claims will be within 5% of the true value 90% of the time. Individual claim amounts have pdf
 , and the number of claims has the Poisson distribution. The recent experience consists of 1,082 claims. Determine the credibility, Z, to be assigned to the recent experience. Use the normal approximation.
, and the number of claims has the Poisson distribution. The recent experience consists of 1,082 claims. Determine the credibility, Z, to be assigned to the recent experience. Use the normal approximation. - 16.7 (*) The average claim size for a group of insureds is 1,500, with a standard deviation of 7,500. Assume that claim counts have the Poisson distribution. Determine the expected number of claims so that the total loss will be within 6% of the expected total loss with probability 0.90.
- 16.8 (*) A group of insureds had 6,000 claims and a total loss of 15,600,000. The prior estimate of the total loss was 16,500,000. Determine the limited fluctuation credibility estimate of the total loss for the group. Use the standard for full credibility determined in Exercise 16.7.
- 16.9 (*) The full-credibility standard is set so that the total number of claims is within 5% of the true value with probability p. This standard is 800 claims. The standard is then altered so that the total cost of claims is to be within 10% of the true value with probability p. The claim frequency has a Poisson distribution and the claim severity distribution has pdf
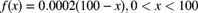 . Determine the expected number of claims necessary to obtain full credibility under the new standard.
. Determine the expected number of claims necessary to obtain full credibility under the new standard. - 16.10 (*) A standard for full credibility of 1,000 claims has been selected so that the actual pure premium will be within 10% of the expected pure premium 95% of the time. The number of claims has the Poisson distribution. Determine the coefficient of variation of the severity distribution.
- 16.11 (*) For a group of insureds, you are given the following information:
- The prior estimate of expected total losses is 20,000,000.
- The observed total losses are 25,000,000.
- The observed number of claims is 10,000.
- The number of claims required for full credibility is 17,500.
Determine the credibility estimate of the group's expected total losses based on all the given information. Use the credibility factor that is appropriate if the goal is to estimate the expected number of losses.
- 16.12 (*) A full-credibility standard is determined so that the total number of claims is within 5% of the expected number with probability 98%. If the same expected number of claims for full credibility is applied to the total cost of claims, the actual total cost would be within
 of the expected cost with 95% probability. Individual claims have severity pdf
of the expected cost with 95% probability. Individual claims have severity pdf  , and the number of claims has a Poisson distribution. Determine K.
, and the number of claims has a Poisson distribution. Determine K. - 16.13 (*) The number of claims has a Poisson distribution. The number of claims and the claim severity are independent. Individual claim amounts can be for 1, 2, or 10, with probabilities 0.5, 0.3, and 0.2, respectively. Determine the expected number of claims needed so that the total cost of claims is within 10% of the expected cost with 90% probability.
- 16.14 (*) The number of claims has a Poisson distribution. The coefficient of variation of the severity distribution is 2. The standard for full credibility in estimating total claims is 3,415. With this standard, the observed pure premium will be within
 of the expected pure premium 95% of the time. Determine k.
of the expected pure premium 95% of the time. Determine k. - 16.15 (*) You are given the following:
 prior estimate of pure premium for a particular class of business.
prior estimate of pure premium for a particular class of business. observed pure premium during the latest experience period for the same class of business.
observed pure premium during the latest experience period for the same class of business. revised estimate of pure premium for the same class following the observations.
revised estimate of pure premium for the same class following the observations. number of claims required for full credibility of the pure premium.
number of claims required for full credibility of the pure premium.
Express the observed number of claims as a function of these four items.
- 16.16 (*) A company's standard for full credibility is 2,000 claims when it is assumed that the number of claims follows a Poisson distribution and the total number of claims is to be within 3% of the true value with probability p. The standard is changed so that the total cost of claims is to be within 5% of the true value with the same probability p and a severity distribution that is uniform from 0 to 10,000, and the frequency distribution is Poisson. Determine the expected number of claims necessary to obtain full credibility under the new standard.




