Appendix C

Public Key Cryptography in a Nutshell

This appendix is not intended to be a comprehensive overview of public key cryptography.¹ There are a number of great books covering cryptography for practitioners as well as researchers [115, 156, 190, 257, 293]. The purpose of this appendix is to introduce the reader to some of the basic concepts of public key cryptography and hopefully provide enough information to enable readers who are new to cryptography to gain a better understanding of this book without having to go elsewhere. Public key cryptography is a technology that is central to the design of advanced malicious software.

C.1 Overview of Cryptography

Cryptology is the study of the hidden word. It is broken down into two subfields called cryptography and cryptanalysis. Cryptography is the science of developing cryptosystems that encipher and decipher data, among other things. Cryptanalysis is the study of breaking cryptosystems. A cryptanalyst is one who seeks to break or find weaknesses in the ciphers that are developed by a cryptographer. One who dabbles in both subfields may be justly referred to as a cryptologist.

Classical cryptography dates back thousands of years and has been employed for such things as concealing command and control information during times of war. Command and control information must be secured, even against the messengers that carry it, so that it does not fall into enemy hands while in transit. In this respect the most basic use of cryptography can be regarded as malicious in nature. It is malicious from the perspective of allied forces whenever it is used by the enemy to hide enemy command and control information from allied forces. This book is the study of malicious cryptography in a more literal sense, since it describes how to use cryptography to craft advanced malicious software agents that traverse hostile networks and execute cryptographic payloads.

A classical cryptosystem consists of an encryption algorithm and a corresponding decryption algorithm. To encrypt data, the encryption algorithm requires the user to supply it with a cryptographic key. When prompted for a key, a user will typically enter a word or phrase that will be easy to remember. This text is then transformed into a binary string that in turn serves as an encryption key. The encryption algorithm then uses the key to algorithmically transform the input message into a cryptogram, or ciphertext. No information is lost in this process and provided that the key is available, the ciphertext can be converted back into the original message using the decryption algorithm.

C.1.1 Classical Cryptography

More formally, a classical cryptosystem consists of an encryption algorithm E, a decryption algorithm D, a message space M, a ciphertext space C, and a key space K. The key space is a large set of numbers from which a key is chosen in order to encipher data. For example, in AES-128 the key space consists of all bit strings of length 128 bits [204]. The key space therefore contains 2¹²⁸ unique encryption keys. To encrypt a message m chosen from the message space, a key k is chosen randomly from K and the ciphertext c is computed. This may be represented as,

The encryption algorithm E takes m and k as input and computes the ciphertext c of the message m. The message m is often referred to as the plaintext, or cleartext of c. Although there typically exist various cryptanalytic methods for making an educated guess at k given a set of plaintext/ciphertext pairs computed using k, a straightforward guess at the value of k in AES-128 would be correct with probably one in 2¹²⁸. In general, the ciphertexts will differ whenever a different key is used to encrypt the message.² The ciphertext c is decrypted using algorithm D and the same key k.

This type of cryptosystem is called a symmetric cipher since decryption requires the same key that was used in encryption. Many symmetric ciphers have been proposed over the years. Examples include DES, Blowfish, Twofish, AES, and so on [204, 210, 258, 259, 261].

In the past it has been the case that various organizations and companies have kept algorithms E and D secret in the implementations that they endorse. For example, the U.S. government proposed a classified block cipher called Skipjack [41, 200] as part of the Clipper Initiative. This algorithm was later declassified and made readily available. Another example is the RC4 cipher which was initially a trade secret of RSA Data Security Inc. [241]. RC4 has since become public. Cryptographers often criticize the practice deploying secret symmetric ciphers. Ciphers are typically regarded as secure because they resist known cryptanalytic methods and because the general public has scrutinized them. Secret ciphers are not subject to public scrutiny, and hence tend to foster little trust within the open research community. Such ciphers can harbor backdoors or at the very least suffer from vulnerabilities or design errors. Kerckhoffs' principle states that the strength of a cryptosystem should reside entirely in the difficulty of determining the key k from specific attacks (e.g., chosen plaintext) not from the secrecy or obscurity of the algorithm. The insistence that both E and D be private is an instance of security by obscurity.

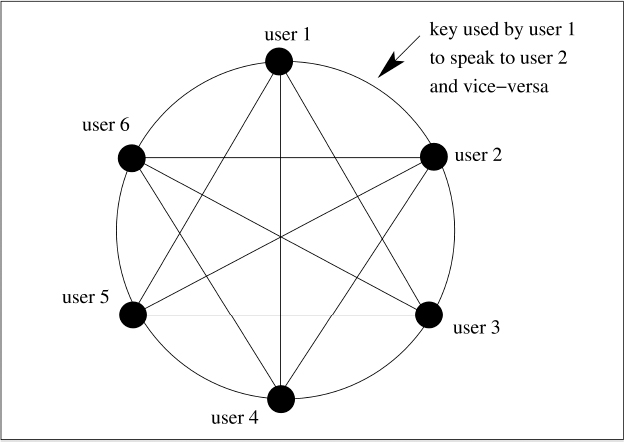
Classical cryptography solves the problem of concealing message traffic over public networks, but it assumes that the sender and receiver have previously agreed upon a randomly chosen key k. In a system consisting of thousands of users, this initial exchange can be at best cumbersome to arrange. Consider a network of n users in which each user fears that the other users will try to read their messages. To guarantee the privacy of communications, each possible pair of users needs a randomly chosen key k. The total number of keys needed to solve this problem is therefore = n (n − 1)/2. This corresponds to the number of edges in the complete graph on n vertices, denoted by K_n. For example, when n = 6 a total of 15 keys is necessary (see Figure C.1). The number of keys is therefore quadratic in the number of users.

C.1.2 The Diffie-Hellman Key Exchange

When two users need to establish a shared secret key k and they have a secure channel at their disposal, then they can do so by communicating over the channel. Once k is agreed upon, messages can be privately sent from one user to the other over a public network such as the Internet. A protocol that allows two users to establish a key over a public network is enormously beneficial since it eliminates the need to establish keys out-of-band. The first solution to this problem was proposed by Whitfield Diffie and Martin Hellman in their seminal 1976 paper covering the Diffie-Hellman key exchange [92]. The algorithm utilizes a large prime p and a generator g of . The values p and g must provide a suitable setting for the discrete-logarithm problem.

The values p and g are publicly known. Let Alice and Bob be two users who want to establish a shared secret key over a public network. To perform the exchange, Alice chooses an integer a uniformly at random such that 1 ≤ a < p − 1. Alice sends Bob the value A = g^a mod p. At the same time Bob chooses an integer b uniformly at random such that 1 ≤ b < p − 1 and sends Alice the value B = g^b mod p. Alice computes k_a = B^a mod p and Bob computes k_b = A^b mod p. Observe that k_a = k_b since,

Both Alice and Bob have therefore agreed upon the symmetric key k = k_a = k_b. The key exchange is based on the Diffie-Hellman assumption (see Appendix B.3.9).

The Diffie-Hellman key exchange solved the problem of negotiating secret keys over an untrusted network wherein there exist passive eavesdroppers.³ However, it does not minimize the total number of keys that are needed to allow each user to communicate privately with each other user. The Diffie-Hellman key exchange is used to establish a symmetric key, so the number of symmetric keys that are needed is still quadratic in the number of users. This provided the motivation for the concept of a public key cryptosystem. In a public key cryptosystem, the number of required keys is only linear in the number of users. W. Diffie and M. Hellman proposed this concept in the original Diffie-Hellman key exchange paper.

Figure C.1 Symmetric keys needed for six users

C.1.3 Public Key Cryptography

A public key cryptosystem consists of an encryption algorithm E, a decryption algorithm D, a message space M, a ciphertext space C, a private key space K, and a public key space P. The public key space typically differs from the private key space. A user chooses a private key x randomly from K. This value is then used to compute the public key y. To encrypt a message m contained in M, the user obtains the public key y of the recipient and computes,

The ciphertext c is then transmitted to the recipient. Using the private key x, the user recovers m as follows,

Only the recipient can recover m from c since only the recipient knows x. This type of cryptosystem is also referred to as an asymmetric cryptosystem since the decryption key is different from the encryption key.

The security of a public key cryptosystem rests on the presumed intractability of one or more computational problems. Under the intractability assumption it is intractable to compute the private key x given the corresponding public key y and other available information. Private communications are conducted as follows. The public keys of the users are displayed in a public database. To send a message to a recipient, the public key y of the recipient is obtained in a secure fashion from the trusted database. The sender computes the encryption of m to be c = E(m, y) and sends c to the recipient. The recipient obtains the secret message by computing m = D(c, x).

C.1.4 Attacks on Cryptosystems

If a cryptanalyst is able to learn the plaintext in every ciphertext then the cryptanalyst has completely broken the encryption scheme. This is accomplished by deducing the secret key, or by other means. The following are attacks that can be mounted on an encryption algorithm. They all assume that both the encryption algorithm and decryption algorithm are publicly known. The attacks are ordered from the weakest threat model to the strongest threat model.⁴

1. Ciphertext-only attack: The threat model for this attack is one in which the cryptanalyst is only given access to ciphertexts above and beyond that which is publicly known. The goal of the cryptanalyst is to try to determine one or more plaintexts correctly. Any scheme that succumbs to this type of attack is insecure.
2. Known-plaintext attack: The threat model for this attack is one in which the cryptanalyst is given access to several ciphertexts and corresponding plaintexts. Furthermore, it may be assumed that all ciphertexts were produced using the same key and that the cryptanalyst is aware of this. The goal of the cryptanalyst is to try to determine one or more plaintexts correctly for one or more ciphertexts that the cryptanalyst has not yet seen.
3. Chosen-plaintext attack: The threat model for this attack is one in which the cryptanalyst is allowed to choose one or more plaintexts to be encrypted and is permitted to submit them to an encryption oracle all at once. The oracle then gives the corresponding ciphertexts to the cryptanalyst. It may be assumed that all ciphertexts are produced using the same key and that the cryptanalyst is aware of this. The goal of the cryptanalyst is to try to determine one or more plaintexts correctly for one or more ciphertexts that the cryptanalyst has not yet seen.
4. Adaptive chosen-plaintext attack: The threat model for this attack is one in which the cryptanalyst is allowed to choose one or more plaintexts to be encrypted and is permitted to submit them to an encryption oracle. The cryptanalyst is permitted to submit a plaintext, receive the corresponding ciphertext, and then formulate another plaintext to submit. Hence, the cryptanalyst can adaptively choose the plaintexts to be encrypted based on previously received ciphertexts. It may be assumed that all ciphertexts are produced using the same key and that the cryptanalyst is aware of this. The goal of the cryptanalyst is to try to determine one or more plaintexts correctly for one or more ciphertexts that the cryptanalyst has not yet seen.
5. Chosen-ciphertext attack: The threat model for this attack is one in which the cryptanalyst is allowed to choose one or more ciphertexts to be decrypted and is permitted to submit them to a decryption oracle all at once. The oracle then gives the corresponding plaintexts to the cryptanalyst. The decryption oracle is a device that the cryptanalyst is given temporary access to, but that is still able to conceal the secret key from the cryptanalyst. The goal of the cryptanalyst is to try to determine one or more plaintexts correctly without access to the device for one or more ciphertexts that the cryptanalyst has not yet submitted to the oracle.
6. Adaptive chosen-ciphertext attack: The threat model for this attack is one in which the cryptanalyst is allowed to choose one or more ciphertexts to be decrypted and is permitted to submit them to a decryption oracle. The cryptanalyst is permitted to submit a ciphertext, receive the corresponding plaintext, and then reformulate another ciphertext to submit. Hence, the cryptanalyst can adaptively choose the ciphertexts to be decrypted based on previously received plaintexts. The decryption oracle is a device that the cryptanalyst is given temporary access to, but that is still able to conceal the secret key from the cryptanalyst. The goal of the cryptanalyst is to try to determine one or more plaintexts correctly without access to the device for one or more ciphertexts that the cryptanalyst has not yet submitted to the oracle.

There is an extensive body of research surrounding security against malleability, chosen-ciphertext attacks, and adaptive chosen ciphertext attacks [32, 78, 95, 199, 238, 342]. To maintain rigorous security, the goal has been to devise an asymmetric cryptosystem that is based on well-accepted (and if possible, very weak) intractability assumptions. Of secondary importance is to make the ciphertexts that are output by the cryptosystem as small as possible.

Similar types of attacks exist against digital signature algorithms. A signature algorithm succumbs to an existential forgery if a cryptanalyst is able to compute a signature for one or more messages. The cryptanalyst need not have any control over which message or messages are signed for an existential forgery attack to be regarded as a success. The mere fact that a valid signature on a message was produced by the cryptanalyst without the involvement of the legitimate signer implies that the scheme is vulnerable to an existential forgery. A signature algorithm succumbs to a selective forgery attack if a cryptanalyst is able to compute digital signatures on a particular class of messages. It must be possible for the signatures to be produced without the involvement of the legitimate signer for the attack to be regarded as a success. A complete break for a signature algorithm occurs when a cryptanalyst is able to forge the signature on any chosen message. For instance, the cryptanalyst could either deduce the private signing key or devise an efficient algorithm that is capable of forging signatures.

As in the case of encryption schemes, signature algorithms can be broken down into various attacks that adhere to different threat models. The following are attacks that can be mounted on a signature algorithm. They all assume that both the signing and verification algorithms are publicly known. The attacks are ordered from the weakest threat model to the strongest threat model.

1. Key-only attack: The threat model for this attack is one in which the cryptanalyst is only given access to the public signature verification key above and beyond that which is publicly known. The goal of the cryptanalyst is to produce a valid signature on any message.
2. Known-message attack: The threat model for this attack is one in which the cryptanalyst is given access to several messages and corresponding signatures. Furthermore, it may be assumed that all signatures were produced using the same signing private key. The goal of the cryptanalyst is to produce a valid signature on a different message.
3. Chosen-message attack: The threat model for this attack is one in which the cryptanalyst is allowed to choose one or more messages to be signed and is permitted to submit them to a signing oracle all at once. The oracle then gives the corresponding signatures to the cryptanalyst. It may be assumed that the oracle always uses the same private signing key. The goal of the cryptanalyst is to produce a valid signature on a different message.
4. Adaptive chosen-message attack: The threat model for this attack is one in which the cryptanalyst is allowed to choose one or more messages to be signed and is permitted to submit them to a signing oracle. The cryptanalyst is permitted to submit a message, receive the corresponding signature, and then formulate another message to submit. Hence, the cryptanalyst can adaptively choose the messages to be signed based on previously received signatures. It may be assumed that the oracle always uses the same private signing key. The goal of the cryptanalyst is to produce a valid signature on a different message.

There is an extensive amount of literature regarding secure signature schemes [125, 126, 131, 191, 198, 213]. Some of these approaches attempt to utilize the weakest possibility intractability assumptions, whereas others try to keep the size of each digital signature at a bare minimum.

C.1.5 The Rabin Encryption Algorithm

The Rabin cryptosystem is based on the computational intractability of factoring [237]. The private key in Rabin is two large primes p and q that are roughly equal in size. The corresponding public key is n = pq. In this rendition of Rabin it will be assumed that p ≡ 3 mod 4 and that q ≡ 3 mod 4 since this gives rise to a very simple decryption algorithm.⁵ The message space for Rabin is . The integers a and b are needed for decryption and are found by solving the following diophantine equation.

The extended Euclidean algorithm can be used to find these two values. They can then be stored along with the private key (p, q).

To encrypt a message m in Rabin the ciphertext c is computed as follows.

Given the special form of p and q the following algorithm can be used to decrypt c.

1. compute r = 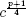mod p
2. compute s = mod p
3. compute t = aps + bqr mod n
4. compute u = aps − bqr mod n

The plaintext m is either t, −t mod n, u, or −u mod n. These are the four square roots of c modulo n. It is possible that gcd(m, n) ≠ 1 in which case there may be only one or two square roots of c.

It is possible to use a redundancy function (e.g., a checksum) to help disambiguate m from the other square roots. For example, this can be done using a hash function. The idea is to shrink the message space and make some of the most significant bits of m the hash of the lower order bits.

This cryptosystem is provably secure against chosen-plaintext attacks. However, it completely succumbs to a chosen-ciphertext attack. To see this, note that the attacker can choose a value r randomly from and compute the ciphertext c = m² mod n. If the attacker has access to the decryption device, the attacker can use the device to obtain a square root m′. With probability 1/2, m′ will not be congruent to ±m mod n in which case gcd(m − m′, n) is a non-trivial divisor of n.

Rabin also works when p and q are not of this special form. In this case c is reduced modulo p and then its two square roots modulo p are found using a probabilistic poly-time root finding algorithm [12]. The two roots of c mod q are also found. Using the Chinese Remainder Theorem these four values can be used to compute the four square roots of c modulo n.

Scott Lindhurst wrote a comprehensive treatise on computing square roots modulo a prime [173]. Also, Kumanduri and Romero provide a nice description of a Las Vegas algorithm for computing a square root of quadratic residue modulo a prime [164]. The Las Vegas version can easily be converted into a Monte Carlo algorithm with fixed polynomial running time and negligible failure probability. The way to do so is as follows. One of the steps in the algorithm finds a randomly chosen quadratic non-residue. By bounding the number of attempts to find such a non-residue in this step, the algorithm can be made Monte Carlo. If a non-residue is not found by the time the bound is reached, then the algorithm halts with failure. Hence, the entire algorithm is Monte Carlo.

C.1.6 The Rabin Signature Algorithm

The Rabin digital signature algorithm is based on the computational intractability of factoring [234]. The public and private keys are the same as those in the Rabin encryption algorithm. To sign a message it is necessary that the message be a quadratic residue modulo n. It is also necessary that the message contain some redundancy to guard against existential forgeries. Let R(·) be a redundancy function that hashes its input message to an appropriate size, adds redundancy, and guarantees that the final output value of R(·) is a square modulo n.

1. compute m′ = R(m)
2. compute a square root r = mod n using p and q

The signature on m is r. There are four unique square roots of m′ modulo n. To verify the signature the verifier computes m′ = R(m) and makes sure that the following equation holds.

If the public key is not current or if Equation C.8 does not hold, then the signature is rejected.

C.1.7 The RSA Encryption Algorithm

The Rivest-Shamir-Adleman (RSA) public key cryptosystem [245] was the first public key cryptosystem to implement the concept of a public key cryptosystem [92]. It is perhaps the most widely used public key cryptosystem today. The RSA primitive may be used for public key encryption and decryption and also for digitally signing and verifying messages. In this appendix the classic RSA algorithm will be described and it will be shown how to use it to encrypt and decrypt messages.

The space of private keys in RSA consists of pairs of randomly chosen large prime numbers. So, to generate an RSA private key the user chooses two large prime numbers p and q randomly. Currently, 384-bit primes or larger are deemed sufficient to use RSA securely. A standard way to generate an RSA prime is to generate a large number randomly and then test it for primality. This process is repeated if the number is found to be composite. The Rabin-Miller probabilistic primality test is often used for this purpose [194, 235], although an efficient method for testing primality was recently discovered that is deterministic [5].

The values p and q must satisfy another requirement in addition to being prime. RSA utilizes a public exponent e that is typically shared by all of the users in the system. The primes p and q must also satisfy the property that e and (p − 1)(q − 1) be relatively prime. In other words, the greatest common divisor of e and (p − 1)(q − 1) must be 1.

The prime number e = 2¹⁶ + 1 is often used in modern RSA implementations. Once p and q are found, the private key d is computed using the extended Euclidean algorithm. The value d is chosen by solving the following diophantine equation for d and w.

The value w is discarded. Finally, the composite number n is computed to be the product of p and q. In RSA, the public key is the pair of values (e, n) and the private key is d. The values e and d are multiplicative inverses of each other modulo (p − 1)(q − 1).

The message space for RSA consists of all messages m such that 1 < m < n and such that gcd(m, n) = 1. The ciphertext space is the same as the message space. The following is how to encrypt a message m using RSA,

The private key d is required to decrypt the public key ciphertext c. The message is recovered as follows,

It may not be immediately clear why decryption should yield m every time. Euler's generalization to Fermat's Little Theorem may be utilized to show that this is indeed the case:

For all u relatively prime to n, u⁽ⁿ⁾ ≡ 1 mod n

Here is Euler's totient function. When n = pq, (n) = (p − 1)(q − 1). The proof that RSA decryption is correct is as follows. Let m be any valid RSA message. Observe that c^d = m^ed = m^{1−w(p−1)(q−1)} = m¹ * m^(n)(−w) mod n. Since m is relatively prime to n, it follows from Euler's generalization that m⁽ⁿ⁾ = 1 mod n, so c^d = m * (1)^−w = m mod n.

It is important to dispel one of the popular misconceptions about RSA. It is not uncommon for industry practitioners to say something along the lines of “breaking RSA is equivalent to factoring.” Whereas this might in fact be true, it is not known as of this writing. RSA as originally defined is based on the computational difficulty of computing e^th roots (see Appendix B.3.2).

C.1.8 The RSA Signature Algorithm

The concept of a digital signature is based on the concept of a digital identity. In its most basic form, the idea is to assign to a user, who for the sake of argument will be called Alice, a large randomly chosen number.⁶ The number must be large enough so that with overwhelming probability Alice's number is unique. Anyone in possession of this number can masquerade as Alice, so she must make sure to keep it secret. This schema would be of little use if Alice were unable to use her number in any meaningful way, so there should be some mechanism for her to use it. One of the most basic usages of such numbers is in a digital signature algorithm. The concept of a digital signature was introduced by Diffie and Hellman [92], but no realization of the primitive appeared until later [236, 245].

In a digital signature algorithm, a private key serves as this secret number and is chosen randomly from the set of all possible private keys. A digital signature algorithm is much like a public key cryptosystem except that it involves algorithms for signing messages and verifying signed messages as opposed to algorithms for encrypting messages and then decrypting them. In a digital signature algorithm, a message m is signed using a private key x to produce a digital signature s. The pair of values (m, s) constitutes a signed message. To verify (m, s) as being a valid signed message, the public key y in addition to (m, s) is supplied as input to the signature verification algorithm. This algorithm returns true if and only if s is a valid digital signature on m. One of the most widespread digital signature algorithms in use today is RSA that utilizes the same keys as the RSA encryption algorithm. RSA is therefore often used to refer to both the RSA public key cryptosystem and the RSA digital signature algorithm.

The original RSA signature algorithm is as follows. To sign a message m contained in , the signer Alice computes,

using her private key d. The message m is accompanied by the digital signature s. In typical e-mail applications, a signed e-mail is transmitted with s as well as the digital certificate needed to verify the signature s on m.

Anyone in possession of (m, s,(e, n)) can verify the digital signature s. The signature is regarded as valid if and only if the following equation holds.

However, this approach is subject to existential forgery attacks. To see this, observe that anyone can choose a signature s randomly from and compute m = s^e mod n. When this is performed, s is a valid signature on m. A well-known heuristic to remedy this problem is to compute the signature s using a cryptographic one-way hash function H as such,

The signature is verified by hashing the message that was signed to obtain H(m) and then verifying that the following equality holds.

C.1.9 The Goldwasser-Micali Algorithm

One of the drawbacks to the RSA encryption algorithm as originally defined is that it leaks a single plaintext bit in every ciphertext. This bit is the Jacobi symbol of the plaintext, and is either “1” or “−1.” Since e is odd it is straightforward to see that J(m/n) = J(m^e/n) for all valid RSA plaintexts m.

This observation pointed to a problem in public key cryptography in general. It should not be possible for an adversary to so much as even distinguish one encryption from another. This problem can be formulated as an experiment. Let an adversary choose any two different plaintexts m₁ and m₂, let the encryption algorithm choose one of the messages randomly, encrypt it, give the resulting ciphertext to the adversary, and then let the adversary guess which message was encrypted. In a truly secure public key cryptosystem the adversary should be able to guess with probability significantly greater than 1/2 which message was encrypted. In RSA, the adversary can choose a message m₁ such that J(m₁/n) = 1 and another message m₂ such that J(m₂/n) = −1 and then distinguish correctly every time.

The GM cryptosystem was the first cryptosystem to provably solve this problem. It was presented by Goldwasser and Micali along with a rigorous definition of security known as semantic security and a proof that the GM cryptosystem is semantically secure against plaintext attacks [117].

The private key in GM is a pair of large primes p and q that are roughly equal in size. This cryptosystem makes use of pseudosquares modulo n. The public key in GM is n and a pseudosquare y modulo n. It is not hard to show that −1 is a pseudosquare modulo n when p ≡ 3 mod 4 and q ≡ 3 mod 4. For other primes a pseudosquare y can be found as follows. Find a quadratic non-residue a modulo p and a quadratic residue b modulo q. By applying the Chinese Remainder Theorem to a and b, the value that results is a pseudosquare modulo n.

A message m = m₁m₂ · · · m_t in GM is represented as a bit string of length t. Each bit m_i for 1 ≤ i ≤ t in m is encrypted by choosing r_i at random from and computing c_i as follows.

The ciphertext on m is c = c₁c₂ · · · c_t. The value c_i is a quadratic residue if and only if m_i = 0. The value c_i is a pseudosquare otherwise. The ciphertext is decrypted as follows. For i ranging from 1 to t the following is computed.

m_i is set to 0 if ℓ_i = 1 and m_i is set to 1 if ℓ_i ≡ −1.

The GM cryptosystem solves the problem in RSA in which Jacobi symbols are revealed by making message distinguishability hold based on the quadratic residuosity assumption (see Appendix B.3.5).

C.1.10 Public Key Infrastructures

When two users decide to use a public key cryptosystem to communicate privately over a public network, there is a danger in having the sender transmit his or her public key to the receiver. If an active adversary is present, the adversary could potentially intercept the public key y and substitute it with another public key y′. The person who wants to send the plaintext message m would then receive y′ thinking that it is the public key of the recipient of m, when in fact it is the public key of the adversary. This same adversary could then intercept the ciphertext c encrypted using y′ and then decrypt c using x′ which only the adversary knows. The plaintext message could then be encrypted using y and the resulting ciphertext could be forwarded on to the intended recipient. This active attack is called a man-in-the-middle attack since the adversary carries out the attack in between the sender and the receiver.

The problem with using a public key cryptosystem by itself is that there is no way to authenticate the public keys of users. The standard way to foil a man-in-the-middle attack is to have a trusted entity securely distribute the public keys of the users. This trusted entity is called a certification authority (CA). The CA has its own key pair and everyone is assumed to have the correct public key of the CA. The CA issues a digital certificate to each user in the public key system. A digital certificate consists of the user's name, public key, and other identifying information, along with the CA's digital signature on this information. This way, when a user obtains a digital certificate, the user can verify the signature on it to be certain that the public key it contains came from the CA. This is a public key infrastructure (PKI) in its most basic form [161].

In addition to establishing secure channels over public networks, public key cryptosystems reduce the complexity of symmetric ciphers since they reduce the total number of keys that are needed by the n users. In a system of n users, only n keys need to be exchanged and only 2n keys are needed in total. These 2n keys consist of the n private keys and n corresponding public keys. The advantages of public key cryptography are therefore twofold: it enables private communication channels to be established over open networks and it minimizes the required number of cryptographic keys.

C.2 Discrete-Log Based Cryptosystems

The discrete-log cryptosystems in this section are all closely related to the Diffie-Hellman key exchange as well as the Decision Diffie-Hellman assumption. They form the basis for many advanced cryptographic protocols such as electronic voting and e-cash.

C.2.1 The ElGamal Encryption Algorithm

The ElGamal public key cryptosystem is an elegant cryptosystem that gets its security from the Diffie-Hellman key exchange [110]. This cryptosystem employs the same parameters (p, g) used in Appendix C.1.2. The private key is an integer x chosen uniformly at random such that 1 ≤ x ≤ p − 1. The corresponding public key is y = g^x mod p. The public key of a user is represented by the three values (y, g, p). The value y will vary from user to user in a public key infrastructure while g and p can be shared by all. The message space in ElGamal is _p. To encrypt a message m, an integer k is chosen uniformly at random such that 1 ≤ k ≤ p − 1. The ciphertext of m is the pair (a, b) = (g^k mod p, y^km mod p). The pair (a, b) is decrypted by computing m = ba^−x mod p. The following equation demonstrates that decryption will always succeed for properly formed ciphertexts.

The inverse of a is denoted by a⁻¹ mod p. This inverse exists, is unique, and can be computed using the extended Euclidean algorithm.

C.2.2 Security of ElGamal

It can be shown via a reduction argument that the Diffie-Hellman key exchange is no more or less secure than ElGamal. Suppose that an oracle O_DH exists that solves the Diffie-Hellman problem. That is, for a random choice of t and u, O_DH(g, p, g^t mod p,g^u mod p) returns g^tu mod p with non-negligible probability.⁷ It will now be shown how to use O_DH to break the ElGamal ciphertext (a, b). Choose the integers r₁, r₂,r₃ uniformly at random such that 1 ≤ r₁, r₂, r₃ < p − 1. Then compute,

and,

The oracle is then invoked and the value w = O_DH (g^r₃ mod p, p, y₁ y₂) is found. With non-negligible probability w will be equal to g^{r₃xkr₁r₂} mod p. To see this, note that with non-negligible probability the oracle returns the Diffie-Hellman secret corresponding to y₁ = g^r₃xr₁ mod p and y₂ = g^r₃kr₂ mod p. Assuming that w is indeed as such, t is as follows,

It is easy to see that bt⁻¹ ≡ m mod p.

The reason that the random values r₁, r₂, and r₃ were used was to demonstrate a randomized reduction. A randomized reduction is a strong form of reduction since it allows the oracle to refuse to give correct answers most of the time but can still be used to break ElGamal with high probability. If the oracle fails to decrypt (a, b), then new random values can be chosen and the oracle can be queried again.

It remains to show that given an oracle O_ElG that breaks ElGamal with non-negligible probability the Diffie-Hellman key exchange can be broken. Let the Diffie-Hellman key exchange problem instance be T = g^t mod p and U = g^u mod p. The key exchange value is g^ut mod p. Suppose that with non-negligible probability O_ElG (g, p, y, a, b) = m. Again, values for r₁, r₂, and r₃ are chosen randomly. An integer b is chosen randomly from G_q. Then compute,

and,

The oracle is then invoked to obtain the value,

With non-negligible probability the value bm⁻¹ mod p will be equal to the Diffie-Hellman secret corresponding to y₁ and y₂ using the generator g^r₃ mod p. Assuming that m is as such, it follows that bm⁻¹ = (g^r₃)^tr₁ur₂ mod p. Therefore, it follows that (bm⁻¹)^{(r₁r₂r₃)−1} mod p = g^tu mod p. It has been shown that Diffie-Hellman is breakable if and only if ElGamal is breakable.

To implement ElGamal in a way that is semantically secure against plaintext attacks the original ElGamal cryptosystem needs to be redefined a little [304]. It is sufficient that the order of g be devoid of small prime factors and that the message space consists only of elements that have the same order as g. In general it is a good practice to choose g so that its order is a large prime and to define the message space to be the prime order subgroup generated by g. For instance, prime numbers of the form p = 2q + 1 can be used where q is prime. Such a prime p is said to be a safe prime. ElGamal is semantically secure against plaintext attacks when p is a safe prime, g has order q, and the message space is the set of quadratic residues modulo p. However, this approach is still not secure against adaptive chosen-ciphertext attacks [238].

C.2.3 The Cramer-Shoup Encryption Algorithm

The Cramer-Shoup public key cryptosystem is secure against adaptive chosen ciphertext attacks [76]. It is based on the Decision Diffie-Hellman problem (see Appendix B.3.10) and the existence of a collision intractable hash function. The scheme involves only a few exponentiations over a group, making it a rather efficient scheme from a computational standpoint.

Cramer-Shoup utilizes a group G of prime order q where q is large. It also uses a collision intractable hash function H that hashes long strings to values contained in . The private key in Cramer-Shoup is the six values (x₁, x₂, y₁, y₂, z₁, z₂), all of which are chosen randomly from . The public key includes the values g₁ and g₂ that are chosen randomly from G. The public key also includes the following three values.

It is assumed that the values are computed within the group G (for example, by performing modular reductions using the prime modulus p). So, the public key is (g₁, g₂, c, d, h).

The message space for Cramer-Shoup is G. To encrypt a message m, a value r is chosen randomly from and the following values are computed,

The ciphertext on m is (u₁, u₂, e, v).

The nice thing about chosen-ciphertext secure cryptosystems is that they allow the receiver to verify that the sender knows the plaintext. In other words, it is not possible to send a message to someone using their public key without knowing what the plaintext is. Such a cryptosystem is said to be plaintext-aware. The first thing that the receiver should do upon obtaining ciphertext computed using Cramer-Shoup is verify its integrity. This is performed by computing a = H(u₁, u₂, e) and then verifying that the following equality holds.

If it does not hold then the decryption algorithm outputs “reject.” This prevents the recipient from going ahead and interpreting the plaintext as if it were valid. It also guarantees that despite any subsequent publication of the plaintext, the sender only learns that which he or she already knows.⁸ If this equality holds then the ciphertext is decrypted as follows.

It will now be shown that a properly constructed ciphertext will always cause the correct plaintext to be output by the decryption algorithm. First, the decryption algorithm will never output “reject” in this case. To see this, note that since u₁ = g^r₁ and u₂ = g^r it follows that,

So, u₁^x₁ u₂^x₂ in Equation C.28 is equal to c^r. Likewise, since u₁^y₁ u₂^y₂ = d^r it follows that the term in the parenthesis in C.28 equals d^r. But then this equality must hold due to the rightmost equality in (C.27).

Since u₁^−z₁ u₂^−z₂ = g₁^−rz₁ g₂^−rz₂ = h^−r it follows that,

The elegant proof of security of Cramer-Shoup can be found in the original paper.

C.2.4 The ElGamal Signature Algorithm

The ElGamal digital signature algorithm utilizes the same parameters as the ElGamal public key cryptosystem. There are numerous variants of this digital signature algorithm [208, 209].

To sign a message m an integer k is chosen uniformly at random such that 1 ≤ k < p − 1 and such that gcd(k, p − 1) = 1. The fact that gcd(k, p − 1) = 1 guarantees the existence of a unique inverse of k. The signature on m is the pair (r, s) = (g^k mod p, k⁻¹ (H(m) − xr) mod p − 1). H is a cryptographic one-way function that may, for instance, be the secure hash algorithm (SHA-1) [202] or MD5 [243]. The digital signature on the message m is the pair of values (r, s).

Anyone who is in possession of (m, (r, s), (y, g, p)) can verify the signature (r, s) on m. The signature is regarded as valid if and only if 1 ≤ a < p and the following equality holds:

In the case that (y, g, p) was obtained from a digital certificate it is also necessary to verify the validity of the digital certificate. This is typically done by verifying the CA signature in the certificate, checking certification revocation lists, and so on.

It will now be shown that signature verification will always succeed for properly computed signatures. Suppose that (r, s) is constructed according to the algorithm. Consider the equation for the signature value s. By multiplying both sides of the equation by k it follows that,

Adding xr modulo p − 1 to both sides of Equation C.33 yields the following equation.

Then, by raising g to the value on each side of this equation the following equation is obtained,

This is the equality that is tested during signature verification. So, signature verification will always succeed for properly constructed signatures.

The use of H is necessary to avoid existential forgery attacks. To see this, suppose that H is not used. Hence, let m be used in place of H(m). The following is a one-parameter forgery attack on ElGamal. Choose a value e uniformly at random such that 1 ≤ e < p − 1 and compute r = g^ey mod p. Then compute s = − r mod p − 1 and m = es mod p − 1. The pair (r, s) is a valid signature on m as illustrated by the following equation.

C.2.5 The Pointcheval-Stern Signature Algorithm

David Pointcheval and Jacques Stern [225] (see also [226]) showed that by altering ElGamal slightly, it can be proven to be secure against adaptive chosen-message attacks. In this model they showed that forgeries are possible if and only if the discrete-logarithm problem is solvable. This proof was shown in the random oracle model.

To sign a message m an integer k is chosen uniformly at random such that 1 ≤ k < p − 1 and such that gcd(k, p − 1) = 1. The fact that gcd(k, p − 1) = 1 guarantees the existence of a unique inverse of k. First, the signature value r is computed.

Once r is computed, the value s is found as follows.

The digital signature on the message m is the pair of values (r, s). Anyone who is in possession of (m, (r, s), (y,g,p)) can verify the signature (r, s) on m. The signature is regarded as valid if and only if 1 ≤ a < p and the following equality holds.

Pointcheval and Stern introduced the notion of a forking lemma and used it to construct their random oracle based proof. The forking lemma technique has since been utilized to show the security of other random oracle based cryptographic algorithms.

C.2.6 The Schnorr Signature Algorithm

The Schnorr algorithm [262, 263] has the nice feature that its signatures are very small. It makes use of a cryptographic one-way hash function H that outputs values in . Let p and q be large primes such that q divides p − 1. Let g be an element of with order q. The signing private key in Schnorr is a value x chosen uniformly at random from . The corresponding public key is y = g^−x mod p. To sign a message m the value k is chosen randomly from . A Schnorr digital signature is the pair (e, s) that is computed as follows.

A signature is regarded as valid if and only if the following equation holds.

C.2.7 The Digital Signature Algorithm (DSA)

The Digital Signature Algorithm is similar to ElGamal except that it is defined using a value g < p that generates a prime order subgroup G of . Let the prime q denote the order of g. It is part of a U.S. government standard called the Digital Signature Standard (DSS) [203]. Let H denote a cryptographic one-way hash function such as SHA-1 and let q be a 160-bit prime number. To sign a message m, an integer k is chosen uniformly at random from . The signature on m is the pair (r, s) = ((g^k mod p) mod q, k⁻¹(H(m) + xr) mod q). Anyone who is in possession of (m, (r,s), (y,g,p)) can verify the validity of the digital signature (r, s) on the message m. Observe that signatures are quite small. The pair (r, s) occupies a mere 320 bits.

The digital signature (r, s) on the message m is regarded as valid if and only if 0 < r, s < q and the following equality holds.

It will now be shown that signature verification will always succeed for properly computed signatures. Suppose that (r, s) is constructed according to the algorithm. Consider the equation for the signature value s. Multiplying both sides of this equation by ks⁻¹ mod q yields,

Raising g to each side of this equation modulo p yields g^k mod p on the left side and,

on the right side. But this implies that r = (g^k mod p) mod q will always equal (g^H(m)s−1 y^rs−1 mod p) mod q and so signature verification will always succeed for properly computed signatures.

An obvious advantage of DSA is that it produces short signatures. A DSA signature consists of two positive integers, both less than q, whereas an ElGamal signature consists of a value less than p and a value less than p − 1. It is not uncommon for q to be 160 bits and p to be 768 bits or more in size.