Chapter 17
Topics in psychometrics
1 INTRODUCTION
We now turn to some optimization problems that occur in psychometrics. Most of these are concerned with the eigenstructure of variance matrices, that is, with their eigenvalues and eigenvectors. Sections 17.2–17.6 deal with principal components analysis. Here, a set of p scalar random variables x1, …, xp is transformed linearly and orthogonally into an equal number of new random variables v1, …, vp. The transformation is such that the new variables are uncorrelated. The first principal component v1 is the normalized linear combination of the x variables with maximum variance, the second principal component v2 is the normalized linear combination having maximum variance out of all linear combinations uncorrelated with v1, and so on. One hopes that the first few components account for a large proportion of the variance of the x variables. Another way of looking at principal components analysis is to approximate the variance matrix of x, say Ω, which is assumed known, ‘as well as possible’ by another positive semidefinite matrix of lower rank. If Ω is not known, we use an estimate S of Ω based on a sample of x and try to approximate S rather than Ω.
Instead of approximating S, which depends on the observation matrix X (containing the sample values of x), we can also attempt to approximate X directly. For example, we could approximate X be a matrix of lower rank, say ![]() . Employing a singular‐value decomposition we can write
. Employing a singular‐value decomposition we can write ![]() , where A is semi‐orthogonal. Hence, X = ZA′ + E, where Z and A have to be determined subject to A being semi‐orthogonal such that tr E′E is minimized. This method of approximating X is called one‐mode component analysis and is discussed in Section 17.7. Generalizations to two‐mode and multimode component analysis are also discussed (Sections 17.9 and 17.10).
, where A is semi‐orthogonal. Hence, X = ZA′ + E, where Z and A have to be determined subject to A being semi‐orthogonal such that tr E′E is minimized. This method of approximating X is called one‐mode component analysis and is discussed in Section 17.7. Generalizations to two‐mode and multimode component analysis are also discussed (Sections 17.9 and 17.10).
In contrast to principal components analysis, which is primarily concerned with explaining the variance structure, factor analysis attempts to explain the covariances of the variables x in terms of a smaller number of nonobservables, called ‘factors’. This typically leads to the model
where y and ɛ are unobservable and independent. One usually assumes that y ~ N(0, Im), ɛ ~ N(0, Φ), where Φ is diagonal. The variance matrix of x is then AA′ + Φ, and the problem is to estimate A and Φ from the data. Interesting optimization problems arise in this context and are discussed in Sections 17.11–17.14.
Section 17.15 deals with canonical correlations. Here, again, the idea is to reduce the number of variables without sacrificing too much information. Whereas principal components analysis regards the variables as arising from a single set, canonical correlation analysis assumes that the variables fall naturally into two sets. Instead of studying the two complete sets, the aim is to select only a few uncorrelated linear combinations of the two sets of variables, which are pairwise highly correlated.
In the final two sections, we briefly touch on correspondence analysis and linear discriminant analysis.
2 POPULATION PRINCIPAL COMPONENTS
Let x be a p × 1 random vector with mean μ and positive definite variance matrix Ω. It is assumed that Ω is known. Let λ1 ≥ λ2 ≥ ⋯ ≥ λp > 0. be the eigenvalues of Ω and let T = (t1, t2, …, tp) be a p × p orthogonal matrix such that
If the eigenvalues λ1, …, λp are distinct, then T is unique apart from possible sign reversals of its columns. If multiple eigenvalues occur, T is not unique. The ith column of T is, of course, an eigenvector of Ω associated with the eigenvalue λi.
We now define the p × 1 vector of transformed random variables
as the vector of principal components of x. The ith element of v, say vi, is called the ith principal component.
3 OPTIMALITY OF PRINCIPAL COMPONENTS
The principal components have the following optimality property.
Notice that, while the principal components are unique (apart from sign) if and only if all eigenvalues are distinct, Theorem 17.2 holds irrespective of multiplicities among the eigenvalues.
Since principal components analysis attempts to ‘explain’ the variability in x, we need some measure of the amount of total variation in x that has been explained by the first r principal components. One such measure is
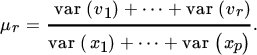
It is clear that
and hence that 0 < μr ≤ 1 and μp = 1.
Principal components analysis is only useful when, for a relatively small value of r, μr is close to one; in that case, a small number of principal components explains most of the variation in x.
4 A RELATED RESULT
Another way of looking at the problem of explaining the variation in x is to try and find a matrix V of specified rank r ≤ p, which provides the ‘best’ approximation of Ω. It turns out that the optimal V is a matrix whose r nonzero eigenvalues are the r largest eigenvalues of Ω.
Exercises
- 1. Show that the explained variation in x as defined in (1) is given by μr = tr V/tr Ω.
- 2. Show that if, in Theorem 17.3, we only require V to be symmetric (rather than positive semidefinite), we obtain the same result.
5 SAMPLE PRINCIPAL COMPONENTS
In applied research, the variance matrix Ω is usually not known and must be estimated. To this end we consider a random sample x1, x2, …, xn of size n > p from the distribution of a random p × 1 vector x. We let
where both μ and Ω are unknown (but finite). We assume that Ω is positive definite and denote its eigenvalues by λ1 ≥ λ2 ≥ ⋯ ≥ λp > 0.
The observations in the sample can be combined into the n × p observation matrix

The sample variance of x, denoted by S, is
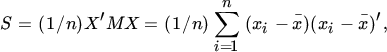
where

The sample variance is more commonly defined as S* = (n/(n − 1))S, which has the advantage of being an unbiased estimator of Ω. We prefer to work with S as given in (5) because, given normality, it is the ML estimator of Ω.
We denote the eigenvalues of S by l1 > l2 > ⋯ > lp, and notice that these are distinct with probability one even when the eigenvalues of Ω are not all distinct. Let Q = (q1, q2, …, qp) be a p × p orthogonal matrix such that
We then define the p × 1 vector
as the vector of sample principal components of x, and its ith element ![]() as the ith sample principal component.
as the ith sample principal component.
Recall that T = (t1, …, tp) denotes a p × p orthogonal matrix such that
We would expect that the matrices S, Q, and L from the sample provide good estimates of the corresponding population matrices Ω, T, and Λ. That this is indeed the case follows from the next theorem.
Exercise
- 1. If Ω is singular, show that r(X) ≤ r(Ω) + 1. Conclude that X cannot have full rank p and S must be singular, if r(Ω) ≤ p − 2.
6 OPTIMALITY OF SAMPLE PRINCIPAL COMPONENTS
In direct analogy with population principal components, the sample principal components have the following optimality property.
7 ONE‐MODE COMPONENT ANALYSIS
Let X be the n × p observation matrix and M = In − (1/n)ιι′. As in ( 5 ), we express the sample variance matrix S as
In Theorem 17.6, we found the best approximation to S by a matrix V of given rank. Of course, instead of approximating S we can also approximate X by a matrix of given (lower) rank. This is attempted in component analysis.
In the one‐mode component model, we try to approximate the p columns of X = (x1, …, xp) by linear combinations of a smaller number of vectors z1, …, zr. In other words, we write
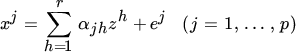
and try to make the residuals ej ‘as small as possible’ by suitable choices of {zh} and {αjh}. In matrix notation, (6) becomes
The n × r matrix Z is known as the core matrix. Without loss of generality, we may assume A′A = Ir (see Exercise 1). Even with this constraint on A, there is some indeterminacy in (7). We can postmultiply Z with an orthogonal matrix R and premultiply A′ with R′ without changing ZA′ or the constraint A′A = Ir.
Let us introduce the set of matrices
This is the set of all semi‐orthogonal p × r matrices, also known as the Stiefel manifold.
With this notation we can now prove Theorem 17.7.
We notice that the ‘best’ approximation to X, say ![]() , is given by (15):
, is given by (15): ![]() . It is important to observe that
. It is important to observe that ![]() is part of a singular‐value decomposition of X, namely the part corresponding to the r largest eigenvalues of X′X. To see this, assume that r(X) = p and that the eigenvalues of X′X are given by λ1 ≥ λ2 ≥ ⋯ ≥ λp > 0. Let Λ = diag(λ1, …, λp) and let
is part of a singular‐value decomposition of X, namely the part corresponding to the r largest eigenvalues of X′X. To see this, assume that r(X) = p and that the eigenvalues of X′X are given by λ1 ≥ λ2 ≥ ⋯ ≥ λp > 0. Let Λ = diag(λ1, …, λp) and let
be a singular‐value decomposition of X, with S′S = T′T = Ip. Let
and partition S and T accordingly as
Then,
From (16)–(18), we see that X′XT1 = T1Λ1, in accordance with (13). The approximation ![]() can then be written as
can then be written as
This result will be helpful in the treatment of two‐mode component analysis in Section 17.9
. Notice that when r(ZA′) = r(X), then ![]() (see also Exercise 3).
(see also Exercise 3).
Exercises
- 1. Suppose r(A) = r′ ≤ r. Use the singular‐value decomposition of A to show that ZA′ = Z*A*′, where A*′A* = Ir. Conclude that we may assume A′A = Ir in ( 7 ).
- 2. Consider the optimization problem

If F(X) is symmetric for all X, prove that the Lagrangian function is

where L is symmetric.
- 3. If X has rank ≤ r show that
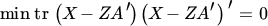
over all A in
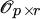 and Z in ℝn × r.
and Z in ℝn × r.
8 ONE‐MODE COMPONENT ANALYSIS AND SAMPLE PRINCIPAL COMPONENTS
In the one‐mode component model we attempted to approximate the n × p matrix X by ZA′ satisfying A′A = Ir. The solution, from Theorem 17.7, is
where T1 is a p × r matrix of eigenvectors associated with the r largest eigenvalues of X′X.
If, instead of X, we approximate MX by ZA′ under the constraint A′A = Ir, we find in precisely the same way
but now T1 is a p × r matrix of eigenvectors associated with the r largest eigenvalues of (MX)′(MX) = X′MX. This suggests that a suitable approximation to X′MX is provided by
where Λ1 is an r × r matrix containing the r largest eigenvalues of X′MX. Now, (19) is precisely the approximation obtained in Theorem 17.6. Thus, one‐mode component analysis and sample principal components are tightly connected.
9 TWO‐MODE COMPONENT ANALYSIS
Suppose that our data set consists of a 27 × 6 matrix X containing the scores given by n = 27 individuals to each of p = 6 television commercials. A onemode component analysis would attempt to reduce p from 6 to 2 (say). There is no reason, however, why we should not also reduce n, say from 27 to 4. This is attempted in two‐mode component analysis, where the purpose is to find matrices A, B, and Z such that
with A′A = Ir1 and B′B = Ir2, and ‘minimal’ residual matrix E. (In our example, r1 = 2, r2 = 4.) When r1 = r2, the result follows directly from Theorem 17.7 and we obtain Theorem 17.8.
In the more general case where r1 ≠ r2, the solution is essentially the same. A better approximation does not exist. Suppose r2 > r1. Then we can extend B with r2 − r1 additional columns such that B′B = Ir2, and we can extend Z with r2 − r1 additional rows of zeros. The approximation is still the same: ![]() . Adding columns to B turns out to be useless; it does not lead to a better approximation to X, since the rank of BZA′ remains r1.
. Adding columns to B turns out to be useless; it does not lead to a better approximation to X, since the rank of BZA′ remains r1.
10 MULTIMODE COMPONENT ANALYSIS
Continuing our example of Section 17.9 , suppose that we now have an enlarged data set consisting of a three‐dimensional matrix X of order 27 × 6 × 5 containing scores by p1 = 27 individuals to each of p2 = 6 television commercials; each commercial is shown p3 = 5 times to every individual. A three‐mode component analysis would attempt to reduce p1, p2, and p3 to, say, r1 = 6, r2 = 2, r3 = 3. Since, in principle, there is no limit to the number of modes we might be interested in, let us consider the s‐mode model. First, however, we reconsider the two‐mode case
We rewrite (20) as
where x = vec X, z = vec Z, and e = vec E. This suggests the following formulation for the s‐mode component case:
where Ai is a pi × ri matrix satisfying ![]() . The data vector x and the ‘core’ vector z can be considered as stacked versions of s‐dimensional matrices X and Z. The elements in x are identified by s indices with the ith index assuming the values 1, 2, …, pi. The elements are arranged in such a way that the first index runs slowly and the last index runs fast. The elements in z are also identified by s indices; the ith index runs from 1 to ri.
. The data vector x and the ‘core’ vector z can be considered as stacked versions of s‐dimensional matrices X and Z. The elements in x are identified by s indices with the ith index assuming the values 1, 2, …, pi. The elements are arranged in such a way that the first index runs slowly and the last index runs fast. The elements in z are also identified by s indices; the ith index runs from 1 to ri.
The mathematical problem is to choose Ai(i = 1, …, s) and z in such a way that the residual e is ‘as small as possible’.
Exercise
11 FACTOR ANALYSIS
Let x be an observable p × 1 random vector with E x = μ and var(x) = Ω. The factor analysis model assumes that the observations are generated by the structure
where y is an m × 1 vector of nonobservable random variables called ‘common factors’, A is a p × m matrix of unknown parameters called ‘factor loadings’, and ɛ is a p × 1 vector of nonobservable random errors. It is assumed that y ~ N(0, Im), ɛ ~ N(0, Φ), where Φ is diagonal positive definite, and that y and ɛ are independent. Given these assumptions, we find that x ~ N(μ, Ω) with
There is clearly a problem of identifying A from AA′, because if A* = AT is an orthogonal transformation of A, then A*A*′ = AA′. We shall see later (Section 17.14 ) how this ambiguity can be resolved.
Suppose that a random sample of n > p observations x1, …, xn of x is obtained. The loglikelihood is
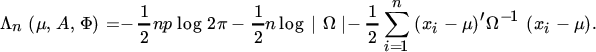
Maximizing Λ with respect to μ yields ![]() . Substituting
. Substituting ![]() for μ in (32) yields the so‐called concentrated loglikelihood
for μ in (32) yields the so‐called concentrated loglikelihood
with

Clearly, maximizing (33) is equivalent to minimizing log |Ω| + tr Ω−1 S with respect to A and Φ. The following theorem assumes Φ known, and thus minimizes with respect to A only.
Notice that the optimal choice for A is such that A′Φ−1 A is a diagonal matrix, even though this was not imposed.
12 A ZIGZAG ROUTINE
Theorem 17.10 provides the basis for (at least) two procedures by which ML estimates of A and Φ in the factor model can be found. The first procedure is to minimize the concentrated function (36) with respect to the p diagonal elements of Φ. The second procedure is based on the first‐order conditions obtained from minimizing the function
The function ψ is the same as the function ϕ defined in (34) except that ϕ is a function of A given Φ, while ψ is a function of A and Φ.
In this section, we investigate the second procedure. The first procedure is discussed in Section 17.13.
From ( 37 ), we see that the first‐order condition of ψ with respect to A is given by
where Ω = AA′ + Φ. To obtain the first‐order condition with respect to Φ, we differentiate ψ holding A constant. This yields
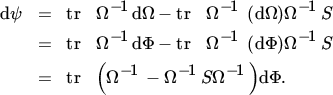
Since Φ is diagonal, the first‐order condition with respect to Φ is
Pre‐ and postmultiplying (46) by Φ, we obtain the equivalent condition
(The equivalence follows from the fact that Φ is diagonal and nonsingular.) Now, given the first‐order condition for A in (45), and writing Ω − AA′ for Φ, we have

so that

using the fact that ΦΩ−1S = SΩ−1 Φ. Hence, given ( 45 ), (47) is equivalent to
that is,
Thus, Theorem 17.10 provides an explicit solution for A as a function of Φ and (48) gives Φ as an explicit function of A. A zigzag routine suggests itself: choose an appropriate starting value for Φ, then calculate AA′ from (43), then Φ from ( 48 ), et cetera. If convergence occurs (which is not guaranteed), then the resulting values for Φ and AA′ correspond to a (local) minimum of ψ.
From ( 43 ) and ( 48 ), we summarize this iterative procedure as

for k = 0, 1, 2, ….Here sii denotes the ith diagonal element of S, ![]() the jth largest eigenvalue of (Φ(k))−1/2S(Φ(k))−1/2, and
the jth largest eigenvalue of (Φ(k))−1/2S(Φ(k))−1/2, and ![]() the corresponding eigenvector.
the corresponding eigenvector.
What is an appropriate starting value for Φ? From ( 48 ), we see that 0 < ϕi < sii (i = 1, …, p). This suggests that we choose our starting value as
for some α satisfying 0 < α < 1. Calculating A from (35) given Φ = Φ(0) leads to
where Λ is a diagonal m × m matrix containing the m largest eigenvalues of S* = (dg S)−1/2 S(dg S)−1/2 and T is a p × m matrix of corresponding orthonormal eigenvectors. This shows that α must be chosen smaller than each of the m largest eigenvalues of S*.
13 NEWTON‐RAPHSON ROUTINE
Instead of using the first‐order conditions to set up a zigzag procedure, we can also use the Newton‐Raphson method in order to find the values of ϕ1, …, ϕp that minimize the concentrated function ( 36 ). The Newton‐Raphson method requires knowledge of the first‐ and second‐order derivatives of this function, and these are provided by the following theorem.
Given knowledge of the gradient g(ϕ) and the Hessian G(ϕ) from (50) and (51), the Newton‐Raphson method proceeds as follows. First choose a starting value ϕ(0). Then, for k = 0, 1, 2, …, compute
This method appears to work well in practice and yields the values ϕ1, …, ϕp, which minimize (49). Given these values we can compute A from ( 35 ), thus completing the solution.
There is, however, one proviso. In Theorem 17.11 we require that the p − m smallest eigenvalues of Φ−1/2 SΦ−1/2 are all distinct. But, by rewriting (31) as
we see that the p − m smallest eigenvalues of Φ−1/2 ΩΦ−1/2 are all one. Therefore, if the sample size increases, the p − m smallest eigenvalues of Φ−1/2 SΦ−1/2 will all converge to one. For large samples, an optimization method based on Theorem 17.11 may therefore not give reliable results.
14 KAISER'S VARIMAX METHOD
The factorization Ω = AA′ + Φ of the variance matrix is not unique. If we transform the ‘loading’ matrix A by an orthogonal matrix T, then we have (AT)(AT)′ = AA′. Thus, we can always rotate A by an orthogonal matrix T, so that A* = AT yields the same Ω. Several approaches have been suggested to use this ambiguity in a factor analysis solution in order to create maximum contrast between the columns of A. A well‐known method, due to Kaiser, is to maximize the raw varimax criterion.
Kaiser defined the simplicity of the kth factor, denoted by sk, as the sample variance of its squared factor loadings. Thus,

The total simplicity is s = s1 + s2 + ⋯ + sm and the raw varimax method selects an orthogonal matrix T such that s is maximized.
An iterative zigzag procedure can be based on (64) and ( 65 ). In ( 64 ), we have B = B(Q) and in ( 65 ) we have Q = Q(B). An obvious starting value for B is B(0) = A. Then calculate Q(1) = Q(B(0)), B(1) = B(Q(1)), Q(2) = Q(B(1)), et cetera. If the procedure converges, which is not guaranteed, then a (local) maximum of (63) has been found.
15 CANONICAL CORRELATIONS AND VARIATES IN THE POPULATION
Let z be a random vector with zero expectations and positive definite variance matrix Σ. Let z and Σ be partitioned as

so that Σ11 is the variance matrix of z(1), Σ22 the variance matrix of z(2), and ![]() the covariance matrix between z(1) and z(2).
the covariance matrix between z(1) and z(2).
The pair of linear combinations u′z(1) and v′z(2), each of unit variance, with maximum correlation (in absolute value) is called the first pair of canonical variates and its correlation is called the first canonical correlation between z(1) and z(2).
The kth pair of canonical variates is the pair u′z(1) and v′z(2), each of unit variance and uncorrelated with the first k − 1 pairs of canonical variates, with maximum correlation (in absolute value). This correlation is the kth canonical correlation.
16 CORRESPONDENCE ANALYSIS
Correspondence analysis is a multivariate statistical technique, conceptually similar to principal component analysis, but applied to categorical rather than to continuous data. It provides a graphical representation of contingency tables, which arise whenever it is possible to place events into two or more categories, such as product and location for purchases in market research or symptom and treatment in medical testing. A well‐known application of correspondence analysis is textual analysis — identifying the author of a text based on examination of its characteristics.
We start with an m × n data matrix P with nonnegative elements which sum to one, that is, ι′Pι = 1, where ι denotes a vector of ones (of unspecified dimension). We let r = Pι and c = P′ι denote the vectors of row and column sums, respectively, and Dr and Dc the diagonal matrices with the components of r and c on the diagonal.
Now define the matrix
Correspondence analysis then amounts to the following approximation problem,

with respect to A and B. The dimension of the approximation is k < n.
To solve this problem, we first maximize with respect to A taking B to be given and satisfying the restriction B′DcB = Ik. Thus, we let
from which we find
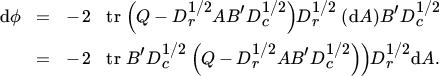
The maximum (with respect to A) is therefore obtained when
and this gives, taking the constraint B′DcB = Ik into account,
Hence,

Our maximization problem thus becomes a minimization problem, namely
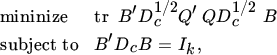
with respect to B. Now let ![]() . Then we can rewrite (75) as
. Then we can rewrite (75) as

with respect to X. But we know the answer to this problem, see Theorem 11.13. The minimum is the sum of the k smallest eigenvalues of Q′Q and the solution ![]() contains the k eigenvectors associated to these eigenvalues. Hence, the complete solution is given by
contains the k eigenvectors associated to these eigenvalues. Hence, the complete solution is given by
so that the data approximation is given by
Exercise
- 1.
Show that the singular values of
 are all between 0 and 1 (Neudecker, Satorra, and van de Velden 1997).
are all between 0 and 1 (Neudecker, Satorra, and van de Velden 1997).
17 LINEAR DISCRIMINANT ANALYSIS
Linear discriminant analysis is used as a signal classification tool in signal processing applications, such as speech recognition and image processing. The aim is to reduce the dimension in a such a way that the discrimination between different signal classes is maximized given a certain measure. The measure that is used to quantify the discrimination between different signal classes is the generalized Rayleigh quotient,
where A is positive semidefinite and B is positive definite.
This measure is appropriate in one dimension. If we wish to measure the discrimination between signal classes in a higher‐ (say k‐)dimensional space, we can use the k‐dimensional version of the quotient, that is,

where X is an n × k matrix of rank k, A is positive semidefinite of rank r ≥ k, and B is positive definite.
Let us define
Then,
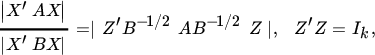
and hence, by Theorem 11.15, this is maximized at ![]() , where
, where ![]() contains the eigenvectors associated with the k largest eigenvalues of B−1/2AB−1/2. The solution matrix
contains the eigenvectors associated with the k largest eigenvalues of B−1/2AB−1/2. The solution matrix ![]() is unique (apart from column permutations), but the resulting matrix
is unique (apart from column permutations), but the resulting matrix ![]() is not unique. In fact, the class of solution matrices is given by
is not unique. In fact, the class of solution matrices is given by
where Q is an arbitrary positive definite matrix. This can be seen as follows. First, it follows from (77) that 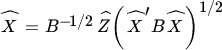 , which implies (78) for
, which implies (78) for  . Next, suppose that (78) holds for some positive definite Q and semi‐orthogonal
. Next, suppose that (78) holds for some positive definite Q and semi‐orthogonal ![]() . Then,
. Then,

so that ( 77 ) holds.
BIBLIOGRAPHICAL NOTES
1. There are some excellent texts on multivariate statistics and psychometrics; for example, Morrison (1976), Anderson (1984), Mardia, Kent, and Bibby (1992), and Adachi (2016).
2–3. See also Lawley and Maxwell (1971), Muirhead (1982), and Anderson (1984).
5–6. See Morrison (1976) and Muirhead (1982). Theorem 17.4 is proved in Anderson (1984). For asymptotic distributional results concerning li and qi, see Kollo and Neudecker (1993). For asymptotic distributional results concerning qi in Hotelling's (1933) model where ![]() , see Kollo and Neudecker (1997a).
, see Kollo and Neudecker (1997a).
7–9. See Eckart and Young (1936), Theil (1971), Ten Berge (1993), Greene (1993), and Chipman (1996). We are grateful to Jos Ten Berge for pointing out a redundancy in (an earlier version of) Theorem 17.8.
10. For three‐mode component analysis, see Tucker (1966). An extension to four models is given in Lastovička (1981) and to an arbitrary number of modes in Kapteyn, Neudecker, and Wansbeek (1986).
11–12. For factor analysis, see Rao (1955), Morrison (1976), and Mardia, Kent, and Bibby (1992). Kano and Ihara (1994) propose a likelihood‐based procedure for identifying a variate as inconsistent in factor analysis. Tsai and Tsay (2010) consider estimation of constrained and partially constrained factor models when the dimension of explanatory variables is high, employing both maximum likelihood and least squares. Yuan, Marshall, and Bentler (2002) extend factor analysis to missing and nonnormal data.
13. See Clarke (1970), Lawley and Maxwell (1971), and Neudecker (1975).
14. See Kaiser (1958, 1959), Sherin (1966), Lawley and Maxwell (1971), and Neudecker (1981). For a generalization of the matrix results for the raw varimax rotation, see Hayashi and Yung (1999).
15. See Muirhead (1982) and Anderson (1984).
16. Correspondence analysis is discussed in Greenacre (1984) and Nishisato (1994). The current discussion follows van de Velden, Iodice d'Enza, and Palumbo (2017). A famous exponent of textual analysis is Foster (2001), who describes how he identified the authors of several anonymous works.
17. See Duda, Hart, and Stork (2001) and Prieto (2003).
