Chapter 14
Investing in Arbitrage
This chapter looks at a number of practical aspects of investing in merger arbitrage strategies. Some topics have been touched on earlier, such as short selling and leverage. Risk management is an area that has not yet been discussed. Despite its exponential growth in finance in general, the tools used in merger arbitrage are still rudimentary. Finally, different vehicles that investors can utilize to participate in merger arbitrage strategies are discussed.
Trading versus Investing
Merger arbitrage investments are held for a short period of time. As we saw in Chapter 5, the average time for the closing of a merger is 128 days. This short holding period qualifies merger arbitrage as a short-term trading strategy by the standards of most investors. For ultra-short-term traders who hold positions for a few days only or even as little as a few minutes or seconds, the time horizon of merger arbitrage is long. Most investors, however, have longer horizons and will consider merger arbitrage a short-term or trading strategy.
The short-term nature of merger arbitrage investing has implications on taxes, which have been discussed in Chapter 5. Merger arbitrage will generate primarily short-term gains and hence will be tax-inefficient. Many institutional investors are pension funds or endowments that are exempt from taxes and do not put much weight on the tax characteristics of merger arbitrage. Taxable individuals, however, often prefer to invest in the strategy through tax-deferred vehicles such as individual retirement accounts (IRAs), variable annuities, or private placement life insurance. The flip side of benefiting from the tax deferral of these vehicles is that the investment must be held long enough for the compounding on the deferral to work as intended. Therefore, an investment in the strategy requires a commitment in the context of an asset allocation strategy. It is not suitable for investors who are chasing after the latest hot strategy. Unfortunately, the nature of financial market is such that asset classes go through cycles and perform well sometimes while underperforming at other times. Merger arbitrage is no different. The market correction in late 2008 is a good example of how short-term cycles can affect merger arbitrage as a strategy. Sharp drawdowns were experienced in 1998, when investors dropped merger arbitrage, only to pile back into the strategy shortly thereafter. Investors who make such tactical withdrawals should have a clear idea of when to reenter the strategy. This is, of course, true not just for merger arbitrage but for any investment. If investors exit simply out of panic and enter for the same reason (more commonly called chasing returns), then they are effectively pursuing a strategy of selling low and buying high.
The asymmetric payoff of merger arbitrage makes the evaluation of a manager more complex than more traditional strategies with a symmetric payoff profiles. As discussed on several occasions in this book, merger arbitrage has a high probability of producing a small payoff and a small probability of generating a large loss. An aggressive investor therefore can be tempted to take large risks, because the probability of loss is low. For an outside investor, it is difficult if not impossible to estimate why these risks have been taken: Is the manager an aggressive risk taker or a compulsive gambler? In the author's experience, both personality types gravitate toward the financial markets, and in particular to short-term trading strategies. It is possible to distinguish between the two types only if one makes a deliberate effort to understand the thought process behind each investment decision. Even then, one must be well familiar with each investment to distinguish between empty financial phraseology and actual thoughtful decisions. It should be noted that this dilemma arises not just in evaluating merger arbitrage manager, but many other investment strategies as well, where payoff profiles are asymmetric. The optionality that is sometimes embedded in strategies can be next to impossible to detect for outside investors.
Many institutional investors have developed elaborate due diligence procedures with due diligence questionnaires (DDQs), manager interviews and onsite visits that are supposed to standardize the selection of investment managers to whom they allocate assets. The risk with these processes is that they become too formulaic so that a clever compulsive gambler will not find it difficult to game the selection process. Check-box investing is necessary if decisions are taken by committee. Unfortunately, it has become widespread, and many institutions will pay the price for this overly simplistic decision making. In my own experience in dealing with due diligence teams at various institutional investment firms, I have found a wide range of expertise that, in some cases, can be highly detailed and question the rationale of specific investments, sometimes going back several quarters in the past.
Leverage and Options
Merger arbitrage is a low-volatility strategy. As such, it lends itself to the use of leverage to boost returns, as is commonly done with other low-volatility strategies. Because leverage is a double-edged sword, amplifying both returns and losses, it is risky to use on investment strategies that produce widely fluctuating returns.
Arbitrageurs have two main sources of leverage: the use of derivatives and borrowing. Borrowing can be done either through margin loans from a broker, which is the most common form of borrowing for hedge funds, or through loans. These forms of leverage were discussed in Chapter 5. Derivatives provide more flexibility to managers seeking leverage than margin loans. Not only can the implied interest rate be more favorable, because derivatives are priced using the risk-free rate rather than the (presumably much higher) actual funding rate that is available to the arbitrageur, but also the leverage that can be achieved is much higher. Margin loans are constrained by Regulation T, as described in Chapter 5. Derivatives can provide much higher levels of leverage. Leverage is constrained only by any collateral required by the counterparty, if any.
Single stock futures have been offered by OneChicago, a joint venture of the Chicago Board Options Exchange and the Chicago Mercantile Exchange, since 2002. Single stock futures are similar to other financial futures in that they are cash settled. They require an initial and maintenance margin of only 20 percent of the underlying and thus offer higher leverage than what can be achieved through a margin loan. In addition, certain positions can be used to offset each other, for example calendar spreads. Each contract is offered on an underlying of 100 shares. However, these futures contracts are offered only on a limited number of stocks. At the time of writing, single stock futures were available on approximately 900 underlying stocks. Liquidity is also a problem: In mid-2015, the aggregate daily volume on all of these contracts on the OneChicago exchange only occasionally exceeded 100,000 and on some days barely exceeded a mere 10,000. This is equivalent to trading of not even 1 million shares. In comparison, the daily volume on each of the New York Stock Exchange and the NASDAQ amounted to several billion shares over the same period.
Options are another source of leverage. Options have already been discussed in Chapter 5 in the context of call writing to enhance returns. Arbitrageurs can also purchase calls to obtain additional leverage. Implied volatilities fall significantly after the announcement of a merger, so that option premia become affordable despite the tight spreads. An arbitrageur probably will acquire in-the-money options to mimic long positions and in-the-money puts for short positions, because they have the highest deltas.
The pricing of options of stocks in a merger is more difficult than that of options on other stocks. The standard model to calculate prices of financial options on stocks it the Black-Scholes model. One of its crucial underlying assumptions is the continuous movement of prices. For stocks that are going through a merger, prices will go through sudden and instantaneous jumps when a merger is called off. The stock will suffer a sharp correction (or a short squeeze in the short leg of a stock-for-stock merger) that is discontinuous. The risk of such a sudden jump in prices is not captured correctly by the Black-Scholes model. A model that captures this effect was developed by Ajay Subramanian.1 It uses a jump diffusion process rather than the continuous diffusion, also called Brownian motion, of the Black-Scholes framework. Subramanian examines options on stocks undergoing stock-for-stock mergers and starts with jump diffusion processes of the form

where
| S1, S2 are the prices of the stocks. |
| t– is a notation for the time just prior to t. |
| d1, d2 are the respective dividend yields. |
| dW1, dW2 are random draws as in a Brownian motion. |
If the merger is called off, the stocks will revert to a standard Black-Scholes process:

where
| dW3, dW4 are random draws as in a Brownian motion. |
Subramanian derives a closed-form solution for the price of a European call option, which is significantly more involved than the classic Black-Scholes equation:

where
 .
.- A1, A2 are chosen so that the stock jumps by a factor.
 if the deal is called off.
if the deal is called off.  is the risk- neutral probability that the deal is called off in the period [t,t+dt] is
is the risk- neutral probability that the deal is called off in the period [t,t+dt] is  dt.
dt.
The integrals can be replaced by

where
Subramanian uses these formulas to invert the problem: Rather than calculating option prices, he uses option prices as the input to derive the implied probability that a merger closes. His results, shown in Table 14.1, show that the options market sets probabilities of the closing of mergers that are good predictors of the actual outcome. The time between announcement and anticipated closing is split into three periods. In each of these periods, the implied probabilities of the options are averaged. The average for the final month before closing or cancellation of the deal is also shown. For successful deals, the average probability implied by the options is twice as high as that for deals that ultimately are successful.
Table 14.1 Implied Probabilities of the Closing of Mergers Derived from Option Prices
| Successful Deals | Unsuccessful Deals | ||||||||||||
| Target | Acquirer | AverageSuccessProbability(First Third) | AverageSuccessProbability(Middle Third) | AverageSuccessProbability(Final Third) | AverageSuccessProbability(Final Month) | OverallAverage | Target | Acquirer | AverageSuccessProbability(First Third) | AverageSuccessProbability(Middle Third) | AverageSuccessProbability(Final Third) | AverageSuccessProbability(Final Month) | OverallAverage |
| DS | MXIM | 0.48 | 0.64 | 0.79 | 0.74 | 0.61 | NTPA | PROX | 0.33 | 0.29 | 0.26 | 0.29 | 0.3 |
| TOS | P | 0.56 | 0.79 | 0.95 | 0.91 | 0.81 | PRXL | CVD | 0.25 | 0.19 | 0.3 | 0.26 | 0.25 |
| CATP | NOVL | 0.79 | 0.8 | 0.95 | 0.93 | 0.86 | AZA | ABT | 0.29 | 0.43 | 0.41 | 0.44 | 0.38 |
| CIT | TYC | 0.4 | 0.63 | 0.74 | 0.74 | 0.58 | NR | TBI | 0.27 | 0.3 | 0.49 | 0.46 | 0.35 |
| BBC | AAS | 0.38 | 0.44 | 0.57 | 0.6 | 0.43 | CYM | AR | 0.3 | 0.25 | 0.49 | 0.49 | 0.36 |
| KNT | AVNT | 0.6 | 0.65 | 0.76 | 0.74 | 0.68 | WLA | AHP | 0.01 | 0.05 | 0.07 | 0.08 | 0.04 |
| AZA | JNJ | 0.81 | 0.85 | 0.95 | 0.94 | 0.87 | GLIA | GLFD | 0.15 | 0.47 | 0.52 | 0.51 | 0.37 |
| SEM | VSH | 0.49 | 0.58 | 0.79 | 0.77 | 0.59 | REL | LUK | 0.49 | 0.47 | 0.6 | 0.53 | 0.52 |
| WB | FTU | 0.43 | 0.68 | 0.86 | 0.91 | 0.68 | FSCO | ZION | 0.18 | 0.22 | 0.09 | 0.11 | 0.17 |
| NIS | USB | 0.69 | 0.93 | 0.98 | 0.97 | 0.87 | |||||||
| SAWS | TQNT | 0.44 | 0.6 | 0.69 | 0.64 | 0.57 | |||||||
| MRL | PDE | 0.38 | 0.61 | 0.76 | 0.77 | 0.55 | |||||||
| HM | ABX | 0.4 | 0.57 | 0.71 | 0.82 | 0.58 | |||||||
| DRMD | BRL | 0.25 | 0.42 | 0.59 | 0.58 | 0.38 | |||||||
| GEN | TER | 0.44 | 0.49 | 0.63 | 0.62 | 0.52 | |||||||
| W | MEA | 0.47 | 0.6 | 0.79 | 0.79 | 0.61 | |||||||
| CPQ | HWP | 0.16 | 0.23 | 0.58 | 0.77 | 0.33 | |||||||
| GLM | SDC | 0.33 | 0.47 | 0.65 | 0.64 | 0.51 | |||||||
| COC | P | 0.29 | 0.35 | 0.58 | 0.82 | 0.41 | |||||||
| AVIR | MEDI | 0.68 | 0.79 | 0.94 | 0.85 | 0.83 | |||||||
| CORR | MLNM | 0.5 | 0.56 | 0.72 | 0.67 | 0.58 | |||||||
| AVNT | SNPS | 0.25 | 0.46 | 0.62 | 0.74 | 0.44 | |||||||
| SRM | TYC | 0.85 | 0.85 | 0.93 | 0.91 | 0.87 | |||||||
| SCI | SNM | 0.29 | 0.45 | 0.67 | 0.73 | 0.45 | |||||||
| Mean | 0.47 | 0.6 | 0.75 | 0.76 | 0.6 | 0.25 | 0.3 | 0.36 | 0.35 | 0.3 | |||
| Median | 0.44 | 0.6 | 0.75 | 0.77 | 0.58 | 0.27 | 0.29 | 0.41 | 0.44 | 0.35 | |||
| q | Max | 0.83 | 0.91 | 0.96 | 0.98 | ||||||||
Source: Ajay Subramanian, “Option Pricing on Stocks in Mergers and Acquisitions,” Journal of Finance 59, no. 2 (April 2004).
This result is consistent with other studies that have found that mergers that close have narrower spreads than those that eventually collapse.
Some of the highest leverage can be achieved through the use of swaps. A total return swap allows an arbitrageur to obtain exposure to an asset without taking possession. As discussed previously, margin borrowing can be expensive, in particular for smaller arbitrageurs or entities that are highly leveraged. A total return swap allows an arbitrageur to borrow the funding capability of a large investment bank or dealer and pay a much smaller spread on the reference rate than if it had taken out a margin loan. The structure of a total return swap resembles that of other swap contracts, such as interest rate swaps. It has two legs: a funding leg and a return leg. In the terminology of total return swaps, the party that receives the return leg, which is the return on the underlying asset, is the buyer. The seller pays the return on the asset. In exchange, the buyer pays the seller a funding cost, which is a spread over the London Interbank Offered Rate (LIBOR). In addition, the buyer pays the seller any depreciation of the underlying assets. The net effect of these cash flows is that the buyer pays the cost of funding and receives any appreciation and dividends on the underlying. If the underlying loses value, the buyer pays the seller.
Sellers of total return swaps are broker/dealers that hedge themselves by acquiring the underlying assets. Therefore, an arbitrageur who acquires a total return swap gets the benefit of paying LIBOR plus a modest spread rather than a higher margin rate.
Contrary to some misinformation that circulates in the media and also literature about the financial crisis, swaps are not an unregulated wild west. In practice, swaps can only be executed by parties that have executed an ISDA agreement between each other. ISDA agreements are standardized and so is the vast majority of swap contracts. Although it is possible to execute a swap with nonstandard terms, this is rarely done. Swaps outside of an ISDA agreement are no more than a hypothetical scenario. A bigger concern, from the point of view of an arbitrageur, is the difficulty of obtaining an ISDA agreement. The number of banks that offer this service has shrunk in the wake of the financial crisis, and those that continue to offer this service do so only for counterparties that promise to generate substantial business, so that smaller arbitrageurs will find it difficult to impossible to use this type of derivative.
Similar levels of leverage can be achieved through contracts for difference (CFD). However, for regulatory reasons, these instruments are not available in the United States at this time.
It is well known to financial practitioners as well as academics that the use of leverage is a double-edged sword. Not only does it amplify positive returns, but it also increases losses. An aspect of leverage that is less well known in academic circles is that the combination of leverage and short selling introduces costs that are a drag on returns. This problem is especially acute for 130/30 strategies. These are investment strategies where 100 percent of the assets are invested in an index, 30 percent are sold short, and an additional 30 percent are invested in long positions. The combination of 30 percent short/30 percent long is supposed to add returns that are independent of the direction of the market and add to the return achieved from the index component.
The academic literature regarding these strategies assumes that the proceeds from the short sales are used to acquire the long position. This is not possible because most brokers do not allow an investor to access all of the proceeds from a short sale. Figure 14.1 illustrates this problem. At least some fraction of the proceeds of the short sale must remain at the broker in cash and cannot be invested. The broker will, of course, pay interest in the form of a short rebate (to be discussed; see also Chapter 5) on the cash balance of short proceeds. Nevertheless, the investor cannot access these funds to purchase additional securities. Therefore, sufficient funds must be borrowed to compensate for the unavailability of the funds retained by the broker. The investor needs to pay a higher rate of interest on the amounts borrowed than received through the short rebate. This is a net cost of the long/short component that must be offset through investment gains. Therefore, even before any gains are made, the long/short component will impose a cost on the fund. This cost also can be viewed as a negative alpha built into the long component of the strategy.

Figure 14.1 Leverage Coupled with Short Selling Leads to Negative Alpha
Some simple calculations can illustrate the extent of a negative alpha. It is determined by three factors:
- The amount of leverage used
- The fraction of the short sale proceeds that the short broker allows the arbitrageur to access for purchases
- The interest rate differential between the short rebate and the borrowing cost.
Table 14.2 shows various levels of negative alpha for different levels of these three variables.
Table 14.2 Negative Alpha for Different Levels of Leverage, Interest Rate Spreads, and Withdrawal Levels from the Brokerage
| Short Proceeds Retained by Broker | ||||
| 20% leverage | 30% | 50% | 100% | |
| Spread | 1.00% | 0.06% | 0.10% | 0.20% |
| 2.00% | 0.12% | 0.20% | 0.40% | |
| 5.00% | 0.30% | 0.50% | 1.00% | |
| Short Proceeds Retained by Broker | ||||
| 30% leverage | 30% | 50% | 100% | |
| Spread | 1.00% | 0.09% | 0.15% | 0.30% |
| 2.00% | 0.18% | 0.30% | 0.60% | |
| 5.00% | 0.45% | 0.75% | 1.50% | |
| Short Proceeds Retained by Broker | ||||
| 50% leverage | 30% | 50% | 100% | |
| Spread | 1.00% | 0.15% | 0.25% | 0.50% |
| 2.00% | 0.30% | 0.50% | 1.00% | |
| 5.00% | 0.75% | 1.25% | 2.50% | |
Merger arbitrageurs face the same challenge when using leverage to finance a portion of the long/short component of their arbitrage portfolio. In a stock-for-stock merger, they cannot utilize all of the proceeds from the short sale for purchasing the long leg of the arbitrage. If they leverage, they must borrow these funds. Their arbitrage position will experience the same type of negative alpha just described.
Shorting Stocks
The shorting of stock is generally regarded as a high-risk activity and sometimes is associated with illegal activities. There is no doubt that short selling exposes the seller to potentially unlimited losses on the short. The short seller takes the opposite position of a buyer; while the buyer has the potential for unlimited gains on their holding, the short seller faces the opposite risk. Short selling as a stand-alone investment strategy is indeed a risky undertaking that is best left to investors who master this discipline well.
Since the stock market goes up most of the time, a simple short position is more likely to generate losses than gains. Returns on funds that specialize in short selling only confirm the difficulty of making a profit on this strategy. Table 14.3 shows the returns of the HFRI Equity Hedge Short Biased Index of short-selling hedge funds. On average, these funds had a negative performance, with an average annual return of –2.66 percent compared to an average annual return of 9.45 percent for the Standard & Poor's (S&P) 500 index. Some observers unfamiliar with arbitrage strategies may argue based on these numbers that using short selling is a losing strategy. However, when short selling is used as an element of a more complex strategy, such as merger arbitrage, comparisons to pure short selling are not relevant. The short position changes its character from a bet on the drop of a stock price to an attempt to capture a price differential.
Table 14.3 Performance (percentage per calendar year) of Short Biased Hedge Funds According to HFRI
| Year | Return (%) |
| 2014 | (3.89) |
| 2013 | (18.60) |
| 2012 | (17.24) |
| 2011 | 0.35 |
| 2010 | (18.01) |
| 2009 | (24.03) |
| 2008 | 28.41 |
| 2007 | 4.72 |
| 2006 | (2.65) |
| 2005 | 7.28 |
| 2004 | (3.83) |
| 2003 | (21.78) |
| 2002 | 29.17 |
| 2001 | 8.99 |
| 2000 | 34.63 |
| 1999 | (24.40) |
| 1998 | (0.54) |
| 1997 | 3.86 |
| 1996 | (4.00) |
| 1995 | (17.14) |
| 1994 | 18.53 |
| 1993 | (7.50) |
| Average | (2.66) |
| S&P 500 Total Return | 9.45 |
Source: Bloomberg, HFRI.
A short seller is required to deliver the shares that have been sold to the buyer. The buyer is not concerned with whether the purchased shares have been sold by someone who held the stock or who sold it short. The buyer simply expects to obtain the acquired shares. Many institutional investors, including public pension funds and endowments, lend their shares to short sellers and charge a fee for that service. In most cases, the actual lending is done not by the institution itself but by the custodian. A securities lending agreement stipulates whether the custodian must obtain permission from the institution before lending the shares, or whether the shares can be lent on a discretionary basis without prior approval.
Lenders receive a fee from the borrower. Table 14.4 shows the fees charged and returns achieved by lenders of securities in the first quarter of the year 2014. In the table, bp stands for basis points, which represent 0.01 percent.
Table 14.4 Fees and Returns Earned by Lenders of Securities
| Asset Class | Lendable Assets (US $m) | Total Balance (US $m) | Utilization (%) | Securities Lending Fee (bp) | Securities Lending Return to Lendable (bp) | Total Return to Lendable (bp) |
| Asian Equity | 394,636.2 | 31,318.4 | 5.85 | 119.21 | 6.82 | 6.93 |
| Of which Australia | 217,052.6 | 14,464.2 | 5.26 | 52.30 | 2.65 | 2.74 |
| USA Equity | 5,299,961.9 | 383,031.41 | 5.22 | 63.04 | 3.24 | 3.78 |
| Of which S&P 500 | 4,053,935.3 | 181,587.0 | 3.11 | 10.95 | 0.42 | 0.84 |
| Western Europe Equity | 1,505,513.6 | 110,883.7 | 4.19 | 68.20 | 3.41 | 3.47 |
| Of which UK Equity | 789,305.0 | 31,672.2 | 3.16 | 35.66 | 1.20 | 1.25 |
Source: Securities Finance Review / Q1 2014: Spring Cleaning (London: markit, May 7, 2014).
Most arbitrageurs that sell short do not borrow shares directly from a lender but instead rely on their broker to borrow the shares either out of their clients' inventory or from other sources. Brokers usually borrow from other sources only if the size of the trade is large enough to make doing so economical. An arbitrageur who borrows shares from the broker does not normally pay a lending fee. Instead, the cost of lending is incorporated into the short rebate in the form of a lower rebate. Only hard-to-borrow shares command extra fees.
Short rebates vary widely and are subject to negotiation. Most retail brokerage firms pay their customers no short rebate at all. One such firm, Interactive Brokers, pays a rate based on the Fed Funds rate, and charges between Fed Funds minus 0.25 percent and Fed Funds minus 1.25 percent, depending on the dollar balance of short proceeds. The section about leverage in this chapter has a more detailed discussion of the impact of the short rebate on the use of leverage. Merger arbitrageurs who want to generate extra income also can take the opposite side and lend out shares that they hold as part of the arbitrage. The income generated thereby can offset some of the borrowing costs. Many arbitrageurs will forgo this additional revenue in order to maintain voting control over the shares that are subject to a merger. When shares are lent out, the ultimate holder of the shares will exercise the voting rights, not the original owner who has lent them. For an arbitrageur who wants a merger to happen, it is more critical to vote in favor than to generate additional revenue. The larger the position, the more relevant this consideration becomes.
The borrowing of shares also can be used to acquire votes beyond the actual number of shares owned. An investor can borrow shares with the sole intent of voting them. The cost of borrowing is minimal in most instances; however, the upside of influencing the outcome of such a vote can be considerable. One of the most prominent examples of such “empty voting” occurred during the failed merger of King Pharmaceuticals and Mylan Laboratories in 2005. Hedge fund Perry Corp. owned shares of King, which had risen following the news of the merger. Perry acquired 9.9 percent of Mylan and hedged all its exposure to the stock price. Therefore, Perry2 had voting rights to Mylan's stock but no economic interest. Perry could have pushed Mylan to pay a higher price for King. The transaction unraveled following the revelation of accounting problems at King, so that Perry's strategy was never tested in practice. However, it has led to calls by Securities and Exchange Commission (SEC) official for action on empty voting. Because the SEC does not want to disrupt the securities lending markets, no action had been proposed by the time of writing, but it is likely that this area will be regulated in the future.3
The SEC has issued a rule that governs all short sales, Regulation SHO. It became mandatory in January 2005. This rule forbids brokers from entering into short sales on behalf of a client unless the stock to be shorted has been borrowed previously. Many brokers will handle both the borrowing and the execution of the short sale. Execution-only brokers now require confirmation from arbitrageurs that the stock has been borrowed (or located for borrowing) prior to placing a short sell.
Short sellers will cover their position only if they cannot borrow the shares from another lender. Under normal market conditions, there are many willing lenders of stock. However, in some instances, an individual stock can be shorted heavily, and only few shares are available to be borrowed. Such stocks are at risk of going through a short squeeze. An arbitrageur who shorts a stock that goes through a short squeeze will suffer a loss, albeit temporarily. The problem with such a loss is that at some point, the arbitrageur will feel compelled to cover the short position to avoid further losses. Unless the arbitrageur is lucky or unusually skilled in timing the market, it is unlikely that it will be possible to reenter the short position at a more favorable level. Market movements in short squeezes are very rapid. The most prominent example of a short squeeze was the increase of Volkswagen (VW) ordinary shares following the revelation that Porsche SE had acquired control over 75 percent of the shares. With 20 percent held by the state of Lower Saxony, the free float amounted to only 5 percent, while short positions were estimated to amount to 15 percent. Within two days, VW's stock price increased from €210 to as much as €1,000. Cumulative losses to short sellers were estimated to amount to €15 billion. It should be noted that the short sellers were for the most part arbitrageurs who had attempted to arbitrage the wide spread between VW's ordinary and preferred shares.
Retail investors usually do not have to worry about borrowing stock themselves. Their clearing broker gives them access to their clients' inventory and will reject orders to sell short if there is insufficient inventory. The direct access to substantial inventory sometimes can give retail investors an edge over institutions when dealing in hard-to-borrow stocks. Retail brokers may have a small number of shares available that are too few to be shown to the street but are still available to their lucky clients.
A short sale in which the arbitrageur is not able to deliver the stock is referred to as a naked short and is illegal. Nevertheless, occasionally naked short sales can happen as trade errors, but this should be an exception and should not occur with any regularity. It has been alleged by anti–short-selling activists and some politicians that some market participants use foreign exchanges to skirt Regulation SHO. Arbitrageurs should refrain from such activities, which are bound to unwind at the time of the closing of the merger. In July 2008, the SEC reiterated Regulation SHO through an emergency order that prohibited naked shorting for equity securities of 19 financial firms.
By issuing this list, the SEC intended to prop up shares of financial companies that had dropped precipitously in the previous weeks. Although this emergency ruling was hailed widely as a tough measure, it merely reiterated the existing prohibition against naked short sales under Regulation SHO. Its impact was more psychological than logical, sending a message that short sellers might face regulatory scrutiny. It worked as intended and led to a rally in financial stocks as short sellers covered their positions in a squeeze. Nevertheless, the effectiveness of the list is at best dubious. Many of the companies listed are not even based in the United States and their principal trading exchange is located in Asia or Europe and does not fall under the purview of the SEC. A short seller who is not subject to SEC oversight, such as a London-based hedge fund, would be able to engage in unlimited naked short selling without violating the SEC's order.
A study conducted shortly after the ban of short selling showed that the effect of the ban was a deterioration of the market quality in the affected stocks.4 This led to a sharper decline in their stock prices than short selling would have. The study analyzed a number of different metrics to determine the effect of the emergency order.
The study started by noting that short selling the 19 stocks on the list had been comparable to that of other financial companies between 2006 and 2008. When controlling for firm and market characteristics, the author, Arturo Bris, found that there had been less short selling for most stocks on the list than for other financial companies. An important difference between the 19 stocks and other financial companies is the propensity of the firms on the list to issue convertible bonds. Many convertible bonds are acquired by arbitrageurs who hedge the conversion feature by selling short stock. As a result, on an absolute level, there is more short selling in these stocks. This higher absolute level is not evidence of bearish activity but of convertible arbitrage that takes no view about the direction of a company's stock.
More important, the SEC's action led to a deterioration of the market quality in the stocks that it was hoping to protect. Measures of daily price volatility as well as quoted spreads deteriorated after the emergency order took effect. Also, the co-movement of the individual stocks with the overall market increased. In more efficient markets, individual stocks should be less dependent on the overall direction of the market and more dependent on company-specific information.
Despite the mixed results of the first short-selling ban, a more comprehensive prohibition against shorting in 800 financial companies was enacted from September 19 to October 8 that same year. Even the nonfinancial company General Motors was included in the prohibition. At the same time, the SEC required the disclosure of short sales that exceed 0.25 percent of an issuer's outstanding shares or $1 million of market value. Only money managers who were already required to file 13F reports are subject to these reporting requirements. These are managers with at least $100 million assets under management.
Regulators outside of the United States were even more drastic in their measures to restrict short selling. The United Kingdom banned short selling of 30 financial stocks for four months. Australia banned all short sales for two months and, like the SEC, instituted reporting requirements. The Netherlands banned naked short sales of financial stocks for three months. Taiwan banned short selling in stocks amounting to 80 percent of the country's market capitalization for three weeks. Ireland and Germany also imposed restrictions on short sales.
A study on the efficiency of short sales that was conducted prior to the worldwide short selling bans found that restrictions on short selling have lower price efficiency.5 Restrictions on short selling were measured through the availability of shares available for shorting, and the level of borrowing fees. Price efficiency was defined as the lag with which an individual stock responds to market shocks. At the same time, the skewness of returns increased. This was associated with an increase of the number of large positive returns on stocks that suffer from short sale restrictions rather than a decrease in the number of large negative drops. Therefore, like Bris's study, this study confirms that short sale restrictions fail to meet their goals of reducing sharp declines in the affected stocks.
Dividend payments complicate the shorting of stocks. When a stock is sold short, there are two holders of the stock: the original buyer who has lent the stock out and the buyer who is the counterparty to the short sale. The buyer of a stock is ignorant as to the nature of the stock acquired. The buyer does not know whether the stock was purchased out of a seller's inventory or whether the stock had been borrowed and was sold short. Each buyer of a stock expects to receive a dividend and obtains the right to receive it through the purchase.
Short-selling activity increases over dividend dates, as shown in Figure 14.2. Both the percentage of shares available for shorting, labeled “Utilization,” and the level of lending fees increase over dividend dates. Arbitrageurs must be careful if they maintain short positions over dividend dates or attempt to short around that time. The data underlying Figure 14.2 are based on a global data set and may not translate identically to each country. Shorting activity around dividend dates probably increases more in countries that give shareholders tax credits along with dividend payments.6
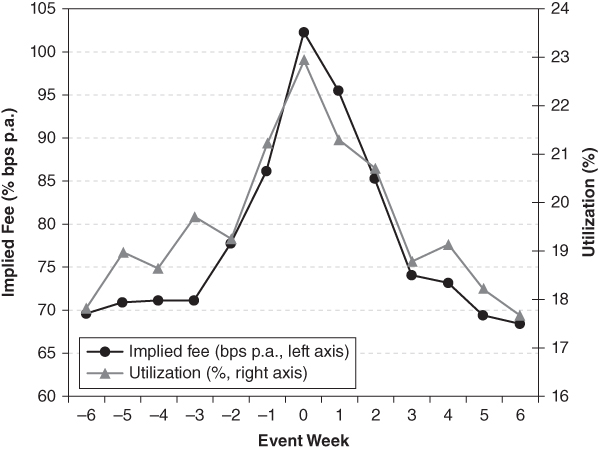
Figure 14.2 Fees and Short Sale Activity (Utilization of Shares Available) around Dividend Payments
Source: P. Saffi, K. Sigurdsson, Price Efficiency and Short Selling. Working Paper, London Business School, January 2007, p. 48.
Transaction Costs
Merger arbitrage spreads are very tight, and arbitrageurs must keep transaction costs under control. Transaction costs come in three forms: brokerage commissions, bid/offer spreads, and market impact.
Brokerage Commissions
As discussed in Chapter 3, commissions have fallen significantly over the last few years. Many mergers would be uneconomical at commission levels of just a few years ago. However, this is somewhat of a chicken-and-egg argument. One of the reasons why spreads have become tighter is the reduction in the overall level of trading commissions. If commissions were larger, then trading costs of arbitrageurs would be higher, and this would be reflected in wider arbitrage spreads. In this way, the fall in the cost of brokerage commissions has benefited not the arbitrage community but, rather, the investors who sell their shares after the announcement of a merger in order to capture the premium. They obtain a higher price from the liquidity providers, the arbitrageurs, because commissions are lower.
Brokerage commissions bundle a number of services into a single fee:
- Execution. This is the basic activity of routing and order to an exchange electronic communication network (ECN) and matching it with a counterparty. Most trades are executed today electronically. Computer algorithms have been developed to split large orders into smaller ones to reduce market impact (to be discussed). Many brokers offer specialized execution services for arbitrageurs and long/short investors, whereby orders are not executed at set price levels; instead, a spread level is entered at which both sides of the trade will be executed. The computer will show one side of the trade in the market in a way that if that side is filled, the other side can be executed instantaneously. For large trades, markets may not be liquid enough to execute the order in a reasonable time frame. Brokers often match buyers and sellers based on knowledge of their clients' investment preferences. Despite increased automation of trading, the human element will remain an important factor for transactions of this type for some time to come. The cost of pure execution without any added value is currently below $0.01 per share.
- Idea generation and market surveillance. Many brokers add value to arbitrageurs by monitoring the market and pointing arbitrageurs to trading activity in stocks going through mergers. Such market intelligence can be very valuable because arbitrageurs generally do not have the time or resources to monitor all trading activity themselves. Commissions charged by brokers who offer such extra services can be as low as $0.02 per share.
- Clearing. Clearing is the act of settlement and paying for the shares bought or sold during the execution of the order. It is a highly automated process that benefits from scale effects. The cost of clearing is below $0.005 per share.
- Soft dollars. In addition to monitoring the market and making suggestions to their customers, many brokers offer added services that they pay for through commissions. This practice is legal and used widely by money managers that seek to reduce costs at the expense of their clients. The idea of soft dollars is that the broker charges a higher commission than necessary and uses the extra payments to purchase services that the investment adviser can use to help with its research. Services typically paid for with soft-dollar commissions are third-party research, data services, and certain investment-related software. The use of soft dollars is particularly pervasive by hedge fund managers, who trade frequently and thereby accrue significant soft-dollar credits. Instead of paying for research out of the management fee, it is paid for by soft dollars, so that the manager's overall profitability increases. For most arbitrageurs, soft dollars are not attractive because they reduce the spread that is already very tight.
Brokerage commissions are highly variable between different firms and even within a single firm for different clients and types of orders or securities. A common fee structure is based on the number of shares that are executed, often coupled with a minimum ticket charge or base fee per ticket.
Bid/Offer Spreads
Bid/offer spreads were discussed in Chapter 3 in the context of liquidity as a determinant of the profitability of merger arbitrage. Arbitrageurs have to place orders carefully in less liquid stocks with wide bid/offer spreads. For wide bid/offer spreads, it is not economic for an arbitrageur to pay the entire spread unless the arbitrage spread is unusually wide. The arbitrageur will try to work with limit orders that are placed within the bid/offer spread. The disadvantage of this strategy is that there is no guarantee that the order will be filled. Other investors may jump ahead of the order. The advantage is that the arbitrageur becomes a genuine provider of liquidity and contributes to the tightening of the bid/offer spread. A tighter spread, in turn, may encourage some sellers to come forward and either hit the arbitrageur's bid or place an offer in the market that is below the previous best offer and thereby again reduce the bid/offer spread.
Mark-to-market valuation adds an impediment to paying the entire bid/offer spread: Many arbitrageurs are required to value their long positions at the bid and short positions on the offer. Some can use midmarket pricing. Under these circumstances, if an arbitrageur pays the entire bid/offer spread, an immediate loss has to be booked. The loss will, of course, be recovered once the spread tightens. Nevertheless, it complicates the setup of an arbitrage position further.
For the short side of stock-for-stock offer, the previous arguments are also true, albeit in reverse.
Market Impact
Whenever an arbitrageur places an order to acquire shares of a target, the order influences the supply and demand balance. The increase in demand will have an impact on the price. This may not necessarily translate into an immediate jump of the target stock price. It could simply prevent the price from making a correction that would have occurred in the absence of the arbitrageur's order. This effect is known as market impact. Although several consulting firms specialize in measuring market impact as part of an evaluation of execution and trading quality, the measurement of market impact is very difficult and is associated with a certain degree of speculation.
Nevertheless, there is no doubt that arbitrage activity does have a market impact. In the aggregate, market impact by all arbitrageurs helps sellers of a target's stock to obtain a better price than they would in the absence of arbitrage activity. This is a corollary of the argument made in Chapter 3 in the discussion of liquidity.
This discussion of market impact applies also to the short sale in a stock-for-stock merger.
Managing the Cash Position
Portfolio managers view cash holdings as a strategic or operational tool. Strategically, cash holdings are treated as an asset class, and operationally, they are needed to meet redemption requests.
Cash can provide a cushion to the downside and represents liquidity that can be put to use when attractive investment opportunities become available. In addition, cash is held in case redemption requests are received from investors. This is a problem that is more acute for mutual fund managers than for arbitrageurs who work in hedge funds or broker/dealers. The latter do not have to worry about cash holdings because cash is part of the firm's overall asset/liability management. Hedge fund managers are in an intermediate position: Typical investment conditions include a 90-day notice period for redemptions, so that the fund manager has sufficient time to liquidate positions and raise cash. Mutual funds have daily redemptions and therefore must keep a portion of their portfolio in cash to meet redemption requests.
The downside of cash holdings is that they do not generate returns. Because the market increases over time, cash holdings act as a drag on performance. This effect is true not only for traditional portfolios but also for merger arbitrage portfolios. Merger arbitrage generates positive returns most of the time, which are higher than the return on cash that is invested in short-term products. Holding cash instead of being fully invested diminishes the overall return on a merger arbitrage portfolio.
For traditional investors, the decision to hold cash beyond the amount required to meet redemption requests is a voluntary choice of the manager. The portfolio can be invested in cash or other assets as the manager sees fit. Increases in cash occur when the manager takes an active decision to sell assets and substitute these investments with cash holdings.
For a merger arbitrageur, cash holdings are based less on choice and more on deal flow. Whenever a merger closes, the arbitrageur will receive cash that must be reinvested. In the case of a cash merger, the position is liquidated when the merger closes. In a stock-for-stock merger, the arbitrageur receives cash indirectly when the proceeds of the short sale become available once the short position is closed out. In both scenarios, the arbitrageur will hold cash rather than an investment. The important difference to a traditional money manager is that this cash holding is not based on the arbitrageur's decision to reallocate assets but is out of the arbitrageur's control. It depends on the timing of the closing of the mergers that the arbitrageur is invested in. Mergers close more or less randomly. Even though the arbitrageur can make a rough guess about the closing, the date cannot be pinpointed precisely. For mergers, the closing date is often within a few days of the shareholder meeting. However, when regulatory approvals are required for a merger, then the shareholder meeting is often well before the actual closing date. Even when the arbitrageur has a high level of confidence in a closing date, there can still be delays in the settlement of the cash or stock proceeds.
Due to this uncertainty, the arbitrageur receives cash as a result of the closing of a merger and now faces the decision to
- Invest in other mergers, currently held in the portfolio or not; or
- Hold on to the cash in case another merger is announced shortly.
Like the liquidation of investments, the decision how to invest cash is different from that faced by a traditional money manager. The traditional manager has a well-defined choice of investment. The arbitrageur also has a defined choice of mergers to invest in. However, mergers are announced at random intervals. In addition to the already announced mergers that the arbitrageur can invest in, there is a probability that another attractive investment opportunity will be announced shortly after the arbitrageur receives a payout from a closing merger.
Assume the arbitrageur spreads the cash across the mergers currently held in the portfolio. The risk characteristics of the portfolio change as the concentration of individual position increases. If another merger is announced shortly thereafter that the arbitrageur deems attractive, all positions must be reduced to free up sufficient funds to invest. In light of the tight absolute spreads, cost of commissions, and bid/offer spreads, this is not a good proposition. Arbitrageurs are more likely to hold the cash until a new merger is announced that is attractive to invest in.
A direct and visible result of this problem is that average cash balances are higher in merger arbitrage funds than in traditional investment vehicles. Cash holdings are considered a cash drag on performance in most portfolios. They are also a drag on performance in merger arbitrage portfolios, but the drag is less of a problem than the alternative. If the cash was invested and subsequently redeployed in a newly announced merger, transaction costs would be much higher than the opportunity cost of holding cash. A back-of-the-envelope calculation illustrates this. Assume the average stock has a price of $20 and the bid/offer spread is 4 cents, while commissions are 2 cents per share. This implies trading costs of 12 cents per share for a round trip, or 0.6 percent. For a long/short merger, the total cost would be twice as high, or 1.2 percent. If cash is held, it can be invested in short-term instruments (money market funds) to yield a return, which reduces the opportunity cost. This compares to a typical monthly return of 1 percent on a merger arbitrage strategy. It is clear that it is best to hold cash rather than incur transaction costs if the arbitrageur thinks that another attractive merger is likely to be announced within no more than a few weeks.
The timing of the closing of mergers is subject to a small seasonality effect. Companies often try to close a merger prior to the end of their fiscal year, which ends on December 31 for most firms. Firms with fiscal years not ending with the calendar year typically have fiscal years that end on another calendar quarter-end. Companies strive to close the transaction in the current fiscal year, or before the completion of a fiscal quarter, in order to simplify the accounting by being able to show financials for the merged entity for an entire fiscal year or quarter.
This effect is apparent from the data. Figure 14.3 shows the number of mergers closing in each calendar month between the years 1990 and 2013. Only cash mergers in the United States with an equity value greater than $50 million were considered, of which there were 3,393 over this period. It can be seen that most mergers closed in the calendar month of December. July is also notable; there may be more merger closings in this month because companies try to close deals before the summer break when many employees take vacation.

Figure 14.3 Frequency of Merger Closings by Calendar Month, 1990–2013
Publicly available mutual funds that employ merger arbitrage are required to report their portfolio holdings periodically, in the United States even quarterly. The annual and semiannual holdings are included in reports sent to shareholders, whereas the holdings at the end of the first and third quarters are reported to the SEC. In the United States, most funds have a fiscal year that ends either October 31 or December 31. Hedge funds do not report their holdings publicly but, depending on their jurisdiction of incorporation and prospectus, may be required to send audited financial statements to their investors. Investors who are unaware of the cash management problem will assume mistakenly that the fund manager has taken the decision to hold a large amount of cash, even though that holding is of a transitory nature only.
A different type of cash management problem faced by a fund manager is the holding of a certain amount of cash to meet redemption requests. This problem arises in all open-ended funds that have a high frequency of redemptions. Hedge funds have normally negotiated a notice period of 90 days prior to the calendar quarter-end, sometimes 45 days. This gives the manager sufficient time to liquidate positions after redemption requests are filed by investors. The cash drag created by a structure of quarterly redemptions will affect all investors and can be worse than in the case of open-ended funds if redemptions represent a large percentage of the hedge fund. In that scenario, the manager will sell positions throughout the quarter to raise cash to the level necessary to pay for the redemption. The period of time for which the cash is held can be up to three months, and all investors will suffer a cash drag in that quarter. For small redemptions, this effect will be negligible, but it can become material for sizable redemptions. In an open-ended fund, in contrast, redemptions occur much more rapidly, and managers have tools (to be described) to minimize the impact of cash holdings on performance. Hedge funds justify the lengthy notice periods for redemptions with illiquidity of investments; this is not a valid reason for merger arbitrage funds, which invest mostly in equity securities that are highly liquid or in derivatives positions that also can be closed easily. It is difficult to understand why merger arbitrage investors are willing to accept 90-day notice periods for merger arbitrage hedge funds despite the high liquidity of the underlying instruments.
A commercial solution has been developed to help open-ended mutual funds minimize cash holdings to meet redemption requests. ReFlow Management Co. of San Francisco will acquire the shares redeemed by investors for up to 30 days and thereby smooth the fluctuation in cash requirements. For the duration of its holding period, ReFlow assumes the full market risk of owning the fund's shares. A fund participating in ReFlow's program benefits in several ways: Overall cash balances can be lower than if the fund were to hold a large cushion against redemptions, and the costs related to selling and buying shares in the fund's investments are eliminated. In addition, the adverse tax effects of realizing gains merely to satisfy redemption requests are avoided. The fund can redeem ReFlow's shares later when cash becomes available through investments, or liquidate investments in a more orderly manner. The key requirement is that under an SEC no-action letter, ReFlow's investment must be redeemed within 30 days. Because ReFlow owns shares in the fund that are not senior to other investors, it is not considered to own senior securities, which would be prohibited under the Investment Company Act. Redemption in kind for ReFlow's shares is also available for funds that seek to avoid triggering tax events.
ReFlow's service does not come for free. Its capital is allocated through an auction mechanism. Funds looking to access ReFlow's funds submit a bid of at least 0.25 percent of the amount requested. ReFlow will fill all requests for fund above the minimum winning bid in a Dutch auction. ReFlow's service has also become available to European funds registered in Luxemburg.
To date, the most sophisticated approach to handle the cash management problem analytically has been developed by Juliana Nascimento and Warren Powell of the Department of Operations Research and Financial Engineering at Princeton University7 in response to an inquiry by this author whether the newsvendor inventory solution can be applied to the mutual fund cash problem. The newsvendor formula is used widely for optimizing inventory when demand is stochastic and there are costs of holding excess inventory.
For a mutual fund, the cash level Rt at time t after new investments, Dti, must be sufficient to cover redemptions Dtl + Dts, which are large and small redemptions. The incidence of large redemptions will have a more dramatic impact on costs than smaller redemptions, so that they should be modeled independently. When the cash holdings after new investments are insufficient to meet redemptions, Rt< Dtl+ Dts, the fund incurs a cost of shortfall, ![]() in liquidating its holdings. A financing cost Ptf will accrue for large amounts of redemptions where positions cannot be liquidated immediately. Whenever the fund holds too much cash, it incurs an opportunity cost in the form of the rate of return on the portfolio, Ptr.
in liquidating its holdings. A financing cost Ptf will accrue for large amounts of redemptions where positions cannot be liquidated immediately. Whenever the fund holds too much cash, it incurs an opportunity cost in the form of the rate of return on the portfolio, Ptr.
The cash management decision xt that must be taken by the fund manager in each period t is the move xt1 from the portfolio into cash and xt2 from cash back into investments: xt =(xt1, xt2). The transaction cost is ![]() (xt1 + xt2). After the decision xt has been taken, the cash level is Rtx.
(xt1 + xt2). After the decision xt has been taken, the cash level is Rtx.
The cost for one period is given by
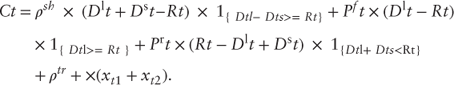
The problem is to minimize this cost.
The variable are combined into a state of the system before and after the decision xt taken at time t:
St = (Wt, Rt) and Stx = (Wt, Rtx), respectively, 14.7
where
| represents the exogenous inputs known at time t. |
The key to dynamic programming is the definition of a Bellman equation. It represents the problem that is to be optimized, coupled with one or several constraints. In the mutual fund cash problem, the Bellman equation is a recursive value function V such that
The problem can be solved through a piecewise-linear optimization using Approximate Dynamic Programming (ADP). Nascimento and Powell use an algorithm SPAR-Mutual, shown in the box, and prove that this algorithm converges. The algorithm breaks the value function into piecewise linear functions ![]() , …,
, …, ![]() that approximate the concave shape of the actual value function. The algorithm determines the slopes of those pieces that are close to optimal cash levels, thereby reducing computational effort.
that approximate the concave shape of the actual value function. The algorithm determines the slopes of those pieces that are close to optimal cash levels, thereby reducing computational effort.
At the beginning of time period t, the algorithm creates a Monte Carlo sample of all the variables in Wt, projecting these values forward over n periods until time N. Temporary approximations of the slopes are calculated in the vector ![]() is a stepsize rule that is state dependent.
is a stepsize rule that is state dependent.
Nascimento and Powell use data to examine the performance of the algorithm based on data from the Center for Research in Security Prices (CRSP) at the University of Chicago Booth School of Business and redemption information from Investment Company Institute for the period from July 2005 until June 2006 for 4,623 stock funds. Further implementation of the algorithm with more granular investment and redemption data is expected to be conducted in the future.
Risk Management
A centerpiece of modern finance is the concept that risk can be calculated and analyzed. The principal parameters that drive the theory of financial risk are standard deviation (volatility) and correlation. In Chapter 4, some of the shortcomings of these measures were discussed when dealing with merger arbitrage and other event-driven strategies. For the measurement and management of the risk of a merger arbitrage portfolio, the metrics used by traditional risk managers are not very useful.
The reason for the inadequacy of financial risk measures based on modern portfolio theory lies in the noncorrelated nature of the risks inherent in merger arbitrage. Most investment strategies rely in one way or another on the dynamics of stocks relative to the overall market. For example, a long/short equity portfolio might hold long positions in stock with high valuations and short positions in stocks with lower valuations. In the short run, it can be expected that these stocks will exhibit similar dynamics relative to the overall market as they have historically. In this case, financial risk management can rely on the plethora of statistical risk measures that have been developed.
For merger arbitrage, the situation is different in that it is known that the dynamics of a stock's behavior have changed at the time of the announcement of a merger. It is not reasonable to assume that it will behave in the near future similarly as it has historically. It was illustrated earlier with Figures 4.2(a) and (b) how the dynamics of stocks change after a merger. Therefore, value at risk, shortfall, and similar risk management techniques do not provide meaningful results for merger arbitrage portfolios.
Merger arbitrageurs are well aware of these restrictions and rely on other methodologies that will appear antiquated to risk managers used to sophisticated statistical techniques. Most arbitrageurs use variations of classic position limits to manage their risk.
In its simplest incarnation, a position limit is a simple cap on the size of any single merger in a portfolio. For example, an arbitrageur may decide not to hold more than 5 percent of the portfolio in a single arbitrage position. Limits can be hard or soft. A hard limit is not exceeded under any circumstance. A soft limit can be exceeded if the arbitrageur has a particularly strong opinion about the likelihood of success of a merger.
A corollary of limiting the percentage of a portfolio that can be invested in a single arbitrage deal is to target the number of transactions in which the arbitrageur invests. There are two types of arbitrageurs, as discussed in Chapter 3: concentrated and diversified. Concentrated arbitrageurs seek to limit the number of transactions in which they invest and seek to minimize the incidence of collapsing deals that generate a loss through extremely deep and thorough analysis. Diversified arbitrageurs try to limit the impact of the inevitable deal failure by spreading the risk over a larger number of transactions. A survey of the risk management practices of risk arbitrageurs8 reveals that the average number of positions held by the 21 arbitrageurs who responded to the questionnaire was 36, with a minimum of 25 and a maximum of 40.
A slightly more sophisticated version of position limits considers the downside risk of a position and limits that to a percentage of the portfolio. The arbitrageur will estimate the severity of each position, as described in Chapter 4, and define a percentage of the portfolio that the aggregate severity (long and short) of any position cannot exceed.
Additional methods for limiting exposure can be set for the types of transactions that an arbitrageur can invest in. For example, arbitrageurs may want to limit their exposure to any individual industry or sector. This is easier said than done, because mergers often occur in waves in certain industries. As a result, deal flow is biased toward the industries undergoing consolidation. An arbitrageur with strong industry limits may have to forgo arbitrages with high risk-adjusted returns. Therefore, sector limits in arbitrage strategies are not comparable to the use of these limits in stock picking or asset allocation strategies, and their effectiveness is less apparent in controlling risk.
Another type of position limit looks at the structure of the transaction. Arbitrageurs may want to restrict the proportion of leveraged buyouts (LBOs) in their portfolio because these transactions have a higher risk due to the purely financial interest of the buyer. In a strategic transaction, a buyer still may proceed with an acquisition even if the financial circumstances change, because the primary reason for the transaction is a strategic fit of the two firms. In contrast, an LBO relies exclusively on financial considerations to be successful.
Similarly, some hedge funds are constrained by implicit position limits on the payment type in a merger. Some hedge funds promise their investors in their offering materials to sell short at least a certain percentage of their portfolio. Many investors believe erroneously that the short positions will protect the arbitrage portfolio from market movements. As a result, they must invest at least that percentage in stock-for-stock transactions. Such a restriction can become as problematic as limits on industries or sectors. At a time when corporations have large amounts of cash available, more cash transactions are likely to be done than stock-for-stock mergers. Arbitrageurs who are subject to a minimum short sale requirement then will all chase after the limited number of stock-for-stock mergers, thereby driving down spreads and annual returns of these transactions.
Besides, as discussed earlier, the belief that the short position in a stock-for-stock merger protects against market movements is misguided. More precisely, the short position is irrelevant to protecting against market risk. This belief has its origin in standard long/short equity strategies, where it is applicable. The idea is that if the market falls and the transaction is canceled, then both the long and the short leg of the arbitrage will trade at lower levels, so the gain on the short side will offset the loss of the long leg. However, this is not necessarily the case for merger arbitrage investments, because market risk is at best a second-order effect. The principal risk remains event risk—the collapse of the merger. In a long/short position, the cancellation of a merger can lead to significantly higher losses than the termination of an otherwise identical cash deal. First, the long side loses value, and, second, the arbitrageur experiences a short squeeze on the short leg. Therefore, the assumption that losses on the long leg will be offset by gains on the short leg is incorrect.
A more quantitative approach to risk management for event-driven investment strategies was introduced recently by Philippe Jorion.9 He relies on correlations between events to compute a value at risk. The approach is modeled after credit default analysis pioneered by Moody's Investor Services in the analysis of collateralized debt obligations. It allows for the use of structural models to determine probabilities of deal failure. It also helps to determine the number of transactions (diversification) needed in an arbitrage portfolio to achieve a certain risk level. Another way of looking at dollar risk is to consider it economic capital needed for survival, which conversely determines the leverage that can be employed by the arbitrageur.
The author believes that the use of correlations is an inadequate approach to determine economic capital, whether for collateralized debt obligations or merger arbitrage portfolios. Economic capital should be set so that the portfolio can withstand a stress scenario. This is the traditional approach used by insurance companies. As recent events have shown, the traditional approach has been more successful than the more modern methodologies used in the evaluation of credit risk. Financial risk managers should familiarize themselves with actuarial techniques. Historical correlations are average values that are of no use in the estimation of stress cases. A better approach in the determination of economic capital is the computation of a distribution of outcomes for the portfolio, either through trees or through Monte Carlo projections. Economic capital should be set so that the portfolio can withstand one of the worst outcomes of this simulation. As in credit, seasoning effects do play some role in the risk assessment of merger arbitrage. This timing dimension is missing from Jorion's approach but can easily be implemented in such a simulation.
Mitchell and Pulvino (see Chapter 3) pointed to the poor performance of merger arbitrage in sharply declining markets. One strategy to mitigate losses that can arise in a sharply declining market is to buy out of the money index put options. Most of the time they will expire worthless, and the arbitrageur will lose the option premium. When there is a decline in the market, these options will be in the money and can at least partially offset the losses suffered from collapsing deals. A portfolio following this strategy will have a slightly lower return in most market conditions due to the cost of acquiring options that expire worthless. However, the benefit is a sharply improved risk profile. In addition to minimizing option premiums by selecting out of the money strike prices other option strategies can be implemented such as barrier options or various types of spreads.
Managing downside risk with equity put options may be insufficient, because this method overhedges most of the time but underhedges when the hedge is most needed. An approach to hedging based on finite mixture models has been developed by Adam Tashman.10 Finite mixture models combine two return distributions from two different states: when the market is in a regular state or in a sell-off state. These two distributions are combined to calculate a hedge ratio that is more accurate than one based solely on linear regression of returns. This approach is similar to hedging through regime switching models.
Merger Arbitrage Indices
Several firms have built indices that seek to replicate mechanically a merger arbitrage portfolio in a way similar to a traditional stock index. The two main providers are IQ Index and Standard & Poors. Both have the major weakness that they do not represent stock-for-stock mergers appropriately.
As part of its efforts to introduce specialty indices, Standard & Poor's developed a series of arbitrage indices, including a long-only merger arbitrage index that began to be calculated in 2008. Data were backfilled to December 31, 2005, where the index value is set to 1,000.
The index contains up to 40 stocks from any developed market11 that are in the process of being acquired. Each company has an index weighting of 2.5 percent at the time it is included, or less if the index contains insufficient cash (more on the indices cash component later). Only companies with an equity of more than $500 million are included if the premium at the time of the announcement is at least 5 percent. Both cash and mixed cash/stock deals are included, but pure stock-for-stock deals are not. For mixed cash/stock deals, the cash component must represent at least 25 percent of the value.
A company is included in the index for one year at the most. If the deal has not closed after one year, the company is removed. A company is also removed once a merger is completed. Similarly, it is removed from the index if the merger is canceled.
No more than 40 companies are in the index at any time. If there are more than 40 eligible merger candidates available, then the company that has the lowest return since entering the index will be replaced by another target. The 2.5 percent weighting of each constituent firm will fluctuate over time with the change in its market value. Therefore, a company can exit the index with a weighting of less than 2.5 percent if its price dropped during the time it was in the index. Its replacement then will be added at that lower weighting. This mimics the management of an actual portfolio. An arbitrageur can put to work only that capital that has been received from the sale of an existing position.
If there are fewer than 40 eligible companies, the index will contain a cash component, because the weighting of each firm is limited to 2.5 percent at the time of inclusion. Interest on that cash balance accrues daily based on U.S. dollar LIBOR. Dividends are added to the cash position on the ex-date. However, the tax treatment of these dividends is assumed to be punitive: It reflects the rates paid by a nonresident institutional investor based in Luxembourg who does not benefit from a double-taxation treaty.
In a similar business model, Index IQ has also developed a number of passive specialty indices that seek to implement hedge fund strategies as varied as market neutral, global macro, and fixed-income arbitrage. Its merger arbitrage index consists of target companies in developed markets that are eligible for inclusion based on their trading prices. The portfolio is rebalanced monthly, when new constituents are included. To determine eligibility, a pseudo-probability is calculated:
where
Several conditions determine whether a target company is included in the index at the monthly rebalancing.
Based on the probability calculated for each transaction with Equation 14.9 a transaction will fall into one of six scenarios listed in Table 14.5. Stocks in scenarios 5 and 6 are not included in the index. Those included based on scenarios 1, 3, and 4 will stay in the index for 180 days or the closing of the merger, whichever occurs first. Stocks included based on scenario 2 can stay in the index for 360 days, or until the closing of the merger if that occurs first.
Table 14.5 Index Scenario Probabilities
| Scenario # | Scenario | Probability Scenario Calculation |
| 1 | Probability less than zero | |
| 2 | Probability between zero and 100 | |
| 3 | Probability greater than 100 | |
| 4 | Probability greater than 100 | |
| 5 | Probability between zero and 100 | |
| 6 | Probability less than zero |
Stocks that are included are then weighted by their seven-day median dollar trading volume on the long side, and various short ETFs weighted so that they replicate the short component of the acquirers in stock-for-stock mergers. The attempt to replicate the short side of stock-for-stock mergers is a crucial point of distinction of this index to that provided by S&P.
The base value of the index, 1,000, was set on October 31, 2007.
Figure 14.4 shows the performance of the two merger arbitrage indices just discussed from their inception in through November 2014 compared to the S&P 500 index and bonds. Table 14.6 shows a number of key statistics for the index over the same period. It can be seen that these passive indices exhibit similar properties as the merger arbitrage hedge fund indices discussed in Chapter 3: The median return is comparable to that of the S&P 500 index, whereas volatility is more akin to that of bonds. The period from 2004 through late 2008 was characterized by an expansive and, as some would argue inflationary, monetary policy that favored stocks over all other investment strategies. Over longer periods of time, the S&P 500 index should perform more like the IQ Index and S&P Merger Arbitrage Indices, although the volatility of the latter will be closer to that of bonds. This is consistent with the experience of merger arbitrage funds discussed in Chapter 3. It can also be seen that the long-only S&P Merger Arbitrage Index exhibits a higher volatility than that of IQ Index. Most likely, this effect is related to the inclusion of short biased ETFs in the index calculated by IQ Index.

Figure 14.4 Performance of the IQ Index and S&P Merger Arbitrage Indices Relative to Other Asset Classes
Table 14.6 Statistics of Monthly Returns of the IQ Index and S&P Merger Arbitrage Indices
| Standard & Poors Merger Arbitrage Index | IQ Index Merger Arbitrage Index | Lehman Aggregate Bond Index | Standard & Poors S&P 500 Index | |
| Observations | 113 | 92 | 113 | 113 |
| NAs | 0 | 22 | 0 | 0 |
| Minimum–0.0697 | –0.0731 | –0.0236 | –0.1679 | |
| Quartile 1 | –0.0037 | –0.0061 | –0.0017 | –0.0158 |
| Median | 0.0035 | 0.0040 | 0.0034 | 0.0134 |
| Arithmetic Mean | 0.0036 | 0.0022 | 0.0039 | 0.0070 |
| Geometric Mean | 0.0034 | 0.0020 | 0.0039 | 0.0060 |
| Quartile 3 | 0.0110 | 0.0142 | 0.0104 | 0.0329 |
| Maximum | 0.0424 | 0.0689 | 0.0373 | 0.1093 |
| SE Mean | 0.0016 | 0.0021 | 0.0009 | 0.0041 |
| LCL Mean (0.95) | 0.0005 | –0.0020 | 0.0021 | –0.0011 |
| UCL Mean (0.95) | 0.0066 | 0.0065 | 0.0057 | 0.0151 |
| Variance | 0.0003 | 0.0004 | 0.0001 | 0.0019 |
| Stdev | 0.0165 | 0.0205 | 0.0095 | 0.0435 |
| Skewness | –0.5705 | –0.7420 | 0.1644 | –0.8440 |
| Kurtosis | 3.0716 | 3.0874 | 1.1906 | 1.8291 |
Figure 14.5 shows the risk/return relationship among the S&P Merger Arbitrage Index, stocks, and bonds. Table 14.7 shows the downside risk. Readers should refer to the explanation of this graph and table in Chapter 3.

Figure 14.5 Risk/Return Trade-off for the S&P Merger Arbitrage Index Since Its Inception
Table 14.7 Various Downside Risk Measures
| Standard & Poors Merger Arbitrage Index | IQ Index Merger Arbitrage Index | Lehman Aggregate Bond Index | Standard & Poors S&P 500 Index | |
| Semi Deviation | 0.0121 | 0.0157 | 0.0066 | 0.0337 |
| Gain Deviation | 0.0109 | 0.0119 | 0.0068 | 0.0236 |
| Loss Deviation | 0.0130 | 0.0173 | 0.0055 | 0.0349 |
| Downside Deviation (MAR=10%) | 0.0146 | 0.0187 | 0.0094 | 0.0344 |
| Downside Deviation (rf=0%) | 0.0105 | 0.0147 | 0.0047 | 0.0306 |
| Maximum Drawdown | –0.1321 | –0.2111 | –0.0383 | –0.5095 |
| Historical VaR (95%) | –0.0242 | –0.0330 | –0.0108 | –0.0750 |
| Historical ES (95%) | –0.0368 | –0.0522 | –0.0161 | –0.1020 |
| Modified VaR (95%) | –0.0250 | –0.0341 | –0.0110 | –0.0723 |
| Modified ES (95%) | –0.0443 | –0.0589 | –0.0157 | –0.1114 |
Separate Accounts
Some merger arbitrage managers offer their clients the management of separate accounts in the strategy. There are a number of advantages to separate accounts over pooled investment vehicles such as hedge funds or mutual funds. The account is held in the name of the client, and all securities are in the name of the client. The manager simply has investment authority with respect to the account. Holders of separate accounts receive statements that show all the holdings in their account. For some institutional investors, notably insurance companies, there are restrictions on their ability to invest in pooled vehicles. It is easier for them to ask an arbitrageur to manage a separate account than to allocate assets to a pooled fund. In fact, variable annuities and other life insurance wrappers of hedge fund strategies need to be established as separate accounts. In the United States, tax reporting can be simplified in certain circumstances because the investor will receive a tax Form 1099 rather than a Schedule K-1. Hedge funds in particular are notorious for sending out their tax information late, requiring their investors to file extensions and potentially incur penalties for underpayment. In fact, for some investors, individualized tax management is one of the biggest advantages of separate accounts. Whether an arbitrage manager should get involved with optimizing taxes for clients is a different question.
For a manager, it is more complicated to manage separate accounts than a pooled vehicle. Managing a plethora of separate accounts requires additional effort compared to a pooled vehicle that is managed in a single account. Most providers of separate account platforms are now offering tools to streamline order placement and integrate seamlessly with the manager's order management systems. Nevertheless, when a new account is opened or an existing account is closed, there is a significant effort in establishing the initial position or liquidating the holdings. In a pooled vehicle, additions or withdrawals of capital are simply one element of the overall cash management.
Some separate accounts established outside of the United States allow investors to obtain leverage substantially in excess of what is allowed under domestic regulations. As a low-volatility strategy, merger arbitrage is well suited for such leverage.
More importantly, the investment ideas of arbitrageurs are proprietary information that they do not want to share with others. If clients access their account and see the deals in which the arbitrageur has invested, information about the positions can leak into the market and potentially can lead to problems such as front running or a squeeze in the lending market for short positions. For this reason, many arbitrage managers prefer to offer their clients only pooled vehicles.
Finally, managing separate accounts adds an additional layer of administrative and compliance burden to the manager's business.
Hedge Funds and Liquid Alternatives
The arbitrage community was a close-knit community of investment houses until the emergence of hedge funds and mutual funds that invest in merger arbitrage. Suddenly, what had been an exclusive niche became available to a much wider group of investors.
Hedge funds and mutual funds are both structured to pool the assets of their investors. Their difference is more one of aura than substance. In fact, hedge funds are modeled after mutual funds: In the United States, a fund is a standalone entity that enters into a management agreement with an investment adviser.12 This is different from other jurisdictions, where funds tend to be sponsored by their adviser and are not independent entities. The principal difference between the structures is one of regulation. Hedge funds are unregulated partnerships that can be made available only to clients who meet qualification requirement in terms income and wealth. At the time of writing, in the United States an annual income of $200,000 (or $300,000 if filing jointly) or a net worth of $1 million are required. These amounts are not indexed to inflation. Therefore, the percentage of households that can invest in hedge funds increases steadily.13 Hedge funds are not required to make regulatory filings or report to their investors. However, the initial offering document must contain information that is equivalent to what would be contained in a mutual fund prospectus.14 This lack of transparency can be an advantage for a fund manager because the fund's investments can be kept confidential. Nevertheless, in the case of a U.S. manager, if the manager has more than $100 million under management, it is required to file a 13-F holdings report quarterly. The public can get an idea from these holdings reports which securities are held by hedge funds, despite the aura of secrecy. Even offshore funds that are managed by U.S. managers will have their holdings revealed through this mechanism. The absence of transparency is also a problem for investors, because it complicates their oversight of the manager to whom they have entrusted their assets.
Mutual funds do not have the transparency problem. They report their holdings on a quarterly basis and offer several other advantages over hedge funds:
- Lower fees. Typical mutual fund expense ratios are between 1.5 and 2 percent, whereas hedge funds charge 2 percent plus a part of the profits as a performance fee in addition to operating expenses.15 A performance fee also can be levied by U.S. mutual funds, but it must be symmetric. For example, if the manager of a U.S. mutual fund were to receive 20 percent of the gains, then the fund would have to be reimbursed for 20 percent of the losses. For hedge funds, however, the performance fee is asymmetric and applies only to gains. Losses are entirely paid out of the investors' assets. In the case of international mutual funds, in particular UCITS funds, hedge-fund style performance fees are allowed and indeed are levied by most managers of these vehicles. Both symmetric and asymmetric performance fees have their advantages and problems. Proponents of performance fees argue that they align the interest of the investor and the manager and are a strong incentive to attract the best managers. An asymmetric performance fee is always more attractive for the manager but creates problems for the investor: Many managers simply close their funds after losses and start new ones so that they can charge performance fees on any rebound. A symmetric performance fee risks bankrupting the manager under extreme market conditions. Therefore, mutual funds that have performance fees limit them in order to avoid reimbursement of potentially devastating amounts. If the incentive argument is true, then a limited symmetric performance fee is inferior to an asymmetric one. The principal problem with asymmetric performance fees in vehicles that have little to no transparency is that investors cannot control whether the manager takes unreasonable risks in order to maximize earnings.
- Performance reporting. Mutual funds report daily net asset values, whereas hedge funds report their performance only monthly.16 This is another aspect of insufficient transparency of hedge funds. For UCITS funds the reporting periodicity varies although most funds choose daily performance reporting.
- Liquidity. Mutual funds allow their investors to redeem on a daily basis. Hedge funds have created complicated withdrawal schedules, under which investors can redeem their shares only quarterly with at least 90 days' notice. If more than a certain percentage of investors seek to redeem in the same quarter, some funds will prevent all others from redeeming in the same quarter. These provisions were introduced originally because many hedge funds use illiquid instruments that can be difficult to unwind. It is hard to see why these provisions should apply to merger arbitrage funds, however, since these funds are invested in liquid publicly traded securities. Some mutual funds have been introduced with periodic liquidity—for example, weekly instead of daily liquidity. However, such structures remain exceptions.
- Lower minimum investments. Mutual funds can be invested in with small amounts, generally a few thousand dollars. Hedge funds have higher minimum investments that are sometimes in the millions of dollars.
- Tax reporting. Tax transparency and reporting varies substantially. Some offshore funds are said to provide next to no tax transparence as to income, capital gains, and unrealized appreciation. U.S. mutual funds furnish their investors with a Form 1099, and most non-U.S. funds have equivalent tax transparency, whereas hedge funds are partnerships that report on a Schedule K-1. The latter complicates tax reporting for their investors. Both entities are pass-through vehicles, whose gains are taxable only on the level of the investor, not on the level of the fund.
- Custody. Mutual funds are required to place their assets with a bank custodian, whereas hedge funds typically hold their assets with a prime broker. The prime broker uses the fund's securities as collateral for margin borrowing. The drawback of this method is that the fund is fully exposed to the well-being of the prime broker. If the prime broker fails, the funds become a credit and may not get their assets back for a long time, and then only at a rate of cents for the dollar. Some hedge funds discovered this problem painfully in the bankruptcy of Lehman Brothers, which acted as prime broker for many funds.
- With more mutual funds adopting hedge fund strategies, the question of holding collateral with prime brokers is become increasingly relevant. Even when a fund holds its asset in a segregated account with a custodian, it still needs to post collateral with a broker for short selling, option activity, or leveraged transactions. Tri-party agreements between a broker, custodian, and fund provide a way to segregate assets from the broker's balance sheet and hold them in an individually identifiable manner in a segregated custodial account. However, even with this structure the fund retains residual exposure to the broker's balance sheet. At the time of writing, the SEC has taken a particular interest in the United States as to the monitoring and implementation of collateral management to eliminate unneeded excess collateral.
One of the biggest misconceptions about mutual funds is their alleged inability to invest in strategies that are the bread-and-butter business of hedge funds. Many commentators claim falsely that mutual funds cannot use leverage or derivatives and sell short. Today, a number of mutual funds are available that use hedge fund strategies, including merger arbitrage, and engage regularly in short selling, leverage, and the use of derivatives.
The use of short selling was banned for mutual funds for a long time. To this day, the Investment Company Act of 1940 (commonly called the 1940 Act) states that
It shall be unlawful for any registered investment company, in contravention of such rules and regulations or orders as the Commission may prescribe as necessary or appropriate in the public interest or for the protection of investors:
[…]
3. to effect a short sale of any security, except in connection with an underwriting in which such registered company is a participant.
Section 12(a) of the Investment Company Act of 1940
The SEC clarified this provision in 1972 in an interpretive release17 and stated that despite the wording of the statute, it was the intention of Congress not to limit shorting per se but to prevent the use of short proceeds as equity for further leveraged transactions. Under the current interpretation of the law, short sales are allowed as long as the shares that have been shorted are delivered to the buyer and the mutual fund has segregated sufficient funds to cover the purchase the shorted assets. The requirement to deliver shares forces a fund to short only shares that can be borrowed and prevents naked short selling. The intent of this rule is to limit the ability of funds to leverage through the proceeds of short sales. Similar rules apply for written options and futures contracts. Nevertheless, the urban myth that mutual funds cannot short continues to make the rounds.
Similarly, U.S. mutual funds can use leverage, albeit not in the form typically used by hedge funds. Leverage is not limited explicitly by U.S. regulations, although there are indirect restrictions through the requirement to have sufficient liquid assets on hand to honor contractual obligations. Effectively, this means that option writing is somewhat restricted, while long option positions do not create contingent obligations that would be restricted and hence can be used to lever. In contrast, in UCITS funds there is an explicit restriction on leverage.
Margin borrowing is a common method for hedge funds to increase their buying and shorting capacity, and it is limited only by the prime brokers' willingness to extend credit. U.S. mutual funds are precluded from using margin borrowing. Instead, they have to use bank lending within strict limitations: The fund must maintain an asset coverage of 300 percent after borrowing. This means that the fund can borrow up to 50 percent of its preborrowing assets from banks. These strict limits on borrowing were imposed because funds also have the ability to leverage through the use of derivatives. The restrictions prevent the excessive use of leverage on top of leverage.
Overall, there are few restrictions on mutual funds to implement strategies such as merger arbitrage that are typically found in hedge funds. Relatively few mutual funds have chosen to implement these strategies. This has more to do with the eagerness of financial intermediaries to sell hedge funds, whose richer management fees allow for higher compensation of the intermediary, than with actual restrictions on the ability of funds to engage in arbitrage strategies.
