Chapter 3
The Role of Merger Arbitrage in a Diversified Portfolio
Portfolio theory reduces investments to two dimensions: risk and return. Both variables are forward looking and hence difficult to assess without perfect foresight. Therefore, analysis relies on historical relationships that are extrapolated to the future. It is assumed, or rather hoped, that the historical relationships will also hold in the future. This may or may not be the case.
Risk is a variable that is particularly difficult to define. The most common substitute for risk is price volatility. An asset's historical price fluctuations are observed, and it is assumed that these historical fluctuations incorporate all the risks that stockholders faced in the past. This historical volatility is then used in forward-looking analysis, and it is assumed that any risks that this stock faces have already occurred in the past and hence are incorporated in the historical volatility. The length of time over which historical volatility is calculated is the most important determinant of whether there is any validity to this approach. It clearly makes no sense to produce 10-year forecasts based on historical volatilities observed over only one or two years.
More fundamentally, it is a strong assumption that all risks inherent in a stock have already manifested themselves in the past. The economy evolves constantly and markets are in flux; assuming that future fluctuations will somehow resemble those of the past is not obvious. However, it is the only practical approach that can be taken when forecasts are made.
An improvement over a static forecast can be achieved through the use of GARCH models. In these models, volatility is autocorrelated. These models are better at replicating some of basic observations about volatility, notably that volatility occurs in clusters and is mean reverting. Volatility clusters are periods in which markets are highly volatile for longer periods of time or exhibit low volatility for long periods of time.1 In the words of B. Mandelbrot, “Large changes tend to be followed by large changes, of either sign, and small changes tend to be followed by small changes.”2
In the long run, however, volatility tends to revert to a mean value.
Other than volatility, another statistical term that plays an important role in the construction of portfolios is correlation. It is just as important as return and risk. Even though the risk/return trade-off has become a household term, correlation somehow has been left out. The popular business press does not refer to risk/return/correlation trade-offs.
Correlation describes the comovement of two different assets and can range from ![]() to
to ![]() . A perfect correlation of
. A perfect correlation of ![]() means that prices of the assets move exactly in parallel, whereas
means that prices of the assets move exactly in parallel, whereas ![]() means that they move exactly in the opposite direction. When building financial portfolios, it is best to have assets that have no correlation at all.
means that they move exactly in the opposite direction. When building financial portfolios, it is best to have assets that have no correlation at all.
Volatility of Stocks Going through a Merger
Once a merger is announced, the volatility of a stock declines markedly. Figure 3.1 shows the stock prices of Autonomy Corporation before and after the announcement of its cash merger. It can be seen that price fluctuations following the announcement of the merger are much smaller than before. Figure 3.1 shows daily price changes of Autonomy Corporation, a U.K.-based infrastructure software firm, that was acquired by Hewlett-Packard Co in 2011. This merger was discussed in more detail in Chapter 2. It is clear from the picture that daily price variations are much smaller following the announcement of the merger on August 11, 2011, than prior to that date.

Figure 3.1 Daily Price Changes (in pence) of Autonomy Corporation before and after the Merger Announcement
Daily total returns differ from daily stock price returns in that they incorporate dividends. For dividend paying stocks, price return will be negative on the ex-date of a dividend, even though the investor receives a separate cash flow from the dividend payment. Therefore, total returns are the appropriate measure that will be used for the remainder of this book.
To demonstrate that this is not just an effect in isolated cases, pre- and post-announcement volatilities of 258 mergers were analyzed. The data set consists of 258 cash mergers for the period of March 31, 2010, until March 31, 2014, retrieved from the Bloomberg database. Total returns for these stocks were retrieved also from Bloomberg. The calculation for premerger volatilities and returns starts 60 trading days before the announcement, and post-merger returns and volatilities are calculated from the day following the announcement for 60 days or until completion, whichever came first. The histogram in Figure 3.2 shows the resulting cross-sectional distribution of returns. The height of the bars in these histograms shows the number of stocks whose returns fell within a given range. The distribution of dark bars is that of pre-announcement returns, that of light bars of the returns post-announcement.

Figure 3.2 Cross-sectional Distribution of Daily Returns (a) before and (b) after the Announcement of a Merger
It can be seen that the distribution of returns is spread out before the announcement but collapses to a much narrower shape once a merger has been announced. Pre-announcement stock returns span a wide range, whereas post-announcement stock returns fall into a very narrow range. A similar phenomenon can be observed for volatilities. This means that daily fluctuations in the prices of stocks going through a merger are much lower once a merger has been announced than the fluctuations of stocks that are not subject to a merger. This effect is even more visible when the variance of returns is plotted, as in Figure 3.3. All volatilities and returns are annualized for comparability.3

Figure 3.3 Variance of Daily Returns (a) before and (b) after the Announcement of a Merger
There are several implications of these observations.
Evaluating stocks going through a merger on the basis of their historical volatility and return characteristics will lead to incorrect conclusions. Many asset managers use value-at-risk (VAR) methodologies in their risk assessments. These methodologies will yield incorrect results for stocks going through a merger. After the announcement of a merger, a VAR system will look back at the recent much higher volatility and extrapolate this into the immediate future. However, actual price fluctuations are much smaller for merger stocks than before the announcement, so that the VAR is overestimated. As the merger seasons, a more dangerous error enters into VAR: The algorithm will look back at recent volatility and project a low volatility into the near future. As Table 5.2 will show, the average time until a merger collapses is about 128 days, or more than four months. Therefore, a VAR methodology will underestimate the price risk of a merger stock. This is even more so if the VAR algorithm is based on the RiskMetrics methodology, which uses exponentially declining moving averages. The VAR will decline soon after the merger announcement and will remain low even as the deal approaches the time of the average deal collapse.
Another implication is that combining stocks that are going through a merger into a portfolio should produce an overall volatility that is significantly lower compared to that of a portfolio of nonmerger stocks for which no merger has been announced. A portfolio of stocks going through a merger is no longer a portfolio of stocks but a portfolio of merger spreads. The characteristics of that portfolio are hence those of merger spreads. Although the analysis for Figure 3.2(a) and (b) was based on cash mergers, the same qualitative observation is also true for stock-for-stock mergers or mixed stock/cash mergers. The difference between these two types of mergers is primarily the degree to which any residual market volatility is contained in the spread.
It was shown in Chapter 2 that spreads in stock-for-stock mergers exhibit negative correlation to the market, all else being equal; refer to Table 2.2 in particular. Cash mergers should exhibit a positive, albeit small, correlation with the overall market. By combining cash and stock-for-stock mergers in a portfolio, arbitrageurs can create a net correlation that is almost zero. Unfortunately, all this theoretical elimination of all correlation is not achievable in practice, and most merger funds do have a small positive correlation with the overall stock market. However, the beta coefficient of merger arbitrage funds tends to be small and is of the magnitude of 0.5 to 0.6 for many funds.
Merger Arbitrage Universe
Corporate merger activity is sensitive to the macroeconomic environment, in particular the risk-taking environment and financial and liquidity conditions. One would expect that the size of the opportunity set will influence the returns that arbitrageurs can generate. In an environment with plenty of mergers, spreads should be wider as the capital available for merger arbitrage is spread of a larger number of opportunities. In a scenario where there is little merger activity, the same capital is spread over fewer mergers, and as a result merger spreads and returns achieved by arbitrageurs should be smaller.
Mergers and acquisitions appeared not long after the formation of the modern corporation. For example, the ill-fated East India Company is known to have merged with one of its competitors in the year 1708. Since the late nineteenth century, mergers and acquisitions have occurred in waves. Economic historians are still debating the reasons for this clustering. Reliable data about M&A activity are only available from the beginning of the 1990s, but the existence of prior M&A waves is well documented and supported by their side effects, most notably, bouts of legislative activity to tame what in each era was perceived as an excess.
For example, U.S. antitrust legislation arose out of a wave of mergers and acquisitions in the late nineteenth and early twentieth centuries that led to the formation of trusts. Similar business empires were built around the same time in Europe, too, where many of the creations of the period survive as major enterprises to this day. In the United States, antitrust legislation of the Sherman Act of 1890 and the Clayton Act of 1914 survives today and is evidence of successful M&A integration efforts.
The first wave lasted from the year 1893 to 1904 and consisted of horizontal integration for the formation of trusts. It ended with a Supreme Court decision of 1904 that made the Sherman Act applicable to mergers. It should be noted that the United Kingdom experienced a similar wave of merger activity at roughly the same time, the turn of the century.
The second wave in the years 1919 to 1929 was a continuation of the first wave and concentrated in particular on the automobile industry. It ended with the crash of 1929.
The third wave in the years 1955 to 1973 accompanied the conglomerate boom. It was hoped that the diversification across different business lines would increase the overall value of the conglomerate. It ended when it became apparent that this premise could not be realized, and conglomerate stocks crashed in the years 1969 and 1970. The legacy of this period is the basis of modern M&A legislation and jurisprudence. The U.K. Takeover Code and, by extension, many of its European and Asian copycat legislations as well as some key Delaware court decisions, have their origin in this period.
The fourth period lasted from 1984 through 1989, with the emergence of the corporate raider, junk bond financing, leveraged buyouts, and the establishment of hostile takeovers. Legislation and interpretation of the law took on a new level of complexity in light of these developments.
The fifth period lasted from the year 1993 to 2000 with a series of mega-mergers, including some unprecedented cross-border mergers of large iconic companies like Mannesmann / Vodafone or Chrysler / Daimler Benz. It ended with the stock market crash of the year 2000.
A sixth period lasted from the year 2003 through 2007 and was characterized by leveraged acquisitions through private equity partnerships. While the leveraged acquisition originally had been designed for hostile transactions, private equity buyers almost always take a friendly approach to acquisitions.
The seventh period began in the year 2010 and persists at the time of this writing (2015).
The evolution of merger and acquisition activity since the year 1895 can be seen in Figure 3.4. The seven waves of merger activity can be identified readily. Note that no single data source covers the entire period until today.

Figure 3.4 Number of Mergers and Waves of Merger Activity since the year 18954
Today it is not known whether arbitrageurs were active prior to the third wave. As discussed in Chapter 1, the earliest documented merger arbitrage trades from the 1960s fall into the third wave, and it can be assumed that by that time the strategy was well established.
Data on the dollar volume of mergers shows its high dependence on the level of the stock market. Figure 3.5 shows the volume of merger activity in dollar terms, as opposed to the number of mergers as in Figure 3.4. Comparing the two figures, it can be seen that peaks in the merger waves correspond to peaks in the stock market, and so do troughs. However, as high stock prices also increase the value of mergers, the merger waves are magnified when looked at through deal values as opposed to through the number of transactions.

Figure 3.5 Worldwide Volume of Mergers (in US$ trillions, left axis) and Level of the S&P 500 Price Index Since 1992 (right axis) Data: Factset Mergerstat
The composition of types of mergers available to arbitrageurs also varies over time, as illustrated by Figure 3.6. It can be seen that cash mergers represent the majority of all mergers, by equity value, announced over the period. Around the year 2000, during the Internet bubble when valuations were uncharacteristically high, stock was the preferred currency for acquisitions. Since the year 2005, cash and mixed cash and stock mergers have dominated the universe while stock-only mergers consistently represent less than one fifth of all transactions. The availability of stock-for-stock mergers will determine what fraction of an arbitrageur's portfolio will have a short component associated with it. As I discuss elsewhere, some investors misunderstand arbitrage portfolios because they look at them from the mindset of a market-neutral investor. In this view, arbitrage portfolios have substantial market exposure because they contain not enough short positions to offset the longs. Of course, this view completely mischaracterizes the risk/return profile of merger arbitrage portfolios. I have been criticized myself at times for not having shorted at a time when the best investment opportunities presented themselves in cash mergers and stock-for-stock mergers were relatively unappealing. Whenever the opportunity set that presents itself to arbitrageurs has few stock-for-stock mergers, one would expect the arbitrage portfolio to be more “long” than at times when stock is used at acquisition currency widely.

Figure 3.6 Percentage Cash and Stock Mergers over Time Data: Factset Mergerstat
It should be noted that the composition of the non-U.S. merger universe resembles that shown in Figure 3.6. The main difference lies in the period around the year 2000, where stock-for-stock mergers represented a much smaller percentage of mergers. Most likely this is due to the Internet bubble having taken on nowhere near the magnitude internationally that it did in the United States, and hence, the use of stock as an acquisition currency was not as widespread internationally.
Merger Arbitrage Spreads
When arbitrageurs talk about the spread on a deal, they refer to the expected or anticipated annualized spread. Because the closing date is not known with certainty and needs to be estimated, the resulting annualized number is also merely an estimate. In contrast, once a merger has closed, or failed, the completion date is known and can be used to calculate the spread that was realized. In the rare cases where the estimate matches the realized closing date the two spreads will be equal. A more detailed and technical discussion of the analytical problems that arise from this distinction is shown in Exhibit 3.1.

Figure 3.7 Average Annualized Merger Arbitrage Spread
The evolution of realized arbitrage spreads since the year 2000 is shown in Figure 3.7, and their distribution in the middle of each calendar year in Figure 3.8. Figure 3.7 shows the average spread that would have been realized had an investor put all capital in all cash mergers above $1 billion on that day. Figure 3.8 gives an overview of the distribution of spreads in the middle of each calendar year shown, again under the assumption that all capital had been invested at that date in each deal with an equity value of at least $1 billion.5 Readers should review the note about calculating spreads for historical time series before proceeding. Readers with experience in merger arbitrage spreads may doubt these numbers based on their experience unless they understand the methodology underlying their calculation.

Figure 3.8 Distribution of Merger Arbitrage Spreads (Annualized) in the Middle of Each Year
It can be seen that average spreads of merger arbitrage have fluctuated widely since the year 2000 but overall have been undergoing a downtrend. This compression of merger arbitrage spreads is reflected in returns generated by merger arbitrage hedge funds over time (see Figure 3.13).
In addition to the overall downtrend the dispersion of spreads at any given point of time is substantial. This is illustrated by the violin chart of mid-year spreads. The middle of the year is chosen for no particular reason other than it avoids potential year-end effects that might arise had 12/31 been selected as the date of reference. While a clear median can be identified, some outliers exist from mergers completing earlier than anticipated by market participants as well as from deal collapses, which leads to significant negative returns. Speaking of a typical merger arbitrage spread at any given time is not very meaningful. It is better to refer to ranges for different categories. For example, safe mergers are, at the time of writing, priced for annualized returns of 2 to 5 percent, whereas mergers with antitrust risk have annualized spreads of 8 to 10 percent. Mergers with political risk have annualized returns above 15 percent. Expressing spreads in this way accounts better for the underlying variability between spreads of different risk characteristics.
Observers blame various factors for the secular decline of the merger arbitrage spread.6 The most obvious ones are capacity constraints and transaction costs. As will be discussed in Chapter 5, transaction costs have declined sharply since the year 2000 as advances in communication technologies have reduced the cost of executing trades, and the replacement of market makers by high-frequency traders has reduced bid/offer spreads. This means that, all else equal, arbitrageurs can generate the same level of returns with tighter spreads. Capacity constraints refer to the number of arbitrageurs and the capital that they deploy in this strategy relative to the opportunities presented to them. Statistical evidence suggests that heightened arbitrage activity, measured through increase in trading volume following the announcement of a merger, coincides with the decline in spreads. This suggests that more and more arbitrageurs chase the same deals, thereby depressing profit opportunities. The sharp increase in capital invested in merger arbitrage is shown in Figure 3.12.
Another important factor is a reduction of risk in merger arbitrage over time. The severity of price declines for targets of failed mergers has lessened over time. This can be seen from Figure 4.11 which shows a modest decline in acquisition premia between the years 1995 and 2009. Since 2009, however, acquisition premia have been rising slightly, yet merger arbitrage spreads have continued their downtrend. Therefore, a reduction in risk may not be the primary driver of the secular decline in merger arbitrage spreads.
A more likely driver for the declining performance of merger arbitrage as a strategy is the fall of interest rates in the quarter century after 1990. Merger arbitrage resembles an investment in a short-dated zero coupon bond: The investor will obtain a slight premium to the invested capital with a high probability, but there exists a small probability of a very large loss of principal. With an average time to close of 128 days, merger arbitrage spreads should therefore behave similarly to short-term interest rates. When interest rates are at 10 percent, merger arbitrage should yield a premium above that rate. Similarly, when interest rates are near zero, as at the time of this writing, merger arbitrage should generate a return that is not much higher than zero.
Interest rates are made up of two components: a risk-free rate and a spread. While the risk-free interest rate is generally considered an indicator of the level of interest rates, the spread is assumed to be an indication of market participants' willingness to assume risks. The tighter the spread, the higher the willingness to assume risk. While these two numbers might be good indicators in an overall macroeconomic sense, the actual interest rate paid by market participants, and the discount rate used in investment decisions, are neither the risk-free rate nor a spread but the actual interest rate available to market participants.
The data confirm the validity of this argument. Correlation between the median merger arbitrage spread and various interest rates are shown in Table 3.1. The correlations are shown for both daily and monthly data. As is often the case, monthly data smooth short-term volatility and hence, give a more stable relationship. However, as most investors look at data daily, it can be misleading if monthly data series are used to draw conclusions about the merits or demerits of an investment strategy.
Table 3.1 Correlation of Merger Arbitrage Spreads to Different Interest Rates
| Interest Rate | Monthly Data | Daily Data |
| Barclays US Corporate High Yield (YTW) | 0.53 | 0.47 |
| Barclays VLI High Yield (YTW) | 0.52 | 0.44 |
| KDP High Yield Daily Yield | 0.57 | 0.53 |
| KDP High Yield Daily Mid Grade Yield | 0.59 | 0.53 |
| 10-year Treasury | 0.39 | 0.34 |
Source: Mergerstat, Bloomberg, Author's calculations.
While the correlation coefficients shown may not appear to be very large by themselves, it should be remembered for context that rolling correlations between the S&P 500 and U.S. Treasury futures (as a substitute for bonds) have historically fluctuated in the range of ![]() to
to ![]() . Therefore, the correlation between merger arbitrage spreads and high-yield interest rates is comparable to the correlation between equities and bonds in a time of extreme crisis or exuberance when bonds and stock appear to move in synch. By most investors' standards, such a correlation is meaningful.
. Therefore, the correlation between merger arbitrage spreads and high-yield interest rates is comparable to the correlation between equities and bonds in a time of extreme crisis or exuberance when bonds and stock appear to move in synch. By most investors' standards, such a correlation is meaningful.
While academic researchers have ignored the impact of interest rates on the merger arbitrage spread this relationship is well known to practitioners. A study by OFI Asset Management7 builds a model of 1,911 merger announcements between the years 1988 and 2010 that incorporates the investment-grade credit spread into the analysis. A change in the credit spread of 10 bps leads to an increase in merger arbitrage spreads by 100 bp, underlining the importance of interest rates.
Another variable that one would expect intuitively to contribute to the level of merger arbitrage spreads is the available universe of mergers that arbitrageurs can invest in. If the median spread is correlated to the outstanding equity value of announced mergers, the correlation coefficient is a mere 0.11 for daily data and 0.15 for monthly spread data. It is also clear that despite record merger activity in recent years, spreads are lower than ever so that merger activity clearly can be no more than a secondary driver of arbitrage spread levels.
The conclusion of this analysis is that interest rates are by far the primary determinant of merger arbitrage spreads.
Performance Characteristics of Merger Arbitrage
Securities dealers have practiced merger arbitrage for a long time. Investments have become available to investors since the 1980s, when private partnerships and mutual funds began to be rolled out more widely. With the growth of hedge funds in the 1990s, various data vendors began to track the performance of merger arbitrage hedge funds, and with the growth in interest in the strategy, academic literature began to investigate the potential of merger arbitrage.
Researchers approach merger arbitrage from two different angles. The first approach is to examine the returns of hedge funds that specialize in merger arbitrage. The second approach is more granular. It seeks to replicate mechanically the actions of an arbitrageur by investing in each announced deal and constructing the evolution over time of a hypothetical portfolio of stocks going through a merger. A number of rules for purchase and sale of investments is assumed, and the return of this portfolio is then measured over time. The second approach mimics an arbitrageur's activities in the construction of a portfolio rather than analyzing descriptive fund data, as the first approach does.
Each approach has its strengths and weaknesses. Using merger arbitrage hedge fund returns is comparing apples and oranges because funds can have different fee and cost structures. Although most hedge funds have a 2 percent management fee and 20 percent performance fee, some funds deviate from this 2/20 fee structure, in particular following the financial crisis of the year 2008. In addition, hedge fund databases are known to suffer from inaccuracies, most notably an incomplete sample of the universe of merger arbitrage funds, and survivorship bias.
The construction of a hypothetical arbitrage portfolio in the second approach is also problematic. It assumes that arbitrageurs follow an index-like investment strategy, whereas actual arbitrageurs select their targets carefully. It also does not incorporate inefficiencies that can make some mergers less investable than others—for example, when an acquirer's stock cannot be borrowed to engage in a short sale. Finally, placing orders carefully around the bid/offer spread is an important ingredient in any arbitrage strategy that deals with tight arbitrage spreads. It is difficult to capture bid/offer spreads accurately.
The Perils of Analyzing Stock-for-Stock Mergers
A complication in the analysis of any long/short strategy is the difficulty to estimate the cost of borrow. When shares are shorted, these shares must be borrowed. Most shares trade as general collateral without an incremental cost of borrow. However, for acquirers in mergers, it is not unusual to see the cost of borrow spike. This cost will be reflected in the arbitrage spread. As a result, the arbitrage spread will appear more profitable than it really is, because the gains that the arbitrageur makes will be paid out in fees to the lender of the security that has been shorted.
Studies about merger arbitrage have consistently ignored this problem. This cavalier attitude is understandable, considering that there is no reliable source for securities lending rates. Even market participants are often in the dark. It is well known among practitioners that prime brokers quote vastly divergent prices from client to client, probably based on the volume of activity of a client as well as the client's ability to get competitive quotes from other providers. Nevertheless, just because the data are difficult to obtain does not justify ignoring this effect.
An illustrative example of how misleading a spread can be is the $6.2 billion acquisition of El Paso by Kinder Morgan in 2012. The spread, shown in Figure 3.9, was at an alarmingly high level from the announcement through closing. Some investors at the time queried me why the market factored in such a high risk on this merger. The answer was not that the market considered this transaction risky, but that the cost of borrow was exceptionally high due to limited supply of shares. Consider one prime broker's securities lending desk's market color on February 29, 2012:

Figure 3.9 Percentage Spread of the Kinder Morgan / El Paso Merger
Kinder Morgan (KMI) - Rose 1% yesterday. Stock available in lending programs approaching 90% utilization. Only small lots of new stock being shown by lenders @ -95%. Mounting recalls coupled with limited supply continuing to squeeze borrow availability and rates to -45%. The desk is not approving new shorts at this time. Pls call for updates.
With no shares available to be lent out, there will be no arbitrage activity and the spread can trade at random levels.
Considering the large market capitalization of $21 billion of this merger, if one were to construct a capitalization-weighted theoretical arbitrage portfolio, then this merger would be by far the largest single constituent of such a portfolio. As a result, the theoretical profitability of merger arbitrage would be vastly overstated.
In order to avoid problems with misleading spreads due to incomplete data on the cost of borrow, I have made all original analysis in the book that incorporates spreads for cash-only deals. Although this approach neglects a substantial fraction of merger arbitrage opportunities, it does provide much more precise insights than a more comprehensive analysis for which it is clear that a good fraction of relevant data, spread and cost of borrow, are unreliable and missing. As the old saying goes: junk in, junk out.
As an aside, some market participants trade on the anticipation of an increase in the cost of borrow of shares. This used to be a business that was carried out by investment banks. However, due to recent cuts in compensation, their securities lending departments fulfill now largely clerical functions. Trading and anticipation of increasing borrow costs has become an area that some very specialized broker/dealers and hedge funds implement. Experience tells these traders for which acquirers an increase in borrowing activity can also lead to an increase in borrow cost. They will then borrow shares at a prevailing market rate and lock in the borrow cost for an extended period of time, usually three months. If the borrow cost then rises, arbitrageurs will have to borrow the shares at a higher rate. The higher rate, in return, forces the arbitrage spread to widen. As already discussed, this widening does not benefit merger arbitrageurs, as the increase is fully attributable to the higher cost of borrowing shares.
Of the two research approaches to merger arbitrage the second approach —that of analyzing merger arbitrage spreads—has been practiced for a longer time than the analysis of merger arbitrage fund data. This is probably caused by the paucity of data on funds for years prior to 1990, because most merger arbitrage occurred in the broker/dealer community and merger arbitrage vehicles open to outside investors are a more recent development. However, now that a quarter century of merger arbitrage fund performance data are available, this approach is viable.
Using the first approach, an early study8 of merger arbitrage investigated 761 cash tender offers that were announced from 1971 to 1985. It concluded that a merger arbitrageur earns a daily abnormal return of 0.47 percent. On an annualized basis, this corresponds to an abnormal return of 171 percent, a return that any merger arbitrageur is dreaming of. The flaw in this study that led to this outsized return is the way in which the return was calculated: For each merger, the return was annualized. These returns were then averaged across all mergers in the sample. The implicit assumption of this cross-sectional approach is that all mergers happen at the same time. In reality, the mergers were spread out over a 14-year period, with only limited overlap, and the average daily return could not have been achieved on a time-weighted basis. A study by Jindra and Walkling9 suffers from the same error. It examines 361 cash tender offers between 1981 and 1995 and finds annual excess returns of up to 115 percent for purchases of target stock on the day after the announcement and a sale one week later.
Bhagat et al.'s10 analysis of cash tender offers describes the nonlinear nature of merger arbitrage. The capital asset pricing model (CAPM) used in it is inadequate because it does not capture all risks, most notably the deal-specific risk of noncompletion.
Mitchell and Pulvino11 find excess returns of almost 4 percent per year using a contingent claims analysis. Their study remains one of the most thorough and detailed studies of merger arbitrage performed to date, and it deserves to be discussed at greater length. They examine 4,750 cash and stock mergers and tender offers between 1963 and 1998. Rather than examining merger arbitrage transactions at a deal level and then averaging over transactions, they create a hypothetical portfolio that is managed on a daily basis. This creates what is effectively a passively managed risk arbitrage index, which is subject to a number of rules that are adhered to mechanically. For example, no single position can amount to more than 10 percent of the portfolio. An important finding of their study is the correlation characteristics of merger arbitrage. Under most market conditions, merger arbitrage is uncorrelated with the returns of the overall stock market. However, in severely declining markets, the correlation becomes positive. Mitchell and Pulvino estimate a piecewise linear regression of a CAPM model that separates returns in upmarket and downmarket series:
where
| is the market return. | |
| is the risk-free rate of return. | |
| is a dummy variable that is 1 when the market return is above a threshold level (upmarket) and 0 when the market return is below that threshold (downmarket). | |
The advantage of running a piecewise linear regression of this type over a normal CAPM model is that the piecewise model takes nonlinear return characteristics into account, albeit limited to those returns that have been observed historically. The model is estimated through trial and error so that the threshold level that is found is the one that yields the highest ![]() for the model.
for the model.
The most important conclusion of this study is that linear mean-variance analysis is inappropriate for evaluating merger arbitrage returns. The authors find a monthly excess return (alpha) of 0.53 percent over the risk-free rate with zero beta in upward-trending markets, but a beta of 0.49 percent in downward-trending markets. The threshold level was a monthly return of ![]() percent, which minimizes the residuals of the model. Therefore, all markets with performance worse than
percent, which minimizes the residuals of the model. Therefore, all markets with performance worse than ![]() percent are considered downmarkets, and those with performance better than
percent are considered downmarkets, and those with performance better than ![]() percent are upmarkets. This result is depicted graphically in Figure 3.10. It can be seen that the slope of the graph has a kink at the –4 percent (monthly) threshold level. The three panels in Figure 3.10 show different periods of time, and the effect can be seen clearly for all three periods. For downmarkets with a worse performance, the beta of the merger arbitrage portfolio increases. This effect is more pronounced for cash transactions than stock-for-stock mergers. For stock-for-stock transactions, the beta remains a modest 0.12 in downmarkets, whereas it increases to 0.72 for cash transactions. Even though this is a large discrepancy, it should be stressed that 0.72 is still a low beta coefficient when compared to other asset classes. It should be noted that the authors also estimate a standard CAPM model that does not incorporate a kink but is one single straight line. This model generates an alpha of 0.29 percent and beta of 0.12 percent. To what extent the finding in the bear market is relevant is another question: There are only few occurrences of monthly returns of less than
percent are upmarkets. This result is depicted graphically in Figure 3.10. It can be seen that the slope of the graph has a kink at the –4 percent (monthly) threshold level. The three panels in Figure 3.10 show different periods of time, and the effect can be seen clearly for all three periods. For downmarkets with a worse performance, the beta of the merger arbitrage portfolio increases. This effect is more pronounced for cash transactions than stock-for-stock mergers. For stock-for-stock transactions, the beta remains a modest 0.12 in downmarkets, whereas it increases to 0.72 for cash transactions. Even though this is a large discrepancy, it should be stressed that 0.72 is still a low beta coefficient when compared to other asset classes. It should be noted that the authors also estimate a standard CAPM model that does not incorporate a kink but is one single straight line. This model generates an alpha of 0.29 percent and beta of 0.12 percent. To what extent the finding in the bear market is relevant is another question: There are only few occurrences of monthly returns of less than ![]() percent, whereas the bulk of the months has a return better than
percent, whereas the bulk of the months has a return better than ![]() percent.
percent.

Figure 3.10 Piecewise Linear Regression of Excess Merger Arbitrage Returns versus Market Returns
Source: Mark Mitchell and Todd Pulvino, “Characteristics of Risk and Return in Risk Arbitrage,” Journal of Finance 56, no. 6 (December 2001).
Mitchell and Pulvino take an additional step in their analysis. Rather than just describing the nonlinear nature of merger arbitrage, they use Black-Scholes analysis to value the optionality. Whenever an investment strategy has nonlinear returns, an option is embedded and hence option theory should be used in its evaluation. Black-Scholes is a good enough approximation for the purposes of this academic study. The authors build a portfolio of written index put options and Treasury bills. The put options are written at a strike price 4 percent below the market at a given time. They find that merger arbitrage generates excess returns of 0.33 percent per month even when options analysis is used based on theoretical Black-Scholes option prices. When actual put option prices are used, the excess return is still a healthy 0.29 percent. Therefore, even if merger arbitrage has characteristics that resemble those of a strategy of writing put options, it still outperforms that strategy.
Mitchell and Pulvino do not limit their analysis of merger arbitrage to a hypothetical portfolio but also apply their analysis to returns of actual merger arbitrage hedge funds. Hedge funds from HFR's database over the period from 1990 to 1998 exhibit the same nonlinear characteristic as the artificial index created in the first part of the study: In upmarkets, the merger arbitrage hedge fund beta is a low 0.10, which rises to 0.60 in downmarkets.
Another conclusion reached by Mitchell and Pulvino is the importance of transaction costs. They find that much of the excessive outperformance of merger arbitrage found by other studies can be explained by the neglect of transaction costs.
Eliezer Fich and Irina Stefanesco12 take a different approach: They construct an equally weighted portfolio of 1,928 cash and stock mergers that occurred between 1985 and 2000 where the bidder is a Standard & Poor's (S&P) 500 firm. They find that such a portfolio yields a monthly excess return of 1.2 percent, which is 85 percent higher than that of a portfolio of non-S&P 500 bidders. Despite the higher return, the likelihood of deal completion is higher when a bidder is in the S&P 500 than when not. These results hold for cash and stock-for-stock transactions.
Malcolm Baker and Serkan Savasoglu13 examine 1,901 mergers between 1981 and 1996 and find excess returns of 0.3 percent per month. Table 3.2 shows their findings in detail. A 2000 study by these authors had found excess returns of approximately 1 percent per month, or annual excess returns of 12.5 percent. Their main concern is the question why the excess returns achieved by merger arbitrage do not disappear. Economic theory suggests that excess returns should disappear as a result of arbitrage activity. Baker and Savasoglu contend that arbitrageurs are limited in number and constrained in capital, and that this limited arbitrage explains excess returns.
Table 3.2 Merger Arbitrage Returns for Different Portfolios
| Value-Weighted | Equal-Weighted | |||||
| Portfolio | Mean (%) | SD (%) | Sharpe ratio | Mean (%) | SD (%) | Sharpe ratio |
| Panel A: Arbitrage portfolios, all offers | ||||||
| All deals | 1.54 | 4.25 | 0.23 | 1.55 | 2.54 | 0.39 |
| Cash deals | 1.62 | 4.84 | 0.22 | 1.48 | 3.13 | 0.29 |
| Stock deals | 1.67 | 4.42 | 0.25 | 1.97 | 4.81 | 0.29 |
| Panel B: Arbitrage portfolios, first offers | ||||||
| All deals | 1.63 | 3.49 | 0.3 | 1.51 | 2.72 | 0.35 |
| Cash deals | 1.76 | 4.32 | 0.28 | 1.4 | 3.3 | 0.25 |
| Stock deals | 1.4 | 4.62 | 0.18 | 1.95 | 5.03 | 0.27 |
| Panel C: Market returns | ||||||
| Market | 1.21 | 4.16 | 0.15 | 1.41 | 5.08 | 0.17 |
| T-bills | 0.57 | 0.24 | 0.57 | 0.24 | ||
Source: M. Baker and S. Savasoglu, “Limited Arbitrage in Mergers and Acquisitions,” Journal of Financial Economics 64, no. 1 (April 2002), 91–115.
Ben Branch and Jia Wang are the first academic researchers to examine stock-for-stock mergers with a collar.14 Their sample consists of 187 collar deals between 1994 and 2003. Their findings replicate the nonlinear return characteristics of merger arbitrage: In severely declining markets, returns from merger arbitrage are highly correlated with the market, but they remain largely uncorrelated under normal market conditions. They quantify the mischaracterization of excess returns if mean-variance analysis is applied to merger arbitrage. Under CAPM, excess returns are 11.88 percent, but they amount to only 6.3 percent when contingent claims analysis is used. The threshold level for severely declining markets found by Branch and Wang is –3.7 percent, which is close to the –4 percent level found by Mitchell and Pulvino.
Branch and Wang constructed two merger arbitrage portfolios. The first, Strategy I, consists of the target common stock, which is held until the closing for fixed value collars, or delta hedged for fixed share collars. The second portfolio, Strategy II, is always delta hedged, irrespective of the type of collar. Figure 3.11 shows the result of these two strategies. It can be seen that merger arbitrage returns are most often negative when the market also has negative returns. These events are the dots in the lower-left quadrants of the charts.

Figure 3.11 Piecewise Linear Regression of Excess Merger Arbitrage Returns
In a 2006 update of the study, Ben Branch and Taewon Yang15 find that fixed-value collars yield better merger arbitrage performance than fixed-share collars.
Performance of Merger Arbitrage outside the United States
While the bulk of mergers and hence arbitrage opportunities occur in the United States there is substantial deal flow in Europe and Asia. The problem with investments in these markets is that market structure and legal frameworks are different enough from one country to the next to make comparisons difficult. Due to the small number of mergers in many countries any single-country study must be conducted with a comparatively small data set. Cross-border mergers complicate the analysis further because two or more jurisdictions are implicated, and special cross-border rules apply.
Several studies show that merger arbitrage can be successful in non-U.S. markets. However, arbitrageurs must be careful because the legal framework differs drastically from that in the United States. Most European countries, for example, have takeover regimes that are based on the U.K. City Code, which will be discussed later. The advantage of these regimes is that the timeline for the closing of a merger is very well defined. The drawback is that shareholders have fewer rights to influence management. On the positive side, this is offset by easier access to courts and generally lower cost of litigation, although shareholders do not have the benefit of pooling resources through class actions.
Andrew Karolyi and John Shannon16 (1999) examined 37 Canadian acquisitions during the year 1997 with a deal value of at least $50 million. They conclude that a portfolio invested in these merger arbitrage transactions has a beta of 0.39 and an annualized excess return of 33.9 percent over the Toronto Stock Exchange index TSE 300.
Christoph Maxheim17 studies merger arbitrage between August 1999 and October 2006 in three countries: Austria, Germany, and Switzerland. The results for Austria look unfavorable due to the uncharacteristically strong performance of the Austrian Traded Index ATX benchmark over the period of the study. He finds that merger arbitrage in Austria outperforms the ATX index by 2.41 percent; in Germany, it outperforms the Deutscher Aktienindex DAX by 3.97 percent; and in Switzerland, it outperforms the Swiss Performance Index SPI by 2.73 percent annually. Maxheim considers stock-for-stock deals, cash deals, and mixed stock and cash deals. His results are difficult to compare with those of other studies because he does not include transaction costs and calculates raw returns rather than risk-adjusted returns.
These results are confirmed by Rohani and Wanzelius,18 who investigate 212 mergers in Europe between the years 1997 and 2005. They find that a passive merger arbitrage strategy generates abnormal returns of between 2.27 and 3.24 percent. For a semi-active portfolio, in which the arbitrageur invests only in mergers with attributes that statistically have a high probability of completion, the excess return is 2.76 percent. Finally, they find that a portfolio that consists of reverse merger arbitrage (see Chapter 4) has a negative excess return; even a portfolio of only reverse arbitraging hostile transactions generates negative excess returns.
Only looking at U.K. mergers, Cao, Goldie, Liang and Petrasek19 find a positive risk-adjusted return of 0.94 percent per month for 975 cash and stock mergers using a Fama-French three-factor model. They confirm the existence of a nonlinearity for severe market downturns. This study is notable for having the largest sample size of all studies outside the United States.
A study of 193 mergers in Australia between 1991 and 2000 by Krishnan Maheswaran and Soon Chin Yeoh20 finds excess returns of 0.84 to 1.20 percent before transaction costs. Once transaction costs of 0.15 percent stamp duty, commissions of 0.30 percent, and 0.50 percent market impact are taken into account, excess returns are no longer significant. They structure a time-weighted portfolio following Mitchell and Pulvino's methodology. Interestingly, they do not find that the market-neutral behavior of merger arbitrage disappears in down markets. The threshold level that minimizes squared residuals in their piecewise linear regression is located at –2 percent rather than the –4 percent found by Mitchell and Pulvino for the U.S. market. However, they do not find that there is a statistically significant difference between the two segments of the piecewise linear regression. In other words, merger arbitrage in Australia does not behave differently in severely declining markets than under normal market conditions.
In China, there are very few investable mergers and acquisitions to date in which arbitrageurs could have invested. The first public tender offer was only made in June 2003 after securities regulators issued Administrative Measures on the Acquisition of Listed Companies. A particularity of the Chinese market is the existence of mandatory tender offers that holders of more than 30 percent of the shares are required to make to the holders of the freely circulating (i.e., not held by the state) shares. Because many 30 percent holders do not actually intend to acquire the firm they are invested in, these tender offers are made at a discount (sometimes at more than a 50 percent discount) to the market price in order to discourage shareholders from tendering their shares. As a result, the only merger arbitrage study21 in the Chinese market has to work with a limited data set of only 22 tender offer bids between 2002 and 2006 in which a real acquisition attempt was made. The results of merger arbitrage in the Chinese market are discouraging for any hopeful arbitrageur: Annualized abnormal returns are –4.14 percent. Therefore, it is better to invest in the Chinese market directly than to conduct merger arbitrage in China.
In connection with Chinese mergers, U.S.-listed Chinese companies deserve a particular mention. During the years 2010 to 2011, these companies went through their own merger wave, which was driven by the valuation discrepancy between high valuations for domestic firms in China and Hong Kong and substantial discounts to these valuations for Chinese firms in the U.S. market. As a result, many management teams sought to take their firms private, most likely with the intention of floating them in the Chinese market at a higher valuation later. However, at that time two securities companies exposed a number of frauds among Chinese firms. This led to a generalized fear of Chinese firms listed in the United States, so that merger spreads for Chinese companies widened substantially. Even in one case of a firm undergoing a private-equity sponsored management buyout, Harbin Electric, allegations of fraud were made. Although the merger spread went through a roller coaster, the merger eventually closed and as the company is private today it cannot be known whether the fraud allegations were valid or not.
Overall, the evidence points to merger arbitrage as a valid strategy not only in the United States but international markets also. In fact, Europe has a well-developed merger arbitrage community, and so does Asia. Some Asian arbitrageurs are now even active in markets that generally are still considered emerging markets like Thailand, South Korea, and Malaysia. Clearly, the less developed a market the less deal flow presents itself, not to mention country-specific risks and language barriers that can make it prohibitive for outside investors to engage in arbitrage.
Risk and Return of Merger Arbitrage Funds
The previous sections discussed academic studies of merger arbitrage analyzed hypothetical passive portfolios. These portfolios were constructed on the basis of some assumption about the allocation of capital in a passive manner to mergers active at any one time. Merger arbitrageurs, however, take an active approach to managing their portfolios. Two types of arbitrageurs are active:
- Concentrated arbitrageurs invest in a small number of mergers only and take big bets on each of these transactions closing. Most arbitrageurs in investment banks and broker/dealers fall into this category. Each transaction they invest in has a high probability of closing and hence provides only a small expected return. In order to get to a double-digit level of return expected by investors, the arbitrageurs leverage their portfolios. In investment banks, the funding can be achieved near the London Interbank Offered Rate (LIBOR), whereas merger arbitrage hedge funds finance their leverage at a higher cost of capital. Therefore, the latter need a higher level of leverage in order to achieve the desired level of return. A drawback of this approach is that any unforeseeable event that leads to a widening of spreads, or even a collapse of a deal, will have a large impact on the portfolio and lead to a substantial drawdown. However, many arbitrageurs and investors find the prospect of extended periods of stable returns appealing, even if they are achieved at the price of short bouts of significant losses.
- Diversified arbitrageurs invest in a larger number of transactions. Therefore, they are more likely to be affected by the collapse of a merger. Through a careful analysis of the severity of each transaction, combined with position limits and diversification, the impact of any losses after a deal's collapse on the overall portfolio can be managed.
The returns of hedge funds are tracked by a number of databases. Each of these databases calculates a number of subindices, including indices of hedge funds that specialize in merger arbitrage.
- Barclay Hedge. Formerly The Barclay Group, this database began collecting hedge fund data in 1985 and has over 6,000 hedge funds with total assets of over $2.1 trillion. Merger arbitrage funds represent a mere $30 billion of assets (Q1 2015).
- Cogent Hedge. This database consists of over 5,000 active hedge funds and 15,000 funds in total.
- Morningstar Crédit Agricole Structured Asset Management Center for International Securities and Derivatives Markets (CASAM CISDM). Formerly known as Managed Accounts Research (MAR), this database was created in 2005 when Crédit Agricole partnered with the University of Massachusetts Amherst and took over the MAR data. MAR started collecting data on hedge funds in 1992, and has data going back to 1990.22 The merger arbitrage index is a category of its own, unlike in the other databases. It contains 4,140 active hedge funds, 5,840 dead funds, and 31 active merger arbitrage funds (Q1 2014). Morningstar also took over the former MSCI Barra hedge fund indices.
- Greenwich Alternative Investments. Formerly known as Van Hedge Fund Advisors, this database covers 7,000 hedge funds going back to 1996. Merger arbitrage is classified as a substrategy of event-driven funds within the market-neutral equity strategy.
- Hedge Fund Research (HFR). The HFR database contains over 16,000 funds in the aggregate. The Merger Arbitrage Index is considered a subcategory of the event-driven index. HFRI is calculated monthly from all hedge funds, both open and closed to new investors, and is available from 1990. HFRX was initially a monthly calculation of investable hedge funds but now is comprised of UCITS-compliant funds with daily NAVs.
- Hennessee Group. This database has collected hedge fund data since 1987. Merger arbitrage is classified as a substrategy of the broader Arbitrage/Event-Driven category and its data are available from July 1994. At the time of writing, Hennessee was reviewing its indices and had last published performance data for March 2014.
- Lipper TASS. Formerly Tremont TASS, it was acquired by Lipper/Reuters in 2005. This database contains over 6,300 hedge funds and over 7,000 “graveyard” funds.
Merger arbitrage hedge funds have grown in size since the 1990s, when they were first offered on a larger scale to the investing public. The growth of total assets managed by merger arbitrage funds is shown in Figure 3.12. During the immediate post-Internet bubble years, growth in assets under management (AUM) was particularly strong. The general decline in hedge fund assets following the financial crisis in the year 2008 is also reflected in merger arbitrage, even though the strategy held up well throughout the meltdown. Since 2011, assets have increased again but at the time of writing have yet to regain their peak of the year 2007. Even though hedge fund assets in general are back to their pre-crisis levels, merger arbitrage assets are still substantially below their peak.

Figure 3.12 Assets Managed in Merger Arbitrage Funds
Source: Barclay Hedge, LTD.
It should be noted that some funds will use leverage to increase their exposure, so that the total dollar amount of merger arbitrage investments controlled by hedge funds is higher than the net shown in the figure. Since merger arbitrage is a low-volatility strategy, a higher level of leverage can be justified than for other hedge fund strategies.
One of the problems encountered when constructing merger arbitrage fund indices is that many merger arbitrage managers do not restrict themselves to a pure merger arbitrage strategy but also invest in related strategies, notably liquidations, spin-offs, activist situations, or restructurings (bankruptcies). These styles are not necessarily constant but can drift over time. Other problems are related to more fundamental weaknesses of the databases that make their numbers biased. Some databases drop funds that close down from the calculation of the returns, not only after the date of the closing of the fund but even for historical returns when the fund was operating. As funds that close typically do so after poor performance, the averages include only well-performing funds and are biased to the upside. Some data providers are said to have fixed this problem and now provide indices without this type of survivorship bias. Nevertheless, other problems remain. For example, the data providers rely on voluntary reporting by managers, and not all managers choose to report. Managers do not necessarily report from the time their fund was started but often run their funds for a year or two before reporting their historical performance since inception. In cases where the fund had poor performance, the manager will simply shut down the fund without ever reporting.
For the remainder of this section, the properties of five of the hedge fund indices will be compared to the S&P 500 and the Barclays Aggregate Bond Index. The S&P 50 and Barclays indices represent the performance of the stock and bond markets overall, respectively. The five merger arbitrage hedge fund indices selected were those of Hedge Fund Research (HFRI and HFRX), CASAM CISDM, Barclay Hedge, and Greenwich. Data for all of these indices are available through the end of the year 2014. However, the indices have different start dates. Hedge Fund Research covers the longest period of time, starting in January 1990. CASAM starts in January 1993. Greenwich starts in January 1997. The Barclay Hedge is by far the shortest index, starting only in January 2001.
Monthly returns for the five indices are shown in Figure 3.13. The S&P 500 index is by far the most volatile. Bonds often move in the opposite direction when the S&P 500 falls, except in some instances where a severe drop in the S&P 500 drags down bonds as well as the hedge fund indices. For the remainder of this chapter, monthly returns are used to analyze performance, unless noted otherwise. Monthly data have the disadvantage of masking the true volatility, because extreme moves are so rare that they are not captured by monthly data that cover, in the longest series, a quarter century. However, since hedge funds report their performance only monthly, daily data is not available. Some hedge fund products with daily NAV calculations have become available recently, and numerous indices discussed in later chapters seek to calculate hypothetical daily merger arbitrage performance. However, all of these potential sources suffer from relatively recent inception and do not lend themselves for meaningful long-term analysis.

Figure 3.13 Monthly Performance of Merger Arbitrage Hedge Funds, the S&P 500, and Bonds
Summary statistics for the selected data are shown in Table 3.3. The comparison of the series is made difficult due to their different length. For example, the worst drawdown of the shortest index, Barclay, appears to be only roughly half as bad as the drawdown of the longest index, HFR. However, the –6.46 percent drop in the HFR merger arbitrage index occurred in January 1990, the first month that this index was constituted. The other indices did not even exist at that time. It is pointless to speculate what their performance might have been in that month, even though most reasonable observers would probably suspect they may have suffered a comparable drawdown. Similarly, the indices that have been in existence for longer appear to have higher returns than the ones that started reporting later. This finding reflects mostly the high returns generated by merger arbitrage during the 1990s, whereas the new millennium saw returns that were generally lower. Therefore, the indices that started later appear to perform more poorly than the older indices.
Table 3.3 Statistics of Monthly Return for Merger Arbitrage Hedge Fund Indices Compared to Stocks and Bonds over a Quarter Century, 1990–2014
| HFRI | CASAM | Barclay | Greenwich | HFRX | Bonds | S&P 500 | |
| Observations | 300 | 300 | 216 | 215 | 204 | 300 | 300 |
| NAs | 0 | 0 | 84 | 85 | 96 | 0 | 0 |
| Minimum | 0.0646 | 0.0561 | 0.0457 | 0.0490 | 0.0456 | 0.0336 | 0.1679 |
| Quartile 1 | 0.0017 | 0.0026 | 0.0017 | 0.0016 | 0.0004 | 0.0009 | 0.0166 |
| Median | 0.0078 | 0.0066 | 0.0067 | 0.0060 | 0.0047 | 0.0062 | 0.0130 |
| Arithmetic Mean | 0.0066 | 0.0070 | 0.0060 | 0.0056 | 0.0044 | 0.0053 | 0.0086 |
| Geometric Mean | 0.0065 | 0.0069 | 0.0060 | 0.0056 | 0.0043 | 0.0053 | 0.0077 |
| Quartile 3 | 0.0137 | 0.0122 | 0.0118 | 0.0118 | 0.0100 | 0.0124 | 0.0356 |
| Maximum | 0.0312 | 0.0474 | 0.0300 | 0.0276 | 0.0329 | 0.0387 | 0.1144 |
| SE Mean | 0.0007 | 0.0006 | 0.0007 | 0.0007 | 0.0007 | 0.0006 | 0.0024 |
| LCL Mean (0.95) | 0.0053 | 0.0057 | 0.0047 | 0.0043 | 0.0030 | 0.0041 | 0.0038 |
| UCL Mean (0.95) | 0.0079 | 0.0082 | 0.0074 | 0.0070 | 0.0057 | 0.0065 | 0.0134 |
| Variance | 0.0001 | 0.0001 | 0.0001 | 0.0001 | 0.0001 | 0.0001 | 0.0018 |
| Stdev | 0.0114 | 0.0109 | 0.0101 | 0.0100 | 0.0101 | 0.0106 | 0.0423 |
| Skewness | –2.0145 | –0.9000 | –1.2458 | –1.3664 | –1.0758 | –0.2542 | –0.6215 |
Figure 3.14 shows the cumulative performance of the five merger arbitrage hedge fund indices, the S&P 500 index, and bonds. It can be seen in the upper chart that the three merger arbitrage indices have a performance that lies close to each other. The S&P 500 overall exhibits a similar cumulative performance, albeit with much larger fluctuations. Bonds have a much lower overall performance but fluctuate in similar ways as the merger arbitrage hedge funds. For this reason, merger arbitrage is often labeled as a strategy with equity-like returns at bond-like volatility.
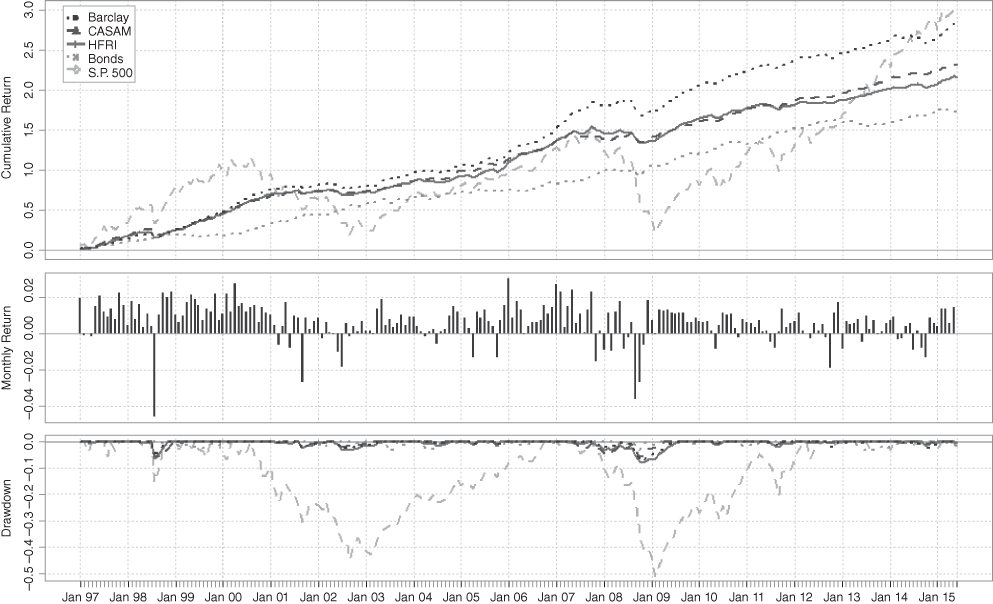
Figure 3.14 Performance of Three Merger Arbitrage Hedge Fund Indices Relative to Stocks and Bonds
The lower chart in Figure 3.14 shows the drawdown from the most recent peak of each index. Drawdowns for the three merger arbitrage fund indices as well as for bonds are so small that they are difficult to discern visually on the chart. In contrast, the S&P 500 index experiences frequent losses. Its most dramatic drawdown occurred between early 2000 and late 2002, where it lost over 40 percent of its value.23
The risk/return trade-off for merger arbitrage compared to the S&P 500 and bonds is shown in Figure 3.15. All indices are shown from their respective inception. All merger arbitrage hedge fund indices exhibit a volatility that is comparable to that of the Barclays Aggregate Bond Index. However, returns are mostly higher. Only the HFRX merger arbitrage fund index underperforms bonds. This can be attributed in part to the shorter length of this index.

Figure 3.15 Risk/Return Trade-off for Merger Arbitrage
Figure 3.16 shows the discrepancy between the merger arbitrage hedge fund indices. The HFR index is used as a baseline, and the performance of HFR is calculated relative to each other index. Overall, the indices are quite close to one another, with a divergence emerging most notably during the market turmoil of 2008.
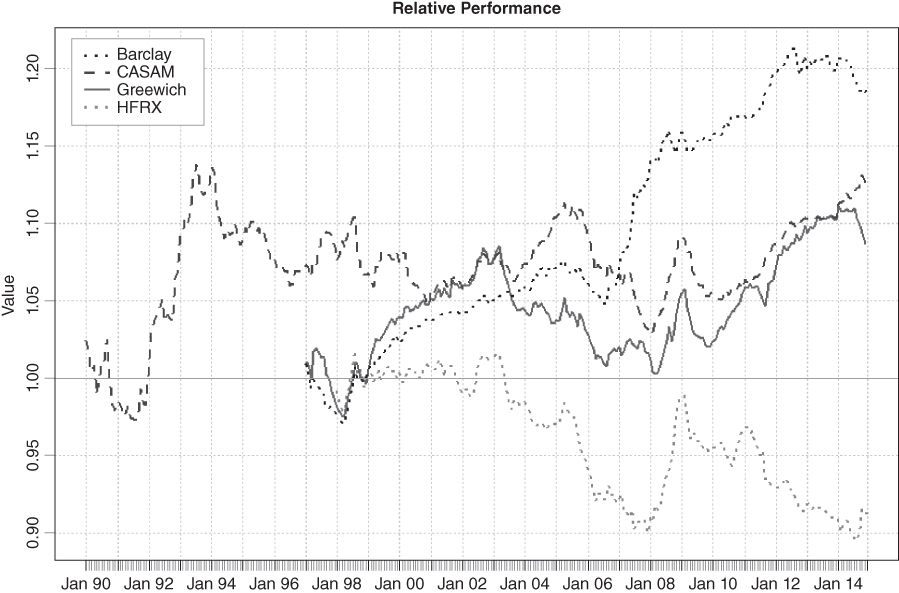
Figure 3.16 Performance of Various Merger Arbitrage Hedge Fund Indices Relative to the HFR Hedge Fund
Similar effects can be seen when the indices are compared to the S&P 500. Table 3.4 shows some risk statistics in a CAPM framework. The statistics shown are frequently used to evaluate performance and risk. Here are some of the less common statistics:
- Beta+ and Beta−. These are betas calculated only for months in which the S&P 500 was up (beta+) or down (beta−).
- Tracking error. The standard deviation of the difference between the portfolio and index returns. It measures how closely an investment follows the benchmark.
- Active premium. The annualized return minus the benchmark's annualized return.
- Information ratio. Measures the active return of an investment manager divided by the amount of risk the manager takes relative to a benchmark. It is defined as active return divided by tracking error.
- Treynor ratio. The excess performance of the portfolio per unit of market risk (beta) assumed.
- Sharpe ratio. The risk-adjusted return. For comparison, the Sharpe ratio for the S&P 500 since 1990 is 0.66 with a risk-free rate of zero.
- Sortino ratio. A variation of the Sharpe ratio that incorporates only volatility to the downside. By excluding volatility to the upside, only the harmful aspect of fluctuations is considered. After all, upside volatility is beneficial to the investor. For comparison, the Sortino ratio for the S&P 500 since 1990 is 0.15.
Table 3.4 CAPM* Statistics of the Merger Arbitrage Hedge Fund Indices, Relative to the S&P 500
| HFRI | CASAM | Barclay | Greenwich | HFRX | |
| Alpha | 0.0007 | 0.0012 | 0.0009 | 0.0005 | –0.0004 |
| Beta | 0.1639 | 0.1522 | 0.1607 | 0.1614 | 0.1466 |
| Beta+ | 0.1034 | 0.0833 | 0.1213 | 0.1262 | 0.1057 |
| Beta− | 0.2576 | 0.2462 | 0.1963 | 0.1894 | 0.1671 |
| R-squared | 0.2227 | 0.2031 | 0.2869 | 0.2912 | 0.2489 |
| Annualized Alpha | 0.0089 | 0.0142 | 0.0113 | 0.0061 | -0.0049 |
| Correlation | 0.4719 | 0.4507 | 0.5357 | 0.5396 | 0.4989 |
| Correlation p-Value | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Tracking Error | 0.1305 | 0.1319 | 0.1414 | 0.1415 | 0.1446 |
| Active Premium | –0.0150 | –0.0099 | –0.0038 | –0.0094 | –0.0118 |
| Information Ratio | –0.1150 | –0.0747 | –0.0267 | –0.0665 | –0.0817 |
| Treynor Ratio | 0.0862 | 0.1249 | 0.0948 | 0.0630 | –0.0200 |
| Sharpe Ratio* | 0.3575 | 0.5027 | 0.4344 | 0.2945 | –0.0841 |
| Sharpe Ratio† | 2.0527 | 2.2839 | 2.1177 | 2.0053 | 1.5185 |
| Sortino Ratio (MAR=0) | 0.9239 | 1.2020 | 1.0483 | 0.9697 | 0.7090 |
* The Barclays Aggregate Bond Index is used as a proxy for the risk-free rate, which averaged 6.4 percent over the period.
† The risk-free rate is set to zero for the calculation of the Sharpe Ratio shown on this line.
It was discussed earlier that CAPM risk measurements are of limited use when nonlinear strategies such as merger arbitrage are evaluated. A number of other measures have been developed that evaluate the risk of loss. Table 3.5 shows these risk metrics for merger arbitrage funds, bonds, and stocks. It can be seen that most of the merger arbitrage measures are of comparable magnitude as those of bonds, confirming the earlier observation:
- Semi deviation. Calculates the standard deviation only for observations that are below the mean.
- Gain deviation. The standard deviation only of observations that generate a gain.
- Loss deviation. The standard deviation in months in which there is a loss. It is a subset of the semi deviation.
- Downside deviation. The standard deviation for months in which the index had a worse performance than the minimum acceptable return (MAR) of 10, and 0 percent.
- Upside/downside capture ratio. It shows the fraction of the up (down) movement of the S&P 500 captured by the index. A negative downside capture means that the index increased when the S&P decreased.
Table 3.5 Various Downside Risk Measures
| Barclay | CASAM | Greenwich | HFRI | HFRX | Bonds | S&P 500 | |
| Semi Deviation | 0.0080 | 0.0082 | 0.0079 | 0.0094 | 0.0079 | 0.0078 | 0.0321 |
| Gain Deviation | 0.0062 | 0.0076 | 0.0060 | 0.0063 | 0.0060 | 0.0070 | 0.0240 |
| Loss Deviation | 0.0098 | 0.0113 | 0.0100 | 0.0128 | 0.0091 | 0.0066 | 0.0309 |
| Downside Deviation (MAR=10%) | 0.0091 | 0.0089 | 0.0092 | 0.0102 | 0.0099 | 0.0095 | 0.0320 |
| Downside Deviation (Rf=0%) | 0.0058 | 0.0058 | 0.0058 | 0.0071 | 0.0061 | 0.0053 | 0.0280 |
| Downside Deviation (0%) | 0.0058 | 0.0058 | 0.0058 | 0.0071 | 0.0061 | 0.0053 | 0.0280 |
| Maximum Drawdown | 0.0718 | 0.0575 | 0.0714 | 0.0806 | 0.0546 | 0.0515 | 0.5095 |
| Historical VaR (95%) | −0.0097 | −0.0096 | −0.0099 | −0.0123 | −0.0136 | −0.0134 | −0.0703 |
| Historical ES (95%) | −0.0214 | −0.0216 | −0.0213 | −0.0261 | −0.0224 | −0.0187 | −0.0952 |
| Modified VaR (95%) | 0.0130 | 0.0123 | 0.0132 | 0.0158 | 0.0143 | 0.0127 | 0.0669 |
| Modified ES (95%) | −0.0276 | −0.0320 | −0.0293 | −0.0410 | −0.0273 | −0.0193 | −0.0992 |
| Upside Capture Ratio | 0.2679 | 0.3174 | 0.2582 | 0.3117 | 0.2158 | 0.1839 | N/A |
| Downside Capture Ratio | −0.0167 | −0.0198 | −0.0015 | 0.0017 | 0.0095 | −0.1117 | N/A |
A different way to look at the performance of merger arbitrage is to rank it relative to other indices and other strategies. Table 3.6 shows the ranking against a number of traditional strategies. This ranking is also referred to as a Callan Chart. Many asset classes, in particular REITs and commodities, rank as top performers in one year or two, followed by bottom performance. Merger arbitrage stands out as a strategy that never delivers an outstanding performance, but also never disappoints. Instead, it is a middle-of-the-road strategy. This is a manifestation of the lower volatility of this asset class compared to the others.
Table 3.6 Ranking of Merger Arbitrage Relative to Traditional Investment Strategies
| 1990 | 1991 | 1992 | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 |
| CTAs 21.02 | Russell 2000 46.04 | Hedge Funds 21.22 | Hedge Funds 30.88 | Merger Arb 8.89 | S&P 37.58 | REITs 36.02 | S&P 33.36 | S&P 28.58 | EAFE 31.68 | REITs 29.61 | Commodities 17.86 | Commodities 16.61 | Russell 2000 47.25 | REITs 32.06 | EAFE 25.96 | REITs 35.35 | Hedge Funds 9.96 | CTAs 14.09 | Midcap 40.48 | REITs 27.70 | Bonds 7.84 | REITs 19.57 | Russell 2000 38.82 | REITs 28.04 |
| Bonds 8.96 | Midcap 41.51 | Russell 2000 18.41 | EAFE 27.17 | Hedge Funds 4.10 | Midcap 34.45 | S&P 22.96 | Midcap 29.01 | MSCI 19.15 | Hedge Funds 31.29 | Merger Arb 18.02 | REITs 13.75 | CTAs 12.36 | Midcap 40.06 | Midcap 20.22 | Commodities 14.34 | Russell 2000 18.37 | CTAs 7.64 | Bonds 5.24 | REITs 28.47 | Russell 2000 26.85 | REITs 7.54 | Midcap 17.28 | Midcap 34.76 | S&P 13.69 |
| T-Bills 8.29 | REITs 37.99 | REITs 16.38 | Merger Arb 20.24 | T-Bills 3.98 | Russell 2000 28.45 | Hedge Funds 21.10 | Russell 2000 22.36 | EAFE 10.63 | MSCI 26.27 | Bonds 11.63 | Bonds 8.44 | Bonds 10.25 | REITs 36.67 | Russell 2000 18.33 | MSCI 13.74 | Commodities 18.02 | Merger Arb 7.05 | T-Bills 2.29 | Russell 2000 27.17 | Midcap 25.48 | Commodities 6.25 | Russell 2000 16.35 | S&P 32.39 | Midcap 13.22 |
| Hedge Funds 5.81 | Hedge Funds 32.19 | Midcap 16.34 | REITs 19.56 | REITs 3.40 | Hedge Funds 21.50 | Midcap 19.00 | MSCI 20.76 | Midcap 10.09 | Russell 2000 21.26 | Commodities 8.89 | Hedge Funds 4.62 | REITs 3.59 | S&P 28.68 | S&P 10.88 | Midcap 12.65 | S&P 15.79 | Bonds 6.97 | Commodities −0.87 | S&P 26.46 | S&P 15.06 | S&P 2.11 | S&P 16.00 | MSCI 26.25 | MSCI 7.71 |
| Merger Arb 0.44 | S&P 30.47 | Merger Arb 7.90 | Russell 2000 18.88 | S&P 1.32 | Bonds 18.47 | Merger Arb 16.61 | REITs 20.07 | Bonds 8.69 | S&P 21.04 | Midcap 8.25 | T-Bills 4.44 | T-Bills 1.80 | MSCI 22.75 | EAFE 10.18 | REITs 11.92 | Midcap 15.26 | Midcap 5.60 | Merger Arb −5.37 | MSCI 22.82 | Hedge Funds 10.25 | Merger Arb 1.50 | Commodities 14.24 | EAFE 23.46 | CTAs 7.61 |
| S&P −3.10 | Merger Arb 17.86 | S&P 7.62 | MSCI 18.86 | CTAs −0.65 | Merger Arb 17.86 | Russell 2000 16.49 | Commodities 17.86 | Commodities 7.90 | Commodities 20.24 | CTAs 7.86 | Merger Arb 2.76 | Merger Arb −0.87 | Hedge Funds 19.55 | MSCI 9.49 | Hedge Funds 9.30 | Merger Arb 14.24 | S&P 5.49 | Hedge Funds −19.03 | EAFE 20.90 | MSCI 7.83 | T-Bills 0.12 | EAFE 13.55 | Hedge Funds 9.13 | Bonds 5.97 |
| Midcap −11.50 | Bonds 16.00 | Bonds 7.40 | Midcap 14.30 | Russell 2000 −1.82 | MSCI 17.43 | MSCI 14.81 | Hedge Funds 16.79 | Merger Arb 7.23 | Midcap 18.23 | T-Bills 6.16 | Russell 2000 2.49 | Hedge Funds −1.45 | EAFE 17.41 | Hedge Funds 9.03 | Merger Arb 6.25 | EAFE 13.81 | T-Bills 4.95 | Russell 2000 −33.79 | Hedge Funds 19.98 | CTAs 7.05 | Midcap −1.55 | MSCI 13.07 | Commodities 7.05 | Russell 2000 4.89 |
| Russell 2000 −19.48 | MSCI 14.02 | T-Bills 3.91 | CTAs 10.37 | Midcap −2.09 | REITs 14.89 | EAFE 9.57 | Merger Arb 16.44 | CTAs 7.01 | Merger Arb 14.34 | Hedge Funds 4.98 | CTAs 0.84 | Midcap −16.19 | Commodities 16.44 | Commodities 7.23 | S&P 4.91 | MSCI 13.52 | MSCI 2.83 | S&P −37.00 | Merger Arb 11.65 | Bonds 6.54 | CTAs −3.09 | Hedge Funds 6.36 | Merger Arb 4.74 | EAFE 3.20 |
| MSCI −22.98 | EAFE 6.82 | CTAs −0.91 | S&P 10.08 | MSCI −2.44 | CTAs 13.64 | CTAs 9.12 | EAFE 11.79 | T-Bills 5.34 | T-Bills 4.65 | Russell 2000 −3.02 | Midcap −5.62 | Russell 2000 −20.48 | CTAs 8.69 | Bonds 4.34 | Russell 2000 4.55 | Hedge Funds 12.89 | Commodities 2.76 | REITs −37.56 | Commodities 7.47 | Merger Arb 4.60 | Russell 2000 −4.18 | Bonds 4.22 | REITs 2.70 | Hedge Funds 2.98 |
| EAFE −30.99 | T-Bills 6.66 | MSCI −3.31 | Bonds 9.75 | Bonds −2.92 | EAFE 7.73 | T-Bills 5.36 | CTAs 10.89 | Hedge Funds 2.62 | Bonds −0.82 | EAFE −8.46 | S&P −11.89 | S&P −22.10 | Merger Arb 7.47 | Merger Arb 4.08 | T-Bills 3.01 | T-Bills 4.78 | EAFE 1.17 | MSCI −40.11 | Bonds 5.93 | Commodities 4.08 | Hedge Funds −5.25 | Merger Arb 2.76 | T-Bills 0.09 | Merger Arb 1.69 |
| Commodities NA | CTAs 3.73 | EAFE −8.01 | T-Bills 3.20 | EAFE −3.43 | T-Bills 6.21 | Bonds 3.63 | Bonds 9.65 | Russell 2000 −2.55 | CTAs −1.19 | S&P −9.10 | MSCI −15.25 | MSCI −25.20 | Bonds 4.10 | CTAs 3.30 | Bonds 2.43 | Bonds 4.33 | Russell 2000 −1.57 | Midcap −41.46 | T-Bills 0.28 | EAFE 2.05 | MSCI −7.56 | T-Bills 0.11 | CTAs −1.42 | T-Bills 0.06 |
| REITs NA | Commodities NA | Commodities NA | Commodities NA | Commodities NA | Commodities NA | Commodities 0.44 | T-Bills 5.47 | REITs −16.96 | REITs −4.33 | MSCI −10.77 | EAFE −17.54 | EAFE −27.45 | T-Bills 1.13 | T-Bills 1.28 | CTAs 1.71 | CTAs 3.54 | REITs −15.59 | EAFE −42.07 | CTAs −0.10 | T-Bills 0.20 | EAFE −14.83 | CTAs −1.70 | Bonds −2.02 | Commodities −5.37 |
When compared to other hedge fund strategies (Table 3.7) this effect is less pronounced but still persists. Most hedge fund strategies have lower volatility than traditional investment indices, albeit higher than merger arbitrage. Therefore, their rankings are clustered around merger arbitrage and are more competitive with merger arbitrage than traditional indices.
Table 3.7 Ranking of Merger Arbitrage Relative to Other Hedge Fund Strategies
| 1990 | 1991 | 1992 | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 |
| Short 36.22 | Macro 46.67 | Emerg. Markets 30.87 | Emerg. Markets 87.10 | Short 18.53 | S&P 37.58 | Emerg. Markets 35.69 | S&P 33.36 | S&P 28.58 | Equity Hedge 44.22 | Short 34.63 | Distress 13.28 | Short 29.17 | Emerg. Markets 32.43 | Distress 18.89 | Emerg. Markets 13.29 | Emerg. Markets 18.15 | Emerg. Markets 20.39 | Short 28.41 | Emerg. Markets 35.00 | S&P 15.06 | Bonds 7.84 | S&P 16.00 | S&P 32.39 | S&P 13.69 |
| Market Neutral 15.45 | Fixed Income 41.83 | Macro 27.17 | Macro 53.31 | Merger Arb 8.89 | Equity Hedge 31.04 | Event-Driven 24.84 | Equity Hedge 23.41 | Equity Hedge 15.98 | Emerg. Markets 40.06 | Merger Arb 18.02 | Event-Driven 12.18 | Bonds 10.25 | Distress 29.56 | Emerg. Markets 15.69 | Equity Hedge 10.60 | Distress 15.94 | Macro 11.11 | Bonds 5.24 | Fixed Income 30.71 | Distress 12.12 | S&P 2.11 | Fixed Income 10.99 | Equity Hedge 14.28 | Bonds 5.97 |
| Equity Hedge 14.43 | Equity Hedge 40.15 | Distress 25.24 | Distress 32.54 | Emerg. Markets 7.65 | Macro 29.32 | S&P 22.96 | Event-Driven 21.23 | Bonds 8.69 | Hedge Funds 31.29 | Market Neutral 14.56 | Emerg. Markets 11.51 | Macro 7.44 | S&P 28.68 | Event-Driven 15.01 | Hedge Funds 9.30 | S&P 15.79 | Equity Hedge 10.48 | Macro 4.83 | Distress 28.14 | Event-Driven 11.86 | Merger Arb 1.50 | Distress 10.12 | Distress 14.05 | Macro 5.58 |
| Macro 12.56 | Distress 35.66 | Equity Hedge 21.32 | Hedge Funds 30.88 | Event-Driven 6.00 | Event-Driven 25.11 | Equity Hedge 21.75 | Emerg. Markets 19.85 | Market Neutral 8.30 | Event-Driven 24.33 | Bonds 11.63 | Short 8.99 | Fixed Income 5.80 | Event-Driven 25.33 | S&P 10.88 | Distress 8.27 | Event-Driven 15.33 | Hedge Funds 9.96 | Merger Arb −5.37 | S&P 26.46 | Fixed Income 11.80 | Fixed Income 0.82 | Event-Driven 8.89 | Event-Driven 12.51 | Market Neutral 3.06 |
| Bonds 8.96 | Hedge Funds 32.19 | Hedge Funds 21.22 | Event-Driven 28.22 | Hedge Funds 4.10 | Hedge Funds 21.50 | Hedge Funds 21.10 | Macro 18.82 | Merger Arb 7.23 | S&P 21.04 | Equity Hedge 9.09 | Bonds 8.44 | Distress 5.28 | Macro 21.42 | Fixed Income 10.49 | Event-Driven 7.29 | Merger Arb 14.24 | Merger Arb 7.05 | Market Neutral −5.92 | Event-Driven 25.04 | Emerg. Markets 11.74 | Short 0.35 | Emerg. Markets 8.62 | Hedge Funds 9.13 | Hedge Funds 2.98 |
| Distress 6.44 | S&P 30.47 | Event-Driven 19.46 | Equity Hedge 27.94 | Distress 3.84 | Distress 19.74 | Distress 20.77 | Hedge Funds 16.79 | Macro 6.19 | Macro 17.62 | Event-Driven 6.74 | Macro 6.87 | Market Neutral 0.98 | Fixed Income 21.30 | Hedge Funds 9.03 | Short 7.28 | Hedge Funds 12.89 | Bonds 6.97 | Hedge Funds −19.03 | Equity Hedge 24.57 | Equity Hedge 10.45 | Distress −1.79 | Equity Hedge 7.41 | Market Neutral 6.46 | Equity Hedge 1.81 |
| Hedge Funds 5.81 | Event-Driven 27.42 | Fixed Income 18.53 | Fixed Income 22.67 | Market Neutral 2.65 | Bonds 18.47 | Merger Arb 16.61 | Merger Arb 16.44 | Hedge Funds 2.62 | Distress 16.94 | Hedge Funds 4.98 | Market Neutral 6.71 | Emerg. Markets −0.03 | Equity Hedge 20.54 | Equity Hedge 7.68 | Macro 6.79 | Equity Hedge 11.71 | Event-Driven 6.61 | Event-Driven −21.82 | Hedge Funds 19.98 | Hedge Funds 10.25 | Market Neutral −2.13 | Hedge Funds 6.36 | Fixed Income 5.68 | Merger Arb 1.69 |
| Merger Arb 0.44 | Merger Arb 17.86 | Short 10.05 | Merger Arb 20.24 | Equity Hedge 2.61 | Merger Arb 17.86 | Fixed Income 16.24 | Distress 15.40 | Event-Driven 1.70 | Merger Arb 14.34 | Distress 2.78 | Fixed Income 5.37 | Merger Arb −0.87 | Hedge Funds 19.55 | Macro 4.63 | Merger Arb 6.25 | Fixed Income 10.78 | S&P 5.49 | Fixed Income −24.18 | Merger Arb 11.65 | Macro 8.06 | Event-Driven −3.30 | Bonds 4.22 | Merger Arb 4.74 | Fixed Income 1.24 |
| Event-Driven −0.47 | Bonds 16.00 | Market Neutral 8.73 | Market Neutral 11.11 | Fixed Income 1.47 | Market Neutral 16.33 | Market Neutral 14.20 | Market Neutral 13.62 | Short −0.54 | Fixed Income 7.35 | Macro 1.97 | Hedge Funds 4.62 | Hedge Funds −1.45 | Merger Arb 7.47 | Bonds 4.34 | Market Neutral 6.22 | Macro 8.15 | Market Neutral 5.29 | Distress −25.20 | Bonds 5.93 | Bonds 6.54 | Macro −4.16 | Market Neutral 2.98 | Emerg. Markets 3.67 | Event-Driven 1.08 |
| S&P −3.10 | Market Neutral 15.65 | Merger Arb 7.90 | S&P 10.08 | S&P 1.32 | Fixed Income 15.20 | Macro 9.32 | Fixed Income 12.52 | Distress −4.23 | Market Neutral 7.09 | Fixed Income −3.03 | Merger Arb 2.76 | Event-Driven −4.30 | Bonds 4.10 | Market Neutral 4.15 | Fixed Income 5.27 | Market Neutral 7.32 | Distress 5.08 | Equity Hedge −26.65 | Macro 4.34 | Merger Arb 4.60 | Hedge Funds −5.25 | Merger Arb 2.76 | Macro −0.44 | Distress −1.39 |
| Fixed Income −12.11 | Short −16.96 | S&P 7.62 | Bonds 9.75 | Bonds −2.92 | Emerg. Markets 9.02 | Bonds 3.63 | Bonds 9.65 | Fixed Income −5.28 | Bonds −0.82 | S&P −9.10 | Equity Hedge 0.40 | Equity Hedge −4.71 | Market Neutral 2.44 | Merger Arb 4.08 | S&P 4.91 | Bonds 4.33 | Short 4.72 | Emerg. Markets −30.87 | Market Neutral 1.43 | Market Neutral 2.85 | Equity Hedge −8.38 | Macro −0.06 | Bonds −2.02 | Emerg. Markets −2.41 |
| Emerg. Markets NA | Emerg. Markets NA | Bonds 7.40 | Short −7.50 | Macro −4.30 | Short −17.14 | Short −4.00 | Short 3.86 | Emerg. Markets −36.39 | Short −24.40 | Emerg. Markets −9.39 | S&P −11.89 | S&P −22.10 | Short −21.78 | Short −3.83 | Bonds 2.43 | Short −2.65 | Fixed Income −0.74 | S&P −37.00 | Short −24.03 | Short −18.01 | Emerg. Markets −9.70 | Short −17.24 | Short −18.60 | Short −3.89 |
Benefits of Merger Arbitrage in a Diversified Portfolio
One of the most important insights of modern portfolio management is that investments should not be judged on a stand-alone basis but in the context of a portfolio. This does not mean that an investment does not need to be evaluated carefully. Investors in merger arbitrage funds regularly go to great lengths to conduct due diligence on each of their funds and its portfolio managers. Rather, what the portfolio context refers to is that the characteristics of a risky investment can change when it is used in connection with other investments. For example, selling short a stock is a risky undertaking, because losses are potentially unlimited if its price rises. However, as we have seen, when short selling is used as part of a merger arbitrage strategy, it is a prudent investment strategy that captures the arbitrage spread in a stock-for-stock deal.
Similar arguments can be made for merger arbitrage as an investment strategy. Although it can be argued that merger arbitrage has a large downside potential, this effect can be mitigated if merger arbitrage is used as one element of a well-diversified portfolio. Diversification is the key: If one investment zigs, the other might zag. This will keep the overall value of the portfolio more stable. The key is to select investments that have a low correlation with one another.
The effect of adding merger arbitrage to an investment portfolio can best be shown graphically. Charts that denote the risk/return trade-off of merger arbitrage have already been presented several times. In modern portfolio construction, these charts usually contain an upward-sloping line referred to as the efficient frontier. The efficient frontier denotes the optimal portfolio for a given level of risk. For example, the lower series of dots in Figure 3.17 shows the efficient frontier for a portfolio consisting of the S&P 500 and the Barclays Aggregate Bond Index. As previously, the Barclays index is used as a proxy for bonds. This portfolio will be referred to as a traditional portfolio because it contains only standard assets. The efficient frontier denotes the best return that can be achieved for a given level of risk. For example, if an investor is willing to accept a risk level of 3 percent (i.e., 0.03), then the best return that can be achieved by combining the S&P 500 and bonds is roughly 0.75 percent per month. The different points along the efficient frontier represent different combinations of stocks and bonds in steps of 2 percent. The leftmost point on the frontier is a portfolio that consists entirely of bonds; it has the lowest risk and the lowest expected return. The rightmost point of the efficient frontier is a portfolio that consists entirely of the S&P 500. It has the highest return of all feasible portfolios but also the highest risk. The middle point represents a portfolio consisting half of stock, half of bonds. The gray part of the efficient frontier to the far left represents linear combinations of the S&P 500 and the Barclays Aggregate Bond Index that are suboptimal. They are included because they are possible. There are three such portfolios: 0 percent stocks with 100 percent bonds, and 2 percent stocks with 98 percent bonds. In these cases, an investor can get the same level of risk but a higher return by selecting a slightly higher level of stocks—these are the black points just above the gray points. The efficient frontier shown here is based on monthly data ranging from January 1990 through December 2014.24
![Graph of Efficient Frontier with Target Risk[Cov] on the horizontal axis, Target Return[mean] on the vertical axis; circular dots plotted for Stocks, bonds and HFRI index, and Stocks and bonds only.](http://images-20200215.ebookreading.net/17/1/1/9781118736357/9781118736357__merger-arbitrage-2nd__9781118736357__images__c03f017.jpg)
Figure 3.17 Efficient Frontiers for Combinations of Stocks and Bonds as well as Stocks, Bonds, and the HFR Index
When merger arbitrage is added to a traditional portfolio consisting of stocks and bonds, the returns that can be achieved for the same level of risks increase. Figure 3.17 shows two efficient frontiers: The lower series of points is the efficient frontier for a portfolio consisting only of the S&P 500 and bonds; the upper efficient frontier represents a portfolio that contains a third asset, the HFR merger arbitrage index. It can be seen that for a given level of risk, the portfolio with merger arbitrage will generate a higher expected return than that consisting only of stocks and bonds.
The weakest aspect of this analysis is that it is impossible to invest in an index. An index is a theoretical construct that assumes frictionless investments without transaction costs and infinite instantaneous liquidity for all of its constituents. This assumption is not even valid for standard stock indices like the S&P 500 index, and index funds inevitably underperform their own indices. For hedge funds, the assumptions implicit in indices are even less valid, because investors can access them only through private placements. Therefore, it is debatable whether hedge fund indices can even be called investable. To make their indices investable, some index providers attempt to include in their indices only funds that are open to new investors. Others seek to build indices that correspond to the entire universe of hedge funds representing the merger arbitrage strategy, including funds that no longer accept new investors. The indices used in the preceding analysis all fall into the latter category. Their advantage is that they represent the performance that can be achieved by the merger arbitrage strategy overall.
Moreover, comparing an actively managed portfolio with an unmanaged index is a conceptually questionable approach. Doing so overstates the performance that can be achieved with an index. An investor could at best invest in an index fund, which will underperform the index. It is not only management fees and expenses that make the fund underperform but also other frictions, such as commission costs and timing differences when constituents are added and removed from an index. A more realistic comparison of any managed vehicle should compare its returns to those of an index fund rather than the index itself, because the index is a purely theoretical construct.
Instead of using merger arbitrage hedge fund indices, the next analysis uses several mutual funds that employ merger arbitrage:
- The Merger Fund (symbol: MERFX) is the oldest mutual fund that invests exclusively in merger arbitrage. It was launched in 1989.
- The Arbitrage Fund (symbol: ARBFX) was launched in 2000 and also invests exclusively in merger arbitrage.
- The Touchstone Merger Arbitrage Fund (symbol: TMGAX) has the shortest track record with a launch in the year 2011.
- The Quaker Event Arbitrage Fund (formerly Pennsylvania Avenue Event-Driven Fund) (symbol: QEAAX) was launched in 2003 and utilizes several event-driven strategies, including merger arbitrage.25
Several other mutual funds invest in merger arbitrage but are not included in this analysis in order to prevent the model from overfitting due to too much data: These funds include The Enterprise M&A Fund (symbol: EMAXX) and the Gabelli ABC Fund (symbol: GABCX). Several funds of Mutual Series also invest in merger arbitrage, among other strategies, going back to the days of Max Heine.
The S&P 500 index and Barclays Aggregate Bond index are replaced, respectively, by these index funds:
- S&P Depositary Receipts, commonly abbreviated SPDR (symbol SPY), an index exchange traded fund (ETF)
- iShares Core Aggregate Bond (symbol AGG), an exchange-traded fund that seeks to replicate the performance of the Barclays U.S. Aggregate Bond Index that was used as a proxy for bond investment earlier in this Chapter
The analysis covers the 11 years from November 2003 through December 2014. The scatter diagram of returns of the five funds can be seen in Figure 3.18. As before, the risk of the merger arbitrage funds is bond-like. However, unlike hedge fund indices, most merger arbitrage mutual funds underperform bonds. EMAAX has higher volatility with returns at the same level as bonds. QEAAX has higher volatility than bonds, which is due to the other event strategies used by this fund in addition to its merger arbitrage portfolio, but compensates for that higher volatility through a higher return that places it overall in an intermediate position between stocks and bonds.

Figure 3.18 Risk/Return Trade-off for Mutual Funds That Use Merger Arbitrage
The efficient frontier is shown in Figure 3.19. The lower frontier shows a portfolio that consists only of the index funds SPY and AGG. The upper frontier shows portfolios that consist of all five funds, the index funds as well as ARBFX, MERFX, GABCX, EMAAX and QEAAX. The same effect that was seen in Figure 3.17 can be observed here: When adding the merger arbitrage funds to a portfolio of stocks and bonds, a higher return can be achieved at the same level of risk.
![Graph of Efficient Frontier with Target Risk[Cov] on the horizontal axis, Target Return[mean] on the vertical axis; circular dots plotted for Stocks, bonds and merger arbitrage funds, and Stocks and bonds only.](http://images-20200215.ebookreading.net/17/1/1/9781118736357/9781118736357__merger-arbitrage-2nd__9781118736357__images__c03f019.jpg)
Figure 3.19 Efficient Frontier for Mutual Funds That Use Merger Arbitrage
Benefits of Merger Arbitrage in a Rising Interest Rate Environment
At the time of writing, interest rates are stagnated at a historically low level. As a result, many investors are concerned about the risk that rising interest rates pose to their portfolios. Merger arbitrage can be an effective diversification tool to mitigate this risk. As already shown, merger arbitrage has, in the long run, risk/return characteristics similar to bonds. Therefore, the relevant question to ask when discussing rising interest rates is whether merger arbitrage will behave similarly during periods of rising interest rates.
In examining this question, rising interest rates were defined as periods of time during which the 10-year Treasury yield realized a short-term trough followed by a short-term peak. Two criteria define a trough:
- The lowest inflection point is between two peaks.
- Inflection point must represent a new low point that is below previous troughs.
Similarly, two criteria define a peak:
- The highest inflection point is between two troughs.
- Inflection point must be greater than 1.5x in value than the most recent trough.
With these criteria, six periods of rising interest rates can be found between the years 1990 and 2014. Comparing the performance of merger arbitrage, bonds and the S&P 500 during these periods (Figure 3.20) it can be seen that merger arbitrage always outperformed bonds in periods of rising interest rates. In addition, it has consistently lower volatility than bonds during these periods of stress. It is clear that replacing bond exposure with merger arbitrage will de-risk a portfolio with respect to the prospects of increasing interest rates.

Figure 3.20 Performance of Merger Arbitrage in Periods of Rising Interest Rates
It is important to note that other hedge fund strategies perform less favorably in rising interest environments. Figure 3.21 compares performance and volatility of several popular hedge fund strategies in these circumstances. It is remarkable that several strategies have both higher volatility and worse performance than long equities, for which the S&P 500 acts as a proxy. Merger arbitrage and the broader event-driven category compare extremely favorably to other hedge fund strategies.

Figure 3.21 Performance of Several Hedge Fund Strategies in Periods of Rising Interest Rates
Quantitative Easing
A similar result as in the previous section can be obtained from splitting the 25-year history of event-driven returns into two distinct periods, prior to and during the unprecedented period of quantitative easing. The Federal Reserve initiated its policy of quantitative easing (QE) in late November 2008 and maintained it in several waves, labeled QE1, QE2, and QE3 by Fed watchers, through October 29, 2014.
The returns achieved by merger arbitrage investments compared to stocks and bonds in the three distinct periods prior to quantitative easing, during quantitative easing, and in the relatively short period since the end of quantitative easing and the writing of this book are shown in Table 3.8.
Table 3.8(a) Performance of Merger Arbitrage Prior to Quantitative Easing (1990–2008)
| Barclay | CASAM | Greenwich | HFRI | HFRX | Bonds | S&P 500 | |
| Median | 0.0082 | 0.0084 | 0.0070 | 0.0096 | 0.0068 | 0.0066 | 0.0123 |
| Arithmetic Mean | 0.0070 | 0.0078 | 0.0063 | 0.0075 | 0.0052 | 0.0056 | 0.0068 |
| Standard Deviation | 0.0113 | 0.0120 | 0.0108 | 0.0125 | 0.0112 | 0.0111 | 0.0422 |
Table 3.8(b) Performance of Merger Arbitrage During Quantitative Easing (2008–2014)
| Barclay | CASAM | Greenwich | HFRI | HFRX | Bonds | S&P 500 | |
| Median | 0.0057 | 0.0042 | 0.0054 | 0.0039 | 0.0031 | 0.0049 | 0.0200 |
| Arithmetic Mean | 0.0040 | 0.0044 | 0.0044 | 0.0036 | 0.0030 | 0.0047 | 0.0130 |
| Standard Deviation | 0.0071 | 0.0055 | 0.0081 | 0.0064 | 0.0077 | 0.0095 | 0.0438 |
Table 3.8(c) Performance of Merger Arbitrage After the End of Quantitative Easing (2014–2015)
| Barclay | CASAM | Greenwich | HFRI | HFRX | Bonds | S&P 500 | |
| Median | 0.0073 | 0.0041 | 0.0041 | 0.0037 | 0.0060 | 0.0009 | 0.0096 |
| Arithmetic Mean | 0.0066 | 0.0034 | 0.0015 | 0.0034 | 0.0055 | 0.0019 | 0.0071 |
| Standard Deviation | 0.0089 | 0.0051 | 0.0097 | 0.0086 | 0.0050 | 0.0100 | 0.0273 |
It can be seen that the historical pattern of merger arbitrage generating bond-like returns and volatility and about half the return of equities with only a quarter of the volatility broke down during the period of unprecedented monetary easing. During those times, merger arbitrage underperformed bonds, albeit with a volatility that was lower. Since the end of quantitative easing, the benefits of merger arbitrage are becoming apparent again: It is outperforming bonds, which generate returns no better than cash. Despite its outperformance, it has nevertheless maintained a volatility well below that of bonds. Compared to equities, merger arbitrage now looks even more attractive than at any time since 1990. Since the end of quantitative easing, merger arbitrage has produced roughly half the performance of equities but with a volatility that is two-thirds to four-fifths lower. It is clear that we are entering an era in which merger arbitrage benefits to a portfolio are higher than in any prior period.
